Similar presentations:
Программирование на языке Python. Тема №4. Числовые типы. Занятие 1
1.
Программирование на языке PythonТема №4
Числовые типы.
Занятие 1
2.
Список используемой литературы.1.
2.
3.
4.
5.
Программирование для детей на языке Python – Москва: Издательство
АСТ – 2017.
Python для детей. Самоучитель по программированию / Джейсон Бриггс
(перевод С. Ломакина) – 2017.
Сам себе программист. Как научиться программировать и устроиться в
Ebay? / Кори Альтхофф – Москва: Эксмо, 2018.
Изучаем Python. том 1. 5-е изд. – СПб. : ООО «Диалектика», 2019.
Изучаем Python. том 2. 5-е изд. – СПб. : ООО «Диалектика», 2019.
В презентациях занятий ссылки на материал из этих книг будут
обозначаться следующим образом:
[2] с.35 – это означает, что книга №2 из списка, страница 35.
То есть число в квадратных скобках – номер книги в списке литературы.
3.
План занятияЧисловые типы
• Базовые числовые типы в Python: int, float.
• Арифметические операции: сложение, вычитание, деление, умножение,
вычисление остатка от деления, возведение в степень, краткие операторы.
• Встроенные математические функции и очень коротко о модуле math.
• Примеры и особенности выполнения.
Используемая литература:
https://www.youtube.com/watch?v=HZrbYY10cJI&list=PLA0M1Bcd0w8yWHh2V70bTtbVxJICrnJHd&index=4
4.
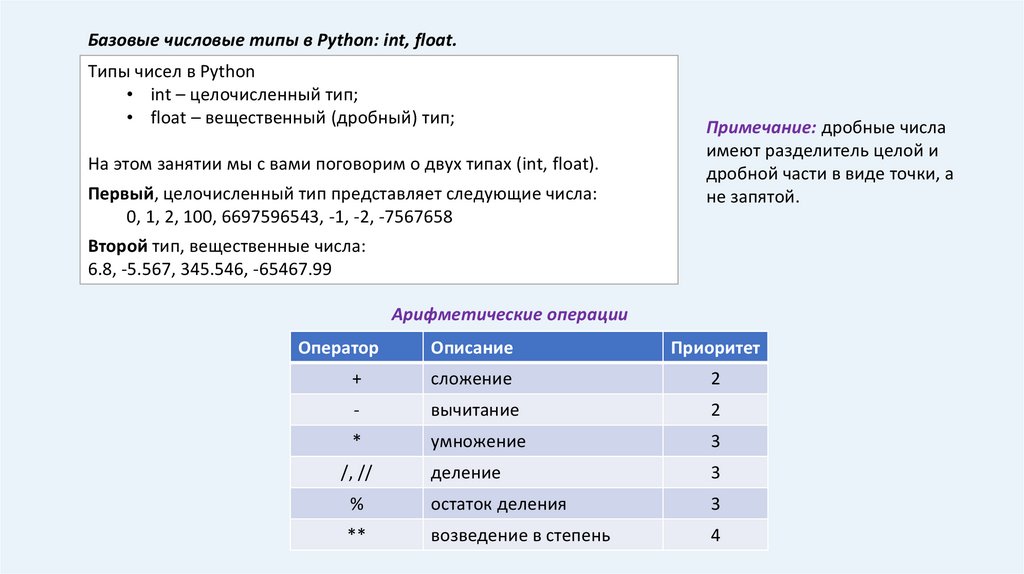
Базовые числовые типы в Python: int, float.Типы чисел в Python
• int – целочисленный тип;
• float – вещественный (дробный) тип;
На этом занятии мы с вами поговорим о двух типах (int, float).
Первый, целочисленный тип представляет следующие числа:
0, 1, 2, 100, 6697596543, -1, -2, -7567658
Примечание: дробные числа
имеют разделитель целой и
дробной части в виде точки, а
не запятой.
Второй тип, вещественные числа:
6.8, -5.567, 345.546, -65467.99
Арифметические операции
Оператор
Описание
Приоритет
+
сложение
2
-
вычитание
2
*
умножение
3
/, //
деление
3
%
остаток деления
3
**
возведение в степень
4
5.
Выполнение арифметических операций на примерах.1
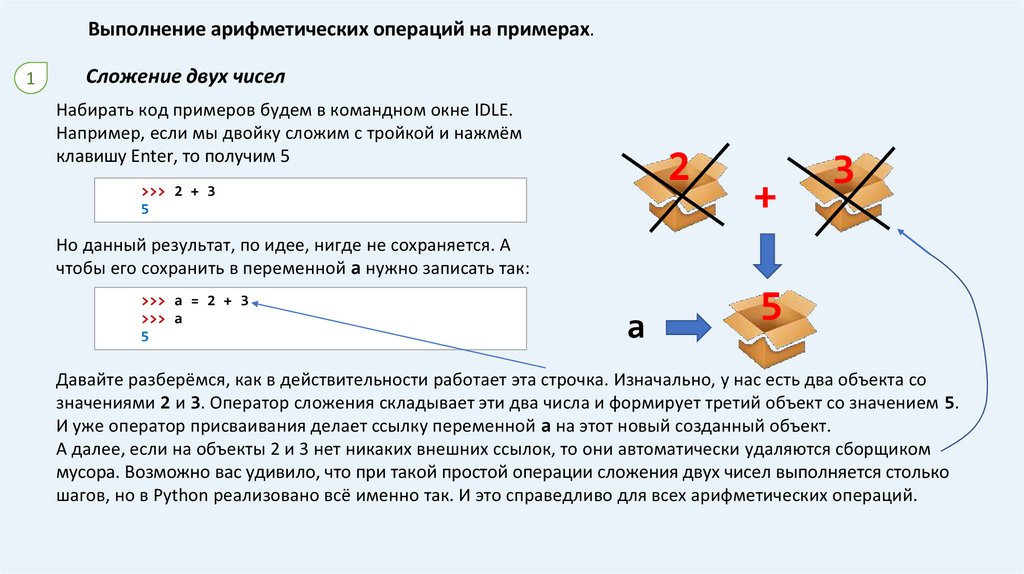
Сложение двух чисел
Набирать код примеров будем в командном окне IDLE.
Например, если мы двойку сложим с тройкой и нажмём
клавишу Enter, то получим 5
2
>>> 2 + 3
5
+
3
Но данный результат, по идее, нигде не сохраняется. А
чтобы его сохранить в переменной а нужно записать так:
>>> a = 2 + 3
>>> a
5
a
5
Давайте разберёмся, как в действительности работает эта строчка. Изначально, у нас есть два объекта со
значениями 2 и 3. Оператор сложения складывает эти два числа и формирует третий объект со значением 5.
И уже оператор присваивания делает ссылку переменной а на этот новый созданный объект.
А далее, если на объекты 2 и 3 нет никаких внешних ссылок, то они автоматически удаляются сборщиком
мусора. Возможно вас удивило, что при такой простой операции сложения двух чисел выполняется столько
шагов, но в Python реализовано всё именно так. И это справедливо для всех арифметических операций.
6.
Мало того, если операция сложения возвращает объект с результатом, то можно сделать и такоесложение:
Как было получено значение 9, сначала было
>>> b = 2 + 3 + 4
вычислено 2 + 3, получили значение 5, а затем
>>> b
9
значение 5 прибавилось к 4 и мы видим 9
2
То есть арифметические операции выполняются слева на право, кроме одной операции возведения в
степень, о которой мы поговорим чуть позже. Нужно заметить, что при выполнении действий с участием
дробных чисел, результат всегда будет иметь тип вещественного числа. Также результат будет всегда
вещественным числом при выполнении деления. Python ещё имеет целочисленное деление, ещё его
называют делением к наименьшему целому, которое записывается следующим образом:
>>> d3 = 7 // 2
>>> d3
3
3
Если мы делим 7 на 2, то результат равен 3.5,
но наименьшее целое здесь и есть 3.
Следующей интересной операцией является получение остатка от деления:
Что это за операция и как она работает?
>>> 10 % 3
1
Из рисунка наглядно видно как получается остаток.
7.
4И последняя арифметическая операция, которую мы рассмотрим – это возведение в степень, она
записывается как две звёздочки, смотрите примеры:
>>> 2 ** 3
8
>>> 36 ** 0.5
6.0
# возведение в куб
# извлечение квадратного корня
Или ещё пример:
>>> 2 ** 3 ** 2
512
Вот эта операция возведения в степень выполняется справа налево, поэтому сначала выполнится
возведение тройки во вторую степень, получится 9, а потом два возводится в девятую степень и будет
число пятьсот двенадцать.
5
Краткие операторы
Обычная форма записи:
>>> i = i + 2
>>> i = i - 1
>>> i = i * 4
>>> i = i / 3
Сокращённая форма записи:
>>> i += 2
>>> i -= 1
>>> i *= 4
>>> i /= 3
8.
6Встроенные математические функции языка Python.
В этом занятии речь пойдёт о наиболее употребимых математических функциях. Первая функция,
которую мы рассмотрим - это функция для вычисления модуля числа, называется она abs() - в
буквальном переводе - абсолютное значение. Пример применения:
>>> abs(-5)
5
Следующая функция - функция min(), она возвращает минимальное из переданных ей чисел, пример:
>>> min(1, 2, -5, 4, 0)
-5
Другая противоположная ей функция - max(), она возвращает максимальное из переданных ей чисел,
пример:
>>> max(0, 0.7, 0.4, 0.3)
0.7
Примечание: Функции min() и max() нельзя вызвать без аргумента или с одним аргументом, т.к. они
должны выбирать из чего-то, хотя бы из двух значений.
Последняя математическая встроенная функция, которую мы рассмотрим - это функция round(), она
позволяет округлять числа. Работает она следующим образом:
>>> round(0.5)
0
То есть, идёт округление к ближайшему целому, а вот если возьмём другой пример:
>>> round(1.5)
2
9.
7Некоторые функции из модуля math.
Мы рассмотрели довольно ограниченный набор математических функций, конечно же в Pythpn есть и
другие. Они находятся в модуле math и чтобы ими воспользоваться нужно импортировать этот модуль.
Делается это при помощи следующей инструкции:
import math
После этого все функции данного модуля будут доступны для использования в программе. Этих функций
довольно много, мы рассмотрим только небольшое количество. Но принцип работы со всеми этими
функциями похож, поэтому вы легко можете применить любые функции из этого модуля. Рассмотрим
распространенную функцию для вычисления квадратного корня math.sqrt(), пример применения:
>>> math.sqrt(49)
7.0
И разумеется, в этом модуле есть набор всех тригонометрических функций, например таких как синус,
косинус и других. Рассмотрим эти две на примере:
>>> math.sin(3.14/2)
0.9999996829318346
>>> math.cos(0)
1
Помимо этого, есть ещё общеизвестные константы:
>>> math.pi
3.141592653589793
>>> math.e
2.718281828459045
10.
По выше приведенным примерам видно как можно легко брать математические функции из модуляmath и применять их в каких-то своих целях. Пока, набор функций, который мы рассмотрели будет
достаточен. Для закрепления изученного материала нужно потренироваться на практических примерах.








 programming
programming








