Критические точки и точки экстремума функции. Алгебра и начала анализа. 11 класс

1.

11 класс
Алгебра и начала анализа

2.

Цель урока:
10.4.1.28
- знать определения критических точек и точек
экстремума функции,
экстремума функции.
условие
существования
Критерии оценивания
Учащийся:
- Использует определение находит критические
(стационарные) точки, используя определение;
- применяет необходимое и достаточное условие для
определение точек экстремума функции.

3.

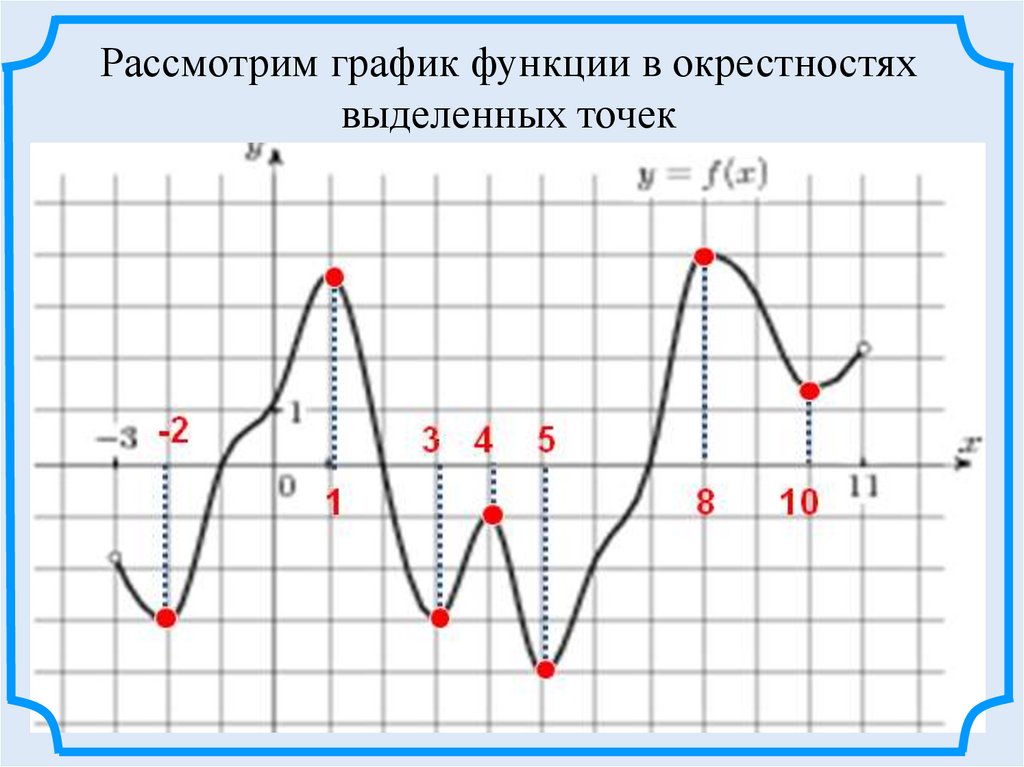
Рассмотрим график функции в окрестностях
выделенных точек

4.

5.

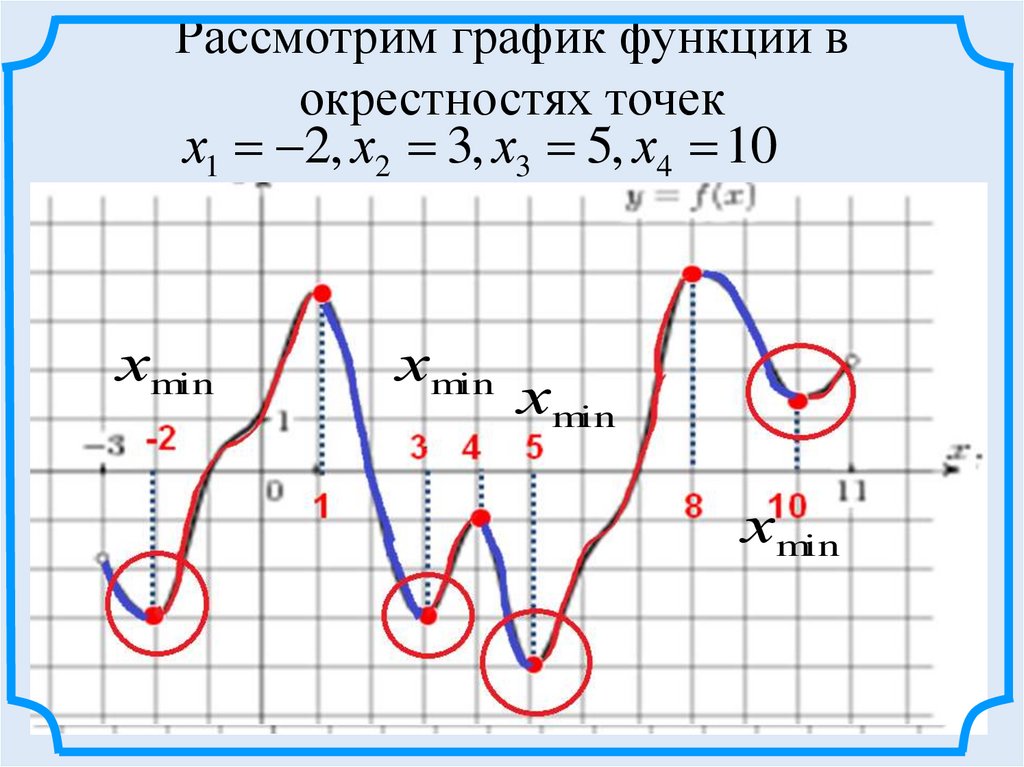
Рассмотрим график функции в
окрестностях точек
х1 2, х2 3, х3 5, х4 10
хmin
хmin
хmin
хmin

6.

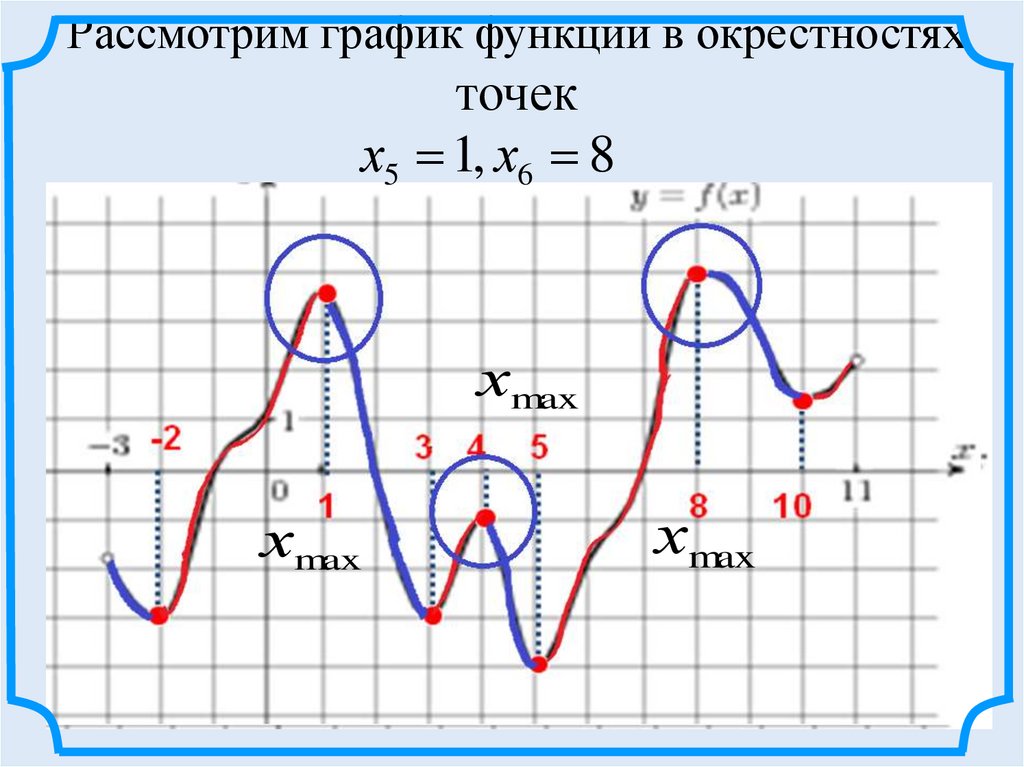
Рассмотрим график функции в окрестностях
точек
х5 1, х6 8
хmax
хmax
хmax

7.

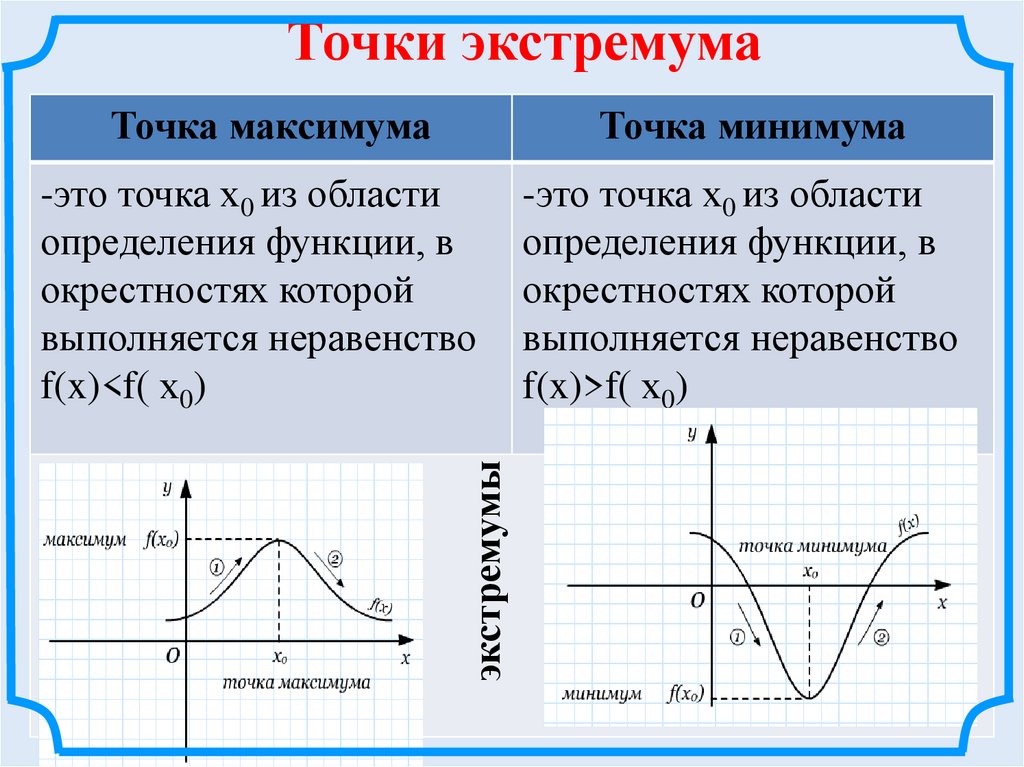
Точки экстремума
Точка минимума
-это точка х0 из области
определения функции, в
окрестностях которой
выполняется неравенство
f(x)<f( х0)
-это точка х0 из области
определения функции, в
окрестностях которой
выполняется неравенство
f(x)>f( х0)
экстремумы
Точка максимума

8.

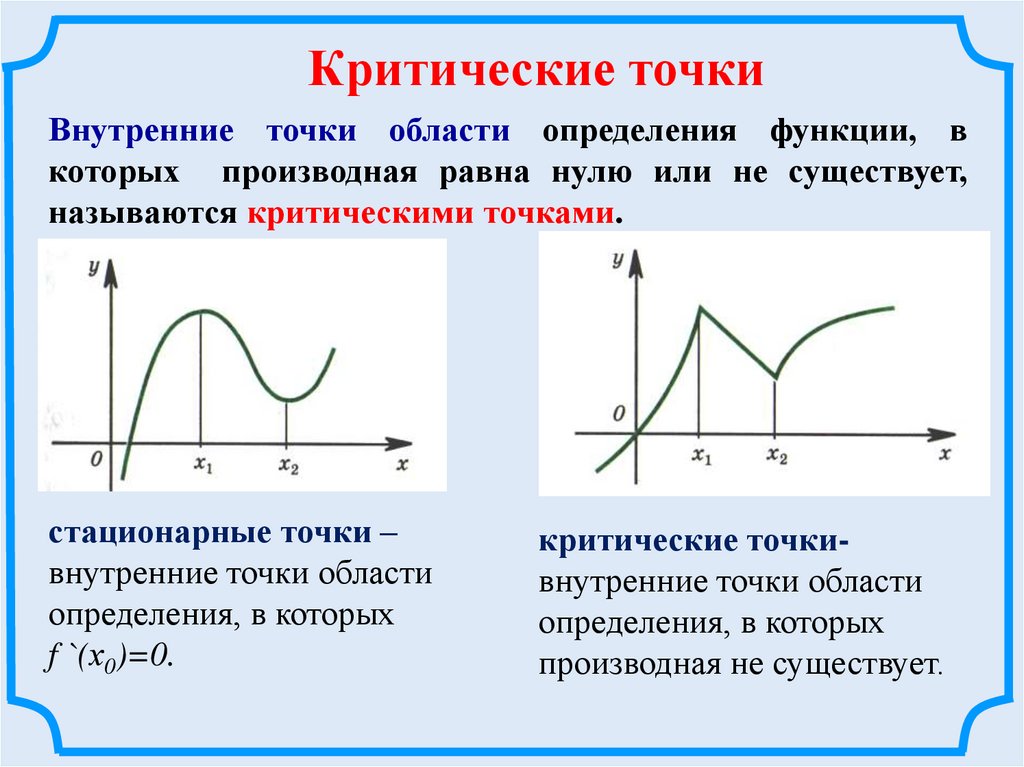
Критические точки
Внутренние точки области определения функции, в
которых производная равна нулю или не существует,
называются критическими точками.
стационарные точки –
внутренние точки области
определения, в которых
f `(х0)=0.
критические точкивнутренние точки области
определения, в которых
производная не существует.

9.

Найти по графику функции точки, с определениями
которых вы только, что познакомились.
Х=4 ..
Х=7…
Х=10….
Х=12…
Х=17…
y
1
O
15
1
4
7
9
12
19
x

10.

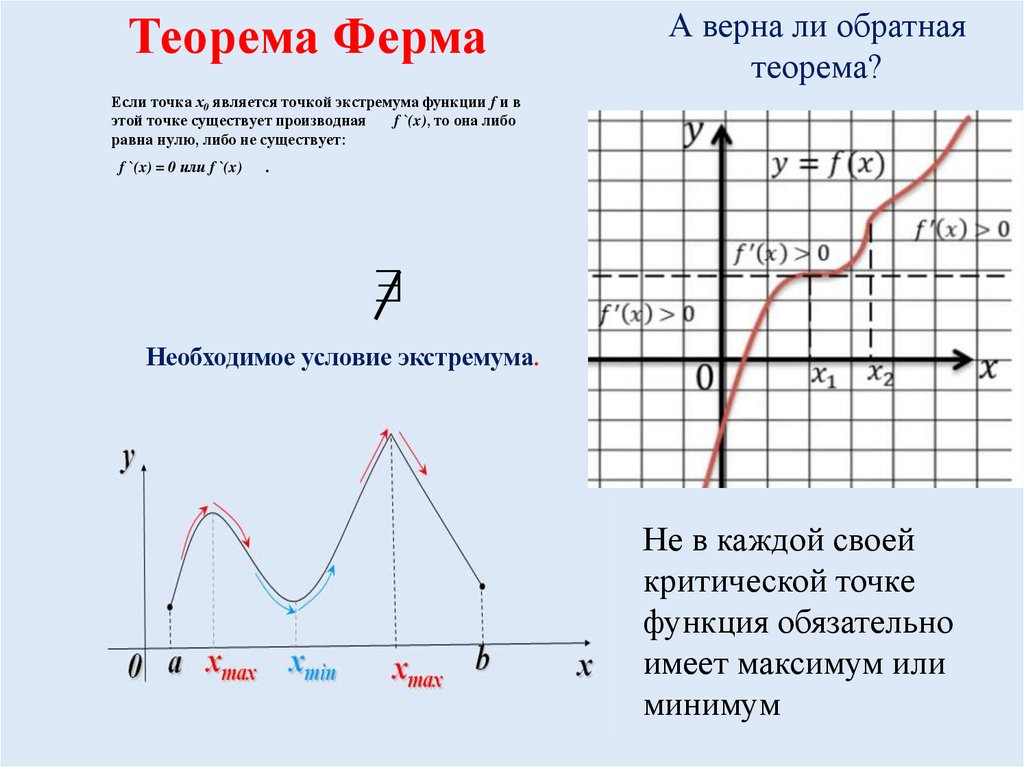
Теорема Ферма
А верна ли обратная
теорема?
Если точка х0 является точкой экстремума функции f и в
этой точке существует производная
f `(x), то она либо
равна нулю, либо не существует:
f `(x) = 0 или f `(x)
.
Необходимое условие экстремума.
Не в каждой своей
критической точке
функция обязательно
имеет максимум или
минимум

11.

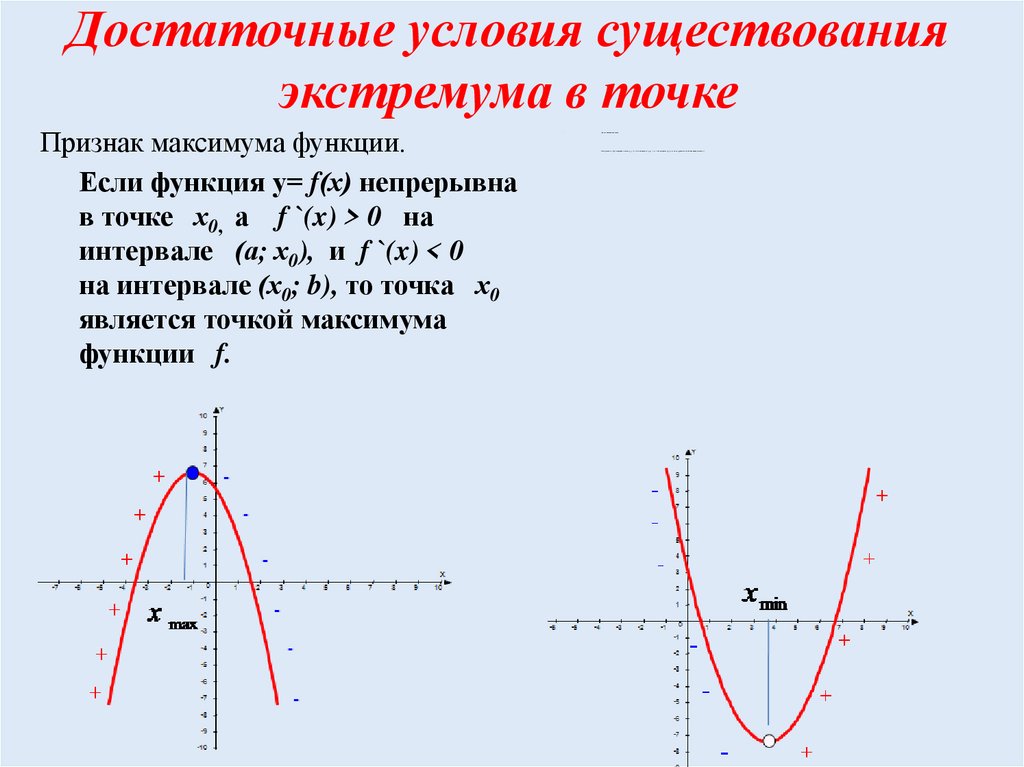
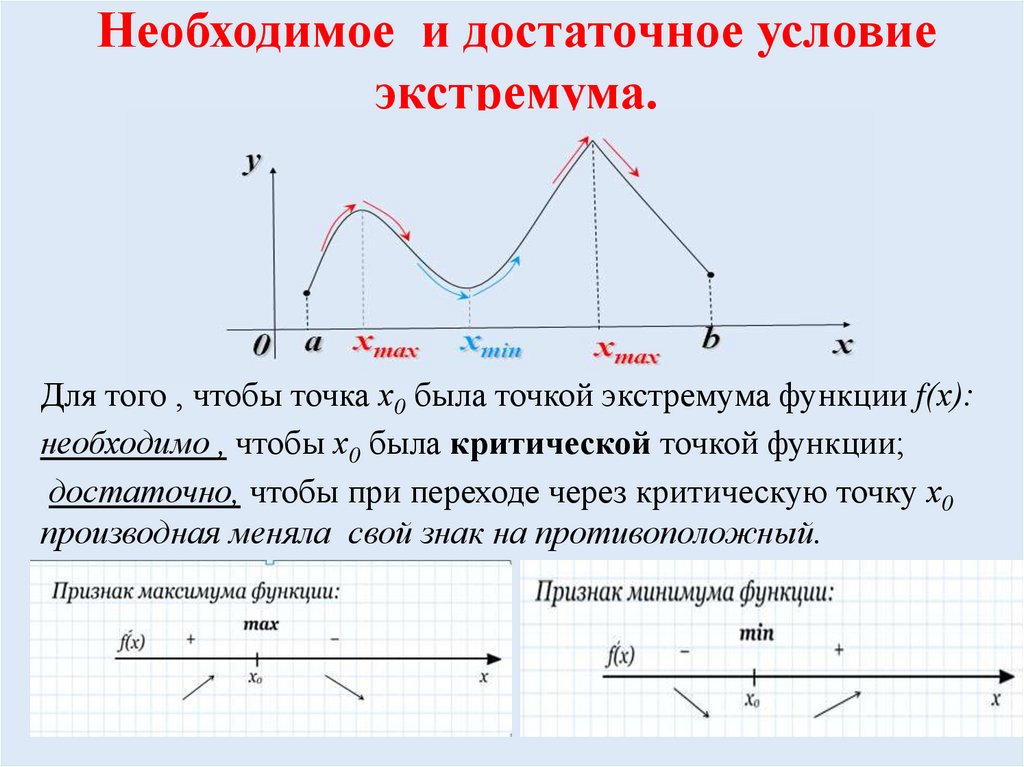
Достаточные условия существования
экстремума в точке
Признак максимума функции.
Если функция у= f(х) непрерывна
в точке х0, а f `(x) > 0 на
интервале (а; х0), и f `(x) < 0
на интервале (х0; b), то точка х0
является точкой максимума
функции f.
Признак миниму ма фу нкции.
Если функция у=f((х) непрерывна в точке х0, f `(x) < 0 на интервале (а; х0) и f `(x) > 0 на интервале (х0; b), то точка х0 является точкой минимума функции f

12.

13.

14.

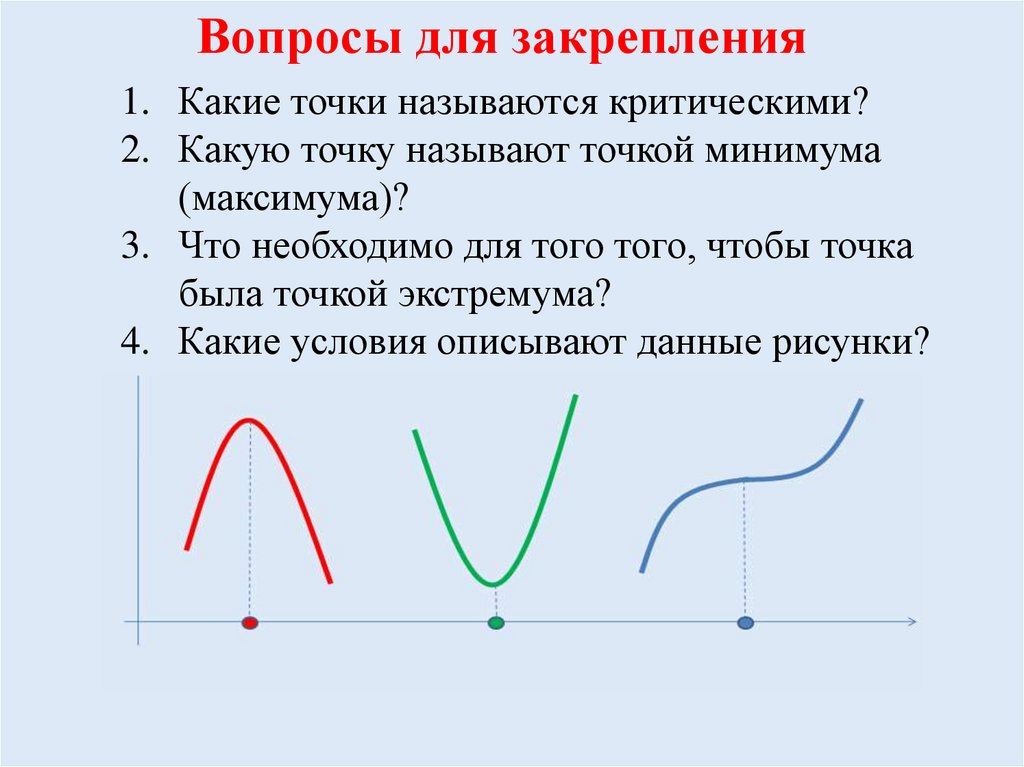
Вопросы для закрепления
1. Какие точки называются критическими?
2. Какую точку называют точкой минимума
(максимума)?
3. Что необходимо для того того, чтобы точка
была точкой экстремума?
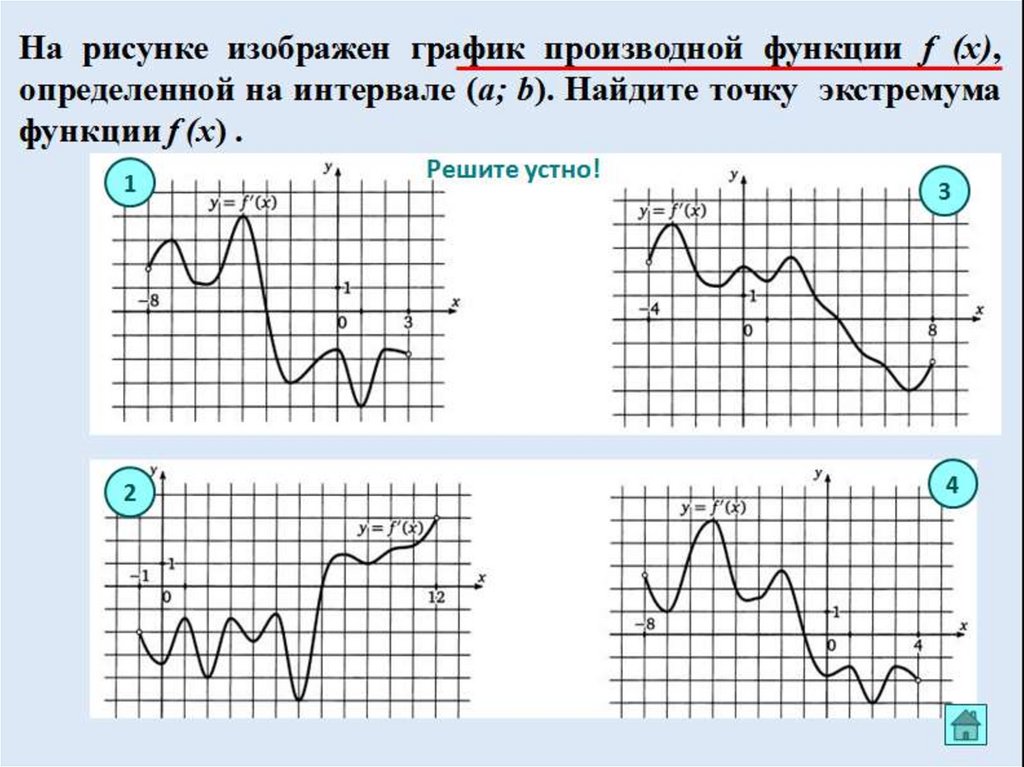
4. Какие условия описывают данные рисунки?

15.

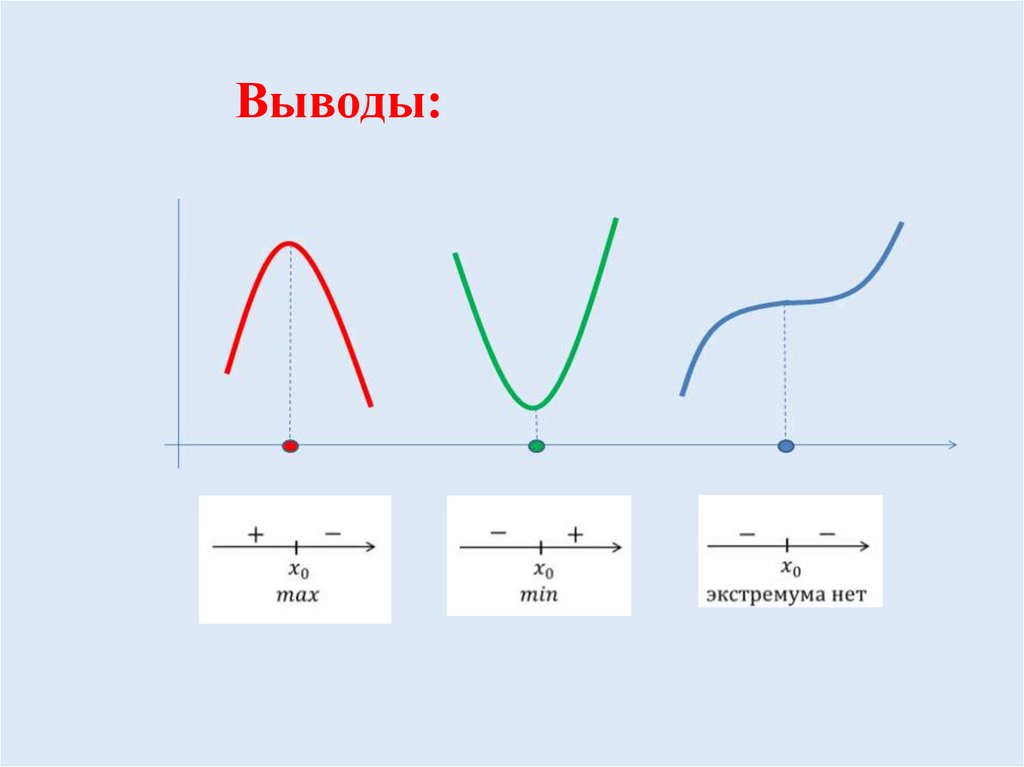
Выводы:

16.

Необходимое и достаточное условие
экстремума.
Для того , чтобы точка х0 была точкой экстремума функции f(х):
необходимо , чтобы х0 была критической точкой функции;
достаточно, чтобы при переходе через критическую точку х0
производная меняла свой знак на противоположный.

17.

18.

Найдите точку минимума
3
функции
2 2
y
3
x 2x 1
Найдите точку максимума
функции
х 2 289
289
y
х 2
х
х
D( y ) : x 0
D( y ) : x 0
1
2
у х 2 х 2
/
х 2 0
х 2
х 4
Ответ : хmin 4
2
1 289 х (17 х)(17 х)
у 1 289 2 2
2
х
х
х
(17 х)(17 х)
/
у 0,
0
2
х
х 17, х 0( 2)
/
Ответ : хmax 17

19.

Задания для самостоятельного решения
1А. (5б) Найдите критические точки функции.
Выясните, какие из этих точек являются:
а) точками минимума; б) точками максимума.
а) у х 2 х 3
4
№
п/п
2
б ) у х 27
3
дескрипторы
балл
1.
2.
Находит правильно производную
Находит критические точки
1
1
3.
4.
Расставляет верно знаки производной
Определяет точки минимума
1
1
5.
Определяет точки максимума
1

20.

Задания для самостоятельного решения
2Б. (6б) Найдите экстремумы функции:
2
б) у
х2
х
№
п/п
дескрипторы
балл
1.
2.
Находит область определения
Находит правильно производную
1
1
3.
4.
Находит критические точки
Расставляет верно знаки производной
1
1
5.
Определяет точки экстремума
1
6.
Находит экстремумы функции
1

21.

Задания для самостоятельного решения
3С.(7б)Найдите промежутки возрастания и
убывания, точки экстремума функции:
6 х
2
а) f ( x)
б ) f ( x) 4 х х
х 6
№ п/п
дескрипторы
балл
1.
2.
3.
4.
5.
6.
7.
Находит область определения
Находит производную
Находит критические точки
Расставляет знаки производной
Исследует поведение функции
Находит промежутки монотонности
Определяет точки экстремума
1
1
1
1
1
1
1

22.

Дополнительные цифровые ресурсы
https://videouroki.net/video/4
5-primienieniie-proizvodnoidlia-otyskaniia-tochiek
ekstriemuma.html
https://infourok.ru/videour
oki/1215

23.

Ссылки на дополнительные ресурсы
для самообразования
bilimland.kz
https://bilimland.kz/ru/subjec
t/algebra/10-klass/kriticheskietochki-dostatochnoe-usloviesushestvovaniyaehkstremuma?mid=%info%
www.yaklass.ru
https://www.yaklass.ru/p/al
gebra/10-klass/proizvodnaia9147/primenenie-proizvodnoidlia-issledovaniia-funktcii-namonotonnost-i-ekstr_-11226

24.

Рефлексия содержания учебного
материала
Теперь я могу…
Было трудно…
Сегодня я узнал…

25.

Дорогие дети!
Вы получили самое основное
содержание по новой теме, другие
материалы вы получите от своего
учителя!
Если у вас есть вопросы, вы их
можете задать учителю!
Удачи в освоении нового материала,
наши юные друзья!