Similar presentations:
Вычисление координат точек замкнутых теодолитных ходов
1.
ГБПОУ КК«Пашковский сельскохозяйственный колледж»
ПМ.01 «Проведение проектно-изыскательских работ для
целей землеустройства и кадастра»
МДК 01.02 Камеральная обработка результатов
полевых измерений
Раздел 1. Производство теодолитной съемки
Тема: «Вычисление координат
точек замкнутых теодолитных
ходов»
2.
Результат освоенияПрофессиональные и общие компетенции:
ПК 1.2 Обрабатывать результаты полевых
измерений
ОК 1 Понимать сущность и социальную
значимость своей будущей профессии,
проявлять к ней устойчивый интерес
3.
Содержание урока:1.Составление схемы замкнутого
теодолитного хода
2.Вычисление ведомости замкнутого
теодолитного хода
4.
Схема замкнутого теодолитногохода
70,47
т.3
91°55ʹ22ʺ
т.4
НОМЕР ТОЧКИ
90°36ʹ08ʺ
Координаты 1 точки
90,63
X1 = 1000,00
Y1 = 1000,00
т.2
184°02ʹ19ʺ
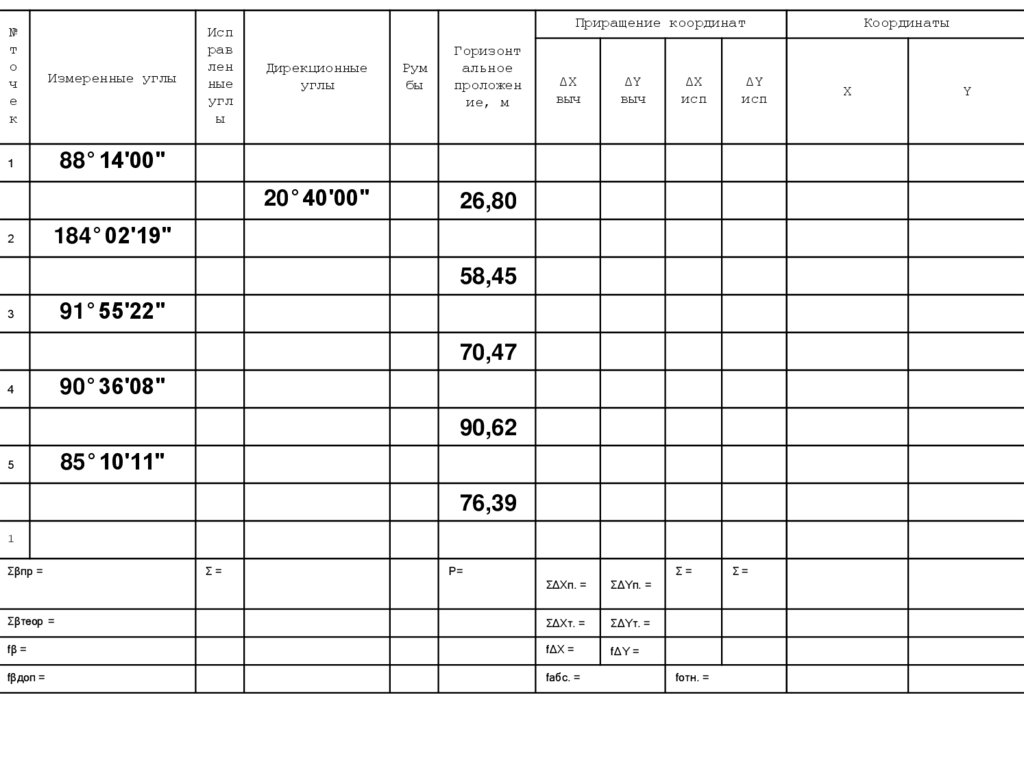
ГОРИЗОНТАЛЬНОЕ ПРОЛОЖЕНИЕ,м
Дирекционный угол
линии 1-2
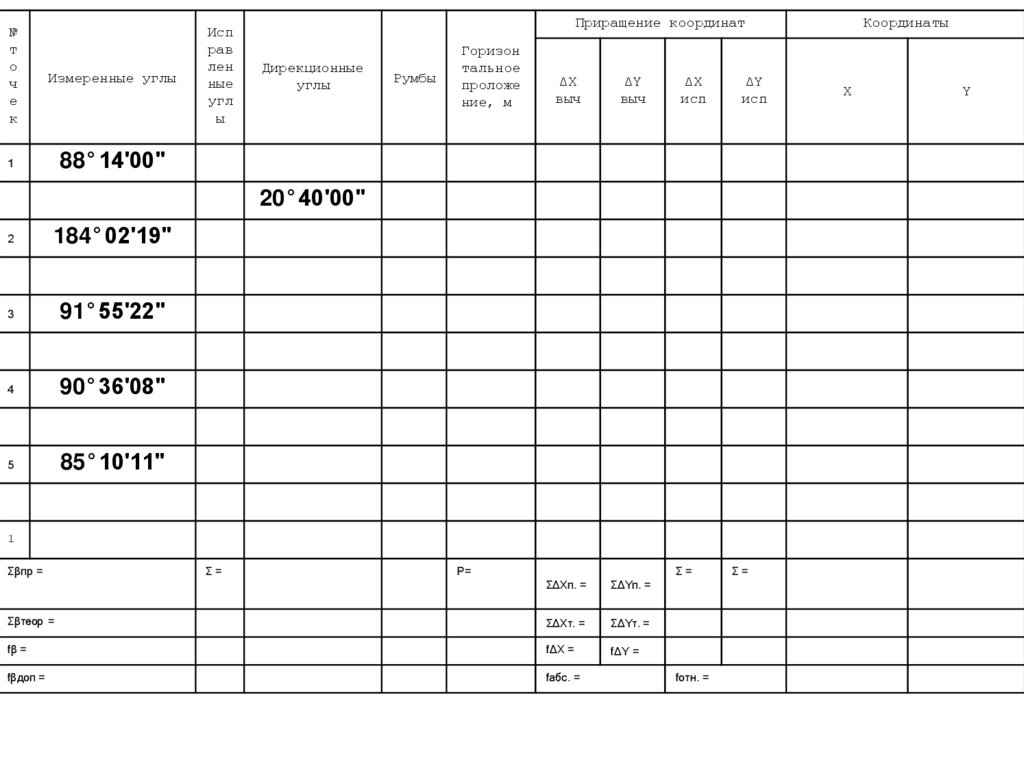
α1-2 = 20°40ʹ00ʺ
88°14ʹ00ʺ 85°10ʹ11ʺ
т.1
т.5
76,39
ИЗМЕРЕННЫЕ УГЛЫ
Углы по ходу - правые
5.
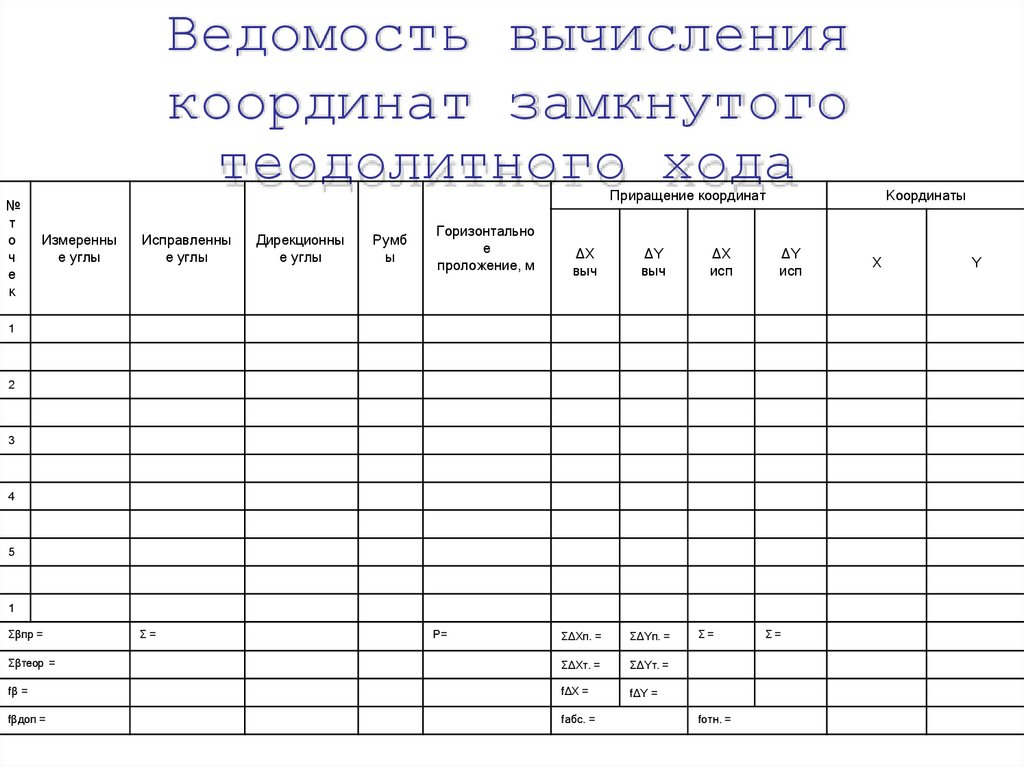
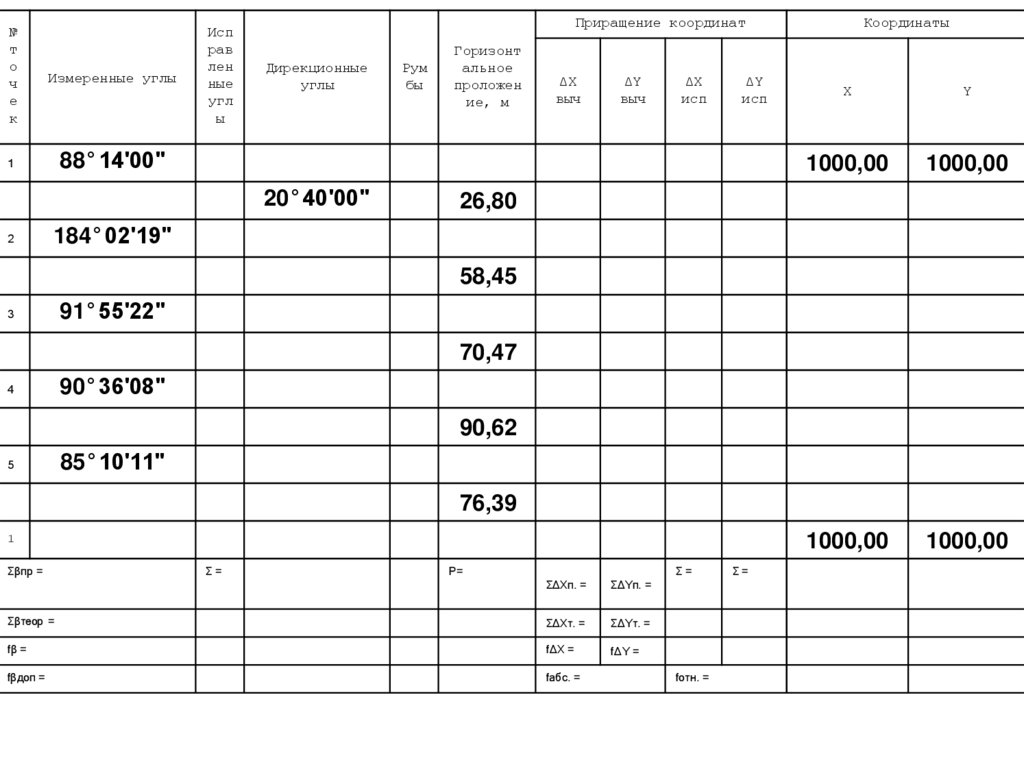
Ведомость вычислениякоординат замкнутого
теодолитного хода
№
т
о
ч
е
к
Приращение координат
Измеренны
е углы
Исправленны
е углы
Дирекционны
е углы
Румб
ы
Горизонтально
е
проложение, м
ΔX
выч
ΔY
выч
Σ∆Xп. =
Σ∆Yп. =
Σβтеор =
Σ∆Xт. =
Σ∆Yт. =
fβ =
f∆X =
f∆Y =
fβдоп =
fабс. =
ΔX
исп
ΔY
исп
1
2
3
4
5
1
Σβпр =
Σ=
Р=
Σ=
fотн. =
Σ=
Координаты
X
Y
6.
№т
о
ч
е
к
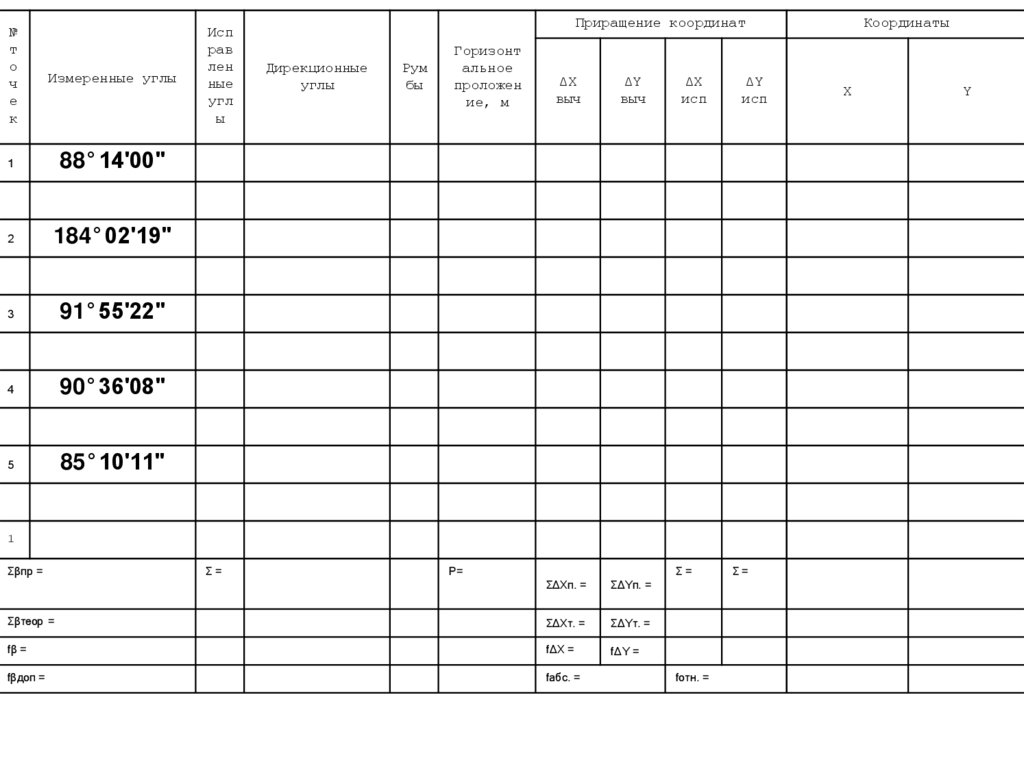
Измеренные углы
1
88°14ʹ00ʺ
2
184°02ʹ19ʺ
3
91°55ʹ22ʺ
4
90°36ʹ08ʺ
5
85°10ʹ11ʺ
Исп
рав
лен
ные
угл
ы
Приращение координат
Дирекционные
углы
Рум
бы
Горизонт
альное
проложен
ие, м
ΔX
выч
ΔY
выч
Σ∆Xп. =
Σ∆Yп. =
Σβтеор =
Σ∆Xт. =
Σ∆Yт. =
fβ =
f∆X =
f∆Y =
fβдоп =
fабс. =
ΔX
исп
ΔY
исп
1
Σβпр =
Σ=
Р=
Σ=
fотн. =
Σ=
Координаты
X
Y
7.
№т
о
ч
е
к
Измеренные углы
1
88°14ʹ00ʺ
Исп
рав
лен
ные
угл
ы
Приращение координат
Дирекционные
углы
Румбы
Горизон
тальное
проложе
ние, м
ΔX
выч
ΔY
выч
Σ∆Xп. =
Σ∆Yп. =
Σβтеор =
Σ∆Xт. =
Σ∆Yт. =
fβ =
f∆X =
f∆Y =
fβдоп =
fабс. =
ΔX
исп
ΔY
исп
20°40ʹ00ʺ
2
184°02ʹ19ʺ
3
91°55ʹ22ʺ
4
90°36ʹ08ʺ
5
85°10ʹ11ʺ
1
Σβпр =
Σ=
Р=
Σ=
fотн. =
Σ=
Координаты
X
Y
8.
№т
о
ч
е
к
Измеренные углы
1
88°14ʹ00ʺ
Исп
рав
лен
ные
угл
ы
Приращение координат
Дирекционные
углы
Рум
бы
Горизонт
альное
проложен
ие, м
ΔX
выч
ΔY
выч
Σ∆Xп. =
Σ∆Yп. =
Σβтеор =
Σ∆Xт. =
Σ∆Yт. =
fβ =
f∆X =
f∆Y =
fβдоп =
fабс. =
20°40ʹ00ʺ
2
ΔX
исп
ΔY
исп
26,80
184°02ʹ19ʺ
58,45
3
91°55ʹ22ʺ
70,47
4
90°36ʹ08ʺ
90,62
5
85°10ʹ11ʺ
76,39
1
Σβпр =
Σ=
Р=
Σ=
fотн. =
Σ=
Координаты
X
Y
9.
№т
о
ч
е
к
Измеренные углы
1
88°14ʹ00ʺ
Исп
рав
лен
ные
угл
ы
Приращение координат
Дирекционные
углы
20°40ʹ00ʺ
2
Рум
бы
Горизонт
альное
проложен
ие, м
ΔX
выч
ΔY
выч
ΔX
исп
ΔY
исп
Координаты
X
Y
1000,00
1000,00
1000,00
1000,00
26,80
184°02ʹ19ʺ
58,45
3
91°55ʹ22ʺ
70,47
4
90°36ʹ08ʺ
90,62
5
85°10ʹ11ʺ
76,39
1
Σβпр =
Σ=
Р=
Σ=
Σ∆Xп. =
Σ∆Yп. =
Σβтеор =
Σ∆Xт. =
Σ∆Yт. =
fβ =
f∆X =
f∆Y =
fβдоп =
fабс. =
fотн. =
Σ=
10.
Этапы вычислениязамкнутого теодолитного хода:
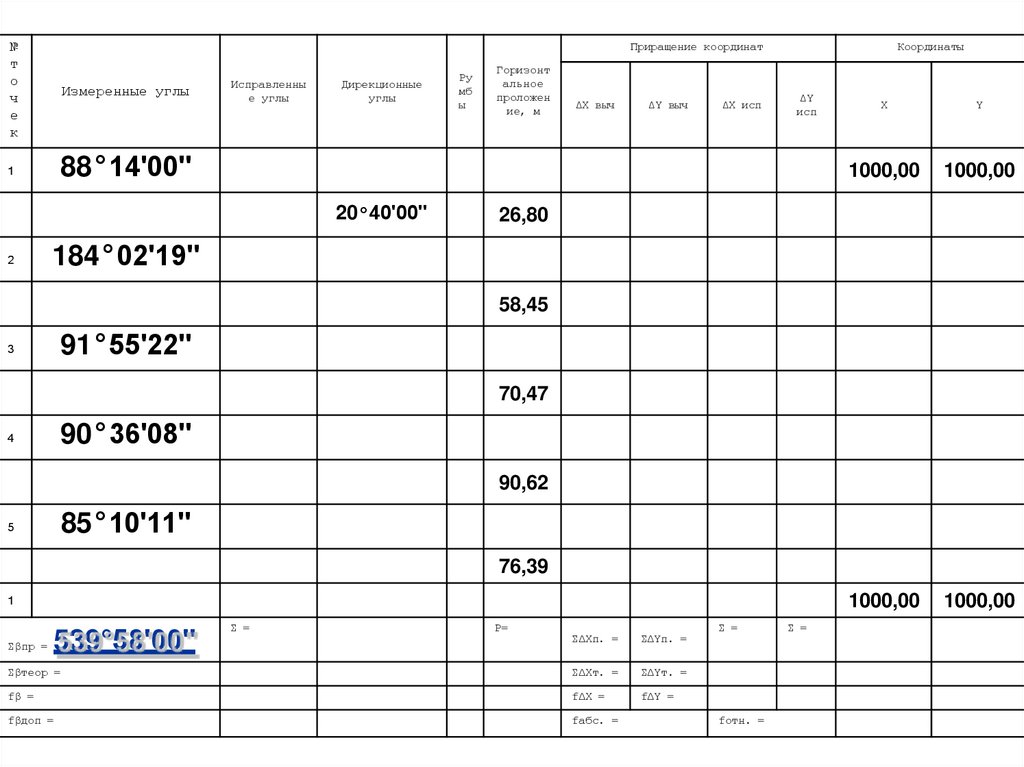
1. Нахождение практической суммы углов, т.е.
суммы измеренных углов
∑βпр. = ∑βизм.
∑βпр. = 88°14ʹ00ʺ+ 184°02ʹ19ʺ+
+91°55ʹ22ʺ+ 90°36ʹ08ʺ+ 85°10ʹ11ʺ =
= 539°58ʹ00ʺ
11.
№т
о
ч
е
к
Измеренные углы
1
88°14ʹ00ʺ
Приращение координат
Исправленны
е углы
Дирекционные
углы
20°40ʹ00ʺ
2
Ру
мб
ы
Горизонт
альное
проложен
ие, м
ΔX выч
ΔY выч
ΔX исп
Координаты
ΔY
исп
X
Y
1000,00
1000,00
1000,00
1000,00
26,80
184°02ʹ19ʺ
58,45
91°55ʹ22ʺ
3
70,47
90°36ʹ08ʺ
4
90,62
85°10ʹ11ʺ
5
76,39
1
539°58ʹ00ʺ
Σ =
Р=
Σ∆Xп. =
Σ∆Yп. =
Σβтеор =
Σ∆Xт. =
Σ∆Yт. =
fβ =
f∆X =
f∆Y =
fβдоп =
fабс. =
Σβпр =
Σ =
fотн. =
Σ =
12.
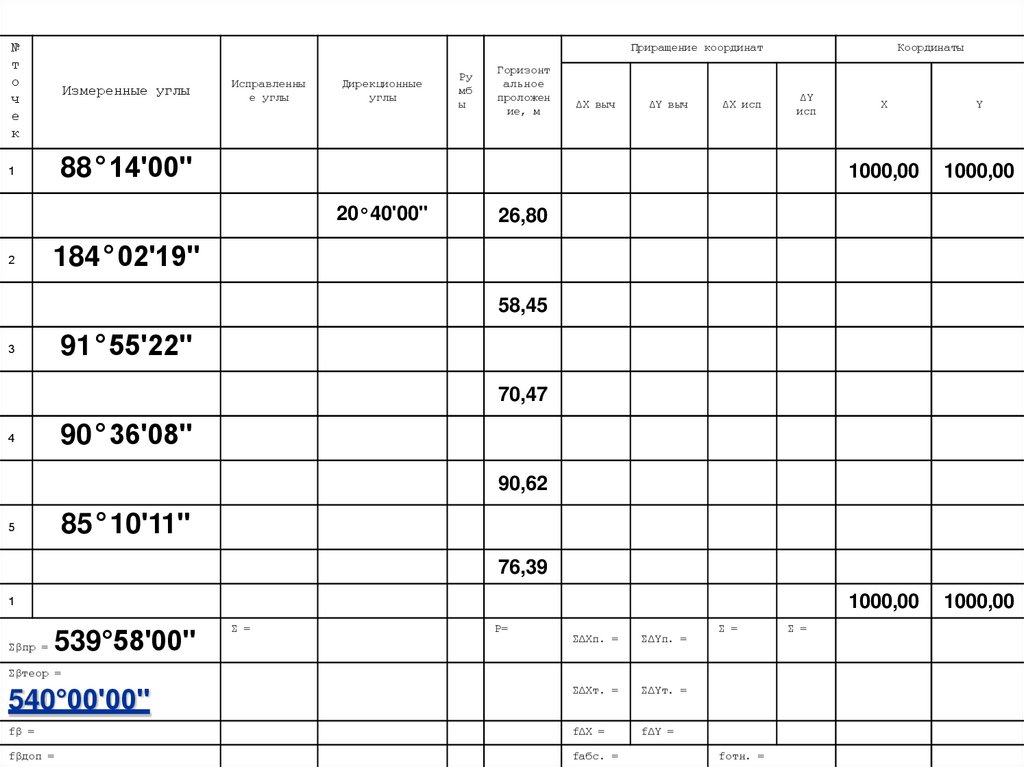
2. Нахождение теоретической суммы углов∑βтеор. = 180˚·(n-2),
где n – число измеренных углов,
т.е. 5 измеренных углов
∑βтеор. = 180°·(5-2) = 540°00ʹ00ʺ
13.
№т
о
ч
е
к
Измеренные углы
1
88°14ʹ00ʺ
Приращение координат
Исправленны
е углы
Дирекционные
углы
20°40ʹ00ʺ
2
Ру
мб
ы
Горизонт
альное
проложен
ие, м
ΔX выч
ΔY выч
ΔX исп
Координаты
ΔY
исп
X
Y
1000,00
1000,00
1000,00
1000,00
26,80
184°02ʹ19ʺ
58,45
91°55ʹ22ʺ
3
70,47
90°36ʹ08ʺ
4
90,62
85°10ʹ11ʺ
5
76,39
1
539°58ʹ00ʺ
Σ =
Р=
Σ∆Xп. =
Σ∆Yп. =
540°00ʹ00ʺ
Σ∆Xт. =
Σ∆Yт. =
fβ =
f∆X =
f∆Y =
fβдоп =
fабс. =
Σβпр =
Σ =
Σβтеор =
fотн. =
Σ =
14.
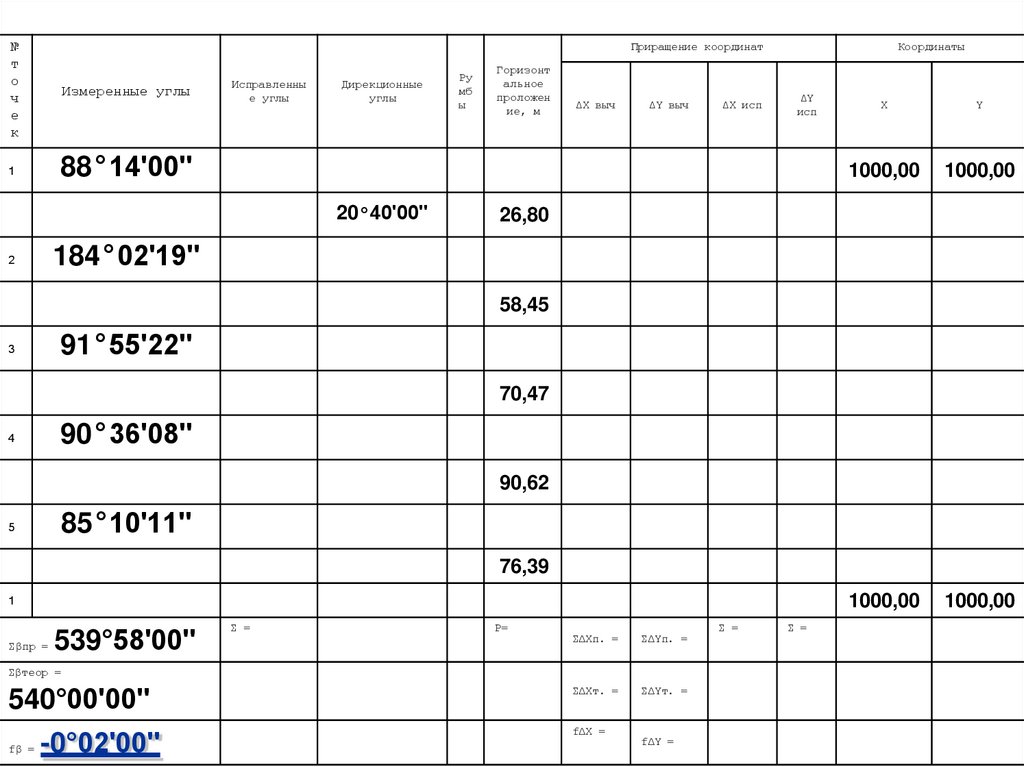
3. Нахождение угловой невязкиfβ = ∑βпр. - ∑βтеор.
fβ = 539°58ʹ00ʺ - 540°00ʹ00ʺ =
= -0°02ʹ00ʺ
15.
№т
о
ч
е
к
Измеренные углы
1
88°14ʹ00ʺ
Приращение координат
Исправленны
е углы
Дирекционные
углы
20°40ʹ00ʺ
Ру
мб
ы
Горизонт
альное
проложен
ие, м
ΔX выч
ΔY выч
ΔX исп
Координаты
ΔY
исп
X
Y
1000,00
1000,00
1000,00
1000,00
26,80
184°02ʹ19ʺ
2
58,45
91°55ʹ22ʺ
3
70,47
90°36ʹ08ʺ
4
90,62
85°10ʹ11ʺ
5
76,39
1
Σβпр =
539°58ʹ00ʺ
Σ =
Р=
Σ∆Xп. =
Σ∆Yп. =
Σ∆Xт. =
Σ∆Yт. =
Σβтеор =
540°00ʹ00ʺ
fβ =
-0°02ʹ00ʺ
f∆X =
f∆Y =
Σ =
Σ =
16.
4. Нахождение допустимой угловой невязкиfβдоп. = ±2· mβ· √n,
где mβ – средняя квадратическая
погрешность измерение угла, т.е. 30ʺ (4Т30П)
n – число измеренных углов, т.е. 5 углов
fβдоп. = ±2·0°00ʹ30ʺ·√5 = ±0°02ʹ14ʺ
17.
№т
о
ч
е
к
Измеренные углы
1
88°14ʹ00ʺ
Приращение координат
Исправленны
е углы
Дирекционные
углы
20°40ʹ00ʺ
Ру
мб
ы
Горизонт
альное
проложен
ие, м
ΔX выч
ΔY выч
ΔX исп
Координаты
ΔY
исп
X
Y
1000,00
1000,00
1000,00
1000,00
26,80
184°02ʹ19ʺ
2
58,45
91°55ʹ22ʺ
3
70,47
90°36ʹ08ʺ
4
90,62
85°10ʹ11ʺ
5
76,39
1
Σβпр =
539°58ʹ00ʺ
Σ =
Р=
Σ∆Xп. =
Σ∆Yп. =
Σ∆Xт. =
Σ∆Yт. =
Σ =
Σβтеор =
540°00ʹ00ʺ
fβ =
-0°02ʹ00ʺ
f∆X =
fабс. =
f∆Y =
fотн. =
Σ =
18.
5. Если полученная невязка fβ не превышаетдопустимую, то ее распределяем поровну на все
углы
Vβ = - f β : n
где Vβ – поправка на измеренные углы
n – число измеренных углов,
т.е. 5 углов
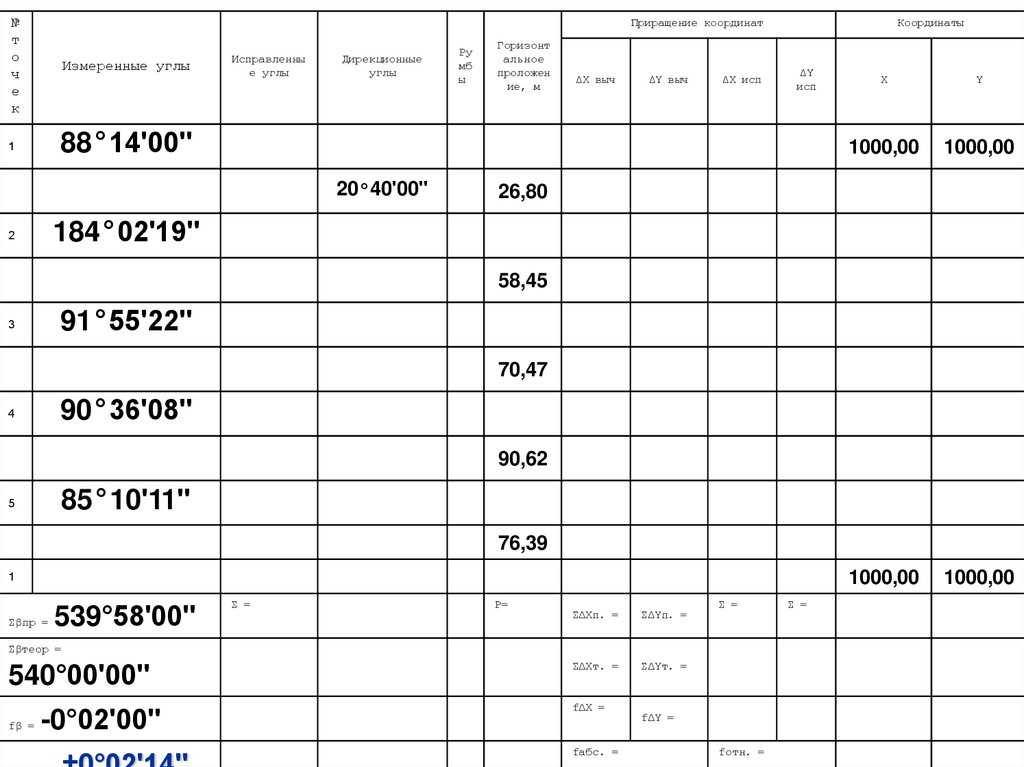
Vβ = - (-0°02ʹ00ʺ) : 5 = +0°00ʹ24ʺ
19.
КОНТРОЛЬ: сумма поправокдолжна равняться невязке с
обратным знаком
∑Vβ = -fβ
∑Vβ = 24ʺ+24ʺ+24ʺ+24ʺ+24ʺ = +0°00ʹ120ʺ
+0°00ʹ120ʺ = -0°02ʹ00ʺ
20.
№т
о
ч
е
к
Приращение координат
Измеренные углы
+24
Исправленны
е углы
Дирекционные
углы
Румб
ы
Горизонт
альное
проложен
ие, м
1
88°14ʹ00ʺ
2
+24
184°02ʹ19ʺ
58,45
3
+24
91°55ʹ22ʺ
70,47
4
+24
90°36ʹ08ʺ
90,62
5
+24
85°10ʹ11ʺ
20°40ʹ00ʺ
ΔX выч
ΔY выч
ΔX исп
Координаты
ΔY
исп
X
Y
1000,00
1000,00
1000,00
1000,00
26,80
76,39
1
Σβпр =
539°58ʹ00ʺ
Σ =
Р=
Σ∆Xп. =
Σ∆Yп. =
Σ∆Xт. =
Σ∆Yт. =
Σ =
Σβтеор =
540°00ʹ00ʺ
fβ =
-0°02ʹ00ʺ
f∆X =
fабс. =
f∆Y =
fотн. =
Σ =
21.
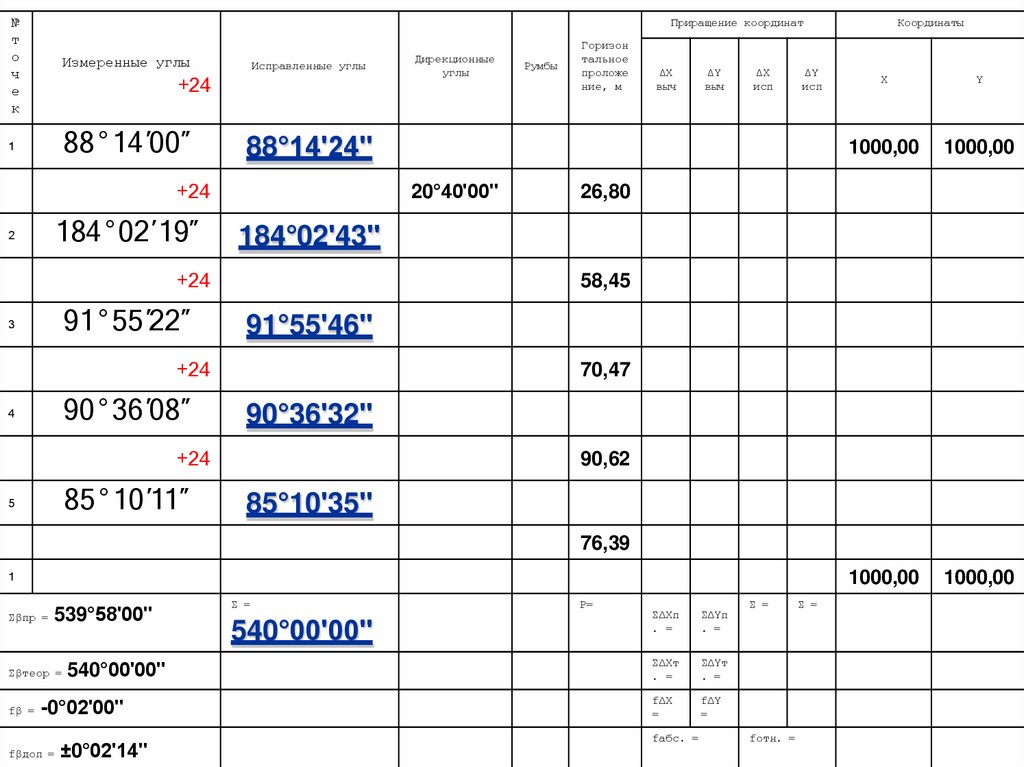
6. Вычисление исправленных угловβn исп. = βn изм. + Vβn
где βn исп. – исправленный n-ый угол
βn изм. – измеренный n-ый угол
Vβn – поправка для измеренного n-ого угла
Пример:
β1исп.=88°14ʹ00ʺ+0°00ʹ24ʺ= 88°14ʹ24ʺ
КОНТРОЛЬ: сумма исправленных углов
должна равняться теоретической сумме
∑βисп. = ∑βтеор.
углов
22.
№т
о
ч
е
к
Измеренные углы
1
88°14ʹ00ʺ
Приращение координат
Исправленные углы
+24
184°02ʹ19ʺ
20°40ʹ00ʺ
91°55ʹ22ʺ
90°36ʹ08ʺ
85°10ʹ11ʺ
ΔX
исп
ΔY
исп
X
Y
1000,00
1000,00
1000,00
1000,00
26,80
91°55ʹ46ʺ
70,47
90°36ʹ32ʺ
+24
5
ΔY
выч
58,45
+24
4
ΔX
выч
184°02ʹ43ʺ
+24
3
Румбы
Горизон
тальное
проложе
ние, м
88°14ʹ24ʺ
+24
2
Дирекционные
углы
Координаты
90,62
85°10ʹ35ʺ
76,39
1
Σβпр =
539°58ʹ00ʺ
Σβтеор =
fβ =
540°00ʹ00ʺ
-0°02ʹ00ʺ
fβдоп =
±0°02ʹ14ʺ
Σ =
540°00ʹ00ʺ
Р=
Σ∆Xп
. =
Σ∆Yп
. =
Σ∆Xт
. =
Σ∆Yт
. =
f∆X
=
f∆Y
=
fабс. =
Σ =
fотн. =
Σ =
23.
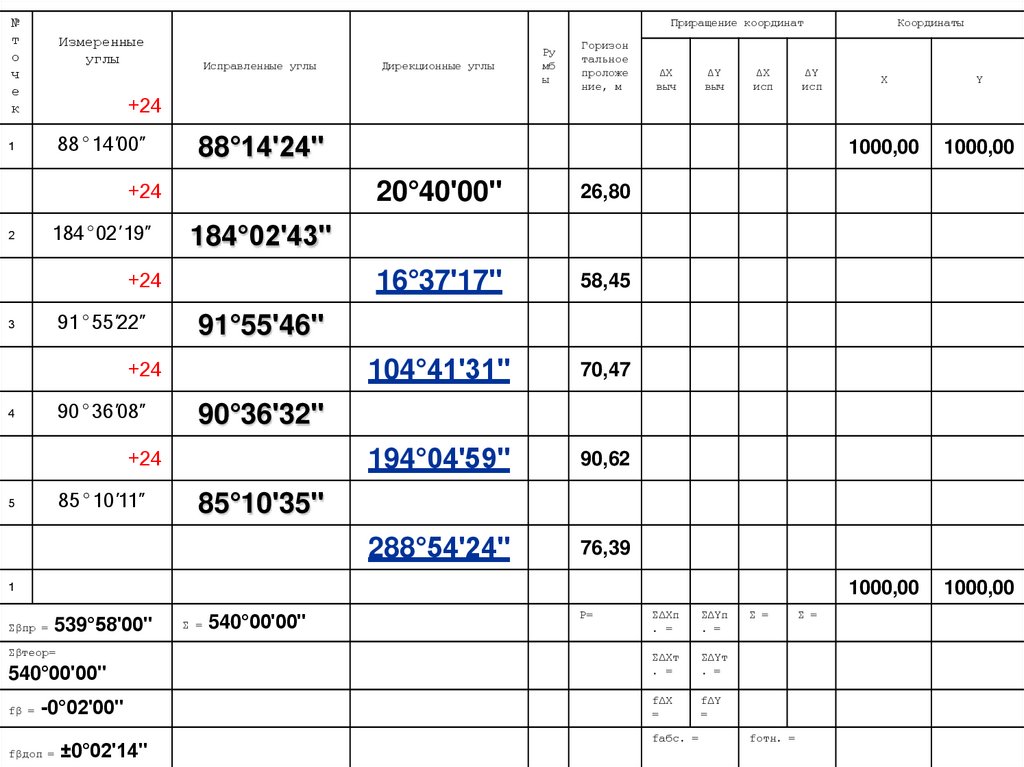
7. Вычисление дирекционных угловαn = αn-1 + 180° - βn – для правых углов
αn = αn-1 - 180° + βn – для левых углов
Пример:
α2-3=20°40ʹ00ʺ+180°-184°02ʹ43ʺ= 16°37ʹ17ʺ
КОНТРОЛЬ: в результате должен получится
начальный дирекционный угол
α1-2 = 20°40ʹ00ʺ
24.
№т
о
ч
е
к
Приращение координат
Измеренные
углы
Исправленные углы
Дирекционные углы
Ру
мб
ы
Горизон
тальное
проложе
ние, м
ΔX
выч
ΔY
выч
ΔX
исп
ΔY
исп
X
Y
1000,00
1000,00
1000,00
1000,00
+24
88°14ʹ00ʺ
1
88°14ʹ24ʺ
+24
184°02ʹ19ʺ
2
91°55ʹ22ʺ
3
90°36ʹ08ʺ
85°10ʹ11ʺ
16°37ʹ17ʺ
58,45
104°41ʹ31ʺ
70,47
194°04ʹ59ʺ
90,62
288°54ʹ24ʺ
76,39
90°36ʹ32ʺ
+24
5
26,80
91°55ʹ46ʺ
+24
4
20°40ʹ00ʺ
184°02ʹ43ʺ
+24
85°10ʹ35ʺ
1
Σβпр =
539°58ʹ00ʺ
Σβтеор=
540°00ʹ00ʺ
fβ =
Координаты
-0°02ʹ00ʺ
fβдоп =
±0°02ʹ14ʺ
Σ =
540°00ʹ00ʺ
Р=
Σ∆Xп
. =
Σ∆Yп
. =
Σ∆Xт
. =
Σ∆Yт
. =
f∆X
=
f∆Y
=
fабс. =
Σ =
fотн. =
Σ =
25.
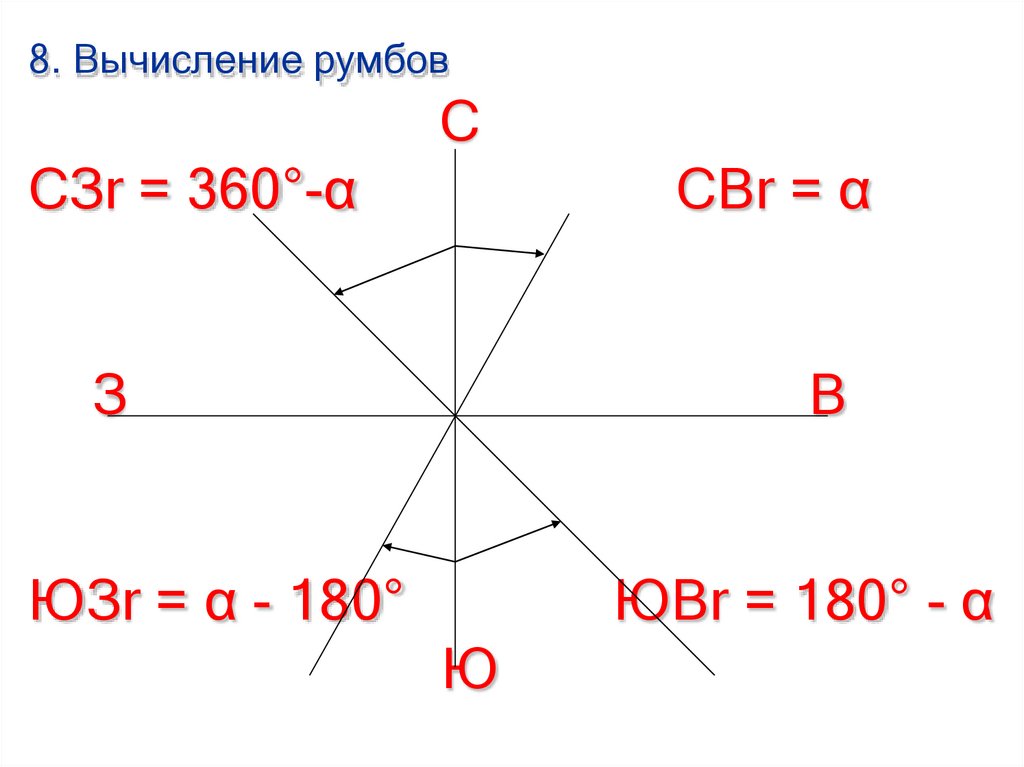
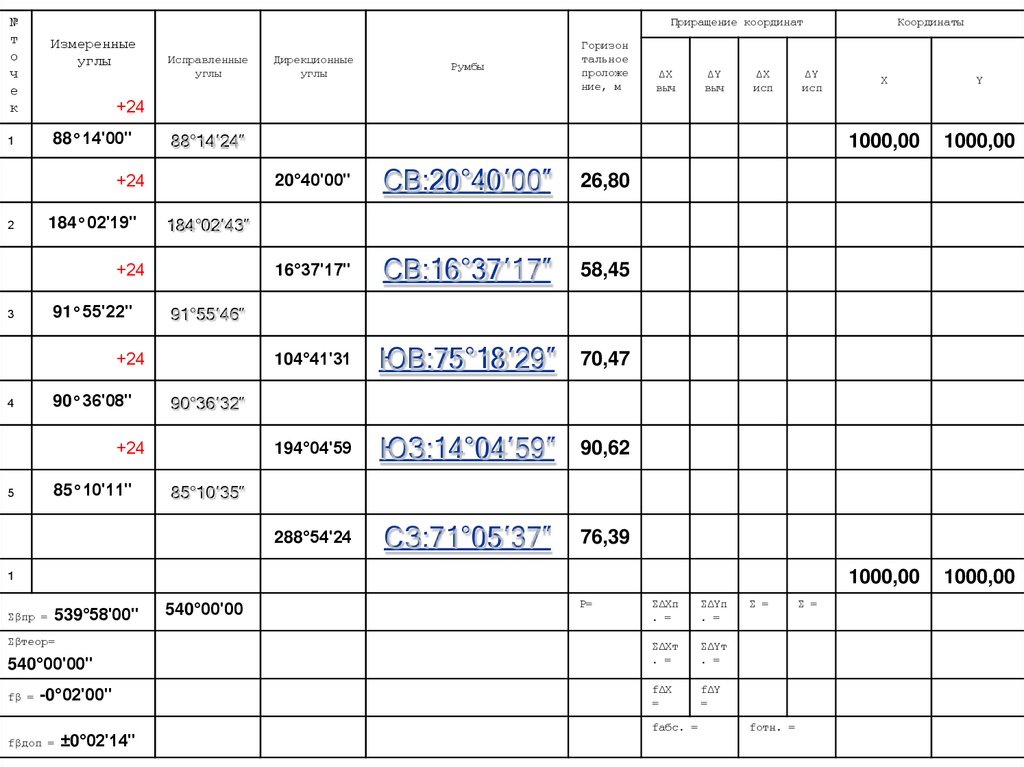
8. Вычисление румбовС
СЗr = 360°-α
СВr = α
З
В
ЮЗr = α - 180°
ЮВr = 180° - α
Ю
26.
№т
о
ч
е
к
1
Приращение координат
Измеренные
углы
Исправленные
углы
88°14ʹ00ʺ
184°02ʹ19ʺ
91°55ʹ22ʺ
ΔX
исп
ΔY
исп
X
Y
1000,00
1000,00
90°36ʹ08ʺ
85°10ʹ11ʺ
20°40ʹ00ʺ
СВ:20°40ʹ00ʺ
26,80
16°37ʹ17ʺ
СВ:16°37ʹ17ʺ
58,45
104°41ʹ31
ЮВ:75°18ʹ29ʺ
70,47
194°04ʹ59
ЮЗ:14°04ʹ59ʺ
90,62
288°54ʹ24
СЗ:71°05ʹ37ʺ
76,39
1000,00
1000,00
91°55ʹ46ʺ
90°36ʹ32ʺ
+24
5
ΔY
выч
184°02ʹ43ʺ
+24
4
ΔX
выч
88°14ʹ24ʺ
+24
3
Румбы
Горизон
тальное
проложе
ние, м
+24
+24
2
Дирекционные
углы
Координаты
85°10ʹ35ʺ
1
Σβпр = 539°58ʹ00ʺ
Σβтеор=
540°00ʹ00ʺ
fβ = -0°02ʹ00ʺ
fβдоп = ±0°02ʹ14ʺ
540°00ʹ00
Р=
Σ∆Xп
. =
Σ∆Yп
. =
Σ∆Xт
. =
Σ∆Yт
. =
f∆X
=
f∆Y
=
fабс. =
Σ =
fотн. =
Σ =
27.
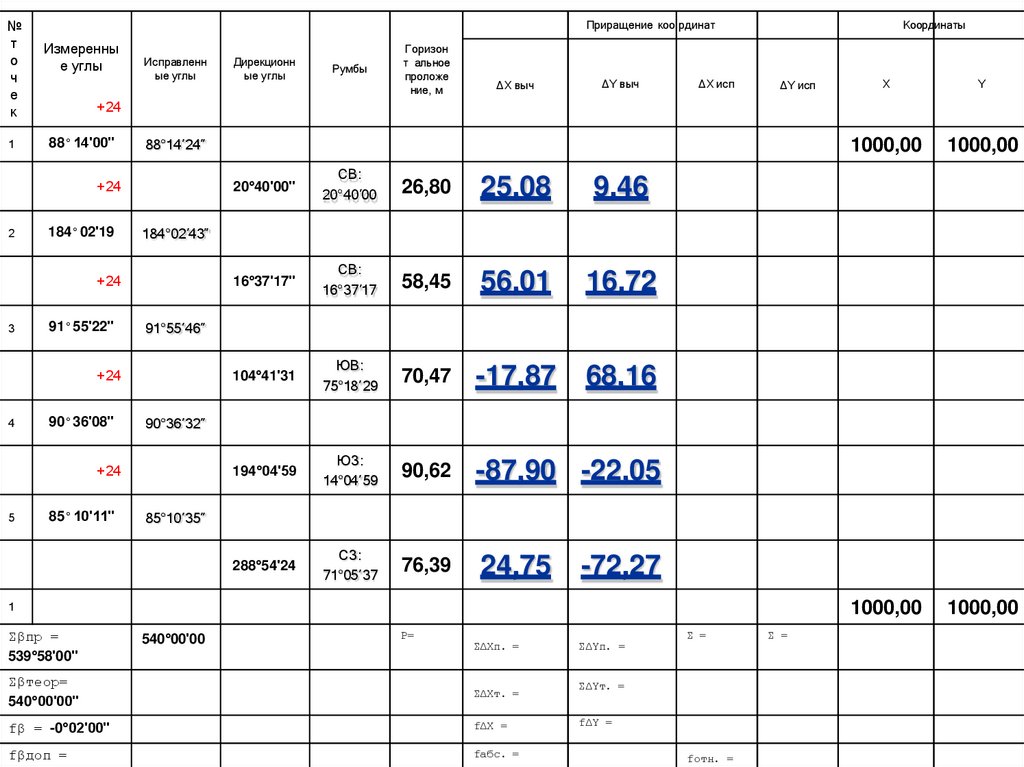
9. Вычисление приращения координат∆Х = Sn · cosαn
∆Y = Sn · sinαn
где ∆Х, ∆Y – приращение координат
Sn – горизонтальное проложение n-ого
направления
αn – дирекционный угол n-ого
направления
Пример:
∆Х1-2 = 26,80 · cos 20°40ʹ00ʺ = 25,08
∆Y1-2 = 26,80 · sin 20°40ʹ00ʺ = 9,46
28.
№т
о
ч
е
к
1
Приращение коо рдинат
Измеренны
е углы
Исправленн
ые углы
88°14ʹ00ʺ
184°02ʹ19
91°55ʹ22ʺ
ΔX исп
ΔY исп
X
Y
1000,00
1000,00
90°36ʹ08ʺ
85°10ʹ11ʺ
20°40ʹ00ʺ
СВ:
20°40ʹ00
26,80
25,08
9,46
16°37ʹ17ʺ
СВ:
16°37ʹ17
58,45
56,01
16,72
104°41ʹ31
ЮВ:
75°18ʹ29
70,47
-17,87
68,16
194°04ʹ59
ЮЗ:
14°04ʹ59
90,62
-87,90 -22,05
288°54ʹ24
СЗ:
71°05ʹ37
76,39
24,75
1000,00
1000,00
91°55ʹ46ʺ
90°36ʹ32ʺ
+24
5
ΔY выч
184°02ʹ43ʺ
+24
4
ΔX выч
88°14ʹ24ʺ
+24
3
Румбы
Горизон
т альное
проложе
ние, м
+24
+24
2
Дирекционн
ые углы
Координаты
85°10ʹ35ʺ
-72,27
1
Σβпр =
539°58ʹ00ʺ
540°00ʹ00
Р=
Σ∆Xп. =
Σβтеор=
540°00ʹ00ʺ
Σ∆Xт. =
fβ = -0°02ʹ00ʺ
f∆X =
fβдоп =
fабс. =
Σ∆Yп. =
Σ =
Σ∆Yт. =
f∆Y =
fотн. =
Σ =
29.
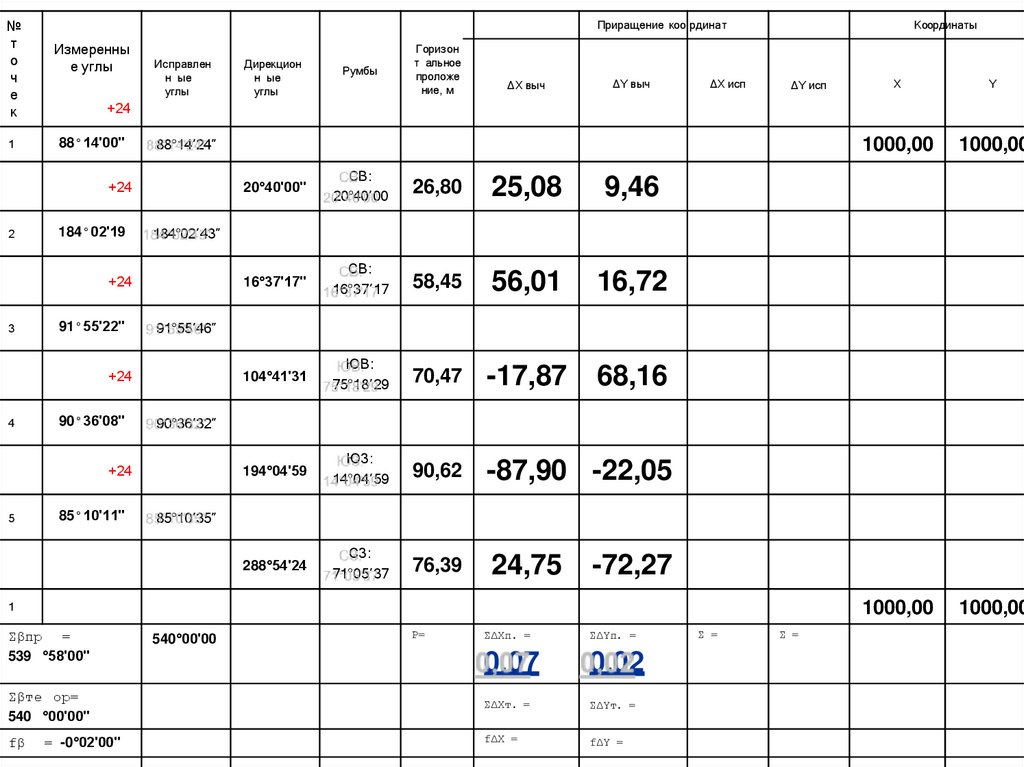
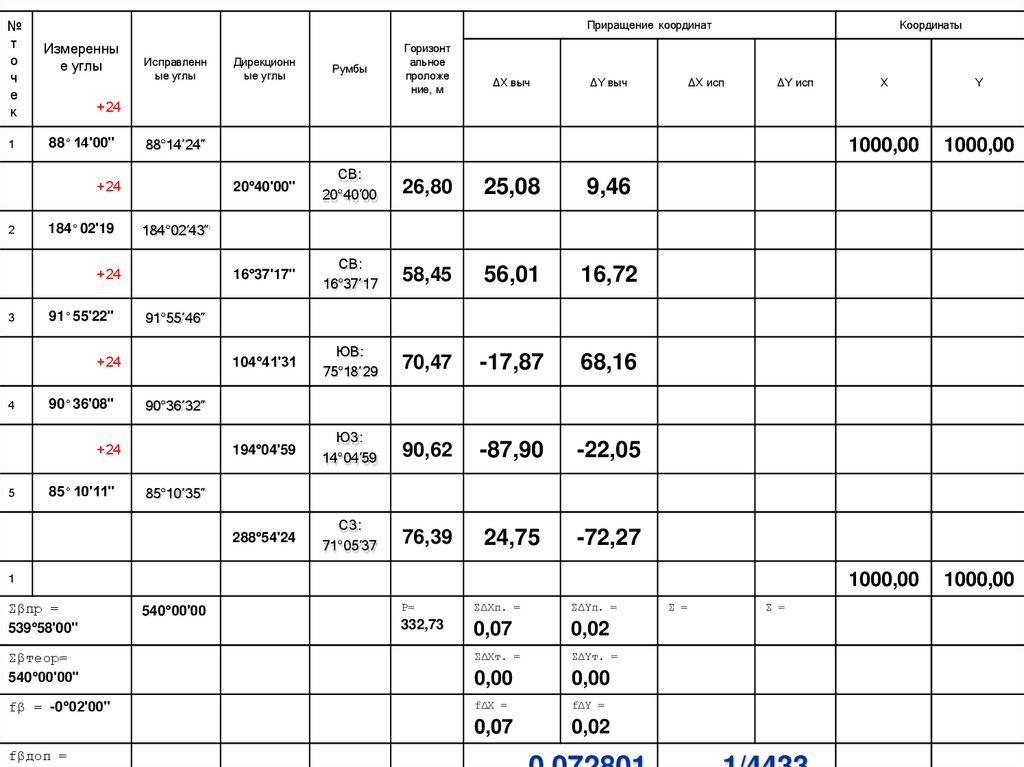
10. Вычисление практической суммы приращениякоординат
∑∆Хпр.= ∑∆Хвыч.
∑∆Yпр.= ∑∆Yвыч.
∑∆Хпр.= 25,08+56,01+(-17,87)+(-87,90)+24,75 =
= 0,07
∑∆Yпр.= 9,46+16,72+68,16+(-22,05)+(-72,27) =
= 0,02
30.
№т
о
ч
е
к
1
Приращение коо рдинат
Измеренны
е углы
Исправлен
н ые
углы
88°14ʹ00ʺ
184°02ʹ19
91°55ʹ22ʺ
ΔX исп
ΔY исп
X
Y
1000,00
1000,00
90°36ʹ08ʺ
85°10ʹ11ʺ
20°40ʹ00ʺ
СВ:
20°40ʹ00
26,80
25,08
9,46
16°37ʹ17ʺ
СВ:
16°37ʹ17
58,45
56,01
16,72
104°41ʹ31
ЮВ:
75°18ʹ29
70,47
-17,87
68,16
194°04ʹ59
ЮЗ:
14°04ʹ59
90,62
-87,90 -22,05
288°54ʹ24
СЗ:
71°05ʹ37
76,39
24,75
1000,00
1000,00
91°55ʹ46ʺ
90°36ʹ32ʺ
+24
5
ΔY выч
184°02ʹ43ʺ
+24
4
ΔX выч
88°14ʹ24ʺ
+24
3
Румбы
Горизон
т альное
проложе
ние, м
+24
+24
2
Дирекцион
н ые
углы
Координаты
85°10ʹ35ʺ
-72,27
1
Σβпр =
539 °58ʹ00ʺ
Р=
Σ∆Xп. =
Σ∆Yп. =
0,07
0,02
Σβте ор=
540 °00ʹ00ʺ
Σ∆Xт. =
Σ∆Yт. =
fβ
f∆X =
f∆Y =
= -0°02ʹ00ʺ
540°00ʹ00
Σ =
Σ =
31.
11. Вычисление теоретической суммы приращениякоординат
∑∆Хтеор.= Хкон.-Хнач.
∑∆Yтеор.= Yкон.-Yнач.
где Хкон., Yкон. – координаты конечной точки
Хнач., Yнач. – координаты начальной точки
∑∆Хтеор.= 1000,00 – 1000,00 = 0,00
∑∆Yтеор.= 1000,00 – 1000,00 = 0,00
32.
№т
о
ч
е
к
1
Приращение координат
Измеренны
е углы
Исправленн
ые углы
88°14ʹ00ʺ
184°02ʹ19
91°55ʹ22ʺ
ΔX исп
ΔY исп
X
Y
1000,00
1000,00
90°36ʹ08ʺ
85°10ʹ11ʺ
20°40ʹ00ʺ
СВ:
20°40ʹ00
26,80
25,08
9,46
16°37ʹ17ʺ
СВ:
16°37ʹ17
58,45
56,01
16,72
104°41ʹ31
ЮВ:
75°18ʹ29
70,47
-17,87
68,16
194°04ʹ59
ЮЗ:
14°04ʹ59
90,62
-87,90
-22,05
288°54ʹ24
СЗ:
71°05ʹ37
76,39
24,75
-72,27
1000,00
1000,00
91°55ʹ46ʺ
90°36ʹ32ʺ
+24
5
ΔY выч
184°02ʹ43ʺ
+24
4
ΔX выч
88°14ʹ24ʺ
+24
3
Румбы
Горизонт
альное
проложе
ние, м
+24
+24
2
Дирекционн
ые углы
Координаты
85°10ʹ35ʺ
1
Σβпр =
539°58ʹ00ʺ
Р=
Σ∆Xп. =
Σ∆Yп. =
0,07
0,02
Σβтеор=
540°00ʹ00ʺ
Σ∆Xт. =
Σ∆Yт. =
0,00
0,00
fβ = -0°02ʹ00ʺ
f∆X =
f∆Y =
fβдоп =
fабс. =
540°00ʹ00
Σ =
fотн. =
Σ =
33.
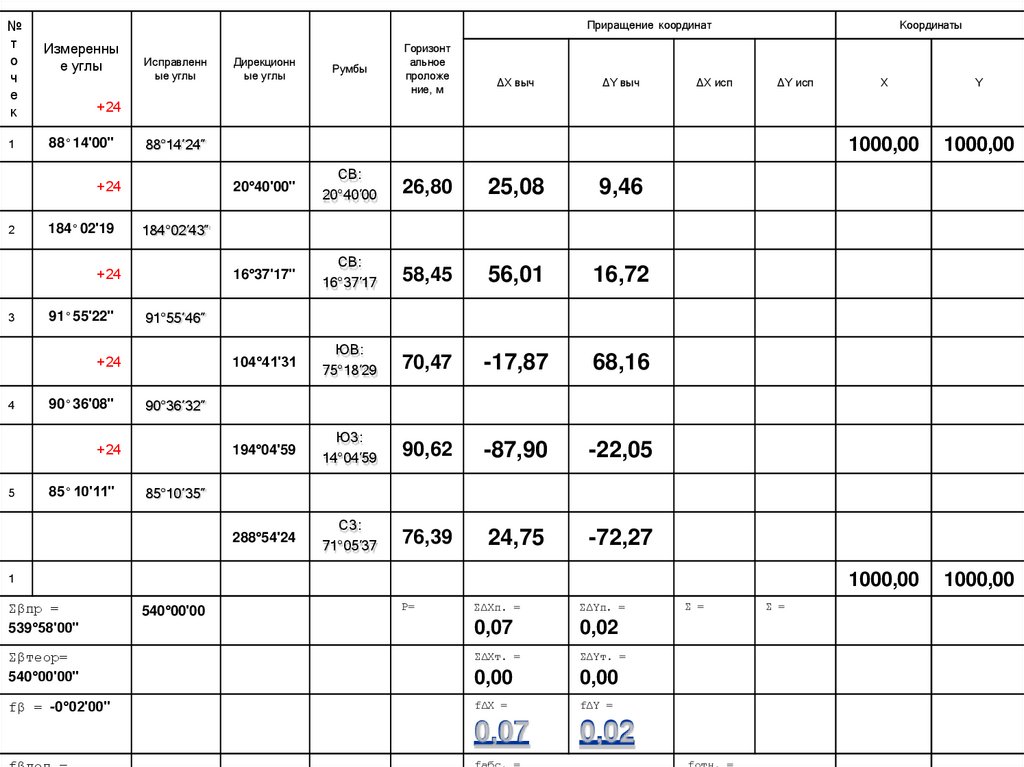
12. Вычисление невязки в приращениях координатf∆Х = ∑∆Хпр. - ∑∆Хтеор.
f∆Y =∑∆Yпр. - ∑∆Yтеор.
f∆Х= 0,07 – 0,00 = 0,07
f∆Y= 0,02 – 0,00 = 0,02
34.
№т
о
ч
е
к
1
Приращение координат
Измеренны
е углы
Исправленн
ые углы
88°14ʹ00ʺ
184°02ʹ19
91°55ʹ22ʺ
ΔX исп
ΔY исп
X
Y
1000,00
1000,00
90°36ʹ08ʺ
85°10ʹ11ʺ
20°40ʹ00ʺ
СВ:
20°40ʹ00
26,80
25,08
9,46
16°37ʹ17ʺ
СВ:
16°37ʹ17
58,45
56,01
16,72
104°41ʹ31
ЮВ:
75°18ʹ29
70,47
-17,87
68,16
194°04ʹ59
ЮЗ:
14°04ʹ59
90,62
-87,90
-22,05
288°54ʹ24
СЗ:
71°05ʹ37
76,39
24,75
-72,27
1000,00
1000,00
91°55ʹ46ʺ
90°36ʹ32ʺ
+24
5
ΔY выч
184°02ʹ43ʺ
+24
4
ΔX выч
88°14ʹ24ʺ
+24
3
Румбы
Горизонт
альное
проложе
ние, м
+24
+24
2
Дирекционн
ые углы
Координаты
85°10ʹ35ʺ
1
Σβпр =
539°58ʹ00ʺ
Р=
Σ∆Xп. =
Σ∆Yп. =
0,07
0,02
Σβтеор=
540°00ʹ00ʺ
Σ∆Xт. =
Σ∆Yт. =
0,00
0,00
fβ = -0°02ʹ00ʺ
f∆X =
f∆Y =
0,07
0,02
540°00ʹ00
fабс. =
Σ =
fотн. =
Σ =
35.
13. Выполнение оценки точности ходаfабс = ±√(f∆Х²+f∆Y²)
fабс = √(0,07²+0,02²) = 0,072801
fотн = fабс / Р = 1 / (Р : fабс.),
где Р – периметр теодолитного хода
fотн. = 1 / (322,73 : 0,072801) = 1/4433
1/3000>1/4433
36.
№т
о
ч
е
к
1
Приращение координат
Измеренны
е углы
Исправленн
ые углы
88°14ʹ00ʺ
184°02ʹ19
91°55ʹ22ʺ
ΔX исп
ΔY исп
X
Y
1000,00
1000,00
90°36ʹ08ʺ
85°10ʹ11ʺ
20°40ʹ00ʺ
СВ:
20°40ʹ00
26,80
25,08
9,46
16°37ʹ17ʺ
СВ:
16°37ʹ17
58,45
56,01
16,72
104°41ʹ31
ЮВ:
75°18ʹ29
70,47
-17,87
68,16
194°04ʹ59
ЮЗ:
14°04ʹ59
90,62
-87,90
-22,05
288°54ʹ24
СЗ:
71°05ʹ37
76,39
24,75
-72,27
1000,00
1000,00
91°55ʹ46ʺ
90°36ʹ32ʺ
+24
5
ΔY выч
184°02ʹ43ʺ
+24
4
ΔX выч
88°14ʹ24ʺ
+24
3
Румбы
Горизонт
альное
проложе
ние, м
+24
+24
2
Дирекционн
ые углы
Координаты
85°10ʹ35ʺ
1
Р=
Σ∆Xп. =
Σ∆Yп. =
332,73
0,07
0,02
Σβтеор=
540°00ʹ00ʺ
Σ∆Xт. =
Σ∆Yт. =
0,00
0,00
fβ = -0°02ʹ00ʺ
f∆X =
f∆Y =
0,07
0,02
Σβпр =
539°58ʹ00ʺ
fβдоп =
540°00ʹ00
Σ =
Σ =
37.
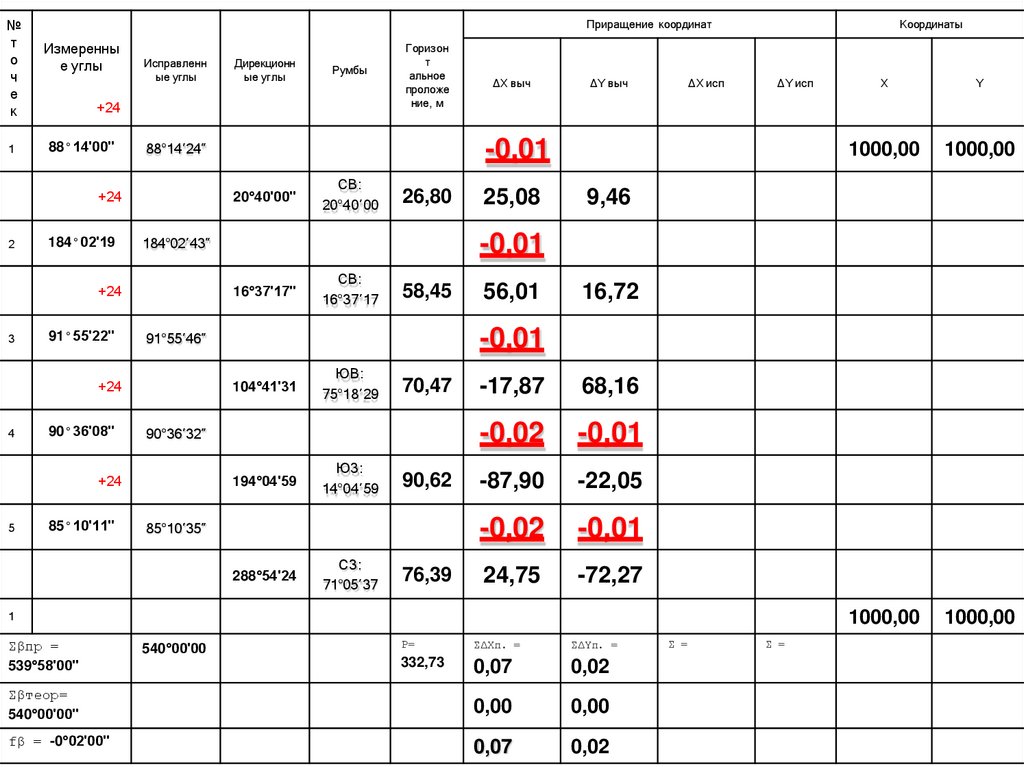
14. Если полученные невязки f∆Х, f∆Y непревышают допустимую, то их распределяем с
обратным знаком на приращения
пропорционально горизонтальному проложению
VXn = -(f∆X / P) · Sn
VYn = -(f∆Y / P) · Sn
где Vхn – поправка на приращение
координат
f∆X,∆Y – невязка в приращениях координат
Р – периметр теодолитного хода
Sn – горизонтальное проложение
38.
Пример:VX1-2 = -(0,07 / 322,73) · 26,80 = -0,01
VY1-2 = -(0,02 / 322,73) · 26,80 = -0,00
КОНТРОЛЬ: сумма поправок должна
равняться невязке с обратным знаком
∑V∆Х = -∑f∆X
∑V∆Y = -∑f∆Y
39.
№т
о
ч
е
к
1
Приращение координат
Измеренны
е углы
Исправленн
ые углы
88°14ʹ00ʺ
184°02ʹ19
91°55ʹ22ʺ
90°36ʹ08ʺ
5
85°10ʹ11ʺ
СВ:
20°40ʹ00
26,80
ΔY выч
ΔX исп
ΔY исп
25,08
16°37ʹ17ʺ
СВ:
16°37ʹ17
58,45
104°41ʹ31
ЮВ:
75°18ʹ29
70,47
90°36ʹ32ʺ
194°04ʹ59
ЮЗ:
14°04ʹ59
90,62
85°10ʹ35ʺ
1000,00
1000,00
1000,00
1000,00
9,46
56,01
16,72
СЗ:
71°05ʹ37
76,39
-17,87
68,16
-0,02
-0,01
-87,90
-22,05
-0,02
-0,01
24,75
-72,27
1
Р=
Σ∆Xп. =
Σ∆Yп. =
332,73
0,07
0,02
Σβтеор=
540°00ʹ00ʺ
0,00
0,00
fβ = -0°02ʹ00ʺ
0,07
0,02
540°00ʹ00
Y
-0,01
91°55ʹ46ʺ
288°54ʹ24
Σβпр =
539°58ʹ00ʺ
X
-0,01
184°02ʹ43ʺ
+24
ΔX выч
-0,01
20°40ʹ00ʺ
+24
4
Горизон
т
альное
проложе
ние, м
88°14ʹ24ʺ
+24
3
Румбы
+24
+24
2
Дирекционн
ые углы
Координаты
Σ =
Σ =
40.
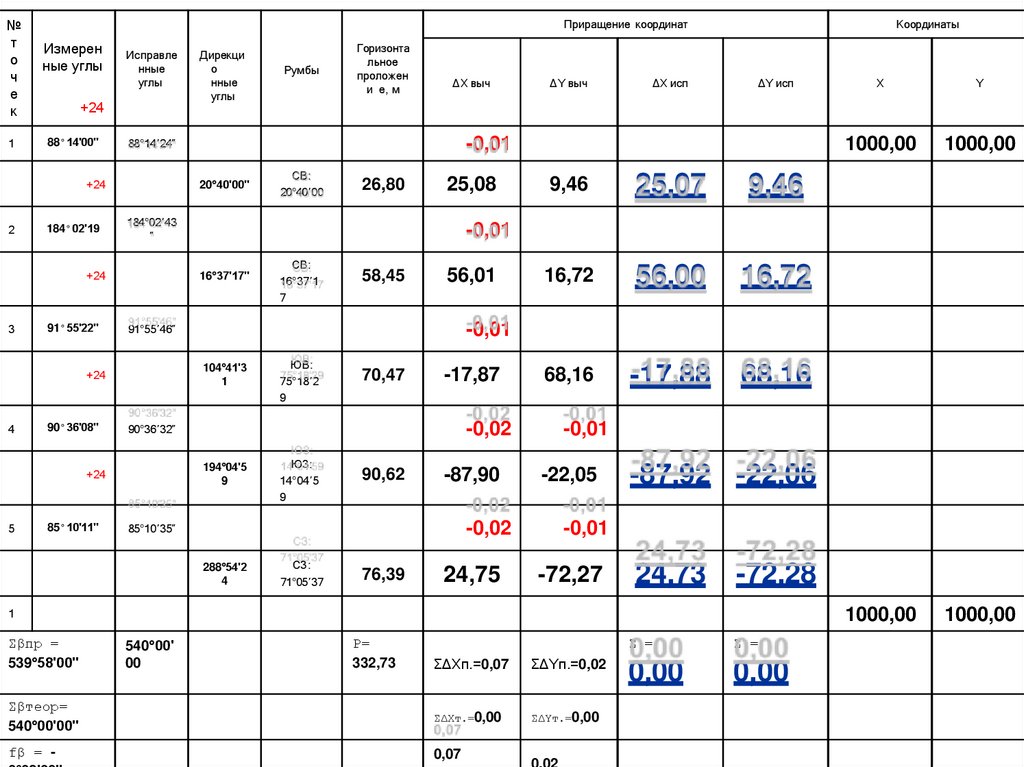
15. Вычисление исправленных приращенийкоординат
∆Хисп. = ∆Х + V∆X
∆Yисп. = ∆Y + V∆Y
Пример:
∆Xисп.1-2 = 25,08+(-0,01) = 25,07
∆Yисп.4-5 = -22,05+(-0,01) = -22,05
КОНТРОЛЬ: сумма исправленных приращений
координат должна равняться теоретической
сумме приращений координат
41.
№т
о
ч
е
к
1
Приращение координат
Измерен
ные углы
Исправле
нные
углы
+24
88°14ʹ00ʺ
184°02ʹ19
91°55ʹ22ʺ
90°36ʹ08ʺ
85°10ʹ11ʺ
ΔY выч
ΔX исп
ΔY исп
26,80
25,08
9,46
25,07
9,46
16,72
56,00
16,72
68,16
-17,88
68,16
СВ:
16°37ʹ1
7
58,45
56,01
104°41ʹ3
1
ЮВ:
75°18ʹ2
9
70,47
-17,87
-0,02
-0,01
-87,90
-22,05
-0,02
-0,01
24,75
-72,27
90°36ʹ32ʺ
194°04ʹ5
9
ЮЗ:
14°04ʹ5
9
90,62
85°10ʹ35ʺ
1000,00
1000,00
СЗ:
71°05ʹ37
76,39
1000,00
1000,00
-87,92 -22,06
24,73
-72,28
1
540°00ʹ
00
Y
-0,01
91°55ʹ46ʺ
288°54ʹ2
4
Σβпр =
539°58ʹ00ʺ
X
-0,01
16°37ʹ17ʺ
+24
5
СВ:
20°40ʹ00
184°02ʹ43
ʺ
+24
4
ΔX выч
-0,01
20°40ʹ00ʺ
+24
3
Румбы
Горизонта
льное
проложен
и е, м
88°14ʹ24ʺ
+24
2
Дирекци
о
нные
углы
Координаты
Р=
332,73
Σ∆Xп.=0,07
Σ∆Yп.=0,02
Σβтеор=
540°00ʹ00ʺ
Σ∆Xт.=0,00
Σ∆Yт.=0,00
fβ = -
0,07
0,02
Σ =
Σ =
0,00
0,00
42.
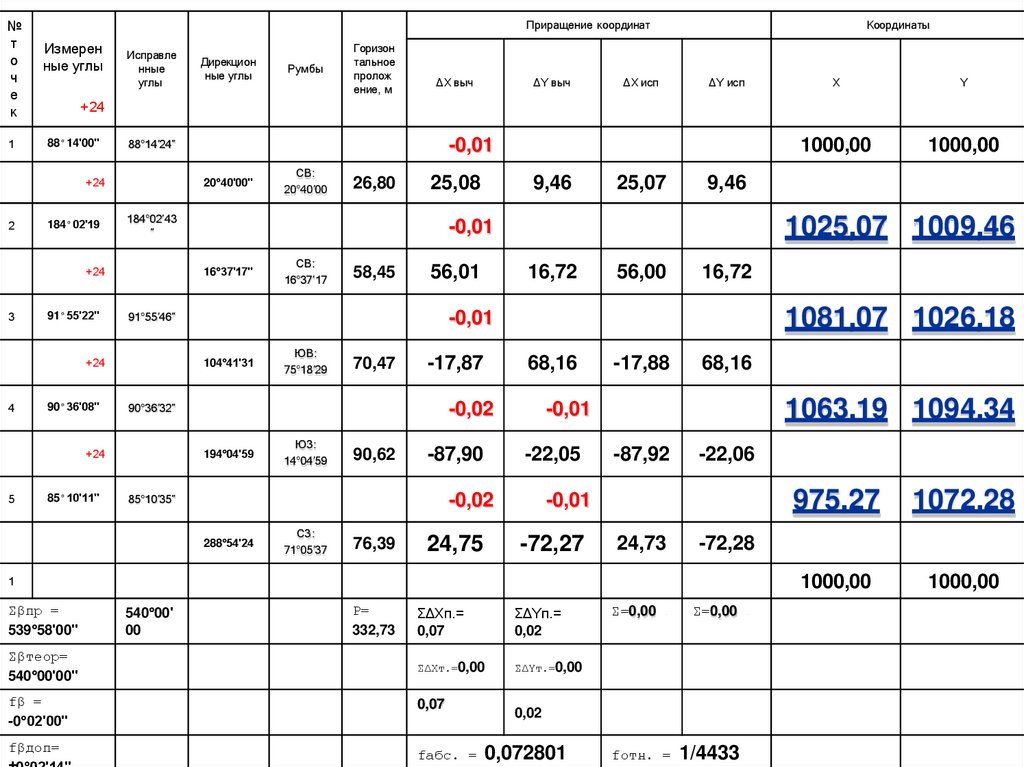
15. Вычисляем координаты точекХn+1 = Хn + ∆Xn-1
Yn+1 = Yn + ∆Yn-1
где n – номер точки теодолитного хода
КОНТРОЛЬ: при вычислении координат
точек должен получиться конечный
результат
43.
Пример:X2 = 1000,00 + 25,07 = 1025,07
Y2 = 1000,00 + 9,46 = 1009,46
44.
№т
о
ч
е
к
1
Приращение координат
Измерен
ные углы
Исправле
нные
углы
88°14ʹ00ʺ
184°02ʹ19
91°55ʹ22ʺ
90°36ʹ08ʺ
85°10ʹ11ʺ
СВ:
20°40ʹ00
26,80
25,08
184°02ʹ43
ʺ
ΔX исп
ΔY исп
9,46
25,07
X
Y
1000,00
1000,00
9,46
1025,07 1009,46
-0,01
16°37ʹ17ʺ
СВ:
16°37ʹ17
58,45
56,01
16,72
56,00
16,72
1081,07 1026,18
-0,01
91°55ʹ46ʺ
104°41ʹ31
ЮВ:
75°18ʹ29
70,47
-17,87
68,16
-0,02
-0,01
-87,90
-22,05
-0,02
-0,01
24,75
-72,27
90°36ʹ32ʺ
+24
5
ΔY выч
-0,01
20°40ʹ00ʺ
+24
4
ΔX выч
88°14ʹ24ʺ
+24
3
Румбы
Горизон
тальное
пролож
ение, м
+24
+24
2
Дирекцион
ные углы
Координаты
194°04ʹ59
ЮЗ:
14°04ʹ59
90,62
85°10ʹ35ʺ
288°54ʹ24
СЗ:
71°05ʹ37
76,39
-17,88
68,16
1063,19 1094,34
-87,92
24,73
-22,06
Σβтеор=
540°00ʹ00ʺ
540°00ʹ
00
Р=
332,73
Σ∆Xп.=
0,07
Σ∆Yп.=
0,02
Σ∆Xт.=0,00
Σ∆Yт.=0,00
fβ =
-0°02ʹ00ʺ
0,07
fβдоп=
fабс. = 0,072801
Σ=0,00
1072,28
1000,00
1000,00
-72,28
1
Σβпр =
539°58ʹ00ʺ
975,27
Σ=0,00
0,02
fотн. = 1/4433

























 mathematics
mathematics








