Similar presentations:
Элементы алгебры логики. Математические основы информатики. Информатика. 8 класс
1.
ЭЛЕМЕНТЫАЛГЕБРЫ ЛОГИКИ
МАТЕМАТИЧЕСКИЕ ОСНОВЫ
ИНФОРМАТИКИ
2.
Простые и сложныевысказывания
Высказывания бывают простые и сложные.
Высказывание называется простым, если никакая его
часть сама не является высказыванием.
Сложные (составные) высказывания строятся из простых с
помощью логических операций.
Название логической операции
Логическая связка
Конъюнкция
«и»; «а»; «но»; «хотя»
Дизъюнкция
«или»
Инверсия
«не»; «неверно, что»
3.
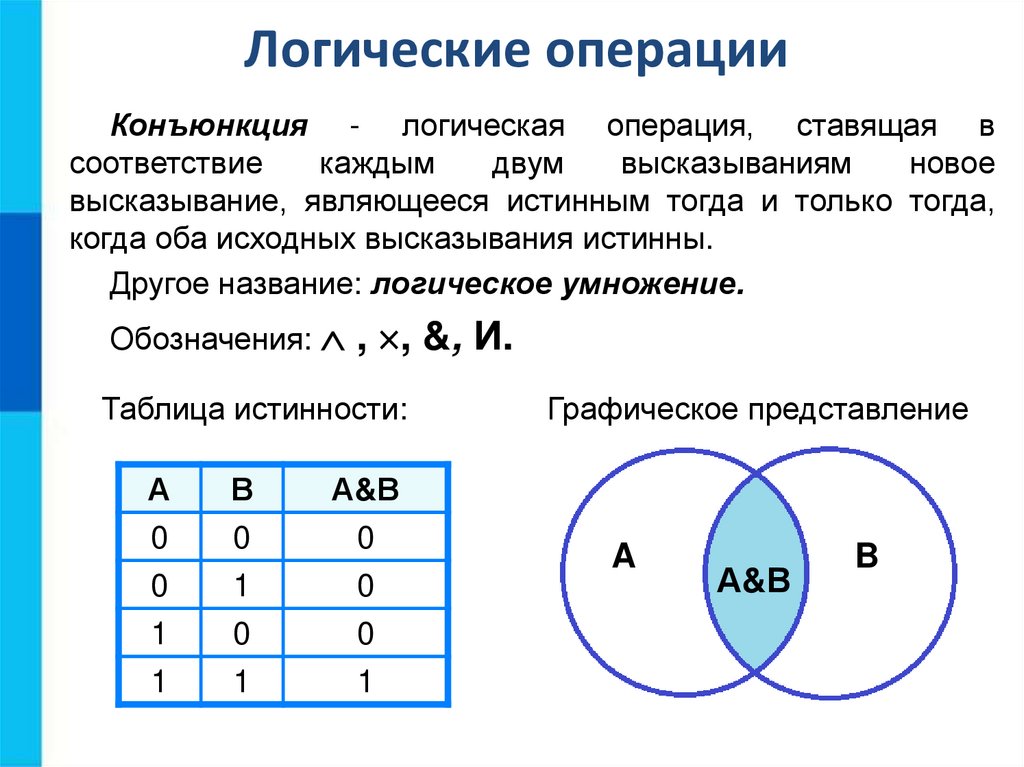
Логические операцииКонъюнкция - логическая операция, ставящая в
соответствие
каждым
двум
высказываниям
новое
высказывание, являющееся истинным тогда и только тогда,
когда оба исходных высказывания истинны.
Другое название: логическое умножение.
Обозначения: , , &, И.
Таблица истинности:
А
В
А&В
0
0
0
0
1
0
1
0
0
1
1
1
Графическое представление
A
А&В
B
4.
Логические операцииДизъюнкция - логическая операция, которая каждым двум
высказываниям ставит в соответствие новое высказывание,
являющееся ложным тогда и только тогда, когда оба исходных
высказывания ложны.
Другое название: логическое сложение.
Обозначения: V, |,
ИЛИ, +.
Таблица истинности:
А
В
АVВ
0
0
0
0
1
1
1
0
1
1
1
1
Графическое представление
A
B
АVВ
5.
Логические операцииИнверсия - логическая операция, которая каждому
высказыванию ставит в соответствие новое высказывание,
значение которого противоположно исходному.
Другое название: логическое отрицание.
Обозначения: НЕ,
¬,¯ .
Таблица истинности:
А
Ā
0
1
1
0
Графическое представление
Ā
A
Логические операции имеют следующий приоритет:
инверсия, конъюнкция, дизъюнкция.
6.
Порядок выполнения операций1) скобки
2) НЕ - инверсия
3) И - конъюнкция
4) ИЛИ- дизъюнкция
5
6
1 3
4
2
X A B (A B B )
7.
Пример построения таблицы истинностиАVA&B
Приоритет операций: &, V
A
B
A&B
AVA&B
0
0
0
0
0
1
0
0
1
0
0
1
1
1
1
1
8.
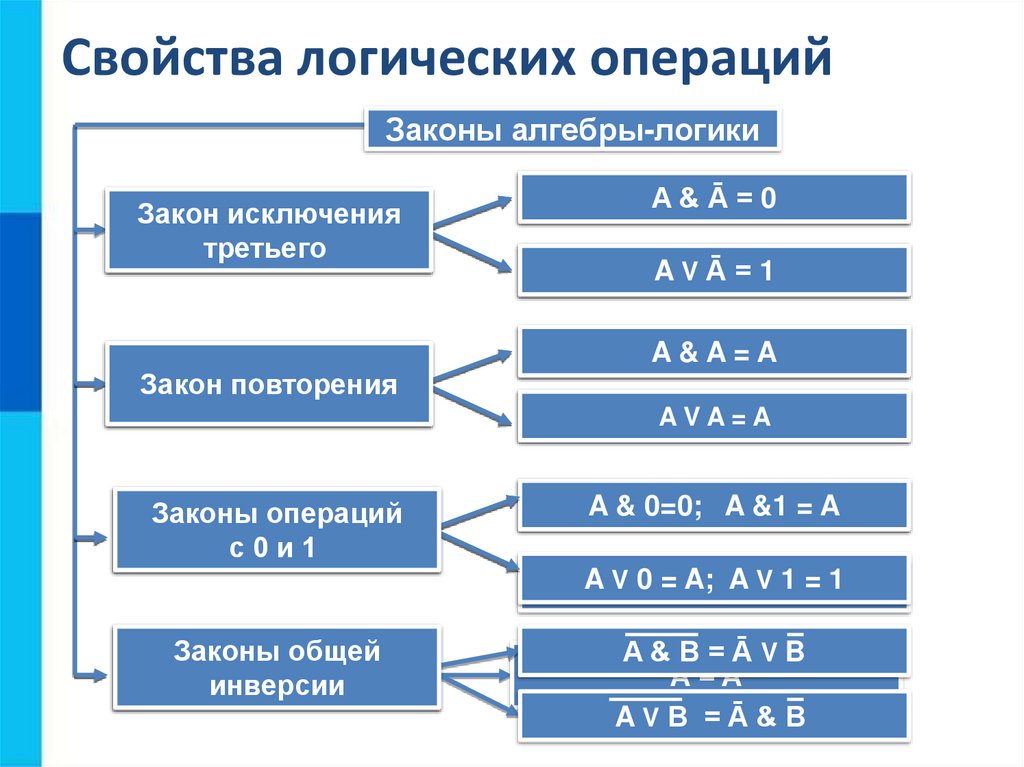
Свойства логических операцийЗаконы алгебры-логики
Закон исключения
Переместительный
третьего
A&
AB
&=
ĀB
=&
0A
AV
AB
VĀ
=B
=V
1A
(A & B) &
AC
& =AA= &
A ( B & C)
Закон
Сочетательный
повторения
(A V B) V
AC
VA
=A=VA( B V C)
Законы операций
Распределительный
с0и1
A&(B
A&
VC)=
0=0;(A&B)
A &1V =(A&C)
A
V 0 ==A;(AA
V1=1
AVA
(B&C)
VB)&(A
VC)
Закон
Законы
двойного
общей
отрицания
инверсии
A&B=ĀVB
Ā=A
AVB =Ā&B
9.
Доказательство законаРаспределительный закон для логического сложения:
A v (B & C) = (A v B) & (A v C).
A
B
C
0
B&C
0
A v (B & C)
0
AvB
0
0
0
0
0
1
0
0
0
1
0
0
1
1
0
1
0
1
0
1
1
0
0
0
1
0
1
1
1
0
1
1
1
0
0
1
A v C (A v B) & (A v C)
0
0
1
0
1
0
1
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
Складываем А и (В&С) и выводим результат.
1
1
10.
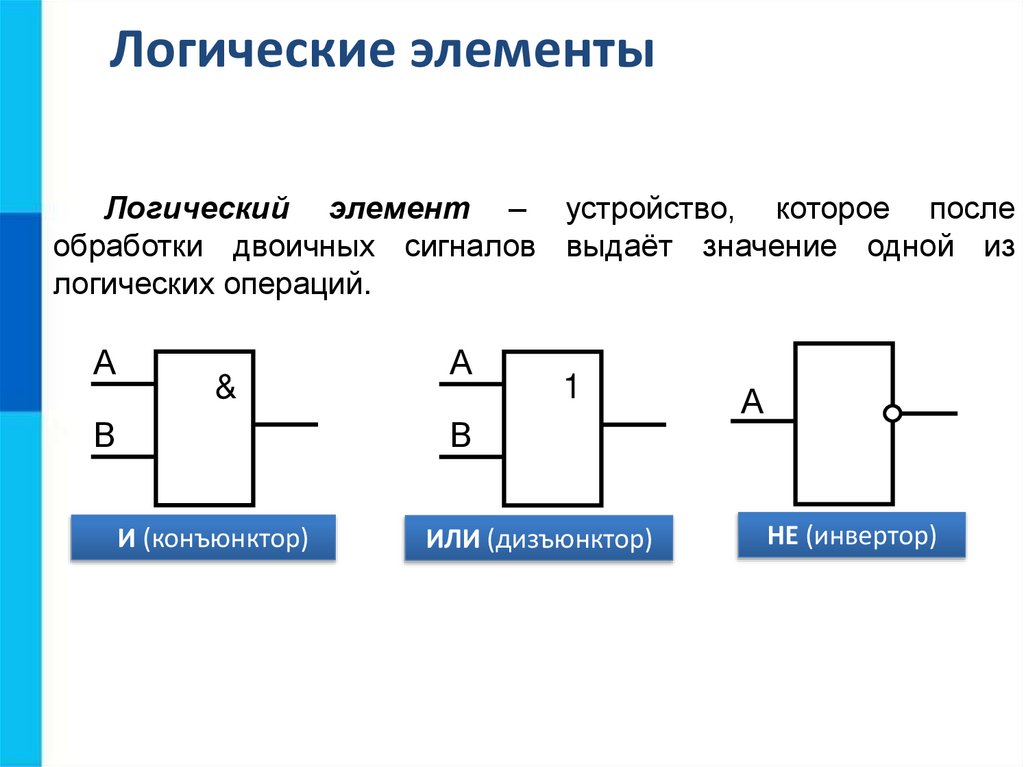
Логические элементыЛогический элемент – устройство, которое после
обработки двоичных сигналов выдаёт значение одной из
логических операций.
А
&
В
А
1
В
И (конъюнктор)
ИЛИ (дизъюнктор)
А
НЕ (инвертор)
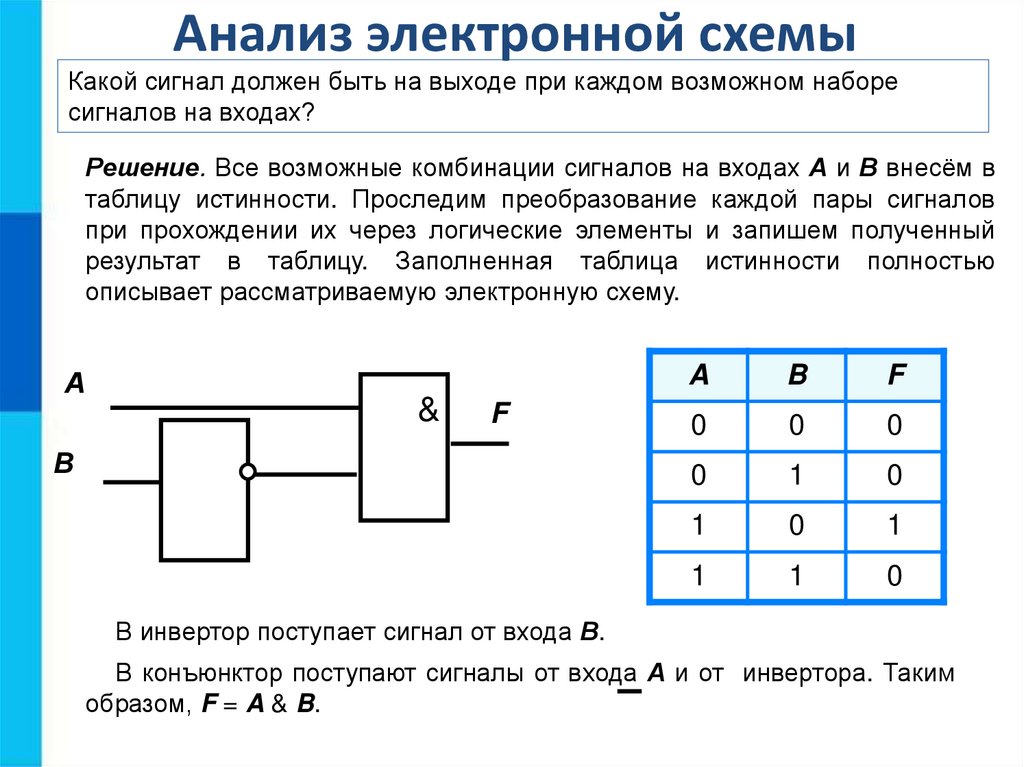
11. Анализ электронной схемы
Какой сигнал должен быть на выходе при каждом возможном наборесигналов на входах?
Решение. Все возможные комбинации сигналов на входах А и В внесём в
таблицу истинности. Проследим преобразование каждой пары сигналов
при прохождении их через логические элементы и запишем полученный
результат в таблицу. Заполненная таблица истинности полностью
описывает рассматриваемую электронную схему.
А
&
F
В
A
B
F
0
0
0
0
1
0
1
0
1
1
1
0
В инвертор поступает сигнал от входа В.
В конъюнктор поступают сигналы от входа А и от инвертора. Таким
образом, F = A & B.
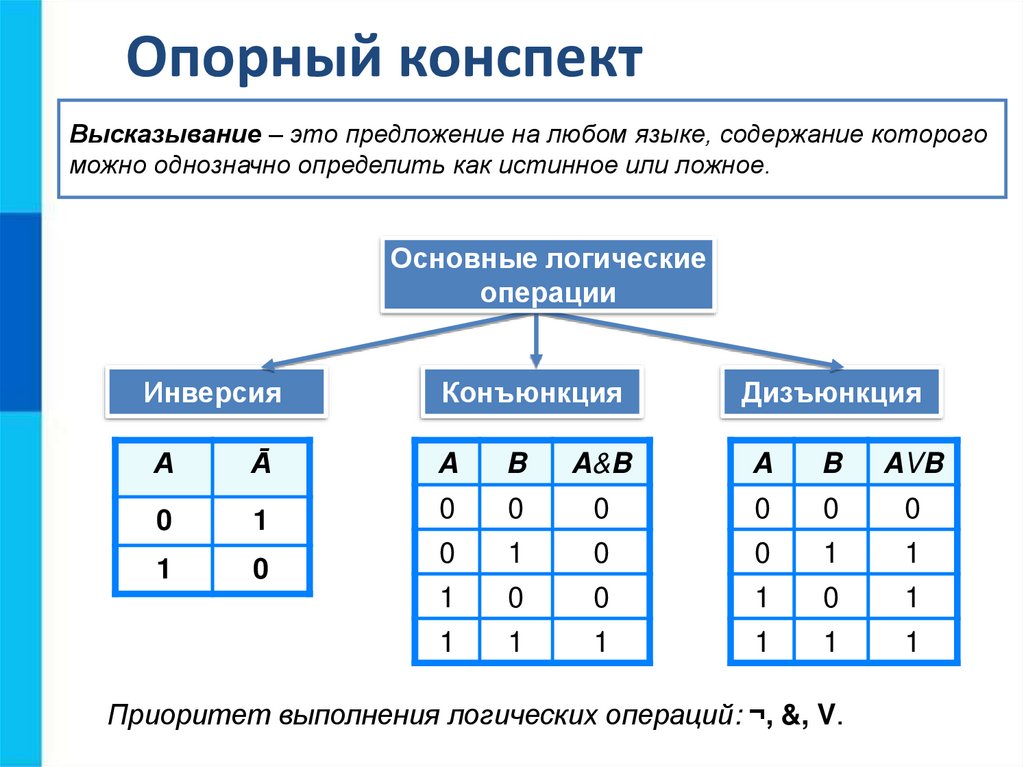
12.
Опорный конспектВысказывание – это предложение на любом языке, содержание которого
можно однозначно определить как истинное или ложное.
Основные логические
операции
Инверсия
Конъюнкция
Дизъюнкция
А
Ā
A
B
A&B
A
B
AVB
0
1
0
0
0
0
0
0
1
0
0
1
0
0
1
1
1
0
0
1
0
1
1
1
1
1
1
1
Приоритет выполнения логических операций: ¬, &, V.







 informatics
informatics