Раздел 1. Тема 1.4. Геометрические построения

1.

Раздел 1
Тема 1.4. Геометрические
построения
1)Деление отрезков и
углов
2) Деление окружности
3) Практическая работа

2.

Тема 1.4. Геометрические построения
• Геометрическим построением называют способ решения задачи, при котором
ответ получают в основном графическим путём без каких - либо математических
расчетов.
• Чтобы построить какой-либо чертеж или выполнить плоскостную разметку
заготовки детали перед ее обработкой, необходимо осуществить ряд
графических операций – геометрических построений
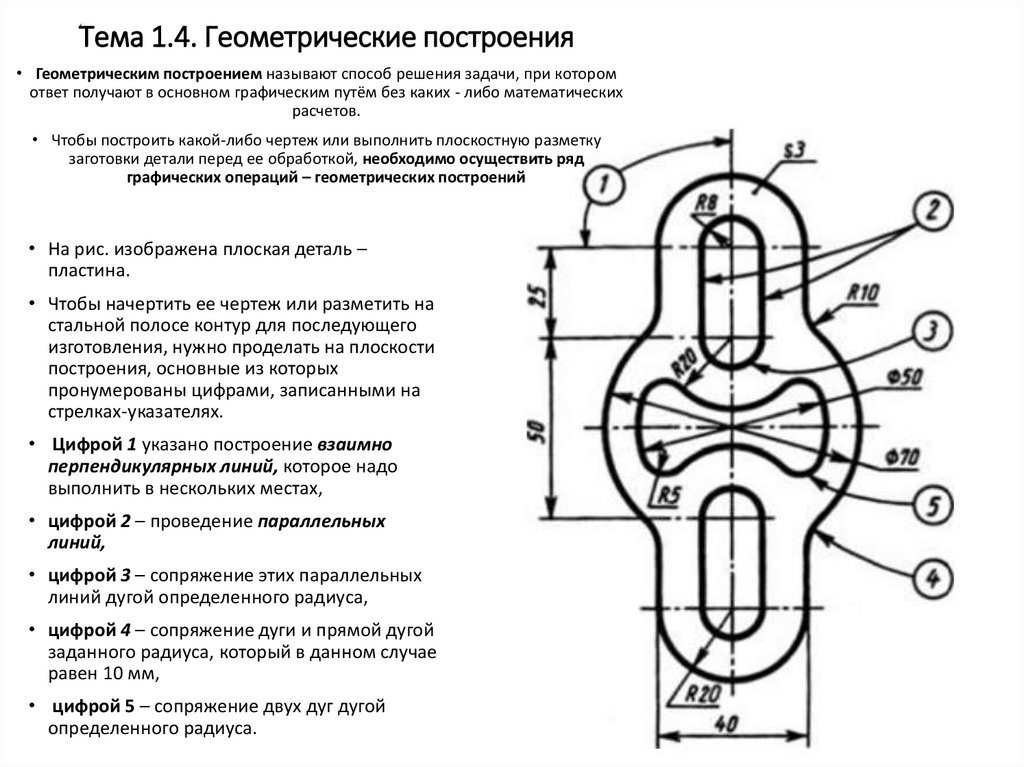
• На рис. изображена плоская деталь –
пластина.
• Чтобы начертить ее чертеж или разметить на
стальной полосе контур для последующего
изготовления, нужно проделать на плоскости
построения, основные из которых
пронумерованы цифрами, записанными на
стрелках-указателях.
• Цифрой 1 указано построение взаимно
перпендикулярных линий, которое надо
выполнить в нескольких местах,
• цифрой 2 – проведение параллельных
линий,
• цифрой 3 – сопряжение этих параллельных
линий дугой определенного радиуса,
• цифрой 4 – сопряжение дуги и прямой дугой
заданного радиуса, который в данном случае
равен 10 мм,
• цифрой 5 – сопряжение двух дуг дугой
определенного радиуса.

3.

Тема 1.4. Геометрические
построения
а
б
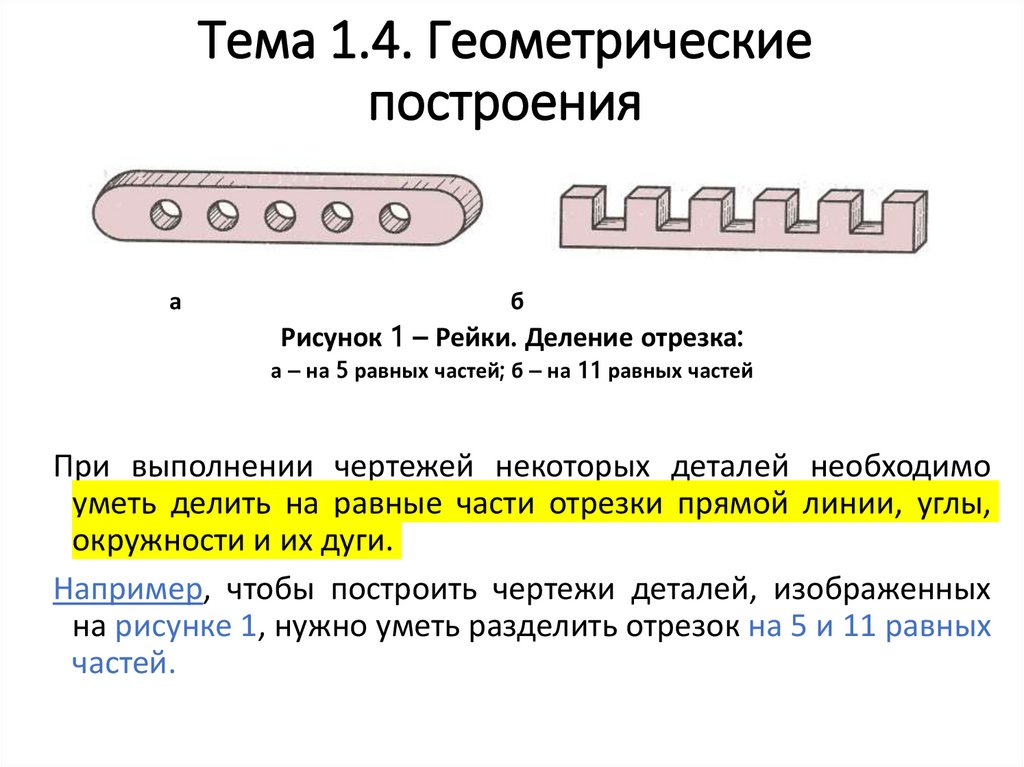
Рисунок 1 – Рейки. Деление отрезка:
а – на 5 равных частей; б – на 11 равных частей
При выполнении чертежей некоторых деталей необходимо
уметь делить на равные части отрезки прямой линии, углы,
окружности и их дуги.
Например, чтобы построить чертежи деталей, изображенных
на рисунке 1, нужно уметь разделить отрезок на 5 и 11 равных
частей.

4.

Деление отрезка на 2,4,8 и т.д. частей
1) Из точек A, B отрезка AB проводим
дуги радиусом R, по величине
превышающим половину отрезка
AB. Они пересекутся в точках C,D.
2) Прямая, проходящая через точки C,
D разделит отрезок в точке K на две
равные части.
Вывод:
АК=КВ,
АВ СD
Пластина с пазами применение
способа деления отрезка

5.

Проведение
перпендикулярной
прямой
• Проведение
перпендикулярной
прямой-задача
решена с помощью
линейки и угольника
Вывод:
МN A

6.

Деление отрезка прямой
на равные части
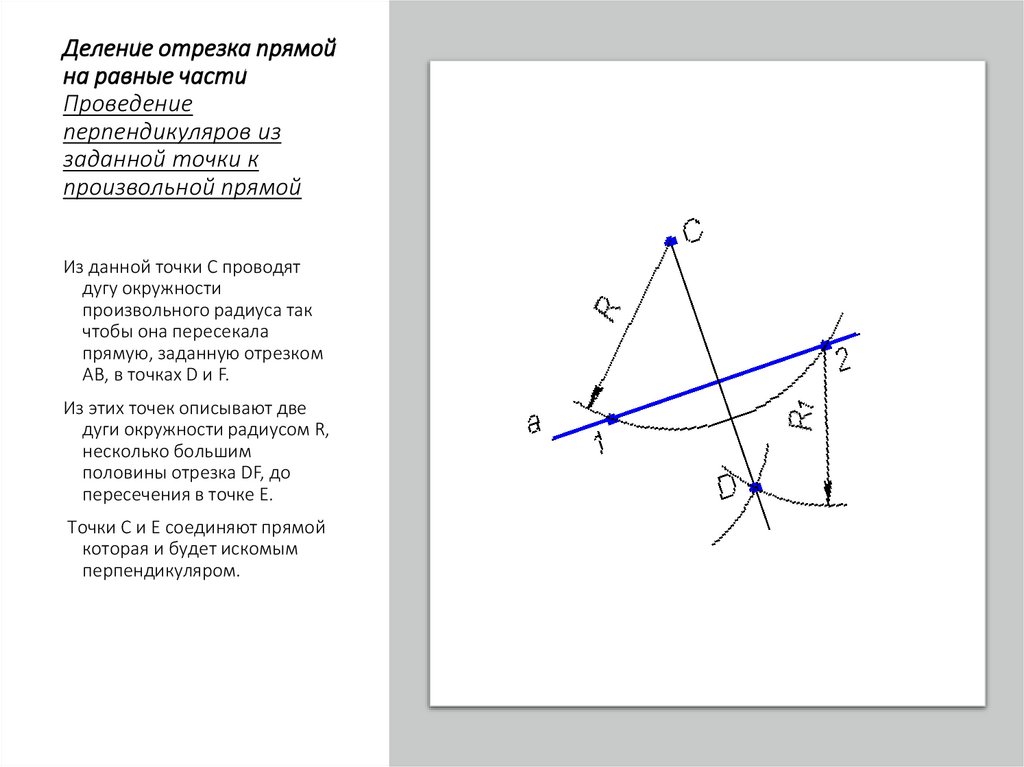
Проведение
перпендикуляров из
заданной точки к
произвольной прямой
Из данной точки С проводят
дугу окружности
произвольного радиуса так
чтобы она пересекала
прямую, заданную отрезком
АВ, в точках D и F.
Из этих точек описывают две
дуги окружности радиусом R,
несколько большим
половины отрезка DF, до
пересечения в точке Е.
Точки С и Е соединяют прямой
которая и будет искомым
перпендикуляром.

7.

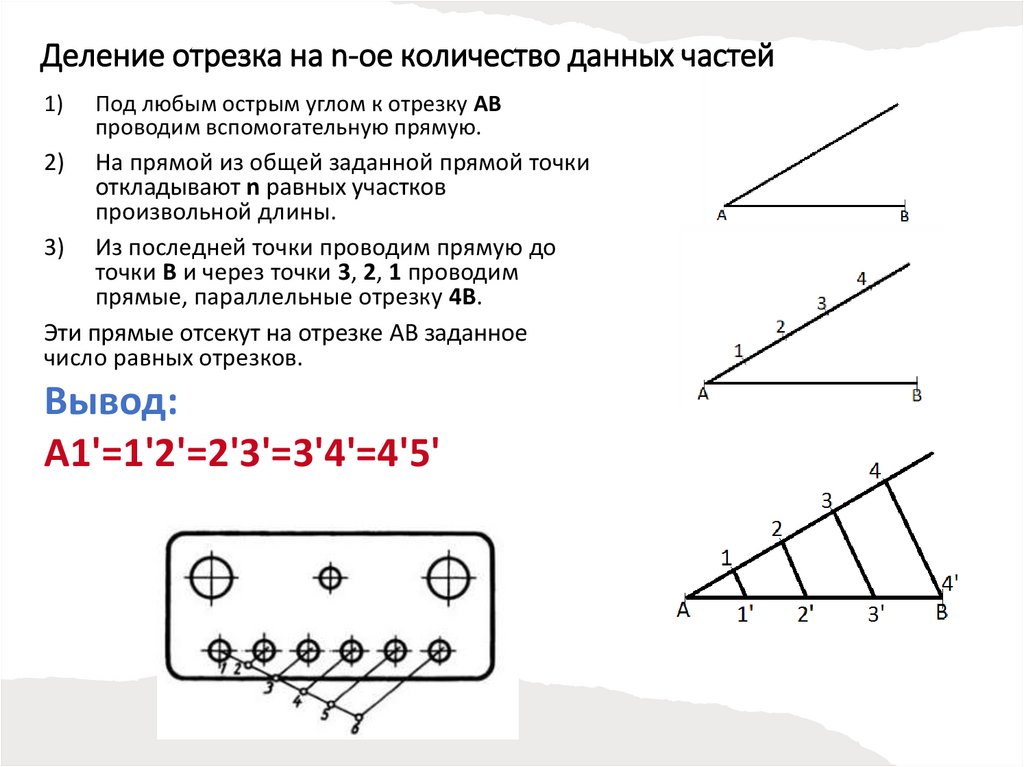
Деление отрезка на n-ое количество данных частей
1)
Под любым острым углом к отрезку AB
проводим вспомогательную прямую.
2)
На прямой из общей заданной прямой точки
откладывают n равных участков
произвольной длины.
3) Из последней точки проводим прямую до
точки B и через точки 3, 2, 1 проводим
прямые, параллельные отрезку 4B.
Эти прямые отсекут на отрезке AB заданное
число равных отрезков.
Вывод:
А1'=1'2'=2'3'=3'4'=4'5'

8.

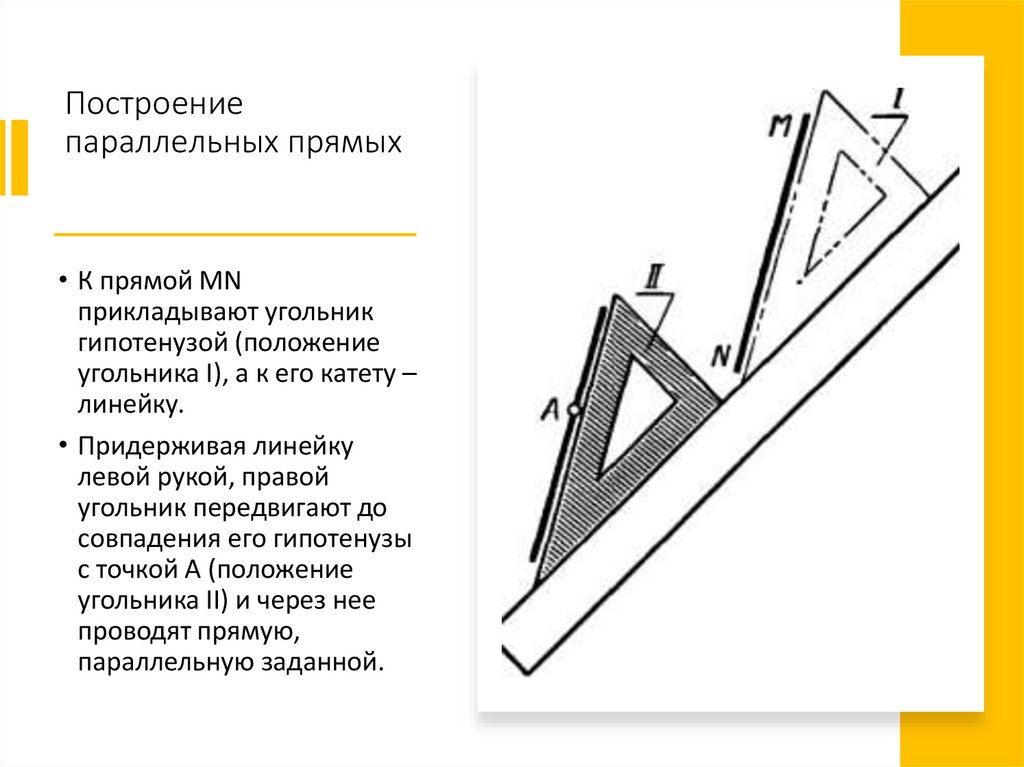
Построение
параллельных прямых
• К прямой MN
прикладывают угольник
гипотенузой (положение
угольника I), а к его катету –
линейку.
• Придерживая линейку
левой рукой, правой
угольник передвигают до
совпадения его гипотенузы
с точкой A (положение
угольника II) и через нее
проводят прямую,
параллельную заданной.

9.

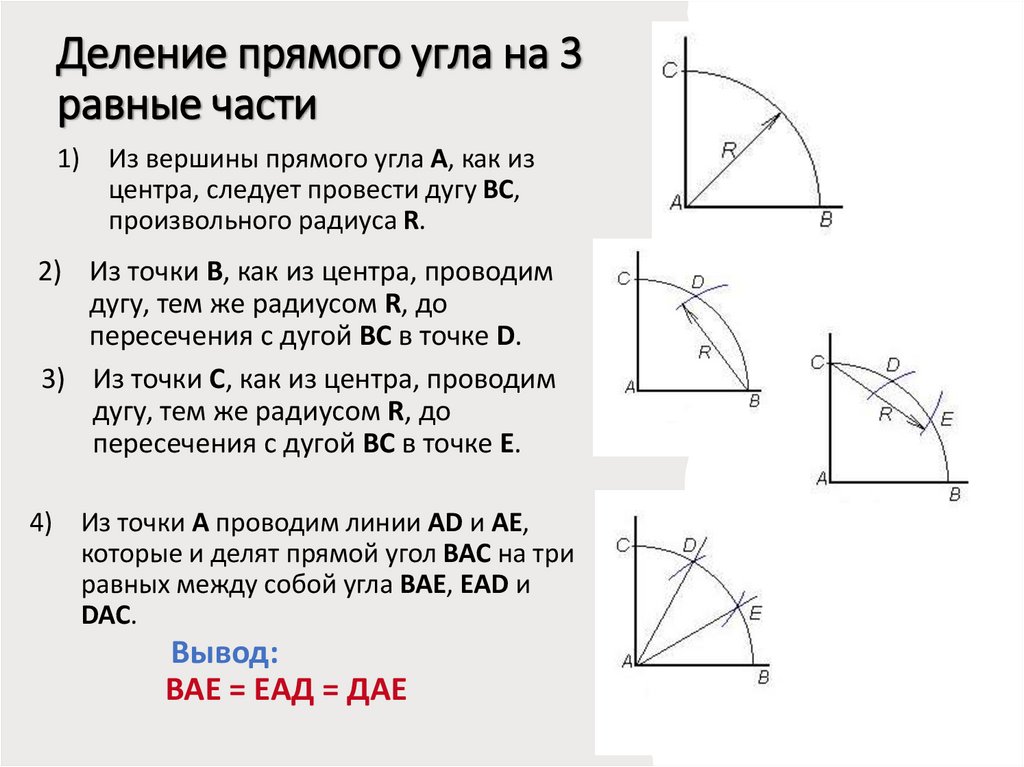
Деление прямого угла на 3
равные части
1) Из вершины прямого угла А, как из
центра, следует провести дугу BC,
произвольного радиуса R.
2) Из точки B, как из центра, проводим
дугу, тем же радиусом R, до
пересечения с дугой BC в точке D.
3) Из точки C, как из центра, проводим
дугу, тем же радиусом R, до
пересечения с дугой BC в точке E.
4) Из точки А проводим линии AD и AE,
которые и делят прямой угол BAC на три
равных между собой угла BAE, EAD и
DAC.
Вывод:
ВАЕ = ЕАД = ДАЕ

10.

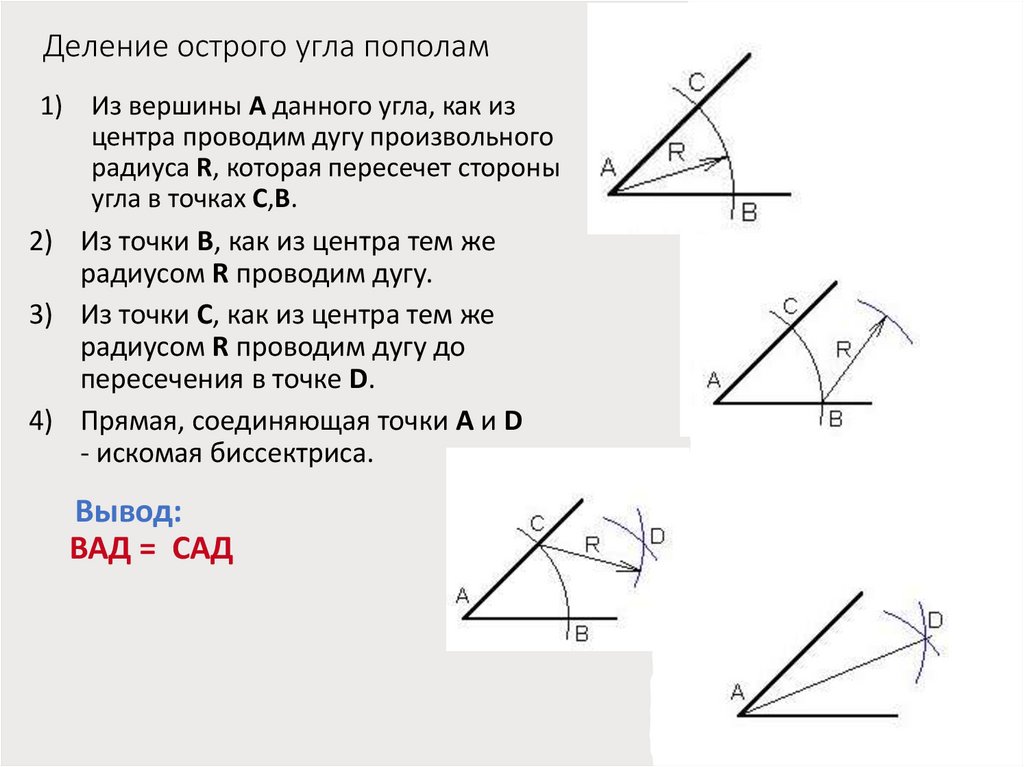
Деление острого угла пополам
1) Из вершины А данного угла, как из
центра проводим дугу произвольного
радиуса R, которая пересечет стороны
угла в точках C,B.
2) Из точки B, как из центра тем же
радиусом R проводим дугу.
3) Из точки С, как из центра тем же
радиусом R проводим дугу до
пересечения в точке D.
4) Прямая, соединяющая точки A и D
- искомая биссектриса.
Вывод:
ВАД = САД

11.

Деление окружности
Рисунок 1 – Прокладки, плашки , гайки
Для построения чертежей некоторых деталей
необходимо уметь делить окружность на равные
части и строить правильные многоугольники.

12.

• Чтобы разделить окружность радиуса R на 3 равные части, из точки пересечения центровой
линии с окружностью (например, из точки А) описывают как из центра дополнительную дугу
радиусом R. Получают точки 2 и 3. Точки 1, 2, 3 делят окружность на три равные части.
• Для деления окружности на шесть равных частей надо из точек 1 и 4 пересечения центровой
линии с окружностью сделать на окружности по две засечки радиусом R , равным радиусу
окружности. Соединив полученные точки отрезками прямых, получим правильный
шестиугольник.
• Чтобы разделить окружность на двенадцать равных частей, надо окружность поделить на
четыре части взаимно перпендикулярными диаметрами. Приняв точки пересечения
диаметров с окружностью А , В , С , D за центры, величиной радиуса проводят четыре дуги до
пересечения с окружностью. Полученные точки 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 и
точки А , В , С , D разделяют окружность на двенадцать равных частей

13.

14.

Деление окружности на 4 и 8 одинаковых частей
Проводим окружность с горизонтальной и вертикальной осями, которые делят её на 4-ре равные части.
• Чтобы разделить окружность на 8 равных частей, дуги, равные четвертой части окружности, делят
пополам. Для этого из двух точек, ограничивающих четверть дуги, как из центров радиусов окружности
выполняют засечки за ее пределами. Полученные точки соединяют с центром окружностей и на пересечении
их с линией окружности получают точки, делящие четвертные участки пополам, т. е. получают восемь равных
участков окружности

15.

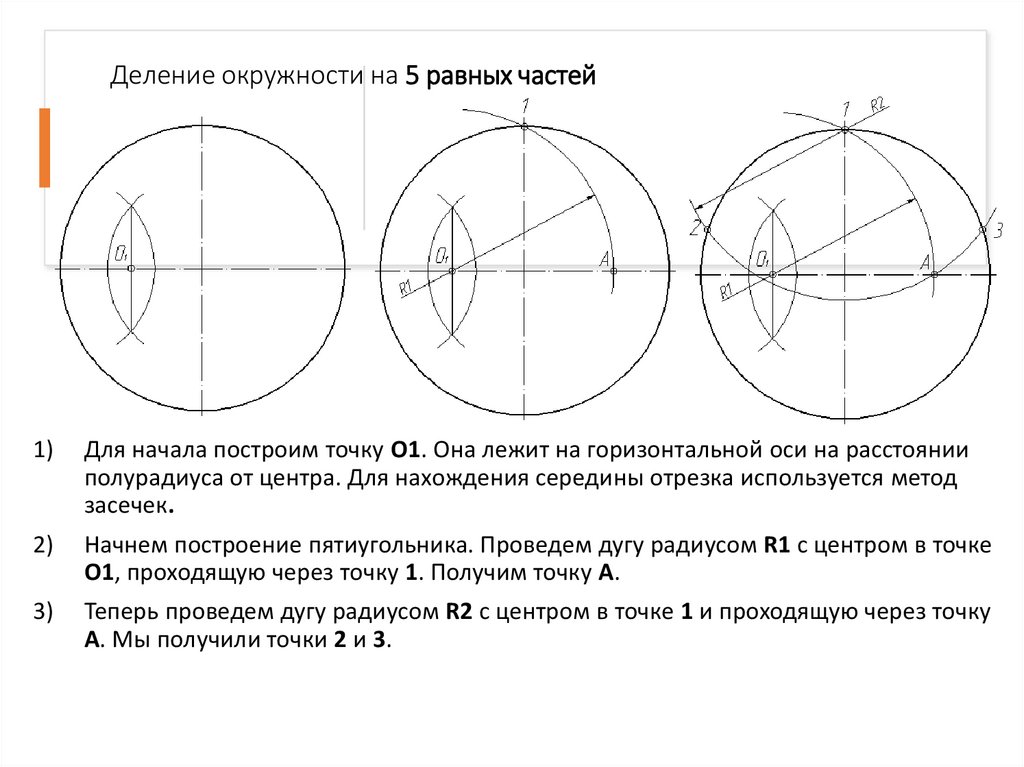
Деление окружности на 5 равных частей
1)
Для начала построим точку О1. Она лежит на горизонтальной оси на расстоянии
полурадиуса от центра. Для нахождения середины отрезка используется метод
засечек.
2)
Начнем построение пятиугольника. Проведем дугу радиусом R1 с центром в точке
О1, проходящую через точку 1. Получим точку А.
3)
Теперь проведем дугу радиусом R2 с центром в точке 1 и проходящую через точку
А. Мы получили точки 2 и 3.

16.

4)
Деление
окружности на 5 5)
равных частей
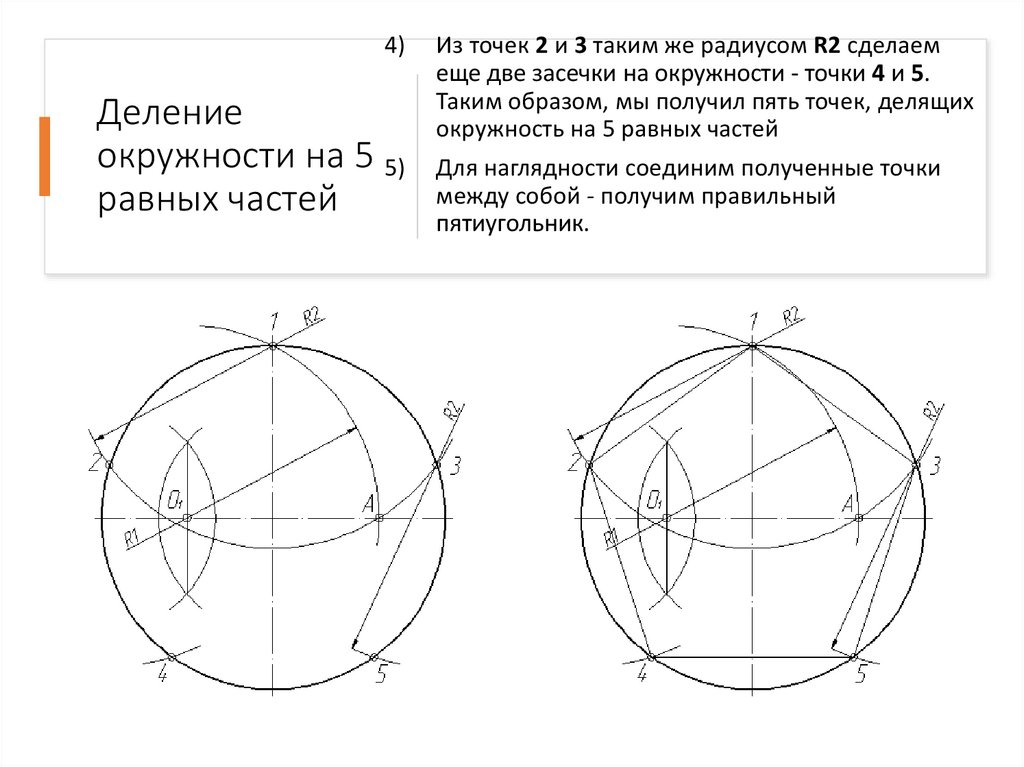
Из точек 2 и 3 таким же радиусом R2 сделаем
еще две засечки на окружности - точки 4 и 5.
Таким образом, мы получил пять точек, делящих
окружность на 5 равных частей
Для наглядности соединим полученные точки
между собой - получим правильный
пятиугольник.

17.

Деление окружности на 7
равных частей
1)
3)
4)
5)
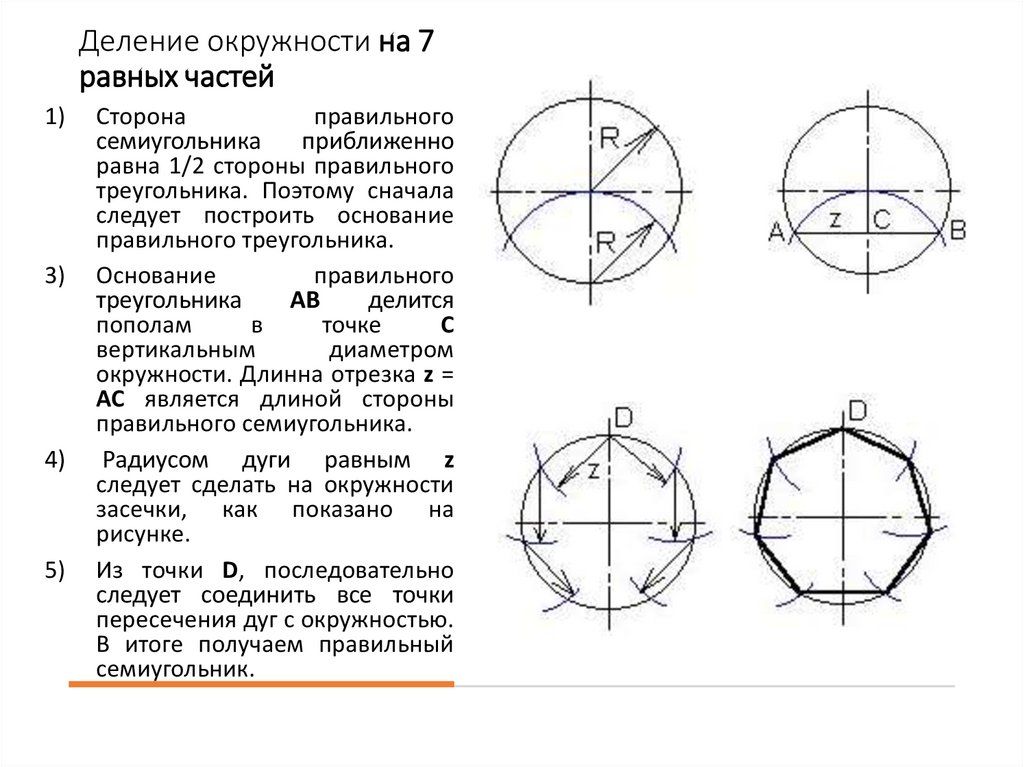
Сторона
правильного
семиугольника
приближенно
равна 1/2 стороны правильного
треугольника. Поэтому сначала
следует построить основание
правильного треугольника.
Основание
правильного
треугольника
AB
делится
пополам
в
точке
С
вертикальным
диаметром
окружности. Длинна отрезка z =
AC является длиной стороны
правильного семиугольника.
Радиусом дуги равным z
следует сделать на окружности
засечки, как показано на
рисунке.
Из точки D, последовательно
следует соединить все точки
пересечения дуг с окружностью.
В итоге получаем правильный
семиугольник.

18.

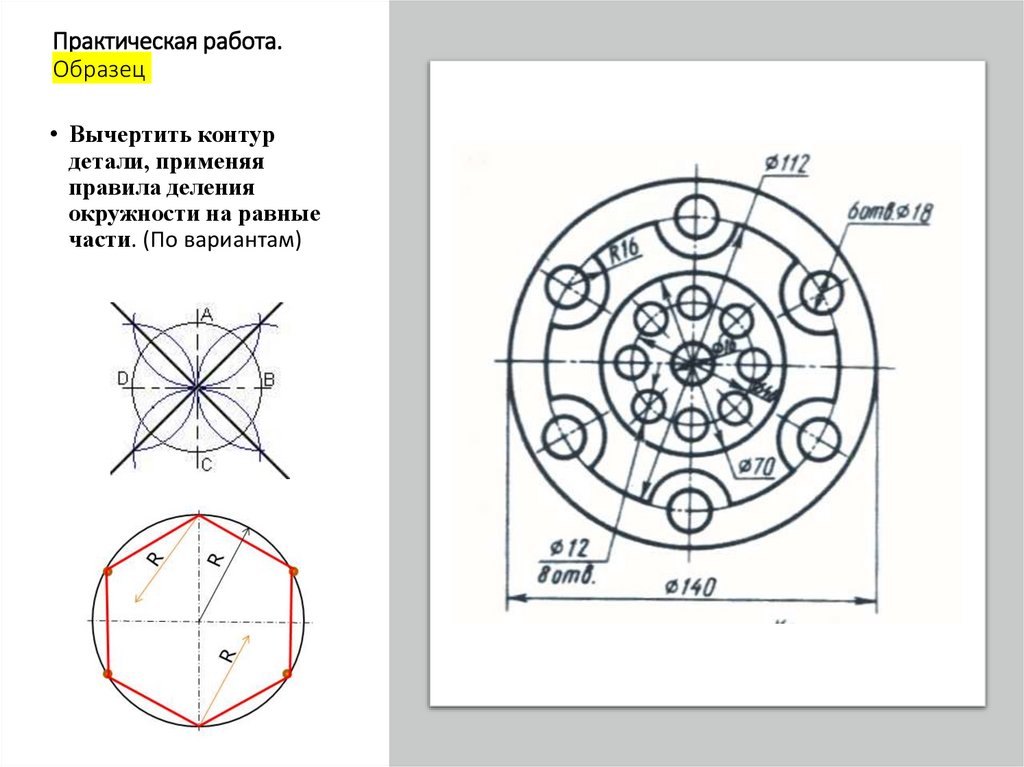
Практическая работа.
Образец
• Вычертить контур
детали, применяя
правила деления
окружности на равные
части. (По вариантам)