Similar presentations:
Проектирование баз данных. Анализ стоимости операций
1.
Дисциплина«Проектирование баз данных»
Маркова Ирина Васильевна,
начальник управления информатизации
markova@miit.ru
2. Стратегия эвристической обработки запросов
Раздел 2.Компиляция и оптимизация. Анализ стоимости операций.
Стратегия эвристической обработки запросов
Улучшение логического плана запроса
Улучшению качества логических планов способны послужить многие из алгебраических
законов, рассмотренных ранее, но наиболее широкое применение в оптимизаторах
запросов находят следующие подходы:
a)
Продвижение операторов выбора «вниз» по дереву до максимально «глубокого»
уровня. Если условие выбора представляет собой конъюнкцию (AND) нескольких
частных условий, его можно расщепить, чтобы продвигать каждый оператор отдельно.
b)
При определенных обстоятельствах целесообразнее вначале продвинуть оператор
выбора «вверх» по дереву выражений, и только затем – «вниз».
c)
Продвижение существующих операторов проекции «вниз» по дереву или добавление
новых операторов, что, как и в случае с операторами выбора, требует тщательного
анализа.
d)
Изъятие операторов удаления кортежей-дубликатов или перемещение в требуемые
позиции дерева.
e)
Сочетание определенных операторов выбора с расположенными ниже по дереву
операторами декартова произведения с целью замены пары операций одной
операцией соединения посредством равенства (equijoin).
2
3. Группирование ассоциативно-коммутативных операторов
Раздел 2.Компиляция и оптимизация. Анализ стоимости операций.
Группирование ассоциативно-коммутативных операторов
a)
Традиционными синтаксическими анализаторами не создаются деревья с вершинами,
обладающими неограниченно большим количеством дочерних вершин, – обычно
операторы пребывают только в унарной или бинарной форме.
b)
Операторы, для которых справедливы ассоциативный и коммутативный законы,
способны обладать произвольным количеством операндов.
c)
Группирование соседних вершин дерева, представляющих одноименные
ассоциативно-коммутативные операторы, в единую вершину со многими дочерними
вершинами (естественное соединение, объединение и пересечение).
d)
Операторы естественного и Θ-соединения допускают возможность взаимного
сочетания при выполнении следующих условий :
операторы естественного соединения заменены Θ-соединениями с условиями
равенства одноименных атрибутов отношений-аргументов;
при переходе от естественного соединения к Θ-соединению с помощью
оператора проекции удаляются дубликаты атрибутов;
условия операторов Θ- соединения ассоциативны.
e)
Оператор декартова произведения, интерпретируемый как частный случай
естественного соединения, может сочетаться с операторами соединения, если они
представлены смежными вершинами дерева выражений.
3
4. Анализ стоимости операций
Раздел 2.Компиляция и оптимизация. Анализ стоимости операций.
Анализ стоимости операций
При подсчете стоимости всех возможных физических планов, которые удается построить
на основе логического плана, учитывается следующая информация:
порядок следования и группирования одноименных, ассоциативно-коммутативных
операторов;
алгоритм реализации каждого оператора логического плана;
дополнительные операторы, необходимые для реализации физического плана, но
отсутствующие в явном виде в логическом плане;
способ передачи значений атрибутов от одного оператора другому.
4
5. Оценка результатов промежуточных отношений
Раздел 2.Компиляция и оптимизация. Анализ стоимости операций.
Оценка результатов промежуточных отношений
Введем обозначения:
k R – кардинальность R;
bR – количество блоков, требуемых для хранения R;
aR – количество различных значений атрибута а в R;
V t R – размер кортежа в R;
Vb – размер блока;
k Rb – коэффициент блокирования.
Цель прогнозирования размеров промежуточных отношений – не получение точных
оценок, а упрощение выбора физического плана по принципу: минимальная стоимость –
наилучший план.
Физический план выбирается таким образом, чтобы свести к минимуму примерную
стоимость выполнения запроса.
5
6. Оценка результата проекции
Раздел 2.Компиляция и оптимизация. Анализ стоимости операций.
Оценка результата проекции
Проекция относится к операторам, объем результата выполнения которых вычисляется
точно. Изменение объема может быть обусловлено только изменением структуры.
Пусть имеется:
R ( a , b, c )
a,b - целые числа;
с - строка (100 байт);
заголовок строки – 12 байт;
Vt R 4 4 100 12 120 ;
Vb 1024 ;
k Rb 8 ;
k R 10000 ;
bR 1250 .
6
7. Оценка результата проекции (пример)
Раздел 2.Компиляция и оптимизация. Анализ стоимости операций.
Оценка результата проекции (пример)
a) Рассмотрим оператор S a b ,c ( R )
Vt S 4 100 12 116 ;
k Rb 8 ;
k S 10000 ;
bS 1250 .
Вывод: объём отношения практически не изменился.
b) Рассмотрим оператор
U a ,b ( R )
VtU 8 12 20 ;
kU 10000 ;
kUb 50(1000 : 20 50) ;
bU 10000 : 50 200 .
Вывод: в результате применения
в 6 раз.
объём результирующего отношения снизился более, чем
7
8. Оценка результата выборки
Раздел 2.Компиляция и оптимизация. Анализ стоимости операций.
Оценка результата выборки
В этом случае размер отдельного кортежа сохраняется, количество кортежей
уменьшается.
Оператор
Оценка
Примечание
1. равенство
const
kS
kR
aR
Оценка точна, если значения a
равновероятны. Эта формула
остаётся наилучшей оценкой «в
среднем», даже если
распределение не равномерное, но
все значения a одинаково часто
упоминаются в запросах, в которых
адресуется атрибут a. Ещё более
точные оценки получаются, если
СУБД обладает соответствующей
статистикой и гистограммами.
2. условие выбора
основано на
неравенстве
kS
kR
3
Эмпирическая оценка.
S a c (R)
S a c (R)
8
9. Оценка результата выборки (продолжение)
Раздел 2.Компиляция и оптимизация. Анализ стоимости операций.
Оценка результата выборки (продолжение)
а )k S k R
3. S a c (R)
4. Условие F – ‘AND’
конъюнкция
(цепочка вложенных
операторов, каждый
из которых
проверяет один
конъюнкт)
в )k S
Исходя из эвристики, что
k R ( а R 1)
aR
1
aR
часть всех кортежей R не
удовлетворяют условию.
k S k R k ( F ( R )) , где
k ( F ( R ))
1
3
1
,
1
a R
k F1ORF2 ( R ) n(1 (1
5. Условие F – ‘OR’
где :
kR n
S F1ORF2 ( R )
k F1 ( R ) т1
m1
m
)(1 2 )),
n
n
k F2 ( R ) т2
Коэффициент избирательности
k( F ( R )) определяется всеми
частными операторами.
m1
– доля кортежей, не
n
удовлетворяющих F1 ,
1
m2
– доля кортежей, не
n
удовлетворяющих F2 .
1
F1 и F2 – независимые условия.
9
10. Оценка результата выборки (примеры)
Раздел 2.Компиляция и оптимизация. Анализ стоимости операций.
Оценка результата выборки (примеры)
a) Пусть есть отношение R ( a , b, c ) и оператор S a 10andb 20 ( R)
kR 10000 ;
aR 50 .
Оценка: k S
kR
10000
67 .
a R 3 50 3
b) Частный случай (внутреннее противоречие): пусть есть отношение R ( a , b, c ) и
оператор S a 10 ANDa 20 ( R) , тогда формально k S
kR
10000
67 , однако
a R 3 50 3
очевидно, что k S .
На практике оптимизатор учитывает множество правил, удовлетворяющих различным
частным случаям. В данном случае оптимизатор должен был применить правило сведения
условия к false.
10
11. Оценка результата выборки (продолжение)
Раздел 2.Компиляция и оптимизация. Анализ стоимости операций.
Оценка результата выборки (продолжение)
c)
Пусть есть отношение R( a, b) и оператор S a 10ORb 20 ( R)
kR 10000 ;
aR 50 .
kR kR
200 3333 3533 .
aR 3
Если принять во внимание, что условия a 10 и b 20 – независимы, то
Оценка: k S
k S n(1 (1
m1
m
200
3333
)(1 2 )) 10000(1 (1
)(1
)) 3466
n
n
10000
10000
В данном случае они мало различаются и не способны повлиять на решение о предпочтении
той или иной оценки.
11
12. Оценка результата соединения
Раздел 2.Компиляция и оптимизация. Анализ стоимости операций.
Оценка результата соединения
Рассмотрим естественное соединение, все остальные варианты соединения могут
трактоваться в соответствии со следующими правилами:
a) размер итогового отношения для соединения на основе равенства после изменения
имен атрибутов вычисляется так же, как и в случае естественного соединения;
b) размер итогового отношения для -соединения оценивается как операция
декартового соединения с последующей выборкой при выполнении следующих
условий:
- количество кортежей в итоговом отношении равно произведению кортежейоперандов;
- количество кортежей, удовлетворяющих условию равенства, можно оценить,
используя приемы для прогнозирования результатов естественного
соединения;
- условия с неравенствами двух атрибутов (вида R.a<S.b) следует трактовать как
неравенства вида R.a c (эвристика в данном случае: коэффициент
избирательности
1
1
– для «сложного» условия и – для простого) .
3
2
12
13. Оценка результата соединения (продолжение)
Раздел 2.Компиляция и оптимизация. Анализ стоимости операций.
Оценка результата соединения (продолжение)
Пусть необходимо выполнить естественное соединение R( X , Y ) S (Y , Z ) .
Возможные варианты связи значений R.Y и S.Y :
a) {R.Y } {S .Y } , соответственно k S 0 ;
b)
S.Y – первичный ключ, R.Y – внешний ключ, соответственно каждый кортеж R
соединяется с единственным кортежем S: k R S k R ;
c) большинство кортежей R и S могут иметь одинаковые значения Y, тогда
k R S k R k S .
13
14. Оценка результата соединения (допущения)
Раздел 2.Компиляция и оптимизация. Анализ стоимости операций.
Оценка результата соединения (допущения)
Упрощающие допущения:
1. принадлежность одного множества значений совпадающего атрибутов
другому:
если Y общий атрибут отношений и S, тогда значения Y в каждом отношении
выбираются в порядке их следования в списке ( y1 , y2 , y3 ,...) , как следствие,
если YR YS , то каждое значение атрибута R.Y будет присутствовать в S.Y ,
т.е. {R.Y } {S .Y } .
2. сохранность множества значений несовпадающих атрибутов:
при соединении отношения R c другим отношением S множество значений
атрибута А, не являющегося общим, не сокращается, т.е. A r (R ) и A r (S )
, то { A( R S ) } { AR } (порядок соединения не важен { A( S R ) } { AR } .
14
15. Оценка результата соединения (один общий атрибут)
Раздел 2.Компиляция и оптимизация. Анализ стоимости операций.
Оценка результата соединения (один общий атрибут)
Принимая во внимание приведенные допущения, оценим размер R( X , Y ) S (Y , Z ) .
Пусть YR YS , тогда каждый кортеж из R может быть соединен с определённым кортежем
отношения S с вероятностью 1
YS
соединению с каждым кортежем R
, прогнозируемое число кортежей S , способных к
kS
YS
, т.к. кортежей в R – k R , то
k R S
kR kS
,
YS
Если же YS YR , то в силу симметрии:
k R S
kS kR
.
YR
Если учитывать оба случая в совокупности, то в качестве знаменателя следует выбрать
наибольшее значение из YR и YS :
k R S
kR kS
.
max( YR , YS )
15
16. Оценка результата соединения с одним общим атрибутом (пример)
Раздел 2.Компиляция и оптимизация. Анализ стоимости операций.
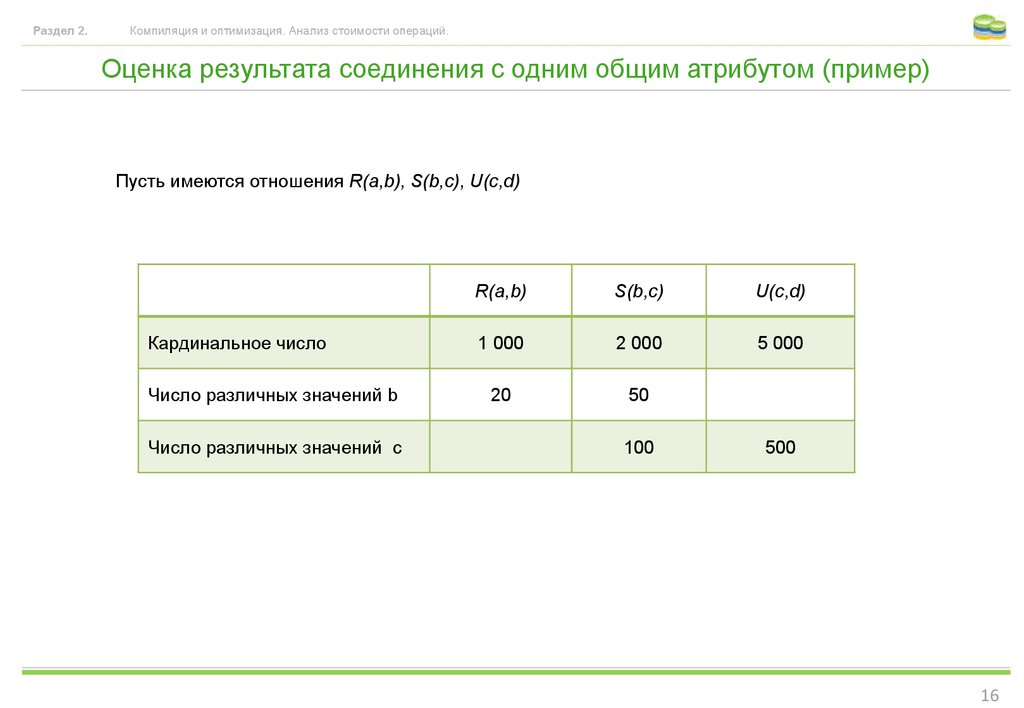
Оценка результата соединения с одним общим атрибутом (пример)
Пусть имеются отношения R(a,b), S(b,c), U(c,d)
Кардинальное число
Число различных значений b
Число различных значений c
R(a,b)
S(b,c)
U(c,d)
1 000
2 000
5 000
20
50
100
500
16
17. Оценка результата соединения с одним общим атрибутом (вариант 1)
Раздел 2.Компиляция и оптимизация. Анализ стоимости операций.
Оценка результата соединения с одним общим атрибутом (вариант 1)
1. Пусть необходимо вычислить R S U .
Сгруппируем ( R S ) U и получим:
k ( R S )
kR kS
1000 2000
40000 ,
max( bR , bS )
50
В соответствии с предположением о сохранности несовпадающих атрибутов
cR S cS 100 :
k ( R S ) U
.
k R S kU
40000 5000
400000
max( cR S , cU )
500
17
18. Оценка результата соединения с одним общим атрибутом (вариант 2)
Раздел 2.Компиляция и оптимизация. Анализ стоимости операций.
Оценка результата соединения с одним общим атрибутом (вариант 2)
2. Пусть необходимо вычислить R S U .
Сгруппируем теперь R ( S U ) и получим:
k( S U )
k R ( S U )
k S kU
2000 5000
20000 ,
max( cS , cU )
500
.
k R k S U
1000 20000
400000
max( bR , bS U )
50
Вывод: результат не зависит от порядка соединения.
18
19. Естественное соединение отношений с несколькими общими атрибутами
Раздел 2.Компиляция и оптимизация. Анализ стоимости операций.
Естественное соединение отношений с несколькими общими атрибутами
Рассмотрим случай, когда Y – не один атрибут, а несколько атрибутов, подлежащих
естественному соединению R( X , Y ) S (Y , Z ) .
Пусть имеется оператор R( x, y1 , y2 ) S ( y1 , y2 , z) .
Вероятность совпадения кортежей в R и S по y1 , если y1R y1S равна 1 / y1R . В силу
симметрии, если y1R y1S , то вероятность равна 1 / y1S .
В общем случае, вероятность того, что кортежи R и S согласуются в атрибуте y1
оценивается следующим образом:
1 / max( y1R , y1S ) .
Аналогично, для y 2 :
1 / max( y2R , y2S )
19
20. Естественное соединение отношений с несколькими общими атрибутами (продолжение)
Раздел 2.Компиляция и оптимизация. Анализ стоимости операций.
Естественное соединение отношений с несколькими общими атрибутами (продолжение)
Так как значения y1 и y 2 независимы, вероятность одновременного равенства – это
произведение двух указанных выше дробей. Поэтому с учетом общего количества различных
пар кортежей R и S, прогнозируемое число пар кортежей, совпадающих одновременно в
компонентах y1 и y 2 , равно:
k R S
kR kS
max( y1R , y1S ) max( y2R , y2S )
При произвольном количестве общих атрибутов в отношениях-операндах справедливо:
k R S
kR kS
,
)
y
,
y
max(
iS
iR
где 1 i n – количество общих атрибутов.
i
20
21. Естественное соединение отношений с несколькими общими атрибутами (пример)
Раздел 2.Компиляция и оптимизация. Анализ стоимости операций.
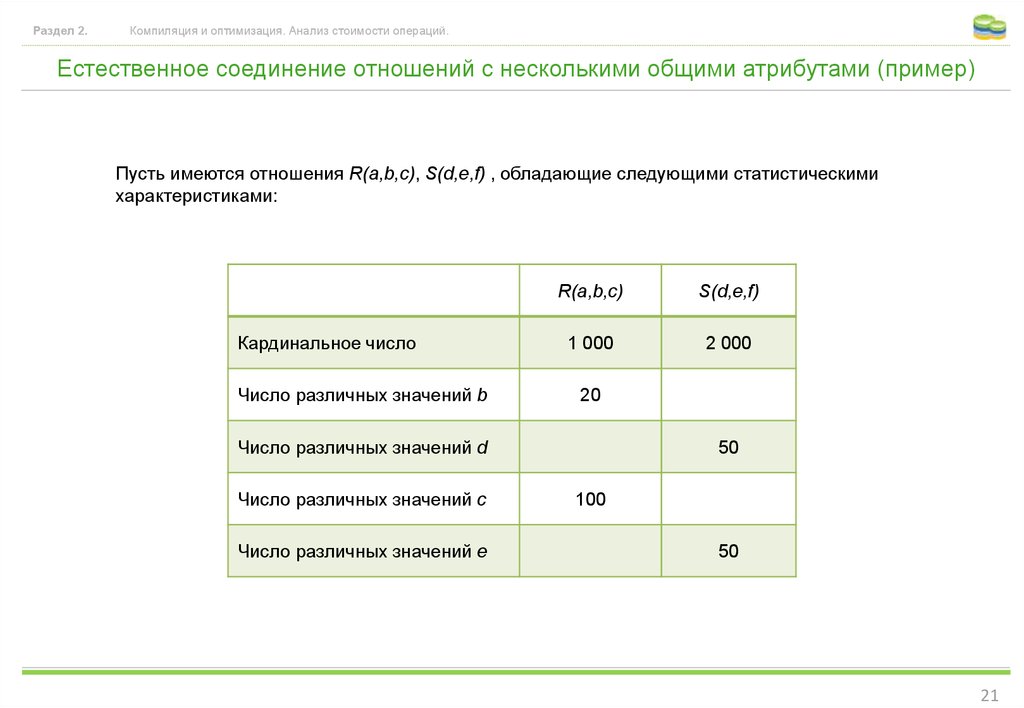
Естественное соединение отношений с несколькими общими атрибутами (пример)
Пусть имеются отношения R(a,b,с), S(d,e,f) , обладающие следующими статистическими
характеристиками:
Кардинальное число
Число различных значений b
R(a,b,с)
S(d,e,f)
1 000
2 000
20
Число различных значений d
Число различных значений c
Число различных значений e
50
100
50
21
22. Естественное соединение отношений с несколькими общими атрибутами (пример)
Раздел 2.Компиляция и оптимизация. Анализ стоимости операций.
Естественное соединение отношений с несколькими общими атрибутами (пример)
Пусть необходимо вычислить ( R ( a, b, c )
k R S
R . b S . dANDR. c S . e
S ( d , e, f ) .
kR kS
1000 2000 2000
400 .
max( y1R , y1S ) max( y2R , y2S )
50 100
5
Выводы, справедливые для естественного соединения, остаются в силе для любых
разновидностей соединения по равенству.
22
23. Соединение нескольких отношений
Раздел 2.Компиляция и оптимизация. Анализ стоимости операций.
Соединение нескольких отношений
Рассмотрим общий случай естественного соединения:
S R1 R2 ... Rn .
Пусть A ri ,
1 i k и a Ri : 1 2 3 ... k . Допустим, что в каждом их k
отношений выбрано по одному кортежу ti .
Какова вероятность того, что все эти кортежи совпадут в атрибуте A?
23
24. Соединение нескольких отношений (продолжение)
Раздел 2.Компиляция и оптимизация. Анализ стоимости операций.
Соединение нескольких отношений (продолжение)
Рассмотрим кортеж t1 (выбран из R с минимальным количеством 1 различных значений
атрибута). В соответствии с допущением о принадлежности одного множества значений
совпадающего атрибута другому каждое из 1 значений можно найти в компонентах A
кортежей всех других k 1 отношений ( 1 2 3 ... k ) . Кортеж ti совпадает с t1
в атрибуте A с вероятностью pi
1
1
. Это утверждение верно для всех i 2,3,..., k .
Вероятность того, что все кортежи совпадут в атрибуте A :
P
1
.
2 3 ... k
Размер итогового отношения, возвращаемого оператором соединения с произвольным
числом аргументов:
kS
k1 k2 ... k R
,
2 3 ... k
для каждого атрибута A, присутствующего, как минимум, в двух отношениях.
24
25. Соединение нескольких отношений (пример)
Раздел 2.Компиляция и оптимизация. Анализ стоимости операций.
Соединение нескольких отношений (пример)
Пусть имеются отношения R(a,b,с), S(b,c,d) и U(b,e), обладающие следующими
статистическими характеристиками:
Кардинальное число
R(a,b,с)
S(b,c,d)
U(b,e)
1 000
2 000
5 000
200
Число различных значений a
100
Число различных значений b
20
50
Число различных значений c
200
100
Число различных значений d
Число различных значений e
400
500
25
26. Пример (продолжение)
Раздел 2.Компиляция и оптимизация. Анализ стоимости операций.
Пример (продолжение)
Пусть необходимо вычислить
R(a, b, c) S (b, c, d ) U (b, e) .
Оценка размера итогового отношения будет иметь вид:
k Rb S U
Таким образом,
k R S U
k R k S kU
k k k
c
и k R S U R S U ,
S U
R
k R k S kU 1000 2000 5000
5000 .
S U R
(50 200) 200
Независимо от группирования и упорядочения аргументов выражения естественного
соединения n отношений, правило, применяемое к каждому частному соединению отдельно,
дает тот же результат, что и в случае применения к соединению всех n отношений.
26
























 database
database








