Similar presentations:
Сравнение отрезков и углов
1.
Урок 3.12.09.2022
2. Проверка домашнего задания
№ 11№ 14
h
А
C
r
l
hr , hl , rl
O
D
№ 13
B
A
M
B
N
3.
1)Что называется углом?4.
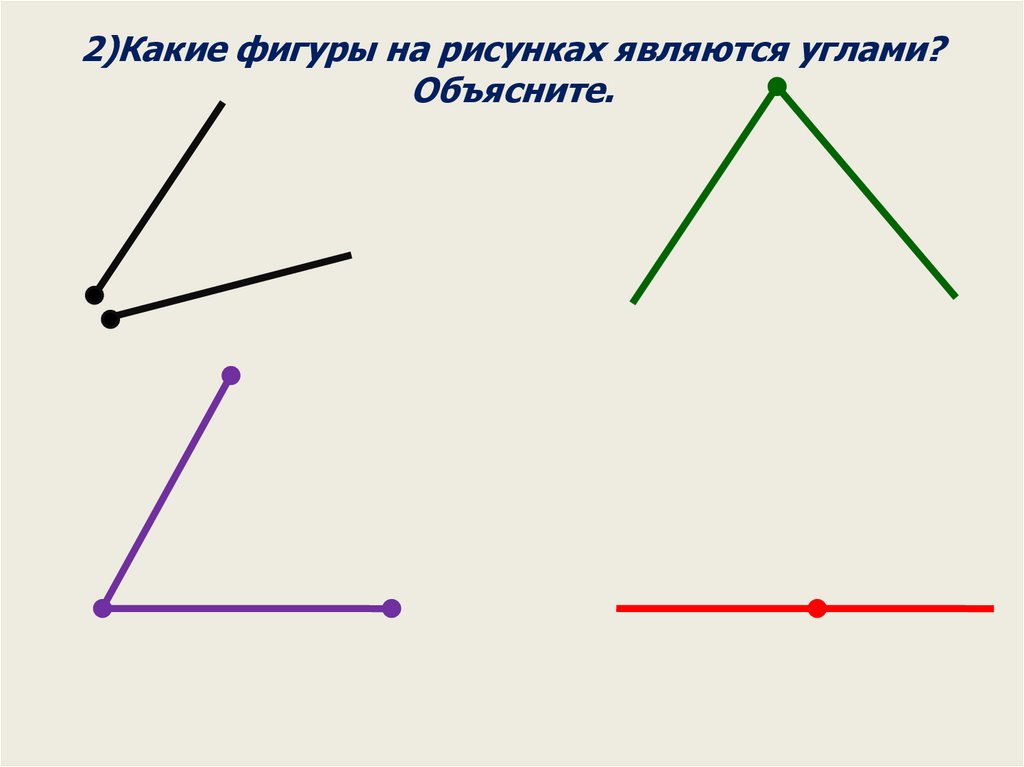
2)Какие фигуры на рисунках являются углами?Объясните.
5.
NM
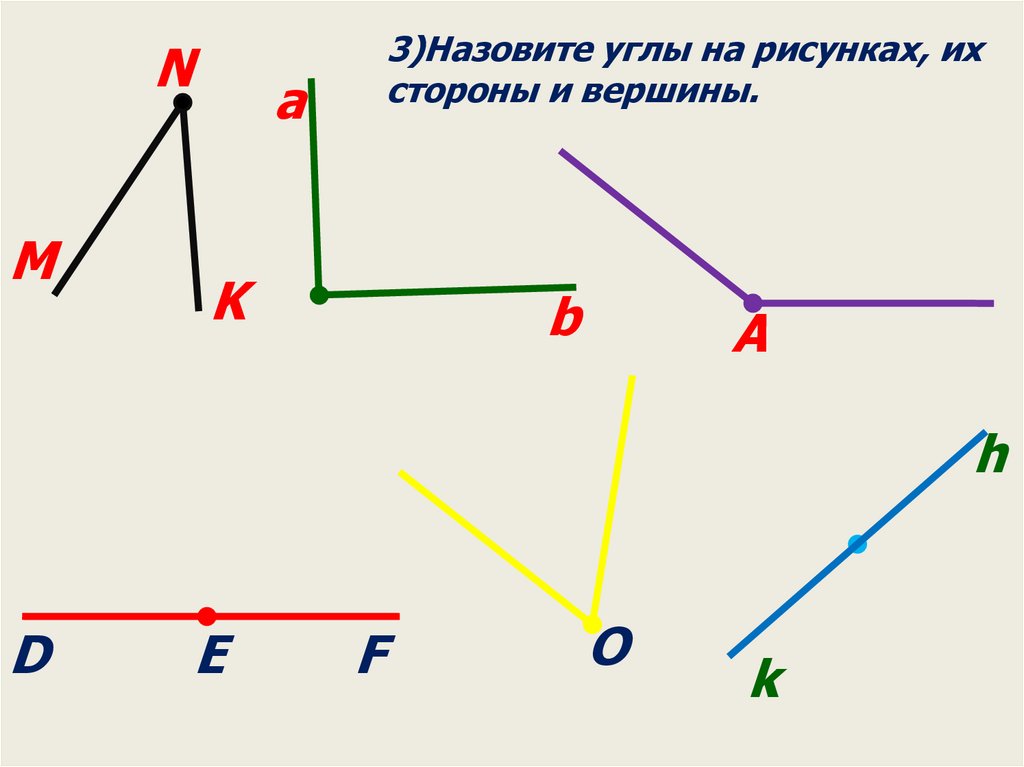
3)Назовите углы на рисунках, их
стороны и вершины.
a
K
b
A
h
D
E
F
O
k
6.
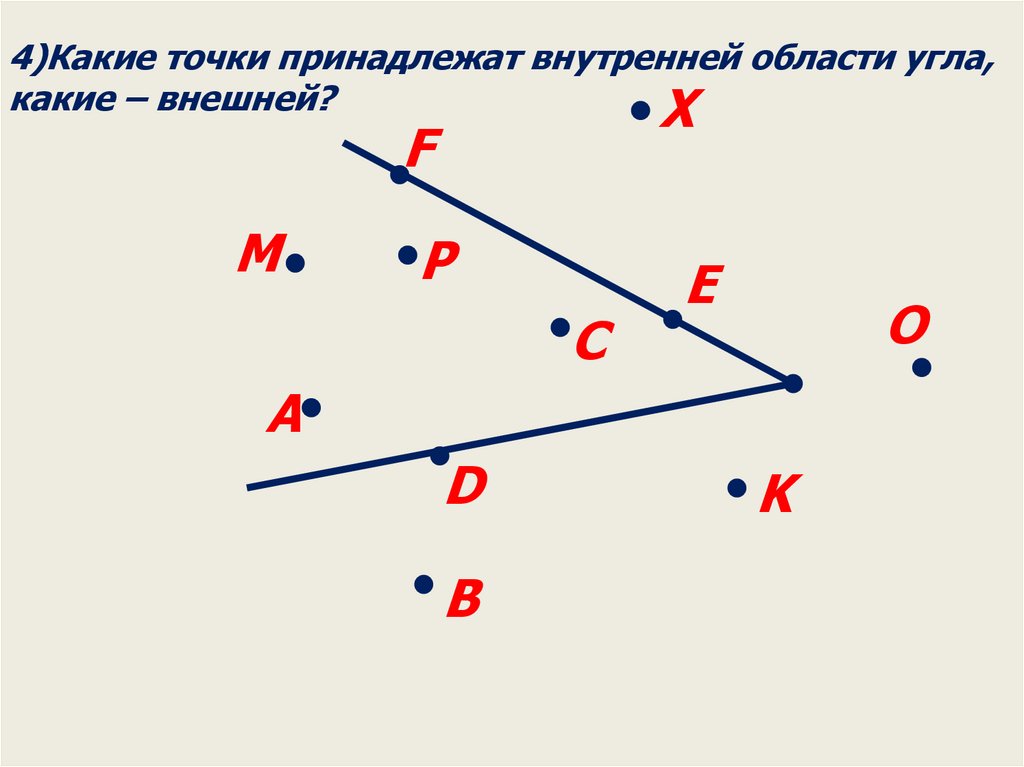
4)Какие точки принадлежат внутренней области угла,какие – внешней?
X
F
M
P
C
E
O
A
D
B
K
7.
8.
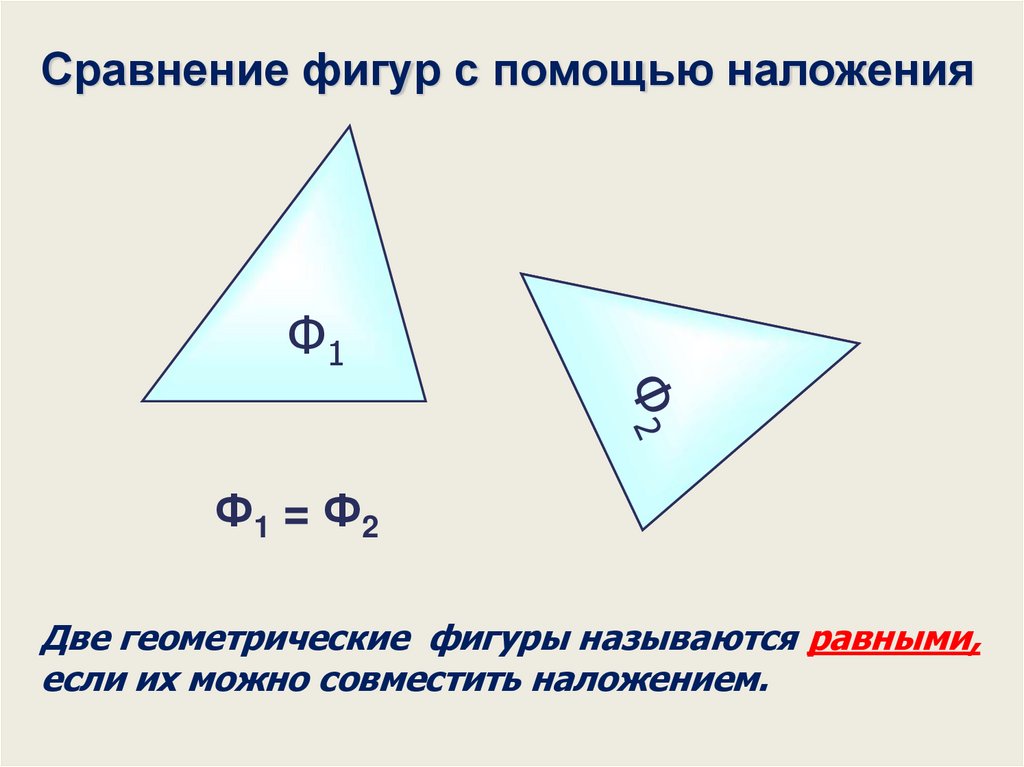
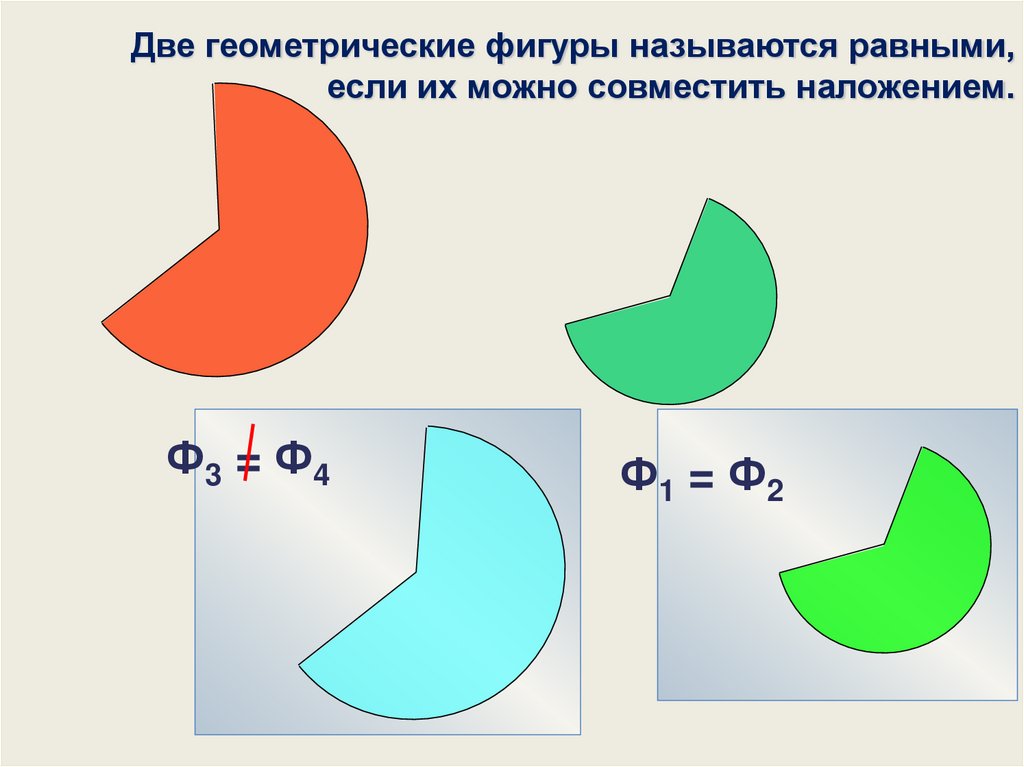
Сравнение фигур с помощью наложенияФ1
Ф1 = Ф2
Две геометрические фигуры называются равными,
если их можно совместить наложением.
9.
Две геометрические фигуры называются равными,если их можно совместить наложением.
Ф3 = Ф4
Ф1 = Ф2
10.
Сравнение отрезковD
С
В
А
АB = CD
M
N
MN > CD
11.
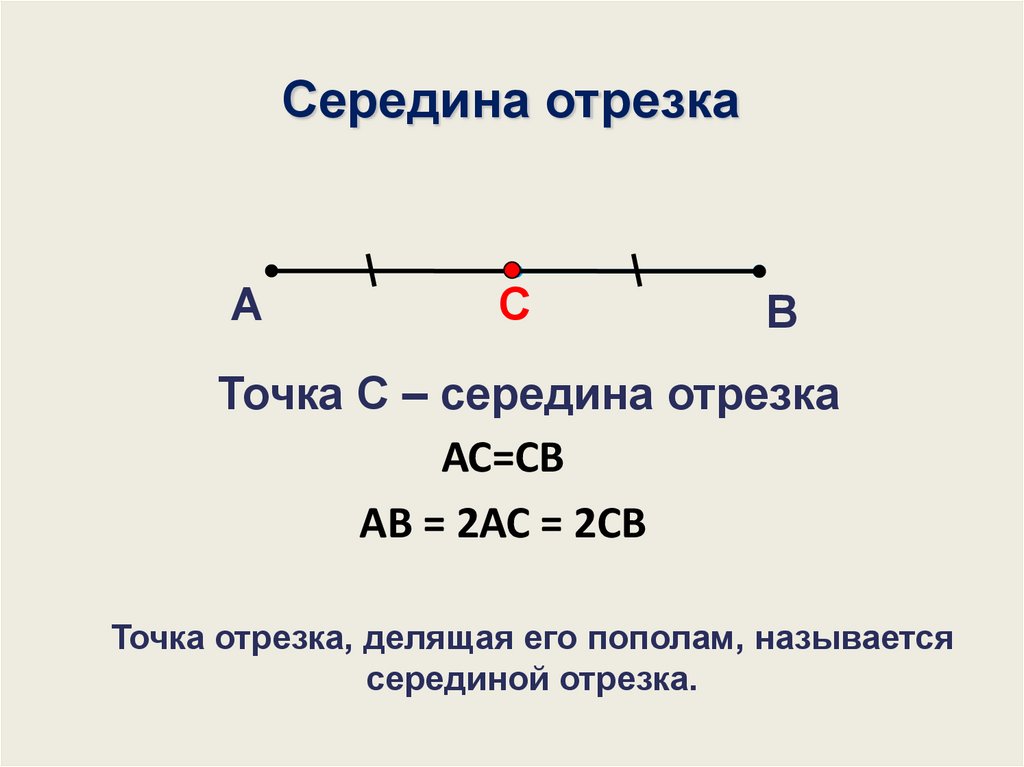
Середина отрезкаА
С
В
Точка С – середина отрезка
АС=СВ
АВ = 2АС = 2СВ
Точка отрезка, делящая его пополам, называется
серединой отрезка.
12.
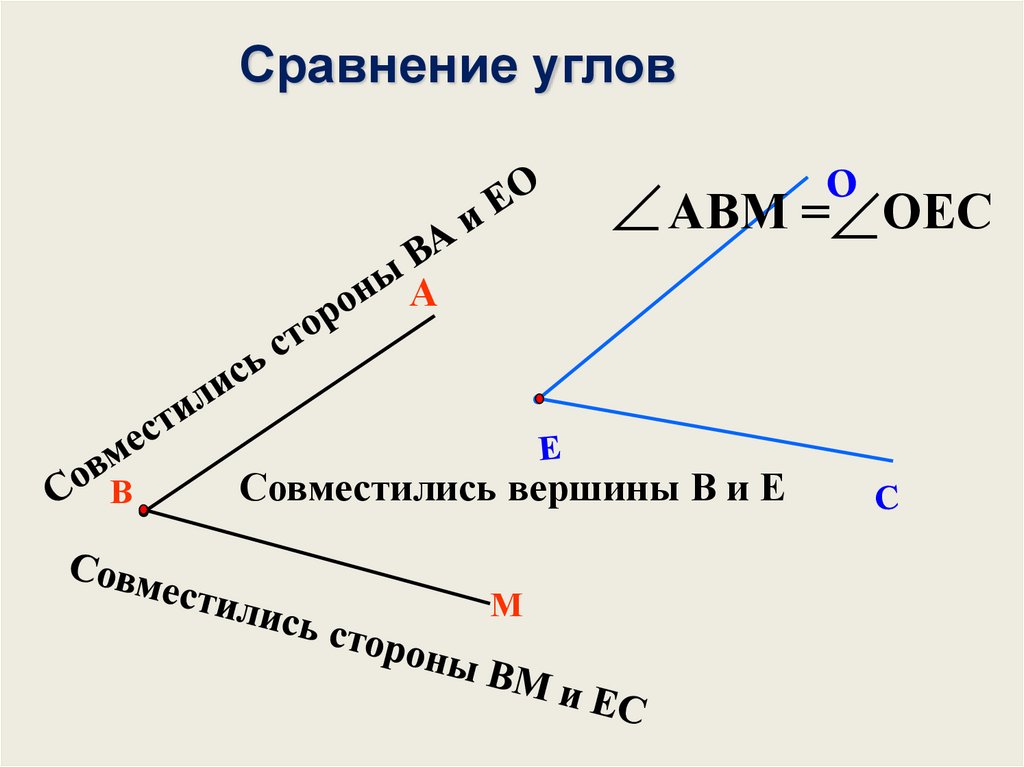
Сравнение угловАВМ = ОЕС
А
В
Совместились вершины В и Е
М
13. Запомни!
1. Вершины должны совпадать;2. Сторона одного угла должна совместиться
со стороной другого угла;
3. Две другие стороны должны оказаться по
одну сторону от совместившихся сторон;
4. Равенство или неравенство углов будет
зависеть только от того, совместятся ли
другие стороны.
14.
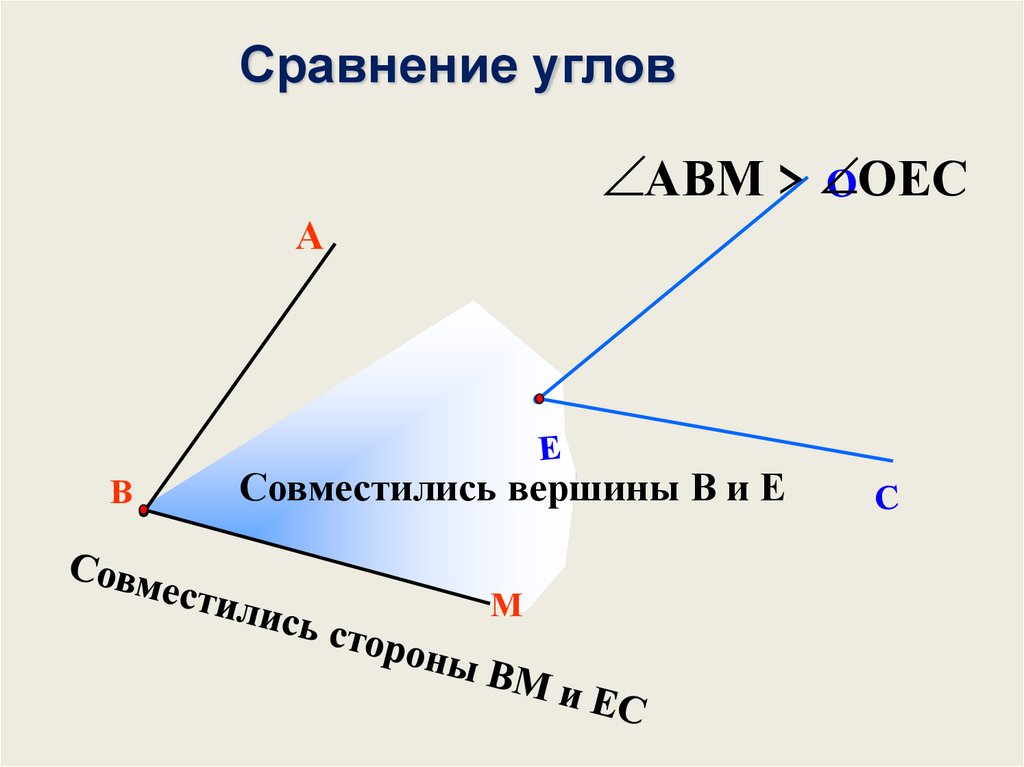
Сравнение угловАВМ > ОЕС
А
В
Совместились вершины В и Е
М
15.
Сравнение угловАВМ < ОЕС
А
В
Совместились вершины В и Е
М
16.
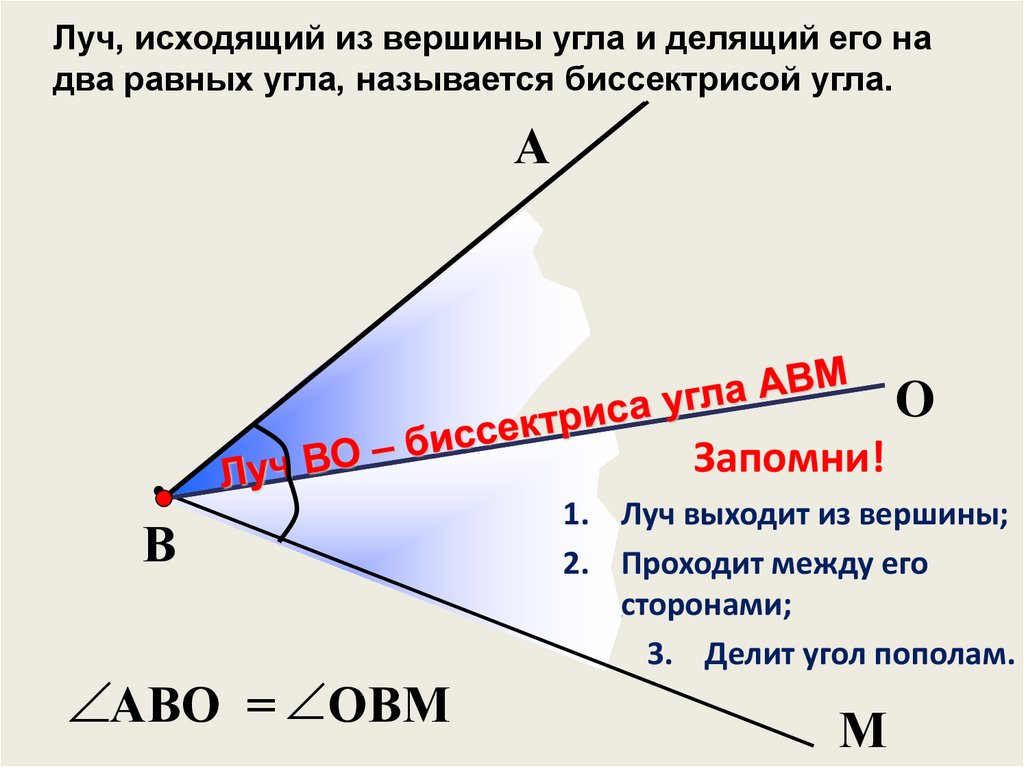
Луч, исходящий из вершины угла и делящий его надва равных угла, называется биссектрисой угла.
А
O
Запомни!
В
АВО = ОВМ
1. Луч выходит из вершины;
2. Проходит между его
сторонами;
3. Делит угол пополам.
М
17.
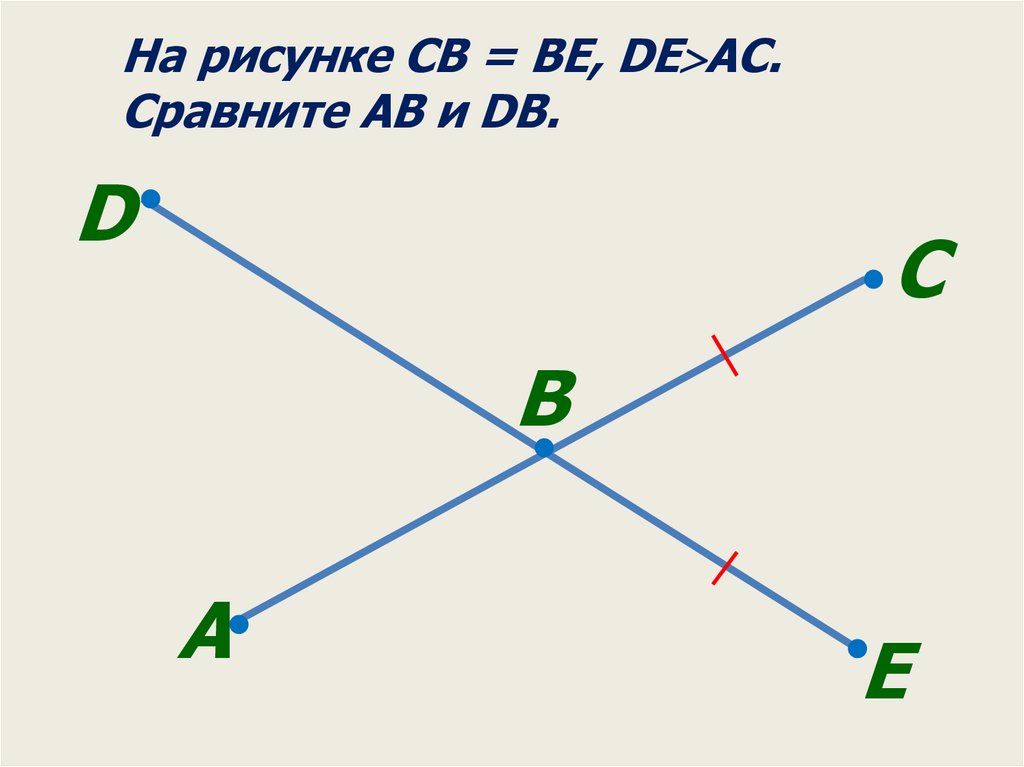
На рисунке CB = BE, DE AC.Сравните AB и DB.
D
С
B
A
E
18.
На рисунке AOB = DOC.Есть ли еще на рисунке равные углы?
С
B
A
O
D
19.
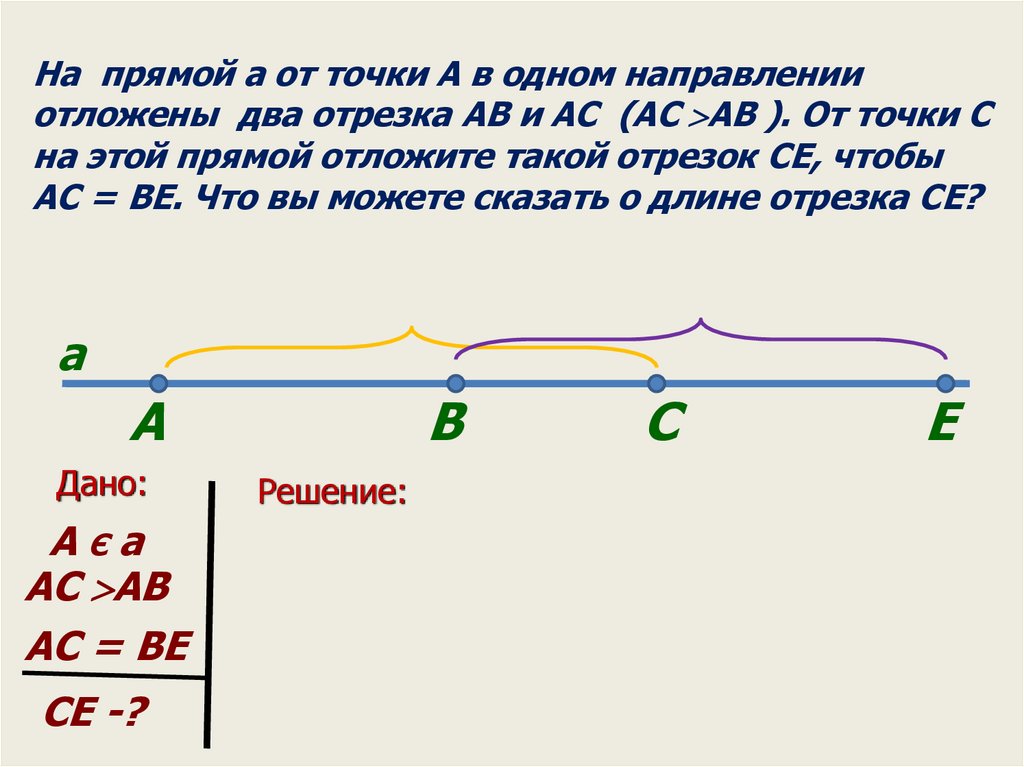
На прямой a от точки A в одном направленииотложены два отрезка AB и AC (AC AB ). От точки С
на этой прямой отложите такой отрезок CE, чтобы
AC = BE. Что вы можете сказать о длине отрезка CE?
a
A
Дано:
АЄа
AC AB
AC = BE
CE -?
B
Решение:
С
E
20.
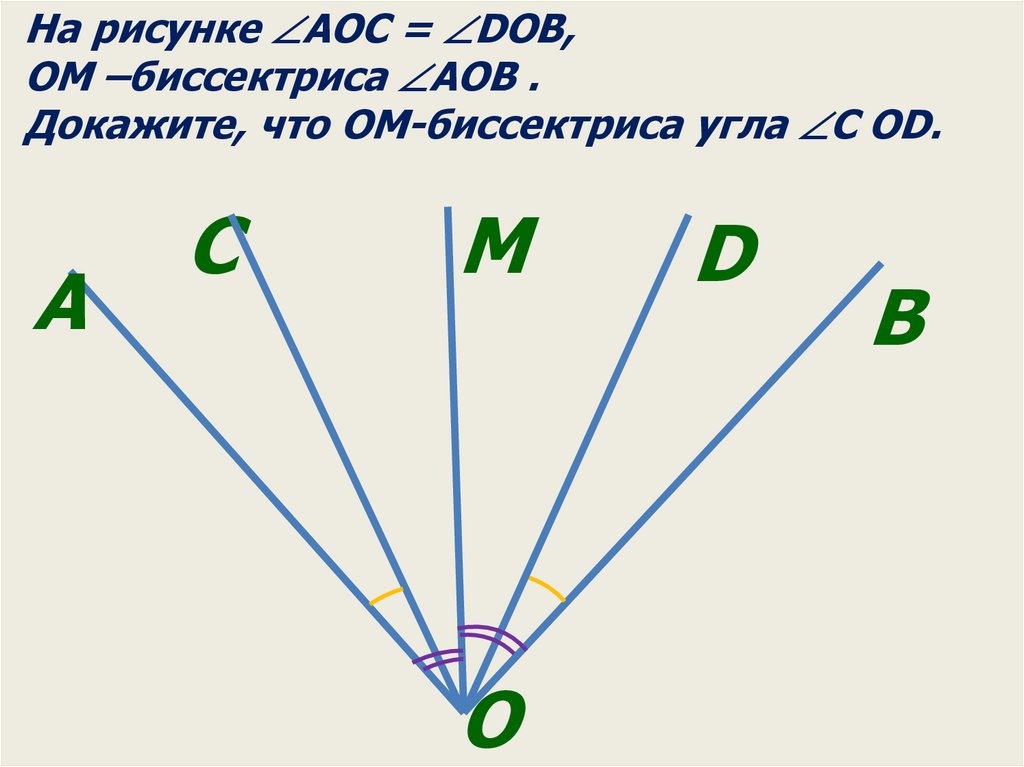
На рисунке AOС = DOB,OM –биссектриса AOB .
Докажите, что OM-биссектриса угла С OD.
A
С
M
O
D
B
21. Домашнее задание
§3, №№18, 20, 2322.
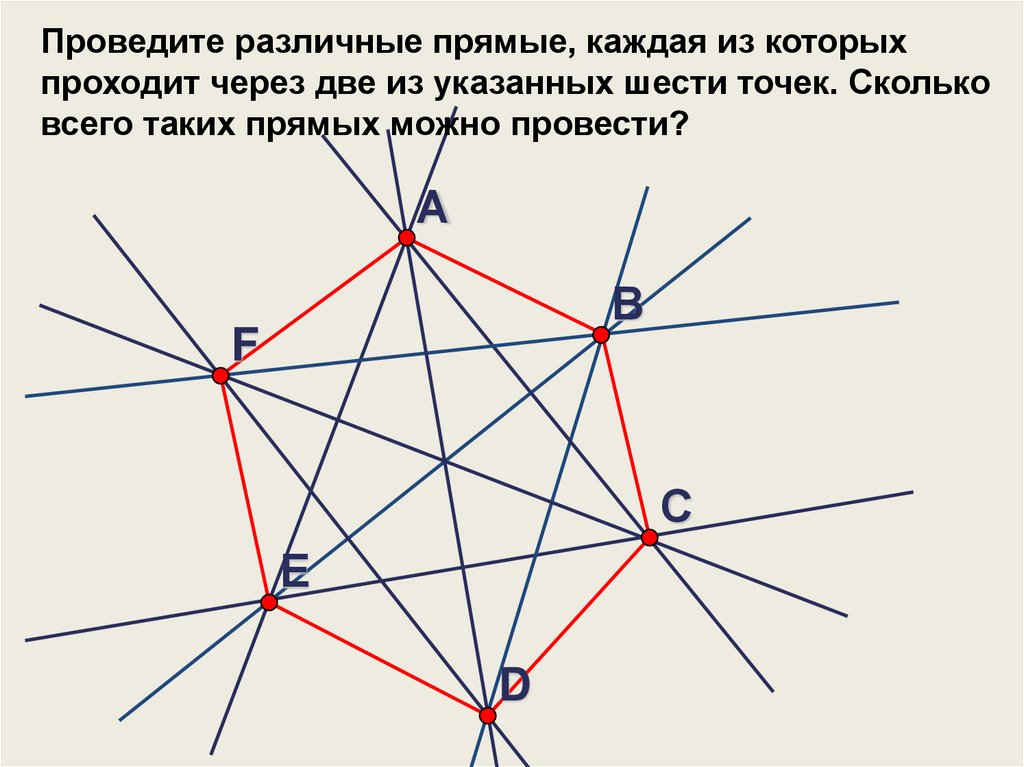
Проведите различные прямые, каждая из которыхпроходит через две из указанных шести точек. Сколько
всего таких прямых можно провести?
А
В
F
С
Е
D









 mathematics
mathematics








