Уравнение окружности

1.

2. Выполнять задания в соответствии с планом урока:

1)Ответить на вопросы математического
диктанта и построить чертеж.
2)Записать определение уравнения
линии (стр. 235 учебника) и построить
чертеж.
3) Записать определение уравнения
окружности и построить чертеж.
4)Записать примеры.
5)Выполнить самостоятельную работу.

3. Математический диктант

1.Как называется геометрическая фигура, состоящая из множества всех
точек, равноудаленных от данной точки?
2. Как называется хорда, проходящая через центр окружности?
3. Как называется отрезок, соединяющий центр окружности с точкой на
окружности?
4. Как называется геометрическая фигура, состоящая из множества всех
точек плоскости, находящихся от данной точки на расстоянии, не
превышающем данного?
5. Пересекаются ли окружности с центрами А и В, если
АВ = 10 см, а радиусы равны 5 см, и 6 см?
6. Найдите координаты точек пересечения окружности с
центром в начале координат и радиусом, равным 7, с
осями координат.

4.

Уравнение линии на плоскости
y
y=x
L
M(x;y)
O
x
D(x;y)
C(x;y)
- Если точка лежит на данной линии, то ее координаты
удовлетворяют уравнению этой линии.
- Координаты любой точки, не лежащей на данной линии,
не удовлетворяют ее уравнению.

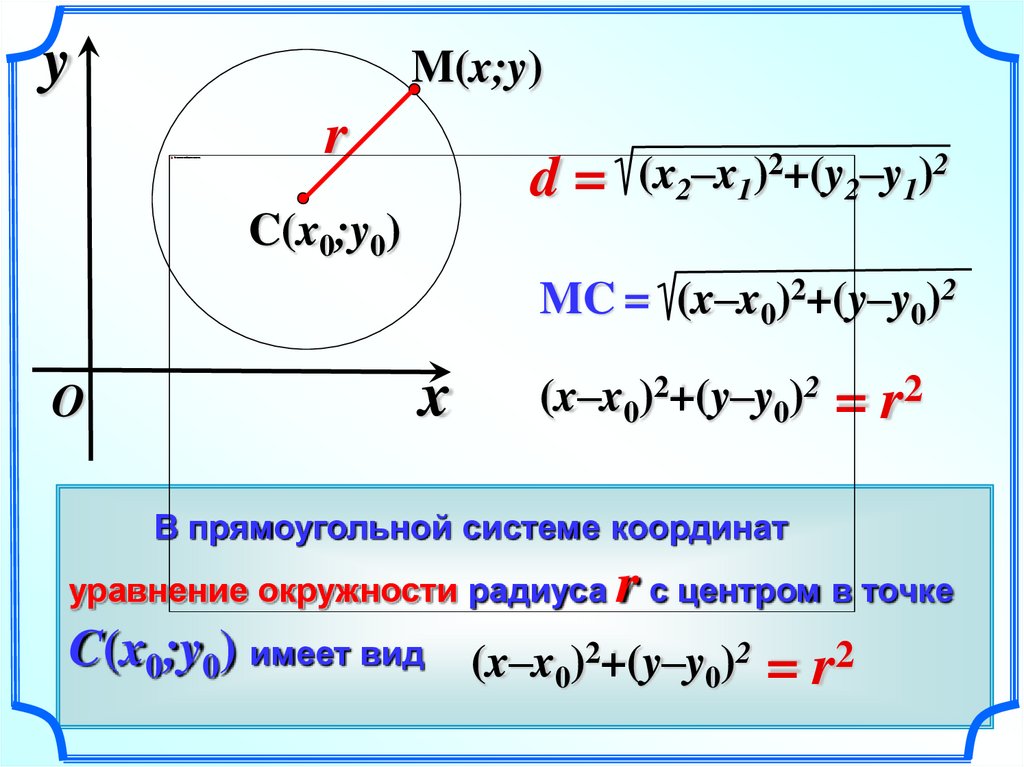
5.

y
M(x;y)
r
d=
(x2–x1)2+(y2–y1)2
C(x0;y0)
MC = (x–x0)2+(y–y0)2
O
x
(x–x0)2+(y–y0)2
= r2
В прямоугольной системе координат
r с центром в точке
(x–x0)2+(y–y0)2 = r2
уравнение окружности радиуса
C(x0;y0) имеет вид

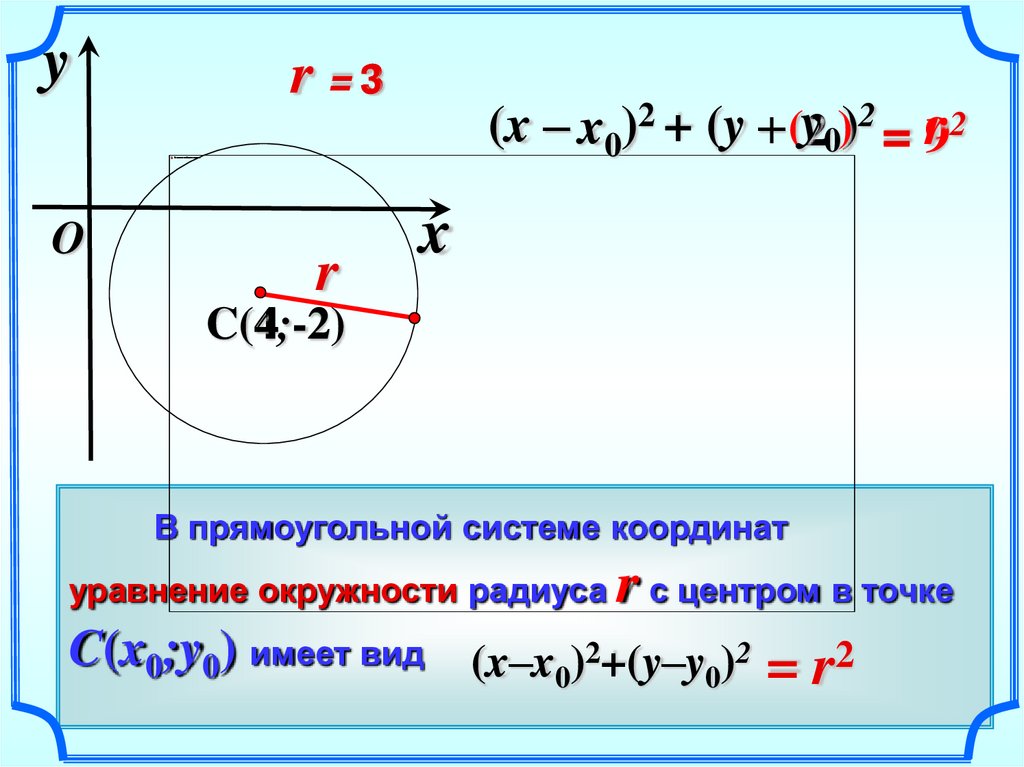
6.

y
O
r =3
r
(x – x0)2 + (y – (y20))2 = 9r 2
x
C(4;-2)
4 -2
В прямоугольной системе координат
r с центром в точке
(x–x0)2+(y–y0)2 = r2
уравнение окружности радиуса
C(x0;y0) имеет вид

7.

y
x0
y0
(x –( -3
3 ))2 + (y – (-2
2 ))2 = 9
32
O
r
x
C( x0; y0)
r=3
C(-3;-2)
В прямоугольной системе координат
r с центром в точке
(x–x0)2+(y–y0)2 = r2
уравнение окружности радиуса
C(x0;y0) имеет вид

8. Выполните самостоятельную работу.

9. Из каждого уравнения окружности выпишите координаты центра и радиус окружности

1)(x – 3)2 + (y – 2)2 = 16;
2)(x – 1 )2 + (y + 2)2 = 4;
3)(x + 5 )2 + (y – 3)2 = 25;
4)(x – 1 )2 + y 2 = 8;
5)x 2 + (y + 2)2 = 2;
6)x 2 + y 2 = 9;
7)(x – 3 )2 + (y – 2)2 = 0,09;
8)(x + 7)2 + (y – 5)2 = 2,5
9)x2 + (y + 4)2 = 6

10. Проверьте свои ответы.

Выполните работу над
ошибками.

11.

Уравнение окружности
Центр
r
(x – 3 )2 + (y – 2)2 = 16
(x – 1 )2 + (y + 2)2 = 4
(x + 5 )2 + (y – 3)2 = 25
(x – 1 )2 + y 2 = 8
x 2 + (y + 2)2 = 2
x 2+ y 2= 9
(x – 3 )2 + (y – 2)2 = 0,09
(x + 7)2 + (y – 5)2 = 2,5
C(3; 2)
r=4
C(1;-2)
r=2
C(-5; 3)
C(1; 0)
r=5
r= 8
C(0;-2)
C(0; 0)
r= 2
r=3
C(3; 2)
C(-7; 5)
r = 0,3
r = 2,5
5
r= 2
x2 +
(y +
4)2 =
1
64
C(0;-4)

12. Выставьте себе оценку:

«5» - верно выполнены все 9 заданий;
«4» - 8 или 7;
«3» – 6 или 5;
«2» – меньше пяти заданий.

13. Домашнее задание.

П.94 учить определения и формулы,
выполнить № 959 (выписать координаты
центра и радиус, построить окружность
(каждую на отдельной координатной
плоскости).