Similar presentations:
Функции и их свойства
1. Функции и их свойства
«Для того, чтобы усовершенствоватьум, надо больше размышлять, чем
заучивать».
« Мыслю, следовательно существую».
Рене Декарт
2. Историческая справка
• Функция – одно из важнейшихматематических понятий, которое уходит
своими корнями в ту далекую эпоху, когда
люди впервые поняли, что окружающие их
предметы взаимосвязаны.
• - чем больше оленей удастся убить на охоте,
тем дольше племя будет избавлено от голода;
• - чем сильнее натянута тетива лука, тем
дальше полетит стрела;
• - чем дольше горит костер, тем теплее будет в
пещере
3. Рене Декарт
• Понятие переменной величины было введенов науку французским ученым Рене Декартом
(1596 - 1650). Он ввел идею числовой
функции числового аргумента. При записи
зависимостей между величинами Декарт стал
применять буквы.
• Он стал геометрически изображать не только
пары чисел, но и уравнения, связывающие
два числа.
4. Определение функции
«Функцией переменнойвеличины называется
количество, образованное
каким угодно способом из
этой переменной
величины и постоянных»
- такое определение
функции дал
швейцарский математик
Иоганн Бернулли (16671748).
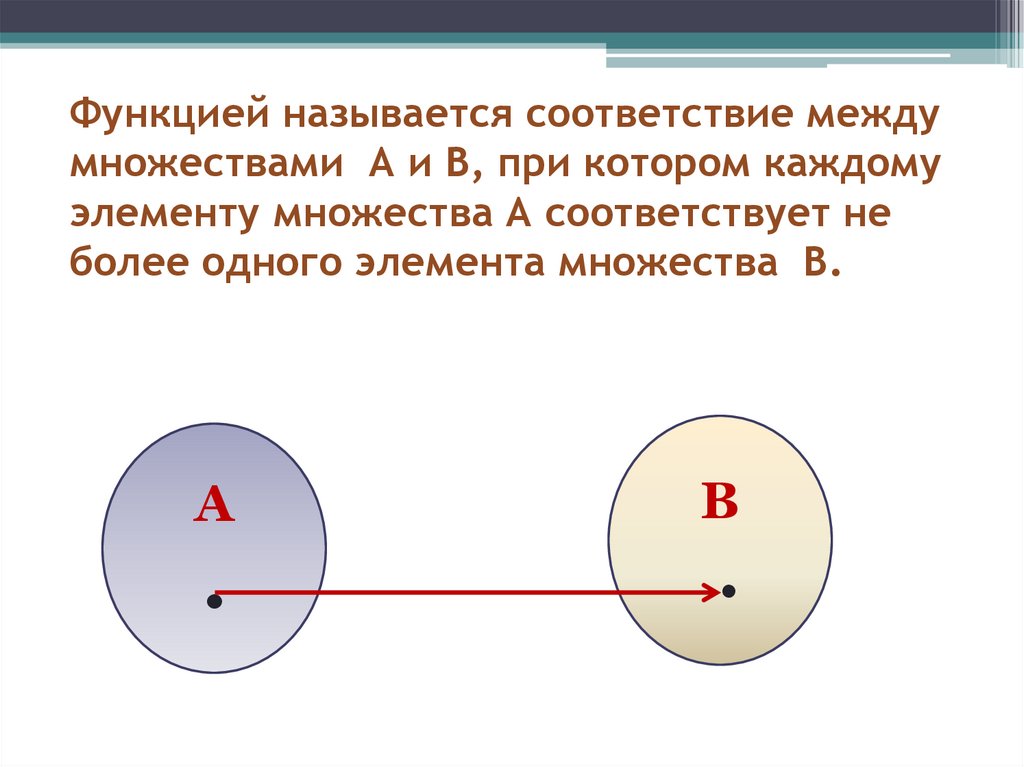
5. Функцией называется соответствие между множествами А и В, при котором каждому элементу множества А соответствует не более
одного элемента множества В.А
В
.
.
6. Функция
• Функцию обозначаютy = f(x), y = g(x), y = h(x)
• Х – аргумент (независимая
переменная)
• У – значение функции (зависимая
переменная)
• D(f) – область определения функции
(множество всех значений аргумента,
при которых функция существует)
• Е(f) – область значений функции
(множество всех значений функции)
7. Способы задания функции
• 1. Словесный• 2. Табличный
• 3. Аналитический (с помощью формулы)
• 4.Графический
Пример.
Функция Е(х) – «целая часть числа х»
Е(1)=1, Е(4,7)= 4, Е(-7,09)= - 7
Пример.
y x 3x 2
y 7 x 6
y
2
x 1
x
2
8.
y n2
y n
3
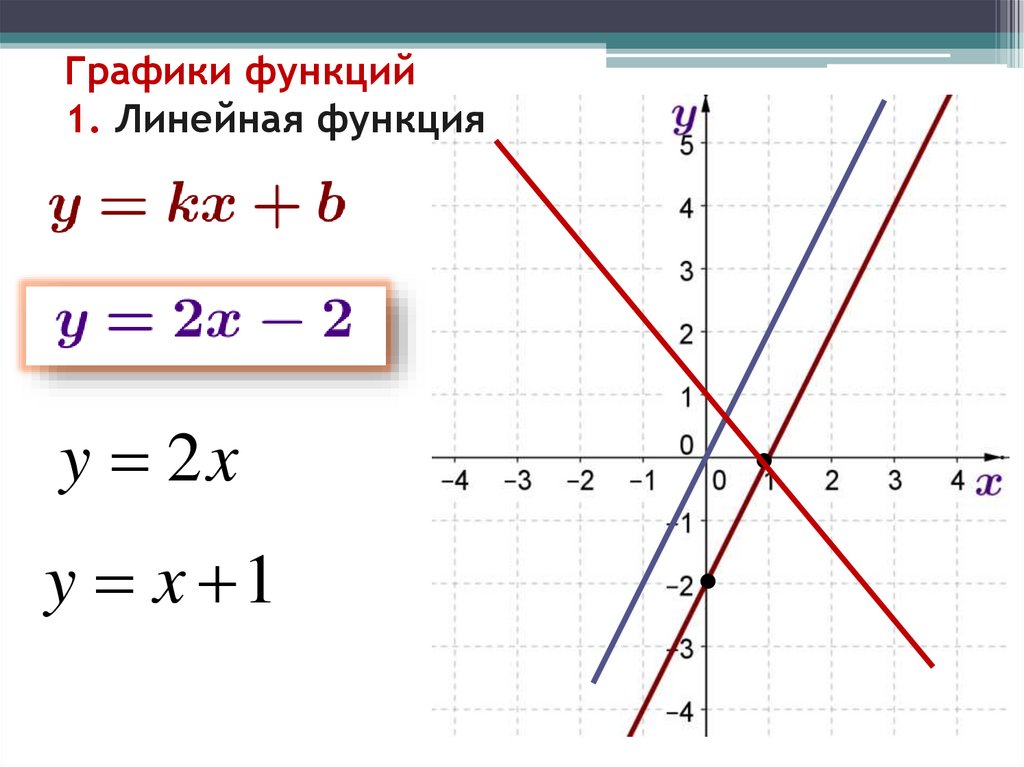
9. Графики функций 1. Линейная функция
y 2xy x 1
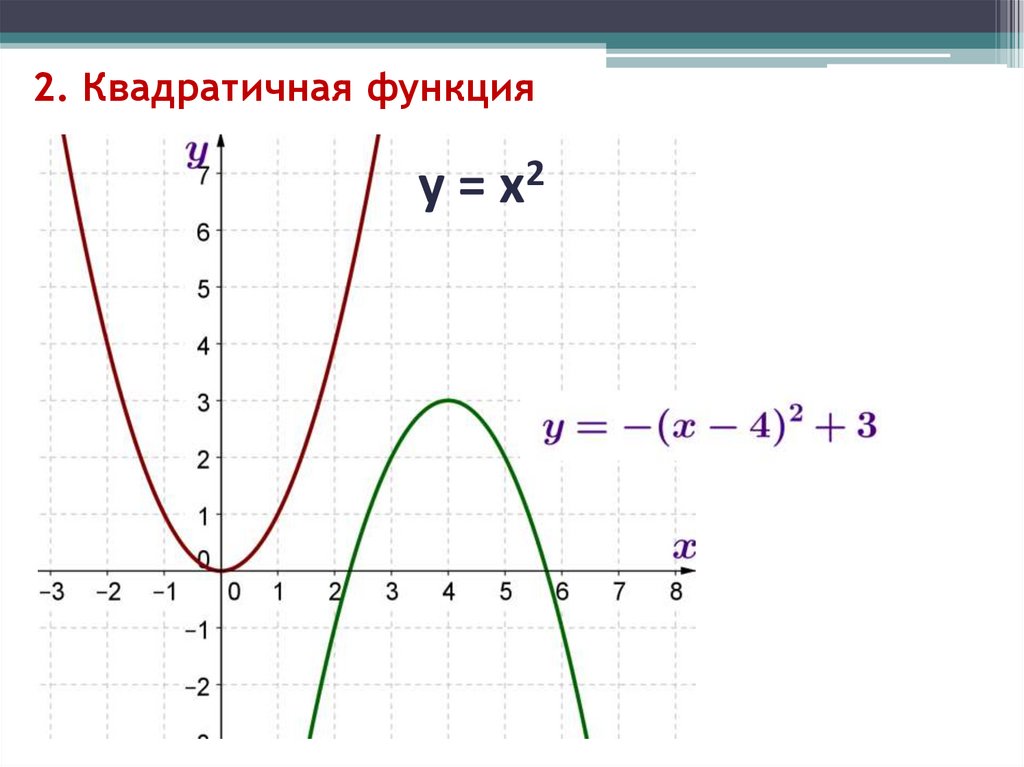
10. 2. Квадратичная функция
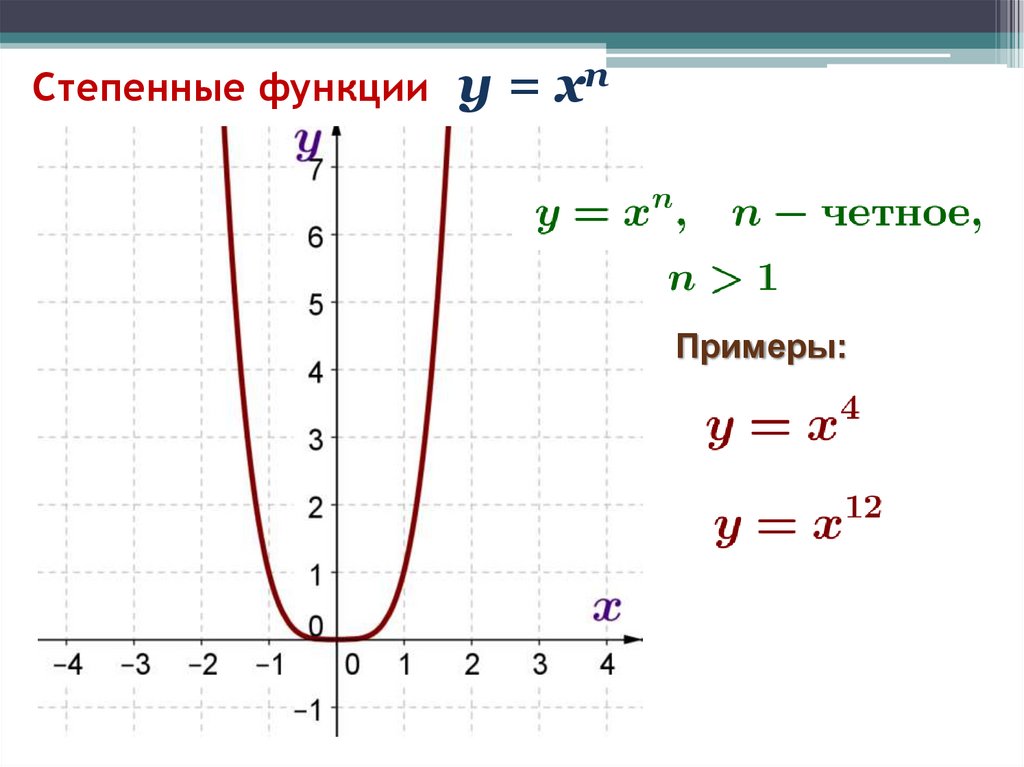
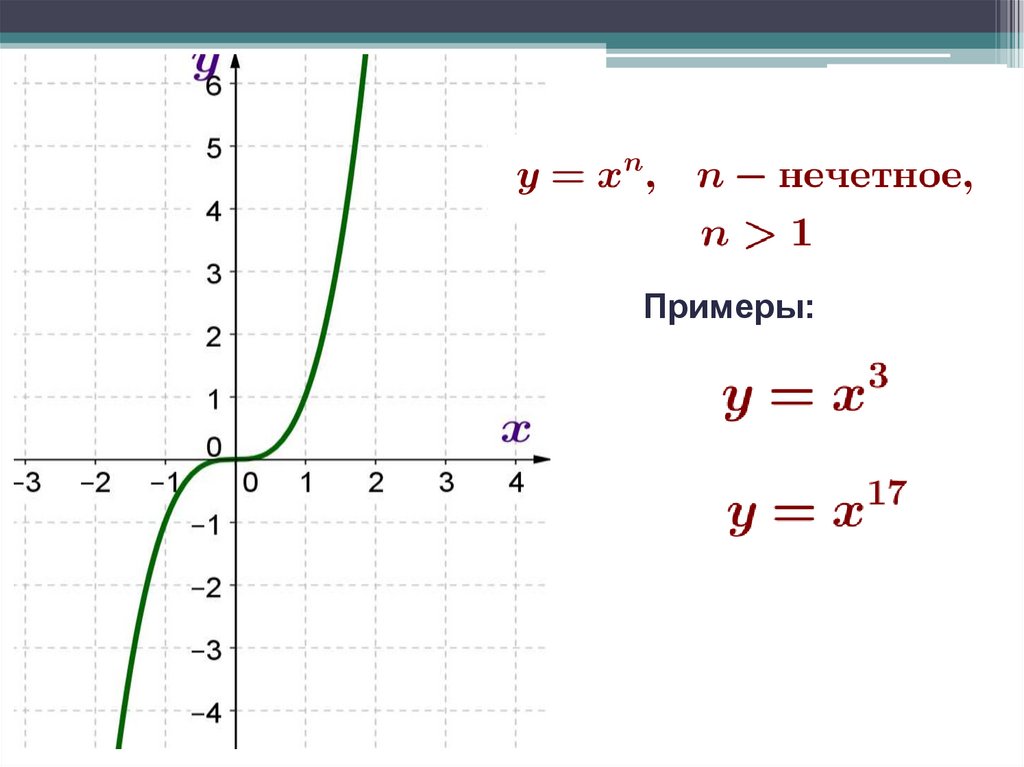
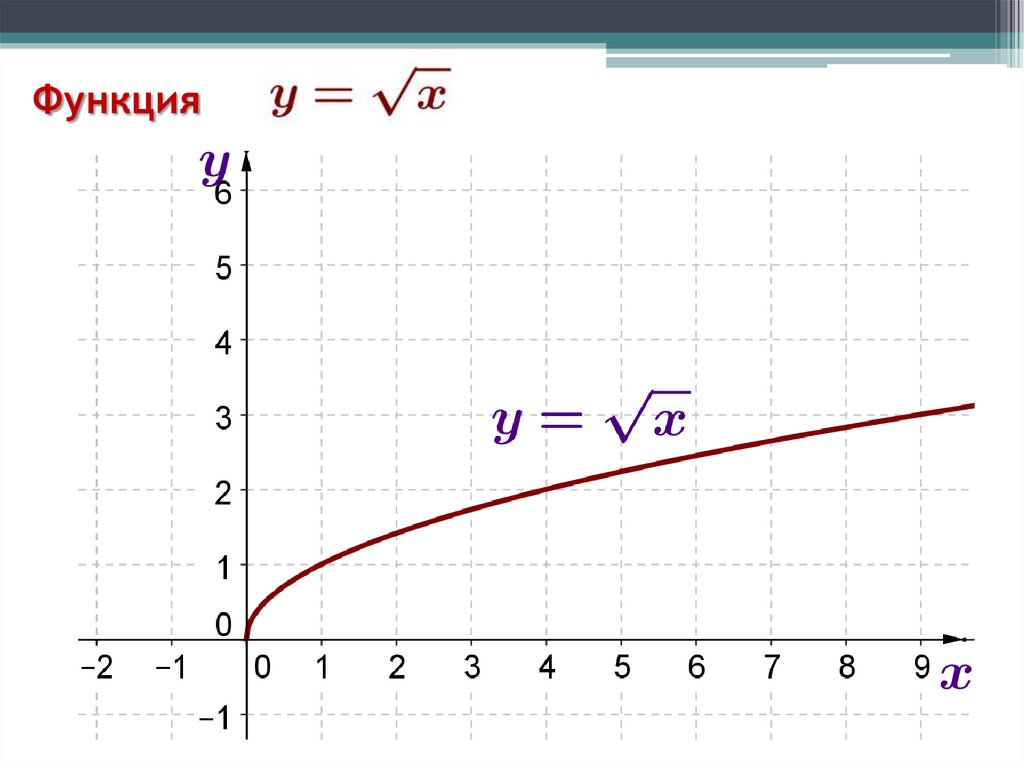
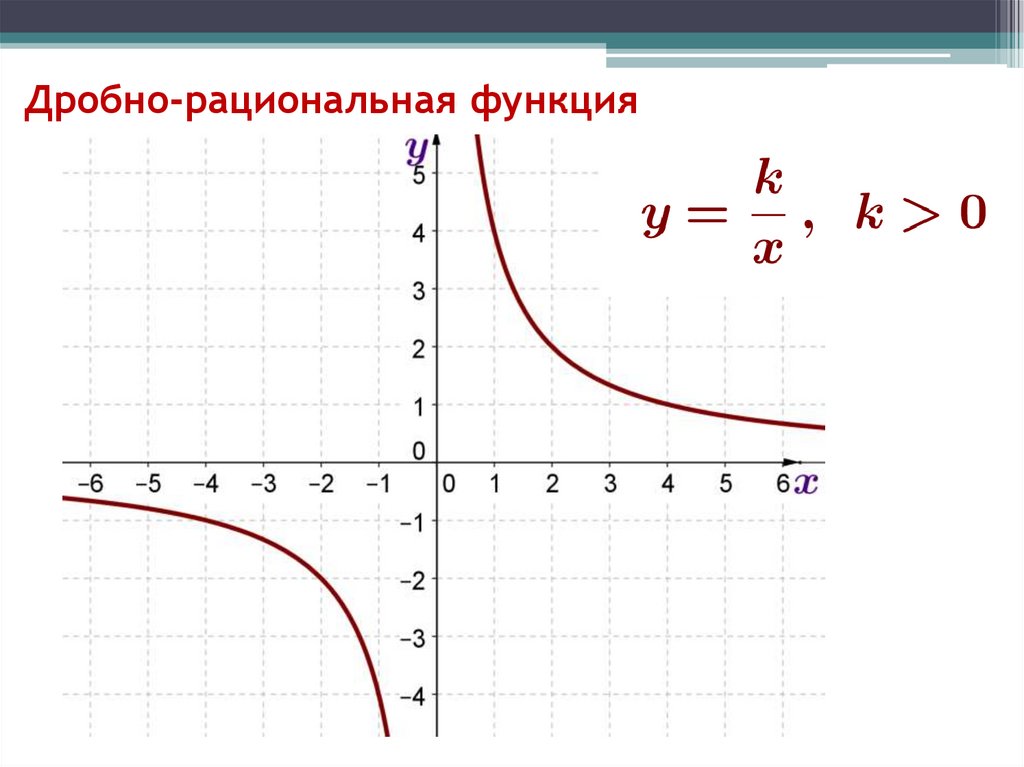
у = х211. Степенные функции
у = хnПримеры:






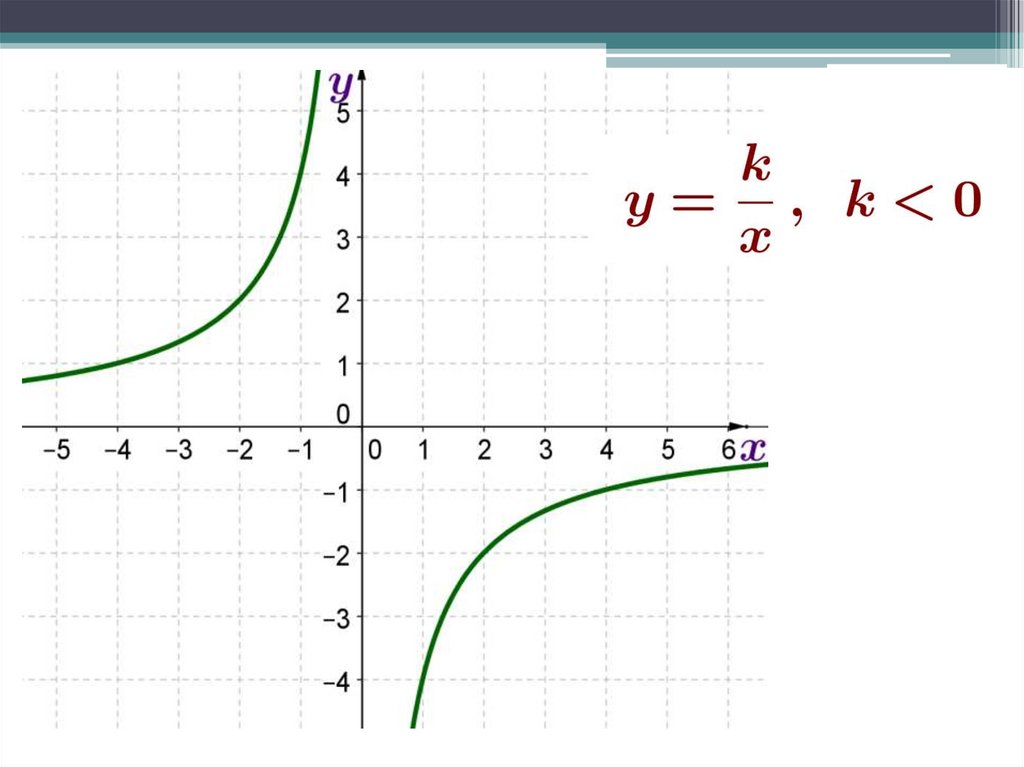

 mathematics
mathematics








