Similar presentations:
Растворы
1. РАСТВОРЫ
2.
Самыми распространёнными химическими системами, скоторыми мы сталкиваемся в лаборатории и в природе,
являются
растворы.
В
лаборатории
специально
приготавливают растворы солей, кислот и оснований, а также
других веществ, чтобы с ними было удобнее обращаться.
Вообще говоря, раствором называют однородную смесь
двух или большего числа молекулярных или ионных
веществ, компоненты которых неразличимы невооружённым
глазом. В отличие от этого, например, компоненты бетона –
песок, цемент, гравий – ясно различимы и поэтому бетон
относят к смесям, а не к растворам.
3.
Более научная формулировка:растворы это взаимодействующие,
однородные,
равновесные
системы
переменного состава.
Растворы могут существовать в любом агрегатном
состоянии: твёрдом, жидком или газообразном, но они
обязательно должны состоять из одной фазы, т.е. из одной
различимой на вид системы.
4.
МЕХАНИЗМЫ И ЭНЕРГЕТИКА РАСТВОРЕНИЯ.Всякий раствор состоит из растворённых веществ и
растворителя, т.е. среды, в которой эти вещества равномерно
распределены
в
виде
молекул
или
ионов.
Обычно
растворителем называют тот компонент, который находится в
большем количестве.
Образование
раствора
идёт
самопроизвольно
до
наступления
устойчивого
равновесия.
Движущей
силой
процесса растворения является уменьшение свободной энергии
Гиббса (ΔG) раствора по сравнению со свободной энергией
раздельно существующих составных частей раствора.
G Gпродукт. Gисходн. 0
(1)
5.
При достижении равновесия ΔG = 0.Энергетической характеристикой процесса растворения
является энтальпия растворения (ΔHраств.). Растворение одних
веществ в других сопровождается обычно заметным
тепловым эффектом. Тепловая энергия, выделяемая при
растворении 1 моля вещества с образованием 1 л раствора,
называется молярной теплотой растворения.
РАСТВОРЕНИЕ ТВЁРДЫХ ТЕЛ.
При растворении твёрдых тел, например, в воде происходят
два главных процесса:
• разрушение кристаллической решетки твёрдого тела;
• сольватация (в случае воды – гидратация) молекул твёрдого
тела.
Сольватацией называется такое взаимодействие между
растворяемым веществом и растворителем, которое не
сопровождается явно выраженной химической реакцией.
6.
Например, 1) растворение твёрдого Al в щёлочисопровождается химической реакцией – выделением водорода:
2 Al + 2 OH– + 2H2O
2) или растворение
источниках воды
→ 2 AlO2–
карбоната
CaCO3 + H2O + CO2
кальция
в
+
3H2
природных
→ Ca2+ + 2HСО3
тоже сопровождается химической реакцией.
7.
В то же время растворение СsBr,сопровождается
заметным
NaI
тепловым
или
NH4NO3
эффектом,
в воде
но
не
химическими реакциями.
Просто сильно полярные
молекулы воды сольватируют или гидратируют молекулы
CsBr
или NaI или NH4NO3 на поверхности кристалла и
переводят их в раствор, новые слои поверхности снова
гидратируются и процесс растворения продолжается до
насыщения раствора.
Итак, теплота растворения:
ΔHраств. = – U + ΔHсольват.
(2)
(В общем случае растворителем может быть не только вода, а ,
скажем, жидкий NH3,
HCN, C2H5OH, CH3OH,
(CH3)2CO, анилин C6H5NH2, жидкая двуокись серы SO2
другие вещества).
и
8.
В общем случае всегда верно это уравнение, где U – энергиярешётки. Обычно, чем больше U , т.е чем больше силы
взаимодействия ионов в кристалле между собой, тем больше и
ΔHсольват и, следовательно, ΔHраств является разностью
двух больших соизмеримых величин. Следовательно, её знак
обычно трудно предсказать.
Например, при растворении 1 моля NaCl в воде происходит
поглощение 5.4 кДж тепла, что обнаруживается по небольшому
понижению температуры. Известно, что энергия решётки NaCl
равна –770 кДж/моль, т.е. это означает, что для разложения
кристалла на моль ионов Na+ и моль ионов Cl– требуется
затратить 184 ккал/моль (770 кДж/моль).
Na+(г) + Cl–(г) → NaCl(кр)
U = –184 ккал/моль ( – 770 кДж/моль).
9.
Это означает, что энергия сольватации NaCl в пересчёте на 1моль ионов Na+ и 1 моль ионов Cl– должна быть равна (184 –
1.3) ккал = 182.7 ккал. Другими словами:
Na+(г) + Cl–(г + H2O → Na+ (водн.) + Cl–(водн.)
ΔHсольват = –182.7 ккал, (– 764.6 кДж).
Итак, затраты энергии при разрушении решётки велики, но
велика и энергия гидратации, суммарная же теплота
растворения невелика.
10.
Третий механизм растворения (помимо рассмотренныххимического и сольватации) обусловлен действием
дисперсионных сил, но энергетика и в этом случае та же. Что
имеется в виду? При растворении инертных газов, например,
Ar, Kr, Xe, CH4, C3H8, N2O и т.д. в воде или, скажем, в
CHCl3, или в C6H6 никакой сольватации и никакого
химического взаимодействия не происходит, силы
взаимодействия этих молекул с молекулами растворителя (в
частности воды) являются дисперсионными (т.е.
достаточно слабыми), кроме того, при переходе молекул из
газовой фазы в раствор резко уменьшается энтропия системы.
11.
И хотя ΔHгидрат < 0, т.е. взаимодействие молекулнеполярных газов с водой слабо экзотермическое, происходит
выделение тепла, но ΔS < 0 и в целом ΔG ≃ 0 и поэтому
растворимость газов и в воде и в других растворителях
весьма мала.
12.
Свойства растворов. Законы Генри, Рауля,Вант Гоффа.
Прежде, чем перейти к рассмотрению этих законов мы
рассмотрим один вам ещё мало известный способ выражения
концентрации.
Все
остальные:
процентная,
молярная,
нормальная и моляльная концентрации вы уже знаете из
занятий на практике и прочтёте в VII главе Общей Химии
Н.Л.Глинки (1980).
Самый удобный и физически осмысленный способ
выражения концентрации – это способ её выражения в
мольных долях Xi.
Если раствор состоит из
n
компонентов, причём имеется
N1 молей вещества 1, N2 молей вещества 2, N3 молей
вещества 3 и т.д., то очевидно, что мольная доля, скажем,
вещества 1 есть:
13.
N1N1
X1
n
N1 N 2 N3 ...N n
Ni
i 1
Для вещества 2:
X2
N2
n
N
i 1
i
для вещества 3:
X3
N3
n
N
i 1
И очевидно, что
X
i
i
1;
i
(3)
14.
поскольку:N1
N1 N 2 N 3 ...N n
N2
N1 N 2 N 3 ...N n
...
Очевидно, что мольные доли
безразмерные единицы концентрации.
Nn
1
N1 N 2 N 3 ...N n
представляют
собой
Рассмотрим равновесие между жидкостью и растворёнными
в ней газами. Молекулы газа, растворённого в жидкости,
способны выделяться из неё. И если скорость выделения газа
из жидкости равна скорости его поступления в неё, то
устанавливается равновесие и при данных температуре и
давлении жидкость насыщается газом. Растворимость газа в
жидкости (его мольная доля в растворе) прямо
пропорциональна парциальному давлению данного газа над
поверхностью жидкости Р2 и если концентрация газа в
жидкости выражается через его мольную долю Х2, то закон
Генри формулируется в виде:
Р2 = kгX2
(4)
15.
В которомпостоянная
растворимости газа.
Генри
kг
является
Таблица 1. Значения постоянной закона Генри для водных
растворов некоторых газов при 25°С
Газ
kг (мм рт. ст./мольная доля)
N2
O2
CO2
CH4
Ar
6.5×107
3.3×107
1.25×106
3.14×107
2.4×107
мерой
16.
Растворимость газов уменьшается:1. при повышении температуры;
2. при растворении в воде полярных или ионных веществ – это
явление объяснимо в терминах сольватации этих веществ
водой. В результате сольватации часть молекул воды
связывается и растворимость газа уменьшается.
Вода гораздо прочнее связывается ионными веществами, чем
неполярными или слабополярными газами. Этот эффект
выделения одного вещества из раствора при добавлении
другого, сильно сольватируемого растворителем называется
высаливанием. Этот эффект используют в практических
целях, например, при изготовлении мыла.
17.
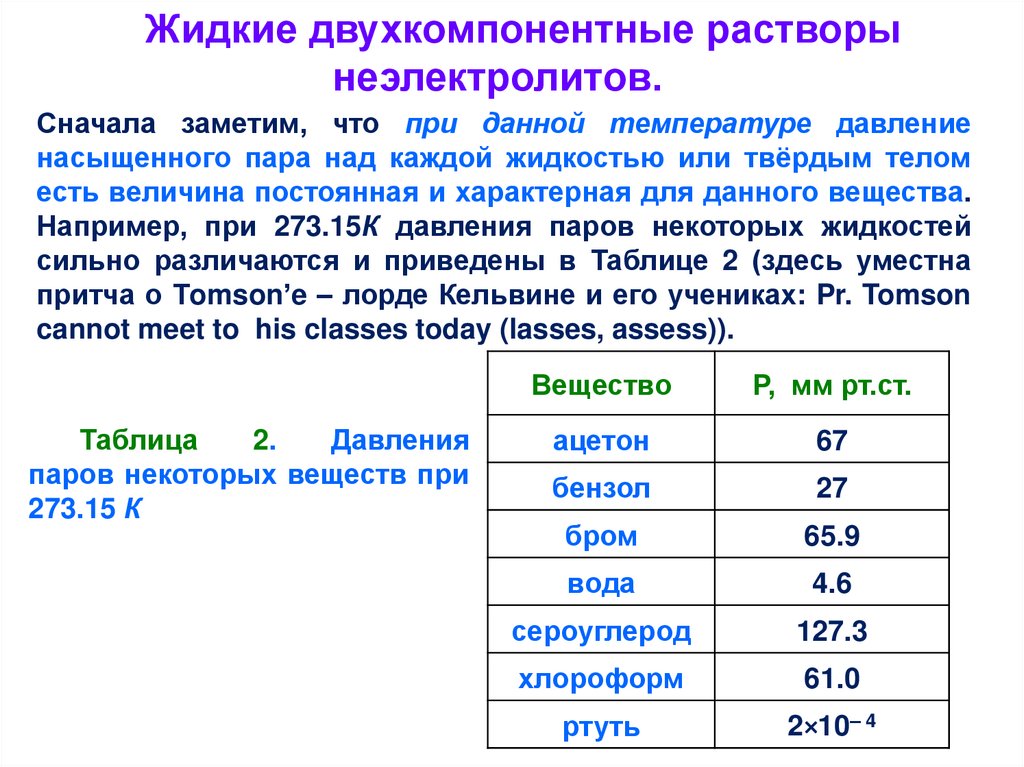
Жидкие двухкомпонентные растворынеэлектролитов.
Сначала заметим, что при данной температуре давление
насыщенного пара над каждой жидкостью или твёрдым телом
есть величина постоянная и характерная для данного вещества.
Например, при 273.15К давления паров некоторых жидкостей
сильно различаются и приведены в Таблице 2 (здесь уместна
притча о Тomson’e – лорде Кельвине и его учениках: Pr. Tomson
cannot meet to his classes today (lasses, assess)).
Таблица
2.
Давления
паров некоторых веществ при
273.15 К
Вещество
Р, мм рт.ст.
ацетон
67
бензол
27
бром
65.9
вода
4.6
сероуглерод
127.3
хлороформ
61.0
ртуть
2×10– 4
18.
Пусть теперь мы растворили в некотором из этих растворителейнелетучее соединение, например сахарозу в воде, т.е.
твёрдое
тело.
Тогда,
оказывается,
как
обнаружил
экспериментально французский исследователь Рауль:
при растворении давление насыщенного пара
растворителя над раствором всегда ниже,
чем над чистым растворителем при той же
температуре.
Итак, если при данной Т давление паров над чистым
растворителем было ро, то после растворения в нём нелетучего
вещества, давление паров растворителя станет р.
Следовательно, понижение давления пара есть
относительное понижение есть
p0 p
.
p0
ро – р , а
19.
Так вот, Рауль показал, что относительное понижениедавления
пара
растворителя
равно
мольной
доле
растворённого вещества. Напомню вам, что мы рассматриваем
2-х компонентные растворы,
т.е. у нас всего 2 вещества: (1)
(5)
растворитель и (2) растворённое вещество, мольная доля
растворителя х1, причём х1 + х2 = 1.
Итак, закон Рауля имеет вид:
p0 p
x2
p0
Отсюда:
или
p
x1 ;
p0
p0 p
p0 p
p
1 x1
1
1 x1
p0
p0 p0
p0
или
p x1 p0
(5)
Следовательно, давление паров растворителя над
раствором пропорционально его мольной доле в растворе x1.
20.
Рассмотрим рисунок:Рис.1. Давление пара растворителя в зависимости от
температуры.
21.
Из рисунка видно, что давление паров растворителя и надчистым растворителем и над раствором растёт при увеличении
температуры. Почему? Можно объяснить это, исходя из принципа
ЛеШателье. Между раствором и паром имеется равновесие,
скажем для воды:
(Н2О)ж
⇄
(Н2О)пар
Причём процесс перехода жидкой воды (как и любой другой
жидкости)
в
парообразное
состояние
есть
процесс
эндотермический. Для испарения моля жидкости надо затратить
теплоту парообразования λ. Следовательно, если мы к этой
равновесной системе подведём теплоту – повысим её
температуру, равновесие сдвинется в сторону парообразования,
т.к. система будет стараться уменьшить внешнее воздействие. Но
всегда, как видно из рисунка,
p
p0
=
ро > р , причём
const.
22.
ТОЧКА ЗАМЕРЗАНИЯ И ТОЧКА КИПЕНИЯ РАСТВОРОВ.Хорошо известно, что раствор замерзает при более низкой
температуре, чем чистый растворитель. Именно поэтому в
районах с холодным климатом принято добавлять в воду,
заливаемую в радиаторы, такие вещества, как спирт, глицерин
или этиленгликоль, чтобы предотвратить её замерзание.
Количественная зависимость понижения точки замерзания Δtзам
имеет вид:
Δtзам = К· m
(6)
Эту зависимость тоже установил Рауль:
понижение точки замерзания, вызываемое различными
растворёнными веществами, взятыми в одинаковых мольных
количествах, одинаково для данного растворителя.
Величина К называется моляльной константой понижения
точки
замерзания
или
криоскопической
постоянной.
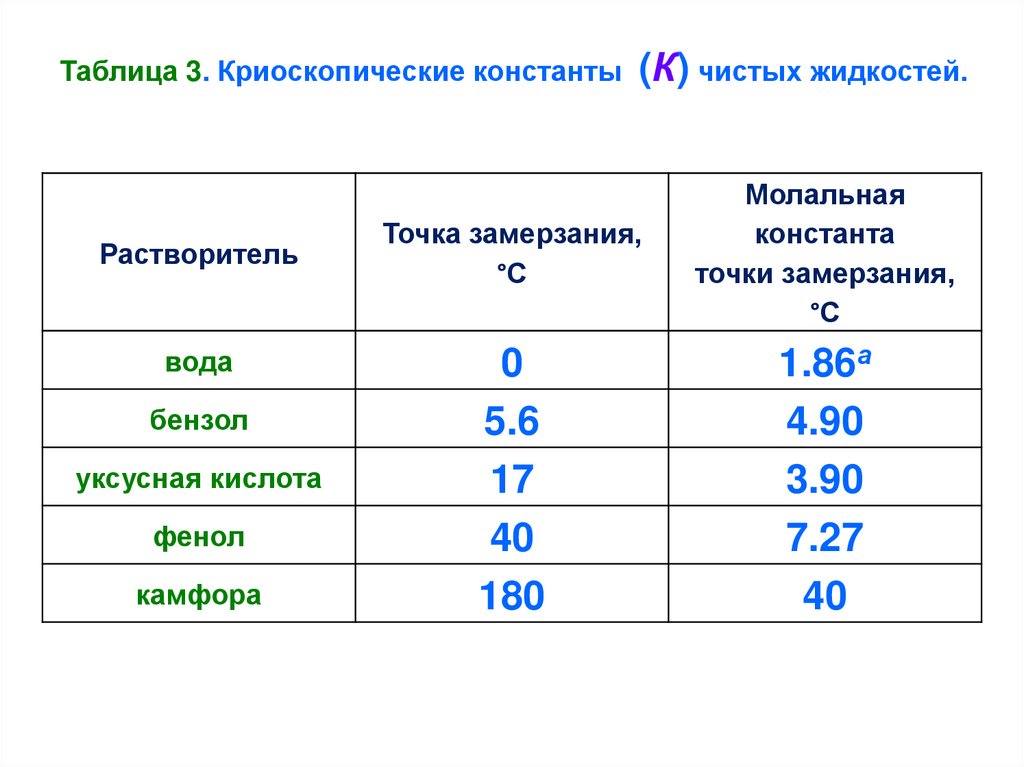
Рассмотрим таблицу 3.
23.
Таблица 3. Криоскопические константыРастворитель
вода
бензол
уксусная кислота
фенол
камфора
(К) чистых жидкостей.
Точка замерзания,
°С
Молальная
константа
точки замерзания,
°С
0
5.6
17
40
180
1.86а
4.90
3.90
7.27
40
24.
Пример. Рассчитать, какое количество этилового спирта.
С2Н5ОН
следует добавить к 5л
воды, чтобы
предотвратить её замерзание в радиаторе автомобиля при
температуре –10°С.
Δtзам
=
К· m,
вещества на 1000 г воды,
t зам
где m число молей растворённого
KH2O 1.86 oC
K g 1000 1.86 g 1000
10
M G
46 5000
25.
Рассмотрим, что происходит при охлаждении растворасоли
NaCl,
скажем, 1М концентрации (например твёрдой
СО2). Оказывается, что этот раствор начинает замерзать, т.е.
в нём появляется лёд при –3.4°С.
Затем по мере образования чистого льда концентрация
соли в растворе растёт и точка замерзания такого раствора
снова понижается. Когда половина всей воды перейдёт в лёд,
концентрация соли станет 2М
замерзания понизится до –6.9°С.
по
NaCl
и температура
В дальнейшем при образовании льда концентрация
раствора продолжает расти и температура замерзания
понизится до –21.1°С. При этой температуре раствор
становится насыщенным по отношению к соли NaCl,
которая начинает выкристаллизовываться в виде твёрдой
фазы NaCl·2H2O. Такая смесь называется эвтектикой.
26.
Точно такое же соотношение, как и (6) имеется дляповышения температуры кипения при растворении вещества
по отношению к точке кипения чистого растворителя:
Δtкип = E·m
(7)
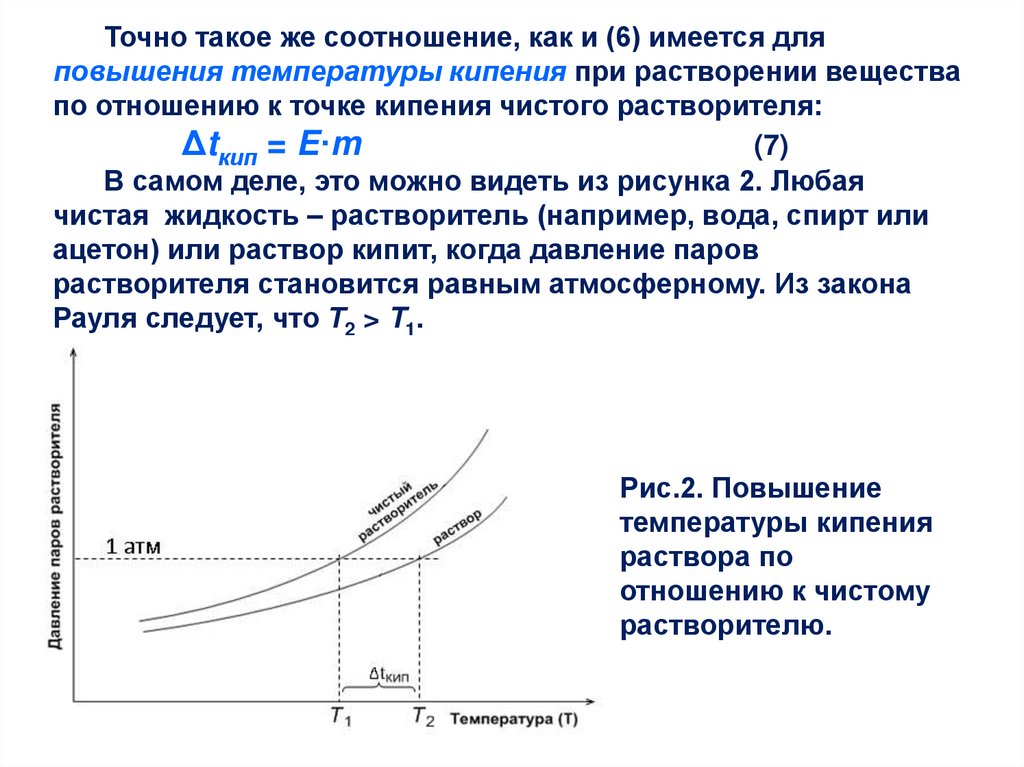
В самом деле, это можно видеть из рисунка 2. Любая
чистая жидкость – растворитель (например, вода, спирт или
ацетон) или раствор кипит, когда давление паров
растворителя становится равным атмосферному. Из закона
Рауля следует, что Т2 > T1.
Рис.2. Повышение
температуры кипения
раствора по
отношению к чистому
растворителю.
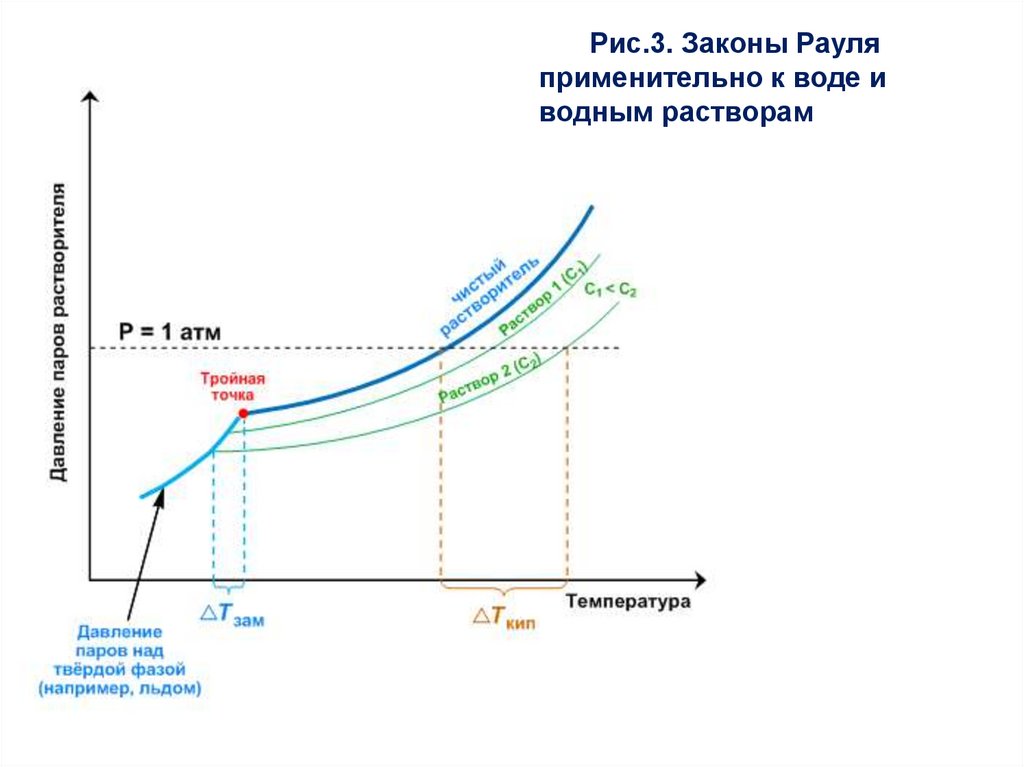
27.
Рис.3. Законы Рауляприменительно к воде и
водным растворам
28.
Осмос29.
Осмосомявление
массопереноса
растворителя (например, воды) через полупроницаемую
мембрану (целлофановую плёнку, пергаментную бумагу,
мочевой пузырь животных, воздушный пузырь рыб и другие
плёнки, сквозь которые могут проходить малые молекулы, но
не могут проходить большие молекулы или ионы) из
разбавленного раствора в концентрированный.
называется
В простейшем случае по одну сторону мембраны находится
чистый растворитель (например, вода), а по другую – раствор.
На Рис.4 изображена схема процесса осмоса – через мембрану
могут
проходить
в
обоих
направлениях
молекулы
растворителя, в данном случае воды, но не могут переходить
молекулы неэлектролита (этилового спирта, ацетона,
глюкозы и т.п.). В данном случае вода, находящаяся в растворе
справа (слева чистая вода), имеет меньшую активность – она
«связывается» молекулами растворённого вещества и поэтому
суммарный водный поток протекает слева направо.
30.
Рис.4. Осмотическоедавление раствора и его
измерение. Два раствора
разделены
полупроницаемой
мембраной
(изготовленной, например,
из керамики).
31.
В результате объём раствора в правой части сосудаувеличивается, что приводит к подъёму воды в узкой трубке
(но это не капилляр !) в этой правой части сосуда. При этом
весь раствор справа оказывается под избыточным по
отношению
к
атмосферному
гидростатическим
давлением. Оно создаётся столбом жидкости над уровнем
воды в левом сосуде. Таким образом, активность воды
увеличивается и в конце концов сравнивается с её
активностью в левом сосуде.
В этом состоянии скорости перехода слева направо и в
обратном направлении равны. И никакого избыточного потока
молекул растворителя теперь нет. Это давление, таким
образом,
прекращает
осмос
и
называется
осмотическим
давлением.
Знаменитый
голландский химик Вант Гофф (первый в истории лауреат
Нобелевской премии) установил экспериментально, что:
32.
πV = n RT , где π – осмотическое давление, V –объёмраствора в правой части сосуда (с учётом раствора,
находящегося в трубке);
n – число молей растворённого вещества (неэлектролита) в
этом объёме V;
T –температура.
nRT
Очевидно:
CM RT
V
– это есть закон Вант – Гоффа для осмотического
давления.
Оговоримся, что уравнение Вант-Гоффа
применимо только к разбавленным растворам (при увеличении
концентрации начинаются отклонения).
33.
Изучая растворы электролитов, исследователи (Аррениус,Вант-Гофф и др.) заметили, что растворы солей, кислот и
оснований
проявляют
коллигативные
свойства,
подобно
растворам
неэлектролитов,
однако
эффекты
(понижение Тзам, повышение Ткип , ΔP – понижение
давления пара над раствором по сравнению с давлением пара
над чистым растворителем, осмотическое давление
π)
всегда
больше.
Например,
практически
Al2(SO4)3
для разбавленных растворов
в 2 раза; для разбавленных
– практически в 5 раз; для раствора
практически в 3 раза и т.д.
NaCl
–
растворов
CaCl2
–
Из этих данных следовало, что при растворении солей,
кислот и оснований они диссоциируют и их ионы оказывают
независимое действие, например, на понижение
температуры замерзания.
34.
Рассмотрим данные по понижениюΔtзам
растворов NaCl;
К = 1.86°С (молальная криоскопическая постоянная).
Таблица 4.
Концентрация
растворов
(молальность)
0
0.1
0.2
0.3
0.4
0.6
0.8
1.0
t замерз.
t замерз.,
(плавления),
°С
вычисленная в
предположении
100% ионизации;
°С
0.00
– 0.36
– 0.71
–1.05
– 1.39
– 2.05
– 2.69
– 3.38
0.00
– 0.372
– 0.744
– 1.118
– 1.49
– 2.23
– 2.98
– 3.72
водных
Кажущаяся
степень
ионизации
соли (%), (α)
93
91
88
87
84
82
81
35.
Из таблицы видно, что при повышении концентрациивлияние NaCl
на температуру замерзания раствора
оказывается таким, как будто соль в растворе не полностью
ионизована. Действительно, в 1Мл растворе NaCl должно
было бы произойти понижение t замерзания от 0°С до – 3.72 °С,
если считать, что все ионы действуют независимо друг от
друга.
На самом деле t зам 1Мл р-ра понижается до – 3.38°С. На
первый взгляд приходится предположить, что NaCl
ионизован в таком растворе на 90%. Однако, дальнейшее
изучение
других
солей,
например,
MgCl2 , MgSO4,
Al2(SO4)3,
привело к выводу, что все эти соли ионизованы
на 100 %, а отклонения свойств их растворов от идеальных, в
предположении 100 % ионизации, объясняется процессом
ассоциации – или образованием ионных пар. Сама
диссоциация, т.е. ионизация электролита, происходит под
действием молекул воды, при этом происходит гидратация:
36.
Итак, указанные отклонения свойств реальных растворов отсвойств «идеальных» растворов с ионизованными на 100%
электролитами
объясняются
взаимным
притяжением
находящихся в них ионов. Поэтому на температуру замерзания,
или температуру кипения, или на осмотическое давление
раствора NaCl влияют не 2×6.02·1023 ионов, а несколько
меньшее число из-за взаимного притяжения гидратированных
ионов Na+ и
Cl–.
37.
ИЗОТОНИЧЕСКИЙ КОЭФФИЦИЕНТ Вант-ГоффаЧтобы описать это отклонение от идеальной 100% ионизации
или электролитической диссоциации существует несколько
способов. Один из них основан на использовании так
называемого изотонического коэффициента, или
коэффициента Вант-Гоффа. Этот коэффициент, который
обозначается буквой i , был введён Вант-Гоффом для
обозначения отклонения от 100% ионизации. А именно: для
растворов электролитов мы должны иметь:
t зам i K m
(a )
tкип i E m
(b )
p p p i p x2
(c )
i CM RT
(d )
0
0
38.
Физический смысл изотонического коэффициента заключается вследующем:
число образовавшихся частиц в растворе
i
число исходных растворённых частиц
Очевидно, что для электролитов i > 1. Изотонические
коэффициенты
находят
путём
сопоставления
величин,
измеренных экспериментально для некоторого электролита: Δtзам
(Δtкип), Δp, π с соответствующими величинами, рассчитанными
по величине концентрации растворённого вещества:
t зам.эксп. tкип.эксп. pэксп. эксп.
i
t расч.
t расч.
p расч. расч.
39.
В таблице 5 приведены значения коэффициента Вант-Гоффа iдля некоторых растворов, причём выбраны молекулы, которые
диссоциируют в водном растворе на 2 частицы.
Таблица 5. Значения
электролитов 1:1
коэффициента
Раствор
0.5 Мл МХ
(идеальный)
0.5 Мл KCl
1.0 Мл H2SO4
1.0 Мл СH3COOH
1.0 Мл H2S
Вант-Гоффа
i для
Коэффициент
2.00
1.80
1.47
1.004
1.00025
i
40.
Посуществу
коэффициент
Вант-Гоффа
указывает
эффективное число ионных или молекулярных частиц,
образующихся
из
единицы
молекулярного
количества
растворённого вещества. Этим эффективным числом и
определяются:
(1) осмотические свойства раствора;
(2) его температуры замерзания и кипения;
(3) давление паров воды над ним.
Уксусная кислота
СH3COOH
и сероводород
H2S
в
растворе очень мало диссоциированы и поэтому коэффициент i
для них лишь немного превышает единицу.
41.
Степень диссоциацииα
Итак,
мы
видим,
что
различные
электролиты
диссоциированы
по-разному.
Количественной
характеристикой способности электролита распадаться на
ионы в данном растворителе является степень диссоциации
α.
Она показывает, какая доля от общего количества
электролита распадается на ионы. В общем случае степень
диссоциации α зависит от:
1) природы электролита;
2) от природы растворителя;
3) от концентрации раствора;
4) от температуры.
Обычно степень диссоциации α определяют из измерений
электропроводности. При бесконечном разбавлении степень
диссоциации α становится равной 1 и вообще 0 < α ≤ 1.
42.
Таблица 6. Степени диссоциации некоторых кислот (α) в водныхрастворах при концентрации 0.001 М и при Т = 25°С.
Сильные кислоты
HCl
0.993
HNO3
0.997
H2SO4
0.960
Слабые кислоты
HCOOH
0.368
(муравьиная)
СH3COOH
0.126
(уксусная)
HCN
0.0011
(цианистоводородная)
43.
Очевидно, что между значениями i и α имеется связь. Пустьчисло молей электролита в данном объёме раствора равно N,
число ионов, образующихся при ионизации 1 молекулы
электролита равно n, и степень диссоциации этого электролита
в данном растворе α. Тогда, согласно определению α, число
молей ионов в растворе равно n·α·N; число молей электролита,
не подвергшихся диссоциации равно (N – N·α), а полное число
растворённых частиц, следовательно: (N – N·α + n·α·N) .
Следовательно:
N N n N
i
;
N
Отсюда: i = 1 – α + n·α
Окончательно:
i 1
n 1
→
i - 1 = α (n – 1)
Из этого выражения следует, что нужно сделать, чтобы
измерить α.
44.
Итак, в растворах сильных электролитов, у которых α близка к1, имеются гидратированные ионы и реакции в растворах – это
реакции между гидратированными ионами. Например:
Na2SO4 +
BaCl2
=
↓ BaSO4
+ 2NaCl
H2SO4 + Ba(CH3COO)2 = ↓ BaSO4 + 2СH3COOH
Взаимодействие сводится к реакции между гидратированными
ионами
Ba2+(aq) и SO42 (aq).
45.
КОНСТАНТА ДИССОЦИАЦИИ СЛАБОГОЭЛЕКТРОЛИТА
К динамическому равновесию, которое устанавливается в
растворе слабого электролита между молекулами и ионами,
применим закон действия масс и законы химического равновесия.
Рассмотрим, к примеру, диссоциацию синильной
(цианистоводородной) кислоты:
HCN ⇄ H+
+
CN–
Для этого равновесия имеем константу равновесия:
[ H ] [CN ]
Ka
[ HCN ]
46.
В числителе стоят концентрации продуктов диссоциации, ав знаменателе – концентрация недиссоциированных молекул.
Эта величина, называемая
константой диссоциации,
зависит, как и α, от природы электролита и природы
растворителя, а также от температуры, но не от
концентрации. Чем выше Ка, тем легче электролит
диссоциирует.
Многоосновные кислоты и основания двух- и более
валентных атомов металлов диссоциируют ступенчато. В
растворах этих электролитов устанавливаются
сложные
равновесия, в которых участвуют ионы различного заряда.
Например, диссоциация фосфорной кислоты происходит в три
ступени:
47.
Равновесие (1) характеризуется константой диссоциации К1:[ H 2 PO4 ] [ H ]
K1
[ H 3 PO4 ]
Равновесие (2) характеризуется константой диссоциации К2:
[ HPO42 ] [ H ]
K2
[ H 2 PO4 ]
и, наконец, равновесие (3) характеризуется константой
диссоциации К3:
[ PO43 ] [ H ]
K3
[ HPO42 ]
48.
Суммарное равновесие::
и ему соответствует константа равновесия:
K K1 K2 K3
(это легко проверить)
Аналогичным
образом
происходит
ступенчатая
диссоциация
оснований
многовалентных
металлов.
Например, двум ступеням диссоциации Mn(OH ) 2
49.
соответствуютдве константы диссоциации:
[ MnOH ] [OH ]
K1
[ Mn(OH )2 ]
и
[Mn2 ] [OH ]
K2
[ MnOH ]
при этом суммарной диссоциации :
соответствует константа:
K K1 K2
50.
При ступенчатой диссоциации распад по каждой следующейступени происходит в значительно меньшей степени, чем по
предыдущей (по 3ей меньше, чем по 2 ой, по 2ой меньше, чем по
1ой). Иначе говоря, соблюдается неравенство:
K1 K 2 K3
ЗАКОН РАЗБАВЛЕНИЯ ОСТВАЛЬДА
Пусть мы имеем бинарный электролит, например, CuSO4 или
СH3COOH, и пусть его степень диссоциации в данных условиях
равна α, а концентрация равна С (моль/л). Тогда концентрация
каждого из ионов будет С·α, а концентрация нераспавшихся
молекул
51.
Тогда константа равновесия:(C )
K
C
C (1 ) 1
2
2
Это уравнение выражает собой закон разбавления
Оствальда. Оно даёт возможность вычислить степень
диссоциации электролита α при различных его концентрациях,
если известна его константа диссоциации. Если α очень мала, то
есть
α << 1,
то :
K C
2
K
C
52.
Следовательно:K
C
Степень диссоциации возрастает при разбавлении раствора
(т.е. при уменьшении его концентрации С ). Этот вывод вытекает
из природы явления диссоциации: два процесса – (1)
диссоциация и (2) образование молекулы из ионов протекают
одновременно в противоположных направлениях и с одинаковой
скоростью
при
равновесии.
Разбавление
раствора
не
препятствует
ассоциации
диссоциации,
но
препятствует
– из-за уменьшения вероятности столкновения
двух ионов. Отсюда и следует вывод об увеличении
разбавлением.
α
с
53.
ИОННОЕ ПРОИЗВЕДЕНИЕ ВОДЫ.ВОДОРОДНЫЙ ПОКАЗАТЕЛЬ.
54.
При обычных условиях вода тоже является слабым электролитом. Онав слабой степени ионизована и равновесие её диссоциации
описывается законом действия масс (имеется в виду равенство
скоростей прямой и обратной реакций):
H2O
Н+
+ OH
Константа равновесия при 25 С (298К) имеет значение:
[ H ] [OH ]
Кд
[ H 2 O]
= 1.86 10–16
Столь ничтожно малая величина константы диссоциации воды позволяет
считать, что:
1000
масса 1л воды
55.56
=
[H2O] = const =
M H 2O
18
Тогда
Кд [H2O] = 1.86 10–16 55.56 = 1 10–14
55.
Отсюда следует, что в чистой воде при 298 К [Н+] = [OH ]1 10 14
=
= 10–7 моль/л.
(Очевидно,
что
при
любой
температуре [Н+] = [OH ] ≠10–7 моль/л).
другой
Введём определение. Обозначим отрицательный логарифм
концентрации ионов водорода {–log[H+]} через символ рН, а
отрицательный логарифм концентрации гидроксильных ионов
–lg[OH–] = pOH.
рН называют водородным показателем, а рОН – гидроксильным
показателем. Очевидно, что поскольку рН непосредственно связан с
концентрацией ионов водорода , его измерения чрезвычайно важны в
химии и особенно в агрохимии.
56.
Также очевидно, что поскольку всегда [H]·[OH]=10–14, торН + рОН = 14.
Также очевидно, что в чистой воде рН = рОН = 7. Очевидно
далее, что если [H+] > 10–7, например, 10–5 или 10–1, или 2, то
рН< 7. Рассмотрим, например, случай [H+] = 10–1, тогда – lg[H+] =
+1, а если [H+] = 2, то –lg[H+] = – lg 2 = –0.301. Очевидно, что и +1 и
–0.3 < 7.
Естественно, что в щелочной среде рН > 7.
Пример. Найти рОН раствора гидроксида аммония NH4OH с
концентрацией [NH4OH] = 0.03 моль/л, если
α- степень
диссоциации NH4OH в этом растворе α= 0.013.
Решение
рОН = –lg[OH–].
Диссоциация
NH4OH
протекает по
уравнению:
NH4OH ⇄ NH4+ + OH–
(1)
57.
По определению α есть отношение числа диссоциированныхмолекул (или молей) NH4OH к числу растворенных молекул
(молей) NH4OH. Следовательно [OH–] равна концентрации
распавшейся части основания, т.е.
[OH–] = α·[NH4OH] = 0.013·0.03 = 3.9×10–4 моль/л
Отсюда pOH = 4 – lg3.9 = 4 – 0.59 = 3.41
58.
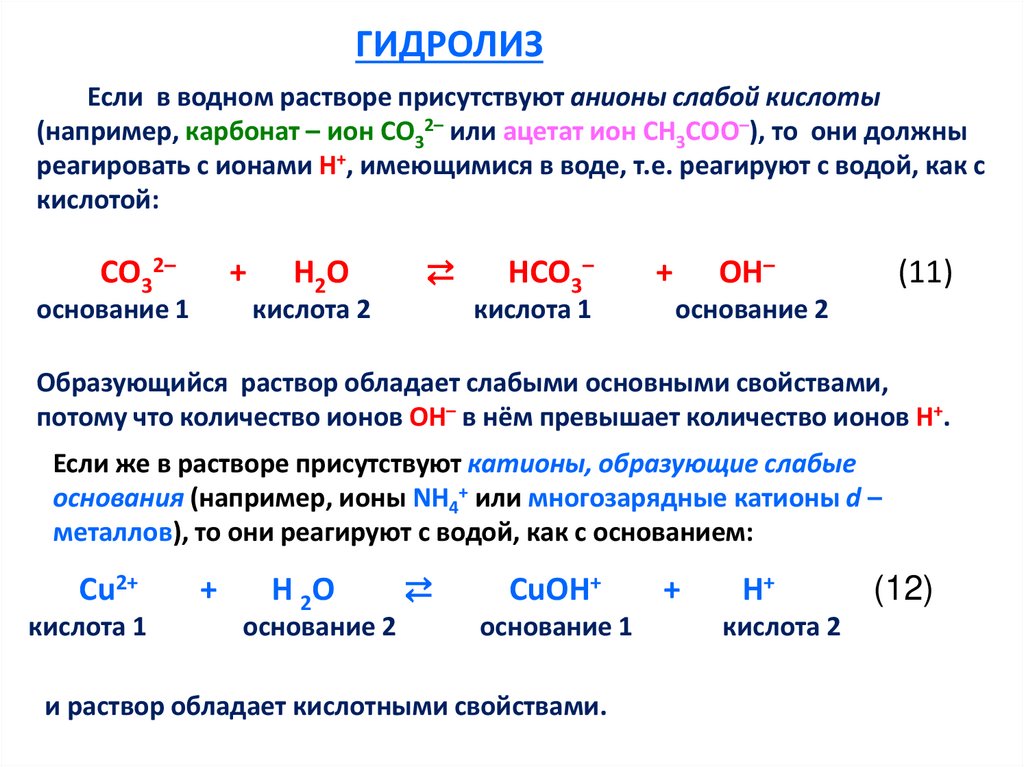
ГИДРОЛИЗЕсли в водном растворе присутствуют анионы слабой кислоты
(например, карбонат – ион СО32– или ацетат ион СН3СОО–), то они должны
реагировать с ионами Н+, имеющимися в воде, т.е. реагируют с водой, как с
кислотой:
СО32–
+
основание 1
Н2О
⇄
кислота 2
НСО3–
кислота 1
ОН–
+
(11)
основание 2
Образующийся раствор обладает слабыми основными свойствами,
потому что количество ионов ОН– в нём превышает количество ионов Н+.
Если же в растворе присутствуют катионы, образующие слабые
основания (например, ионы NH4+ или многозарядные катионы d –
металлов), то они реагируют с водой, как с основанием:
Cu2+
кислота 1
+
Н 2О
основание 2
⇄
CuOH+
основание 1
и раствор обладает кислотными свойствами.
+
H+
кислота 2
(12)
59.
Говорят, что в этих случаях соли, а точнее ионы подвергаютсягидролизу (в приведённых примерах ионы СО32– и Cu2+).
Итак, гидролиз это обменная химическая реакция ионов солей с
водой.
Если в воде растворяют соль, содержащую указанные ионы (катион
слабого основания или анион слабой кислоты, или оба таких иона), то
она гидролизуется.
Глубина или степень гидролиза h, зависит от констант диссоциации
(ионизации), соответственно слабой кислоты Ка, или слабого
основания Кb, или их произведения. Чем меньше эти константы Ка и
Кb , тем сильнее гидролизуется соль. Покажем это.
60.
Пусть мы наблюдаем гидролиз соли, содержащей анион А– слабойкислоты НА:
А– +
НОН
⇄
НА
+
ОН–
(13)
Устанавливается так называемое гидролитическое равновесие (13),
которое описывается соответствующей константой равновесия:
[ HA] [OH ]
Kр
[ A ] [ H 2O ]
Считая, как и прежде, [H2O] практически постоянной, введём её в константу;
получим новую константу, называемую константой гидролиза Кг ,
[ HA] [OH ]
K р [ H 2O] K г
[A ]
61.
[H ]Умножим это уравнение на дробь
1
[H ]
, тогда получим:
[ HA] [OH ] [ H ] K H 2O
Kг
[ A ] [H ]
Ka
(15)
62.
В этом случае константа гидролиза есть отношение ионногопроизведения воды
к константе ионизации слабой кислоты.
Очевидно, что чем меньше знаменатель этой дроби, тем больше вся
дробь, т.е.
есть отношение произведения концентраций продуктов реакции (13)
к концентрации соли. Следовательно, если некоторая кислота НА1 имеет
Ка1
меньшую, чем Ка2 для второй кислоты НА2, то соли этих кислот с
одним и тем же основанием будут гидролизованы по-разному, а именно,
соль кислоты (1) будет гидролизована сильнее чем соль кислоты (2).
63.
Аналогичным способом можно получить выражение для константыгидролиза соли, образованной слабым основанием и сильной
кислотой, например:
M n+ + HOH
=
MOH (n-1)+
+
H+
для этой реакции будем иметь:
[ MOH ( n 1) ] [ H ] [OH ] K H 2O
Kг
n
[ M ] [OH ]
Kb
и для подобных реакций всегда
Kг
K H 2O
Kb
, где Кb – константа ионизации слабого основания.
Если же соль образована и катионом и анионом слабых электролитов
(т.е. кислоты и основания), то
K
Kг
H 2O
K a Kb
64.
Степень гидролиза hСтепень гидролиза
h
соли (s) по смыслу очень близка к степени
диссоциации слабого электролита α. А именно, она (h) показывает, как
глубоко в данных условиях гидролизуется соль. h есть отношение числа
гидролизованных молей соли к числу растворённых молей этой соли (Сs):
Cг
h
Сs
(16)
Как и раньше, в случае диссоциации слабого электролита, легко
получить связь между константой гидролиза Кг и степенью гидролиза
h. Например, в случае гидролиза соли сильного основания и слабой
кислоты имеем уравнение (13):
65.
А– +НОН
и
⇄
НА
+
ОН–
(13)
[ HA] [OH ]
Kг
[ A ]
И поскольку из (13) очевидно , что [НА] = [ ОН–], то:
[OH ]2
Kг
[ A ]
Пусть имеется Сs молей соли в растворе, из них h· Сs = Сг молей
подверглись гидролизу, осталось негидролизованных Сs – h· Сs = Сs (1 – h)
молей. Очевидно, что каждый 1 гидролизованный моль даёт 1 моль ионов
ОН– и один моль молекул НА. Тогда очевидно, что
hCs hCs h Cs
Kг
Cs (1 h) 1 h
2
(17)
66.
В огромном числе случаев h очень мало по сравнению с 1, поэтому (h ≪1)Кг ≃ h2·Cs
и
h
Kг
Сs
Это выражение для h полностью совпадает по форме с законом разведения
Оствальда для диссоциации слабых электролитов.
Если же соль образована и анионом слабой кислоты и катионом слабого
основания, то тогда h уже сравнима с 1, и тогда в знаменателе уравнения
(17) нельзя пренебрегать величиной h. Тогда для нахождения степени
гидролиза h необходимо решать квадратное уравнение ( из уравнения 17):
Kг
h2
1 h Сs
где
Kг
K H 2O
K a Kb
Величины, входящие в Кг берутся из таблиц, а Cs - концентрация
задана. Но очевидно, что чем более разбавлен раствор, тем больше
степень гидролиза h.
67.
Пример. Найти степень гидролиза соли Zn(CH3COO)2 в растворе сконцентрацией 0.05 моль/л. Эта соль образована слабой кислотой –
уксусной, для неё Ка = 1.8×10–5 и слабым основанием Zn(OH)2. Для
него, вообще говоря, имеются две ступени диссоциации:
(1)
(2)
Нам следует учитывать только гидролиз по первой ступени, т.к. при
диссоциации соли Zn(CH3COO)2 образуются ионы Zn2+, то они
сразу же гидролизуются:
Zn2+ + НОН →
ZnOH+
+ H+
Гидролиз по второй ступени
проходит значительно слабее,
Это видно хотя бы из сравнения констант диссоциации:
Итак, при гидролизе имеем:
68.
Zn2+ + СН3СОО– + НОН →2
Kг
h
Имеем:
1 h Сs
Kг
ZnOH+
+ СН3СООН
K H 2O
K ZnOH KCH3COOH
10 14
1.8 10 5 1.5 10 9
69.
Решение задач по теме РАСТВОРЫ70.
Задачи1. Сколько г Ni(HCOO)2 содержится в 11л 0.3M раствора? Найти
его нормальность.
2. Написать реакцию гидролиза соли NaHCO3 и рассчитать рН
раствора, полученного при растворении 6.3 г соли в 2 л воды,
если Ка1 = 4.45 10-7.
3.Связь между i и степенью диссоциации . Рассчитать i в 0.02
M растворе Cr2(SO4)3, если = 0.92.
4. Написать реакцию гидролиза соли Sr(ClO)2 и рассчитать рН
раствора при растворении 14 г соли в 1 л воды, если Ка = 3 10-8.
5. Рассчитать молярность 10% раствора H2SO4, если его
плотность d =1.18 г/мл, какой объём 0.268 н NaОН пойдёт на
нейтрализацию 20 мл раствора серной кислоты?
71.
6. В двух стаканах приготовлены растворы 2х солей: в одномZn(CH3COO)2, в другом ZnBr2 одинаковой концентрации, 002н.
Обе соли подвергнутся гидролизу. Написать обе реакции
гидролиза и определить, в каком из этих 2-х растворов степень
гидролиза h будет больше и в каком из них рН будет выше?
7. Рассчитать pOH водного раствора KH2BO3, если Сs = 0.02M
и Ka1= 5.83 10 10
8. Какой должна быть концентрация изопропилового спирта (iC3H7OH) в водном растворе изотоничным (имеющим такое же
осмотическое давление) c 0.2 M водным раствором KBr с
кажущейся степенью диссоциации =0.85 ?
9. Какой должна быть концентрация этанола C2H5OH в водном
растворе изотоничным (имеющим такое же осмотическое
давление) с 0.2 M водным раствором СaCl2 с кажущейся степенью
диссоциации = 0.75?
10. Написать реакцию гидролиза соли Ba(NO2)2 и рассчитать рН
раствора при растворении 22.9 г соли в 1 л воды, если Ка =5.1 10 4 .
72.
73.
РЕШЕНИЕЗАДАЧ
74.
1. Задача.Сколько г Ni(HCOO)2 содержится в 11л 0.3M раствора? Найти его
нормальность.
В 11л 0.3М раствора содержится : 0.3× 11 = 3.3 моля соли
Ni(HCOO)2.
1 моль Ni(HCOO)2 имеет молярную массу :
58.7 (Ni) + (1+12+16×2)×2 = 58.7 + 90= 148.7 г .
Следовательно, в 11 л раствора масса соли равна :
m = 148.7 × 3.3 = 490,71 г
2. Задача
Написать реакцию гидролиза соли NaHCO3 и рассчитать рН
раствора, полученного при растворении 6.3 г соли в 2 л воды,
если Ка1 = 4.45 10-7.
75.
Реакция гидролиза соли NaHCO3 записывается так :1.
Na+ + HCO3‒ + H2O ⇄ Na+ + H2CO3 + OH‒
то есть реально происходит реакция гидролиза аниона HCO3‒
(поскольку ионы Na+ в реакции не участвуют):
(2)
HCO3‒ + H2O ⇄ H2CO3 + OH‒.
Мы видим, что среда стала щелочной, т.е. рН должен быть > 7
Расчёт рН среды:
Подсчитаем Молярную массу соли М NaHCO3 : 23 + 1 + 12 + 48 = 84г
Следовательно, 6.3г соли в растворе составляют : 6.3/84 = 0.075 моля
и они растворены в 2 л воды, следовательно: концентрация соли
Сs = 0.075:2= 0.0375 М
Равновесие (2) описывается константой равновесия Кравнов. ,
называемой константой гидролиза Кг*:
76.
Здесь поставлен верхний индекс (*), потому что далее мыперенесём концентрацию [H2O] (считая её константой) из
знаменателя в левую часть уравнения, как показывает стрелка,
и теперь получим слева произведение Кг*∙[H2O], которое мы и
назовём константой гидролиза Кг.
Заметим, что из уравнения (2) следует, что в нём справа:
[H2CO3] = [OH‒] поскольку обе эти частицы образуются в
соотношении 1:1 и потому их концентрации в растворе равны.
Тогда можно написать (поскольку, хотя частицы разные, но их
концентрации, т.е. числа молей в единице объёма
одинаковые):
77.
Ранее при рассмотрении темы гидролиза (см. лекцию) мыполучили, что
Кг = Kw/Ka1 ,
где Kw – ионное произведение воды Kw = 10‒14, а Ка1 = 4.45 10‒7
по условию задачи.
(Заметим, что в уравнении (2) участвуют две формы угольной
кислоты:
H2CO3 и HCO3‒ , т.е. это формы первой ступени
диссоциации угольной кислоты H2CO3 ⇄ Н+ + HCO3‒
(ведь есть ещё вторая ступень диссоциации: HCO3‒ ⇄ Н+ + СО32‒ )
Поэтому сразу находим:
[OH‒]2 = Кг · [HCO3‒] = Kw/Ka1 · [HCO3‒],
[OH‒] = √ Kw/Ka1 · [HCO3‒]
= 2.9·10‒5
и отсюда:
= √ (10‒14/4.45·10‒7) · 0.0375
И, следовательно, [Н+] = 10‒14 /2.9·10‒5 = (10/2.9)·10‒10 = 3.45·10‒10
и pH = 10 – lg3.45 = 9,46
Итак, мы имеем щелочную среду, в которой
рН = 9.46
78.
Задача 3Связь между изотоническим коэффициентом i и кажущейся
степенью диссоциации . Рассчитать i в 0.02 M растворе
Cr2(SO4)3, если = 0.92.
Молекула Cr2(SO4)3 распадается (диссоциирует) на 5 ионов,
следовательно, n = 5.
По уравнению Вант-Гоффа:
т.е.:
i = 1 + α(n – 1)= 1 + 0.92·4 = 4.68
Написать реакцию гидролиза соли Sr(ClO)2 и рассчитать рН раствора при
растворении 14 г соли в 1 л воды, если Ка = 3 10-8.
Пишем реакцию диссоциации соли Sr(ClO)2:
(1)
Sr(ClO)2 = Sr2+ + 2 ClO‒ .
В этом полученном растворе соли ионы Sr2+ не образуют слабого
основания, поскольку Sr щёлочно – земельный металл, который образует
сильное основание Sr(OH)2, которое полностью диссоциирует.
Но ион ClO‒ образует слабую хлорноватистую кислоту HClO с константой
диссоциации Ка = 3 10-8, поэтому ион ClO‒ гидролизуется:
(2)
ClO‒ + H2O ⇄ HClO + OH‒
т.е. раствор становится щелочным, т.к. в нём накапливаются ионы OH‒.
79.
Задача 4.Написать реакцию гидролиза соли Sr(ClO)2 и рассчитать рН
раствора при растворении 14 г соли в 1 л воды, если Ка = 3 10-8.
Пишем реакцию диссоциации соли Sr(ClO)2:
(1)
Sr(ClO)2 = Sr2+ + 2 ClO‒ .
В этом полученном растворе соли ионы Sr2+ не образуют
слабого основания, поскольку Sr щёлочно – земельный металл,
который образует сильное основание Sr(OH)2, которое
полностью диссоциирует.
Но ион ClO‒ образует слабую хлорноватистую кислоту HClO с
константой диссоциации Ка = 3 10-8, поэтому ион ClO‒
гидролизуется:
(2)
ClO‒ + H2O ⇄ HClO + OH‒
т.е. раствор становится щелочным, т.к. в нём накапливаются
ионы OH‒.
80.
По аналогии с соображениями, приведёнными в задаче 2, можемзаписать:
(3)
[OH‒]2 = Кг · [ClO‒] = Kw/Ka · [ClO‒]
Здесь: [ClO‒] ‒ концентрация ионов ClO‒, образовавшихся в
растворе соли Sr(ClO)2 в результате её диссоциации по ур. (1) и
из этого уравнения
следует, что [ClO‒] = 2[Sr(ClO)2], т.к. из 1 моля соли Sr(ClO)2
образуется 2 моля ионов ClO‒ (по уравнению (1) См. выделение
жёлтым цветом).
Рассчитаем концентрацию соли [Sr(ClO)2] в растворе по данным
задачи: 14 г соли в 1 л воды.
Масса 1 моля Sr(ClO)2 равна 87.6 + 2(35.5 + 16) =87.6 + 103 = 190.6
Следовательно, концентрация соли равна 14/190,6 = 0,0734
моль/л, а [ClO‒] = 2· 0.0734 =0,147 Моль/л
Далее, по уравнению (3):
81.
[OH‒] = √(10‒14/3·10‒8)· 0,147 = 2.21·10‒4 ;Следовательно [H+] = 10‒14 /2.21·10‒4 = 4.52·10‒11 и наконец
pH = ‒lg[H+] = 11 – 0.655 = 10.345. Среда щелочная.
82.
Задача 5Рассчитать молярность 10% раствора H2SO4, если его
плотность d =1.18 г/мл, какой объём 0.00268 н NaОН пойдёт на
нейтрализацию 20 мл данного раствора серной кислоты?
Решение
Итак, 10% раствор H2SO4 имеет d = 1.18 г/мл; Следовательно,
1000 мл = 1л раствора имеет массу 1180 г. и 10% от этой массы
приходится на H2SO4, т.е. 118 г. Молярная масса H2SO4 равна 98
г, следовательно в 1 л этого раствора содержится : 118/98 =
1,204 моля H2SO4 или
2×1,204 = 2,408 эквивалента H2SO4, или 0.0024 экв. в 1 мл этого
раствора. Поэтому раствор H2SO4 является 1.204 М и 2.408 н.
Вторая часть задачи.
Все вещества реагируют в эквивалентных соотношениях,
следовательно, число эквивалентов H2SO4, содержащихся в 20
мл её раствора, обязано равняться числу эквивалентов
0.00268 н NaОН, содержащихся в объёме Х мл.
Составим равенство
0.00268 · Х мл = 0.0024 · 20 мл ;
Следовательно: Х = (0.0024 × 20)/ 0.00268 = 17,9 мл
83.
Задача 6Какой должна быть концентрация изопропилового спирта
(i-C3H7OH) в водном растворе изотоничным (имеющим такое
же осмотическое давление) c 0.2 M водным раствором KBr с
кажущейся степенью диссоциации =0.85 ?
Решение
По закону Вант-Гоффа осмотическое давление раствора
неэлектролита (в нашем случае спирта i-C3H7OH) равно:
= СM RT
Здесь СМ – молярная концентрация этого раствора.
Для раствора электролита этот закон имеет вид:
= i СM*RT , где i-изотонический
коэффициент
Поскольку наши изотонические растворы оба имеют разные
концентрации, но одно и то же осмотическое давление,
концентрацию раствора электролита обозначим См*.
Очевидно: СM = i СM*.
84.
Найдём i , воспользовавшись уравнением, связывающимi и :
где n - число ионов, на которые распадается молекула соли в
растворе, у нас n = 2 (KBr)
Следовательно n – 1 = 1 и i = +1 = 0.85 + 1 = 1.85. Отсюда
следует, что
СM = iСM* = 1.85 · 0.2 M = 0.37М
Ответ: концентрация изопропилового спирта должна быть
0.37М.
85.
Решение задач дома по задачнику Н.Л. ГлинкиГлава VI.
РАСТВОРЫ
№№ : 397, 398, 400, 401, 404, 406, 407, 411, 414, 415, 416, 418, 421,
428, 429, 431, 440, 444, 445, 446
464, 468, 474, 480, 490, 493, 498, 499
516, 517, 518, 522, 525
А также нерешённые мной задачи из списка 10 задач,
приведённых выше на стр.1
86.
Задача 6В двух стаканах приготовлены водные растворы 2х солей: в одном
Zn(CH3COO)2, в другом ZnBr2 одинаковой концентрации, 0.04н (0.02М)
Обе соли подвергнутся гидролизу. Написать обе реакции гидролиза и
определить, в каком из этих 2-х растворов степень гидролиза h будет
больше и в каком из них рН будет выше?
Решение
Сначала вернёмся к лекции РАСТВОРЫ (слайд 64 Степень гидролиза h)
И рассмотрим понятие степень гидролиза h
Найдём степень гидролиза соли Zn(CH3COO)2 в растворе с
концентрацией 0.02 н. Эта соль образована слабой кислотой – уксусной,
для неё Ка = 1.8×10–5 и слабым основанием Zn(OH)2. Для него имеются
две ступени диссоциации:
(1)
(2)
87.
Нам следует учитывать только гидролиз по первой ступени, т.к. придиссоциации соли Zn(CH3COO)2 образуются ионы Zn2+, то они
сразу же гидролизуются:
Zn2+ + НОН →
ZnOH+
+ H+
Гидролиз по второй ступени
проходит значительно слабее,
Это видно хотя бы из сравнения констант диссоциации (см. реакции
(1) и (2) на предыдущем слайде. Из них видно, что диссоциация по
второй ступени более чем в 10000 раз слабее, чем по первой).
Итак, при гидролизе имеем:
Zn2+ + СН3СОО– + НОН →
Имеем:
2
K
h
г
1 h Сs
Kг
ZnOH+
+ СН3СООН
K H 2O
K ZnOH KCH3COOH
10 14
1.8 10 5 1.5 10 9
88.
илиh = 95%
Найдём теперь степень гидролиза соли ZnBr2 в растворе с
концентрацией 0.04 н (0.02 M). Эта соль образована сильной кислотой –
HBr, и слабым основанием Zn(OH)2. Для него имеются две ступени
диссоциации, но как говорилось выше следует учитывать только
гидролиз по 1 ступени:
Zn2+ + НОН →
ZnOH+
+ H+
а по второй он протекает в ничтожной степени.
В огромном числе подобных случаев h очень мало по сравнению с 1,
поэтому (h ≪1)
Кг ≃ h2·Cs
и
h
Kг
Сs
89.
ТеперьПолучим в результате h = 0,018, т.е. h = 1.8%
Очевидно, что соль Zn(CH3COO)2 гидролизовалась практически
полностью (на 95%) и реакция раствора должна быть близкой к 7, т.к.
образовавшиеся ионы H+ и OH- нейтрализуют друг друга. А соль
ZnBr2 при гидролизе на 1.8% образует ионы H+ и раствор становится
слегка кислым; следовательно , его рН <7.
Задача 7. Рассчитать pOH водного раствора KH2BO3, если Сs = 0.02M
и Ka1= 5.83 10 10
Пишем реакцию гидролиза этой кислой соли, содержащей
слабую ортоборную кислоту H3BO3, диссоциирующую по
первой ступени по уравнению:
90.
Гидролизу подвергается ион H2BO3‒ по реакции:H2BO3‒ + HOH ⇄ H3BO3 + OH‒
По аналогии с соображениями, приведёнными в задаче 2, можем
записать:
[OH‒]2 = Кг· [H2BO3‒ ] = Kw/Ka1 · [H2BO3‒ ]
Отсюда следует :[OH]2 = (Kw/Ka1) ·Cs = 10‒14 / 5.83 10 10 =
1·10-4/5.83 = 1.72·10-5
Далее: [OH‒] = √17.2·10-6 = 4.15·10‒3
Находим pOH:
pOH = -lg[OH‒] = -lg4.15·10‒3 = 3 -0,62 =2.38
и, наконец, рН = 14 – 2.38 = 11.62
91.
Задача № 8 Какой водный раствор быстрей замёрзнет 0.1 m1 растворглюкозы или 0.024 m2 раствор Fe2(SO4)3 ? Считать, что кажущаяся
степень диссоциации Fe2(SO4)3 α = 0.92. Криоскопическая постоянная
воды K = 1.86 (oC/моль/кг).
Согласно второму следствию закона Рауля понижение ΔТ замерзания
раствора пропорционально его молальности:
ΔTзам = K∙ m1, где m1 ‒ молальность раствора (число молей растворённого
вещества на 1 кг растворителя).
Для раствора электролита закон выглядит так : ΔTзам = i K∙ m2,
где i ‒ изотонический коэффициент Вант-Гоффа
m1 и m2 – молальности естественно различны.
Для раствора Fe2(SO4)3 надо рассчитать коэффициент i по формуле ВантГоффа: α = (i - 1)/(n - 1). Для соли Fe2(SO4)3
n = 5 → отсюда n -1 = 4. Сл-но : 4 α = i – 1 и i = 1 + 4α
Следовательно i = 1 + 4·0.92 = 4,68
Рассчитываем ΔTзам р-ра спирта и ΔTзам р-ра соли
ΔTзам р-ра спирта = 1.86· 0.1 = 0.186 оС
ΔTзам р-ра соли = 1.86·0.024·4.68 = 0,209оС
Следовательно, раствор спирта замёрзнет первым при –0.186оС, а
раствор соли замёрзнет чуть позже при ‒0,209оС
92.
Задача № 8 Какой водный раствор быстрей закипит 0.3 m1раствор сахарозы или 0.08 m2 раствор AlCl3 ?
Считать, что кажущаяся степень диссоциации AlCl3 α = 0.90.
Эбуллиоскопическая постоянная воды Е = 0.52 oC.
Решение
Имеем 2 раствора : раствор 1 (неэлектролита – сахарозы) и раствор 2
(соли AlCl3)
m2,сахар.= 0.3 моль/кг и m2, AlCl3 = 0.08 моль/кг
эбуллиоскопическая постоянная воды Е = 0.52оС
Считаем повышения ΔТ кипения для двух растворов:
ΔТ кип.1 = 0.52·0.3 = 0,156оС
Для раствора соли ΔТ кип.2 = i · 0.52·0.08
Рассчитаем i по уравнению Вант-Гоффа:
α = (i – 1) / (n – 1); у нас n = 4; поэтому n -1 = 3 и
i = 1 + 3 α = 1 + 3·0.90 = 3.7
Тогда: ΔТкип.2 = 0.52·0.08·3.7 = 0,154 оС
Очевидно, что ΔТ кип.1 = 0,156оС почти не отличается от ΔТкип.2 = 0,154 оС,
но всё же несколько больше: раствор сахарозы кипит всё же при
немного более высокой Т. чем раствор соли AlCl3
93.
Задача (Глинка)В каком объёме 1М раствора и в каком объёме 1н раствора содержится
114 г Al2(SO4)3 ?
Решение
Для начала подсчитаем молярную массу Al2(SO4)3 .
МAl2(SO4)3 = 27 2 + (32 +4 16)·3 = 342 и очевидно, что 1 моль Al2(SO4)3
содержит 6 эквивалентов (напомню, что эквивалентом вещества
называется такое его весовое количество, которое реагирует (вытесняет,
соединяется и т.п.) с 1 весовой частью водорода. Поскольку ион Al3+ имеет
заряд +3, он эквивалентен 3 ионам Н+ . В соли Al2(SO4)3 содержится 2
иона Al3+ . Поэтому 1 моль соли эквивалентен 6 молям иона Н+ .
По определению 1 л 1М раствора Al2(SO4)3 содержит 342 г соли,
следовательно 114 г Al2(SO4)3 содержатся в 333 мл.
По определению 1 л 1н раствора Al2(SO4)3 содержит 342/6 = 57 г соли,
следовательно 114 г Al2(SO4)3 содержатся в 2л раствора.
94.
Задача № 402 (Глинка)К 500 мл 32% - ной (по массе ) HNO3 (ρ = 1,20 г/мл) прибавили 1 л воды.
Чему равна массовая доля HNO3 в полученном растворе?
Решение
Найдём массу 500 мл исходной кислоты HNO3 .
M = 500 мл × 1,20 г/мл = 600 г. Из них 600 0.32 = 192 г приходится
на 100% ‒ ную HNO3 . После прибавления 1 л воды к 500 мл
исходной кислоты масса раствора стала 1000 + 600 = 1600 г.
Массовая доля (процентное содержание ) HNO3 стало равным
Х = (192×100)/1600 = 12%
95.
Задача № 442 (Глинка)Для нейтрализации 20 мл 0.1н раствора кислоты потребовалось 8 мл
раствора NaOH. Сколько граммов NaOH содержит 1 л этого раствора?
Решение
Вещества всегда реагируют в эквивалентном соотношении – это
закон эквивалентов.
В 20 мл 0.1 н раствора кислоты (любой !!! ) содержится
(20 × 0.1)/1000 эквивалентов. Это следует из определения нормальности
раствора: нормальностью раствора называется число эквивалентов в 1л = 1000
мл раствора, отсюда - в 20 мл содержится (20 × 0.1)/1000 эквивалентов.
Такое же количество эквивалентов щёлочи NaOH пошло на титрование
(нейтрализацию) этой кислоты:
Следовательно (8 мл × Cн )/1000 = (20 × 0.1)/1000
Отсюда: 8 мл × Cн = 20 × 0.1 и Cн = 2/8 = 0,25н
1 эквивалент NaOH = 1 молю = 40 г. Отсюда количество г NaOH в 1 л 0.25н
раствора равно 40×0,25 = 10г
96.
Задача № 428 (Глинка)В 1 кг воды растворено 666 г KOH; плотность раствора равна 1,395 г/мл.
Найти: а)массовую долю КОН ; б) молярность; в) молальность; г) мольные
доли щёлочи и воды.
Решение
Прежде всего напомним, что единицы концентрации могут быть объёмные
(б) , весовые (а) и (в) и безразмерные (г).
1.Находим (а) - массовую долю КОН в растворе: (666×100)/1666 = 0, 39976 = 0.4
2. Находим (в) – молальность раствора КОН – число молей КОН на 1 кг растворителя. 1
моль КОН имеет массу 39.1 +17 = 56.1г, отсюда число молей
КОН, растворённых в 1 кг воды равно: 666/56.1 = 11,87 и это есть молальность раствора
3. Находим (в) – молярность раствора КОН – число молей КОН в 1 л раствора.
Наш раствор имеет массу 1666 г и плотность ρ = 1,395 г/мл. Следовательно, его
объём равен 1666г / 1,395 г/мл = 1194,265 мл = 1194,3 мл и потому молярность
раствора есть (11.87/1194,3)×1000 = 9,9 моль/л
4. Находим мольные доли KOH и H2O в полученном растворе:
Мы знаем число молей KOH , оно равно 11,87, а число молей H2O в 1 кг равно
1000/18 = 55,56. Суммарное число молей 67.63. И следовательно мольные доли равны :
X H2O = 55,56/67,63 =0,82;
X KOH = 11,87/67,63 = 0,18



























































































 chemistry
chemistry








