Similar presentations:
Строение атома водорода
1. СТРОЕНИЕ АТОМА ВОДОРОДА
2.
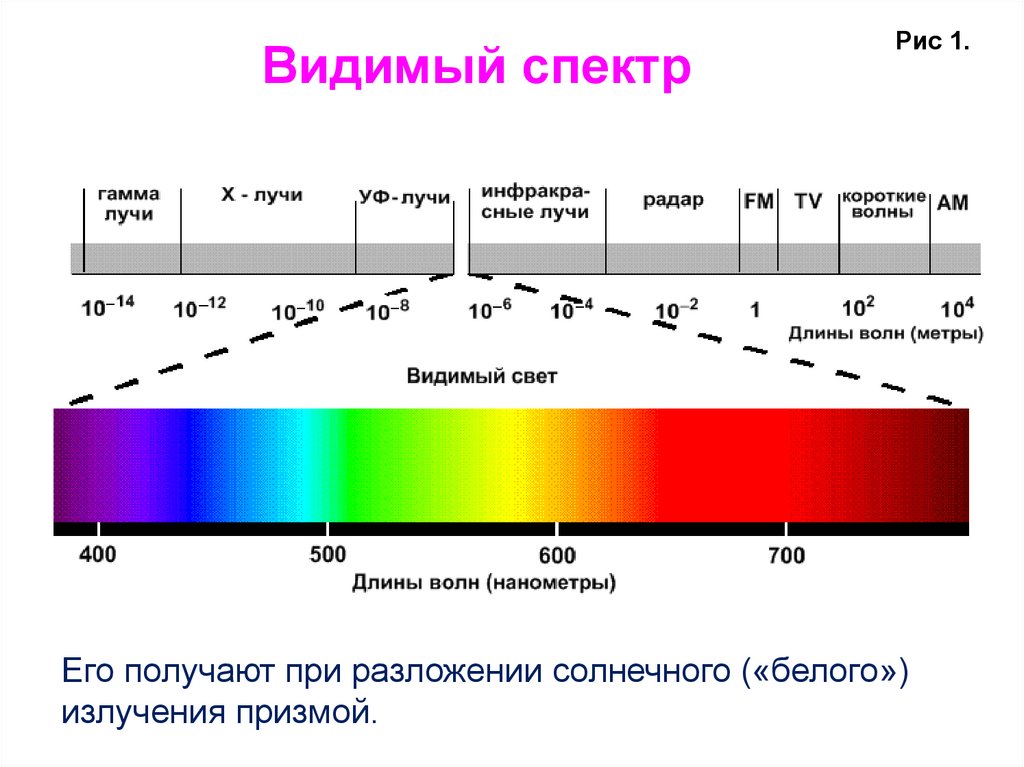
Видимый спектрРис 1.
Его получают при разложении солнечного («белого»)
излучения призмой.
3.
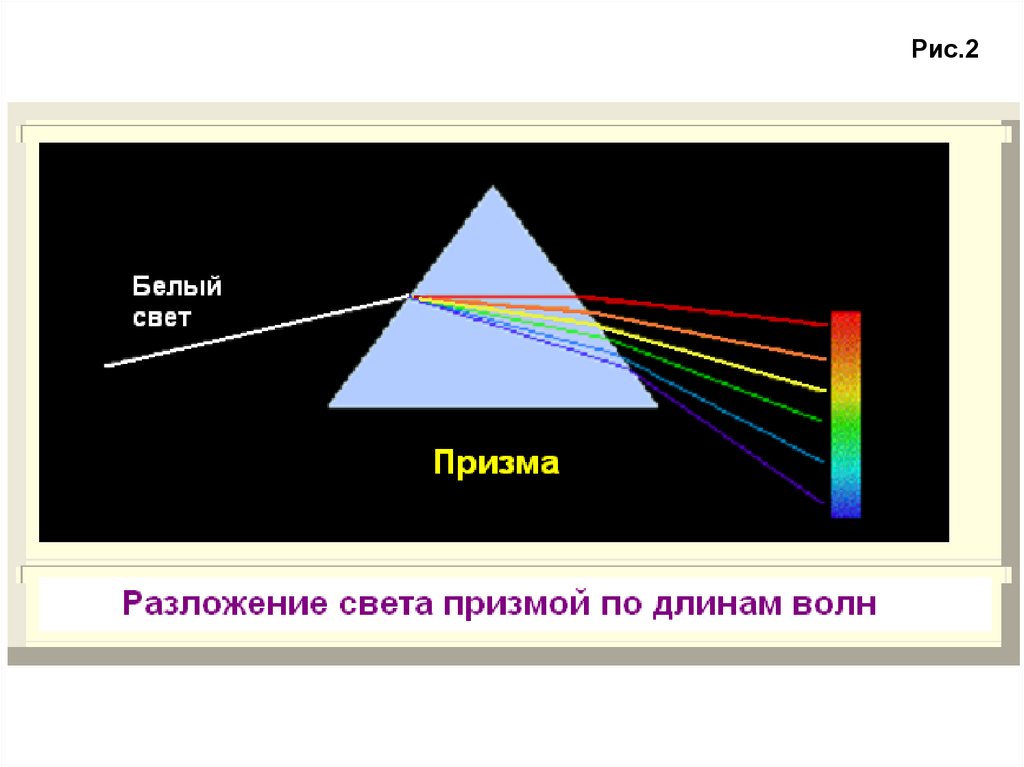
Рис.24.
Однако, если вместо источника белого света перед призмойпоместить излучающую среду (например, сильно нагретый газ
или газ с зажжённым в нём разрядом), то на белом экране за
призмой появится эмиссионный спектр соответствующего
газа: в нём на бледном фоне сплошного спектра (сильно
ослабленного по сравнению с сплошным спектром сильно
нагретого – раскалённого тела или Солнца) будут ярко светиться
несколько (иногда много) ярких линий, характерных именно для
этого вещества.
Если же на пути интенсивного пучка белого света поставить
прозрачную кювету с поглощающим веществом, то наоборот, на
ярком фоне сплошного спектра будут видны тёмные (чёрные)
линии (т.е. отсутствие в спектре некоторых длин волн.
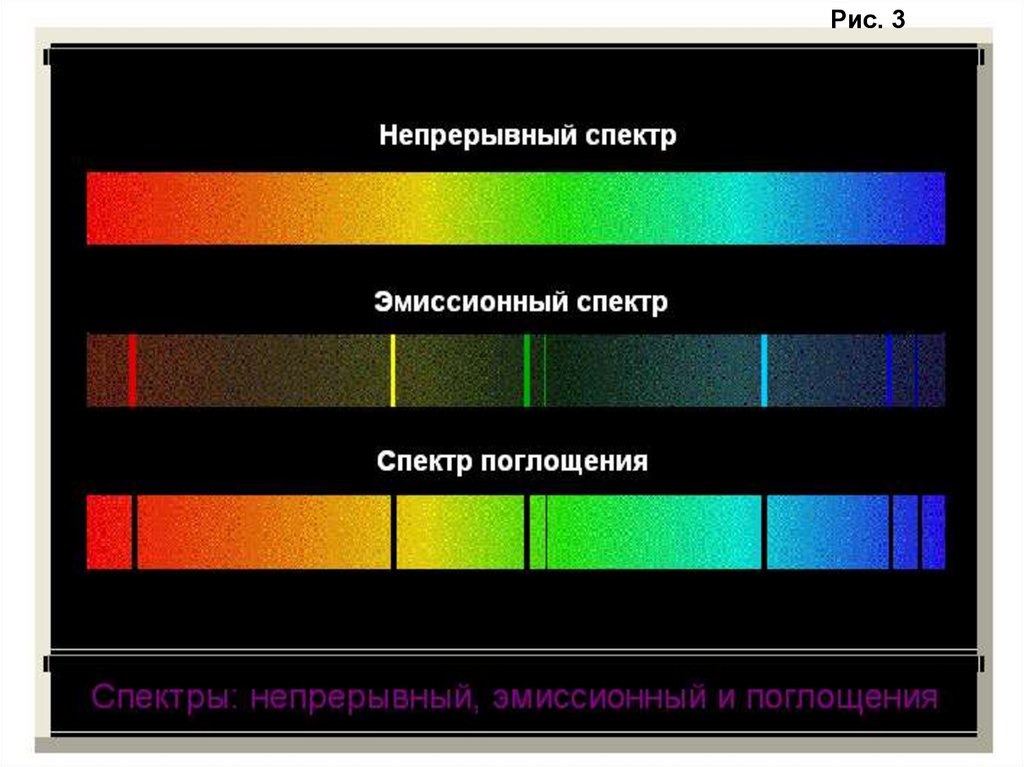
Эти виды спектров показаны на нижеследующем рисунке.
5.
Рис. 36.
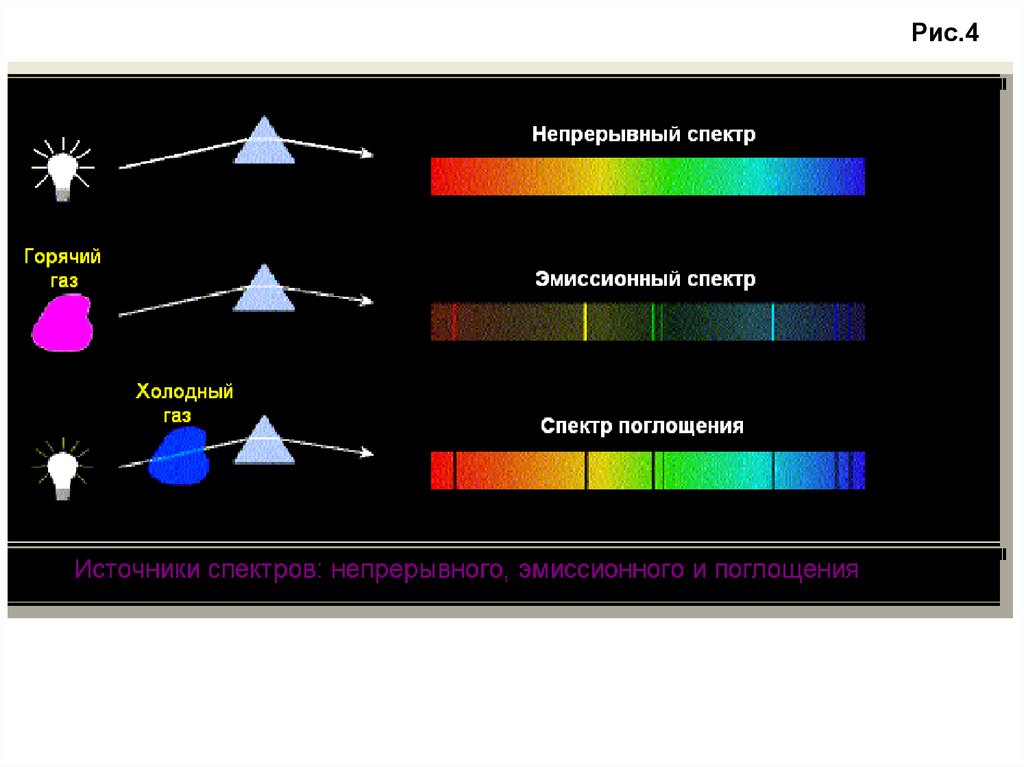
Рис.47.
Итак, эмиссионные спектры производят разреженныегазы, когда атомы не участвуют во множестве столкновений (изза низкой плотности газа). Эмиссионные линии соответствуют
фотонам с дискретными энергиями, которые испускаются,
когда возбуждённые атомные состояния совершают переходы
назад на низколежащие уровни.
Непрерывный спектр получается, когда газ находится
при весьма высоких давлениях. В общем, твёрдые тела,
жидкости, или плотные газы при нагревании испускают свет на
всех длинах волн.
Спектр поглощения образуется, когда свет проходит
через холодный, разреженный газ, и атомы в газе поглощают
на характерных частотах; поскольку невероятно, чтобы свет,
вслед за тем испущенный возбуждённым атомом, был
испущен точно в том же направлении, как и поглощённый
фотон, и в результате образуются тёмные линии (отсутствие
излучения) в спектре.
8.
КВАНТОВАЯ МЕХАНИКАЧтобы понять строение атомов, мы рассмотрим простейший
атом — атом водорода (Н). Нам бы хотелось описать
«динамику движения» электрона, который движется вблизи
протона. Под динамикой движения подразумевается энергия
электрона, импульс, траектория и изменение этих величин во
времени. Можно надеяться, что такое описание поможет нам
понять, почему два атома водорода соединяются и образуют
молекулу Н2, но из трех атомов водорода молекула Н3 не
образуется. Классическая физика — в эпоху до Е
не могла дать ответа на эти вопросы.
= тс2 —
9.
ЛИНЕЙЧАТЫЙ СПЕКТР АТОМАН
Атомы водорода образуются при электрическом разряде в
газообразном водороде. Наличие атомов можно установить по
испускаемому ими свету; этот факт был известен задолго до того,
как было предложено объяснение наблюдаемого цветного спектра.
В отличие от излучения нагретого источника свечение
электрического
разряда
приводит
к
появлению
только
определенных цветов в виде линейчатого спектра. Если
Е = hν
воспользоваться выражением
, это значит, что атом
водорода может излучать в виде квантов света лишь
некоторые определенные количества энергии. При более
детальном исследовании оказалось, что имеются фотоны с
энергией 15,35-10–11 эрг (235,2 ккал на 1 моль квантов) и
19,36·10–11эрг (278,8 ккал/моль); между этими двумя значениями
энергии никаких других квантов не наблюдается.
Ситуация стала еще более интересной, когда были обнаружены
дополнительно фотоны с энергией, в точности равной разности
этих двух энергий: (19,36 –15,35)·10–11 =
4,01·10–11эрг (43,6
ккал/моль).
10.
Очевидно, что для объяснения этих фактов необходимопостулировать, что атом Н может содержать только какие–то
определенные энергии. Из такого постулата автоматически
следовало бы, что при изменении энергии атома от одного
разрешенного значения Е1 до другого разрешенного
значения
Е2
может
высвобождаться
только
строго
определенное количество энергии (Е1 – Е2). Необходимо
было разумное, объяснение такого маловероятного по тем
временам предположения.
11.
В 1913 г. Нильс Бор предложил считать, что в атоме Нэлектрон движется по некоторым специальным планетарным
орбитам,
угловой момент которых
является
целым
числом, кратным величине h/2π).
Это спорное
предположение оказалось приемлемым,
поскольку хорошо увязывалось с рядом других явлений
(излучение с нагретой поверхности, связанное с величиной
h), а также из – за возможности сохранить планетарную модель
атома.
Это предположение Бора открыло дорогу квантовой
механике, несмотря на то что почти все его детали были
впоследствии опровергнуты. На основе общепринятого сейчас
квантовомеханического описания атома можно перечислить
следующие недостатки планетарного атома Бора:
12.
Планетарный КвантовомеханическийВодород.
атом
атом
Таблица 1
Сопоставление
импульсов электрона
в атоме водорода в
различных состояниях
атома: планетарная
модель Бора и
квантовомеханический
атом
Атомное
p = n(h/2π)
состояни
p l (l 1) (h / 2 )
(n – целое
е
число)
(l – целое число)
1s
1 (h/2π)
0
2s
2 (h/2π)
0
2p
2 (h/2π)
1,41
3s
3 (h/2π)
0
3p
3 (h/2π)
1,41
(h/2π)
3d
3 (h/2π)
2,45
(h/2π)
4s
4 (h/2π)
0
4p
4 (h/2π)
1,41
(h/2π)
4d
4 (h/2π)
2,45
(h/2π)
(h/2π)
13.
электрон не движется по планетарной траектории;как видно из табл. 1.1, предположение о том, что значения
импульсов являются кратными некоторому числу,
оказалось неверным;
использованный для одноэлектронного атома водорода
критерий импульса непригоден для объяснения
наблюдаемых уровней энергии любого атома с двумя или
более электронами;
модель не позволяет понять природу химической связи;
модель не может дать логичного объяснения того, почему
происходит квантование и почему электрон на орбите
не излучает энергию, как этого требует электродинамика;
Оба
эти свойства были введены
обоснования или объяснения.
без
14.
Несмотря на этот список, Бор заслуженно занял своеместо в истории, ибо он первым признал необходимость
отхода от классической физики. И сейчас разрешенные
энергетические состояния
атома
называются
стационарными
состояниями
– так, как их
назвал сам Бор. Стационарные состояния, как и раньше,
характеризуются квантовыми числами – целыми
числами, которые позволяют передать удивительный характер
спектра атома водорода. Прошло несколько десятков лет, пока
ограниченные
возможности
атома
Бора
не
стали
общепризнанными, но вклад Бора привел к решительному
отказу от представлений физики макромира.
Наконец в 1926 г. все стало на свои места, когда Эрвин
Шредингер нашёл связь между стационарными состояниями
Бора и наличием у электрона волновых свойств, по де
Бройлю. Этот шаг в развитии квантовой механики следует
рассматривать как одно из самых крупных научных
достижений – достижение, которое стоит в одном ряду с
вкладами Галилея, Ньютона и Максвелла.
15.
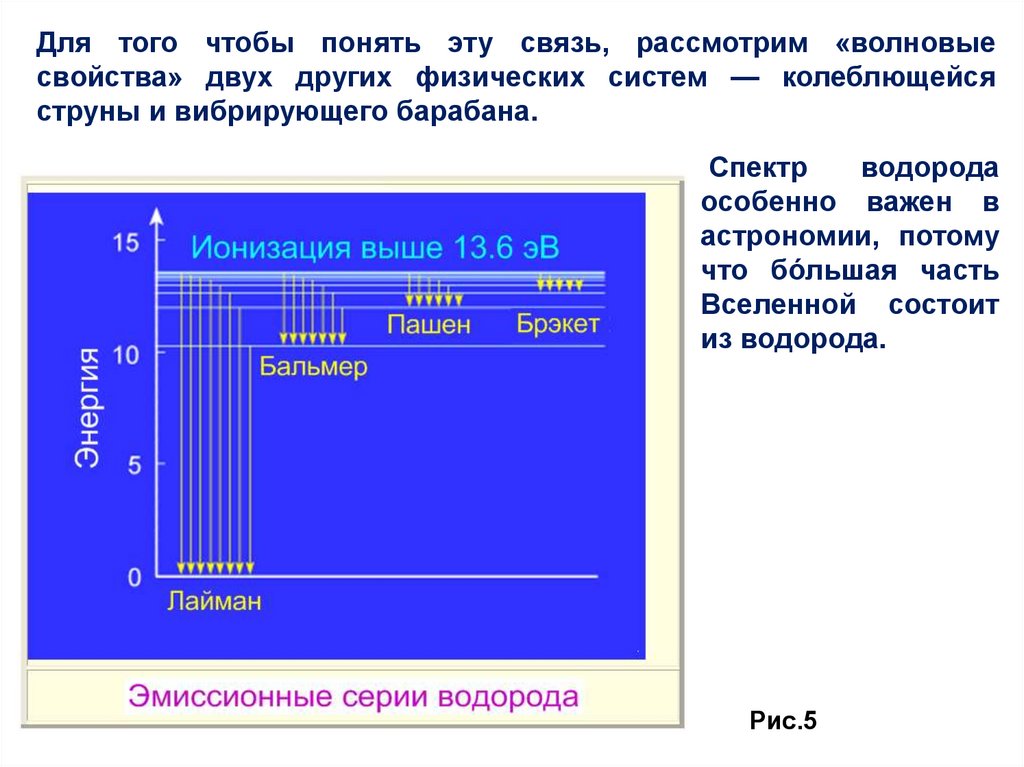
Для того чтобы понять эту связь, рассмотрим «волновыесвойства» двух других физических систем — колеблющейся
струны и вибрирующего барабана.
Спектр
водорода
особенно важен в
астрономии, потому
что бόльшая часть
Вселенной состоит
из водорода.
Рис.5
16.
Процессы испускания или поглощения в атомарномводороде приводят к образованию серий, которые
представляют
собой
последовательности
линий,
соответствующих атомарным переходам, и каждая серия
заканчивается или начинается с одного и того же состояния
атома водорода. Так, например, Серия
Бальмера
включает переходы, начинающиеся (в процессах поглощения)
или заканчивающиеся (в процессах эмиссии) с первого
возбуждённого состояния атома водорода, в то же время
Серия
Лаймана
включает переходы, которые
начинаются
или
заканчиваются
основным
состоянием
водорода. Рядом
расположенные изображения этих серий
иллюстрируют атомные переходы, которые происходят в этих
двух сериях при эмиссии.
17.
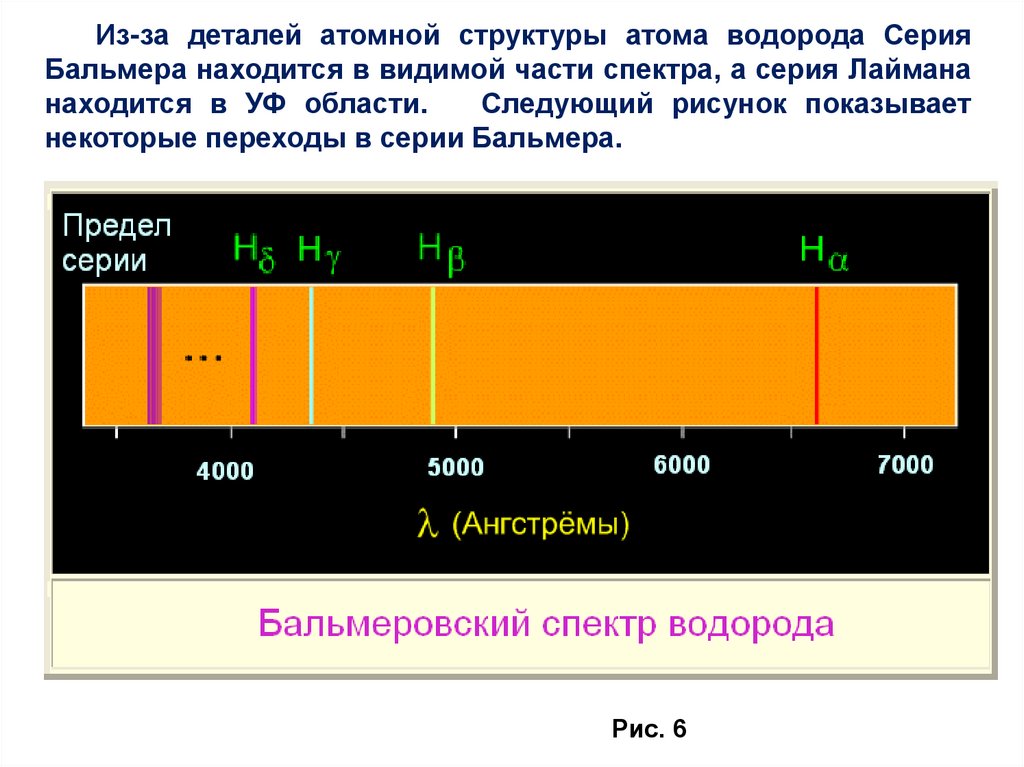
Из-за деталей атомной структуры атома водорода СерияБальмера находится в видимой части спектра, а серия Лаймана
находится в УФ области.
Следующий рисунок показывает
некоторые переходы в серии Бальмера.
Рис. 6
18.
Нас окружает множество систем, способных отдавать илипринимать энергию в любом количестве: автомобиль можно
разогнать до любой скорости; футбольный мяч можно слабо
ударить, выбить за пределы поля или забросить в любое
промежуточное положение; некоторую массу можно поднять
на любую высоту. Но есть ли вокруг нас макроскопические
системы, которые вели бы себя как атомы, т. е. системы,
поглощающие
или
испускающие
энергию
какими-то
определенными порциями? Да, есть, например,
струна
гитары.
Если
тронуть
гитарную
струну,
раздается
звук
определенной высоты и тембра. Если струну прижать к
одному из ладов, изменив тем самым ее эффективную длину,
высота звука изменится. В этом примере можно увидеть
элементы квантовой механики и сущность стационарных
состояний в атоме.
19.
Очевидно, что высота звука, который производит задетаяструна, зависит от частоты ее колебания, сообщающего
акустические колебания воздуху. Когда струна вибрирует
вперед и назад, ее движение в любой точке вдоль длины
струны и частота ее колебания характеризуют вибрацию.
Рассматривая более подробно это движение, мы увидим, что
есть только две точки, в которых струна неподвижна, — ее
концы. Струна закреплена на кобылке, а также вдоль грифа
одним
из
ладов
(соответственно
аппликатуре).
Эти
ограничения, накладываемые на движение гитарной струны,
называются граничными условиями. Границами в
данном случае являются концы струны, а условие состоит в
том, что смещение струны на концах всегда должно быть
равно нулю. Ниже будет показано, что в данном случае из-за
наличия граничных условий могут происходить только
определенные колебания: колебания квантуются.
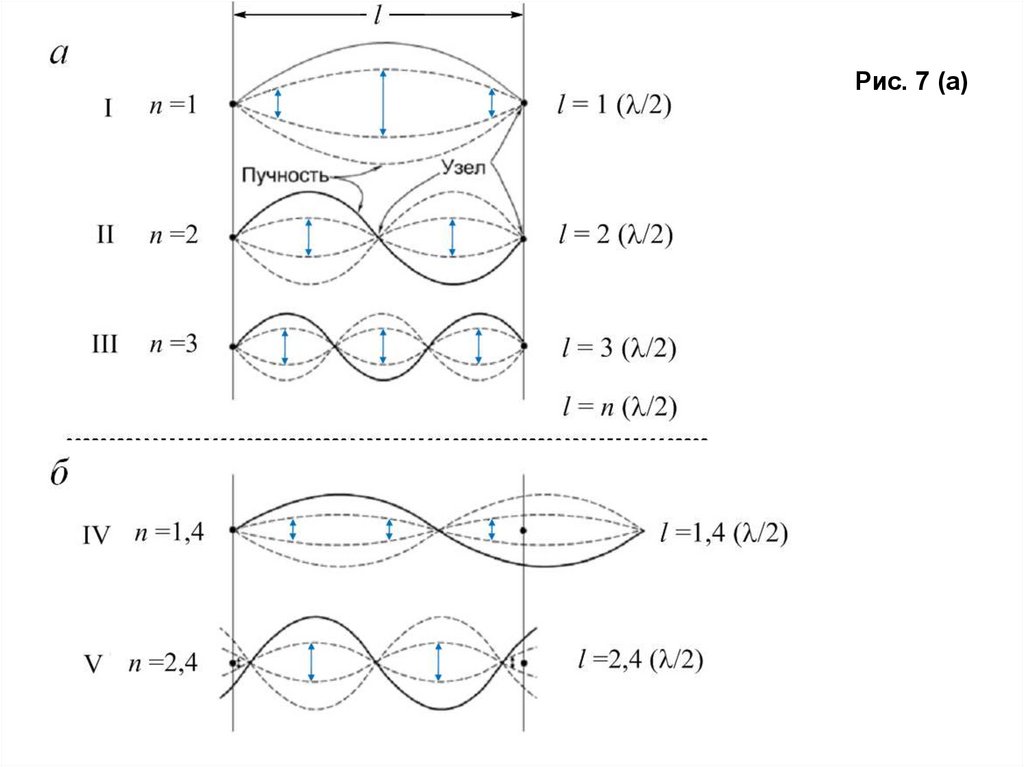
На рис. 7 изображены несколько возможных колебаний
струны.
20.
Рис. 7 (а)21.
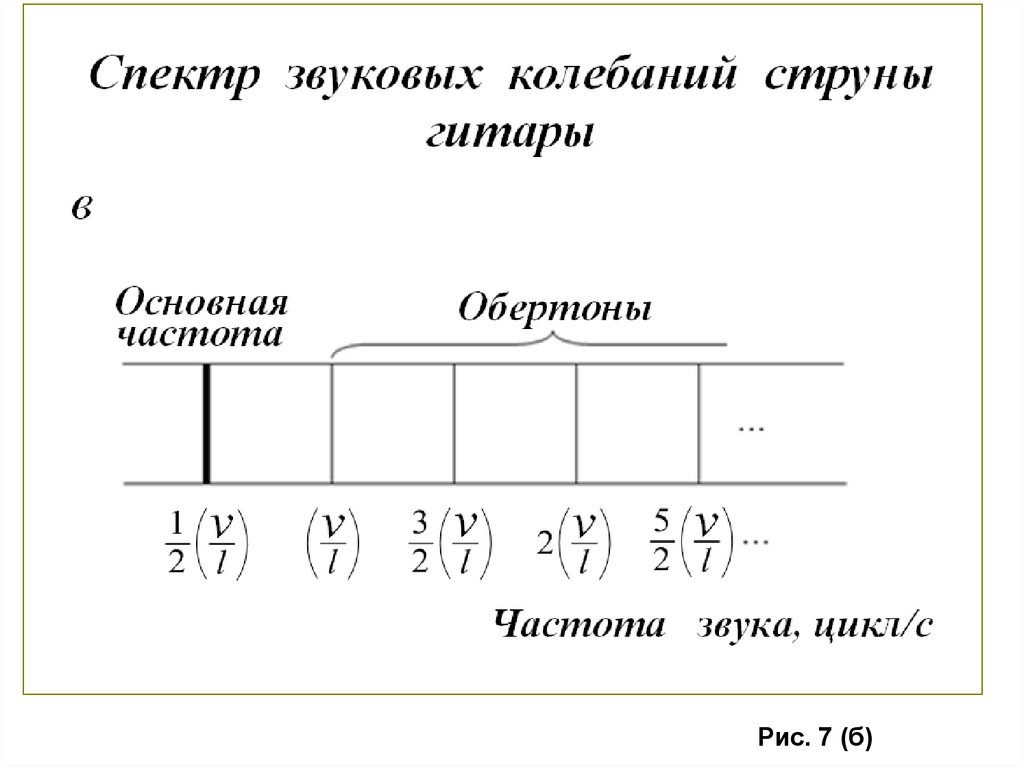
Рис. 7 (б)22.
Простейшее колебание I называется основным, и именнооно определяет основной тон, или высоту. Следующее
простейшее колебание II превращает струну в синусоиду. По
мере колебания струны вперед и назад ее точки
периодически проходят через нулевое смещение. В центре,
однако, смещения нет никогда; эта точка называется узлом.
Те точки, где струна имеет максимальное смещение, называются
пучностями. Как видно, колебание I имеет два узла (на
концах, где выполняются граничные условия) и одну
пучность. Колебание II характеризуется тремя узлами (два на
концах и один в центре) и двумя пучностями. Для этого
колебания длина l совпадает с длиной волны. Колебание III
имеет четыре узла и три пучности; здесь на длине l
укладывается полторы длины волны. Колебания типов II, III
и далее в теории музыки называют гармониками; они
определяют тембр звуков гитары.
23.
Для нас важно то, что гитарная струна может колебатьсятолько с определенными частотами и, следовательно,
издавать
лишь определенные звуки. Каждое из этих
специальных колебаний можно охарактеризовать основной
частотой и целым квантовым числом п. Квантовое число п
определяет число длин полуволн в одном колебании,
а величина (п + 1) дает нам число узлов (включая и узлы на
концах).
Рассмотрим еще один аспект таких колебаний. Можно
заметить, что для колебания II на струне наблюдаются две
пучности в одно и то же время, но в противоположных
направлениях. Тогда как в левой пучности струна поднята
вверх, в правой она опускается вниз. При продолжении
колебания эти положения меняются на противоположные. В
этом случае говорят, что две пучности находятся в
противофазе. Каждый раз при прохождении через узел фаза
меняется.
24.
На рис. 7(б) изображено несколько случаев, когда струнане может вибрировать. Для таких смещений
необходимо, чтобы струна двигалась вверх и вниз у
основания гитары или вблизи ладов, но в каждой из этих
точек струна закреплена. Таким образом, граничные
условия
обусловливают
квантование. Когда
имеются
граничные
условия,
волновому
движению
колеблющейся
струны
соответствует
линейчатый
спектр, частоты которого характеризуются целыми
квантовыми числами, расположением узлов и соотношением
фаз.
Все
эти
характеристики
имеются
и
в
квантовомеханическом описании атома.
25.
АТОМ ВОДОРОДАРаз уж мы убедились в том, что квантовая механика
объясняет свойства атомов и молекул, то нам следует
приспособить ход наших рассуждений к этой модели.
Атом водорода – это пример, из которого можно получить
наибольшее количество информации, ибо для него возможно
точное решение уравнения Шредингера. Ни для какой другой
системы из атомов (или молекул), включающей два или более
электрона, точного решения нет, хотя можно ввести
приближения, которые позволят подойти очень близко к
истинным решениям.
Такие многоэлектронные атомы будут рассмотрены позже,
когда можно будет воспользоваться всеми преимуществами
четкого понимания строения атома водорода.
26.
а) Квантовые числаМы уже знаем, что атом водорода может содержать
только определенные количества энергии. Эти определенные
энергии, именуемые уровнями энергии, а также карту
электронной «плотности» (орбиталь) дает уравнение
Шредингера. Как энергия, так и вероятность распределения
электронов зависят от целых чисел, аналогичных тем,
которые характеризуют узловые свойства колеблющейся
струны или кожи барабана.
У струны смещение может происходить только в одном
измерении (в направлении у), и для того, чтобы описать ее
разрешенные движения, понадобится только одно число.
С другой стороны, для двумерных колебаний кожи
барабана требуются уже два числа, одно из которых
описывало бы радиальные, а другое — угловые узловые
свойства.
27.
Волновое уравнение Шредингера для атома водородаописывает электрон
как волну в трех измерениях.
Совершенно
естественно поэтому, что для полной
атома Н
необходим набор
из трёх целых чисел. Эти
величины называются квантовыми числами.
характеристики каждого такого состояния энергии
Каждый набор квантовых чисел определяет:
1. одну из возможных энергий атома,
2. совершенно определённую картину распределения
вероятности,
по
которой можно судить о положении
электрона (т.е. его орбиталь).
28.
Пространственныераспределения
в
случае
атома
соответствуют орбитальным траекториям, которые описывают
классическое движение планет в солнечной системе. Если бы
можно было сжимать солнечную систему до любого размера, то,
когда Солнце достигло бы массы протона,
орбитальная
траектория
превратилась
бы
в квантовомеханическое
распределение
вероятности
и
выражалась бы через ψ2.
Поэтому такую картину распределения вероятности ученые
также называют орбиталью.
Три
квантовых
числа,
определяющие
конкретное
распределение
вероятности
(конкретную
орбиталь),
обозначают латинскими буквами п, l и m соответственно.
Первое из них, п, наиболее важно, поэтому оно называется
главным квантовым числом; оно может принимать любые
целые значения: 1, 2, 3, 4, ....
Энергия атома водорода
определяется формулой
29.
Энергия атома водорода определяется формулой2
(1)
n
2
Z
E R
n
где R = 313,6 ккал/(моль атомов Н) – константа, Z – заряд ядра
(для атома водорода +1) и п – главное квантовое число (1, 2, 3, 4,
...).
Знак минус в правой части выражения (1) указывает на
понижение энергии относительно начала отсчета –
состояния, в котором протон и электрон удалены друг от друга на
бесконечно большое расстояние.
Главное квантовое число определяет также узловые
свойства орбитали. Колеблющаяся струна обладает узловыми
точками (см. рис. 7(a)), колеблющийся барабан – узловыми
линиями;
у
атома
водорода
имеются
узловые
поверхности. На такой поверхности волновая функция ψ
меняет фазу, подобно изменению фазы – вверх–вниз – в узле
гитарной струны. На узловой поверхности величина ψ2 равна
нулю – здесь электрона быть не может.
30.
Главное квантовое число определяет также узловые свойстваорбитали. Колеблющаяся струна обладает узловыми точками (см.
рис. 7(a)), колеблющийся барабан – узловыми линиями; у атома
водорода имеются узловые поверхности. На такой поверхности
волновая функция ψ меняет фазу, подобно изменению фазы – вверх–
вниз – в узле гитарной струны. На узловой поверхности величина
равна нулю – здесь электрона быть не может.
Число узловых поверхностей равно
ψ
2
n причем одна из этих
поверхностей соответствует граничному условию для бесконечного r.
31.
Пространственные характеристики орбитали определяютсядвумя квантовыми числами n и l. Например, в квантовой
механике среднее расстояние
электрона от ядра
определяется как
n2
r a
Z
3 l (l 1)
2 2n 2
где а = 0,529 Å – постоянная,
(2)
Z – заряд ядра (для атома водорода +1,
п — главное квантовое число и l — угловое квантовое число.
32.
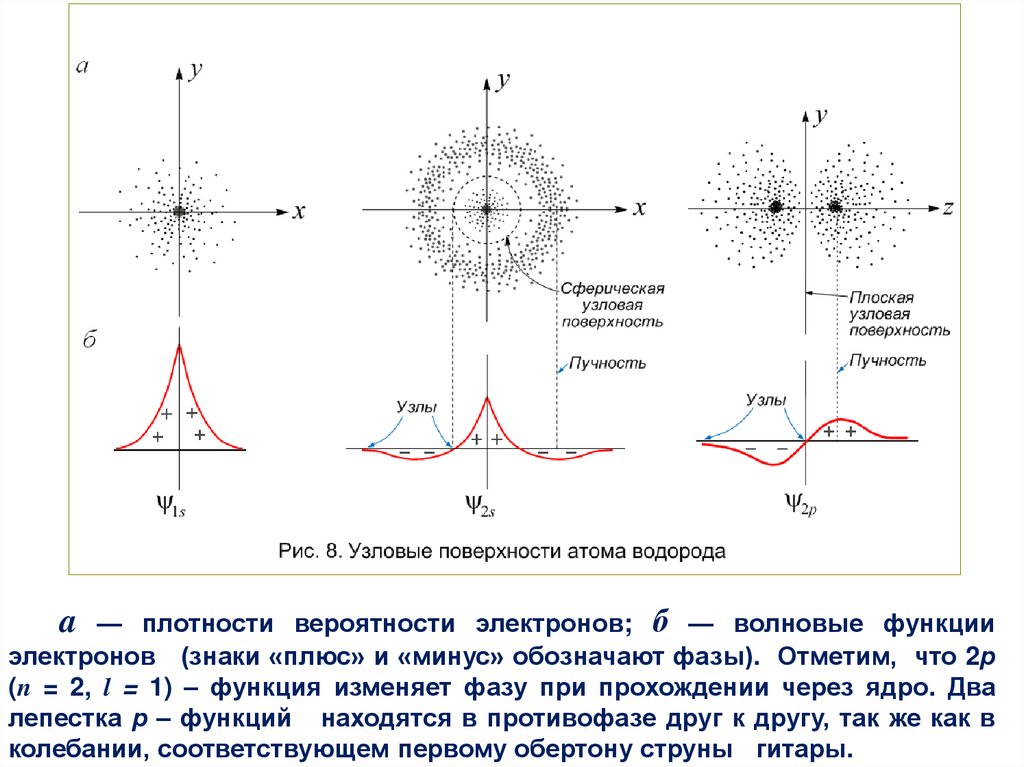
— плотности вероятности электронов; б — волновые функцииэлектронов (знаки «плюс» и «минус» обозначают фазы). Отметим, что 2р
(n = 2, l = 1) – функция изменяет фазу при прохождении через ядро. Два
лепестка р – функций находятся в противофазе друг к другу, так же как в
колебании, соответствующем первому обертону струны гитары.
a
33.
Второе квантовое число l может принимать целые значения винтервале от нуля до (п –1). Так, при п = 3 l может принимать
любое из значений: 0, 1 или 2; при п = 1 l может быть равно
только нулю.
Величина l также связана с узловой картиной орбитали.
Существует l узловых поверхностей, зависящих от углов.
Поскольку всего имеется п узловых поверхностей, то должно
быть еще (п – l) узловых поверхностей без угловой зависимости, т.
е. сферически симметричных. Например, если п = 2, то l может
быть равно либо 0, либо 1. При l = 0 зависящих от угла узловых
поверхностей не будет вовсе, а обе радиальные узловые
поверхности являются сферами. Одна из этих поверхностей лежит
при r = ∞. При l = 1 одна из узловых поверхностей зависит от угла
— это плоскость. Вторая узловая поверхность (п – l = 2 – 1 = 1)
представляет собой сферу; и в этом случае она также уходит в
бесконечность. На рис. 1.13 представлены поперечные разрезы
распределений вероятности, соответствующих п = 2.
34.
Изменение фазы на узловой поверхности обозначено знаками«плюс» и «минус». Эти знаки связаны со свойственными волне
смещениями вверх и вниз по вертикали. На рис. 8а орбиталь с п =
2 и l = 1 изображена направленной вдоль оси х так, что
плоскость уz — узловая плоскость. Это заставляет подумать и о
других возможных ориентациях. Ведь существуют три измерения,
почему же предпочтение отдается оси x ?
На самом деле это не так. Значениям п = 2 и l = 1
соответствуют три орбитали, каждую из которых можно
направить вдоль любой из трех осей координат, как на рис. 1.14.
Эти три орбитали отличаются друг от друга значением третьего
квантового числа m. Оно называется магнитным квантовым
числом и может принимать как положительные, так и
отрицательные значения, не превышающие l по величине:
m = l, l – 1 , l – 2, …, 1, 0, –1, –2, …, – l
(3)
Если мы снова обратимся к примеру с п = 2, получим
следующий набор
орбиталей,
обладающих
одинаковой
энергией:
35.
Z1
1
E R 2 R 2 R
n
2
4
(9)
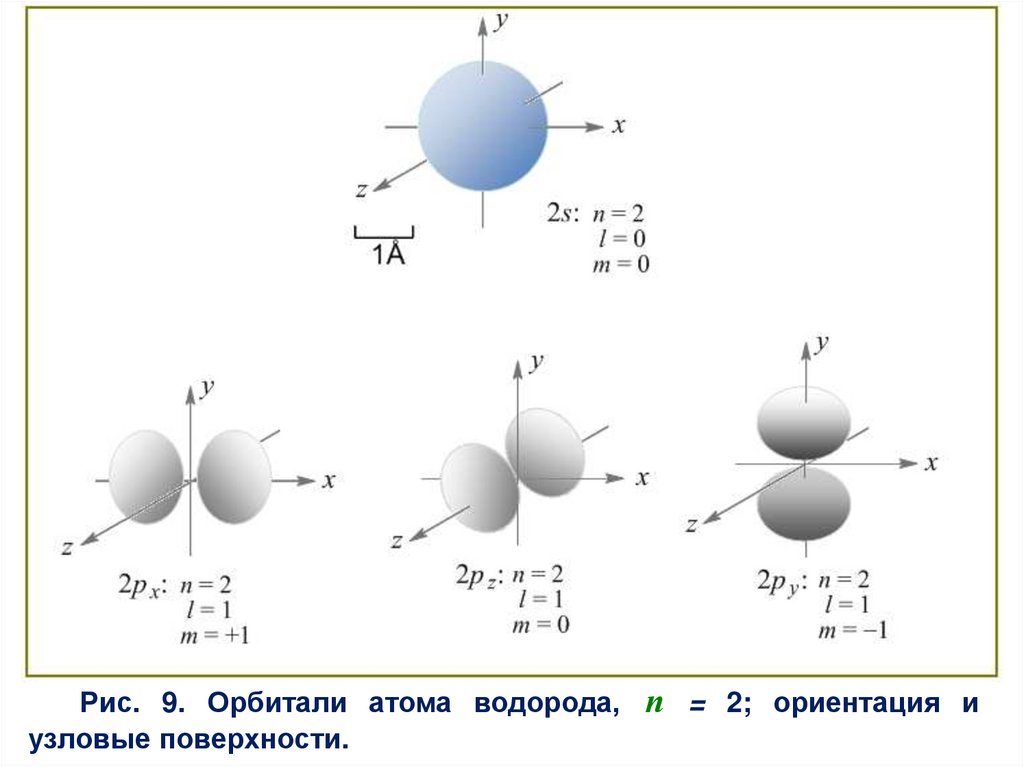
Все четыре орбитали представлены на рис. 9.
36.
Рис. 9. Орбитали атома водорода, п = 2; ориентация иузловые поверхности.
37.
Легко видеть, что для п = 1 возможна только одна орбиталь(п = 1, l = 0, m = 0). При п = 2 существуют четыре орбитали (9);
отметим, что число орбиталей (четыре) равно п2. Этот вывод
справедлив для любого значения п – данному главному
квантовому числу п соответствуют п2 орбиталей.
б) Схема уровней энергии атома водорода
Подытоживая все сказанное выше, можно сказать, что три
квантовых числа п, l и т определяют возможные энергетические
состояния атома водорода и соответствующие распределения
вероятности, или орбитали. Полная энергия и число орбиталей с
данной энергией, зависят от значения п; узловые свойства
зависят также от l и т.
38.
В Таблице 2 показано, как с увеличением п возрастает числосостояний; в ней приведены общепринятые обозначения каждой
орбитали. Обычно для обозначения орбитали не приводят
значения всех трех чисел п, l и т . Сначала записывают значение
п, а затем латинские буквы s, р, d или f, которые соответствуют
определенным значениям l. Так, орбиталь, для которой п = 2 и l =
0, называется 2s – орбиталью. Далее будет показано, что все
орбитали с l = 0 обладают сферической симметрией, поэтому
можно считать, что символ «s» (spherical) означает «сферическая».
Орбиталь с п = 2 и l = 1 называется 2р – орбиталью. 2р –
орбиталей может быть три, что соответствует трем возможным
значениям т (+1, 0, –1). Поскольку три 2р–орбитали можно
представить себе ориентированными перпендикулярно друг к
другу, символ «p» можно считать сокращением от латинского
слова «perpendicular» (перпендикуляр) и три 2р-орбитали
обозначить рх, ру и рz соответственно.
39.
Таблица 2. Квантовые числа атома водорода40.
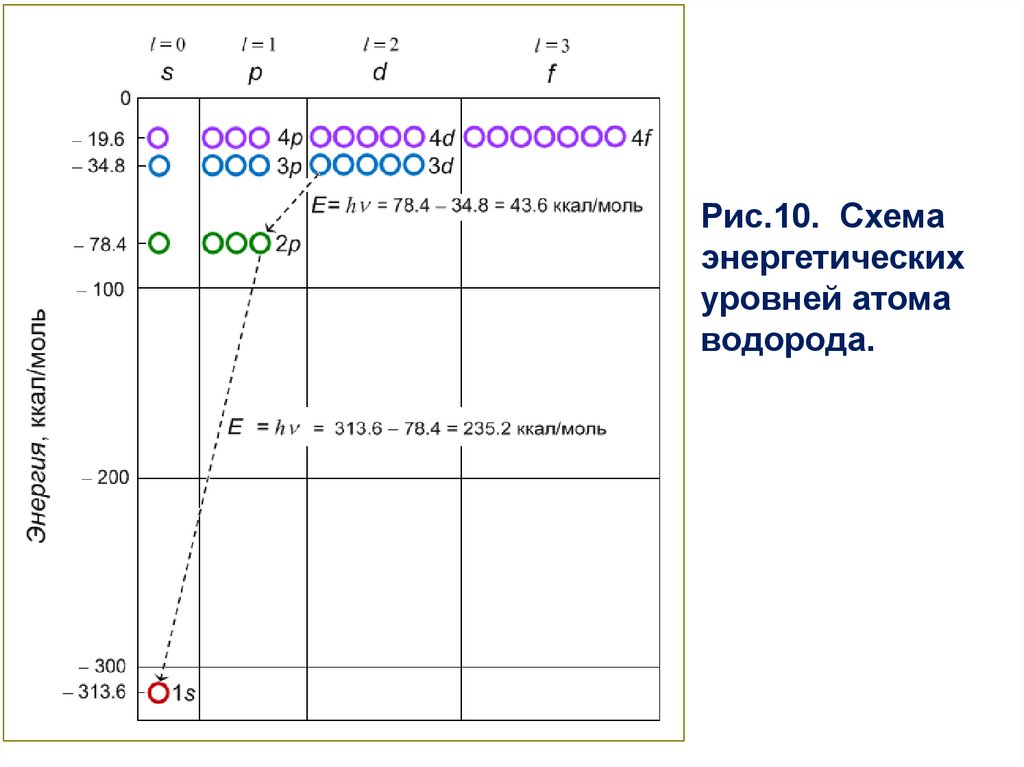
Информацию, заключенную в Таблице 2, можно представитьграфически с помощью диаграммы атомных уровней энергии
(рис. 10). По горизонтали изображены орбитали в виде ячеек,
которые могут быть заполнены электронами. Орбиталям
сопоставлена вертикальная шкала энергий, показывающая,
насколько понижается энергия при захвате протоном электрона
на данную орбиталь.
Такая диаграмма очень полезна при рассмотрении атомных
спектров. Представим себе электрон на 2р – орбитали водорода.
Энергия этого атома на 78,4 ккал/моль ниже энергии
изолированных протона и электрона.
41.
Теперь предположим, чтоатом перешел в некоторое
более низкое энергетическое состояние, испустив энергию. И
квантовая механика, и эксперимент утверждают, что возможно
только одно такое состояние, а именно орбиталь 1s. Этот самый
низкий уровень энергии расположен на 313,6 ккал/моль ниже
нашей точки отсчета. Следовательно, атом может осуществить
переход 2р → 1s, только излучая свет с энергией, равной
разности указанных значений:
(–78,4) – (–313,6) = 235,2 ккал/моль.
Это и есть один из переходов, которые действительно
наблюдаются в спектре атома водорода.
Каждой линии в спектре можно сопоставить
разность энергий, соответствующую одному
из переходов между уровнями на рис. 10.
42.
Рис.10. Схемаэнергетических
уровней атома
водорода.































 chemistry
chemistry








