Маятниковые позиционные акселерометры

1. ВЫСОКОТОЧНЫЕ СИСТЕМЫ НАВИГАЦИИ Лекция №2.5

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ИМЕНИ Н.Э.БАУМАНА
ВЫСОКОТОЧНЫЕ СИСТЕМЫ
НАВИГАЦИИ
Лекция №2.5
Маятниковые позиционные
акселерометры

2.

Акселерометрами называются устройства для измерения
составляющих кажущегося линейного ускорения подвижных
объектов на соответствующим образом выбранные направления.
Под
кажущимся
ускорением
понимают
ускорение
объекта, созданное силами негравитационного происхождения.
Это такое ускорение, которое имел бы объект в пространстве,
где отсутствуют гравитационные силы.
К силам негравитационного происхождения относятся сила
тяги, аэродинамические силы (подъемная сила и сила лобового
сопротивления)

3.

К гравитационным силам относятся силы притяжения
объекта Землей, Луной, Солнцем и другими небесными телами.
Акселерометры,
действие
которых
основано
классической механики, позволяют измерить лишь
на
законах
кажущееся
ускорение геометрическую разность между абсолютным (т.е. по
отношению к инерциальной системе) ускорением и ускорением
силы тяготения (абсолютным ускорением свободной материальной
точки в данном месте пространства из-за притяжения к Земле и
другим небесным телам).

4.

Принципиальная схема измерений с
помощью силового акселерометра
Пусть опорное тело массой m связано с корпусом пружиной 1.
Если пружина не нагружена, то центр тела m находится в точке А,
являющейся началом отсчета деформации пружины.
При равномерном и прямолинейном движении объекта и
отсутствии начальных деформаций пружины тело m движется
вместе с объектом как единая инерциальная система.

5.

Приложим к корпусу объекта силу P , под действием которой
он будет двигаться согласно второму закону Ньютона, с ускорением
a, направленным в сторону действия силы. Тело m, сохраняя
равномерное движение, будет отставать от корпуса и растягивать
пружину на величину r . Сила F упругости пружины, зависящая от
r ( в простейшем случае F kr , где k постоянный коэффициент),
прикладывается, с одной стороны, к телу m, а с другой стороны,
к корпусу объекта. В результате тело будет двигаться с ускорением:
F ,
ar
m
P F
a
а корпус объекта – с ускорением:
,
об
Mo
где M o масса корпуса объекта.

6.

После окончания переходного процесса объект и тело m
будут двигаться как единое целое с одинаковым ускорением:
aоб ar a.
Учитывая значения ускорений, получим на основании этого
равенства следующее выражение:
откуда
Mo m
P
F
m
где M o m
(1)
P F F
,
Mo
m
,
полная масса объекта вместе с присоединенным
опорным телом.
На основании (1) формулируется теорема о динамическом
подобии:
Динамика движения опорного тела под действием сил
реакции связей с объектом подобна динамике самого объекта
под действием внешних активных сил.

7.

Следовательно, измеряя вектор силы F (например по
деформации
r пружины), можно в масштабе
Mo m
m
определить вектор активной силы P , действующей на объект.

8.

КЛАССИФИКАЦИЯ АКСЕЛЕРОМЕТРОВ
по количеству степеней свободы перемещения инерционной
массы относительно корпуса (одномерные, двумерные и
трехмерные);
по характеру зависимости между силой реакции подвеса и
выходным сигналом (простые, интегрирующие и дважды
интегрирующие);
по характеру перемещения инерционной массы (линейные и
маятниковые);
по способу подвеса инерционной массы ;

9.

по виду выходных сигналов (механические, у которых
выходной сигнал получается в виде перемещений;
электрические – с выходным сигналом в виде силы тока или
напряжения;
параметрические, у которых выходной сигнал получается в
виде изменяющегося физического параметра: сопротивления,
размеров тел, напряженности и т.д.;
временные – в виде частот, периодов и т.п.).

10.

11.

12.

13.

14.

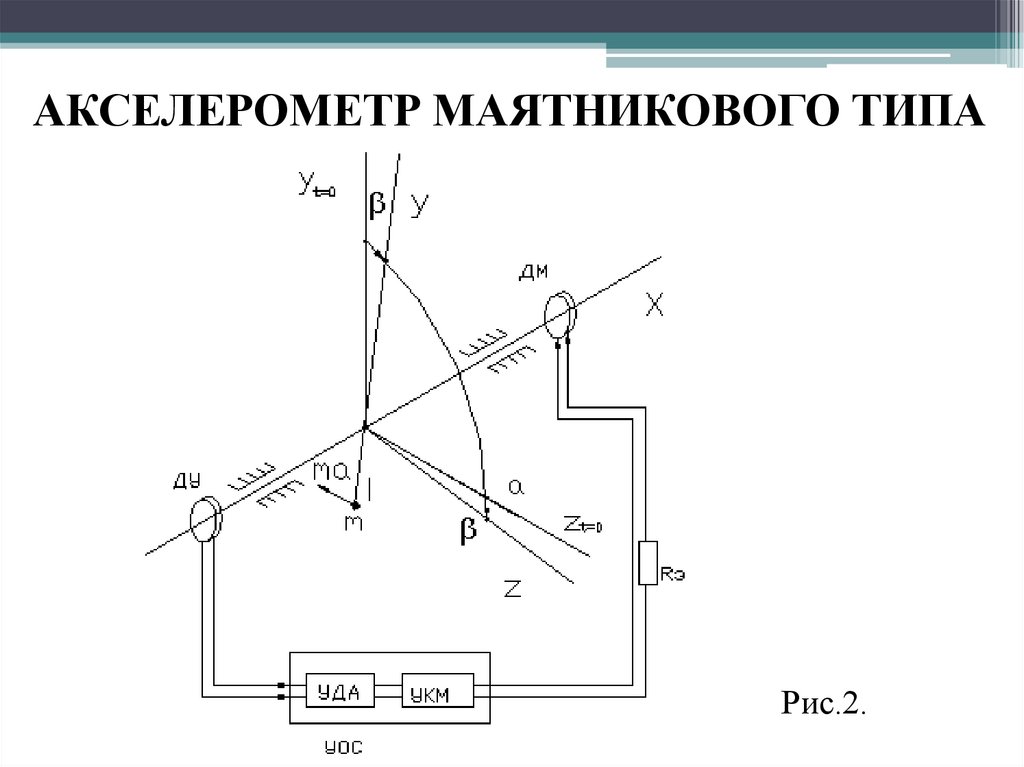
АКСЕЛЕРОМЕТР МАЯТНИКОВОГО ТИПА
Рис.2.

15.

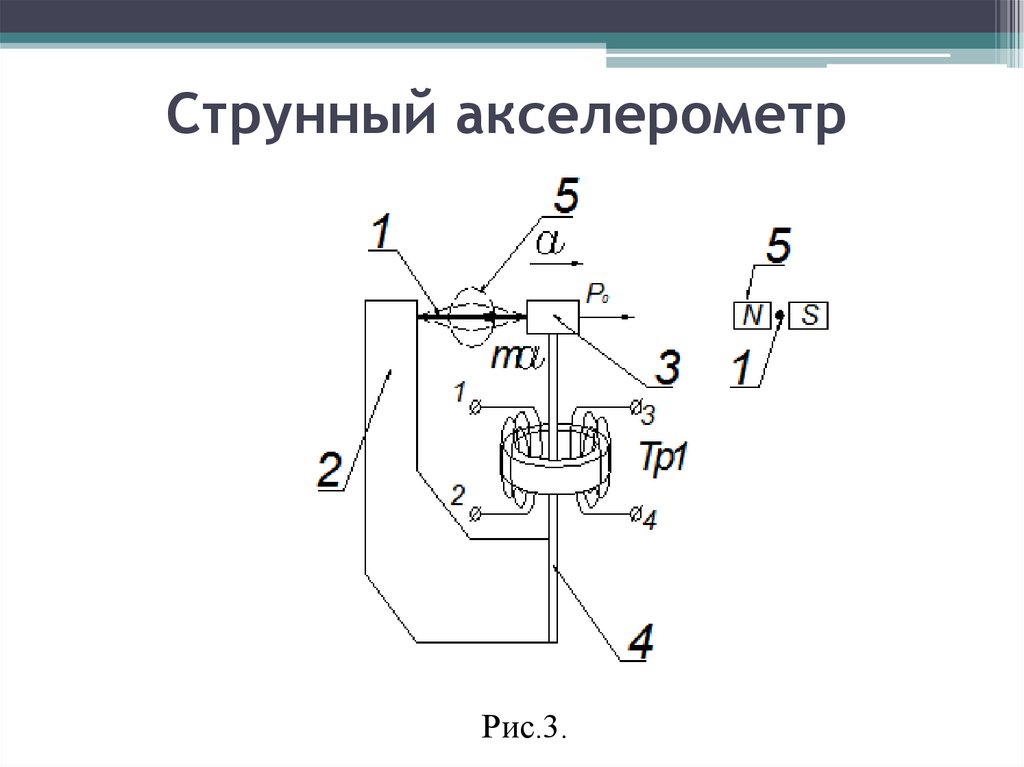
16. Струнный акселерометр

Рис.3.

17.

Струна 1 скреплена концами с кронштейном 2 и инерционной
массой — грузом 3. Начальное натяжение создается плоской
пружиной 4.
Струна 1, кронштейн 2 и пружина 4 с грузом 3 образуют виток
тороидального трансформатора Тр1 с обмотками 1-2, 3-4.
Струна 1 размещается между полюсами N, S постоянного
магнита 5.
Для возбуждения и поддержания незатухающих колебаний
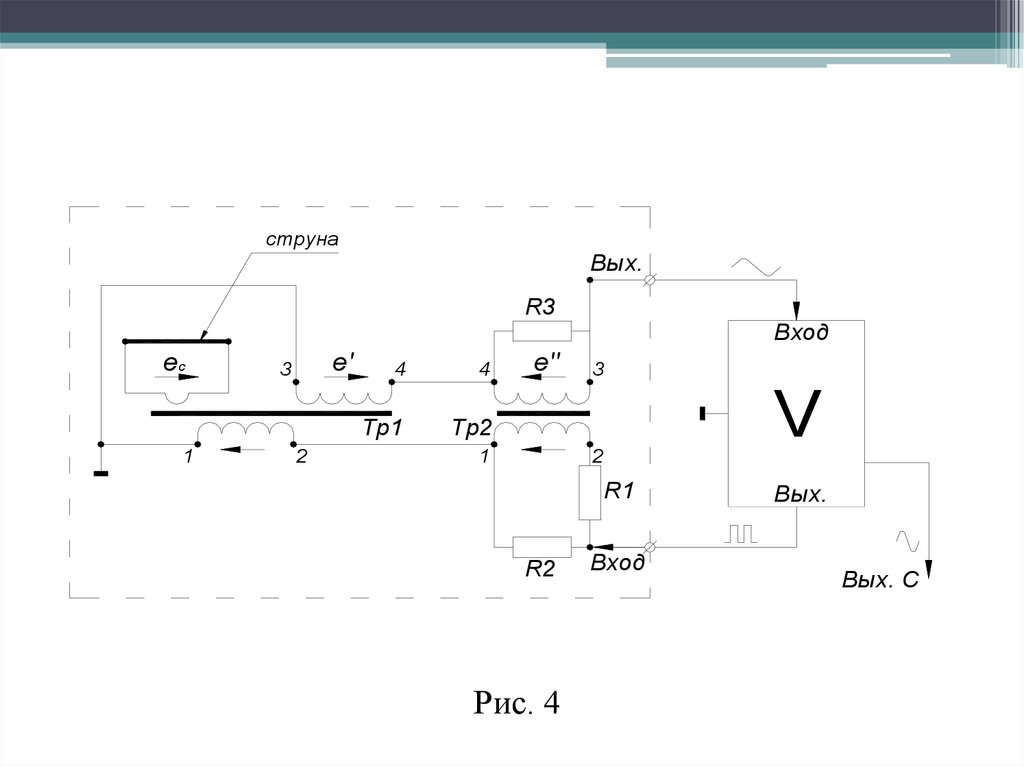
струны реализована электрическая схема, изображенная на рис. 4.

18.

струна
Вых.
R3
ес
1
е'
3
2
4
4
Тр1
Тр2
е''
1
Вход
3
2
R1
R2
Рис. 4
Вход
V
Вых.
Вых. C

19.

Принцип действия струнного акселерометра.
Струнный акселерометр предназначен для измерения величины
проекции кажущегося линейного ускорения объекта на ось
чувствительности и выдачи соответствующей цифровой
информации в инерциальную систему навигации или в систему
управления движением объекта. Принцип действия струнного
акселерометра основан на свойстве натянутой струны изменять
частоту поперечных колебаний при изменении силы ее натяжения.

20.

Частота поперечных колебаний струны определяется формулой:
f 1 P
(1)
2l S
где
Р — сила натяжения струны,
l — длина струны,
r — плотность материала струны,
S — площадь поперечного сечения струны.
Кажущееся ускорение представляет собой вектор, равный
разности абсолютного (действительного) и гравитационного
ускорений. В дальнейшем с целью упрощения будем называть
просто ускорением.

21.

Если со струной 1, предварительно натянутой силой P0 ,
скрепить груз 3 массой m (рис.1) , то при ускорении а сила сила
натяжения струны
P P0 ma
и частота поперечных
колебаний струны f будет определяться формулой:
1
f
2l
P0 ma
S
(2)
Из формулы (2) получим:
f f0 1
a
a
f 0 (1 )1/ 2
a0
a0
,
(3)

22.

1 P0
частота колебаний струны при начальном
2l S
натяжении, определяемая силой P0 (при отсутствии ускорения),
где
f
a проекция ускорения на продольную ось струны,
P
a0 0 конструктивный параметр.
m
При a a0 сила натяжения струны становится равной нулю.
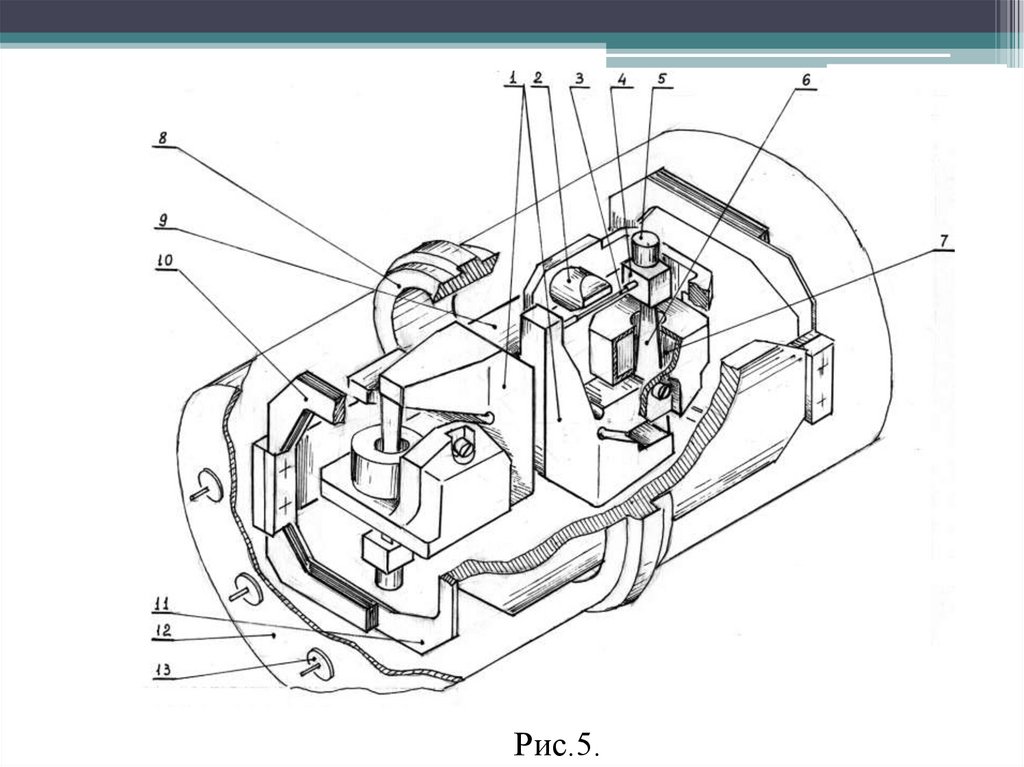
На рис.5. изображена упрощенная конструктивная схема
чувствительного элемента струнного акселерометра (ЧЭ),
называемого струнным резонатором.

23.

Рис.5.

24.

Наименование позиций:
1. кронштейн ЧЭ,
2. постоянный магнит (один полюс),
3. струна,
4. инерционная масса,
5. груз,
6. пружина ЧЭ,
7. тороидальный трансформатор Тр1,
8. корпус,
9. основание,
10. демпфер,
11. пружина амортизатора,
12. крышка,
13. гермовывод.