Similar presentations:
Эффект Зеемана. Эффект Штарка. Электронный парамагнитный резонанс (ЭПР)
1. Кислицын А.А. Физика атома, атомного ядра и элементарных частиц
24 (2). Эффект Зеемана.Эффект Штарка. Электронный
парамагнитный резонанс (ЭПР)
2.
Эффект Зеемана (Zeeman P.) является одним изубедительных экспериментальных доказательств
существования магнитного момента атома и правил
его квантования. Эффект Зеемана заключается в
расщеплении спектральных линий источника света,
помещенного в магнитное поле. При этом в простейшем случае нормального эффекта Зеемана в
направлении, перпендикулярном магнитному полю
линия расщепляется на 3 компонента: 0, 0 +∆ 0,
0 -∆ 0, а в направлении вдоль поля – на 2 компонента: 0 +∆ 0, 0 -∆ 0, где
eB
0
4 me
(24.1)
3. Простой (нормальный) эффект Зеемана
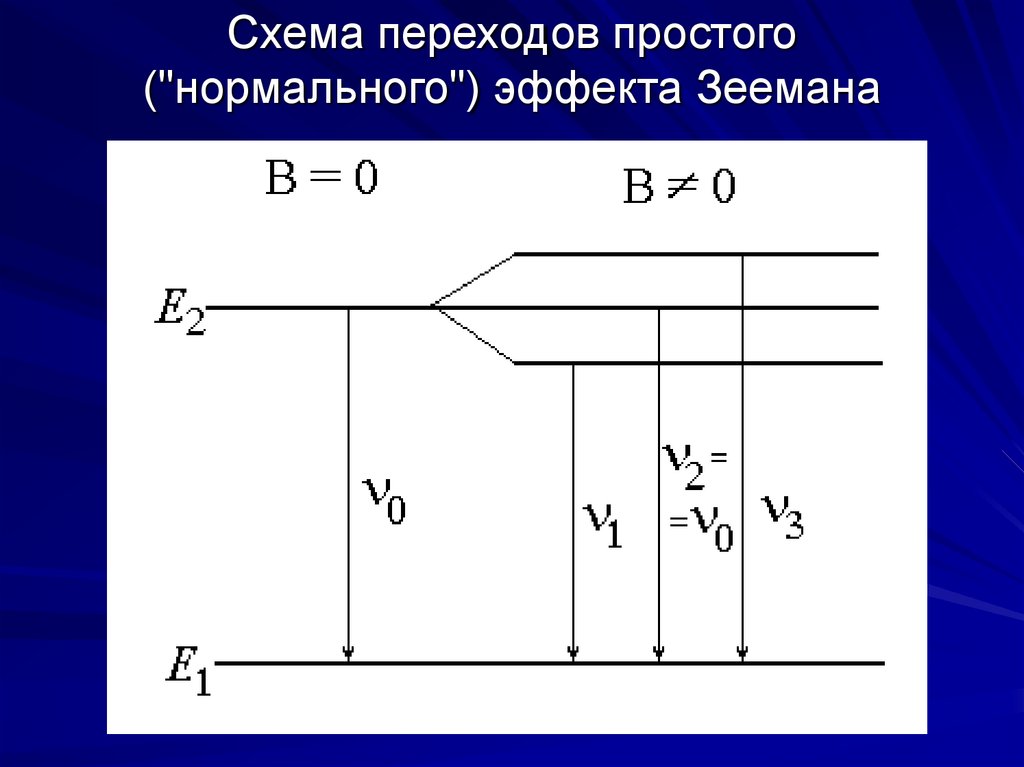
Схематическое изображение простого эффекта приведено на рисунке. Внаправлении вдоль магнитного поля
линия, имеющая частоту , представляется в виде двух линий с круговыми поляризациями и с частотами
+ и - .
В направлении перпендикулярном
магнитному полю, спектральная линия расщепляется на 3 компонента с
частотами + , и - . Смещение
eB
4 me
где e и me - заряд и масса электрона,
В - индукция магнитного поля.
4.
В более сложном аномальном эффекте Зееманалиния расщепляется на большее число компонент, причем сдвиг частоты ∆ не равен ∆ 0. Теория, основанная на законах классической физики (теория Лоренца) смогла объяснить только
нормальный эффект, а аномальный эффект,
встречающийся гораздо чаще, классическая физика объяснить не в состоянии. Нормальный эффект Зеемана наблюдается лишь на одиночных
(синглетных) линиях, возникающих при переходах между уровнями с суммарным спином S=0.
Во всех остальных случаях наблюдается аномальный эффект.
5. Сложный (аномальный) эффект Зеемана
Простой эффект объяснил голландский физик Хендрик Лоренц (Lorentz H.)в рамках классической электронной
теории (поэтому эффект называется
нормальным). Сложный эффект наблюдается гораздо чаще, но его может
объяснить только квантовая теория,
поэтому
его называют аномальным.
6.
Для объяснения эффекта Зеемана воспользуемся векторной моделью атома. Пусть в отсутствие магнитного поля атом находится в некотором состоянии, которому соответствует энергияE. Поместим его в магнитное поле. В результате взаимодействия магнитного момента атома с
полем его энергия изменится и станет равной
(см формулу (23.5) ):
E E E J B
E JB B E 0 gBM J
(24.2)
где MJ, как уже указывалось, может принимать
2J+1 значений.
7.
Таким образом, в магнитном поле каждый энергетический уровень Е (терм) атома расщепляетсяна 2J+1 подуровней с энергиями, определяемыми формулой (24.2), что и приводит к появлению
новых линий в спектре. Действительно, пусть в
отсутствие поля атом при переходе из состояния
E2 в состояние E1 излучал линию с частотой 0:
h 0 E2 E1
В магнитном поле оба уровня расщепляются на
подуровни, поэтому теперь будут излучаться
частоты:
h i E2 0 g 2 M J 2 B E1 0 g1M J 1 B
E2 E1 0 B g 2 M J 2 g1M J 1
8.
или:i 0 0 g2 M J 2 g1M J 1
где
0 B
E2 E1
eB
0
, 0
h
h
4 me
(24.3)
Рассмотрим пример: Переход между уровнями 1S0
и 1P1 атома гелия. Оба терма имеют S=0. В
магнитном поле терм 1S0 не расщепляется, т.к.
J=0, значит MJ1=0, и по формуле (24.2) ∆E=0.
Терм 1P1 расщепляется на три подуровня, т.к.
J=1, и магнитное квантовое число MJ2 принимает три значения: +1, 0, -1.
9.
Подсчитаем значение множителя Ланде для состояния 1P1:J ( J 1) S ( S 1) L( L 1)
g2 1
2 J ( J 1)
1 2 0 1 2
1
1
2 1 2
Таким образом, по формуле (24.3) получаем
i 0 0 M J 2
или
1 0 0 , 2 0 , 3 0 0
- нормальный эффект Зеемана.
10. Схема переходов простого ("нормального") эффекта Зеемана
Схема переходов простого("нормального") эффекта Зеемана
11. Теперь рассмотрим пример аномального эффек-та Зеемана.
Теперь рассмотрим пример аномального эффекта Зеемана.Рассмотрим переход 2P1/2 → 2S1/2 атома натрия. В
магнитном поле уровень 2S1/2 (L=0, S=1/2, J=1/2)
расщепляется на два подуровня, т.к. MJ может
принимать 2 значения: +1/2, -1/2. Множитель
Ланде для этого состояния:
1 1 1 1
1 1 0
2 2 2 2
g1 1
1 1 2
1 1
2 1
2 2
12.
Уровень 2P1/2 также расщепится на два подуров-ня,для него множитель Ланде:
1 1 1 1
1 1 1 1 1
1
2
2 2 2 2
g2 1
1
1 1
3
3
2 1
2 2
Таким образом, в магнитном поле будут излучаться 4 линии:
i 0
0 g 2 M J 2 g1M J 1
13.
Частоты этих линий по формуле (24.3) равны:или
2
i 0 0 M J 2 2M J1
3
4
1 0 0
3
2
2 0 0
3
2
3 0 0
3
4
4 0 0
3
14. Схема переходов сложного ("аномального") эффекта Зеемана
Схема переходов сложного("аномального") эффекта Зеемана
15. Эффект Штарка
В сильных электрических полях также наблюдаетсярасщепление спектральных линий. Это явление открыл немецкий физик Иоганн Штарк (Stark J.) в 1913г
(нобелевская премия 1919г). Светящиеся атомы вводятся через каналы К. Зазор ЕК очень мал (ок.1мм),
а разность потенциалов 10кВ, поэтому напряженность достигает 100000 В/см.
16. Магнитные свойства веществ
Магнитные свойства в той или иной форме присущивсем без исключения веществам: у всех веществ
во внешнем магнитном поле появляется или изменяется магнитный момент (все вещества "намагничиваются"). Поэтому при описании магнитных
свойств веществ часто используется термин "магнетики".
Все магнетики по их поведению во внешнем магнитном поле можно разделить на два класса:
Диамагнетики, которые намагничиваются навстречу
направлению внешнего магнитного поля,
Парамагнетики (в широком смысле), которые во внешнем магнитном поле намагничиваются в направлении поля.
17.
Класс парамагнетиков (в широком смысле) включаетв себя:
Парамагнетики (в узком смысле): вещества, которые
намагничиваются в направлении внешнего поля, и
у которых практически отсутствует взаимодействие между магнитными моментами атомов. В
дальнейшем только такие вещества мы и будем
называть парамагнетиками);
Ферромагнетики: твердые (кристаллические) магнетики, у которых магнитные моменты атомов, вследствие межатомного взаимодействия, самопроизвольно, без воздействия внешнего магнитного поля,
ориентируются параллельно друг к другу. Из-за
этого ферромагнетики в отсутствие внешнего поля
могут обладать намагниченностью.
18.
Антиферромагнетики: твердые (кристаллические)магнетики, у которых магнитные моменты атомов
самопроизвольно (межатомными силами) ориентируются антипараллельно, и полностью компенсируют друг друга. Поэтому, в отличие от ферромагнетиков, антиферромагнетики в отсутствие внешнего поля не обладают намагниченностью.
Ферримагнетики: кристаллические вещества, у которых так же, как у антиферромагнетиков, из-за межатомного взаимодействия магнитные моменты атомов самопроизвольно стремятся ориентироваться
антипараллельно, но не полностью компенсируют
друг друга. Поэтому, в отличие от антиферромагнетиков, ферримагнетики в отсутствие внешнего
поля могут обладать намагниченностью.
19.
Намагниченность (магнитный момент единицы объема магнетика) связан с величиной индукции магнитного поля соотношением:M = χB,
(24.4)
где χ - коэффициент магнитной восприимчивости.
У всех диамагнетиков коэффициент χ отрицателен, а
у парамагнетиков и антиферромагнетиков положителен, причем у этих веществ χ практически не зависит от индукции внешнего магнитного поля, а по
абсолютной величине лежит в пределах от 10-4 до
10-6 см3/моль.
У ферро- и ферримагнетиков магнитная восприимчивость χ достигает значений 104 - 106 см3/моль, и
при этом сильно и сложным образом зависит от B.
20.
Правило Ленца гласит, что всякое изменение магнитного потока через электрический контур индуцирует в нем ток, магнитный момент которого противодействует изменению этого магнитного потока.В модели атома Бора электронные оболочки атомов
можно рассматривать как проводящие контуры без
сопротивления. При включении внешнего магнитного поля в этих оболочках появляются индукционные токи, и возникает дополнительный магнитный
момент, направленный против внешнего поля. Это
и есть явление диамагнетизма.
Таким образом, диамагнетизм наблюдается у всех
веществ без исключения. Но у некоторых веществ
он перекрывается парамагнетизмом, ферро- или
ферримагнетизмом.
21. Парамагнетики
Рассмотрим магнитные свойства веществ, у которыхмагнитные моменты атомов обусловлены только
спином одного электрона, причем эти моменты
практически не взаимодействуют друг с другом
(электронный спиновый парамагнетизм).
Обозначим через E0 энергию атома в отсутствие магнитного поля. В магнитном поле B энергия станет
равной (формула (24.2)):
E0 J B E0 JB B E0 0 gBM J E0 0 B (24.5)
т.к. в данном случае L = 0, S = 1/2, J=1/2, фактор Ланде равен 2, а внутреннее магнитное квантовое число MJ = ±1/2. Другими словами, энергетический
уровень E0 расщепится на два подуровня:
нижний E1 = E0 - μ0B и верхний
E2 = E0 + μ0B.
22.
Обозначим полное число атомов в единице объемавещества через N0, а числа атомов на нижнем и
верхнем уровнях через N1 и N2 соответственно. В
условиях теплового равновесия
2 0 B
(24.7)
N2
e kT
N1
Учитывая, что
N0 = N1 + N2
(24.6)
0 B
находим
N0
e kT
N1
N 0 0 B
2 0 B
B
0
(24.7)
1 e kT
e kT e kT
N 2 N1e
2 0 B
kT
N0
e
0 B
0 B
kT
e kT e
0 B
kT
(24.8)
23.
Согласно формуле (24.5), проекция магнитного момента атома на верхнем уровне E2 на направлениемагнитного поля B равна μ0, и направлена против
поля B, а на нижнем уровне E1 она равна -μ0, и направлена по полю B., т.к. заряд электрона отрицательный. Отсюда следует, что результирующий
магнитный момент M единицы объема равен:
M = μ0N1 - μ0N2.
(24.9)
Подставляя сюда значения N1 и N2 из формул (24.7) и
(24.8), получаем:
0 B
M 0 N 0
e kT e
0 B
e
kT
e
0 B
kT
0 B
kT
0 N 0th
0 B
kT
(24.10)
24.
Если μ0B << kT, тоth
0 B
0 B
(24.11)
kT
kT
Тогда магнитный момент единицы объема:
0 B 02 N0
(24.12)
M 0 N 0
B
kT
kT
Сравнивая (24.12) и (24.4), находим:
02 N 0
(24.13)
kT
Таким образом, магнитная восприимчивость парамагнетика χ > 0, и обратно пропорциональна его
абсолютной температуре (закон Кюри):
C
(24.14)
T
где C = μ02N0/k = const.
25. Магнитный резонанс
Многие вещества в намагниченном состоянии приобретают способность резонансного поглощенияэнергии падающих на них электромагнитных волн.
Резонансный характер означает, что поглощение
происходит лишь при определенном соотношении
между длиной электромагнитной волны и индукцией магнитного поля, намагничивающего вещество.
Явления такого рода (ферромагнитный резонанс)
впервые наблюдал в 1913 году профессор физфака МГУ Владимир Константинович Аркадьев; их
общее название: магнитный резонанс.
Явления магнитного резонанса используются как эффективное средство исследования свойств и строения вещества.
26.
В настоящее время известны:Электронный парамагнитный резонанс (ЭПР), обусловленный магнитными моментами неспаренных
электронов в парамагнетиках;
Ядерный магнитный резонанс (ЯМР), при котором
поглощение энергии осуществляется ядрами атомов в результате изменения ориентации их спинов
в магнитном поле;
Ферромагнитный резонанс (ФМР), антиферромагнитный резонанс (АФМР), ферримагнитный резонанс эти виды магнитного резонанса наблюдаются в
магнитоупорядоченых веществах (соответственно
в ферро-, антиферро- и ферримагнетиках).
27.
Для объяснения явлений магнитного резонанса вернемся к формуле (24.2)E E E J B E 0 gBM J
из которой следует, что в магнитном поле каждый
энергетический уровень расщепляется на 2J+1
компонент (подуровней); их количество равно числу возможных значений внутреннего магнитного
квантового числа MJ. Эти компоненты иногда называют зеемановскими подуровнями. Если переходы
происходят между зеемановскими подуровнями
разных основных уровней, то возникает расщепление спектральной линии, т.е. вместо одной линии
появляется несколько линий, частота которых отличается от частоты спектральной линии до расщепления - это эффект Зеемана.
28.
Переходы между зеемановскими подуровнями одного и того же уровня обуславливают возможностьтой или иной разновидности магнитного резонанса. Вероятность спонтанных переходов между такими подуровнями очень мала, поэтому спонтанное излучение, обусловленное такими переходами, не наблюдается. Между этими подуровнями
происходят вынужденные переходы: поглощение и
вынужденное излучение.
Вынужденные переходы с поглощением между зеемановскими подуровнями одного исходного уровня
и представляют собой магнитный резонанс: избирательное поглощение энергии электромагнитных
волн веществом, находящимся в магнитном поле.
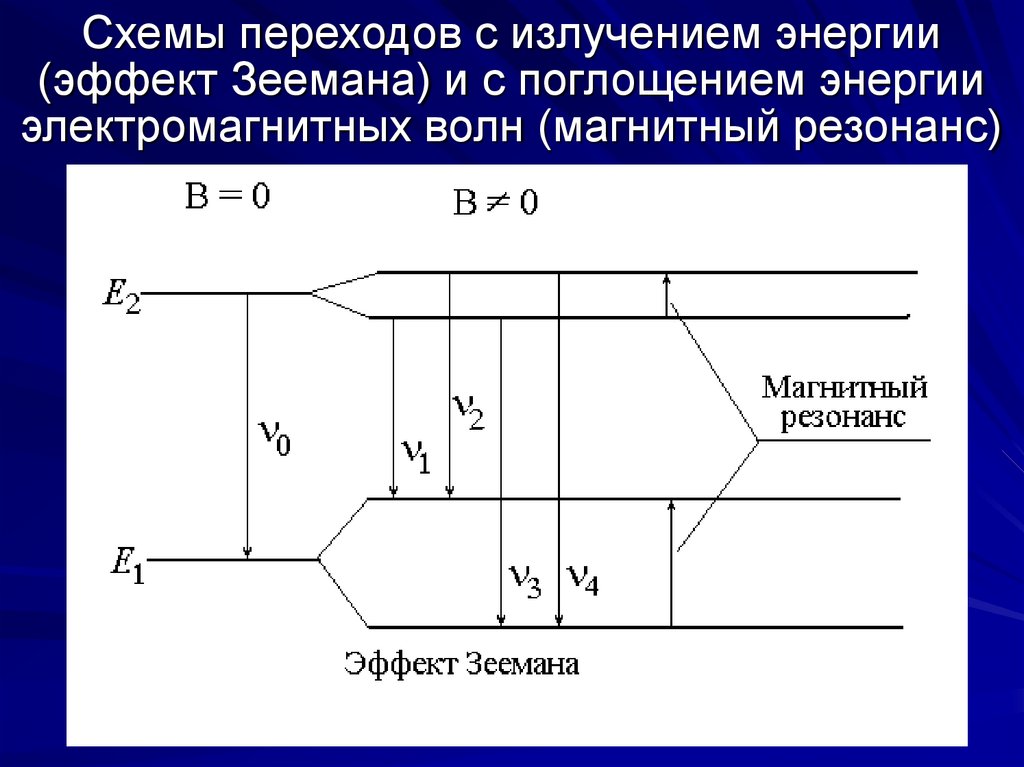
29. Схемы переходов с излучением энергии (эффект Зеемана) и с поглощением энергии электромагнитных волн (магнитный резонанс)
30. Электронный парамагнитный резонанс (ЭПР)
Электронным парамагнитным резонансом (ЭПР) называется явление резонансного поглощения энергии электромагнитного поля намагниченным веществом, содержащим парамагнитные атомы, молекулы, ионы.ЭПР был открыт в 1944г российским (советским) физиком Евгением Константиновичем Завойским.
Первый ЭПР-спектрометр работал на волнах дециметрового диапазона, поэтому в нем использовались магнитные поля небольшой индукции ~ 0.1Тл.
Позднее в методе ЭПР стали применять радиоволны сантиметрового диапазона и, соответственно, более сильные магнитные поля с индукцией ~
1 Тл.
31.
32.
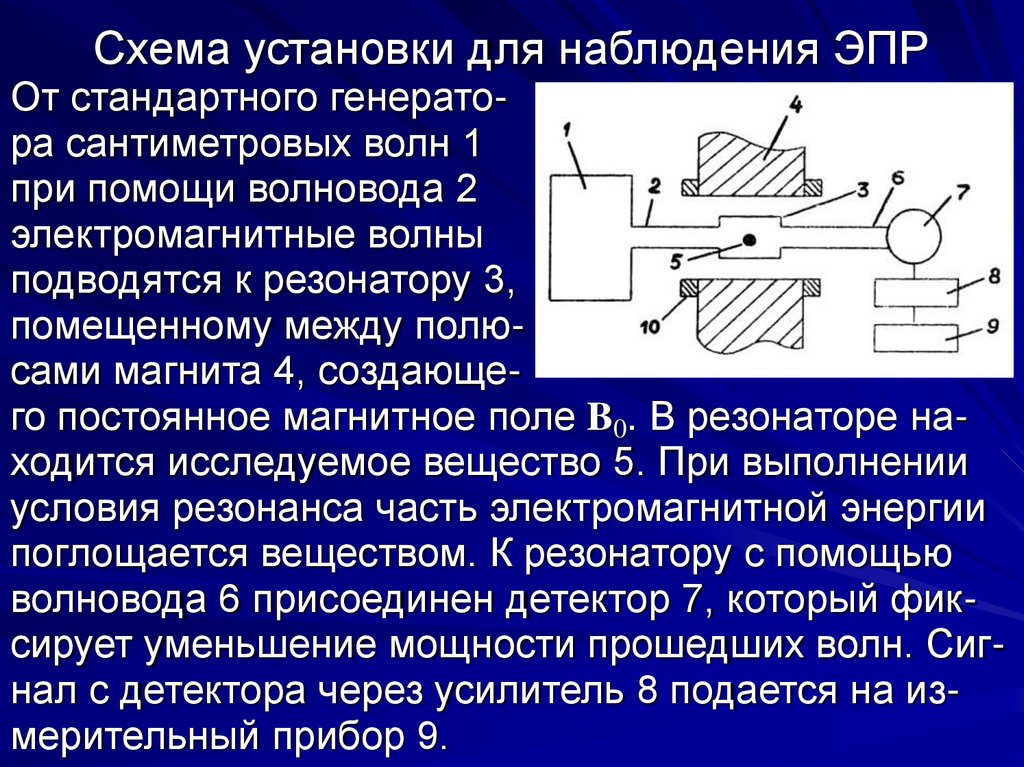
Схема установки для наблюдения ЭПРОт стандартного генератора сантиметровых волн 1
при помощи волновода 2
электромагнитные волны
подводятся к резонатору 3,
помещенному между полюсами магнита 4, создающего постоянное магнитное поле B0. В резонаторе находится исследуемое вещество 5. При выполнении
условия резонанса часть электромагнитной энергии
поглощается веществом. К резонатору с помощью
волновода 6 присоединен детектор 7, который фиксирует уменьшение мощности прошедших волн. Сигнал с детектора через усилитель 8 подается на измерительный прибор 9.
33.
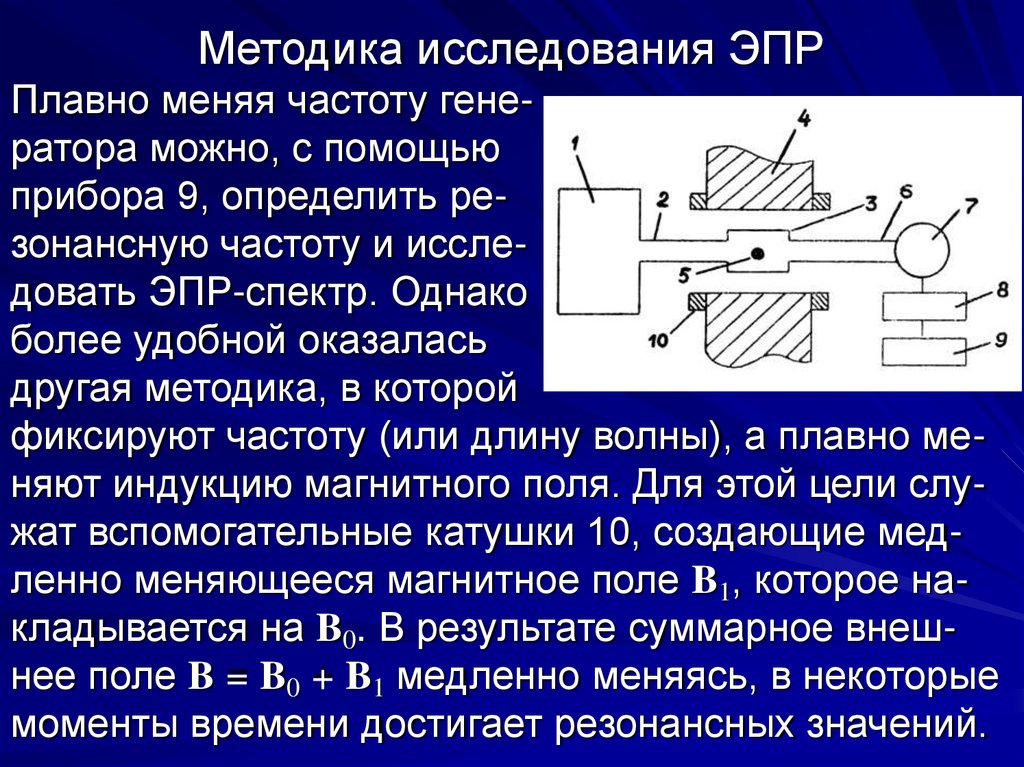
Методика исследования ЭПРПлавно меняя частоту генератора можно, с помощью
прибора 9, определить резонансную частоту и исследовать ЭПР-спектр. Однако
более удобной оказалась
другая методика, в которой
фиксируют частоту (или длину волны), а плавно меняют индукцию магнитного поля. Для этой цели служат вспомогательные катушки 10, создающие медленно меняющееся магнитное поле B1, которое накладывается на B0. В результате суммарное внешнее поле B = B0 + B1 медленно меняясь, в некоторые
моменты времени достигает резонансных значений.
34.
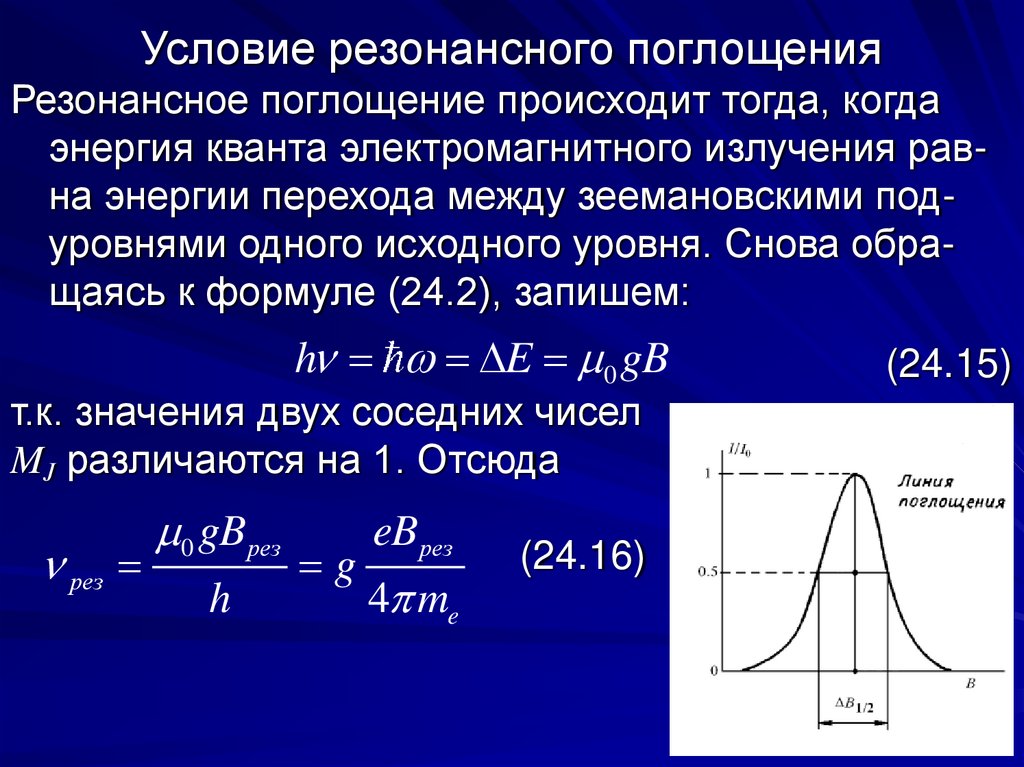
Условие резонансного поглощенияРезонансное поглощение происходит тогда, когда
энергия кванта электромагнитного излучения равна энергии перехода между зеемановскими подуровнями одного исходного уровня. Снова обращаясь к формуле (24.2), запишем:
h E 0 gB
т.к. значения двух соседних чисел
MJ различаются на 1. Отсюда
рез
0 gBрез
h
g
eBрез
4 me
(24.16)
(24.15)
35.
В эксперименте по заданному Bрез определяют резонансную частоту νрез, а также ширину резонанснойлинии поглощения ΔB, и далее по формуле (24.16)
вычисляют фактор Ланде. Это позволяет с большой точностью установить структуру уровней энергии исследуемого парамагнитного вещества. По
ширине линии поглощения можно получить информацию об интенсивности различных взаимодействий между пара- и диамагнитными частицами и о
механизме спин-решеточной релаксации.
В тех случаях, когда ЭПР может быть исследован, он
дает прямые и наиболее точные сведения об основном состоянии парамагнитных атомов и о влиянии кристаллической решетки на энергетические
уровни этих атомов.
36.
Магнитные свойствавещества тесно связаны с его структурой,
поэтому ЭПР является одним из наиболее
важных методов изучения строения вещества, позволяет получить ценнейшие данные, и широко применяется в различных
областях физики и
химии.































 physics
physics








