Оптика

1. Оптика

Лекция 1-2

2. План

Развитие представлений о
природе света.
Основные законы
геометрической оптики.
Полное отражение.
Тонкие линзы.

3. Развитие представлений о природе света

4.

Развитие представлений о природе света
Ньютон
(Newton)
Исаак
(1643–1727)
Согласно
корпускулярной
теории, свет представляет
собой
поток
частиц
(корпускул),
испускаемых
светящимися телами.
Гюйгенс
(Huygens)
Христиан
(1629–95)
Волновая теория, в отличие
от корпускулярной, рассматривала свет как волновой
процесс, подобный механическим волнам.
В конце XVII века возникли две теории света:
корпускулярная (И. Ньютон) и волновая (Р. Гук и
Х. Гюйгенс).

5.

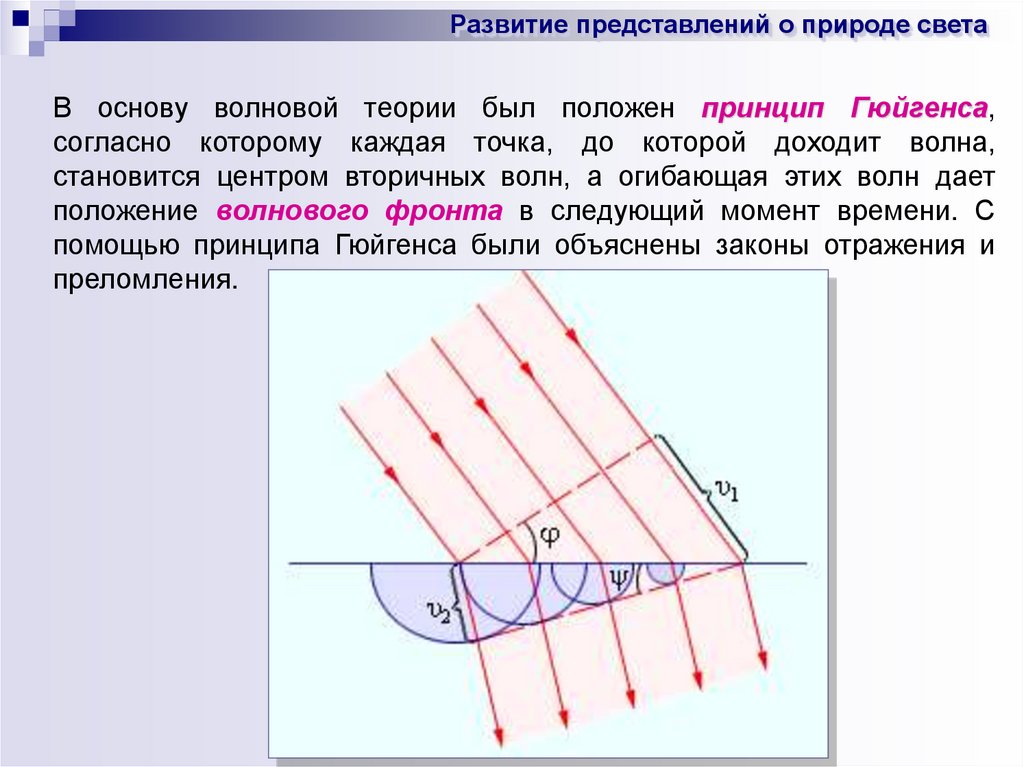
Развитие представлений о природе света
В основу волновой теории был положен принцип Гюйгенса,
согласно которому каждая точка, до которой доходит волна,
становится центром вторичных волн, а огибающая этих волн дает
положение волнового фронта в следующий момент времени. С
помощью принципа Гюйгенса были объяснены законы отражения и
преломления.

6.

Развитие представлений о природе света
Корпускулярная
(И. Ньютон)
Конец XIX в. — Герц
опытным путем открыл
явление фотоэффекта.
В1905 г. Эйнштейн
создал квантовую
теорию света.
Волновая
(Р.
Гук и Х. Гюйгенс)
Начало XIX в. —
Френель открыл
явление
интерференции.
Конец XIX в. —
Максвелл создал
электромагнитную
теорию света.
1888 г. — Герц опытным
путем открыл
электромагнитные
волны.

7.

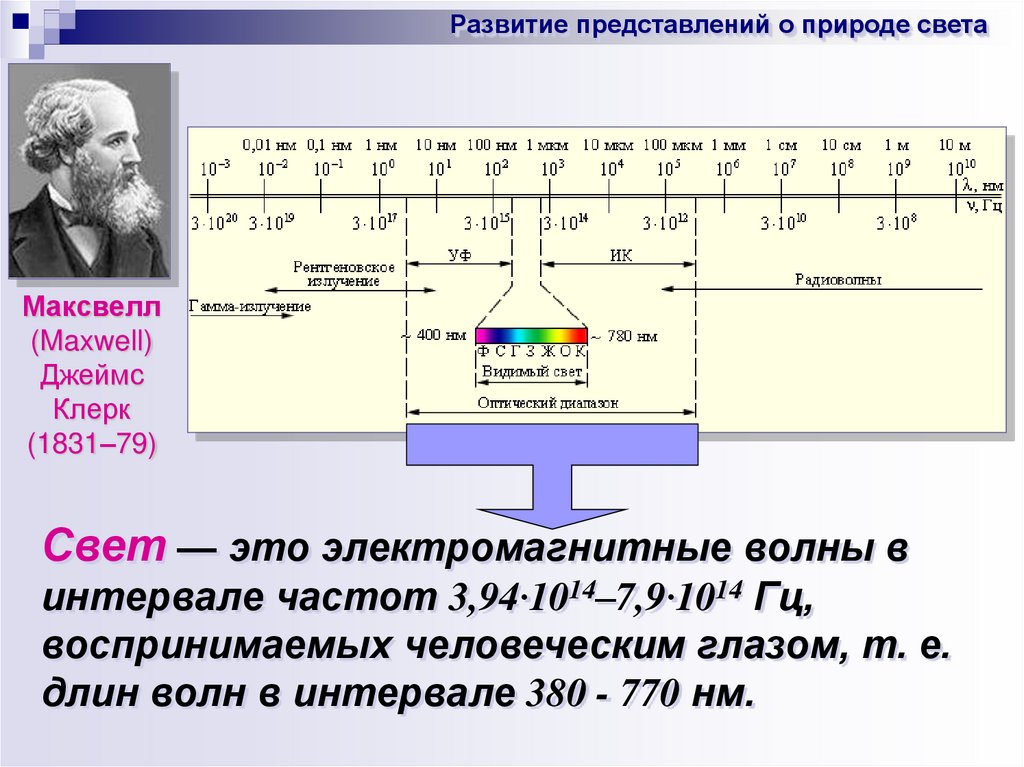
Развитие представлений о природе света
Максвелл
(Maxwell)
Джеймс
Клерк
(1831–79)
Свет — это электромагнитные волны в
интервале частот 3,94·1014–7,9·1014 Гц,
воспринимаемых человеческим глазом, т. е.
длин волн в интервале 380 - 770 нм.

8.

Развитие представлений о природе света
Свету
присущи
все
свойства
электромагнитных волн: отражение,
преломление, интерференция, дифракция, поляризация.
Свет может оказывать давление на вещество,
поглощаться
средой,
вызывать
явление
фотоэффекта.
Имеет
конечную
скорость
распространения в вакууме 300 000 км/с, а в среде
скорость убывает.

9.

Развитие представлений о природе света
Тот факт, что свет в одних опытах
обнаруживает волновые свойства, а
в других – корпускулярные, означает,
что свет имеет сложную
двойственную природу, которую
принято характеризовать термином
корпускулярно-волновой дуализм.

10. Основные законы геометрической оптики

11.

Основные законы геометрической оптики
1. Закон
прямолинейного
распространения света:
в оптически однородной
среде свет
распространяется
прямолинейно.
При прохождении света через очень малое отверстие — отклоняется.

12.

Основные законы геометрической оптики
Опытным
доказательством
этого закона могут служить
резкие тени, отбрасываемые
непрозрачными телами при
освещении светом источника
достаточно малых размеров
(«точечный источник»).

13.

Основные законы геометрической оптики
2. Закон независимости световых
лучей: при пересечении световые
лучи не возмущают друг друга и
каждый
луч
распространяется
независимо от другого.
Закон выполняется при не слишком больших
интенсивностях света.

14.

Основные законы геометрической оптики
На границе раздела двух прозрачных сред свет может частично
отразиться
так,
что
часть
световой
энергии
будет
распространяться после отражения по новому направлению, а
частично пройти через границу и распространяться во второй
среде.

15.

Основные законы геометрической оптики
3. Принцип Ферма: свет
распространяется по такому пути,
для прохождения которого ему
требуется минимальное время.
Этому соответствует путь, оптическая длина
которого минимальна.

16.

Основные законы геометрической оптики
Среда 1
Среда 2
i1 i1
'
i1 = i1'
i2
4. Закон отражения света: падающий и
отраженный лучи, а также перпендикуляр к
границе
раздела
двух
сред,
восстановленный в точке падения луча,
лежат в одной плоскости (плоскость
падения). Угол отражения i1' равен углу
падения i1.

17.

Основные законы геометрической оптики
Среда 1
Среда 2
i1 i1
i2
'
i1 = i1'

18.

Основные законы геометрической оптики
5. Закон преломления света: падающий и
преломленный
лучи,
а
также
перпендикуляр к границе раздела двух
сред, восстановленный в точке падения
луча, лежат в одной плоскости. Отношение
синуса угла падения i1 к синусу угла
преломления i2 есть величина постоянная
для двух данных сред:
sin i1
n12
sin i2
n
(1)
Постоянную
величину
называют
относительным
12
показателем преломления второй среды относительно первой.

19.

Основные законы геометрической оптики
Показатель преломления среды
относительно вакуума называют
абсолютным показателем преломления.
Относительный показатель
преломления двух сред равен отношению
их абсолютных показателей преломления:
n12 = n2 / n1
(2)
Среду с меньшим абсолютным показателем
преломления называют оптически менее плотной.

20.

Основные законы геометрической оптики
Физический смысл показателя преломления –
это отношение скорости распространения
волн в первой среде υ1 к скорости их
распространения во второй среде υ2:
1
n12
2
Абсолютный показатель преломления среды равен отношению
скорости света c в вакууме к скорости света υ в среде:
n
c

21.

Основные законы геометрической оптики
Учитывая (1):
n2 sin i1
n12
n1 sin i2
Следовательно, закон преломления можно записать
в виде:
n1 sin i1 n2 sin i2
(3)
Световые лучи обладают свойством обратимости.
1
n21
n12
(4)

22.

Основные законы геометрической оптики
При переходе света из оптически более плотной среды в
оптически менее плотную n2 < n1 (например, из воды в воздух)
можно наблюдать явление полного отражения, то есть
исчезновение преломленного луча. Это явление наблюдается
при углах падения, превышающих некоторый критический
(предельный) угол iпр, который называется предельным углом
полного внутреннего отражения.
n2
iпр
n1

23.

Основные законы геометрической оптики
Угол
преломления,
соответствующий
равен 90°.
iпр,
Для
определения
предельного
угла
подставим
в
(3)
i2 = π/2
n1 sin iпр n2 sin
Откуда
n2
sin iпр
n12
n1
или
2
n2
iпр arcsin n12

24.

Основные законы геометрической оптики
Явление полного внутреннего отражения
находит применение во многих оптических
устройствах.
Наиболее интересным и практически
важным применением является создание
волоконных
световодов,
которые
представляют собой тонкие (от нескольких
микрометров
до
миллиметров)
произвольно изогнутые нити из оптически
прозрачного материала (стекло, кварц).
Свет, попадающий на торец световода,
может распространяться по нему на
большие расстояния за счет полного
внутреннего
отражения
от
боковых
поверхностей.
Научно-техническое направление, занимающееся разработкой и
применением оптических световодов, называется волоконной
оптикой.

25.

Тонкие линзы
Линзой называется прозрачное тело, ограниченное двумя
сферическими поверхностями.
Если толщина самой линзы мала по сравнению с радиусами
кривизны сферических поверхностей, то линзу называют
тонкой.
Линзы входят в состав
практически всех оптических
приборов. Линзы бывают
собирающими и
рассеивающими.
Собирающая линза в середине
толще, чем у краев,
рассеивающая линза,
наоборот, в средней части
тоньше.

26.

Тонкие линзы

27.

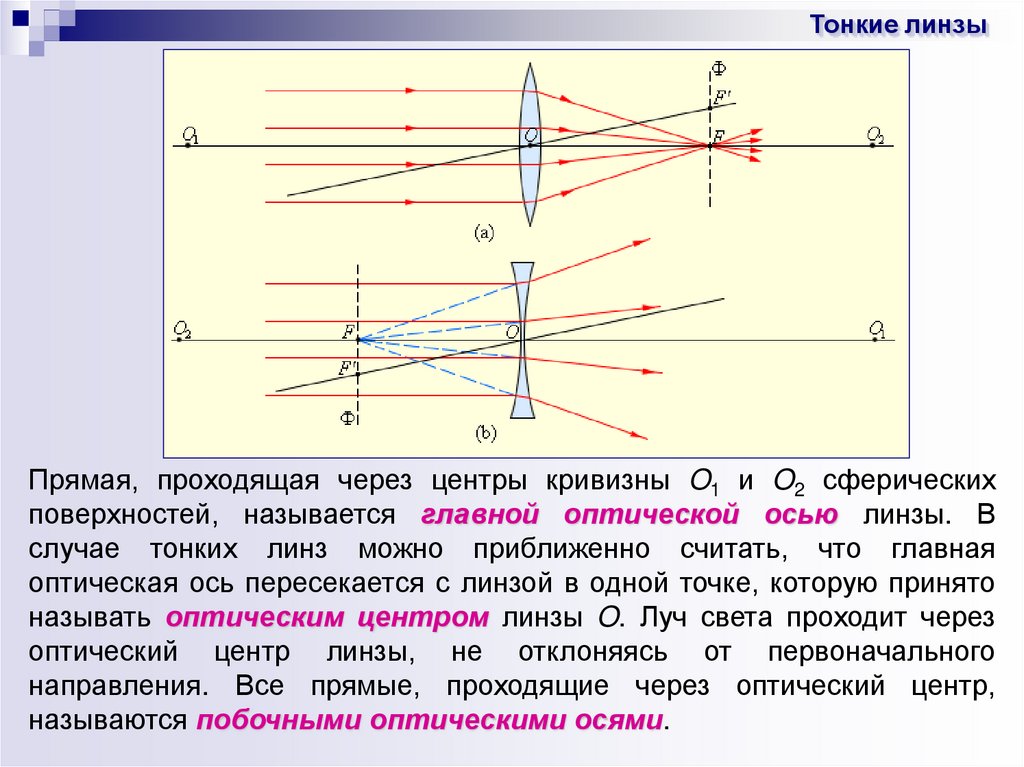
Тонкие линзы
Прямая, проходящая через центры кривизны O1 и O2 сферических
поверхностей, называется главной оптической осью линзы. В
случае тонких линз можно приближенно считать, что главная
оптическая ось пересекается с линзой в одной точке, которую принято
называть оптическим центром линзы O. Луч света проходит через
оптический центр линзы, не отклоняясь от первоначального
направления. Все прямые, проходящие через оптический центр,
называются побочными оптическими осями.

28.

Тонкие линзы
Если на линзу направить пучок лучей, параллельных
главной оптической оси, то после прохождения через линзу
лучи (или их продолжения) соберутся в одной точке F,
которая называется главным фокусом линзы.

29.

Тонкие линзы
У тонкой линзы имеются два главных фокуса, симметрично
расположенных относительно линзы на главной оптической оси. У
собирающих линз фокусы действительные, у рассеивающих –
мнимые. Пучки лучей, параллельных одной из побочных оптических
осей, также фокусируются после прохождения через линзу в точку F',
которая расположена при пересечении побочной оси с фокальной
плоскостью Ф, то есть плоскостью перпендикулярной главной
оптической оси и проходящей через главный фокус. Расстояние между
оптическим центром линзы O и главным фокусом F называется
фокусным расстоянием. Оно обозначается той же буквой F.

30.

Тонкие линзы
Основное свойство линз – способность давать
изображения предметов. Изображения бывают
прямыми и перевернутыми, действительными и
мнимыми, увеличенными и уменьшенными.
Положение изображения и его характер можно
определить с помощью геометрических построений.
Для
этого
используют
свойства
некоторых
стандартных лучей, ход которых известен. Это лучи,
проходящие через оптический центр или один из
фокусов линзы, а также лучи, параллельные главной
или одной из побочных оптических осей.

31.

Тонкие линзы
Построение изображения в собирающей линзе

32.

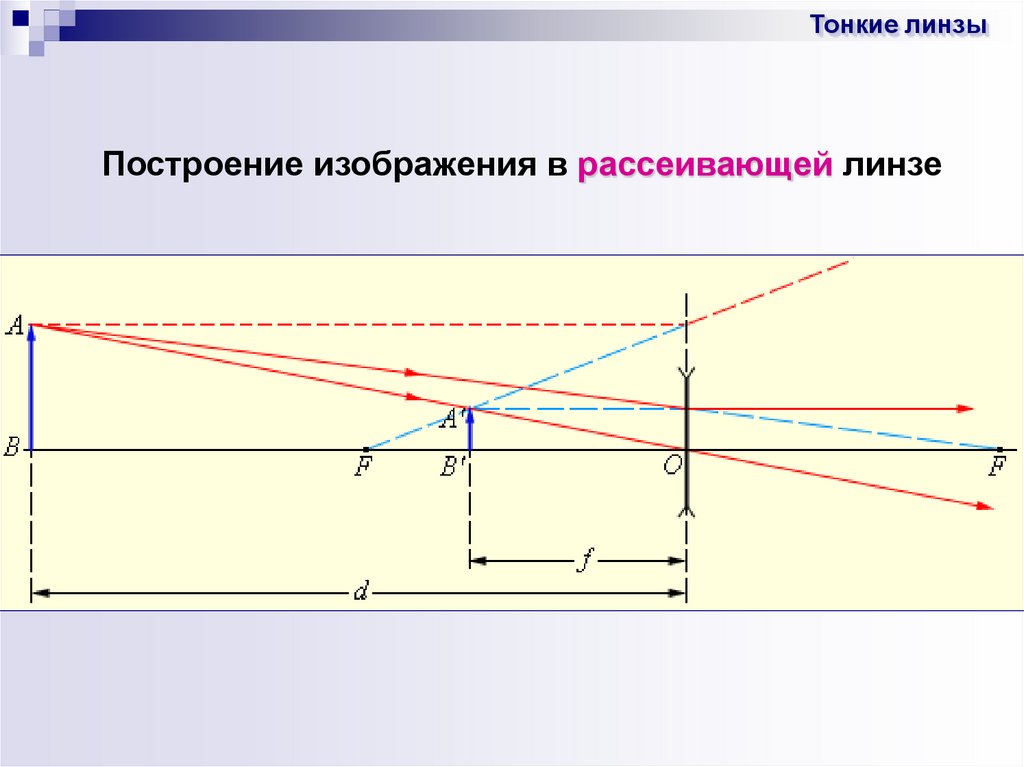
Тонкие линзы
Построение изображения в рассеивающей линзе

33.

34.

Тонкие линзы
Изображения можно также рассчитать с помощью формулы
тонкой линзы. Если расстояние от предмета до линзы
обозначить через d, а расстояние от линзы до изображения
через f, то формулу тонкой линзы можно записать в виде:

35.

Величину D, обратную фокусному расстоянию. называют
оптической силой линзы. Единица измерения оптической силы
является 1 диоптрия (дптр). Диоптрия – оптическая сила линзы с
фокусным расстоянием 1 м: 1 дптр = м–1.

36.

Тонкие линзы
Фокусным расстояниям линз принято приписывать
определенные знаки: для собирающей линзы F > 0, для
рассеивающей F < 0.
Величины d и
правилу знаков:
f
также подчиняются определенному
d>0иf
> 0 – для действительных предметов (то есть
реальных источников света, а не продолжений лучей,
сходящихся за линзой) и изображений;
d < 0 и f < 0 – для мнимых источников и изображений.

37.

В зависимости от положения предмета по отношению к
линзе изменяются линейные размеры изображения.
Линейным увеличением линзы Γ называют отношение
линейных размеров изображения h' и предмета h.
Величине h' удобно приписывать знаки плюс или минус в
зависимости от того, является изображение прямым или
перевернутым.
Величина h всегда считается положительной. Поэтому
для прямых изображений Γ > 0, для перевернутых Γ < 0.

38.

Оптическая сила D линзы зависит как от радиусов
кривизны R1 и R2 ее сферических поверхностей, так и от
показателя преломления n материала, из которого
изготовлена линза. В курсах оптики доказывается
следующая формула:
Радиус кривизны выпуклой поверхности считается положительным,
вогнутой – отрицательным. Эта формула используется при
изготовлении линз с заданной оптической силой.

39.

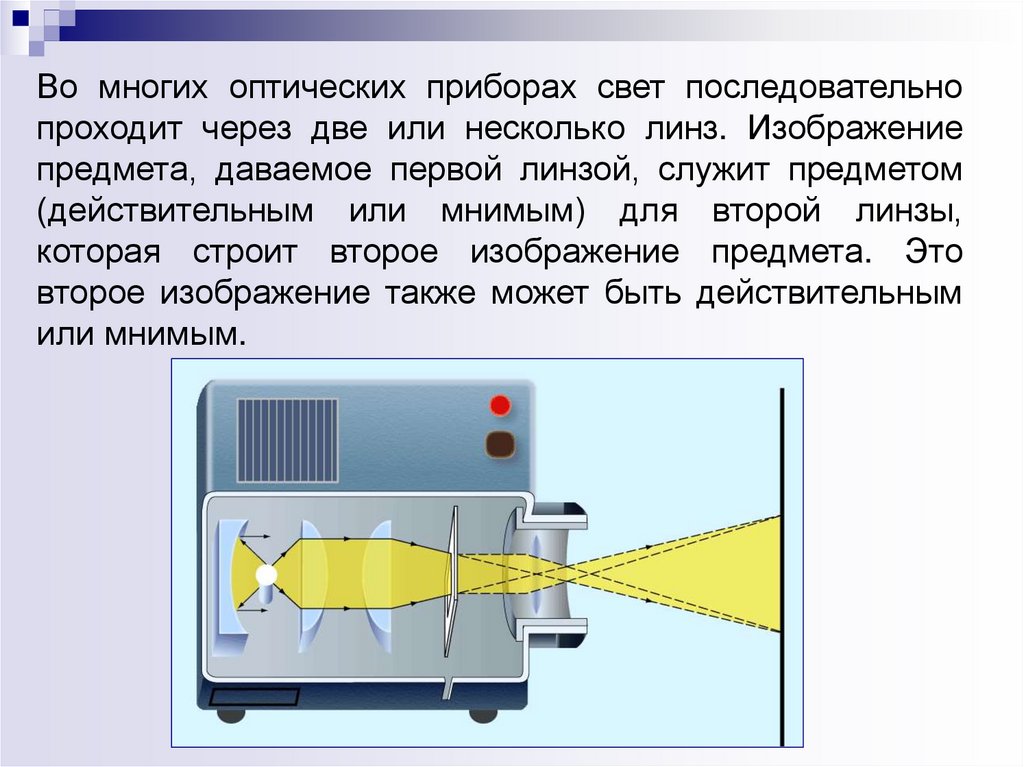
Во многих оптических приборах свет последовательно
проходит через две или несколько линз. Изображение
предмета, даваемое первой линзой, служит предметом
(действительным или мнимым) для второй линзы,
которая строит второе изображение предмета. Это
второе изображение также может быть действительным
или мнимым.

40.

Тонкие линзы обладают рядом недостатков, не
позволяющих получать высококачественные
изображения.
Искажения, возникающие при формировании
изображения, называются аберрациями.
Главные
из
них
–
сферическая
хроматическая аберрации.
и

41.

Сферическая аберрация проявляется в том, что
в случае широких световых пучков лучи, далекие
от оптической оси, пересекают ее не в фокусе.
Формула тонкой линзы справедлива только для
лучей, близких к оптической оси. Изображение
удаленного точечного источника, создаваемое
широким пучком лучей, преломленных линзой,
оказывается размытым.

42.

Хроматическая
аберрация
возникает
вследствие того, что показатель преломления
материала линзы зависит от длины волны
света λ. Это свойство прозрачных сред
называется дисперсией. Фокусное расстояние
линзы оказывается различным для света с
разными длинами волн, что приводит к
размытию изображения при использовании
немонохроматического света.

43.

Поэтому в современных оптических приборах
применяются не тонкие линзы, а сложные
многолинзовые
системы,
в
которых
удается
приближенно устранить различные аберрации.
Формирование собирающей линзой действительного
изображения предмета используется во многих
оптических приборах, таких как фотоаппарат,
проектор и т. д.

44.

Лекцию подготовила к.п.н.
доцент Симдянкина Е.Е.