Similar presentations:
О сколько нам открытий чудных готовит Архимеда труд
1. О сколько нам открытий чудных готовит Архимеда труд!
бюджетное профессиональное образовательное учреждениеВологодской области
«Череповецкий лесомеханический техникум им. В.П.Чкалова»
Специальность 38.02.03 Операционная деятельность в логистике
О сколько нам открытий чудных готовит Архимеда труд!
Научно-исследовательская работа
по дисциплине: Математика.
Выполнила: студентка группы ОЛ-11
Добрынина Ксения
Руководитель Белихина М.Е.
преподаватель математики
Номинация в конкурсе: гуманитарные и
социально-экономические дисциплины,
математический и естественнонаучный цикл
Череповец
2020г.
2. Содержание
ВведениеI Основная часть
1.Биография
1.1 Обучение
1.2 Научная работа
1.3 Конфликт в Сиракузах
1.4 Смерть
2.Научный вклад Архимеда
2.1 Принцип Архимеда
2.2 Механический метод
2.3 Объяснение закона рычага
2.4 Разработка метода исчерпания или истощения для научной демонстрации
2.5 Мера круга
2.6 Геометрия сфер и цилиндров
3.Изобретения
3.1 Одометр
3.2 Первый планетарий
3.3 Архимедов винт
3.4 Коготь Архимеда
Другие исследования
II Исследовательская часть
•1 Я в роли Архимеда ( доказательство аксиом)
•2. Результаты опроса Приложение 1
•3.Решение «Задачи Герона» Приложение 2
•4 «Вспомнить все» (Кроссворды) Приложение 3
III Заключение
•Список источников и литературы
3.
«Дайте мне точку опоры, и я сдвину Землю. »Архимед
Кто не слышал знаменитую фразу «ЭВРИКА!» .Нашел решение задачи,
проблемы - ЭВРИКА! Придумал новый метод решения - ЭВРИКА! Сделал
открытие - ЭВРИКА! Да! Да! Именно о нем моя работа.
Древнегреческий ученый
Архимед Сиракузский (287 до
н.э. - 212 до н.э.) был
математиком, физиком,
изобретателем, инженером,
греческим астрономом и
механиком из древнего города
Сиракузы, на острове Сицилия.
Его вклад означал важные
научные достижения в то время в
области вычислений, физики,
геометрии и астрономии. В свою
очередь, это и делает его одним
из самых выдающихся ученых в
истории человечества.
4.
Актуальность темы: ознакомиться с биографией Архимеда и его открытиями полезно хотя бы потому,что последние изменили ход развития науки.
Гипотеза: Во времена высоких технологий и научных открытий мы привыкли воспринимать
достижения как нечто обыденное, забывая о том, что основы существующих знаний были заложены
древними учёными. Именно они были первопроходцами.
Цель исследования: Показать значимость и важность трудов Архимеда в развитии науки и математики.
Задачи исследования:
•Изучить учебную, методическую, энциклопедическую литературу.
•Определить сущность научных открытий Архимеда.
•Описать основные открытия, сделанные Архимедом.
•Доказать леммы Архимеда.
•Решить задачу Гиерона на основе физики и математики.
•Провести социологический опрос студентов 1 курса.
•Подобрать материал для кроссвордов.
Предмет исследования: научный гений Архимеда
Объект исследования: математическая составляющая в трудах Архимеда
Методы исследования: анализ учебной, методической, энциклопедической, научно-популярной
литературы; сравнительный анализ, выявление аналогий
5. Биография
Архимед Сиракузский родился примерно в 287 году до нашей эры. Оего ранних годах известно немного. Родился в Сиракузах, городе,
который сегодня считается главным морским портом острова Сицилия,
сегодня в Италии.
Его детство пришлось на тот период, когда царь Пирр вёл войны с
карфагенянами и римлянами.
Нет никаких известных фактов о матери Архимеда. Что касается
отца, известно, что его звали Фидий и что он был посвящен
астрономии.
Биограф Плутарко указал в своей книге «Параллельные жизни»,
что у Архимеда были кровные отношения с Гиероном II, царем
Сиракуз с 265 года до нашей эры.
6.
ОбучениеРазличные историографы считают, что Архимед учился
в Александрии, которая была самым важным греческим
культурным и образовательным центром.
Здесь Птолемеями – правителями Египта – были собраны
лучшие греческие учёные и мыслители того времени.
В Александрии находилась самая большая в мире
библиотека, где Архимед на протяжении долгого времени
изучал математику и труды Евдокса, Демокрита и т.д.
7.
Научная работаПосле учёбы Архимед, вернулся в Сиракузы и стал придворным астрономом.
Начал придумывать разные артефакты, которые вскоре завоевали ему
определенную популярность среди жителей этого города.
Создал труд «О равновесии плоских фигур». Эта работа учёного стала
краеугольным камнем «Параболы квадратуры» (интегрального исчисления),
которую откроют через 2000 лет.
В сочинении «Об измерении круга» исследователь вычислил отношение
диаметра окружности к её длине - число Пи (3.14)
В последние годы он занимался вычислительно-астрономической
деятельностью.
8.
Оборона СиракузОткрытия Архимеда в сфере инженерного дела принесли ему
наибольшую славу
Ярко его инженерный гений проявился в 214 г. до н. э. при осаде его
родных Сиракуз.
9.
КончинаИстории его гибели, рассказанные разными историками той эпохи, несколько
отличаются :
Архимед находился в процессе решения математической задачи, когда к нему
подошел римский солдат. Говорят, что Архимед попросил его некоторое время , что
бы решить проблему, поэтому солдат убил бы его.
Римский солдат вошел в его состав и приказал ему встретиться с Марсело, Архимед
ответил, что он должен решить проблему, над которой он работал в первую очередь. В
результате солдат убил его.
Архимед имел в руках много инструментов для математики. Его увидел солдат и
подумал, что он может нести ценные вещи, поэтому он убил его.
Архимед присел у земли, обдумывая планы. Сзади пришел римский солдат и, не
зная, что это был Архимед, застрелил его.
10.
Научный вклад АрхимедаБиография Архимеда описывает два его самых значимых научных
достижения: учение о центре тяжести и формулировка принципа
рычага.
Архимед не только доказал несколько главных положений о
физических характеристиках атомов жидкости, но и подтвердил
целый ряд атомистических идей Демокрита.
Архимед был тем, кто определил, что объем, связанный со сферой,
соответствует удвоенному размеру цилиндра, в котором она находится, и
тем, кто изобрел составной шкив.
11.
Принцип АрхимедаПринцип Архимеда рассматривается современной наукой как одно из важнейших наследий
древней эпохи.
Царь Гиерон заказал мастеру венец из чистого золота. Царь пожелал проверить, не подменил ли
мастер часть золота- серебром и обратился к Архимеду. Он должен был выполнить это, не разрушая
корону.
«Задача Гиерона» (Приложение 2)
Принцип означает, что жидкости оказывают подъемную силу - толкая вверх - на любой погруженный
в них объект, и что величина этой толкающей силы равна весу жидкости, вытесняемой погруженным
телом, независимо от его веса.
12.
Механический методВключил чисто механический, то есть технический метод,
в аргументацию геометрических задач
В контексте Архимеда геометрия считалась
исключительно теоретической наукой.
Сказал что этот метод позволяет решать вопросы
математики с помощью механики и что несколько проще
построить демонстрацию геометрической теоремы, если она
уже имеет некоторые предварительные практические знания
13.
Объяснение закона рычагаВ работе «О равновесии плоскостей» Архимед исследовал центры тяжести
различных фигур.
Закон: два тела, которые можно измерить (соизмеримые), расположенные на
рычаге, сбалансированы, когда они находятся на расстояниях, обратно
пропорциональных их весу.
После открытия рычага Архимед активно развивал свою теорию и находил ей
полезное практическое применение.
Открытия Архимеда наглядно показывают, насколько этот человек
обогнал свое время и во что мог превратиться наш мир, если бы высокие
технологии усваивались в античности
Архимед специализировался в
математике и геометрии — двух
важнейших науках, лежащих в
основе технического прогресса.
14.
Разработка метода исчерпания или исчерпывания длянаучной демонстрации
Исчерпание - это метод, используемый в геометрии, который состоит в аппроксимации
геометрических фигур, чья область известна посредством надписи и круглой надписи, на
другой, чья область должна быть известна.
Архимед, используя метод исчерпывания вписал и описал шестиугольники на
окружности диаметром 1, уменьшив до абсурда разницу между площадью
шестиугольников и площадью окружности. Для этого он разделил пополам
шестиугольники, создавая до 16 сторон многоугольников.
Архимед мастерски использовал метод исчерпания, потому что ему удалось не
только приблизить вычисление значения Pi с достаточно малым и, следовательно,
желательным пределом погрешности, но и потому, что число Pi является
иррациональным числом. Через этот метод и полученные результаты заложили
основы, которые могли бы прорасти в бесконечно малой системе вычислений, а затем
и в современном интегральном исчислении.
15.
Мера кругаЧтобы определить площадь круга, Архимед использовал метод, который
заключался в рисовании квадрата, который точно вписывался в круг
Стомахион, остомахион — древнегреческий математический трактат,
приписываемый Архимеду. Это была своего рода игра, суть которой заключалась в
том ,чтобы собрать из треугольников ровный квадрат или же другие предметы.
Однажды, играя в стомахион, ему в голову пришла идея ,что площадь любой
плоской фигуры можно рассчитать с помощью треугольников, раз треугольнике
позволяют вычислить площадь ,то пирамиды объем.
16.
Геометрия сфер и цилиндровСреди девяти трактатов, составляющих работу Архимеда по математике и физике, есть
два тома по геометрии сфер и цилиндров.
Эта работа посвящена определению того, что поверхность любой сферы радиуса в
четыре раза больше ее наибольшего круга и что объем сферы в две трети превышает
объем цилиндра, в который она вписана.
Главная математическая деятельность ученого была направлена на решения проблем,
касающихся области математического анализа.
Архимед отыскал более простой метод нахождения объемов и площадей, для этого он
усовершенствовал и мастерски применял метод для вычисления площади или объёма
криволинейных фигур, который когда-то открыл Евдокс Книдский.
До Архимеда никто не мог установить объем шара, поэтому он считал это
открытие главным и наилучшим из своих достижений, что даже попросил после
своей смерти выбить на надгробной плите шар, который вписан в цилиндр, потому
что эти фигуры являются идеальными.
17.
Вот соображения, с помощью которых он получил точную формулу для объема шара. Пусть [AC] и[BD] – два взаимно перпендикулярных диаметра большого круга шара с центром К, а AFE – осевое
сечение конуса, основания которого шар касается в центре – точке С. Второй конец диаметра АС
совпадает с вершиной конуса. На круге с диаметром
(основе конуса) построим еще цилиндр,
Осевое сечение цилиндра – GFEL.
высота которого равна
Отложим
и рассмотрим равноплечный рычаг HAC с точкой опоры в A. Через любую точку
S диаметра AC построим плоскость, перпендикулярную АС. Она пересечет цилиндр по кругу
шар – по кругу диаметром
Очевидно, что
и конус – по кругу диаметром
диаметром
,потом
и
Поэтому
Поскольку
то,
или, на основе предыдущего равенства,
В одной из работ Архимеда «Квадратура параболы», было доказано, что сегмент параболы,
отсекаемый от неё прямой, равняется 4/3 площади вписанного в данный сегмент треугольника.
Данную теорему он теоретически подтвердил, высчитав сумму бесконечного ряда:
Всякое слагаемое последовательности является общей площадью треугольников, которые
вписаны в неохваченную предыдущими членами ряда часть сегмента параболы.
Не менее значительны и другие сочинения: «О коноидах и сфероидах», «О
спиралях», «Измерение круга», «Квадратура параболы».
18.
в других опытах, Архимед определил объёмы:сегментов шара – определенных частей шара, отсеченных от него плоскостями
эллипсоида – трехмерного аналога эллипса, описываемого тремя полуосями (a,b,c)
параболоида – поверхности второго порядка, не имеющей центра симметрии,
описываемой каноническим уравнением
Двуполостного гиперболоида вращения – поверхность, которая в некоторой декартовой
системе координат, описывается уравнением
19.
Одометрсоздал конструкцию, чем-то напоминающую тележку. Ее можно было катить рукой, а
можно было прикрепить к повозке.
Это устройство было построено по принципу колеса, которое при повороте
активирует шестерни, позволяющие рассчитать пройденное расстояние.
20.
Первый планетарийМногие ученые приписывают Архимеду создание первого
элементарного планетария. ( Впервые он упоминается в I веке до н.э., а
последнее принадлежит римскому поэту Клавдиану в V веке.)
По словам Цицерона, планетариев, построенных Архимедом, было два. В
одном из них были изображены Земля и различные созвездия рядом с ней,
в другом, с единственным вращением, солнце, луна и планеты делали свои
собственные независимые движения относительно неподвижных звезд точно
так же, как они делали в реальном дне.
21.
.Винт Архимеда
Винт Архимеда - это устройство, которое используется для транспортировки воды снизу
вверх по склону с использованием трубки или цилиндра.
Согласно греческому историку Диодоро, благодаря этому изобретению было
облегчено орошение плодородных земель
Изобретение винта позволило собирать воду из низко расположенных водоемов и
поднимать ее на большую высоту. Это было важное достижение, так доставка воды
представляла серьезную проблему. Оросительные каналы наполнились живительной
влагой и бесперебойно снабжали жителей острова
22.
Коготь АрхимедаКоготь Архимеда, или железная рука, был одним из самых страшных
орудий войны
это был большой рычаг, к которому прикреплен захватный крюк с
помощью цепочки, которая свисала с него.
23.
Другие исследованияКроме механики, физики и математики, Архимед занимался
метеорологической и геометрической оптикой.
Провёл ряд экспериментов по преломлению света.
Проводил эксперименты по преломлению света в водной и
воздушной средах, а также имел представление о свойствах
изображений в вогнутых, выпуклых и плоских зеркалах.
24.
Я в роли АрхимедаСложно переоценить достижения великого математика, физика и естествоиспытателя
Архимеда. Ведь благодаря его открытиям, во многом сформировались принципы
современной науки и инженерного дела.
Открытия в области математики были настоящей страстью ученого. Согласно
утверждениям Плутарха, Архимед забывал о пище и уходе за собой, когда стоял на
пороге очередного изобретения в этой сфере.
Наименее известными из всех его трудов являются аксиомы Архимеда.
В переводе с греческого слова axioma – утверждение,
положение принимаемое без доказательства.
Толковый словарь Даля : аксиома — это «основная истина, очевидность,
ясная сама по себе».
В рамках современного научного подхода, аксиома- некое
фундаментальное положение, с которого начинается логическое
доказательство.
Я доказала некоторые из аксиом Архимеда и в решила задачу Гиерона
двумя способами. Решение лемм оформлено в программе Paint.
Задачи показаны в Приложении 2
25.
1.Лемма о параллельных диаметрах.26.
2. Лемма о перпендикулярах из концовдиаметра.
27.
3.Лемма о перпендикулярных хордах.28.
ЗаключениеРаботая над выбранной темой, я изучила много литературы, рассказывающей о жизни и деятельности
Архимеда, его открытиях. Нашла подтверждение своей гипотезы: открытия, которые совершил великий
философ и гениальный математик Архимед, просто необходимы для человечества, так как произвели
огромный скачек в разделах математики и физики. И хотя большинство опрошенных студентов помнят
лишь закон Архимеда, сам Архимед считал своим самым главным открытием определение соотношения
объемов шара, цилиндра и конуса, чьи диаметры одинаковы и прямо пропорциональны высотам.
Архимед подтвердил большинство собственных идей на практике, решил много математических задач,
сформулировал законы кинематики и гидростатики, применил винт для перекачивания воды, изобрел
подъемный кран и множество видов катапульт, построил лабиринты в городских стенах,
сконструировал зажигательные зеркала и мощные редукторы, построил движущиеся модели небесной
сферы.
В III в. до н.э. греческая цивилизация породила выдающихся ученых: математик и физик Евклид,
инженер и архитектор Сострат Книдский, математик и географ Эратосфен, корабельный мастер
Архелай, математик и астроном Аполлоний Пергский, математик и астроном Аристарх Самосский и
др. Выполняя работу я прикоснулась к этому миру.
Доказав леммы Архимеда, почувствовала себя ученым.
Этот ученый достоин того, чтобы его имя знали все. Поэтому изучая просторы интернет- я
нашла прекрасный сайт позволяющий студентам самим окунуться в ту эпоху. А чтобы
смотрелось веселей организовала ребят на командный квест– «Вспомнить ВСЕ» (разгадай
кроссворд). Работа по данной теме оказалась очень интересной, увлекательной и полезной.
Думаю, что подобранный материал пригодится преподавателям для популяризации истории
математики.
29.
ЛитератураСписок литературы:
1. Арский Ф.Н. Перикл. — М.: Молодая гвардия, 1971. — 224 с.
2. Архимед. Сочинения. — М.: Физматгиз, 1962. -— 640 с.
3. Бондаренко С.Б. Философские взгляды Архимеда//Философия науки, 2013, №2.
4. Боннар А Греческая цивилизация.— М.: Искусство, 1995.— 583 с.
5. Бернштейн С.Н. О квадратуре круга: [пер. с яз. оригинала работ Архимеда, Гюйгенса, Ламберта,
Лежандра, Рудио] / Пер.под ред., с предисл. и примеч.. Одесса. 1911 .VIII. 155 с.
6. Веселовский И.Н. Архимед.— М.: ГУП, 1957.— 111с.
7. Гейберг И.Л. Естествознание и математика в классической древности. — М.-—Л.:ОНТИ, 1936.—139 с.
8. Лурье С.Я. Архимед. — М.— Л.: Изд—во АН СССР, 1945.—256 с. 14. Плутарх. Марцелл//Плутарх.
Сравнительные жизнеописания в 2—х т.— М.: Наука, 1994.— Т.1—С. 340—362.
9. Порфирий. Жизнь Пифагора//Диоген Лаэртский. О жизни, учениях и изречениях знаменитых
философов.— М.: Мысль, 1979.— С.449—461.
10. Суриков И.Е. Пифагор.— М.: Молодая гвардия, 2013.— 269 с.
11. Ямвлих. О Пифагоровой жизни.— М.: Алетейа, 2002.-—192 с.
Ссылки:
1.АССИС, А. (2008). Архимед, центр тяжести и первый закон механики [онлайн]. bourabai.ru.
2.DIJKSTERHUIS, E. (1956). Архимед [онлайн]. books.google.co.ve/books.
3.МОЛИНА А. (2008). Метод исследования Архимеда Сиракузского: интуиция, механика и истощение
[онлайн]. WorldWide Webproduccioncientifica.luz.edu.
4.O'CONNOR, J. & ROBERTSON, R. (1999). Архимед Сиракузский [онлайн]. history.mcs.st-and.ac.uk.
5.PARRA, E. (2009). Архимед: его жизнь, творчество и вклад в современную математику
[онлайн].lfunes.uniandes.edu.co.
https://fb.ru/article/169109/biografiya-arhimeda-vyidayuschiesya-otkryitiya-arhimeda
30.
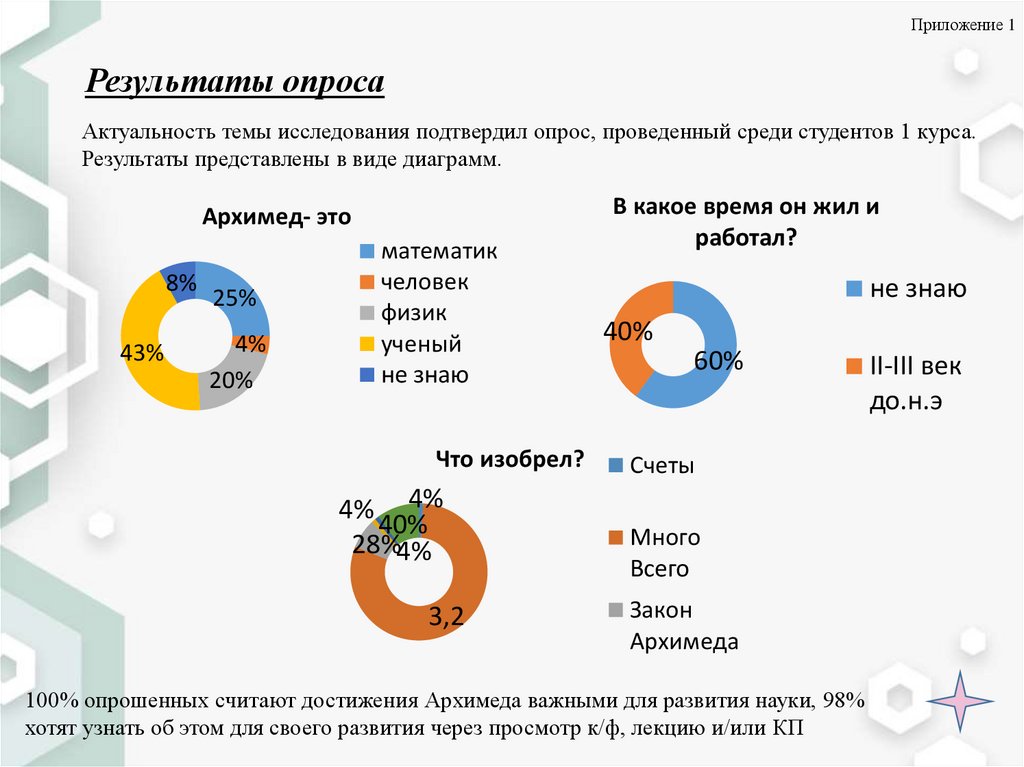
Приложение 1Результаты опроса
Актуальность темы исследования подтвердил опрос, проведенный среди студентов 1 курса.
Результаты представлены в виде диаграмм.
Архимед- это
8%
43%
25%
4%
20%
математик
человек
физик
ученый
не знаю
Что изобрел?
4% 4%
40%
28%4%
3,2
В какое время он жил и
работал?
не знаю
40%
60%
Счеты
Много
Всего
Закон
Архимеда
100% опрошенных считают достижения Архимеда важными для развития науки, 98%
хотят узнать об этом для своего развития через просмотр к/ф, лекцию и/или КП
II-III век
до.н.э
31.
Приложение 2Задача Гиерона
Решение задачи с точки зрения физики:
32.
Решение задачи с точки зрения математики.Чистое золото теряет в воде 20-ю долю своего веса, а серебро
10-ю долю. Обман мы раскрыли, но последуем примеру Архимеда и
выясним, сколько золота мастер заменил серебром?
Корона потеряла в весе 1,25Н= Н, а должна бы потерять 1Н. Это потому,
что она содержит серебро, которое теряет в воде не долю веса, а .
Серебра должно быть в короне столько, чтобы венец терял в воде не 1Н, а
Н, т.е. на Н более.
Если в короне из чистого золота мысленно заменить 1Н золота серебром,
то корона потеряет в воде больше, чем прежде на - = Н.
Следовательно, чтобы получилось требуемое увеличение потери веса на
Н, необходимо заменить серебром столько золота, во сколько раз Н
больше Н, т.е. := в 5 раз.
Итак, в венце было 5 Н серебра и 15 Н золота.
33.
Приложение 3Кроссворд
Вопросы:
1. Один из главных школьных предметов?
2. Упражнение ,для выполнения которого
нужно думать, вычислять, записывать ответ?
3.Великий ученый, математик из Сицилии,
живший в 3 веке до н.э.?
4.Где родился Архимед?
5.Кто преподавал в школе, в которой обучался
и чью труды читал Архимед?
6.Во время шторма, на корабле Архимед
соорудил прибор, для откачивания воды из
трюмов, это приспособление называлось
Архимедов…?































 biography
biography physics
physics mechanics
mechanics








