Similar presentations:
Прямоугольник. Ромб. Квадрат
1. Прямоугольник. Ромб. Квадрат.
НачалоПРЯМОУГОЛЬНИК. РОМБ. КВАДРАТ.
1
2. Цели урока:
ЦЕЛИ УРОКА:Повторить понятие параллелограмма;
Дать определение прямоугольника, ромба,
квадрата.
Познакомиться со свойствами данных фигур;
Научиться применять свойства при решении задач.
2
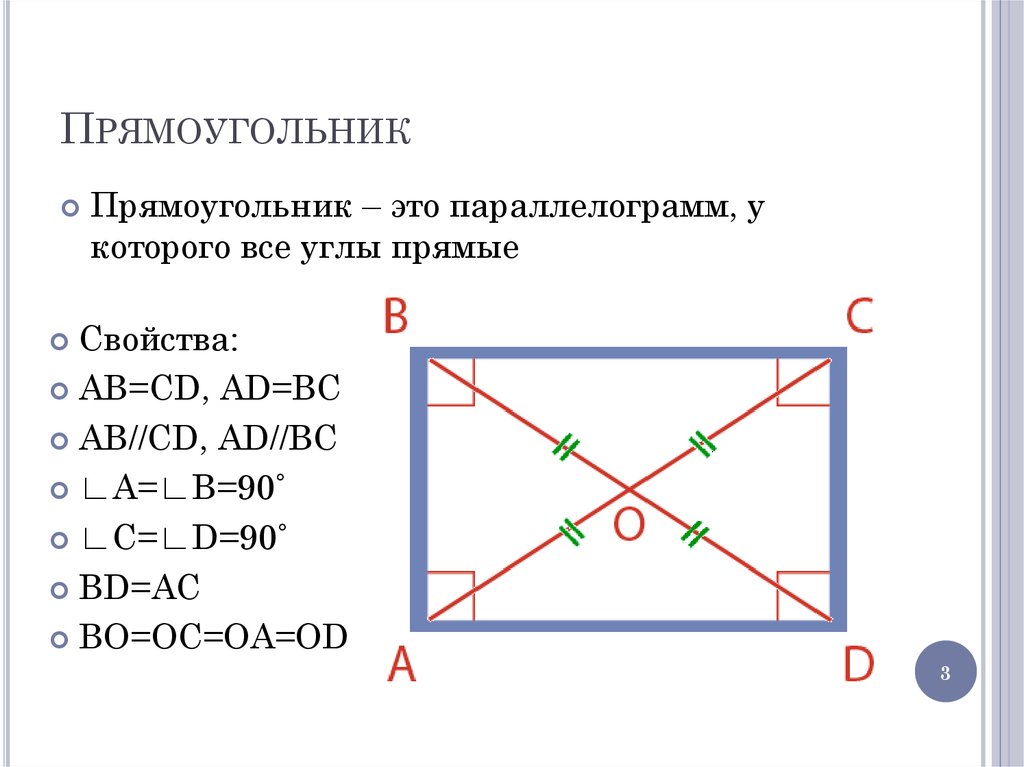
3. Прямоугольник
ПРЯМОУГОЛЬНИКПрямоугольник – это параллелограмм, у
которого все углы прямые
Свойства:
AB=CD, AD=BC
AB//CD, AD//BC
∟A=∟B=90˚
∟C=∟D=90˚
ВD=АС
ВО=ОС=ОА=ОD
3
4. Прямоугольник и параллелограмм
ПРЯМОУГОЛЬНИК И ПАРАЛЛЕЛОГРАММПараллелограмм
Прямоугольник
Противоположные стороны:
- равны
- параллельны
Противоположные стороны:
- равны
- параллельны
Углы:
- противоположные равны
- соседние в сумме = 180˚
Углы:
- противоположные равны
- соседние в сумме = 180˚
- все углы = 90˚
Диагонали:
- точкой пересечения делятся пополам
Диагонали:
- точкой пересечения делятся пополам
- равны
4
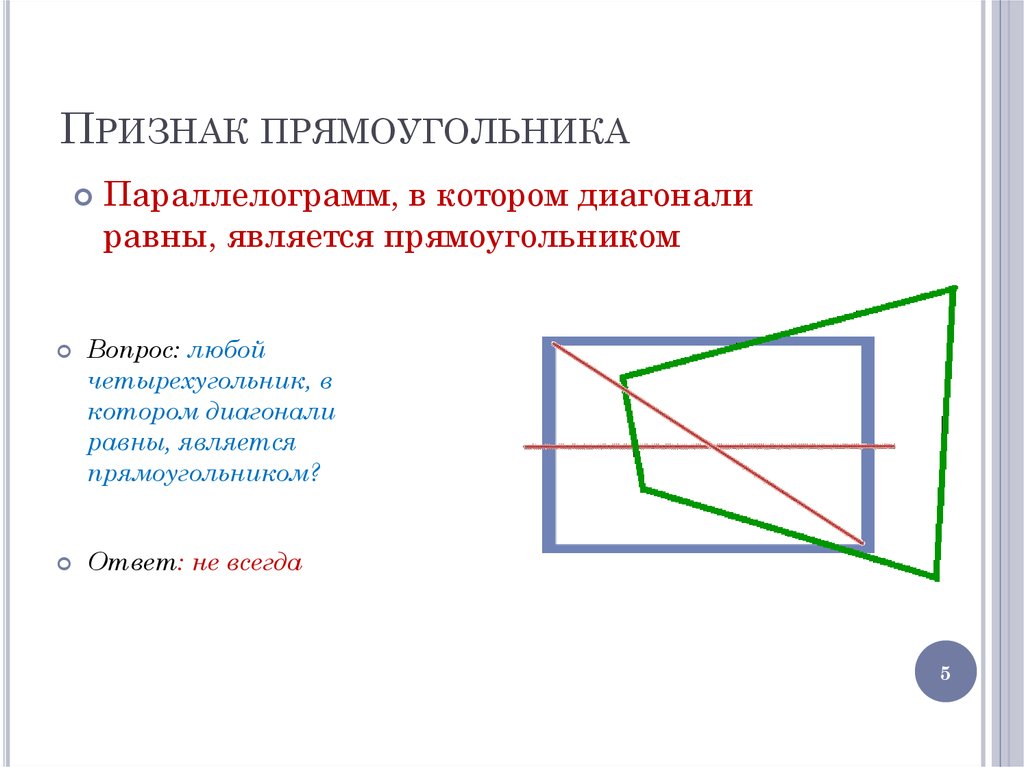
5. Признак прямоугольника
ПРИЗНАК ПРЯМОУГОЛЬНИКАПараллелограмм, в котором диагонали
равны, является прямоугольником
Вопрос: любой
четырехугольник, в
котором диагонали
равны, является
прямоугольником?
Ответ: не всегда
5
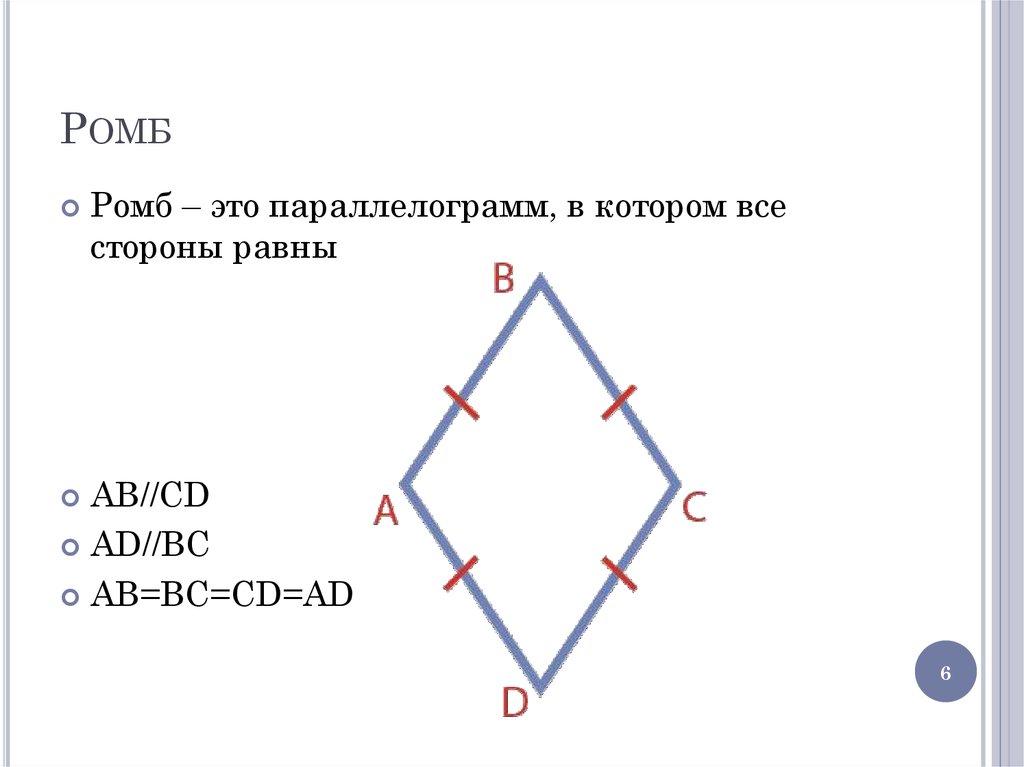
6. Ромб
РОМБРомб – это параллелограмм, в котором все
стороны равны
AB//CD
AD//BC
AB=BC=CD=AD
6
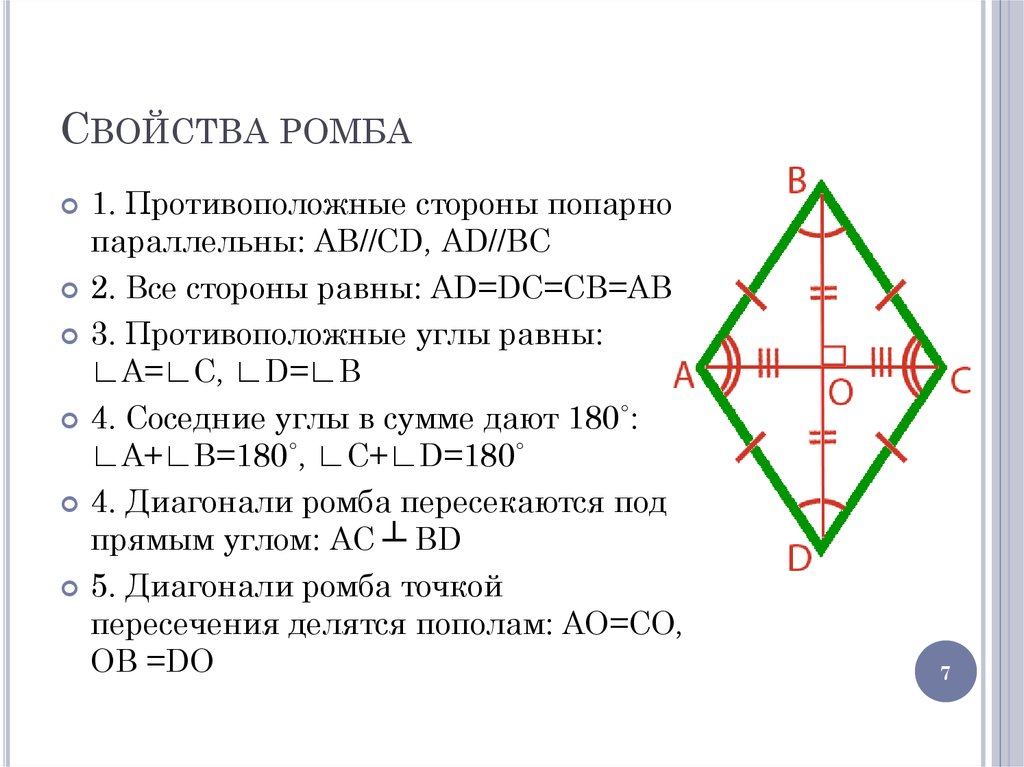
7. Свойства ромба
СВОЙСТВА РОМБА1. Противоположные стороны попарно
параллельны: AB//CD, AD//BC
2. Все стороны равны: AD=DC=CB=AB
3. Противоположные углы равны:
∟A=∟C, ∟D=∟B
4. Соседние углы в сумме дают 180˚:
∟A+∟B=180˚, ∟C+∟D=180˚
4. Диагонали ромба пересекаются под
прямым углом: AC ┴ BD
5. Диагонали ромба точкой
пересечения делятся пополам: AО=CО,
ОB =DО
7
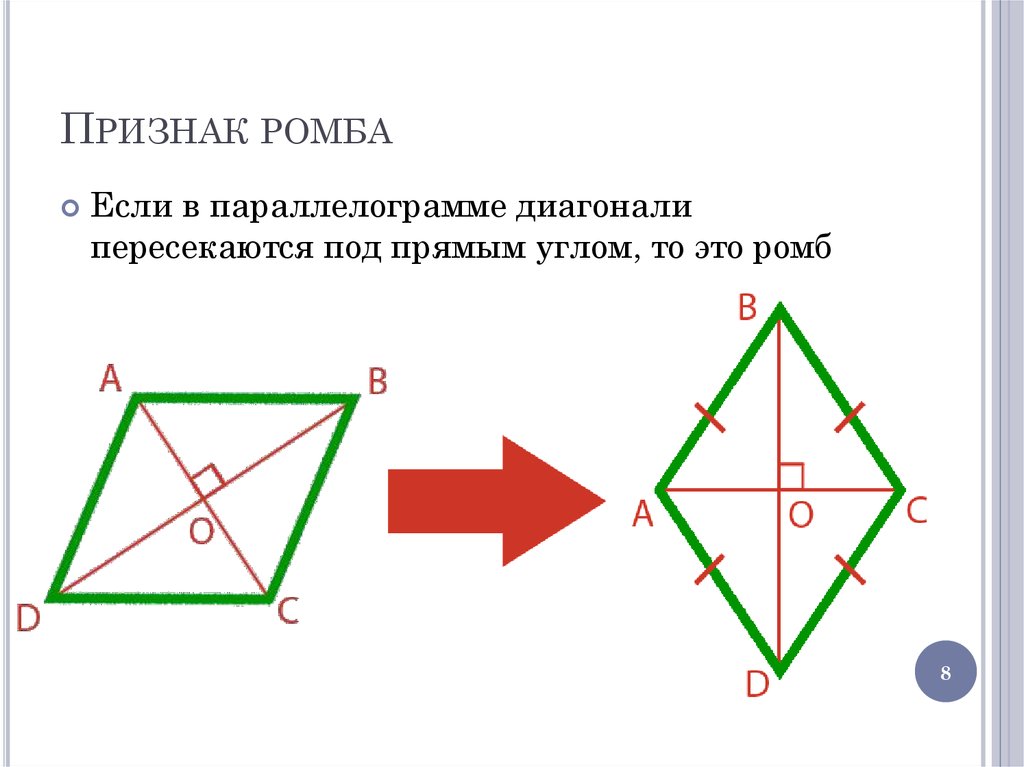
8. Признак ромба
ПРИЗНАК РОМБАЕсли в параллелограмме диагонали
пересекаются под прямым углом, то это ромб
8
9. Квадрат
КВАДРАТЕсли соединить в одной фигуре свойства
прямоугольника и ромба, то мы получим
КВАДРАТ
9
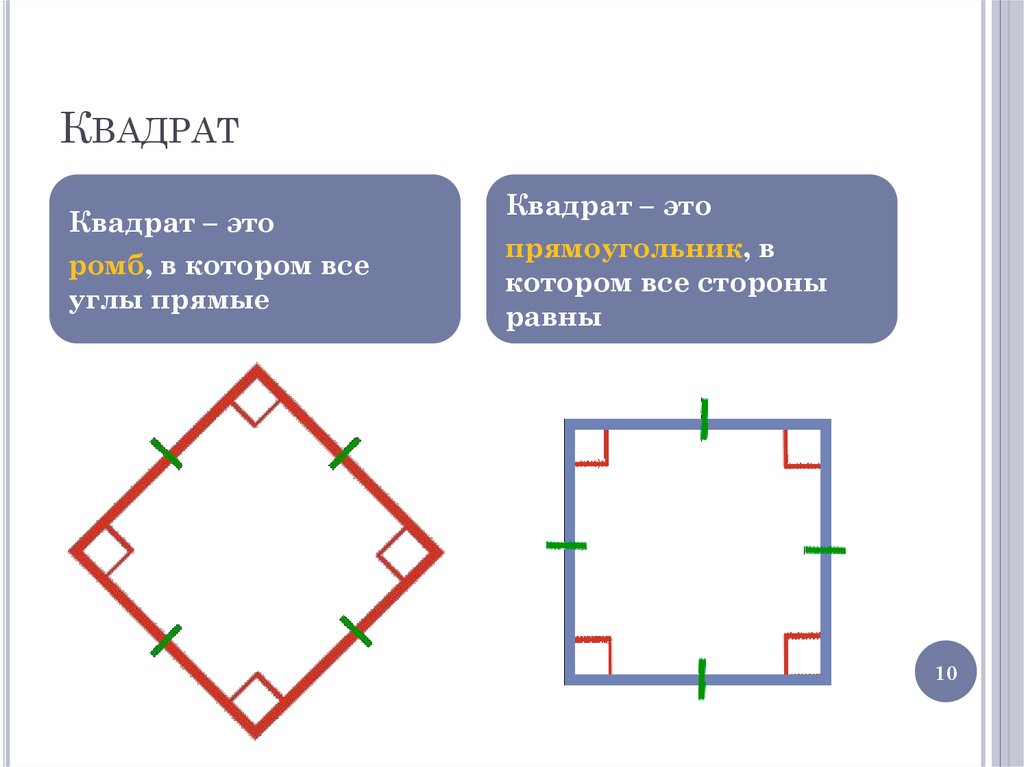
10. Квадрат
КВАДРАТКвадрат – это
ромб, в котором все
углы прямые
Квадрат – это
прямоугольник, в
котором все стороны
равны
10
11. Свойства квадрата
СВОЙСТВА КВАДРАТА1. Все стороны равны
2. Все углы прямые
3. Диагонали равны
4. Диагонали точкой
пересечения делятся
пополам
5. Диагонали
пересекаются под
прямым углом
AC=BD
AO=OC, BO=OD
AC ┴ BD
11
12. Признаки квадрата
ПРИЗНАКИ КВАДРАТАЕсли в прямоугольнике диагонали
перпендикулярны – это квадрат
Если в ромбе диагонали равны – это квадрат
Если в параллелограмме диагонали
перпендикулярны и равны – это квадрат
12
13. Прямоугольник. Ромб. Квадрат.
КонецПРЯМОУГОЛЬНИК. РОМБ. КВАДРАТ.
13






 mathematics
mathematics