Similar presentations:
Философский аспект компьютерного моделирования. Введение в КМ (лекция 2)
1.
Философский аспекткомпьютерного моделирования
Сэр Карл Раймунд Поппер
Австрийский и британский философ. Один
из влиятельных философов ХХ столетия
Годы
жизни:
28.07.1902 –
17.09.1994
2.
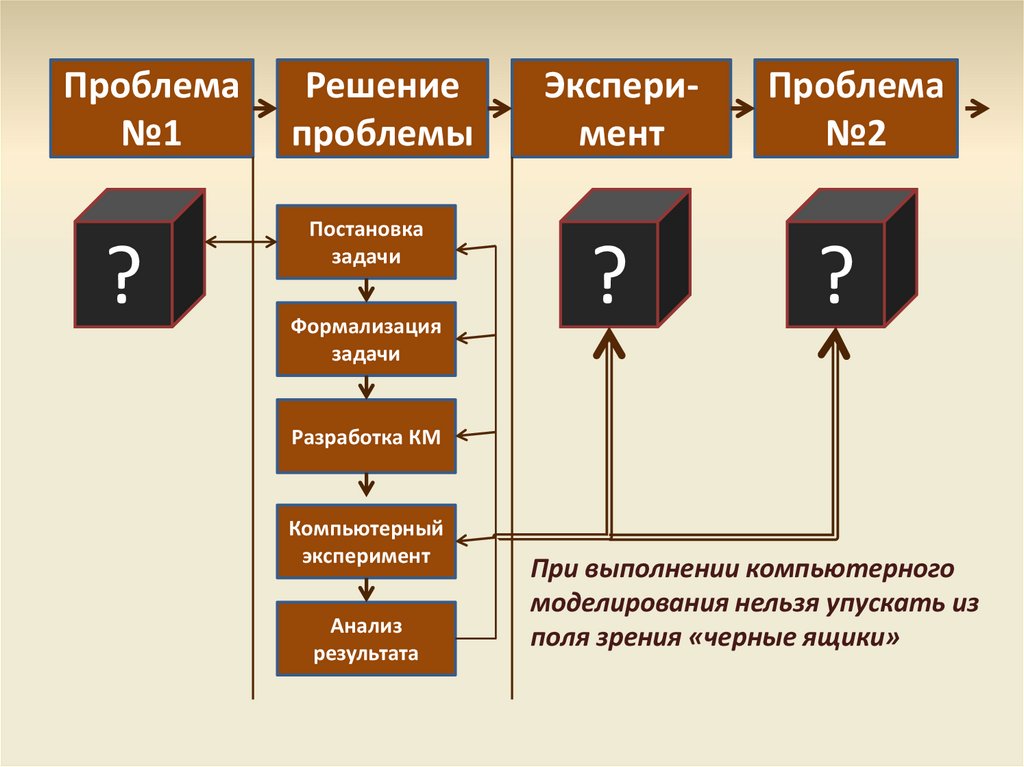
Проблема№1
?
Решение
проблемы
Постановка
задачи
Формализация
задачи
Эксперимент
?
Проблема
№2
?
Разработка КМ
Компьютерный
эксперимент
Анализ
результата
При выполнении компьютерного
моделирования нельзя упускать из
поля зрения «черные ящики»
3.
Проблема№1
?
Районная
больница
Социально- значимая проблема –
Здоровье населения России.
Например, такая болезнь как гипертония
«помолодела» до 30-летнего возраста.
Информационнокоммуникационная сеть
Прибор
Электроника
...
Диагностический
центр
Алтайского края
ПК врача
Сервер
Телефонный кабель,
витая пара,
оптоволоконный
кабель, спутниковая
связь, интернет
База
данных
Алгоритм преобразования
«цифры» в состояние:
- математическая модель,
- программа
4.
Решениепроблемы
...
1
Цель.
Концепция.
...
Постановка
задачи
Разработать прибор контроля изменения
состояния систем человеческого организма
Использовать метод Фолля. Измерять
биопотенциалы в биологически активных
точках (БАТ)
Входная
Пропускать сигнал в виде прямоугольных
информация. импульсов с известной амплитудой через
меридианы человека
Выходная
Анализировать амплитуду выходного
информация. сигнала с каждой БАТ
5.
Решениепроблемы
...
...
Формализация
задачи
2
Поиск и/или разработка математической модели
1. Фрикке в 1925 году экспериментально установил,
что живую клетку можно представить в виде
эквивалентной электрической схемы параллельного
соединения конденсатора и резистора:
Rм
См
6.
2Формализация
задачи
Выводы
1. Берем эту модель за основу получения информации.
Следовательно, эта электрическая модель меридиана
определяет состояние биологически активной точки
(БАТ), а значит состояние определенного органа
нашего организма.
2. Выходной информацией является амплитуда
выходного сигнала. На основе электрической модели
можно определить математическую модель
изменения амплитуды тестового сигнала от
изменения параметров СМ и RM .
3. Для вывода информации необходимо разработать
модель компьютеризированного прибора.
7.
2Формализация
задачи
Накопление знаний
Закон Ома для участка цепи:
U=I R,
где
U – напряжение,
[U] = В;
I – сила тока,
[I] = A;
R – сопротивление, [R] = Ом;
8.
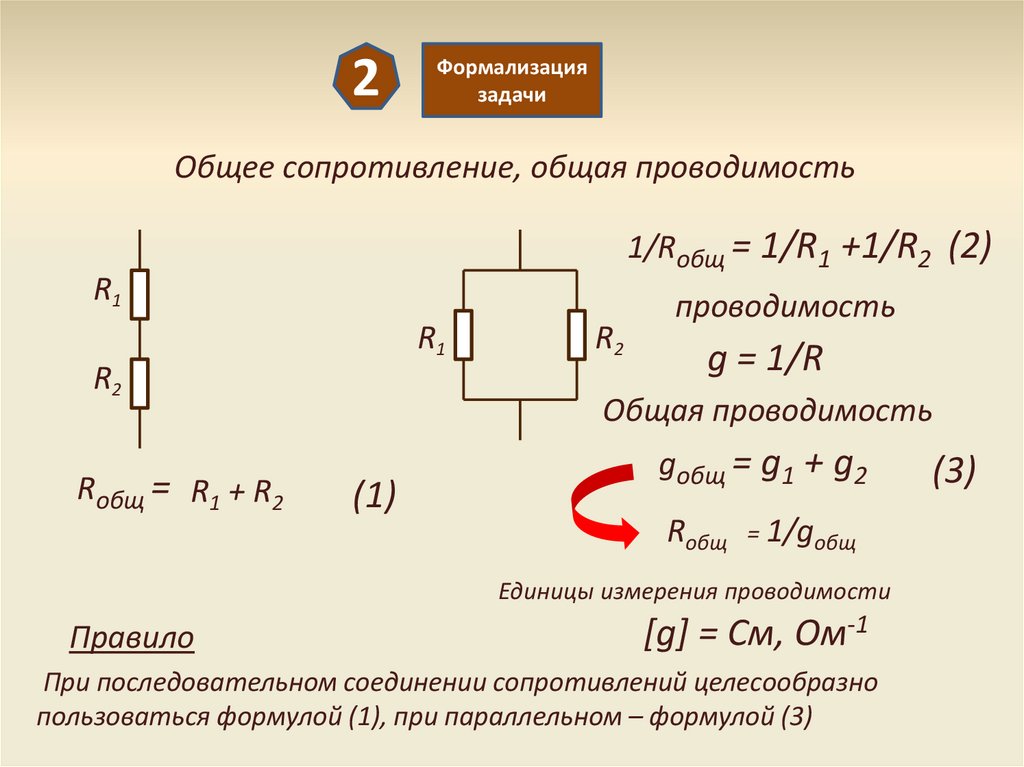
2Формализация
задачи
Общее сопротивление, общая проводимость
1/Rобщ = 1/R1 +1/R2 (2)
R1
R1
R2
Rобщ = R1 + R2
Правило
R2
проводимость
g = 1/R
Общая проводимость
(1)
gобщ = g1 + g2
Rобщ
= 1/gобщ
Единицы измерения проводимости
[g] = См, Ом-1
При последовательном соединении сопротивлений целесообразно
пользоваться формулой (1), при параллельном – формулой (3)
(3)
9.
2Формализация
задачи
Емкость, емкостное сопротивление, емкостная
проводимость
С
Единицы
измерения
емкости
Емкостное
сопротивление
[С] = Ф
= 2 - циклическая частота;
= 1/Т - частота;
Xc = 1/ C
Т – период гармонич. колебаний
Единицы измерения
[ ] = Гц ;
[Т] = с
10.
2Формализация
задачи
Емкостная проводимость:
Вc = 1/Хс = C = 2 С
Единицы измерения
емкостного сопротивления :
[Хс] = Ом
Единицы измерения
емкостной проводимости :
[Вс] = См, Ом-1
11.
2Формализация
задачи
Полное сопротивление схемы параллельного соединения
сопротивления и конденсатора
Модель электрическая
Rм
Zм
См
Zм - полное сопротивление
Yм - полная проводимость
Yм = g2 + Bc2 =
= (1/Rм)2 + (2 С)2
Модель математическая №1
Zм = 1/Yм









 electronics
electronics








