Математические методы анализа динамики цен рыночных активов в работах американских экономистов

1. МИНОБРНАУКИ РОССИИ РГУ НЕФТИ И ГАЗА (НИУ) ИМЕНИ И.М. ГУБКИНА

ДИПЛОМНАЯ РАБОТА
на тему:
«Математические методы анализа динамики цен рыночных
активов в работах американских экономистов и их применения для
анализа нефтегазовых рынков»
Группа: АМ-15-06
Студент: Буянов Максим Олегович
Руководитель: Жолков Сергей Юрьевич
проф. кафедры, доц. с.н.с.
Москва 2019
1

2.

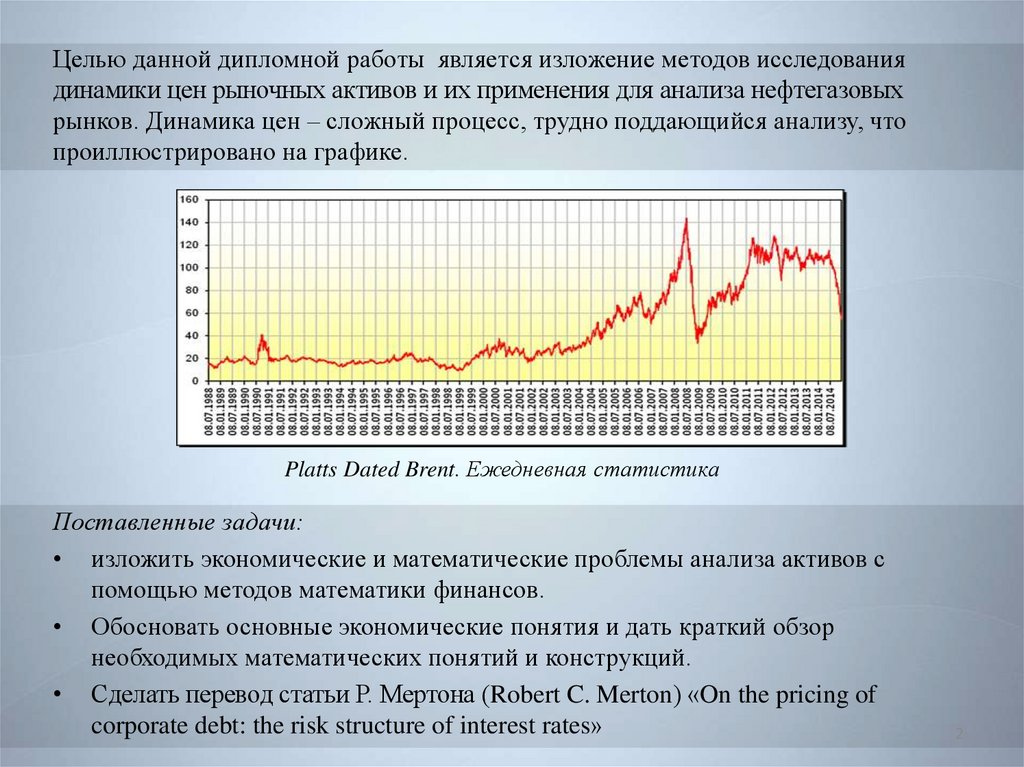
Целью данной дипломной работы является изложение методов исследования
динамики цен рыночных активов и их применения для анализа нефтегазовых
рынков. Динамика цен – сложный процесс, трудно поддающийся анализу, что
проиллюстрировано на графике.
Platts Dated Brent. Ежедневная статистика
Поставленные задачи:
• изложить экономические и математические проблемы анализа активов с
помощью методов математики финансов.
• Обосновать основные экономические понятия и дать краткий обзор
необходимых математических понятий и конструкций.
• Сделать перевод статьи Р. Мертона (Robert C. Merton) «On the pricing of
corporate debt: the risk structure of interest rates»
2

3. Поль Энтони Самуэльсон

«В последнее время я работаю над очень трудной
проблемой анализа стохастической спекулятивной цены»
«Столкнувшись при этом с неудобоваримой системой
нелинейных разностных уравнений и неравенств, я было
отчаялся найти в математической литературе
доказательство хотя бы существования решения»
«Сам предмет исследования выступает в количественной
форме: уберите численные значения цен или пропорции
бартерных обменов – и у вас просто ничего не останется»
«В этом случае сам здравый смысл обнаруживается только
под прожектором математики»
П. Самуэльсон
(15 мая 1915 - 13 декабря 2009)
Из нобелевской речи 11 декабря 1970 г.
Samuelson Paul A. Maximum Principle in Analytical Economics // The American Economic Review, June
1972, V.62, No.3, p.249–262. © Nobel Foundation. 1971. /Цит. по рус. пер. к.э.н. Н.В. Павлова. THESIS.
3
1993. Вып.1. С.184–202.

4. Работы авторов:

1965 г. «Rational Theory of Warrant Pricing»
(Рациональная теория ценообразования (на варранты))
Работы авторов:
Robert C. Merton (Роберт Мертон), Fischer Black
(Фишер Блэк), Myron Scholes (Майрон Шоулз), John C.
Cox (Джон Кокс), Stephen A. Ross ( Стефан Росс), Mark
Rubinstein (Марк Рубинштейн), Eduardo Schwartz
(Эдуардо Шварц), James E. Smith (Джеймс Смит),
Robert S. Pindyck (Роберт Пиндайк), Daniel R. Siegel
(Дэниэл Сигел) и др.
4

5. Основные математические конструкции

Описание динамики актива во всех указанных выше статьях использует
конструкцию:
b
t dt
a
– интеграла (римановского типа) от стохастического процесса ξt и
конструкцию стохастического интеграла (Винера) от неслучайных функций
g(t) по процессу ξt с некоррелированными и ортогональными
приращениями:
b
g (t )d t
a
Вентцель А.Д. Курс теории случайных процессов. :Наука. М. 1975.
Дэвис М.Х.А. Линейное оценивание и стохастическое управление. :Наука. М. 1984.
Ширяев А.Н. Основы стохастической финансовой математики. :Фазис. М. 1998. 5

6.

Основные математические конструкции
Стохастические дифференциальные уравнения:
dxt A(t ) xt dt Ct dw t
Формулируется задача фильтрации Калмана:
dxt A(t ) xt dt Ct dw t
dyt H (t ) xt dt Gt dw t
6

7.

Основные математические конструкции,
используемые в экономике
Стохастическое дифференциальное уравнением Ито - Самюэльсона:
dSt St ( t dt t dBt )
Стохастический интеграл Ито:
T
I ( g ) g (t ,ω)dwt
0
В случае μt, σt = const получаем стохастическое уравнение,
задающее диффузионную модель Самуэльсона для
«геометрического броуновского движения»:
dSt St ( dt dBt )
Вентцель А.Д. Курс теории случайных процессов. :Наука. М. 1975.
7

8.

Основные математические конструкции
рынка активов
Модель Блэка–Мертона–Шоулза (BMS-модель)
B ( Bt )t 0
– динамика неслучайного актива (банковского счета)
S ( St ) t 0
– динамика цены случайного актива
dBt rBt dt
dSt St ( dt dwt )
Решения первого уравнения очевидно:
Bt B0e rt
Решение второго уравнения следует из формулы Ито, и было получено П.
Самуэльсоном. Это решение:
St S 0 e
H (t )
, где H (t )
t w
t
То есть St – «геометрическое броуновское движение» Самуэльсона
8

9. Black F., Scholes M. The pricing of options and corporate liabilities Journal of Political Economy. V.81. N3. 1973. Pр.637–659.

Merton Robert C. On the pricing of corporate debt: the risk
structure of interest rates 684–73.
Уравнение Блэка–Шоулза:
2
1 2
Y
2 Y
(t , s) (t , s) S
(t , s) 0 ,
2
t
2
s
0≤ t < T, s>0
С краевым условием:
Y(T,s) = f(T,s), s>0
9

10.

Идеи и методы стохастической теории управления портфелем
активов с 80-х годов были применены для решения проблем
инвестирования в нефтяную и другие отрасли добывающей
промышленности.
• Dias M.A.G., Rocha K.M.C. Petroleum Concessions with Extendible
Options Using Mean Reversion with Jumps to Model Oil Prices. Working
Paper, first presented at the present at "Workshop on Real Options",
Stavanger, Norway, May 1998. Revised version presented in the 3rd
Annual International Conference on Real Options. Netherlands, June 1999.
• Paddock J.L., Siegel D.R., Smith J.L. Option Valuation of Claims on Real
Assets: The Case of Offshore Petroleum Leases. // Quarterly Journal of
Economies, August 1988. Pp.479–508.
• Schwartz E., Smith J.E. Short-Term Variations and Long-Term Dynamics
in Commodity Prices.// Management Science. 2000. Vol.46. N.7;
10

11.

Во 2 главе представлен полный перевод статьи Роберта К.
Мертона (Robert C. Merton)
«On the pricing of corporate debt: the risk structure of
interest rates».
«Об установлении цены корпоративной задолженности:
структура риска процентных ставок»
Данная статья является основополагающей для многих
исследований. Найти в литературе перевода этой статьи на
русский язык не удалось. Однако детали этой работы могут
оказаться важными для понимания и анализа последующих
работ.
11

12. МИНОБРНАУКИ РОССИИ РГУ НЕФТИ И ГАЗА (НИУ) ИМЕНИ И.М. ГУБКИНА

English Русский Rules