Логика - наука о высказываниях

1. Логика-наука о высказываниях

Высказывание –
повествовательное предложение,
в котором что-либо утверждается
или отрицается

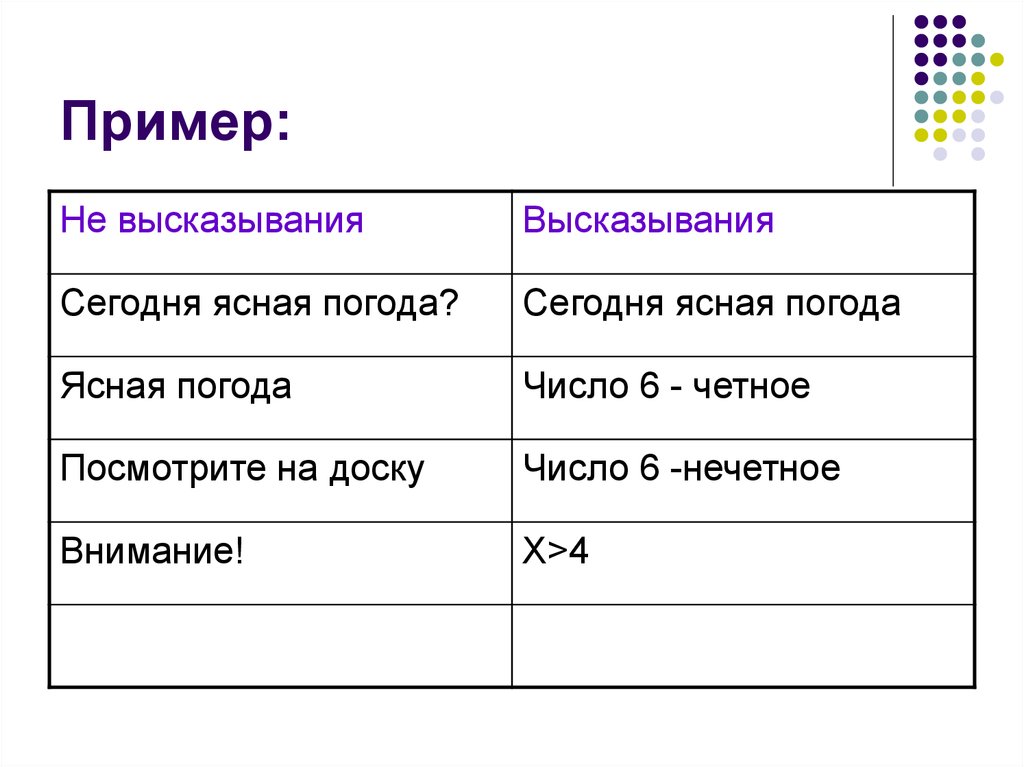
2. Пример:

Не высказывания
Высказывания
Сегодня ясная погода?
Сегодня ясная погода
Ясная погода
Число 6 - четное
Посмотрите на доску
Число 6 -нечетное
Внимание!
Х>4

3. Высказывания бывают:

Общими (можно
начать со слов ВСЕ,
ВСЯКИЙ, КАЖДЫЙ)
Частными
(НЕКОТОРЫЕ,
БОЛЬШИНСТВО)
Единичными (в
остальных случаях)

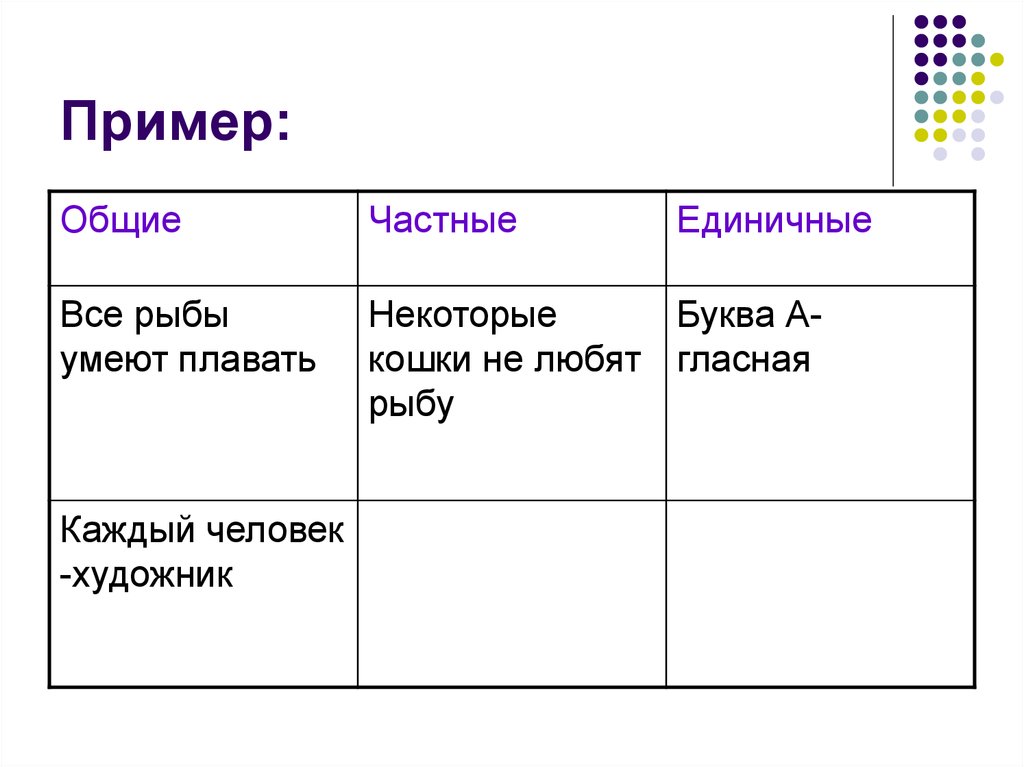
4. Пример:

Общие
Частные
Все рыбы
умеют плавать
Некоторые
Буква Акошки не любят гласная
рыбу
Каждый человек
-художник
Единичные

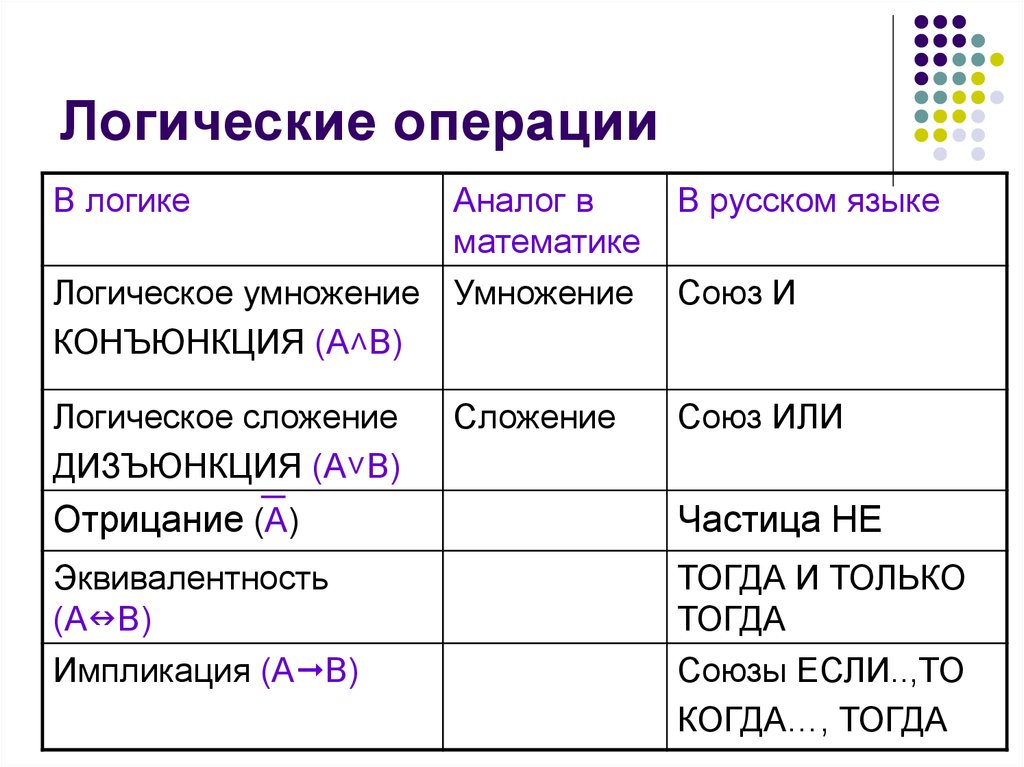
5. Логические операции

В логике
Аналог в
математике
Логическое умножение Умножение
КОНЪЮНКЦИЯ (А˄В)
В русском языке
Логическое сложение
ДИЗЪЮНКЦИЯ (А˅В)
Союз ИЛИ
Сложение
Союз И
Отрицание (А)
Частица НЕ
Эквивалентность
(А В)
ТОГДА И ТОЛЬКО
ТОГДА
Импликация (А В)
Союзы ЕСЛИ..,ТО
КОГДА…, ТОГДА

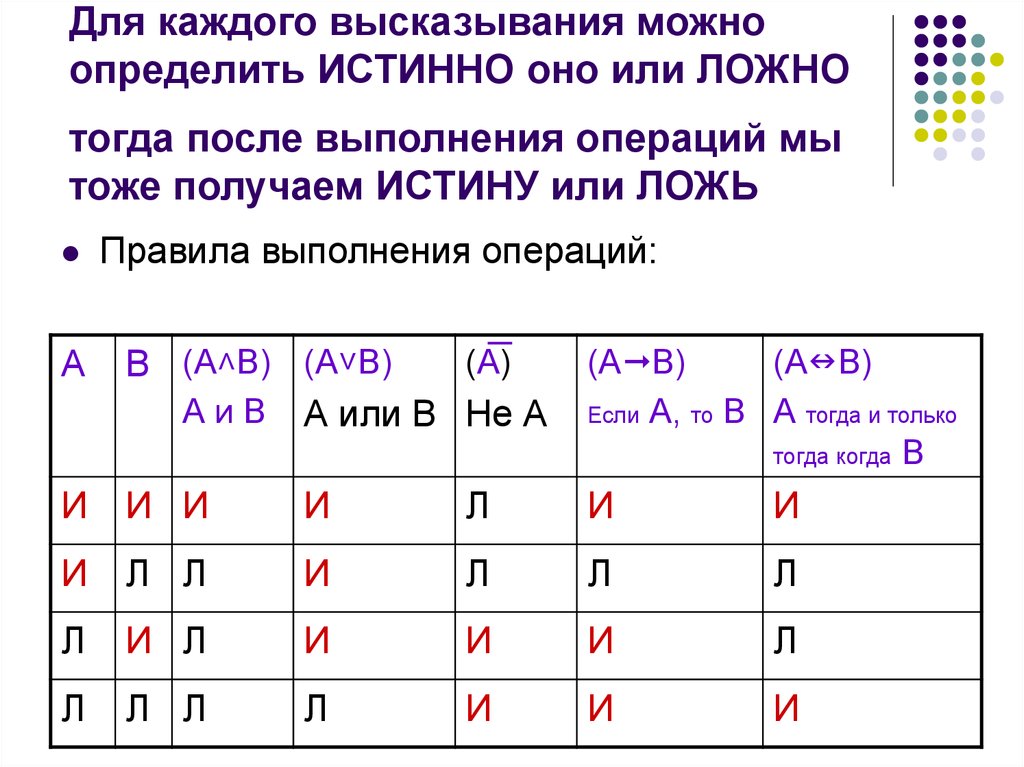
6. Для каждого высказывания можно определить ИСТИННО оно или ЛОЖНО тогда после выполнения операций мы тоже получаем ИСТИНУ или ЛОЖЬ

Правила выполнения операций:
А
(А)
В (А˄В) (А˅В)
А и В А или В Не А
(А В)
(А В)
Если А, то В А тогда и только
тогда когда В
И
И И
И
Л
И
И
И
Л Л
И
Л
Л
Л
Л
И Л
И
И
И
Л
Л
Л Л
Л
И
И
И

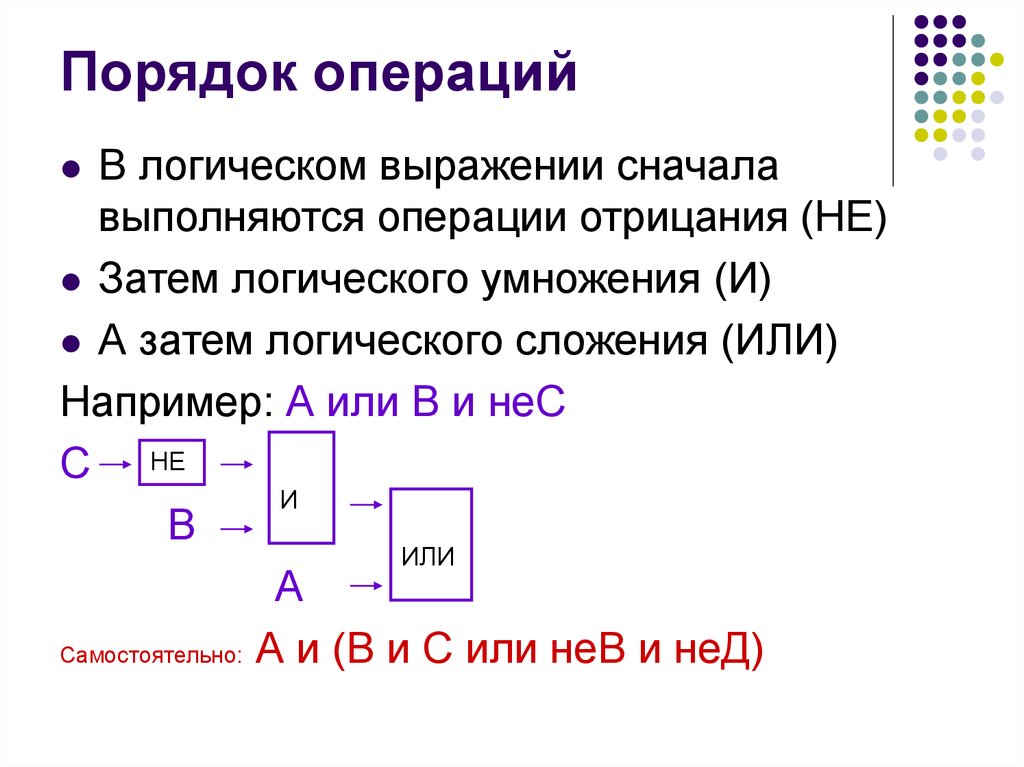
7. Порядок операций

В логическом выражении сначала
выполняются операции отрицания (НЕ)
Затем логического умножения (И)
А затем логического сложения (ИЛИ)
Например: А или В и неС
С НЕ
И
В
ИЛИ
А
Самостоятельно: А и (В и С или неВ и неД)

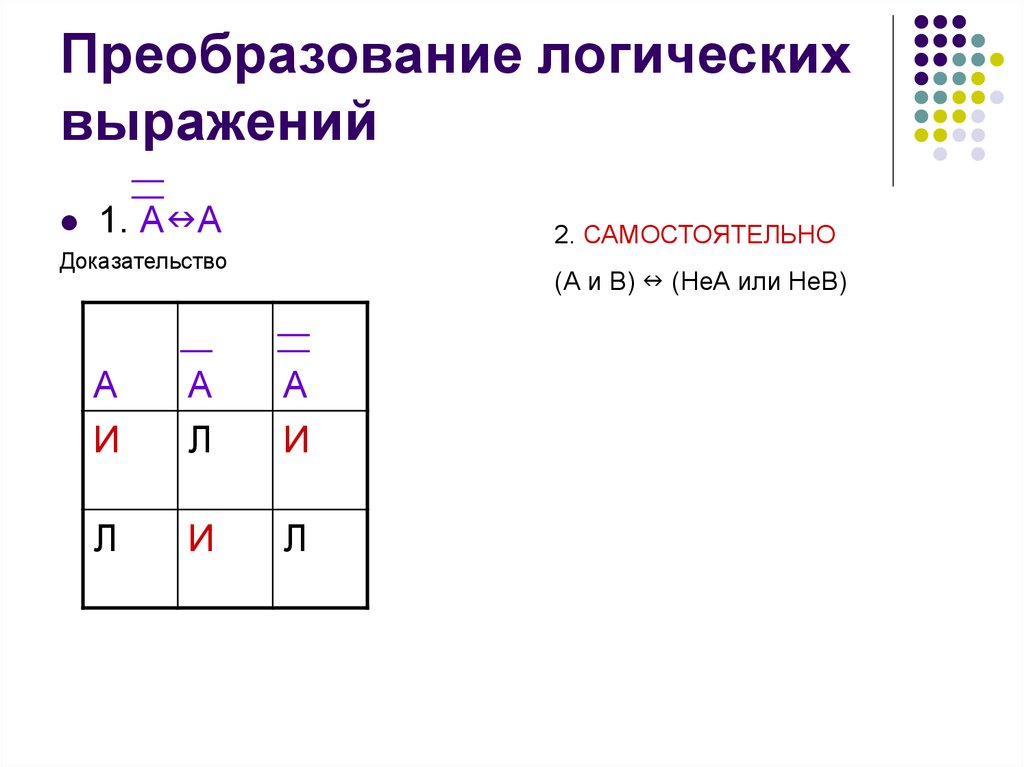
8. Преобразование логических выражений

1. А А
2. САМОСТОЯТЕЛЬНО
Доказательство
(А и В) (НеА или НеВ)
А
И
А
Л
А
И
Л
И
Л

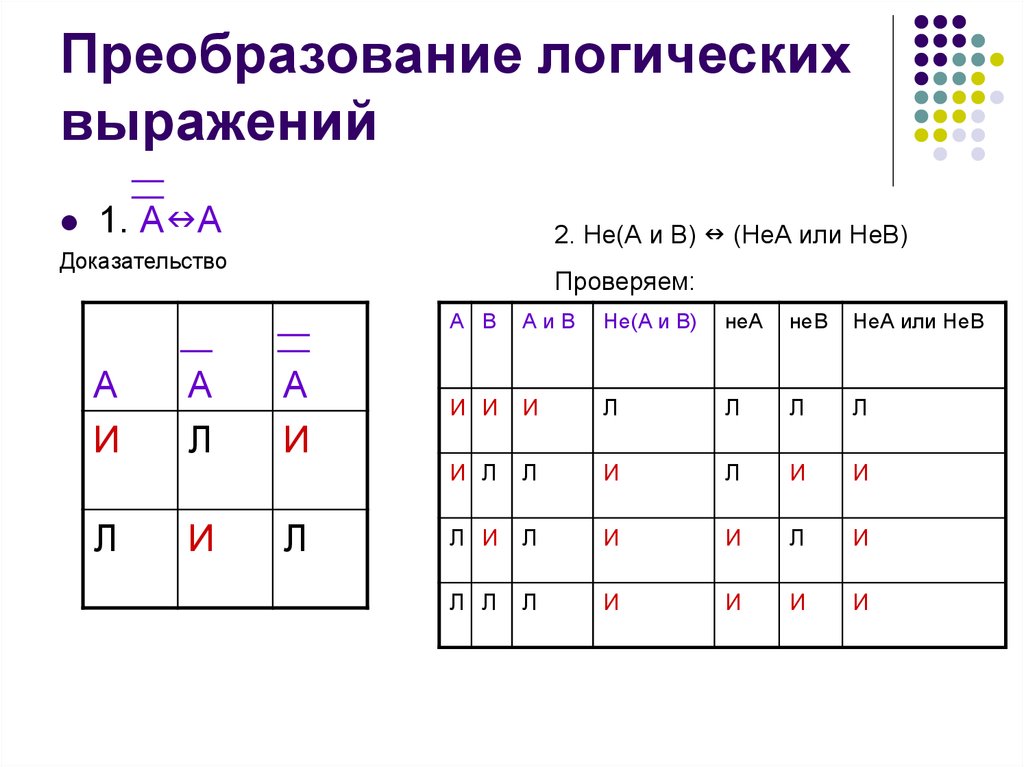
9. Преобразование логических выражений

1. А А
2. Не(А и В) (НеА или НеВ)
Доказательство
Проверяем:
А В
АиВ
Не(А и В)
неА
неВ
НеА или НеВ
А
И
А
Л
А
И
И И
И
Л
Л
Л
Л
И Л
Л
И
Л
И
И
Л
И
Л
Л И
Л
И
И
Л
И
Л Л
Л
И
И
И
И

10. Д/З: Доказать законы преобразования

1. А или А и В А
2. А или НеА и В А или В
3. А и (В или С) (А и В) или (А и С)
4. А или (В и С) (А или В) И (А или С)
5. НеА и (А или В) Не А и В