Similar presentations:
Среднее арифметическое. Среднее значение величины
1.
13.05.Среднее арифметическое.
Среднее значение
величины
2. Задача
Миша, Юра и Петя были в походе. Подойдя к лесу, решилисделать привал. У Миши было 2 пирожка, у Пети – 4, а у Юры – 6.
Все пирожки мальчики поделили поровну и съели. Сколько
пирожков съел каждый?
Решение:
1) 2 + 4 + 6 = 12 (п.) всего было у мальчиков.
2) 12 : 3 = 4 (п.) досталось каждому.
Ответ: по 4 пирожка.
Решение:
(2 + 4 + 6) : 3 = 4 (п.) досталось
каждому.
Ответ: по 4 пирожка.
3.
(2 + 4 + 6) : 3 = 4Средним арифметическим нескольких чисел
называют частное от деления суммы этих чисел
на число слагаемых.
Лексическое значение слов “среднее арифметическое”
среднее - находящееся посередине
арифметическое – от слова aritmos – число
Значит, среднее арифметическое означает - среднее число
4. Где применяется среднее арифметическое?
1. Подсчет среднего месячного балла по математикеЗадача:
У Вани за месяц стоят оценки 4 5 3 4 3 4 1 4 4 4 3 3,
найдите среднее арифметическое.
Решение:
(4+5+3+4+3+4+1+4+4+4+3+3) : 12 = 42 : 12 = 3,5
округлим до целых = 4 балла
Ответ: 4 балла.
5. Где применяется среднее арифметическое?
2. Средний балл для выставления оценкиЗадача:
Фигуристка, выступая, получила оценки 5,3; 5,5; 5,4;
5,2; 5,6; 5,7. Каков средний балл ее выступления?
Решение:
(5,3 + 5,5 + 5,4 + 5,2 + 5,6 + 5,7) : 6 = 32,7 : 6 =5,45
округлим до десятых = 5,5 балла
Ответ: 5,5 балла.
6. Где применяется среднее арифметическое?
3. Средняя масса (среднесуточный привес) используется при подсчете массы телят, поросят, цыплятЗадача:
Масса трех поросят оказалась равной соответственно
25,4 кг, 19,8 кг, 22,6 кг. Найти среднюю массу поросенка.
Решение: (25,4 + 19,8 + 22,6) : 3 = 67,8 : 3 = 22,6 кг
Ответ: 22,6 кг средняя масса.
7. Где применяется среднее арифметическое?
4. Среднее арифметическое используется дляподсчета средней месячной заработной платы
Задача:
Для оформления детского пособия маме потребовались данные
ее средней месячной заработной платы. Ее заработок:
январь – 6200 руб.; февраль – 6000 руб.; март – 5800 руб.
Решение: (6200 + 6000 + 5800) : 3 = 18000 : 3 = 6000 руб.
Ответ: 6000 руб.
8. Где применяется среднее арифметическое?
5. Среднее арифметическое используется дляопределения средней урожайности, средней
производительности
Задача:
Первый год с огорода накопали 320 ведер картошки, во второй
год – 280 ведер, в третий год – 300 ведер, в четвертый год –
400 ведер. Какова средняя урожайность?
Решение:
(320 + 280 + 300 + 400) : 4 =
= 1300 : 4 = 325 ведер
Ответ: 325 ведер
9. Где применяется среднее арифметическое?
6. Определение средней длины шага человекаЗадача:
Решение: 8 : 10 = 0,8 (м) средней длины шаг.
Ответ: 0,8 метра.
10. Где применяется среднее арифметическое?
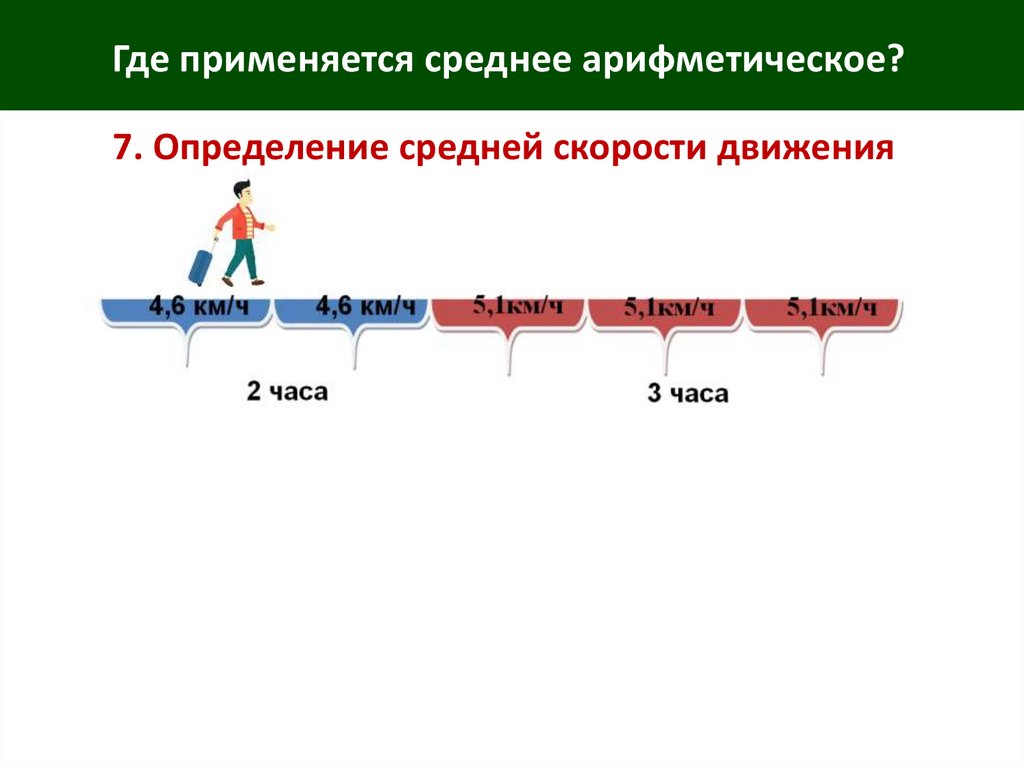
7. Определение средней скорости движенияЗадача:
Человек шел 2 ч со скоростью 4,6 км/ч и 3 ч со скоростью
5,1 км/ч. С какой постоянной скоростью он должен был идти,
чтобы пройти тоже расстояние за то же время?
11. Где применяется среднее арифметическое?
7. Определение средней скорости движенияРешение:
1) 4,6 · 2 + 5,1 · 3 = 9,2 + 15,3 = 24,5 (км) расстояние, которое
прошел пешеход.
2) 2 + 3 = 5 (ч) был в дороге пешеход.
3) 24,5 : 5 = 4,9 (км/ч) средняя скорость.
Ответ: 4,9 км/ч должен идти пешеход.
12. Где применяется среднее арифметическое?
Задача №1:Найти второе число, если среднее арифметическое
двух чисел равно 3,1, а первое число равно 3,8.
Решение:
Пусть второе число – х
(3,8 + х) : 2 = 3,1
3,8 + х = 3,1 · 2
3,8 + х = 6,2
х = 6,2 – 3,8
х = 2,4
Ответ: второе число равно 2,4.
13. Где применяется среднее арифметическое?
Задача №2:Среднее арифметическое двух чисел, одно из которых в 3 раза
меньше второго, равно 16. Найдите эти числа.
Решение:
Пусть меньшее число – х,
(х + 3х) : 2 = 16
тогда большее число – 3х
х + 3х = 16 · 2
4х = 32
х = 32 : 4
х = 8 – меньшее число
3 · 8 = 24 – большее число
Ответ: 8 и 24












 mathematics
mathematics








