Общая экология. Тема 2. Системный подход в экологии. Принципы количественного описания и элементы математического моделирования

1.

Общая экология
Тема 2
Системный подход в экологии. Принципы
количественного описания и элементы
математического моделирования
динамических систем

2.

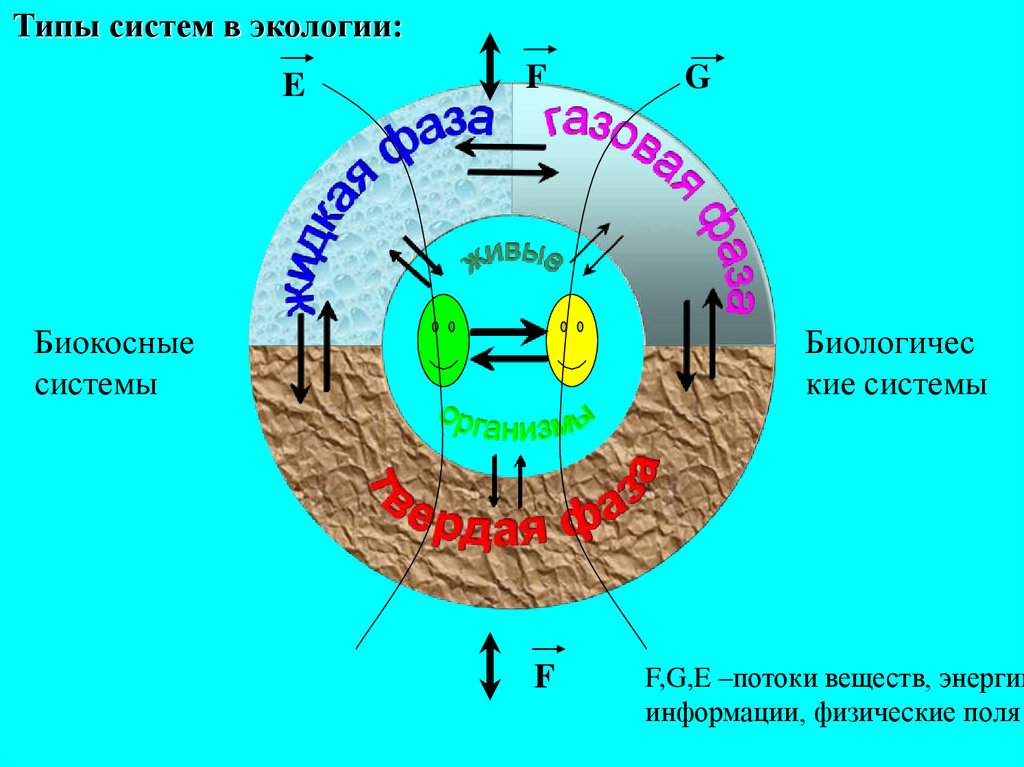
Типы систем в экологии:
E
F
Биокосные
системы
G
Биологичес
кие системы
F
F,G,E –потоки веществ, энергии
информации, физические поля

3.

Задачи исследований и границы выделения системы во времени и
пространстве; целостность системы; принцип эмерджентности:
1 подход: Объект - организм (биосистема) – целостная система в
собственных границах и с собственным характерным временем
существования. Все остальное – внешняя (по отношению к
границам организма) или окружающая среда (факторы среды)
2 подход: Объект - экосистема (биокосная система) –система
объединяющая организмы и косные компоненты ближайшего
окружения, представленные твердой, жидкой и газовой фазами.
Как провести границы чтобы отделить такую систему от
внешнего окружения? Где временные рамки? По-видимому,
главный принцип - выделение системы не должно нарушать ее
целостности. При исследованиях на различных соподчиненных
уровнях , решении задач отдельных дисциплин можно изучать
отдельные компоненты экосистемы. Но при этом следует
помнить о принципе эмерджентности; целое не есть
совокупность компонентов, у целого появляются новые качества
и целое это связи между компонентами, от которых зависят сами
компоненты.

4.

Почва и фитоценоз (сообщество растений) образуют
целостную биокосную систему более высокого порядка –
биогеоценоз (наземную экосистему)
Нелинейность, замкнутость (по веществу) таких систем
наличие взаимообусловленных прямых и обратных связей не
позволяют управлять продуктивностью (урожаем) их
компонентов (фитоценоза, почвы…), прогнозировать
динамику и устойчивость только на основе изучения
отдельных «элементарных» процессов и факторов внешнего
воздействия.
Почва и биогеоценоз (целостная биокосная система)

5.

Задачи исследований и границы выделения системы во времени и
пространстве; целостность системы; принцип эмерджентности:
А.А. Роде «Почвообразовательный процесс нельзя считать процессом
самостоятельным, независимым, ввиду того, что часть биологического
цикла миграции веществ, как важнейшего элемента почвообразования
протекает вне почвы. Это обстоятельство ничуть не умаляет
«самостоятельности» почвы как объекта исследования. Тезис В.В.
Докучаева о том, что почва есть самостоятельное естественноисторическое образование означает, что ей присущи совершенно особые,
специфические, ни в каких других природных телах не встречающиеся
процессы и явления. Но надо ясно понимать, что эти специфические,
присущие только почве процессы и явления, могут идти лишь при
взаимодействии почвы с другими природными телами – компонентами
биогеоценозов».
В.Н.Сукачев «Лишь при изучении биогеоценоза как целого мы в
полной мере можем выявить место фитоценозов в природе и их роль в
превращении веществ и энергии…изучение жизни фитоценоза не
может быть оторвано от изучения биогеоценоза как целого»

6.

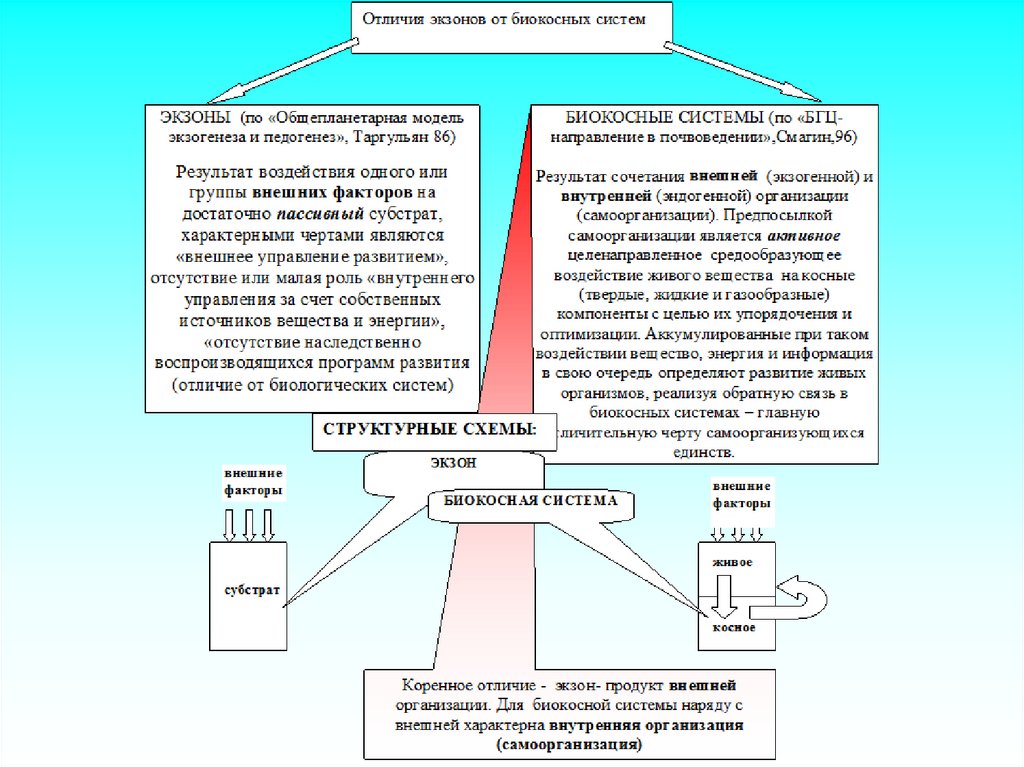
Концептуальные принципы выделения систем в разных научных направлениях:
Биоцентризм. В основе организации биокосного единства
– ведущее значение
принадлежит внутреннему биологическому фактору: средообразующая деятельность
взаимодействующих живых организмов (биоценоза) и обратное влияние со стороны
абиотических компонентов (экотопа). Биогеоценоз это экосистема в границах фитоценоза.
Поскольку круговорот веществ определяется потоком лучистой энергии – естественные
границы – по ареалу однородного фитоценоза, автотрофного блока, улавливающего эту
энергию и трансформирующего ее в биомассу. (биогеоценоз, экосистема, биосфера))
Типично для биогеоценологии, системной экологии, учения о биосфере…
Равенство факторов. В природе все факторы и компоненты равнозначны и биотические и
абиотические как на низшем уровне организации (ландшафт, геосистема), так и на
глобальном (географическая оболочка). На деле здесь чаще всего умаляется роль живых
организмов и превозносятся абиотические факторы (космические и геодинамические) в
организации и динамике геосистем различного уровня. Типично для географических и
геологических учений (ландшафтоведения, физ. географии, учения о геосистемах,
географической оболочке,факторного генетического почвоведения …
Антропоцентризм. Человеческий фактор стал определяющим по силе воздействия на биосферу и ее
компоненты. Природных экосистем практически не осталось. С другой стороны и изучаем и изменяем
природу мы в своих интересах – отсюда необходимость включения человека с его арсеналом
организующих и разрушающих природу средств в состав биокосных систем на правах компонента
(антропоэкеосистема, антропосфера) или в список внешних факторов организации биокосных
единств Земли (агроэкосистемы, урбосистемы, ноосфера…).

7.

Концептуальные принципы выделения систем в разных научных направлениях:
ГРАНИЦЫ В ПРОСТРАНСТВЕ: Выделение объекта и проведение соответствующих
границ диктуется целью исследования. Например, если исследователя интересует
структура связей, перенос и трансформация веществ и энергии в биогеоценозе (БГЦ),
границы этой биокосной системы в пространстве совпадают с границами ее автотрофного
блока ― фитоценоза, поскольку существование остальных подсистем напрямую зависит от
поступления веществ и энергии, продуцируемых растениями. Выделение почвенного
индивидуума, как биокосной системы формально проводится в вертикальном направлении
по двум границам ― верхней, с атмосферой, и нижней ― с грунтовыми водами.
Латеральное расчленение удобно проводить по границам биокосной системы более
высокого ранга ― БГЦ или его структурных элементов (парцелл). Во всех случаях,
независимо от цели исследования, проведение границ не должно нарушать
целостности биокосного единства, что, кстати, типично для представителей
географического направления в естествознании, отрицающих принцип биоцентричности.
Например, лесной биогеоценоз, выделенный по границам доминирующего на данной
территории типа леса ― целостная система, способная к самоорганизации и устойчивому
функционированию. Урочище или фация, выделенные по границам рельефа местности или
доминирующей материнской породе будут целостными лишь в том случае, если эти
границы совпадут с границами господствующего типа растительности и связанных с ним
единой трофической цепью зоо- и микроценозов. В противном случае, это лишь
абстрактные категории для географического описания распространения (встречаемости на
данной территории) тех или иных объектов, но не для анализа закономерностей их
функционирования.

8.

Концептуальные принципы выделения систем в разных научных направлениях:
ГРАНИЦЫ ВО ВРЕМЕНИ: Границы существования биокосной системы во времени, опять
таки целесообразно выделять по принципу биоцентричности. Это не означает, что с
гибелью определенного поколения биокосная система перестает существовать. Напротив,
генетическая информация, передающаяся от поколения к поколению, определяет
однотипность и устойчивость функционирования системы, имеющей поэтому больший
масштаб характерного времени существования. Смена одних биоценозов другими
неминуемо ведет к смене режимов функционирования биокосной системы и,
соответственно, ее экологического состояния. При этом, благодаря инертности твердой
фазы почвы, определяющей ее морфологические характеристики, создается впечатление,
что никаких изменений не произошло. Возникает довольно распространенная ситуация ―
на "одной и той же почве ― два типа растительности". Ошибка становится очевидной,
если вспомнить, почва не просто органоминеральная субстанция, а биокосное тело со
своим "живым веществом" в виде микробо- и зооценозов. Последние довольно быстро
реагируют на смены в автотрофном блоке БГЦ, приспосабливаясь к новому режиму
функционирования и влияя на него через функции утилизации органической материи и
снабжение растений минеральными веществами. Поэтому морфологические особенности
почвы как физического субстрата, далеко не всегда
отражают особенности ее
функционирования как биокосного тела в текущий момент времени.

9.

10.

11.

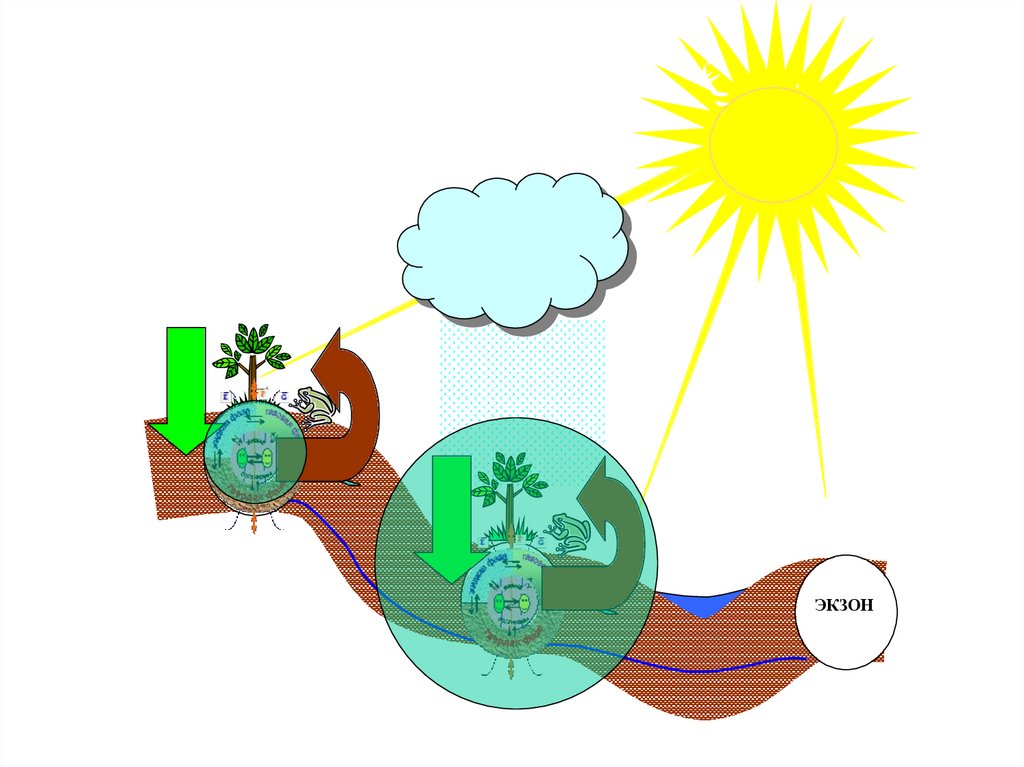
ЭКЗОН
ЭКЗОН
ЭКЗОН

12.

Экология – количественная наука, принципы количественного описания систем:
После обособления (выделения) системы в координатах пространства (x,y,z) и времени (t), необходимо
определить показатели состояния системы (переменные, параметры). Чаще всего при этом используются
интенсивные показатели (то есть не зависящие от количества вещества). Они могут быть первого рода
(температура, давление), или второго – удельные (нормированные) характеристики, являющееся комбинацией
двух или более экстенсивных величин, зависящих от количества вещества. Например, численность
организмов (популяции) – N – экстенсивная величина, а ее интенсивный аналог – плотность популяции –
отношение численности к площади (ареалу), который занимает популяция (S): С=N/S. Аналогично,
характеристики абиотических факторов – например, влажность почвы (W) – отношение экстенсивных
величин – массы воды (ml) и массы твердой фазы почвы(mS): W= ml/ mS.
Между показателями системы устанавливаются связи (отношения), которые могут быть формализованы в вид
графических, функциональных, логических зависимостей и иных способов выражения. Эти связи формирую
структуру объекта и являются основным предметом изучения. В простейшем случае связи представляю
собою линейные зависимости (пропорциональность типа У=аХ+в, где У,Х – показатели системы (факторы)
Однако в природе линейные связи достаточно редки, а доминируют – нелинейные отношения. Линейные связи
допущение, возникающее на начальных стадиях и при ограниченных масштабах изучения объекта в качеств
первого приближения. По направленности различают прямые (воздействие компонента А на компонент Б)
обратные (реакция компонента Б на воздействие А) связи.Наличие в системе прямых и обратных связе
является предпосылкой ее целостности и самоорганизации.
Наиболее общие (универсальные) связи, характерные для всех объектов природы или ее больших множеств
составляют теоретическую базу науки о природе – ее фундаментальные законы и принципы. (например –
закон сохранения вещества и энергии). Менее универсальные законы характерны для определенных классов
объектов и явлений и являются теоретической базой отдельных отраслей науки (например закон состояния
идеального газа, характерный для большинства газообразных веществ природной среды). Наконец
существуют индивидуальные зависимости, характерные лишь для данного объекта и для их получения
требуется как правило экспериментальное исследование (зависимость дыхания почвы от температуры и
влажности). Развитие точных наук идет по пути селекции (отбора) наиболее универсальных, значимых связей
и отношений, составляющих фундамент науки и позволяющих характеризовать класс объектов при
минимизации экспериментальных исследований.

13.

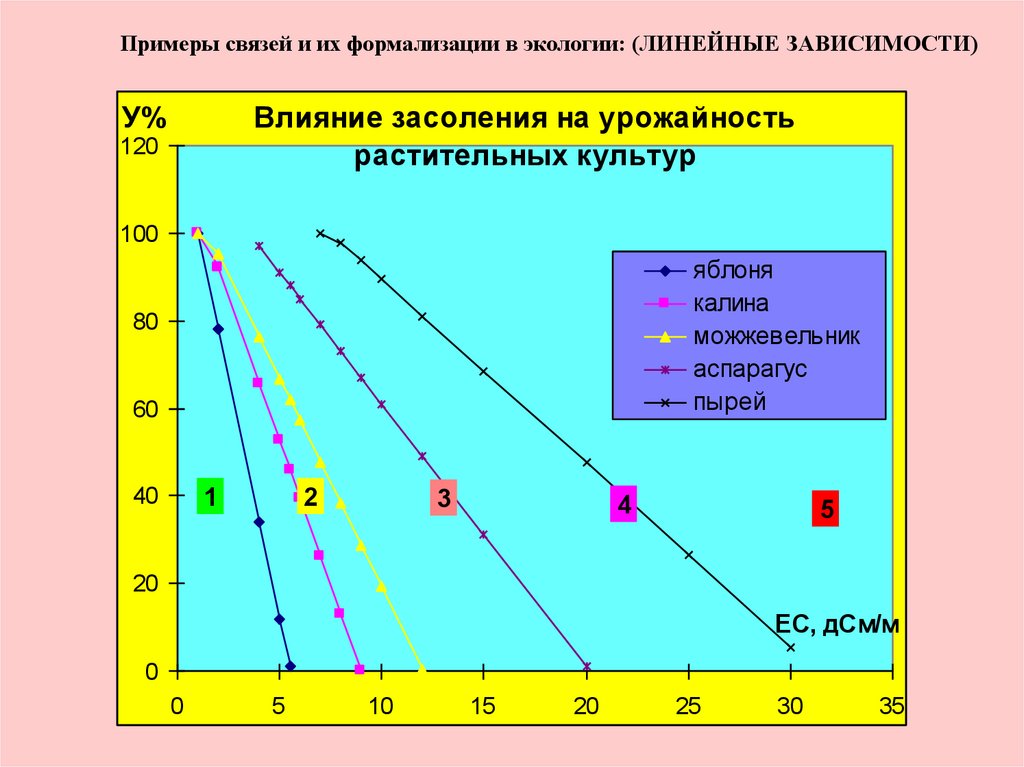
Примеры связей и их формализации в экологии: (ЛИНЕЙНЫЕ ЗАВИСИМОСТИ)
У%
Влияние засоления на урожайность
растительных культур
120
100
яблоня
калина
можжевельник
аспарагус
пырей
80
60
40
1
2
3
4
5
20
ЕС, дСм/м
0
0
5
10
15
20
25
30
35

14.

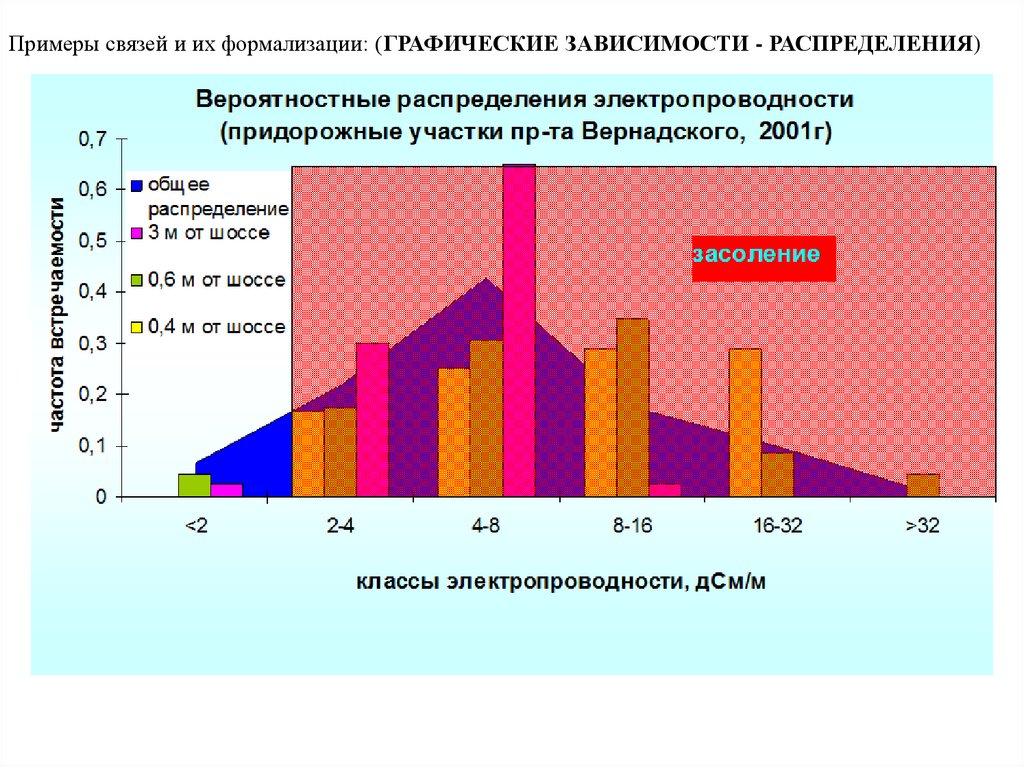
Примеры связей и их формализации: (ГРАФИЧЕСКИЕ ЗАВИСИМОСТИ - РАСПРЕДЕЛЕНИЯ)

15.

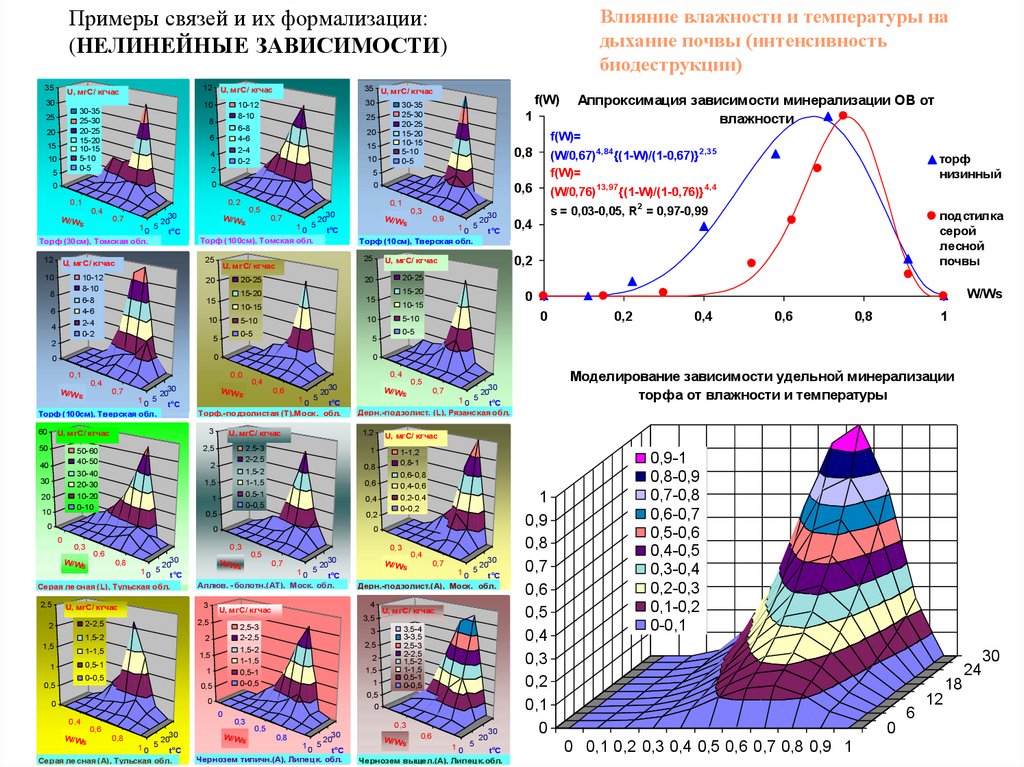
Влияние влажности и температуры на
дыхание почвы (интенсивность
биодеструкции)
Примеры связей и их формализации:
(НЕЛИНЕЙНЫЕ ЗАВИСИМОСТИ)
35
U, мгС/ кгчас
30
30-35
25-30
20-25
15-20
10-15
5-10
0-5
25
20
15
10
5
12
U, мгС/ кгчас
10
10-12
8-10
8
4
2
0
0,1
0,4
12
0,7
8
6
4
0,5
0,1
30
20
1 0 5 t oC
Торф (100см), Томская обл.
W/Ws
25
U, мгС/ кгчас
10
10-12
8-10
20
6-8
4-6
2-4
0-2
15
0,7
U, мгС/ кгчас
20-25
15-20
0-5
5
0,1
0,4
0,7
40
3
30
20
10
0,6
U, мгС/ кгчас
2,5-3
2-2,5
2
30-40
20-30
10-20
0-10
0,3
1
0,6
0,4
0,2
U, мгС/ кгчас
2
1,5
1,5-2
2
1-1,5
1,5
0-0,5
0,5
3
2-2,5
0,5-1
1
0,5
0,7
0,4
30
W /Ws
0,8
20
1 0 5 t oC
Серая ле сная (А), Тульская обл.
0,5
0,7
0,2
подстилка
серой
лесной
почвы
0
W/Ws
0,4
0,2
0,4
0,6
0,8
1
3
2,5
1,5-2
1-1,5
0,5-1
0-0,5
1
0,5
1-1,2
0,8-1
0,6-0,8
0,4-0,6
0,2-0,4
0-0,2
0,4
2
1,5
1
0,7
10 5
U, мгС/ кгчас
3,5-4
3-3,5
2,5-3
2-2,5
1,5-2
1-1,5
0,5-1
0-0,5
0,5
0
0,3
0,5
0,3
30
20
10 5
t oC
Чернозем типичн.(А), Липец к. обл.
W/Ws
0,8
Моделирование зависимости удельной минерализации
торфа от влажности и температуры
10 5
30
20
t oC
Дерн.-по дзолист.(А), Моск. обл.
3,5
2,5-3
2-2,5
0
0,6
s = 0,03-0,05, R2 = 0,97-0,99
U, мгС/ кгчас
W/Ws
4
U, мгС/ кгчас
0
0
(W/0,76)13,97 {(1-W)/(1-0,76)}4,4
торф
низинный
0-5
0,3
30
20
1 0 5 t oC
Аллюв. - болотн.(АТ), Моск. обл.
W/W s
2,5
0,6
0
5-10
0
0,3
0,8
1,2
0,6
0,5
30
20
1 0 5 t oC
Серая ле сная (L), Тульская о бл.
W /Ws
(W/0,67)4,84 {(1-W)/(1-0,67)}2,35
f(W)=
30
20
t oC
Дерн.-по дзолист. (L), Рязанская обл.
0,8
0
0
10-15
W/Ws
1
1,5-2
1-1,5
0,5-1
0-0,5
1,5
0
15-20
0,4
30
20
1 0 5 t oC
Торф.-по дзолистая (Т),Моск . обл.
2,5
50-60
40-50
0,4
W/W s
U, мгС/ кгчас
50
20-25
0,8
0
0,0
30
20
10 5
t oC
Торф (100см), Тверская обл.
W/W s
U, мгС/ кгчас
20
5
0
0
0,9
25
10
5-10
0,3
Аппроксимация зависимости минерализации ОВ от
влажности
f(W)=
30
20
1 0 5 t oC
Торф (10см), Тверская обл.
W/Ws
15
10-15
10
2
f(W)
1
0
0,2
30
20
10 5
t oC
Торф (30см), Томская обл.
W/Ws
2,5
6-8
4-6
2-4
0-2
6
0
60
35 U, мгС/ кгчас
30
30-35
25-30
25
20-25
20
15-20
10-15
15
5-10
10
0-5
5
0,6
20
30
W/Ws
10 5
t oC
Чернозем выщел.(А), Липец к.обл.
1
0,9
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0
0,9-1
0,8-0,9
0,7-0,8
0,6-0,7
0,5-0,6
0,4-0,5
0,3-0,4
0,2-0,3
0,1-0,2
0-0,1
0
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
6
12
18
24
30

16.

ПРОСТРАНСТВЕННО-ВРЕМЕННАЯ ДИНАМИКА систем и ее количественные показатели:
C
dC
1. Скорость: U
или при t 0 U
t
dt
C =С2-С1 - изменение интенсивного показателя С
C
C
за интервал времени t=t2-t1.
C C C
2. Градиент : grad
или
x y z
dC dC dC
при x , y, z 0grad
dx dy dz
U= C / t
t
С1
х
С2
C - изменение интенсивного показателя С по мере изменения
расстояния по пространственным координатам х, у, z .
3. Поток веществ, энергии : q
m
K gradC
S t
К - проводимость среды (величина показывающая насколько хорошо
среда проводит данный поток. К=1/R, R – сопротивление среды)
t

17.

ПРОСТРАНСТВЕННО-ВРЕМЕННАЯ ДИНАМИКА систем и ее количественные показатели:
Линейные и нелинейные системы: Если скорости изменения в системе прямо
пропорциональны самим интенсивным свойствам: U=dC/dt= kC, а потоки –
градиентам: q=-K gradC, k, K=const, такие системы относятся к линейным.
Линейные феноменологические уравнения переноса:
Процесс
переноса
Уравнение
Показатели состояния
Название
закона
1. Движение
тепла
q= λgradT
Т температура
λ κоэффициент
теплопроводности
З-н Фурье
2. Диффузия
веществ
q= DgradC
С концентрация
D κоэффициент
диффузии
З-н Фика
U напряжение
R сопротивление
проводника
З-н Ома
Р гидравлический
напор
KФ κоэффициент
фильтрации
З-н Дарси
3.Электрический ток
4. Фильтрация
воды в
пористых
средах
q= (1/R)gradU
q= KФgradP

18.

ПРОСТРАНСТВЕННО-ВРЕМЕННАЯ ДИНАМИКА систем и ее количественные показатели:
Комбинация процессов переноса (потоков) и внутренних, локальных процессов
(скоростей) изменения свойств системы, уравнение неразрывности (модель
динамической системы), начальные и граничные условия:
Рассмотрим резервуар с постоянным сечением (S) и высотой z, в котором происходит поступление и удаление
жидкости в виде потоков на верхней и нижней границе, а также осуществляется выделение или поглощение
жидкости благодаря гипотетической химической реакции внутри сосуда. Очевидно, общее изменение количества
(массы) жидкости за время t в такой системе будет определяться разностью входящего и выходящего потоков, а
также интенсивностью (U) поглощения (выделения) жидкости при локальном процессе:
m=S q t ± U tS z.
Например, если поток втекающей жидкости равен 10 г/см2час, а вытекающей 5 г/см2час и известно, что
происходит поглощение жидкости внутри сосуда со скоростью 0,3 г/см3час, можно подсчитать на сколько изменится
количество жидкости в резервуаре с площадью сечения S=10см2 и высотой z=10см за время
t=1час: m=10см(10г/см2час 5г/см2час)1час 0,3г/см3час 1час 10см2 10см=50г 30г=20г. Если известно начальное
условие сосуд был пустой (m0=0 при t=0), то за час в нем окажется 20 г воды.
Масса жидкости является экстенсивной величиной, поэтому для того, чтобы сравнить динамику двух сосудов с
разными объемами (S z), необходимо перейти к интенсивным характеристикам концентрациям жидкости в
объеме: C=m/(S z) . Тогда уравнение примет вид:
q
С
m
t
или в предельном случае при t 0 и z 0.
S z t
z
С q
U
t z
Эта зависимость является универсальной, поскольку
отражает закон сохранения вещества и энергии в
системе, и носит название уравнения неразрывности.
U
(одномерный перенос
вдоль координаты z)
Уравнение неразрывности, снабженное
условиями на границах и начальными
условиями представляет собою
математическую модель пространственновременной динамики системы

19.

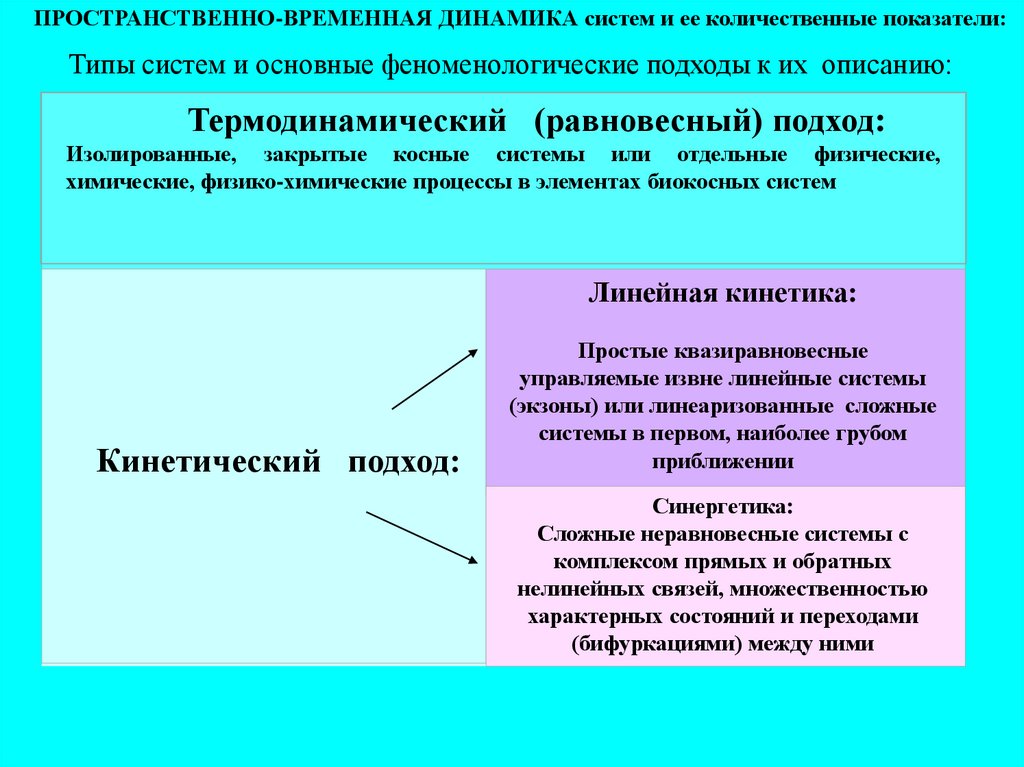
ПРОСТРАНСТВЕННО-ВРЕМЕННАЯ ДИНАМИКА систем и ее количественные показатели:
Типы систем и основные феноменологические подходы к их описанию:
Термодинамический (равновесный) подход:
Изолированные, закрытые косные системы или отдельные физические,
химические, физико-химические процессы в элементах биокосных систем
Линейная кинетика:
Кинетический подход:
Простые квазиравновесные
управляемые извне линейные системы
(экзоны) или линеаризованные сложные
системы в первом, наиболее грубом
приближении
Синергетика:
Сложные неравновесные системы с
комплексом прямых и обратных
нелинейных связей, множественностью
характерных состояний и переходами
(бифуркациями) между ними

20.

Равновесный термодинамический подход
Равновесный термодинамический подход – система, будучи предоставлена самой себе стремится
занять наиболее выгодное состояние термодинамического равновесия с максимумом энтропии
(беспорядка) и минимумом внутренней энергии. При равновесном термодинамическом описании
систем используются две основные функции состояния энтропия (S) и термодинамический
потенциал (ψ) (энергия), связь между которыми задается в дифференциальном виде объединенной
формой первого и второго начал термодинамики:
TdS=dU+PdV+dA
(1)
где ТdS – подвод тепла, (Т – абсолютная температура), PdV – работа расширения, dA – другие виды
полезной работы, совершаемой системой.
Напомним, что энергия есть мера определенной формы движения материи при ее превращении из
одного вида в другой. Она отражает способность системы производить работу. С формальной точки
зрения энергия есть произведение интенсивной и экстенсивной переменной состояния, например,
механическая энергия выражается как РV, тепловая ТS, химическая – μm(μ – υимический
потенциал), поверхностная σ (σ – οоверхностное натяжение) и т.д. Мерой рассеивания энергии (ее
деградации) является энтропия. В качестве специальной функции ψ термодинамического
потенциала, которая определяет возможность существования того или иного состояния физической
системы и наиболее вероятные направления его изменения выбирается одна из перечисленных
характеристик: а) Внутренняя энергия U= f(S,V,xi), б) Энтальпия H=f(S,P,xi), в) Свободная
энергия Гельмгольца F=(T,V,xi), г) Свободная энергия Гиббса G=f(T,P,xi) – xi другие
макроскопические параметры системы (масса (m), число частиц (n)), поверхность раздела фаз (s)).

21.

Равновесный термодинамический подход
Выбор функции диктуется природными условиями существования системы или искусственными условиями
проведение эксперимента по изучению свойств системы. Например, в условиях теплоизоляции (адиабатический
процесс S=const) термодинамическим потенциалом, характеризующим систему, будет ее внутренняя энергия. Из
(1) следует, что элементарная работа, совершаемая системой, включая работу расширения, будет равна убыли
внутренней энергии: dA+PdV=-dU. Если существует теплообмен с внешним окружением, резервуаром при
постоянстве его температуры T=const и объема (V=const), работа совершается не только за счет внутренней
энергии, но и за счет поступающей в систему теплоты: dA=-d(U-TS). Функция состояния A =F=U-TS носит
название свободной энергии Гельмгольца (изохорно-изотермический потенциал). При наличии обмена веществом
с резервуаром и постоянстве его Т и Р, в качестве функции состояния удобно выбрать изобарно-изотермичекий
потенциал (энергию Гиббса). Из (1) имеем, dG =–dA=d(U–TS+PV), откуда G=U– TS+PV. Дифференцирование
функции G с учетом уравнения (1) дает следующую формулу:
dG= –SdT+Vdp
(2) Решение
дифференциального уравнения (2) осуществляется путем подстановки функции состояния из соответствующего
уравнения состояния физической системы с последующим интегрированием. Например, для компонента
однофазной газовой системы (атмосферы), подчиняющейся уравнению состояния идеального газа (PV= mRT/M,
m- масса, М – молярная масса, R – универсальная газовая постоянная), в изотермических условиях (dT=0), имеем:
dG=VdP, откуда
Ψ= Ψ 0+RT/M ln(P/P0)
(3)
где Ψ=G/m – удельный термодинамический потенциал (удельная энергия Гиббса), Ψ0 – удельный
термодинамический потенциал в стандартном состоянии при
Т=Т0 и Р=Р0. Иногда удобнее пользоваться
удельным термодинамическим потенциалом, нормированным не массой компонента (m), а числом его молей
(n=m/M). Для этого обе части формулы (4) надо умножить на молярную массу компонента (М), после чего она
примет вид:
= 0+RT ln(P/P0)
(4)
где - химический (удельный термодинамический потенциал), μ0―химический потенциал в стандартном
состоянии. Величины μ и ψ по физическому смыслу тождественны друг другу и отличаются численно лишь на
постоянный сомножитель (М).

22.

Равновесный термодинамический подход
Уравнения (3,4) могут быть записаны в общем виде для любой гомогенной (однофазной) системы, содержащей
конечное число компонентов с активностями (α):
μ= μ 0+RTlnα
(5)
α=γC (жидкая фаза (раствор)), α=P/P0 (газовая фаза (воздух)), где α – активность компонента, С – равновесная
концентрация, γ ― коэффициент активности.
Знание удельных термодинамических потенциалов системы тождественно ее полному количественному описанию в
рамках равновесной термодинамики. Изолированная система, будучи представлена самой себе, займет наиболее
вероятное устойчивое состояние (термодинамическое равновесие), при котором она будет иметь относительный
максимум энтропии и минимум энергии (термодинамического потенциала). Если компоненты системы, или
совокупность взаимодействующих систем
изолированы от внешней среды, в процессе их внутреннего
взаимодействия устанавливается термодинамическое равновесие, характеризуемое в общем виде равенством
термодинамических потенциалов. Отдельные составляющие термодинамического равновесия определяются
равенством соответствующих интенсивных показателей. Так при тепловом равновесии наступает равенство
температур (Т1=Т2=Т3...=Тi или ΔТi=0), при механическом – равенство давлений (Р1=Р2=Р3...=Рi или ΔРi=0), при
равновесии фаз – равенство удельных термодинамических (химических) потенциалов (μ1=μ2=μ3, Δμ=0), при
химическом равновесии реагирующих веществ – равенство химических потенциалов с учетом стехиометрических
коэффициентов ν1 μ1= ν2 μ2= ν3 μ3...= νi μi или Δνi μi=0). Если разница в интенсивных свойствах (ΔI) не равна нулю (ΔТ,
ΔР,Δμ Δνμ≠0), изолированная система претерпевает изменения до тех пор, пока не исчезнет породившая их причина
(ΔI), то есть пока не наступит термодинамическое равновесие, являющееся закономерным итогом динамики
системы.
Из условия равновесия легко найти законы распределения веществ и энергии во взаимодействующих системах и их
отдельных частях, оценив тем самым равновесное физическое состояние объектов исследования. Так для процесса
растворения газа в жидкости из условия равенства химических потенциалов (4), (5) при термодинамическом
равновесии получаем :
γC= P/P0 или С=КгР или С=аСg,
(6)
где Кг =1/γP0 – константа Генри растворимости, а= КгRT/M – растворимость газа., Сg – концентрация газа в
атмосфере. Уравнение (6) показывает,что в условиях равновесия жидкость содержит а объемов газа. Так при
концентрации СО2 в воздухе почвы 18г/м3 (около 1%) и растворимости 1,4 , раствор будет содержать 25 г/м3 СО2.

23.

В качестве другого о примера рассмотрим химическое равновесие. Пусть в системе протекает химическая реакция
общего вида:
ν1А↔ν2B,
где А, B – исходный реагент и продукт реакции, ν1,2 – стехиометрические коэффициенты. Определим по уравнению
(5) химические потенциалы реагирующих веществ и приравняем их друг к другу:
ν1 (μ 0 А + RTln α A)= ν2 (μ 0 B + RTln α B) или ν1 μ 0 А – ν2 μ 0 B = RTln α B – RTln α A, откуда
A1
(7)
RT ln 2 RT ln K const 0
B
Величина К постоянна в данных термодинамических условиях и носит название константы равновесия химической
реакции. В целом, любое равновесие в изолированной системе может быть охарактеризовано соответствующей
константой (К), связанной со стандартным термодинамическим потенциалом:
d μ 0 =dG0= -RTlnK
(8)
Поскольку для многих веществ величина dG0 известна и приводится в специальных термодинамических
справочниках, ее удобно использовать для расчетов констант равновесий и термодинамической устойчивости.
Рассмотрим, например, выветривание каолинита в почве, при котором возникает гиббсит, согласно реакции
гидролиза [Спозито, 1984]:
Al2Si2O5(OH)4+5H2O ↔ 2H4SiO4+2Al(OH)3
Для расчета величины dG0 реакции воспользуемся законом Гесса, по которому стандартное изменение удельной
энергии Гиббса реакции равно сумме стандартных энергий Гиббса образования продуктов реакции за вычетом
суммы стандартных энергий Гиббса образования исходных веществ с учетом стехиометрических коэффициентов
реакции: . Имеем: при Т=298К, Р=101,3 кПа: dG0 каолинита = -3799,4 кДж/моль, воды = -237,1 кДж/моль, H4SiO4= 1308,0 кДж/моль, гиббсита = -1154,9 кДж/моль. Общее изменение свободной энергии: dG0 =2(-1308,0) + 2(-1154,9) 1(-3799,4) - 5(-237,1)=59,1 кДж/моль. Так как dG0 >0 реакция в стандартных условиях термодинамически невыгодна,
поскольку требует затрат энергии, и смесь каолинита с водой устойчива. То же следует из анализа константы
равновесия реакции. Подставляя величину dG0 в уравнение (8) и потенцируя с учетом соотношения lnK=2,3lgK,
получаем K=10-10. Отсюда следует, что равновесие сильно сдвинуто влево и равновесные концентрации исходных
веществ на 10 порядков превышают таковые для продуктов реакции. Осуществление такой реакции требует либо смены
термодинамических условий (Т, Р), либо затрат энергии, поступающей извне, например, из биоценоза (микробоценоза) при

24.

Типы систем и основные феноменологические подходы к их описанию:
Количественный аппарат равновесной термодинамики активно применяется в экологии и почвоведении
при описании сорбционных процессов, других вариантов межфазных взаимодействий, оценки химических
равновесий. Он хорошо удовлетворяет результатам лабораторных экспериментов над изолированными
«мертвыми» органоминеральными телами. Однако, для описания функционирования «живой» открытой
биокосной системы в целом равновесные подходы не применимы, поскольку состояние
термодинамического равновесия означает смерть для живого. Биокосные системы суть неравновесные
открытые системы. Их существование поддерживается благодаря постоянному обмену веществом и
энергией с окружающей средой. При этом живые организмы выступают в роли активного фактора,
поддерживающего неравновесность в биокосной системе, поскольку из всех компонентов системы лишь
живому веществу необходимо существование в неравновесном состоянии. Сама по себе система, как любой
физический объект, стремится спонтанно занять состояние термодинамического равновесия, и лишь
деятельность живых организмов целенаправленно препятствует этому, борясь с повышением энтропии как
внутри
себя, так и в ближайшем окружении. Например, для многих организмов свойственна
терморегуляция поддержание температуры тела на определенном постоянном уровне. Такие живые
вещества неравновесны по отношению к окружающей среде по критерию теплообмена: их температура
практически всегда не совпадает с температурой окружающей среды. Неравновесность по отношению к
веществу заложена самой структурой организмов, в которых концентрируются жизненно важные элементы
и их соединения и удерживаются в телах, пока они существуют. Аналогичным образом поддерживается
неравновесность и упорядоченность в ближайшем окружении организмов в биокосных системах.
Концентрация веществ и энергии здесь осуществляется трудами не одного, а множества поколений
организмов, и не исчезает при отмирании сиюминутных «владельцев» этого достояния, «дома». Подобно
социальным богатствам, природные «дома» почвы, биогеоценозы наследуются из поколения в поколение,
приумножаются и обеспечивают жизнь на планете. Их количественное описание требует иных, не
равновесных подходов. Для открытых систем в потоках веществ и энергии аналогом термодинамически
выгодного равновесия служит стационарное состояние, при котором уравновешиваются скорости
изменения интенсивных показателей системы (скорости противоположных процессов). (U1=U2=U3...=Ui или
ΔU/Δti=0), то есть никаких изменений не происходит. Аналог – уровень воды в бассейне при одинаковых
скоростях потока на входе и выходе. Для линейных систем это единственный закономерный итог динамики
(линейная кинетика).

25.

ПРОСТРАНСТВЕННО-ВРЕМЕННАЯ ДИНАМИКА систем и ее количественные показатели:
Типы систем и основные феноменологические подходы к их описанию:
Для нелинейных систем существует множество подобных состояний (аттракторов), к которым
может стремиться система в процессе развития (динамики), причем часть из них может быть устойчива,
а часть нет. В процессе изменения характеристик системы устойчивые состояния могут терять
устойчивость. Если в нелинейной системе несколько состояний, она может переходить скачкообразно из
одного в другое (триггерный режим). Возможна стабилизация системы за пределами равновесных
(стационарных) состояний с появлением сложных эндогенных режимов поведения (колебаний, хаоса..) и
контрастных тка называемых диссипативных структур в пространстве с неравномерным, периодическим
распределением вещества (энергии). Такие формы поведения, присущие сложным нелинейным системам
исследует синергетика. Биологическим и биокосным объектам присуще подобные формы, поскольку
они являются нелинейными, неравновесными открытыми системами в потоках веществ, энергии и
информации. Термодинамическое (равновесное) состояние означает для живых организмов смерть,
поэтому живое всеми силами стремиться избежать этого состояния как внутри себя, так и в ближайшем
окружении (принцип сопротивления повышению энтропии, целенаправленного производства
негэнтропии).
1
2
3
4
Формы равновесий: 1 неустойчивое равновесие, 2 устойчивое равновесие, 3
нейтральное состояние, 4 локальная устойчивость (к малым возмущением)

26.

ПРОСТРАНСТВЕННО-ВРЕМЕННАЯ ДИНАМИКА систем и ее количественные показатели:
Линейный анализ устойчивости динамических систем: основной принцип –задать отклонение от
равновесия (возмущение) «толкнуть шарик» и посмотреть что будет дальше – вернется в исходное
состояние или нет. Критерий устойчивости (по Ляпунову) – отрицательное значение первой
производной скорости по интенсивному параметру в характерной точке соответствующей равновесию
(стационарному состоянию).
Простейшие примеры (система с одной переменной):
1)
L, опад
C, детрит
2)
dB
B
rB 1
dt
K
dC
L kC
dt
kC, деструкция
Линейная модель динамики органического вещества
почвы, где L – функция поступления опада, С – запасы
ОВ почвы, k – константа разложения ОВ Найдем
стационарное
состояние
dC/dt=0
или C=L/k.
Рассмотрим его устойчивость: U’=(L-kC)’C=-k <0 –
состояние устойчиво, система стремится попасть в
него из любых начальных значений С=С0 (см дальше
аналитические и численные методы..)
Нелинейная модель роста организма (популяции), где В – запасы
биомассы или численность организмов, r –мальтузианский параметр
скорости роста, К – фактор «емкости» среды для данного вида
организмов (популяции). Найдем стационарные состояния dB/dt=0 их
будет два: В=0 и B=K. Рассмотрим их устойчивость: U’=r(1-B/K)’B=
r(1-2B/K). Отсюда состояние В=0 – неустойчиво ( r(1-2 0/K)=r>0), а
B=K. ( r(1-2 K/K)=-r<0), ) – устойчиво.
Система 2) будет стремиться попасть в него из любых начальных значений В=В0 , включая
состояния с нулевой численностью.

27.

Линейный анализ устойчивости динамических систем:
Простейшие примеры (система с двумя переменными): Общий вид модели:
dX
F2 U 2 (B, X)
dt
dB
U1 (B, X ) F1
dt
где В,Х – переменные состояния, U1,2 –
скорости их изменения, F1,2 =const внешние связи (потоки)
Критерии устойчивости по Ляпунову:
(a 11 a 22 )
1, 2 0,5 4
Δ=a11a22–a12a21
U1
U
U1
U
a
a 22 2
a11
a 21 2
12
X B, X
X B, X
B B, X
B B, X
2
B, X
X X
B B
В зависимости от вида корней характеристического уравнения выделяются шесть основных типов
стационарных состояний и соответствующих режимов поведения системы в их окрестности:
1. λ1,2 – действительные числа При этом возможны следующие случаи:
а) Оба корня отрицательны (λ1,2<0). Стационарное состояние называется устойчивым узлом.
б) Оба корня положительны (λ1,2>0). Неустойчивый узел.
в) Корни разных знаков. Стационарное состояние, называемое седлом, также будет неустойчивым,
2. λ1,2 – комплексно-сопряженные числа (подкоренное выражение отрицательно, корни λ содержат
действительную λRe и мнимую λIm части).
а) Действительная часть корней отрицательна (а11+а12<0, или σ>0). Устойчивый фокус.
б) Действительная часть корней положительна (а11+а12>0 или σ<0). Неустойчивый фокус.
в) Действительная часть корней λRe равна нулю (σ=0). Стационарное состояние (центр) будет нейтрально
устойчивым.

28.

Простейшие примеры (линейная система с двумя переменными):
Модель:
dC
L (k 1 k 2 )C,
dt
dH
k 2 C k 3 H,
dt
L
C
,
k1 k 2
здесь С, Н – запасы детрита и
гумусовых веществ, L– количество
ежегодно поступающих в почву
растительных остатков (опада), k1,2
– кинетические константы
минерализации и гумификации
детрита, k3 – константа
минерализации гумусовых веществ
kC
H 2 ,
k3
1, 2 0,5 a 11 a 22 (a 11 a 22 ) 2 4a 12a 21 4a 11a 22
Найдем корни характеристического уравнения:
а11 = (L-(k1+k2)C)’C= -(k1+k2)
а21 = (L-(k1+k2)C)’H= 0
а12 = (k2C – k3H)’C= k2
а22 = (k2C – k3H)’H= -k3
Стационарные
состояния
1, 2 0,5 (k1 k 2 k 3 ) (k1 k 2 k 3 ) 2 4k 3 (k1 k 2 )
0,5 (k 1 k 2 k 3 ) (k1 k 2 k 3 )
отсюда 1=-k3<0; 2=-(k1+k2)<0
Оба корня действительны и отрицательны. Стационарное состояние –
устойчивый узел. Сложные эндогенные режимы невозможны.
Поведение системы во времени – экспоненциальное приближение к
равновесному (стационарному) состоянию.

29.

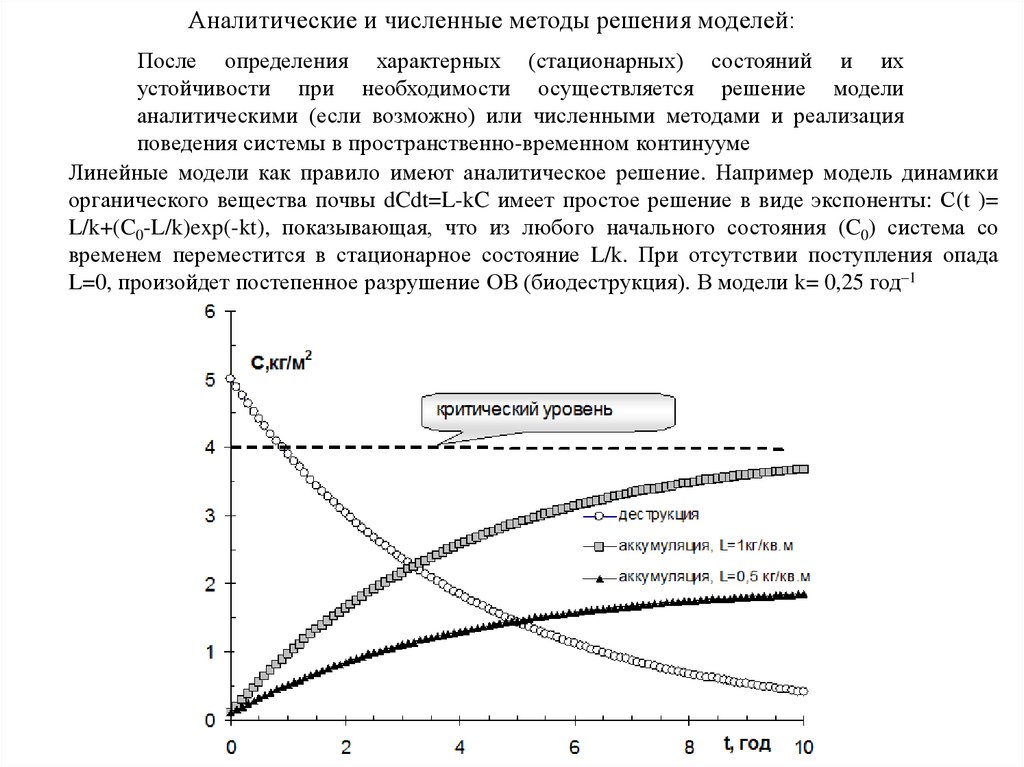
Аналитические и численные методы решения моделей:
После определения характерных (стационарных) состояний и их
устойчивости при необходимости осуществляется решение модели
аналитическими (если возможно) или численными методами и реализация
поведения системы в пространственно-временном континууме
Линейные модели как правило имеют аналитическое решение. Например модель динамики
органического вещества почвы dCdt=L-kC имеет простое решение в виде экспоненты: С(t )=
L/k+(C0-L/k)exp(-kt), показывающая, что из любого начального состояния (C0) система со
временем переместится в стационарное состояние L/k. При отсутствии поступления опада
L=0, произойдет постепенное разрушение ОВ (биодеструкция). В модели k= 0,25 год–1

30.

Для нелинейных моделей аналитические решения получить чаще всего невозможно и
приходится использовать приближенные или численные методы решения. В нашем курсе
с этой целью используется программа MATLAB
Примеры численного моделирования развития микроорганизмов-деструкторов
и динамики субстрата - органического вещества почвы (по Смагин и др.,2001)

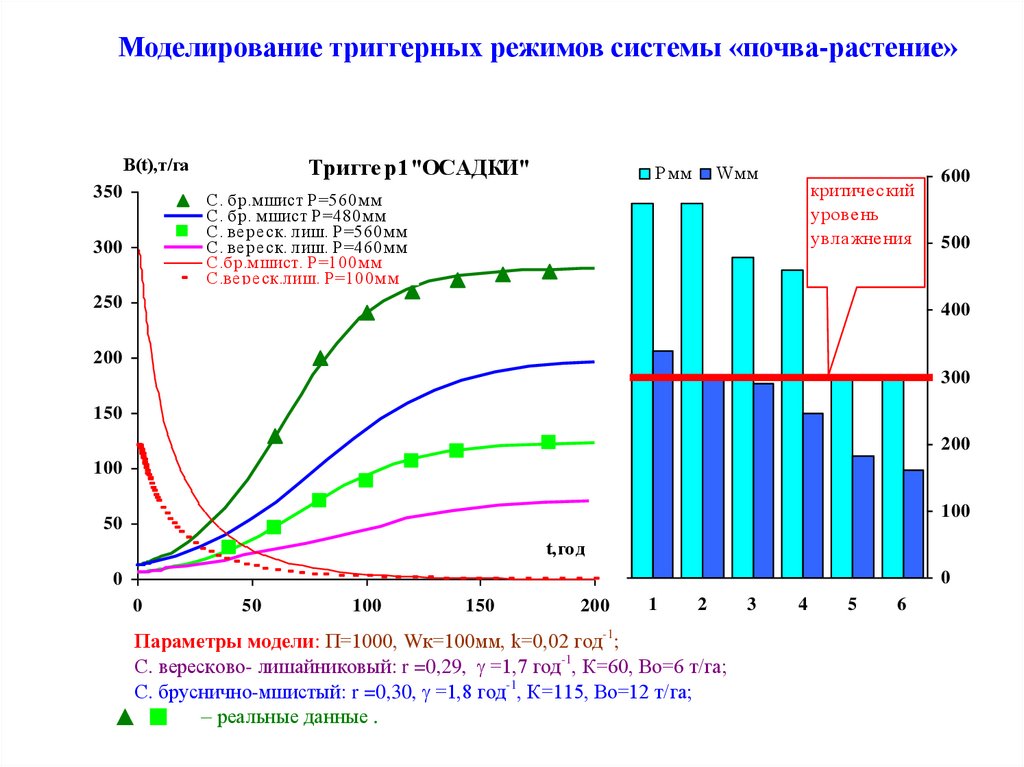
31.

Моделирование триггерных режимов системы «почва-растение»
B(t),т/га
350
Тригге р1"ОСАДКИ"
Р мм
Wмм
критический
уровень
увлажнения
С. бр.м шист Р =560м м
С. бр. м шист Р =480м м
С. ве ре ск. лиш. Р =560м м
С. ве ре ск. лиш. Р =460м м
С.бр.м шист. Р =100м м
С.ве ре ск.лиш. Р =100м м
300
250
600
500
400
200
300
150
200
100
100
50
t,го д
0
0
0
50
100
150
200
1
2
Параметры модели: П=1000, Wк=100мм, k=0,02 год-1;
С. вересково- лишайниковый: r =0,29, =1,7 год-1, К=60, Во=6 т/га;
С. бруснично-мшистый: r =0,30, =1,8 год-1, К=115, Во=12 т/га;
реальные данные .
3
4
5
6

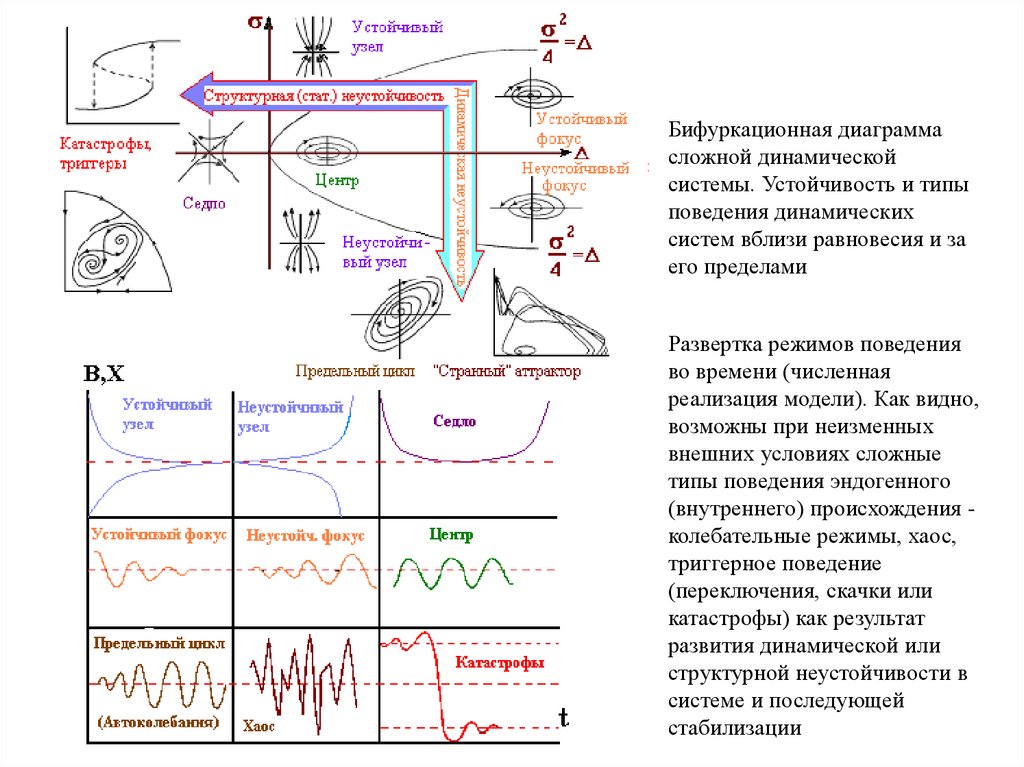
32.

Бифуркационная диаграмма
сложной динамической
системы. Устойчивость и типы
поведения динамических
систем вблизи равновесия и за
его пределами
Развертка режимов поведения
во времени (численная
реализация модели). Как видно,
возможны при неизменных
внешних условиях сложные
типы поведения эндогенного
(внутреннего) происхождения колебательные режимы, хаос,
триггерное поведение
(переключения, скачки или
катастрофы) как результат
развития динамической или
структурной неустойчивости в
системе и последующей
стабилизации