Similar presentations:
Фундаментальные типы данных (тема 1 - 4)
1.
Тема 1-4.Фундаментальные типы данных
для АСУб и ЭВМб
2.
ПланФундаментальные типы данных и константы
Целые числа со знаком и без
Числа с плавающей точкой
Символы и кодировки
3.
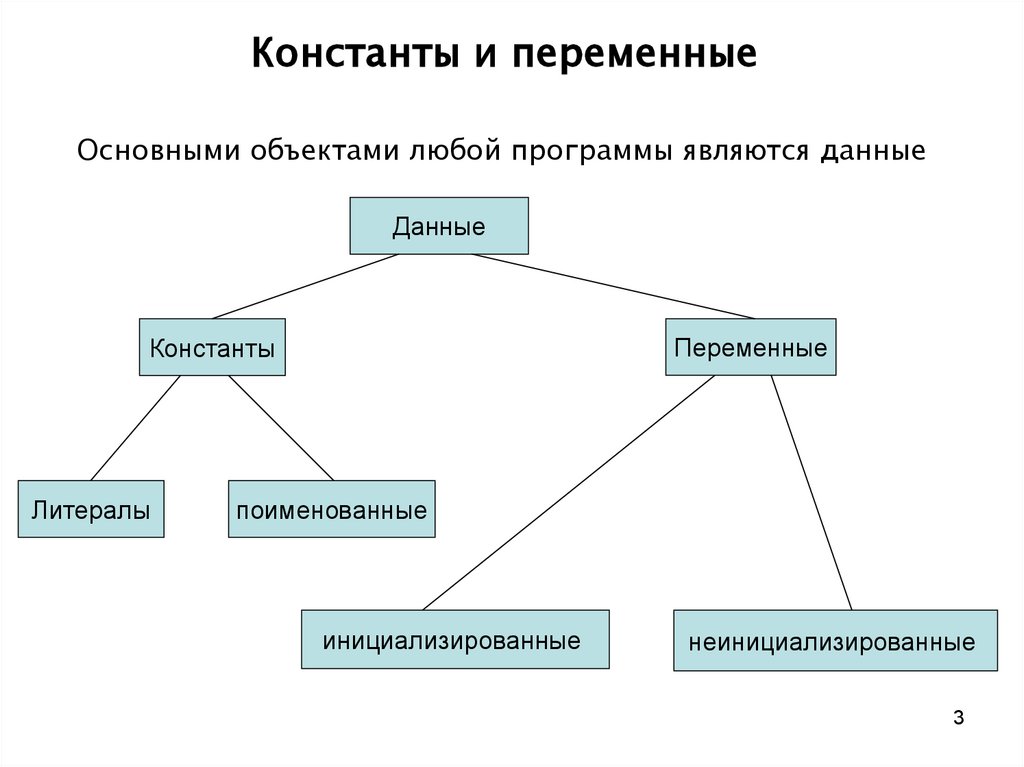
Константы и переменныеОсновными объектами любой программы являются данные
Данные
Переменные
Константы
Литералы
поименованные
инициализированные
неинициализированные
3
4.
1.4 Типы данныхТип данных определяет:
а) диапазон изменения значения, задавая размер ее
внутреннего представления;
б) множество операций, которые могут выполняться над этой
переменной
в) требуемое для переменной количество памяти при ее
начальном распределении
г) интерпретацию двоичного кода значений при последующих
обращениях к переменным.
Кроме того, тип используется для контроля типов с целью
обнаружения возможных случаев недопустимого
присваивания.
В С++ стандартно определено большое количество типов,
которые программист может использовать без
предварительного описания.
5.
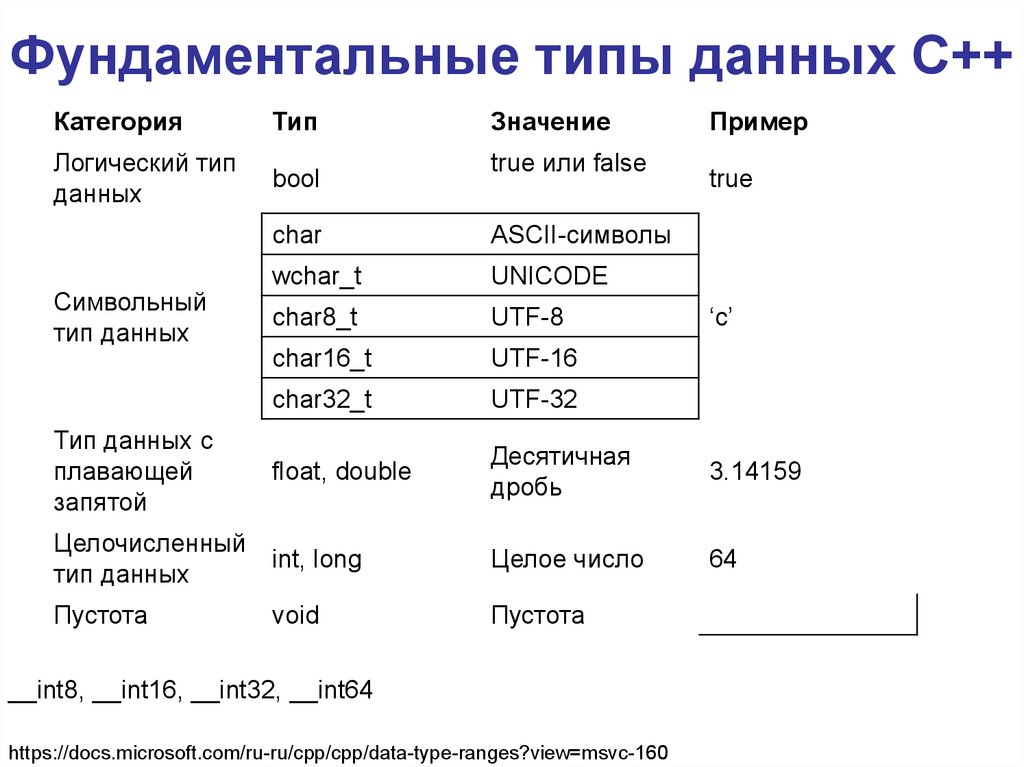
Фундаментальные типы данных С++Категория
Тип
Логический тип
данных
bool
Значение
true или false
Пример
true
char
ASCII-символы
wchar_t
UNICODE
char8_t
UTF-8
char16_t
UTF-16
char32_t
UTF-32
Тип данных с
плавающей
запятой
float, double
Десятичная
дробь
3.14159
Целочисленный
тип данных
int, long
Целое число
64
Пустота
void
Пустота
Символьный
тип данных
__int8, __int16, __int32, __int64
https://docs.microsoft.com/ru-ru/cpp/cpp/data-type-ranges?view=msvc-160
‘c’
6.
Типы данных С++: модификаторыМодификаторы знака
• unsigned – тип данных может содержать
только неотрицательные значения
• unsigned int,
• unsigned char
• signed – целое число со знаком, используется
по умолчанию
7.
Типы данных С++: модификаторыМодификаторы размера
• short – тип данных занимает меньше места
• short int,
• short double
• long – тип данных занимает больше места
• long int
• long double
• 1 == sizeof(char) <= sizeof(short) <= sizeof(int)
<= sizeof(long) <= sizeof(long long)
8.
КонстантыКонстанты – данные, не изменяемые в процессе выполнения
программы.
Поименованные константы – константы, обращение к которым
выполняется по имени. Они описываются в разделе описаний.
Литералы – это лексема, представляющая изображение
фиксированного числового, строкового или символьного
значения, записанная в тексте программы.
Константы делятся на пять групп:
- целые,
- вещественные,
- перечислимые,
- символьные,
- строковые.
Компилятор, выделив константу, относит ее к той или другой
группе по ее «внешнему виду» (по форме записи) в исходном
тексте и по числовому значению.
9.
Целые константыДесятичные константы
123, -15, +9, -100
Восьмеричные константы
• начинаются с цифры нуль (0)
• цифры только от 0 до 7
0123, -015
Шестнадцатеричные константы
• начинаются с приставок 0x,
• цифр от 0 до 9,
• латинские буквы a, b, c, d, e, f (A, B, C, D, E, F)
0xA (это 10), 0Xf (это 15), 0x41(это 65)
10.
Целые константыВ зависимости от значения целой константы
компилятор представляет ее в памяти в
соответствии с типом.
Для явного указания способа представления
программист может использовать суффиксы
• L, l
• 64L – long
• U,u
•067u – unsigned
• F, f
• 0f - float
11.
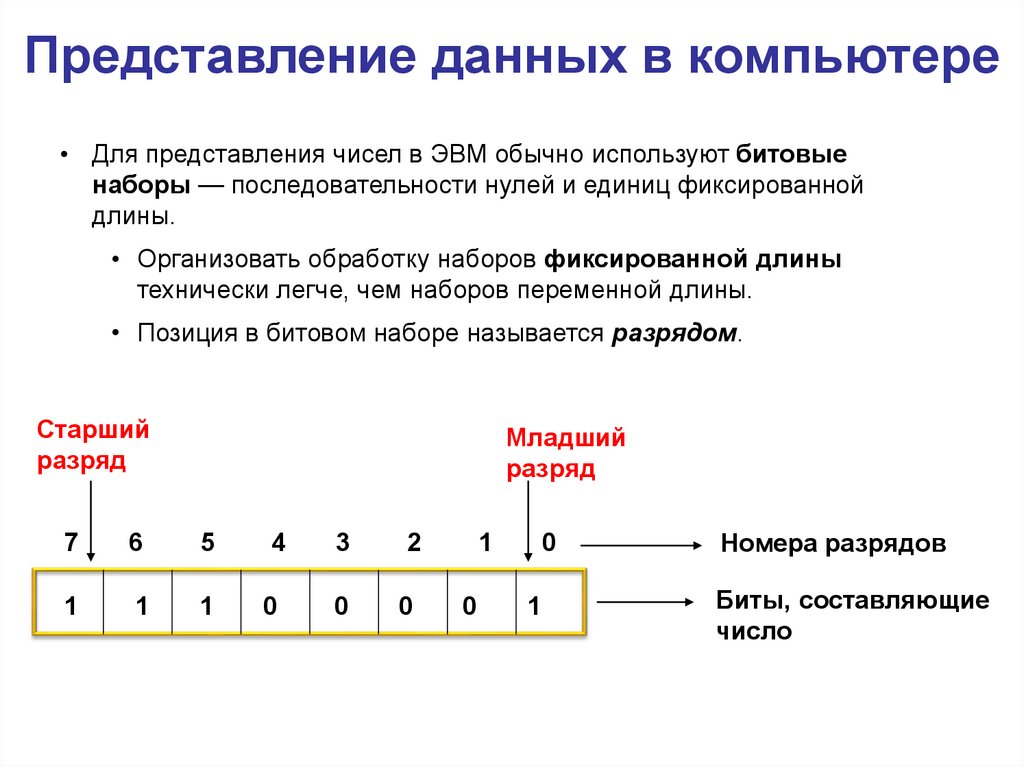
Представление данных в компьютере• Для представления чисел в ЭВМ обычно используют битовые
наборы — последовательности нулей и единиц фиксированной
длины.
• Организовать обработку наборов фиксированной длины
технически легче, чем наборов переменной длины.
• Позиция в битовом наборе называется разрядом.
Старший
разряд
Младший
разряд
7
6
5
1
1
1
4
0
3
0
2
0
1
0
0
1
Номера разрядов
Биты, составляющие
число
12.
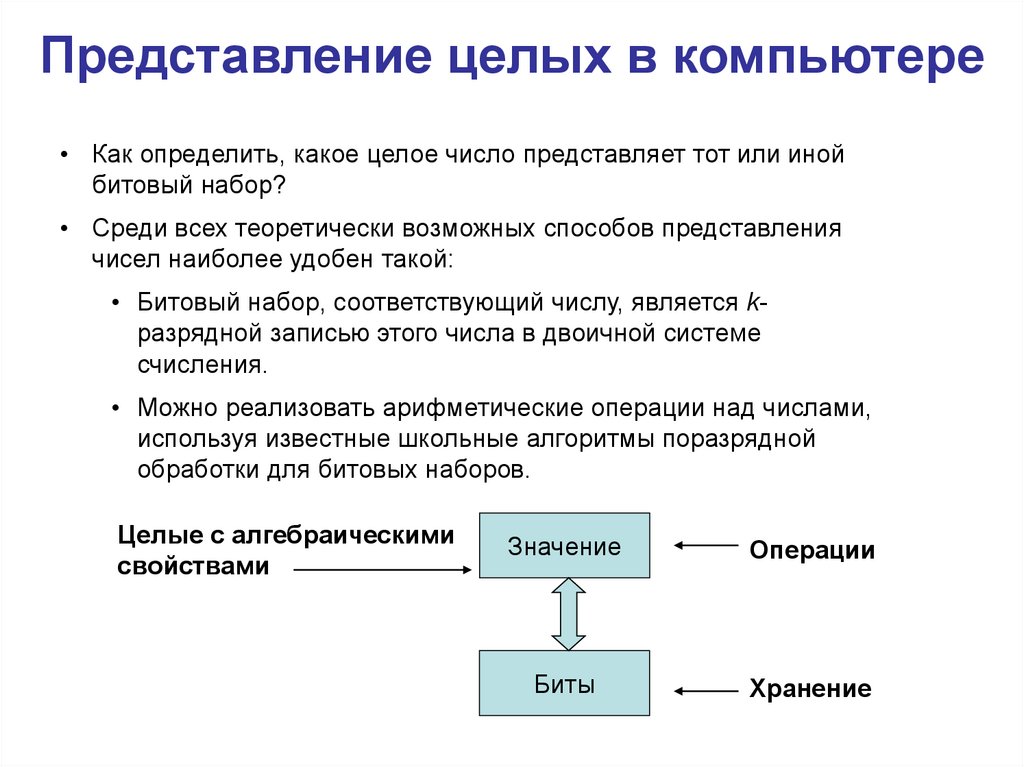
Представление целых в компьютере• Как определить, какое целое число представляет тот или иной
битовый набор?
• Среди всех теоретически возможных способов представления
чисел наиболее удобен такой:
• Битовый набор, соответствующий числу, является kразрядной записью этого числа в двоичной системе
счисления.
• Можно реализовать арифметические операции над числами,
используя известные школьные алгоритмы поразрядной
обработки для битовых наборов.
Целые с алгебраическими
свойствами
Значение
Операции
Биты
Хранение
13.
Двоичное представление целых:без знака
27
26
25
1
1
1
24
0
23
0
22
0
21
0
20
1
Хранение целого неотрицательного числа без знака (unsigned
int) на примере 8 битов.
225
= 1*20 + 0*21+ 0*22 + 0*23 + 0*24 + 1*25 + 1*26 + 1*27 =
= 1+ 32 + 64 +128
Операция сложения и вычитания целого неотрицательного
числа без знака (unsigned int) на примере 8 битов в С++.
unsigned char Min(0),
X(10), Res;
Res=Min + X;
printf("%d", Res);
unsigned char Max=255,
X=10, Res;
Res = Max - X;
printf("%d", Res);
14.
Двоичное представление целых:без знака, допустимость операций
Операция вычитания целого неотрицательного числа без
знака (unsigned int) на примере 8 битов в С++.
unsigned char Min(0), X(10), Res;
Res=Min - X;
ошибка во время компиляции?
printf("%d", Res);
ошибка во время выполнения?
непредсказуемое поведение?
Операция сложения целого неотрицательного числа без знака
(unsigned int) на примере 8 битов в С++.
unsigned char Max=255, X=10, Res;
Res = Max + X;
printf("%d", Res);
15.
Модульная арифметикаМодульная арифметика - это система арифметики для целых чисел,
где числа «оборачиваются» при достижении определенного значения,
называемого модулем .
9+4=1
16.
Двоичное представление целых:без знака, допустимость операций
В модульной арифметике (с целыми без знака)
не используется обнаружение переполнения.
Операция вычитания целого неотрицательного числа без
знака (unsigned int) на примере 8 битов в С++.
unsigned char Min(0), X(10), Res;
Res=Min - X;
printf("%d", Res);
246
Операция сложения целого неотрицательного числа без знака
(unsigned int) на примере 8 битов в С++.
unsigned char Max=255, X=10, Res;
Res = Max + X;
printf("%d", Res);
9
17.
Двоичное представление целых:Старший
со знаком
разряд
для
знака
7
6
5
1
1
1
4
0
3
0
2
0
1
0
0
Номера разрядов
1
Биты, составляющие
цифровую часть
Самый левый (старший) разряд битового набора длины k (называемый
знаковый разряд) используется для кодирования знака числа
• знак “плюс” кодируется нулем,
• знак “минус” кодируется единицей.
Остальные k-1 разрядов (называемые цифровой частью или
значащими разрядами) используются для представления абсолютной
величины числа.
225
≠ 1*20 + 0*21+ 0*22 + 0*23 + 0*24 + 1*25 + 1*26 + 1*27
18.
Целые числа со знаком• Для представления знаковых целых чисел используются три
способа
• прямой код
• обратный код
• дополнительный код
• Кодом ( франц. code, от лат. codex — свод законов) называют как
сам способ отображения, так и множество слов (кодовых
комбинаций), используемых при кодировании.
• Положительные числа в прямом, обратном и дополнительном
кодах изображаются одинаково — цифровая часть содержит
двоичную запись числа, в знаковом разряде содержится 0
0
1
1
0
0
0
0
1
97 = 1*20 + 0*21+ 0*22 + 0*23 + 0*24 + 1*25 + 1*26 = 1+32+64
19.
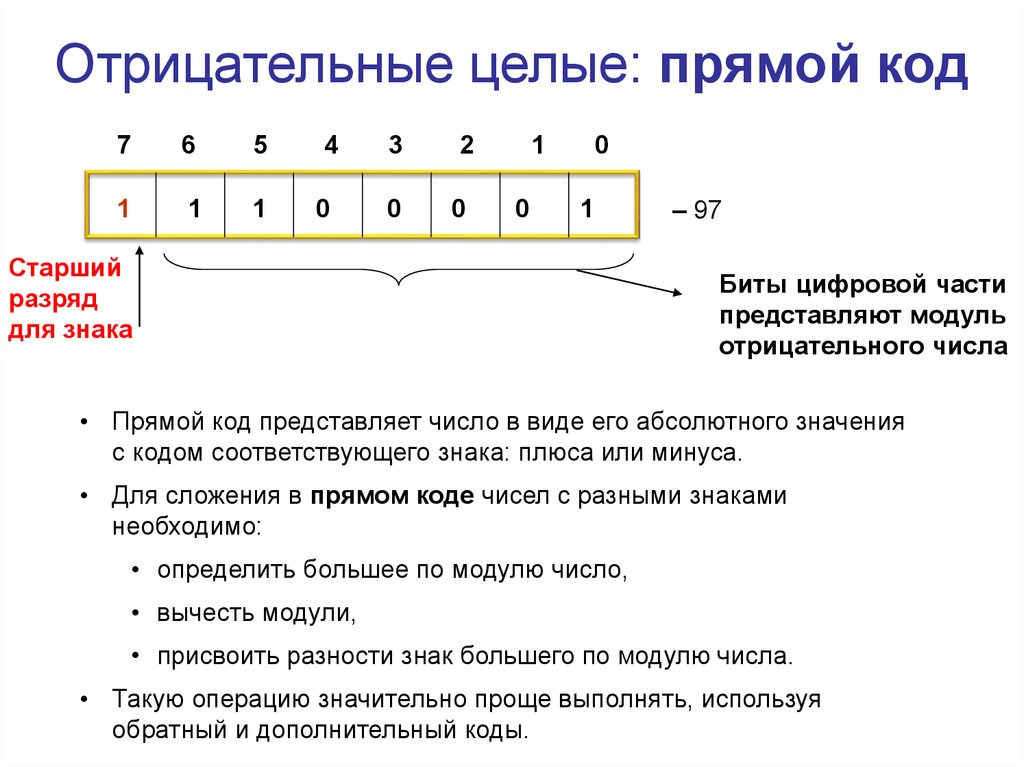
Отрицательные целые: прямой код7
6
5
1
1
1
4
0
3
0
2
0
1
0
0
1
Старший
разряд
для знака
– 97
Биты цифровой части
представляют модуль
отрицательного числа
• Прямой код представляет число в виде его абсолютного значения
с кодом соответствующего знака: плюса или минуса.
• Для сложения в прямом коде чисел с разными знаками
необходимо:
• определить большее по модулю число,
• вычесть модули,
• присвоить разности знак большего по модулю числа.
• Такую операцию значительно проще выполнять, используя
обратный и дополнительный коды.
20.
Отрицательные целые: обратный кодОбратный код отрицательного числа содержит:
• единицу в знаковом разряде,
• поразрядно инверсные значения цифровой части прямого кода
1
1
1
0
0
0
0
1
Прямой код числа -97
1
0
0
1
1
1
1
0
Обратный код числа -97
21.
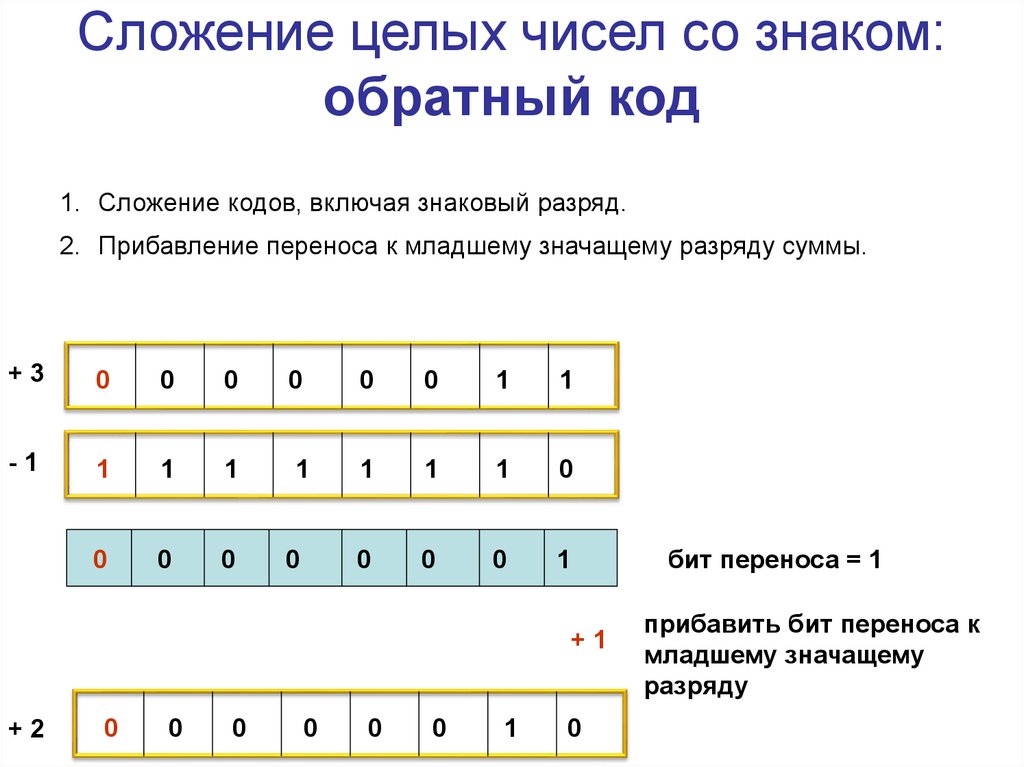
Сложение целых чисел со знаком:обратный код
1. Сложение кодов, включая знаковый разряд.
2. Прибавление переноса к младшему значащему разряду суммы.
+3
0
0
0
0
0
0
1
1
-1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
1
0
+1
+2
0
0
0
0
0
0
1
0
бит переноса = 1
прибавить бит переноса к
младшему значащему
разряду
22.
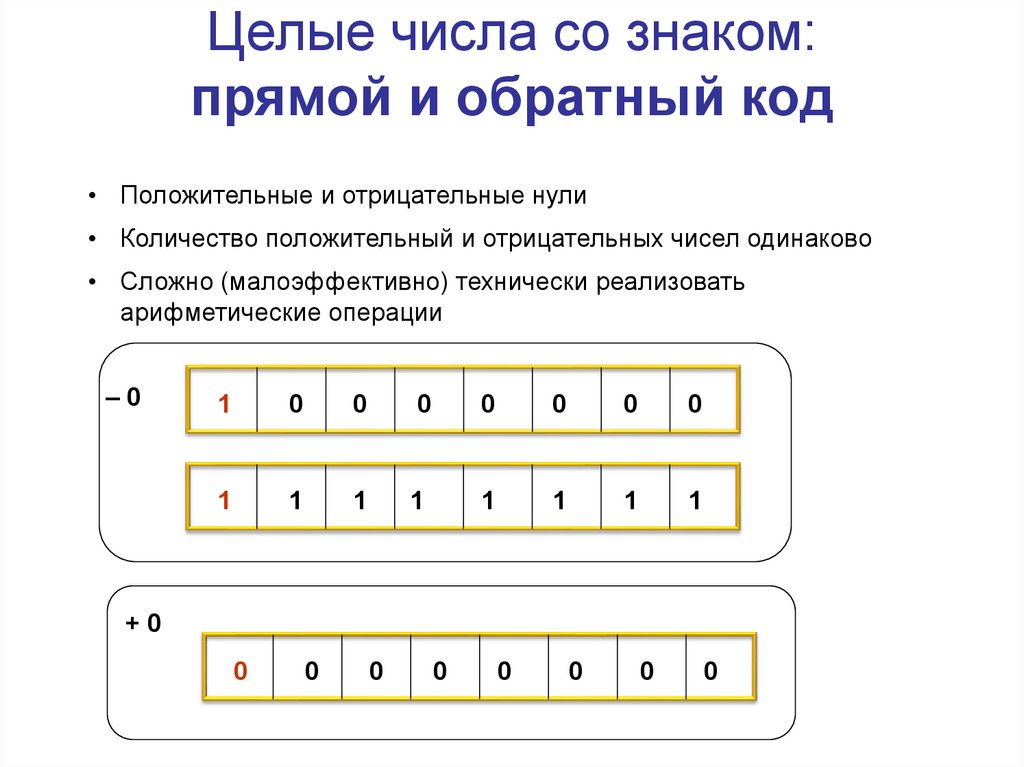
Целые числа со знаком:прямой и обратный код
• Положительные и отрицательные нули
• Количество положительный и отрицательных чисел одинаково
• Сложно (малоэффективно) технически реализовать
арифметические операции
–0
1
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
+0
0
0
0
0
0
0
0
0
23.
Отрицательные целые:дополнительный код
Обратный код отрицательного числа содержит:
• единицу в знаковом разряде,
• поразрядно инвертированные значения в цифровой части плюс
единица в младшем разряде
1
1
1
0
0
0
0
1
Прямой код числа -97
1
0
0
1
1
1
1
0
Обратный код числа -97
+1
1
0
0
1
1
1
1
1
Дополнительный код
числа -97
24.
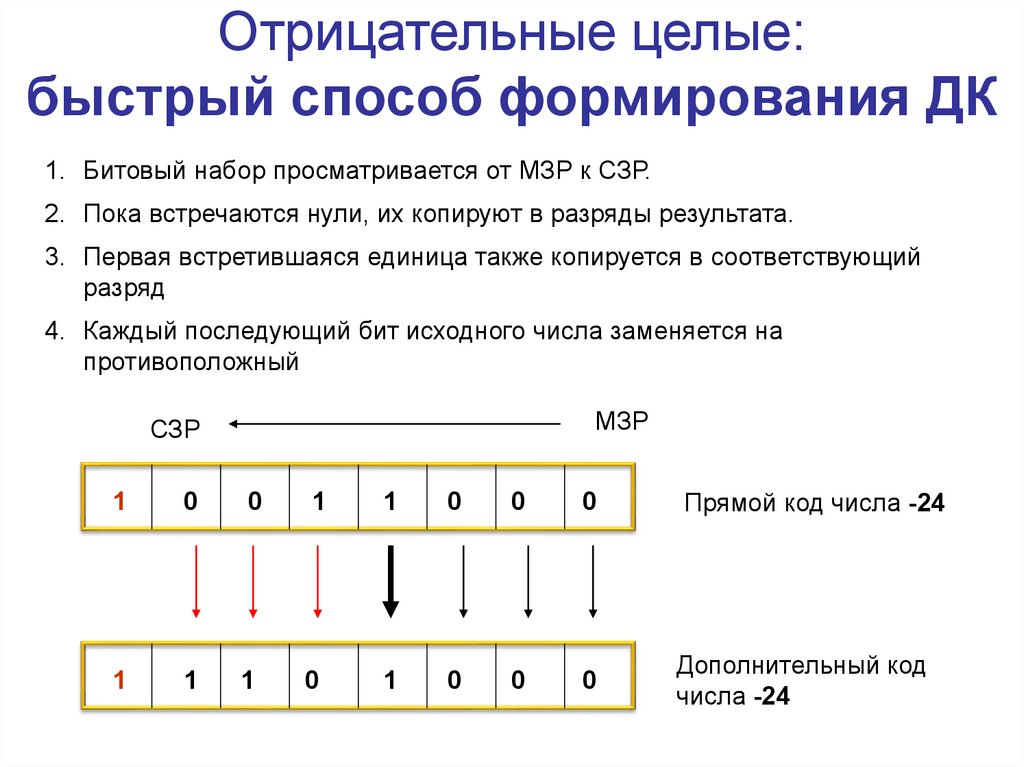
Отрицательные целые:быстрый способ формирования ДК
1. Битовый набор просматривается от МЗР к СЗР.
2. Пока встречаются нули, их копируют в разряды результата.
3. Первая встретившаяся единица также копируется в соответствующий
разряд
4. Каждый последующий бит исходного числа заменяется на
противоположный
МЗР
СЗР
1
0
0
1
1
0
0
0
1
1
1
0
1
0
0
0
Прямой код числа -24
Дополнительный код
числа -24
25.
Целые числа со знаком:дополнительный код
• Нуль единственный
• Количество положительный и отрицательных чисел НЕ одинаково
• Для сложения в обратном коде необходимо:
• сложить числа, включая знаковый разряд,
• бит переноса отбрасывается
+3
0
0
0
0
0
0
1
1
-1
1
1
1
1
1
1
1
1
бит переноса
отбрасывается
+2
0
0
0
0
0
0
1
0
26.
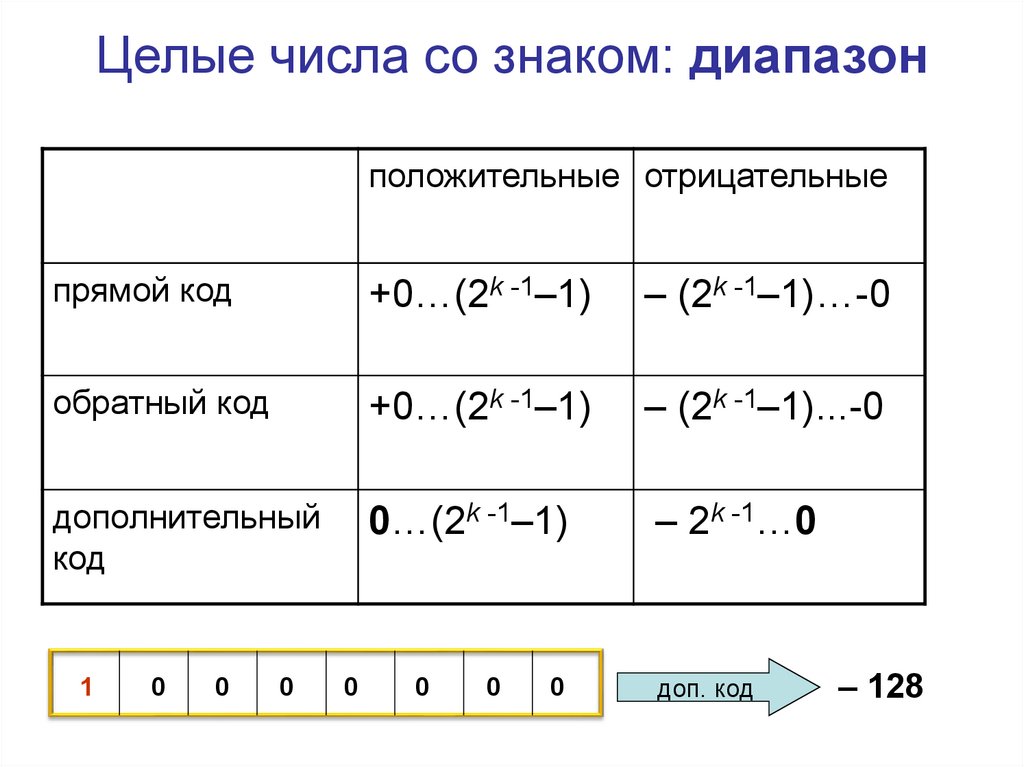
Целые числа со знаком: диапазонположительные отрицательные
прямой код
+0…(2k -1–1)
– (2k -1–1)…-0
обратный код
+0…(2k -1–1)
– (2k -1–1)...-0
дополнительный
код
0…(2k -1–1)
– 2k -1…0
1
0
0
0
0
0
0
0
доп. код
– 128
27.
Целые со знаком:неопределенное поведение
Операция вычитания целого числа со знаком (int) на примере 8
битов в С++.
char M;
M = -128 - 1;
printf("%d", M);
127
Операция сложения целого числа со знаком (int) на примере 8
битов в С++.
char M;
M = 127+1;
printf("%d", M);
-128
28.
Побитовые операции целых: отрицаниеunsigned char UnA = 1;
unsigned char notUnA = ~UnA;
254
std::cout << "uA = " << std::bitset<8>(UnA) << std::endl;
std::cout << "~uA = " << std::bitset<8>(notUnA) <<
std::endl;
std::cout << "~uA = " << (unsigned int)notUnA << std::endl;
char A = 1;
char notA = ~A;
-2
std::cout << "A = " << std::bitset<8>(A) << std::endl;
std::cout << "~A = " << std::bitset<8>(notA) <<
std::endl;
std::cout << "~A = " << (int)notA << std::endl;
29.
Операции сдвига• Операция сдвига – это одновременное перемещение
значений битов операнда на фиксированное количество
разрядов влево или вправо.
• Различают три типа сдвига
• Логический – освобожденные регистры заполняются
нулями.
• Арифметический – выполняется с учётом знака
операнда и зависит от кода числа
• Циклический – значения выдвигаемых битов
записываются на место освобождаемых.
30.
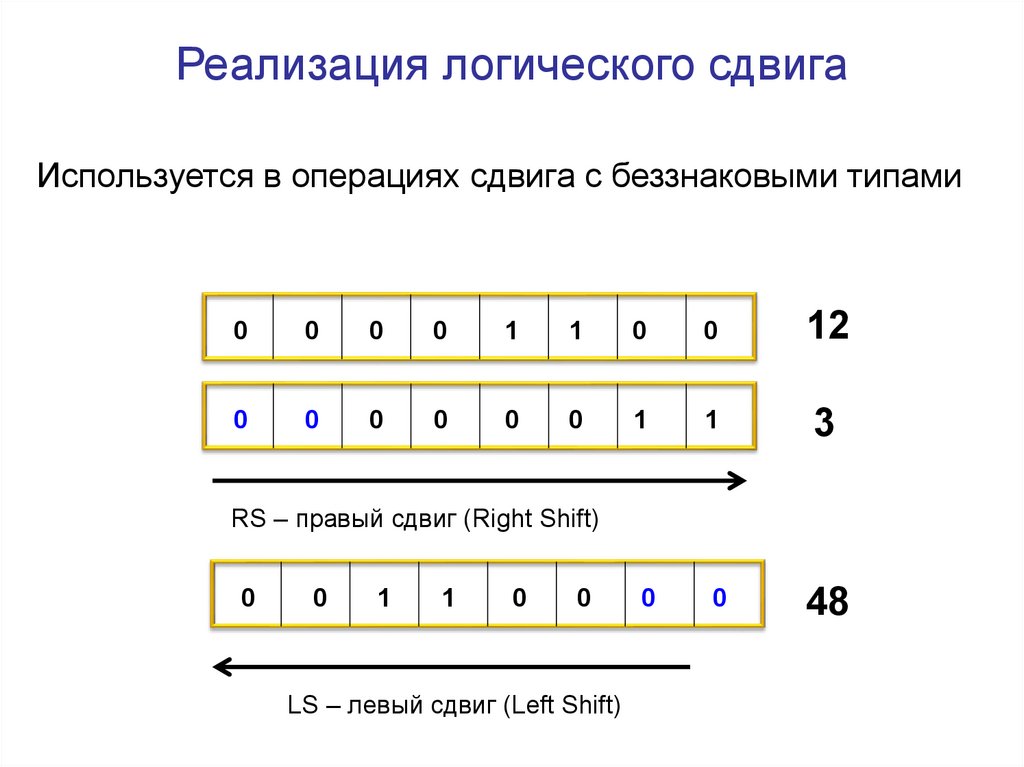
Реализация логического сдвигаИспользуется в операциях сдвига с беззнаковыми типами
0
0
0
0
1
1
0
0
12
0
0
0
0
0
0
1
1
3
RS – правый сдвиг (Right Shift)
0
0
1
1
0
0
LS – левый сдвиг (Left Shift)
0
0
48
31.
Реализация арифметического сдвигаВ прямом коде
• Cдвигается только цифровая часть, знак остаётся на месте,
• Освобождающиеся биты заполняются нулями
В дополнительном коде
• Eсли влево, то освобождающиеся биты заполняются нулями
• для отрицательных в С++ – неопределенное поведение
• для положительных в С++, если смещение не представимо в
беззнаковом виде, то неопределенное поведение
• Eсли вправо, то освобождающиеся биты заполняются
битом знака
• для отрицательных – зависит о реализации
32.
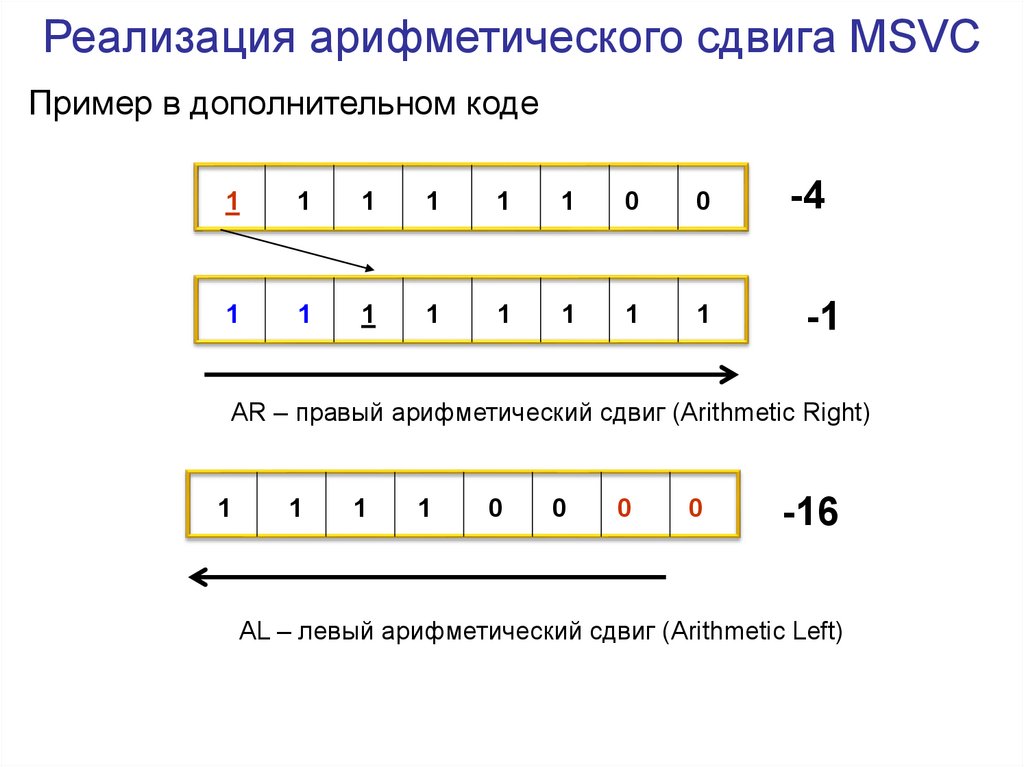
Реализация арифметического сдвига MSVCПример в дополнительном коде
1
1
1
1
1
1
0
0
1
1
1
1
1
1
1
1
-4
-1
AR – правый арифметический сдвиг (Arithmetic Right)
1
1
1
1
0
0
0
0
-16
AL – левый арифметический сдвиг (Arithmetic Left)
33.
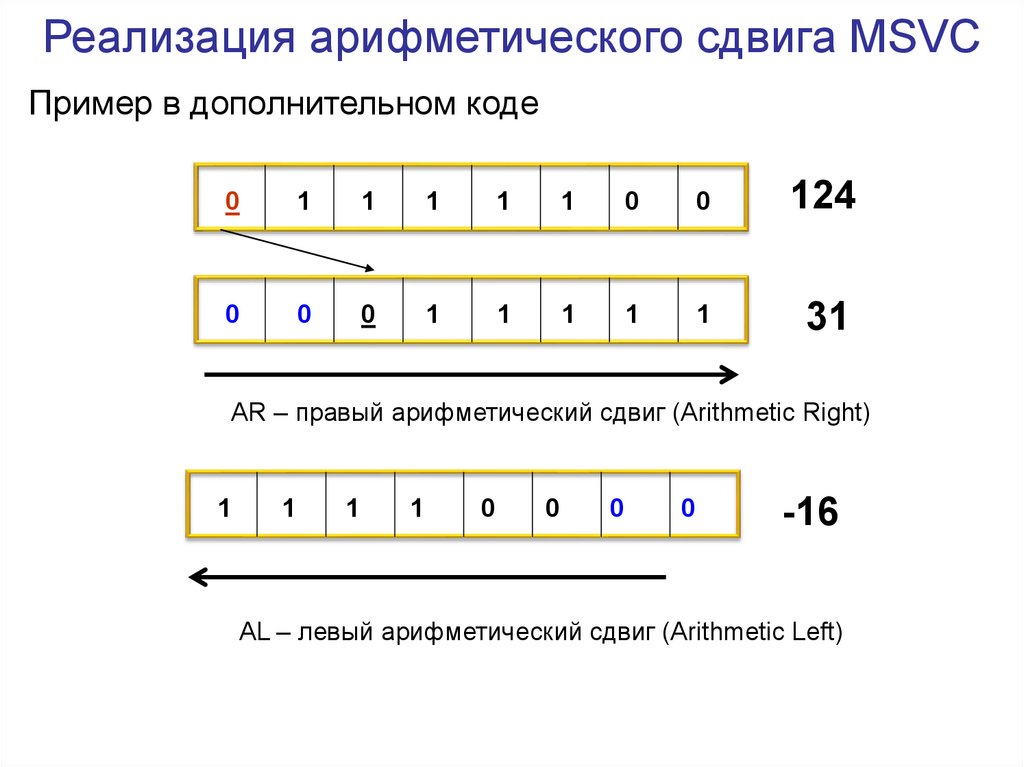
Реализация арифметического сдвига MSVCПример в дополнительном коде
0
1
1
1
1
1
0
0
124
0
0
0
1
1
1
1
1
31
AR – правый арифметический сдвиг (Arithmetic Right)
1
1
1
1
0
0
0
0
-16
AL – левый арифметический сдвиг (Arithmetic Left)
34.
Побитовые операции целых: сдвиг MSVCunsigned char LogicBase = 12;
unsigned char RS2 = LogicBase >>2;
unsigned char LS2 = LogicBase << 2;
std::cout << (int)LogicBase << ": RS2= " <<
std::bitset<8>(RS2) << std::endl;
std::cout << (int)LogicBase << ": LS2= " <<
std::bitset<8>(LS2) << std::endl;
char ArithmeticBase = -4;
char AR2 = ArithmeticBase >> 2;
char AL2 = ArithmeticBase << 2;
std::cout << (int)ArithmeticBase << ": AR2= " <<
std::bitset<8>(AR2) << std::endl;
std::cout << (int)ArithmeticBase << ": AL2= " <<
std::bitset<8>(AL2) << std::endl;
35.
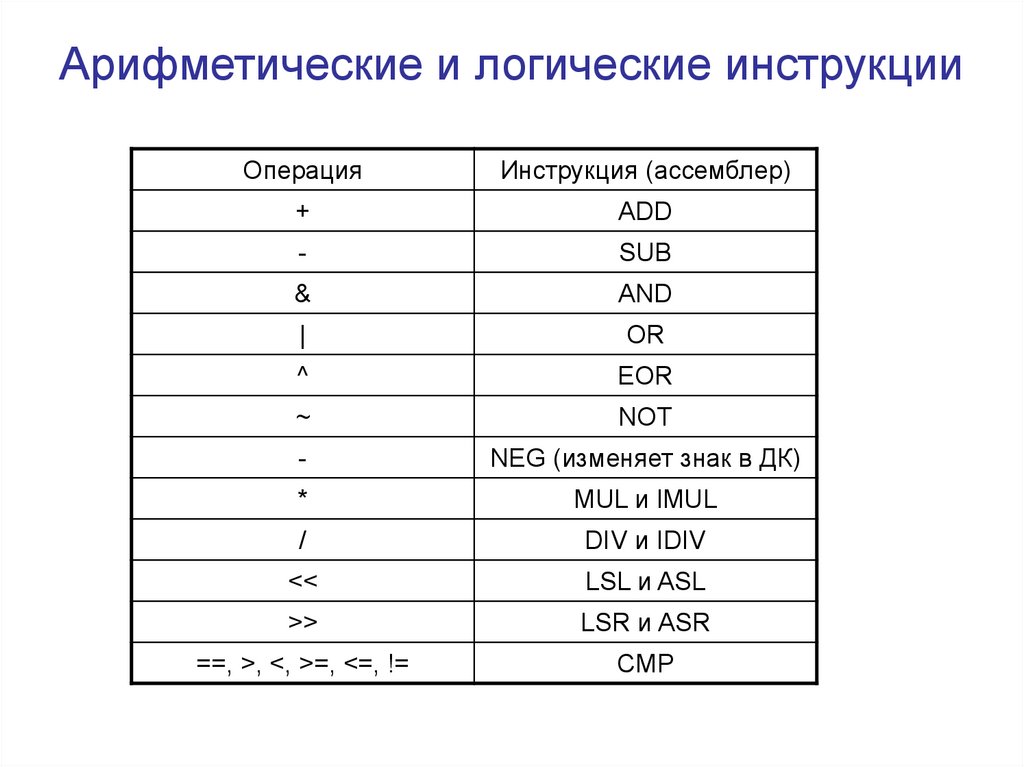
Арифметические и логические инструкцииОперация
Инструкция (ассемблер)
+
ADD
-
SUB
&
AND
|
OR
^
EOR
~
NOT
-
NEG (изменяет знак в ДК)
*
MUL и IMUL
/
DIV и IDIV
<<
LSL и ASL
>>
LSR и ASR
==, >, <, >=, <=, !=
CMP
36.
Дополнительные темы по целымчислам на самостоятельное изучение
• Умножение целых чисел, алгоритм умножения Бута
• Признак переполнения разрядной сетки
• Модифицированные коды
• Числа с фиксированной запятой
• Арифметические операции в системе команд
процессоров, замена вычитание сложением
• Двоично-десятичные числа
• Деление целых чисел
37.
Вещественные константыВещественные константы представлены в формате с плавающей
точкой.
Константа с плавающей точкой может включать семь частей:
- целая часть (десятичная целая константа);
- десятичная точка ;
- дробная часть (десятичная целая константа) ;
- признак экспоненты (символ e или E);
- показатель десятичной степени (десятичная целая константа,
возможно со знаком) ;
- суффикс F(или f) либо L(или l).
В записи вещественного числа
могут опускаться целая или
дробная часть (но не одновременно), десятичная точка или
признак экспоненты с показателем степени, суффикс.
Пример: 66. .045 .0 3.1459F 1.34e-12 45E+6L
56.891
Без суффиксов F или L под вещественную константу отводится 8
байт.
38.
Представления вещественных чиселДля
работы
с
вещественными
числами
могут
использоваться различные способы покрытия вещественной
оси (конечным) набором представимых чисел:
дроби вида m/n: пара целых чисел (m, n)
числа с фиксированной запятой
m·r–p,
где r и p заранее заданные константы, целое число m
• числа с плавающей запятой/точкой
m·rp,
где заранее задано только r, пара целых чисел (m, p)
39.
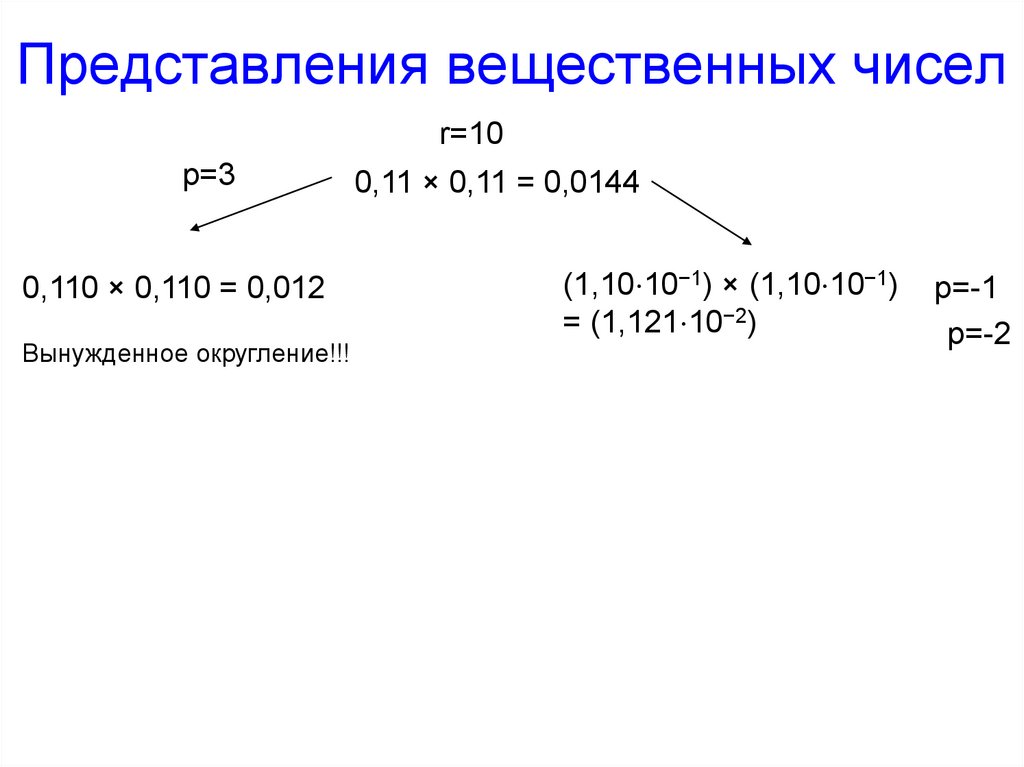
Представления вещественных чиселr=10
p=3
0,110 × 0,110 = 0,012
Вынужденное округление!!!
0,11 × 0,11 = 0,0144
(1,10⋅10−1) × (1,10⋅10−1)
= (1,121⋅10−2)
p=-1
p=-2
40.
Число с плавающей точкой• Вместо слова запятая часто используется слово точка,
так как в англоязычных странах для разделения целой и
дробной части числа традиционно используется точка.
Поэтому оба этих варианта можно считать синонимами.
• Не все действительные числа возможно представить в
виде числа с плавающей точкой
• Сравнительно с числами с фиксированной запятой
числа с плавающей запятой, имеющие тот же размер
представления,
позволяют
существенно
расширить
покрываемый диапазон вещественной оси, однако при
этом теряется однородность покрытия: чем дальше от
нуля, тем больше шаг между соседними представимыми
числами:
– относительная точность постоянная
– абсолютная погрешность изменяется
41.
Погрешность операций• x — приближённое значение некоторой величины x*.
• |x – x*| – это абсолютная погрешность x
• |x – x*|/|x*| – это относительная погрешность x, при
условии x* ≠ 0
• Машинная эпсилон – наибольшее положительное
число ε, такое что, 1⊕ε=1, где ⊕ - машинное сложение
– компьютер не различает числа x и y, если 1<x/y<1+ε
• Машинная эпсилон – числовое значение, меньше
которого невозможно задавать относительную точность
для любого алгоритма, возвращающего вещественные
числа, т.е. такое минимальное ε, что 1+ε>1
– компьютер не различает числа x и y, если |x-y|<ε
– ε = 2−23 ≈ 1.19e-07 для float в С++
42.
Число с плавающей точкойx=(−1)sign×mantissa×baseexp
sign – бит, отвечающий за знак,
mantissa – мантисса, целое число фиксированной длины,
которое выражает значение числа без учёта порядка
base – основание степени, exp – показатель степени
Когорта – совокупность представлений
0,01 =(-1)0×1×10-2=(-1)0×10×10-3=(-1)0×0,1×10-1
Нормальная форма, если mantissa [0,1)
0,01 = (-1)0×0,1×10-1 = (-1)0×0,001×102
43.
Нормализованная формаВ нормализованной форме mantissa [1,base)
В нормализованной форме любое число (кроме 0)
записывается единственным образом.
mantissa [1, 2)
mantissa [1, 10)
0,01 = (-1)0× 1,28 ×2-7=
0,01 = (-1)0×1×10-2
=…приведение к
двоичному виду…
Целая часть числа мантиссы двоичного числа (кроме 0) в
нормализованном виде равен 1 (так называемая неявная
единица), поэтому при записи мантиссы числа в ЭВМ
старший разряд можно не записывать.
44.
Стандарт IEEE 754• Используется в программных (компиляторы разных
языков программирования) и аппаратных (CPU и
FPU) реализациях арифметических действий
• Стандарт определяет пять основных форматов,
которые названы по их числовой базе и числу бит,
используемых в их кодировке
– В C++ поддерживается одинарная (float), двойная
(double) точность, а также long double, реализация
которого зависит от компилятора. Например, в MSVC
long double совпадает с double.
45.
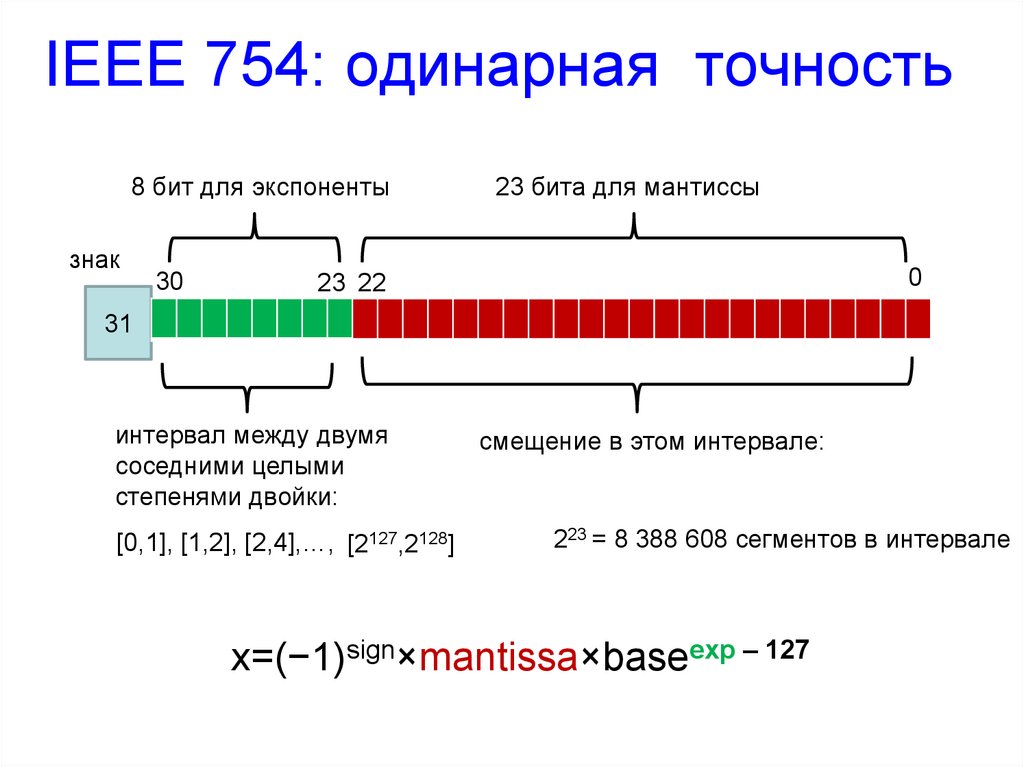
IEEE 754: одинарная точность8 бит для экспоненты
знак
30
23 бита для мантиссы
0
23 22
31
интервал между двумя
соседними целыми
степенями двойки:
[0,1], [1,2], [2,4],…, [2127,2128]
смещение в этом интервале:
223 = 8 388 608 сегментов в интервале
x=(−1)sign×mantissa×baseexp – 127
46.
IEEE 754: особые значения• Ноль и бесконечность (со знаком) – в стандарте
зарезервированы специальные значения мантиссы и
экспоненты
0
или
1
00 0 0 0 0 0 000 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
±0
0
или 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1
±∞
1
11 1 1 1 1 1 111 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
NaN
47.
Перевод числа 3,14• 3,14 => sign = 0
• 2 < 3,14 < 4 => 21= 2(128-127)
• (3,14-2)/(4-2)=0,57 внутри интервала
3,14 = (–1)0× (1+0,57)× 2(128-127)
• 128=1000 0000
• В ячейке 0,57*223=4781506,56=> 4781507=>
mantissa = 100 1000 1111 0101 1100 0011
0
1 0 0 0 0 0 0 010 0 1 0 0 0 1 1 1 1 0 1 0 1 1 1 0 0 0 0 1 1
(1+4781507*2-23)*2 = 3,1400001049041748046875
48.
Особенности сравнения чисел IEEE754Из-за округлений при вычислениях накапливается погрешность, вместо
прямого сравнения чисел с плавающей точкой на равенство или неравенство,
необходимо выполнять оценку расстояния между ними.
Абсолютная погрешность
fabs(a - b) <= eps;
Относительная погрешность
abs(a - b) <= eps * fmax(abs(a), abs(b));
Невозможно подобрать
фиксированное значение
константы eps для сравнения
произвольных чисел!
•Некоммутативность
•Разные знаки
49.
Особенности сравнения чисел IEEE754setlocale(LC_ALL, "Russian");
cout << "проверки для float" << endl;
float f01 = 0.1, f02 = 0.2, fEps = 0.001;
if (f02 == 0.2) cout << " 0.2 по умолчанию double" << endl;
if (f01 + f02 == 0.3f) cout << " обчныное равнство" << endl;
if (0.1f + 0.2f == 0.3f) cout << " обчныное равнство для констант" << endl;
if (abs(f01 + f02 - 0.3f) < fEps) cout << " eps: равенство" << endl;
cout << "проверки для double" << endl;
double d01 = 0.1, d02 = 0.2, dEps = 0.001;
if (d02 == 0.2) cout << " 0.2 по умолчанию double"<<endl;
if (d01 + d02 == 0.3 ) cout << " обчныное равнство" << endl;
if (0.1 + 0.2 == 0.3) cout << " обчныное равнство и константа" << endl;
if ( abs(d01 + d02 - 0.3) < dEps) cout << " eps: равенство" << endl;
50.
Функции и вещественные числа• Сумма и произведение чисел с плавающей запятой не
являются ассоциативными операциями
• Новые математические функции из стандарта С++11
сохраняют высокую точность при x ≈ 0 по сравнению со
старыми вариантами функций: expm1, log1p и др.
• Для некоторых функций С++ если их предел определён
(включая значения ±∞), то он берётся в качестве значения
этой функции в соответствующих предельных точках.
Например, log(-0).
• Для сравнения вещественных чисел можно использовать
не знаки операций, а функции: isless, islessequal и т.п.
• Для явного указания того, что аргумент и результат
функции “абсолютное значение” имеют тип double, следует
использовать функцию fabs вместо abs.
51.
Дополнительные темы по ЧсПТ насамостоятельное изучение
• Режимы округления, управление режимом
округления
• Денормализованные числа
• Особые ситуации при работе с числами с
плавающей точкой (переполнение мантиссы и
экспоненты, исчезновение порядка)
52.
53.
СИМВОЛ ТЕКСТАБазовый тип данных char понимается трояко:
1. как байт - минимальная адресуемая единица
представления данных в компьютере
2. как целое со знаком (в диапазоне –127…+127)
3. как символ текста.
54.
КонстантыСимвольные константы – это один или два символа, заключенные
в апострофы.
Примеры:
‘Z’
‘db’
‘*’ ’$’ ‘\012’ ‘\0’ ‘\n’ – односимвольные константы.
‘\x07\x07’
‘\n\t’
- двухсимвольные константы.
Символ ‘\’ используется для
- записи кодов , не имеющих графического изображения
- символов (‘),(\),(?),(“)
- Задания символьных констант, указывая их коды в 8-ричном
или 16 -ричном виде.
Последовательность символов, начинающаяся с символа ‘\’
называется эскейп-последовательностью.
-
55.
СИМВОЛЬНЫЕ КОНСТАНТЫ• Для представления отдельных символов можно
пользоваться
символьными
(литерными)
константами.
• Транслятор вместо такой константы всегда
подставляет код соответствующего символа.
• char c;
• for (c= 'A'; c <= 'Z'; c++) ...
• for (c=0x41; c <=0x5A; c++) ...
56.
НЕОТОБРАЖАЕМЫЕ СИМВОЛЫКод
Действие
\a
0x07
Звуковой сигнал
\b
0x08
Курсор на одну позицию назад
\f
0x0C
Переход к началу (перевод формата)
\n
0x0A
Переход на одну строку вниз(перевод строки)
\r
0x0D
Возврат на первую позицию строки
\t
0x09
Переход к позиции, кратной 8 (табуляция)
\v
0x0B
Вертикальная табуляция по строкам
________________________________________________________________
\\ \' \" \? Представление символов \, ', ", ?
\Onn
Символ с восьмеричным кодом nn
\xnn
Символ с шестнадцатеричным кодом nn
\0
Символ с кодом 0
57.
Таблица кодировки1. Таблица, в которой всем символам
компьютерного алфавита поставлены в
соответствие порядковые номера (коды),
называется таблицей кодировки.
2. Для разных типов ЭВМ используются
различные кодировки. С распространением
IBM PC международным стандартом стала
таблица кодировки ASCII (American
Standart Code for Information Interchange)
– Американский стандартный код для
информационного обмена.
58.
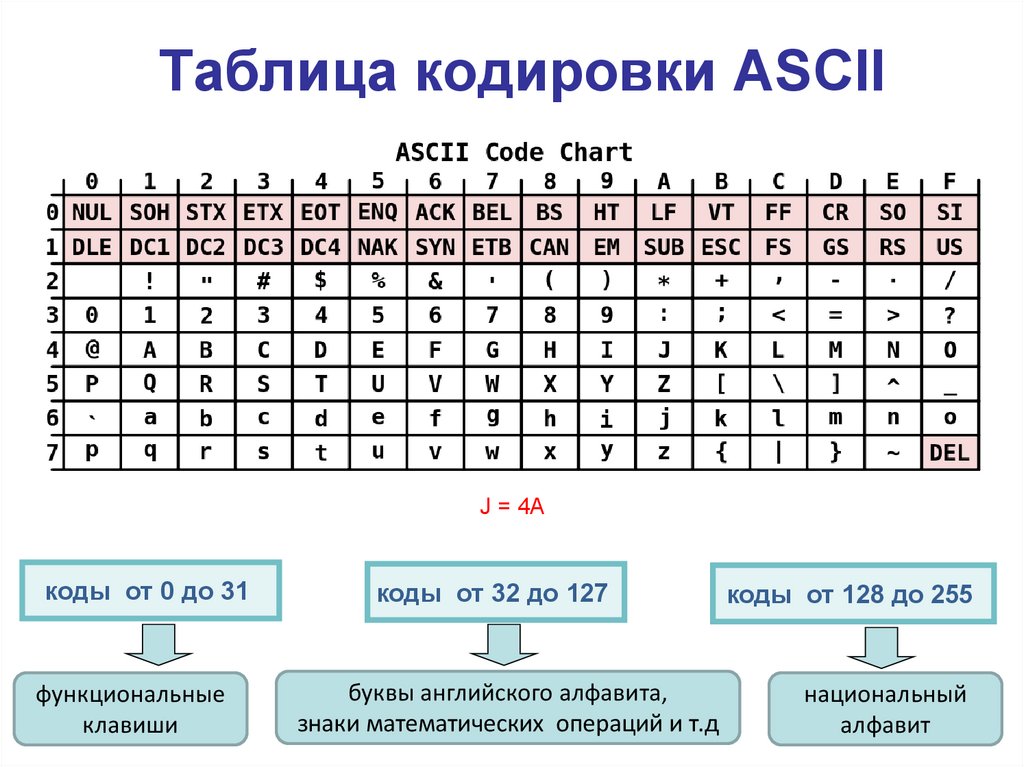
Таблица кодировки ASCII1.
Для кодирования одного символа требуется один
байт информации 28=256
2.
Стандартной в этой таблице является только
первая половина, т.е. символы с номерами от 0
(00000000) до 127 (0111111). Сюда входят
буква латинского алфавита, цифры, знаки
препинания, скобки и некоторые другие
символы.
Остальные 128 кодов используются в разных
вариантах. В русских кодировках размещаются
символы русского алфавита.
В настоящее время существует несколько
кодовых таблиц для русских букв.
3.
4.
59.
КОДОВЫЕ ТАБЛИЦЫКИРИЛЛИЦА В РАЗЛИЧНЫХ КОДИРОВКАХ
• ASCII – ISO/IEC 8859 (коды 128-255)
• Семейство KOI8 (КОИ-8R)
• Альтернативная (IBM code page 866)
60.
КОДОВЫЕ ТАБЛИЦЫКИРИЛЛИЦА В РАЗЛИЧНЫХ КОДИРОВКАХ
• Windows-1251 (CP1251)
• x-mac-cyrillic (CP10007)
61.
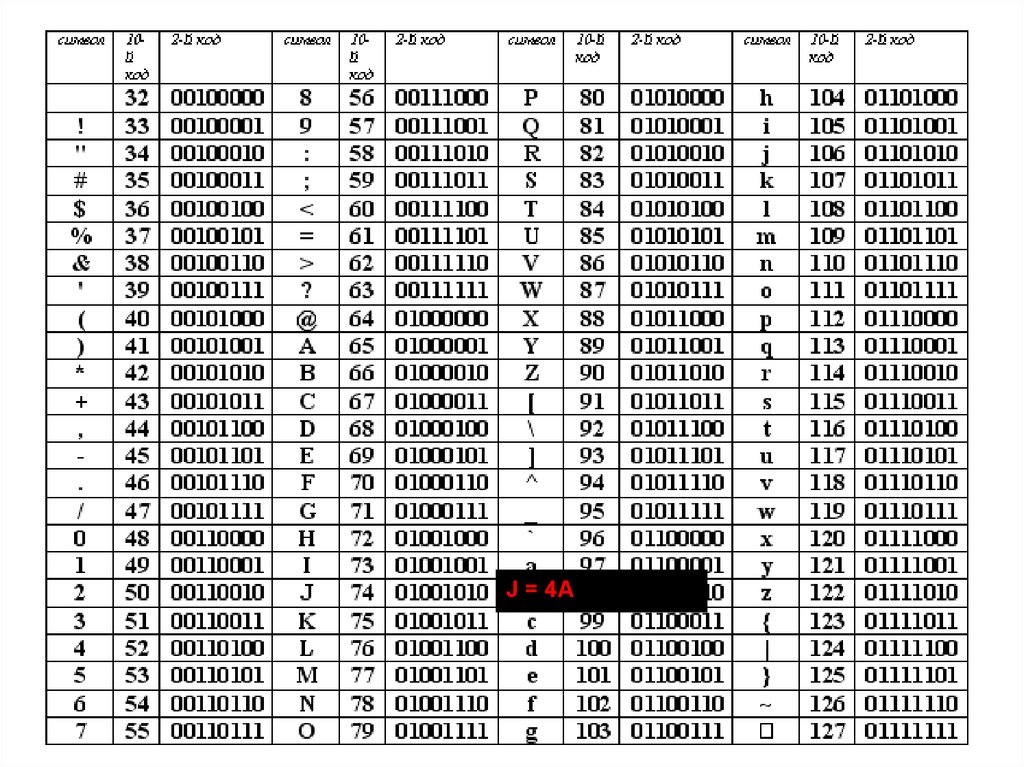
Таблица кодировки ASCIIJ = 4A
коды от 0 до 31
функциональные
клавиши
коды от 32 до 127
буквы английского алфавита,
знаки математических операций и т.д
коды от 128 до 255
национальный
алфавит
62.
J = 4A63.
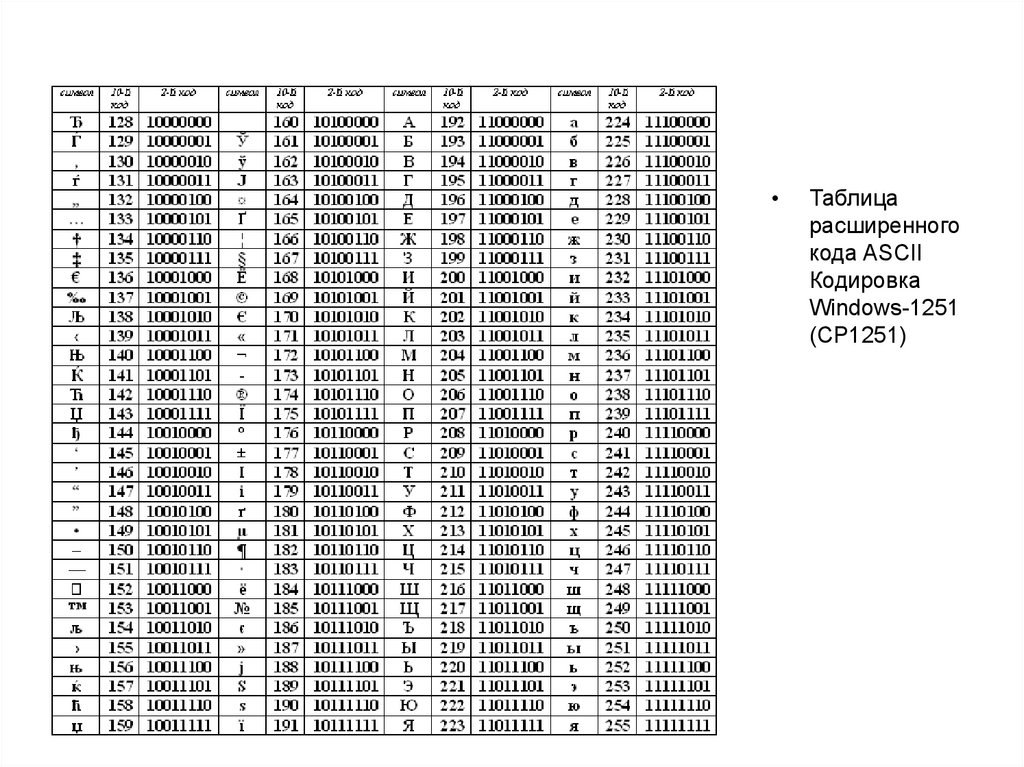
Таблица
расширенного
кода ASCII
Кодировка
Windows-1251
(CP1251)
64.
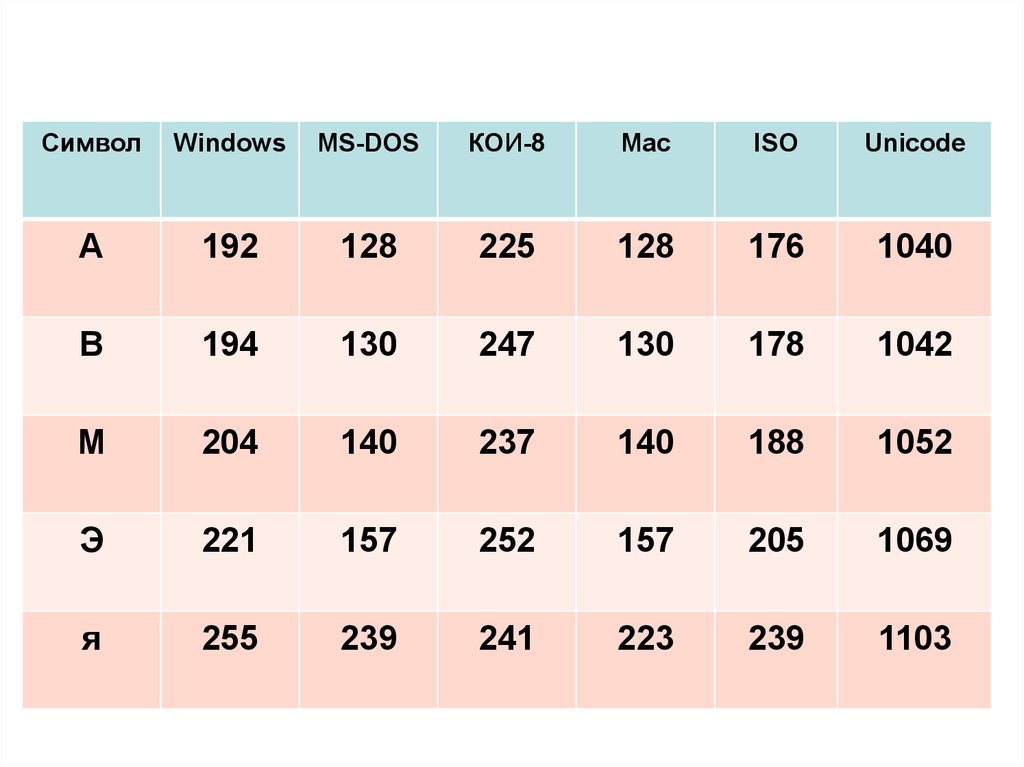
СимволWindows
MS-DOS
КОИ-8
Mac
ISO
Unicode
А
192
128
225
128
176
1040
В
194
130
247
130
178
1042
М
204
140
237
140
188
1052
Э
221
157
252
157
205
1069
я
255
239
241
223
239
1103
65.
Проблемы кодировки ASCII1.
2.
3.
Проблема неправильной раскодировки
Проблема ограниченности набора символов
Проблема преобразования одной кодировки в другую.
4.
Юникод— стандарт кодирования символов, позволяющий
представить знаки практически всех письменных языков.
5.
Первая версия Юникода представляла собой кодировку с
фиксированным размером символа в 16 бит, то есть общее
число кодов было 216 (65 536)
В дальнейшем было принято решение увеличить количество
кодируемых символов.
Одновременно с этим, коды символов стали
рассматриваться не как 16-битные значения, а как
абстрактные числа, которые в компьютере могут
представляться множеством разных способов
6.
7.
66.
UnicodeСтандарт кодирования символов предложен в 1991
году некоммерческой организацией «Консорциум
Юникода» (англ. Unicode Consortium, Unicode Inc.)
Применение этого стандарта позволяет закодировать
очень большое число символов из разных систем
письменности: в документах, закодированных по
стандарту Юникод, могут соседствовать
1.
2.
3.
китайские иероглифы,
математические символы,
буквы греческого алфавита, латиницы и кириллицы,
символы музыкальной нотной нотации,
при этом становится ненужным переключение кодовых
страниц
Стандарт состоит из двух основных частей:
универсального набора символов (Universal character set, UCS)
семейства кодировок ( Unicode transformation format, UTF)
67.
UnicodeУниверсальный набор символов перечисляет допустимые
по стандарту Юникод символы и присваивает каждому
символу код в виде неотрицательного целого числа,
записываемого обычно в шестнадцатеричной форме с
префиксом U+, например, U+040F
1.
Область с кодами от U+0000 до U+007F содержит символы
набора ASCII, и коды этих символов совпадают с их кодами в
ASCII
Под символы кириллицы выделены области знаков с кодами от
U+0400 до U+052F, от U+2DE0 до U+2DFF, от U+A640 до U+A69F
Часть кодов зарезервирована для использования в будущем
Семейство кодировок определяет способы преобразования
кодов символов для передачи в потоке или в файле
Для указания на использование Юникода, в начале
текстового файла или потока может передаваться Маркер
последовательности байтов (byte order mark (BOM))
2.
3.
UTF-8 (EF BB BF )
UTF-16
UTF-32
68.
Unicode: UTF-81.
UTF-8 — представление Юникода, обеспечивающее
наибольшую компактность и обратную совместимость с 7битной системой ASCII;
2.
Текст, состоящий только из символов с номерами меньше
128, при записи в UTF-8 превращается в обычный текст ASCII
и может быть отображён любой программой, работающей с
ASCII; и наоборот, текст, закодированный 7-битной ASCII
может быть отображён программой, предназначенной для
работы с UTF-8.
3.
Остальные символы Юникода изображаются
последовательностями длиной от 2 до 4 байт, в которых
• первый байт всегда имеет маску 11xxxxxx,
• а остальные — 10xxxxxx.
4.
Формат UTF-8 был изобретён 2 сентября 1992 года Кеном
Томпсоном и Робом Пайком
5.
Сейчас стандарт UTF-8 официально закреплён в документах
RFC 3629 и ISO/IEC 10646 Annex D.
69.
Unicode: UTF-16 и UTF-32UTF-16 является компромиссом: все символы как минимум
двухбайтные, но их размер может увеличиваться до 4 байт,
если нужно.
UTF-32 — способ представления Юникода, при котором
каждый символ занимает ровно 4 байта.
1.
2.
Главное преимущество UTF-32 перед кодировками переменной
длины заключается в том, что символы Юникод в ней
непосредственно индексируемы, поэтому найти символ по
номеру его позиции в файле можно чрезвычайно быстро, и
получение любого символа n-й позиции при этом является
операцией, занимающей всегда одинаковое время. Это также
делает замену символов в строках UTF-32 очень простой.
Главный недостаток UTF-32 — это неэффективное
использование пространства, так как для хранения любого
символа используется четыре байта
70.
71.
СтрокаСтрока или строковая константа определяется как последовательность
символов, заключенная в кавычки.
Пример:
“Это пример строки, называемой строковой константой”
Среди символов строки могут быть эскейп-последовательности, то есть
сочетания,
соответствующие
неизображаемым
символьным
константам или символам, задаваемых их внутренними кодами. В
этом случае они начинаются с символа ‘\’ .
“\nЭто строка,\nиначе -\”стринг\”,\nиначе - \”строковый литерал\”.”
72.
Обработка строковых данных1. string (строки Unicode) — это тип данных
С++ для работы со строками.
тип string, задаёт строки переменной длины
тип string представляет последовательность из
нуля или более символов в кодировке Юникод
2. Тип string обеспечивает множество
методов, которые призваны выполнить за
вас всю черновую работу:
–
–
возвратить количество символов в строке,
найти подстроки,
73.
Вывод служебных символовПомимо управляющих последовательностей,
в С++ (C++11) предусмотрен также специальный
синтаксис для дословного вывода строк вне
зависимости от наличия в них управляющих
последовательностей (raw string literals ).
string finalString =R"("quoted string")" ;
74.
75.
Объявление переменных и поименованныхконстант
[<Изменчивость>] [<Тип>]<Список идентификаторов>
[=<Значение>];
где <Изменчивость> – описатель возможности изменения
значений: const – поименованная константа,
volatile – переменная, меняющаяся в промежутках
между явными обращениями к ней
без указания изменчивости – обычная переменная
<Тип> – описатель типа: int, char, float, double и т.д.;
<Список идентификаторов> – список имен переменных или
констант;
<Значение> – начальное значение переменной или значение
константы.
76
76.
Примеры объявлений переменных и константНеинициализированные переменные:
int f,c,d; float r;
I,j;unsigned int max,min;
сhar c1,c2; unsigned char c5;
Инициализированные переменные
double k=89.34; char ch=‘G’;
Поименованные константы
const long a=6; const float pp=6.6e-34;
На практике все объявления могут быть перемешаны в
описаниях программы:
const char simt=‘T’;float max=100,min=-100;
double f,s,eps=0.001;
Переменные и поименованные константы могут быть
объявлены в любом месте программы:
вне всех функций, внутри функций, в любом месте функции.
Основное условие – объявление должно стоять до обращения к
переменной или константе.
77.
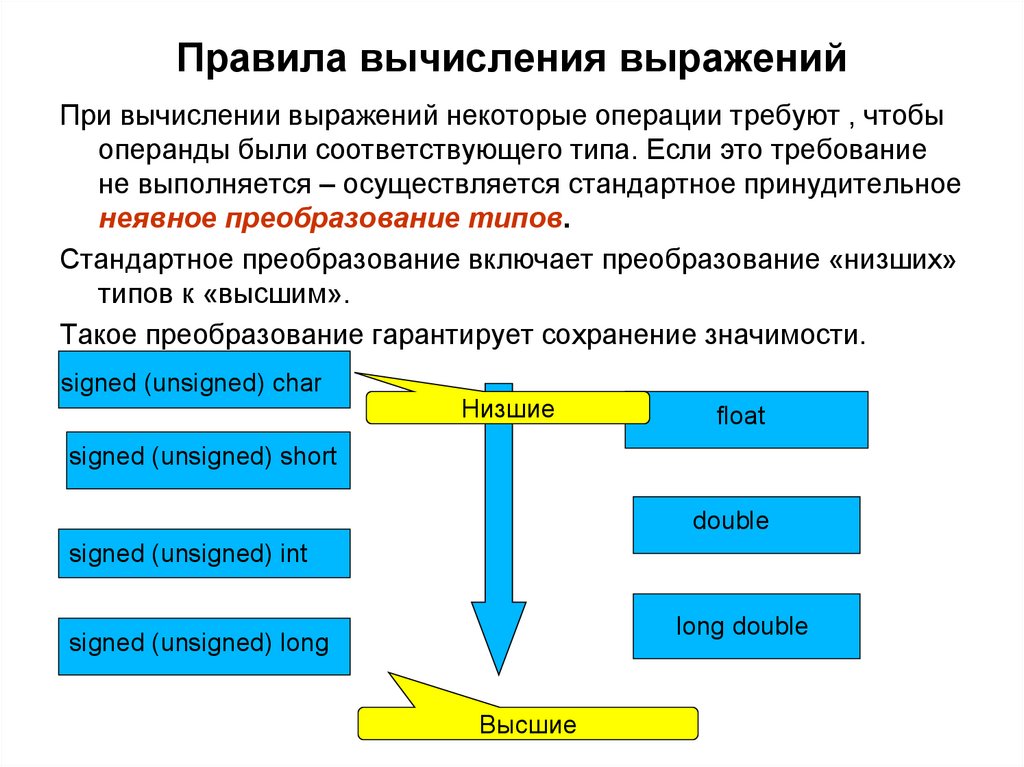
Правила вычисления выраженийПри вычислении выражений некоторые операции требуют , чтобы
операнды были соответствующего типа. Если это требование
не выполняется – осуществляется стандартное принудительное
неявное преобразование типов.
Стандартное преобразование включает преобразование «низших»
типов к «высшим».
Такое преобразование гарантирует сохранение значимости.
signed (unsigned) char
Низшие
float
signed (unsigned) short
double
signed (unsigned) int
long double
signed (unsigned) long
Высшие
78.
Правила вычисления выраженийДля выполнения операций над некоторыми типами данных
требуется явное переопределение типов.
Различают:
Функциональное преобразование
<имя типа> (Список выражений)
Примеры:
int(3.14); float(2/3);
int(‘A’);
Однако, функциональная запись не подходит для сложного
типа.
В этом случае применяется каноническая форма
преобразования:
(имя типа)<выражение>
Примеры:
(unsigned long)(x/3+2); (long)25;(char)123;
79.
• Функции преобразования из строки втип
– stoi
• http://www.cplusplus.com/reference/string/stoi/
• выдает исключения invalid_argument или
out_of_range, если преобразование не может
быть выполнено.



























































 programming
programming








