7.28M

Category: $mathematics$ mathematics

Математика в современном мире

Математика
• В переводе с греческого mathema знание, учение, наука.
• Понимание самостоятельного положения мат
ематики как
особой науки возникло в Древней Греции на
рубеже 6 и 5 вв. до нашей эры.
• Абстрактность и
общность понятий математики позволяют оди
н и тот же математический аппарат применять
в различных науках.

3.

Периоды развития математики
Предистория (до 6 века до н.э.)
Математика постоянных величин (6 в. до
н.э. – 17 в.)
Математика переменных величин (17 в. –
первая треть 19 в.)
Современная математика (первая треть 19
в. – настоящее время)

4.

Цитата
• Если мы посмотрим на решающий в
развитии математики момент, когда она
сделала первый и самый значительный для
человечества шаг и возникла та основа, на
которой она зиждется – логическое
доказательство, то увидим, что произошло
это на материале, который просто исключал
возможность практических приложений.

5.

Продолжение цитаты
• Первые теоремы Фалеса Милетского
устанавливали истины, очевидные для
каждого здравомыслящего человека –
вроде того, что диаметр делит круг на две
равные части. Гениальность нужна была не
для того, чтобы увериться в справедливости
этих положений, а для того, чтобы понять,
что они нуждаются в доказательстве.

6.

Автор цитаты
И́горь Ростисла́вович
Шафаре́вич
(3 июня 1923, Житомир — 19
февраля 2017, Москва) —
советский и
российский математик, доктор
физико-математических наук,
профессор, академик РАН (1991,
член-корреспондент АН СССР с
1958). Основные труды
посвящены алгебре, теории
чисел и алгебраической
геометрии. Лауреат Ленинской
премии. Известен также
как диссидент, публицист, обще
ственный деятель.

7.

Евклид
Евкли́ д или Эвкли́ д (др.греч. Εὐκλείδης, от «добрая
слава», время расцвета —
около 300 года до н. э.) —
древнегреческий математик
, автор первого из
дошедших до нас
теоретических трактатов по
математике.
Биографические сведения
об Евклиде крайне скудны.
Достоверным можно
считать лишь то, что его
научная деятельность
протекала в Александрии в
III в. до н. э.

8.

Математика переменных величин
• Аналитическая геометрия (Р.Декарт,
П.Ферма).
• Теория вероятностей (П.Ферма, Б.Паскаль).
• Исчисление бесконечно малых
(математический анализ) (И.Ньютон,
Г.Лейбниц).

9.

Задачи кавалера де Мере
• Первая состояла в том, чтобы узнать,
сколько раз надо метать две кости, чтобы
надеяться получить наибольшее число
очков, то есть двенадцать. Вторая задача
много сложнее. Страстный игрок, де Мере
чрезвычайно интересовался следующим
вопросом: каким образом разделить ставку
между игроками в случае, если игра не
была окончена?

10.

Блез Паскаль
Блез Паска́ль (фр. Blaise
Pascal [blɛz pasˈkal]; 19
июня 1623, КлермонФерран, Франция — 19
августа 1662, Париж, Франц
ия) —
французский математик, ме
ханик, физик, литератор и ф
илософ. Классик
французской литературы,
один из
основателей математическо
го анализа, теории
вероятностей и проективно
й геометрии, создатель
первых образцов счётной
техники, автор основного
закона гидростатики.

11.

Решение второй задачи
Предположим, говорит Б. Паскаль, что играют два игрока и что выигрыш
считается окончательным после выигрыша одним из них трех партий. Пусть
ставка каждого игрока составляет 32 луидора, и предположим, что первый
уже выиграл две партии (ему не хватает одной), второй выиграл одну (ему не
хватает двух). Им предстоит сыграть еще партию. Если ее выиграет первый, он
получит всю сумму, то есть 64 луидора; если второй, у каждого будет по две
выигранные партии, шансы обеих будут равны, и в случае прекращения игры
каждому, очевидно, надо дать поровну.Итак, если выиграет первый, он
получит 64 луидора. Если выиграет второй, то первый получит лишь 32
луидора. Поэтому, если оба согласны не играть предстоящей партии, то
первый вправе сказать:— Тридцать два луидора я получу во всяком случае,
даже если я проиграю предстоящую партию, которую мы согласились
признать последней. Стало быть, 32 луидора мои. Что касается остальных 32,
может быть, их выиграю, я, может быть, вы. Поэтому разделим сомнительную
сумму пополам!Значит, если игроки разойдутся, не сыграв последней партии,
то первому надо дать 48 луидоров, или же три четверти всей суммы, второму
16 луидоров, или одну четверть, из чего видно, что шансы первого из них на
выигрыш втрое больше, чем второго (а не вдвое, как можно было бы
подумать при поверхностном рассуждении).

12.

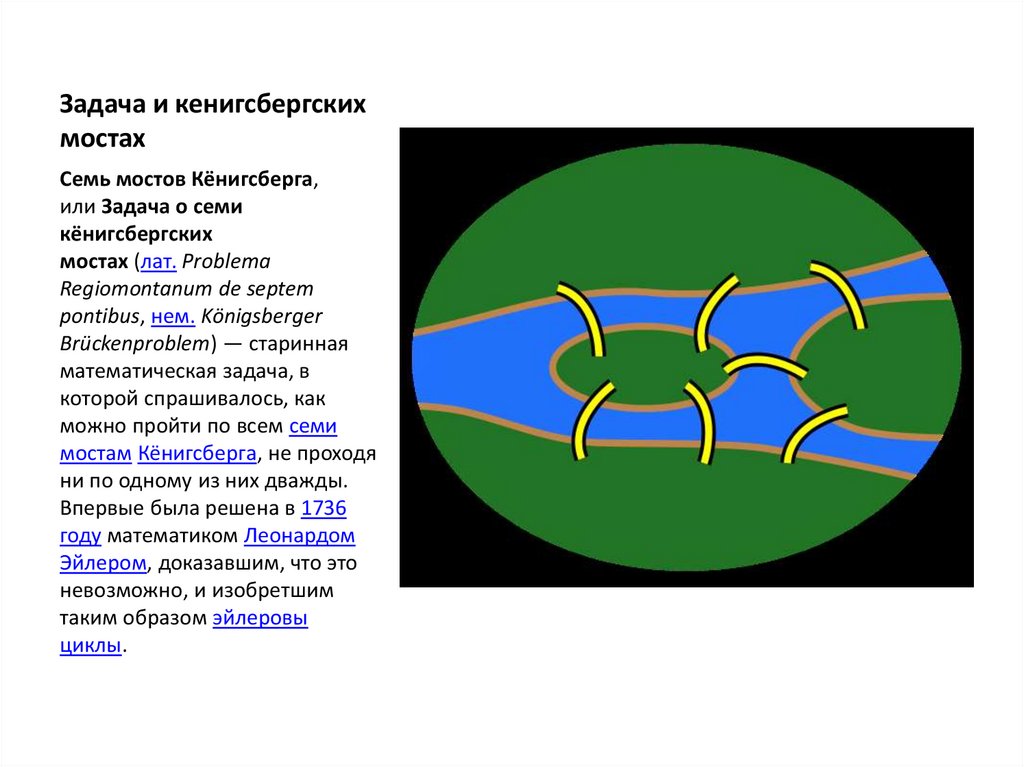
Задача и кенигсбергских
мостах
Семь мостов Кёнигсберга,
или Задача о семи
кёнигсбергских
мостах (лат. Problema
Regiomontanum de septem
pontibus, нем. Königsberger
Brückenproblem) — старинная
математическая задача, в
которой спрашивалось, как
можно пройти по всем семи
мостам Кёнигсберга, не проходя
ни по одному из них дважды.
Впервые была решена в 1736
году математиком Леонардом
Эйлером, доказавшим, что это
невозможно, и изобретшим
таким образом эйлеровы
циклы.

13.

Отцы современной математики
• Неевклидова геометрия (К.Ф.Гаусс, Я.Бояи,
Н.И.Лобачевский)
• Алгебраические структуры (Э.Галуа, Амалия
Эмми Нетер).
• Теория множеств (Георг Кантор).

14.

Н.И.Лобачевский
Никола́й Ива́нович
Лобаче́вский (20 ноября
(1 декабря) 1792, Нижний
Новгород — 12 (24)
февраля 1856, Казань) —
русский математик, один из
создателей неевклидовой ге
ометрии, деятель
университетского
образования и народного
просвещения. Известный
английский
математик Уильям
Клиффорд назвал
Лобачевского
«Коперником геометрии».

15.

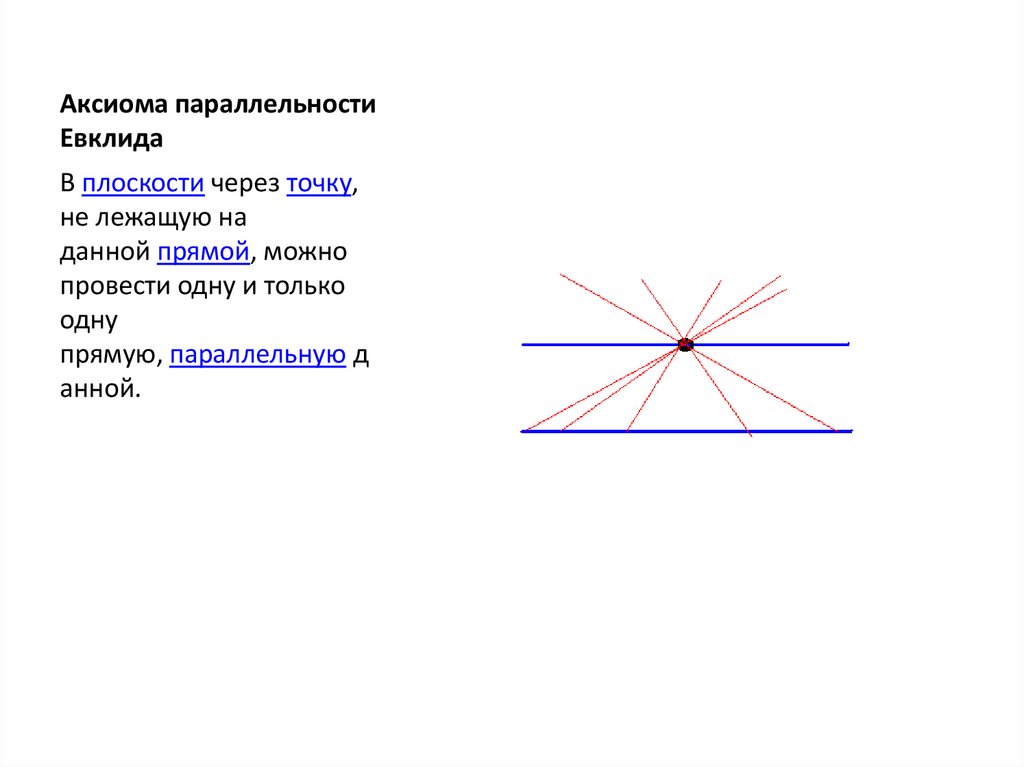
Аксиома параллельности
Евклида
В плоскости через точку,
не лежащую на
данной прямой, можно
провести одну и только
одну
прямую, параллельную д
анной.

16.

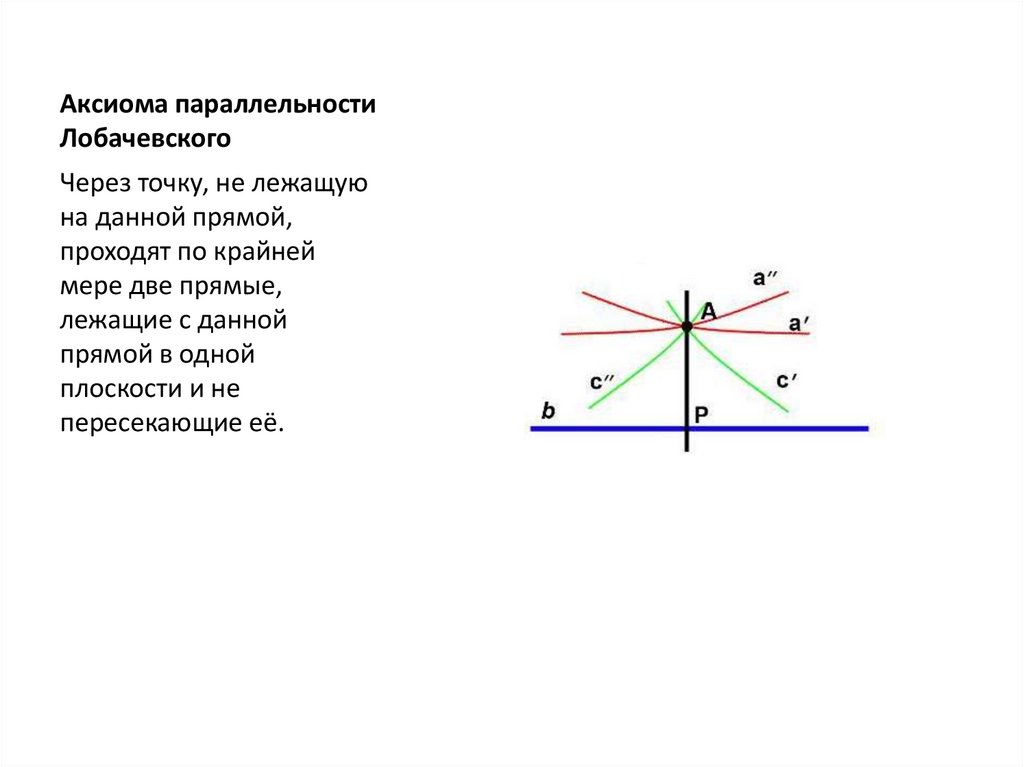
Аксиома параллельности
Лобачевского
Через точку, не лежащую
на данной прямой,
проходят по крайней
мере две прямые,
лежащие с данной
прямой в одной
плоскости и не
пересекающие её.

17.

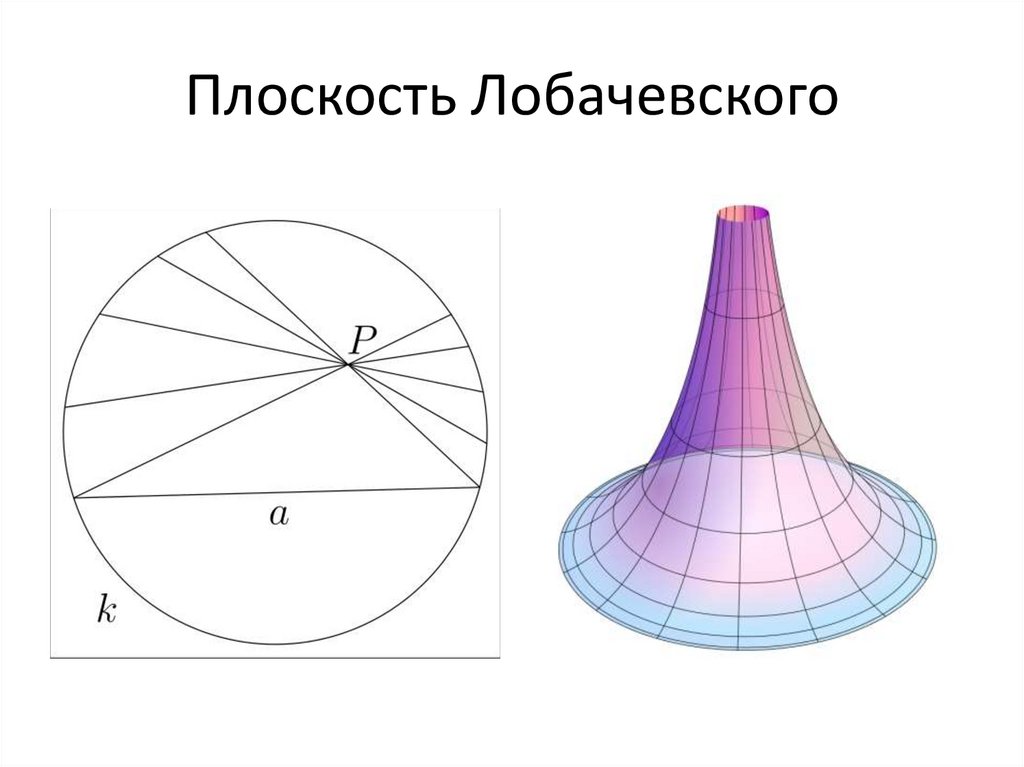
Плоскость Лобачевского

18.

Эварист Галуа
Эвари́ ст Галуа́ (фр. Évariste
Galois; 25 октября 1811, Бурля-Рене (фр.), О-деСен, Франция — 31
мая 1832, Париж,
Франция) —
французский математик,
основатель
современной высшей
алгебры. Радикальный
революционерреспубликанец, был
застрелен на дуэли в
возрасте двадцати лет.

19.

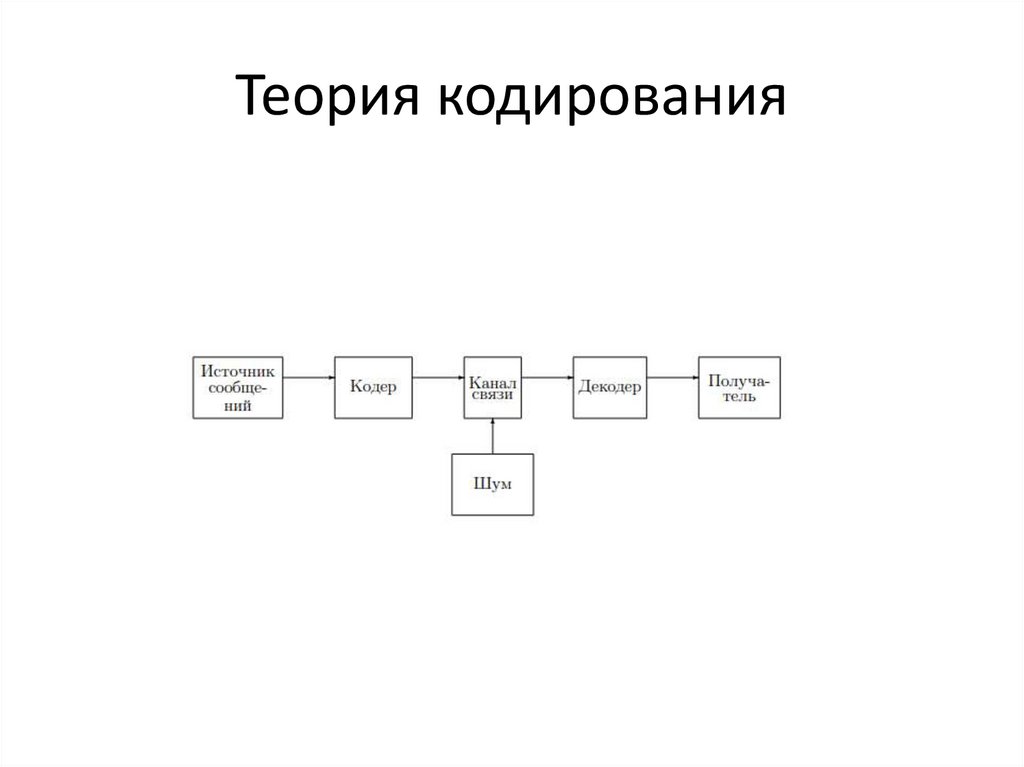
Теория кодирования

20.

21.

Кризисы в истории математики
Первый связан с открытием
несоизмеримых отрезков
Второй – с открытием бесконечно малых
величин
Третий – с созданием теории множеств

22.

Математические методы
• Математические методы наиболее широко
используются при проведении системных
исследований. При этом решение практических
задач математическими методами
последовательно осуществляется по следующему
алгоритму:
• • математическая формулировка задачи
(разработки математической модели);
• • выбор метода проведения исследования
полученной математической модели;
• • анализ полученного математического результата.

23.

Математическая модель
• Математическая формулировка задачи обычно
представляется в виде чисел, геометрических образов,
функций, систем уравнений и т. п. Описание объекта
(явления) может быть представлено с помощью
непрерывной или дискретной, детерминированной или
стохастической и другими математическими формами.
• Математическая модель представляет собой систему
математических соотношений (формул, функций,
уравнений, систем уравнений), описывающих те или
иные стороны изучаемого объекта, явления, процесса
или объект (процесс) в целом.

24.

Линейное
программирование
В 1939 году Леонид
Витальевич
Канторович (1912-1986)
опубликовал работу
«Математические методы
организации и
планирования
производства», в которой
сформулировал новый
класс экстремальных задач
с ограничениями и
разработал эффективный
метод их решения, таким
образом были заложены
основы линейного
программирования
(Нобелевская премия 1975
года по экономике).

25.

Задача
Условие
Компания производит полки для ванных
комнат двух размеров – А и В. Агенты по
продаже считают, что в неделю на рынке
может быть реализовано до 550 полок. Для
каждой полки типа А требуется 2 м2
материала, а для полки типа В – 3 м2
материала. Компания может получить до
1200 м2 материала в неделю. Для
изготовления одной полки типа А требуется
12 мин машинного времени, а для
изготовления одной полки типа В – 30 мин;
машину можно использовать 160 час в
неделю. Если прибыль от продажи полок
типа А составляет 3 денежных единицы, а от
полок типа В – 4 денежных единицы, то
сколько полок каждого типа следует
выпускать в неделю, чтобы получить
максимальную прибыль?
Математическая модель

26.

Ответ
• Ответ: Чтобы получить максимальную
прибыль предприятию необходимо
производить 450 полок вида A и 100 полок
вида В, при этом прибыль составит 1750
ден. ед., а останется неиспользованными
1200 минут машинного времени.

27.

Числа Фибоначчи
На Западе эта последовательность была исследована Леонардо Пизанским,
известным как Фибоначчи, в его труде «Liber Abaci» (1202). Он рассматривает
развитие идеализированной (биологически нереальной) популяции кроликов,
предполагая, что: изначально есть новорожденная пара кроликов (самец и самка);
со второго месяца после своего рождения кролики начинают спариваться и
каждый месяц производить новую пару кроликов; кролики никогда не умирают.
Сколько пар кроликов будет через год?
В начале первого месяца есть только одна новорожденная пара (1).
В конце первого месяца по-прежнему только одна пара кроликов, но уже
спарившаяся (1)
В конце второго месяца первая пара рождает новую пару и опять спаривается (2)
В конце третьего месяца первая пара рождает ещё одну новую пару и
спаривается, вторая пара только спаривается (3)
В конце четвёртого месяца первая пара рождает ещё одну новую пару и
спаривается, вторая пара рождает новую пару и спаривается, третья пара только
спаривается (5)
В конце n-го месяца количество пар кроликов будет равно количеству пар в
предыдущем месяце плюс количество новорожденных пар, которых будет столько
же, сколько пар было два месяца назад. Таким образом:

28.

29.

30.

31.

Аксиомы геометрии
Аксиомы геометрии можно разбить на пять групп.
1. Аксиомы принадлежности
1.1 Какова бы ни была прямая, существуют точки, принадлежащие ей и не
принадлежащие ей.
1.2 Через любые две точки можно провести прямую и притом только одну.
1.3 Какова бы ни была плоскость, существуют точки, принадлежащие этой
плоскости и точки, не принадлежащие ей.
2. Аксиомы расположения
2.1 Из трех точек на прямой одна и только одна лежит между двумя другими.
2.2 Прямая разбивает плоскость на две полуплоскости.
2.3 Если две различные прямые имеют общую точку, то через них можно
провести плоскость и притом только одну.
2.4 Если две различные плоскости имеют общую точку, то они пересекаются
по прямой, проходящей через эту точку.

32.

Аксиомы геометрии
3. Аксиомы измерения
3.1 Каждый отрезок имеет определенную длину, большую нуля. Длина
отрезка равна сумме длин частей, на которые он разбивается любой его
точкой.
3.2 Каждый угол имеет определенную градусную меру, большую нуля.
Развернутый угол равен 180 градусам. Градусная мера угла равна сумме
градусных мер углов, на которые он разбивается любым лучом, проходящим
между его сторонами.
4. Аксиомы откладывания.
4.1 На любой полупрямой от ее начальной точки можно отложить отрезок
заданной длины и притом только один.
4.2 От любой полупрямой в заданную полуплоскость можно отложить угол, с
заданной градусной мерой, меньшей и притом только один.
4.3 Каков бы ни был треугольник, существует треугольник, равный ему, в
заданном расположении относительно данной полупрямой.
5. Аксиома параллельности.
5.1 Через точку, не лежащую на данной прямой можно провести не более
одной прямой, параллельной данной.