Similar presentations:
Эйлеровы и гамильтоновы графы
1.
Авторы: Кляпнева Ангелина (417 гр.)Семиков Алексей (419 гр.)
Научные руководители: Павлов Игорь Сергеевич
Харчева Анна Александровна
ННГУ им. Н.И. Лобачевского, радиофизический факультет,
Нижний Новгород, май 2021 г.
2.
В целях упрощения работы сСодержимое
презентации в
голосовым
сопровождением
В данной
презентации
будут
даны
большинстве
своём
будет
презентации в определенное время
определения автоматически
эйлеровым и
переключаться
в углу экрана будет появляться
гамильтоновым
а также
и не
спеша,графам,
поэтому
значок,
означающий,
что можно
усаживайтесь
поудобнее
и
описаны
их некоторые
особенности.
перейти
далее,
не оборвав
впитывайте
знания!
звуковой
ряд презентации.
3.
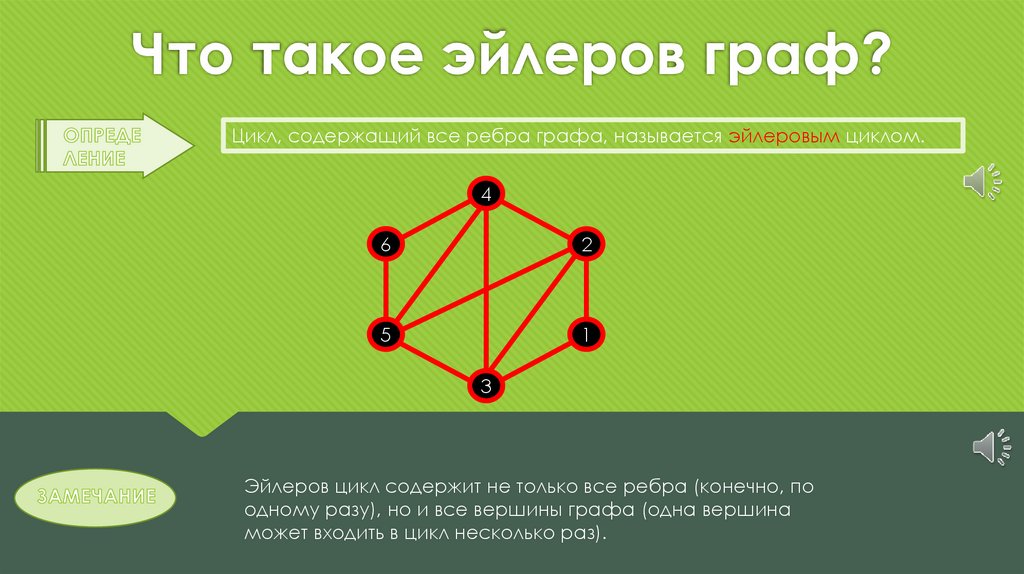
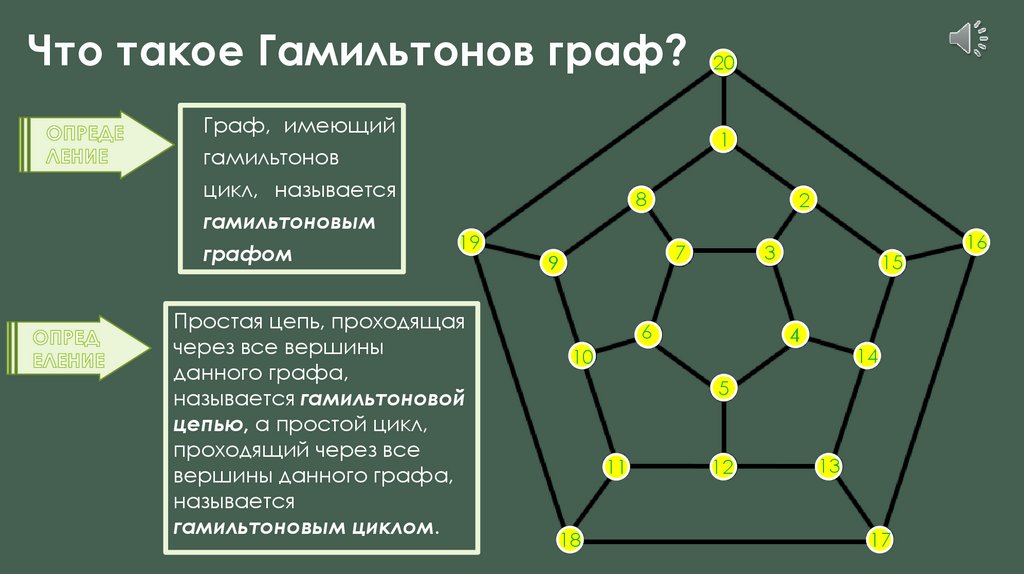
Что такое эйлеров граф?Цикл, содержащий все ребра графа, называется эйлеровым циклом.
4
6
2
5
1
3
Эйлеров цикл содержит не только все ребра (конечно, по
одному разу), но и все вершины графа (одна вершина
может входить в цикл несколько раз).
4.
Связный граф, в котором существует эйлеров цикл, называетсяэйлеровым графом.
Задача о кенигсбергских мостах
C
B
A
D
5.
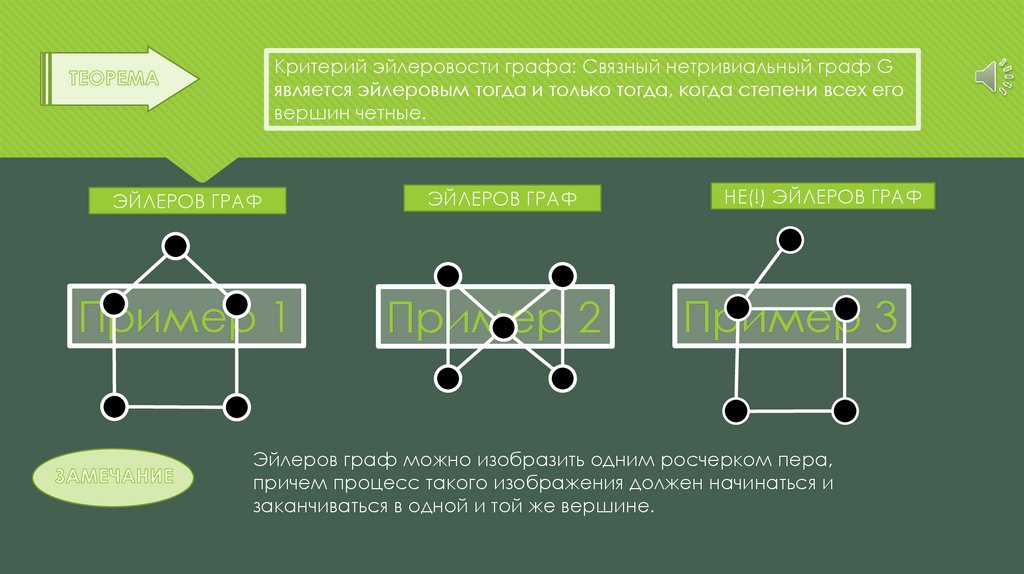
Критерий эйлеровости графа: Связный нетривиальный граф Gявляется эйлеровым тогда и только тогда, когда степени всех его
вершин четные.
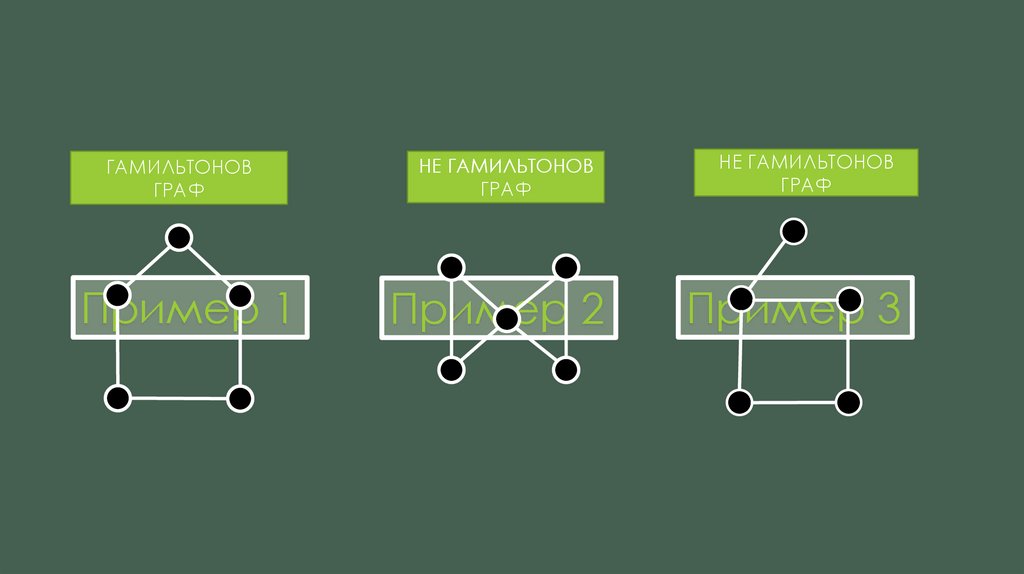
ЭЙЛЕРОВ ГРАФ
Пример 1
ЭЙЛЕРОВ ГРАФ
Пример 2
НЕ(!) ЭЙЛЕРОВ ГРАФ
Пример 3
Эйлеров граф можно изобразить одним росчерком пера,
причем процесс такого изображения должен начинаться и
заканчиваться в одной и той же вершине.
6.
Последнее условие (процесс такого изображения должен начинаться изаканчиваться в одной и той же вершине) чрезвычайно важное, его
несоблюдение приводит к ошибочному увеличению числа эйлеровых графов.
7.
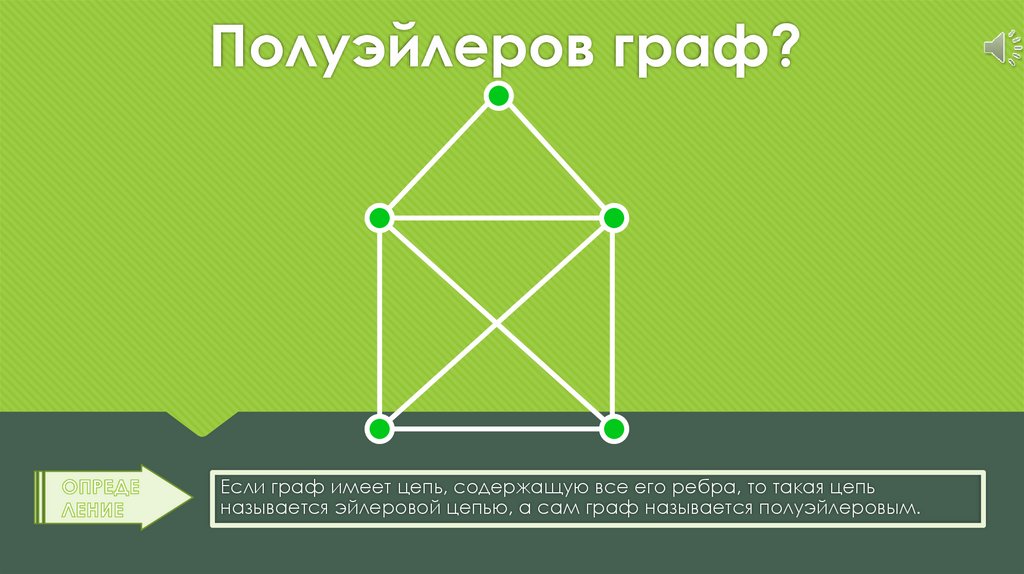
Полуэйлеров граф?Если граф имеет цепь, содержащую все его ребра, то такая цепь
называется эйлеровой цепью, а сам граф называется полуэйлеровым.
8.
Критерий полуэйлеровости графа: Cвязный граф Gобладает эйлеровой цепью в том и только том случае,
если он имеет ровно 2 вершины нечетной степени.
Теорема об оценке числа эйлеровых графов:
Э(р)
lim
= 0, где G(р) – множество всех графов с р










 mathematics
mathematics








