Оценка параметров местного геохимического фона и определение минимально аномальных содержаний

1.

Оценка параметров местного геохимического фона и
определение минимально аномальных содержаний

2.

Оценка параметров местного геохимического фона и
определение минимально аномальных содержаний
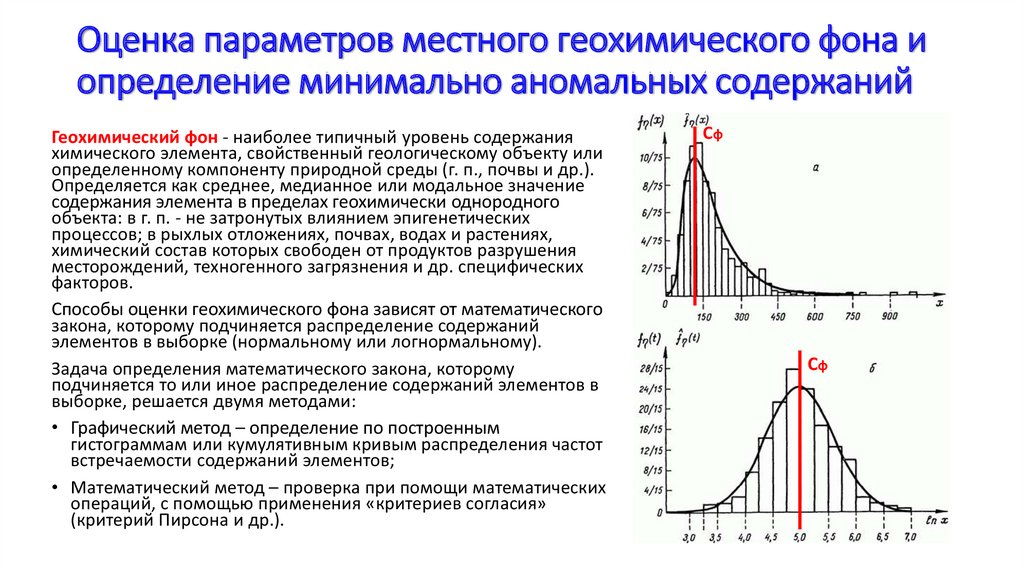
Геохимический фон - наиболее типичный уровень содержания
химического элемента, свойственный геологическому объекту или
определенному компоненту природной среды (г. п., почвы и др.).
Определяется как среднее, медианное или модальное значение
содержания элемента в пределах геохимически однородного
объекта: в г. п. - не затронутых влиянием эпигенетических
процессов; в рыхлых отложениях, почвах, водах и растениях,
химический состав которых свободен от продуктов разрушения
месторождений, техногенного загрязнения и др. специфических
факторов.
Способы оценки геохимического фона зависят от математического
закона, которому подчиняется распределение содержаний
элементов в выборке (нормальному или логнормальному).
Задача определения математического закона, которому
подчиняется то или иное распределение содержаний элементов в
выборке, решается двумя методами:
• Графический метод – определение по построенным
гистограммам или кумулятивным кривым распределения частот
встречаемости содержаний элементов;
• Математический метод – проверка при помощи математических
операций, с помощью применения «критериев согласия»
(критерий Пирсона и др.).
Сф
Сф

3.

Оценка параметров местного геохимического фона и
определение минимально аномальных содержаний
Минимально аномальное содержание элемента – нижнее значение
вероятных аномалий для одиночных (изолированных) точек с
повышенным содержанием элементов. В зависимости от закона
распределения принимается величина:
Са = Сф + 3S – норм. закон распределения
Са = Сф + 3ɛ – логнорм. закон распределения
Где S – стандартное отклонение, ɛ - стандартный множитель
В этих пределах с вероятностью 99,86 % лежат значения фоновых содержаний
элементов, поэтому вероятность ошибочного отнесения к числу аномалий точек,
характеризующихся только случайным колебаниями фона, очень мала.

4.

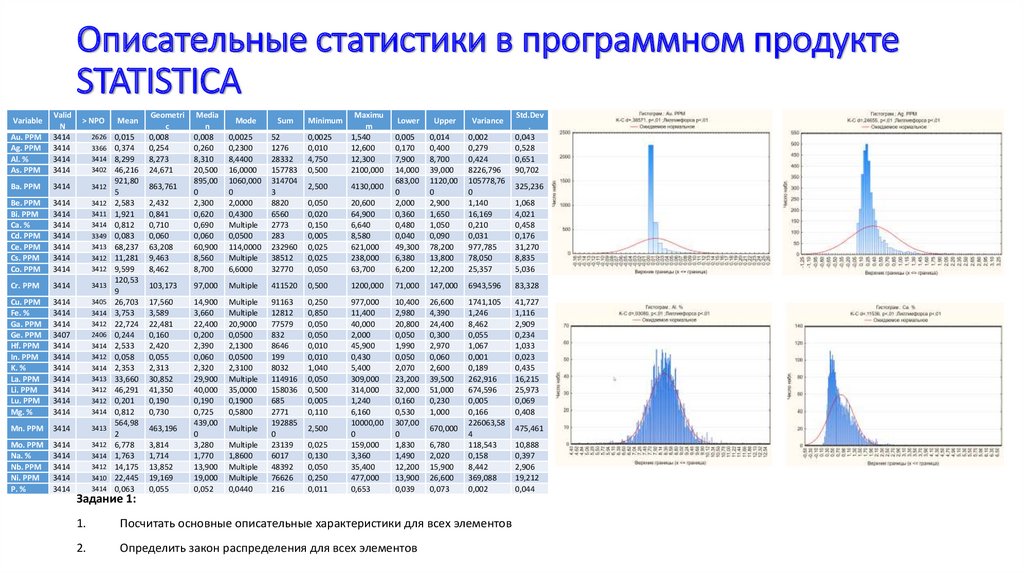
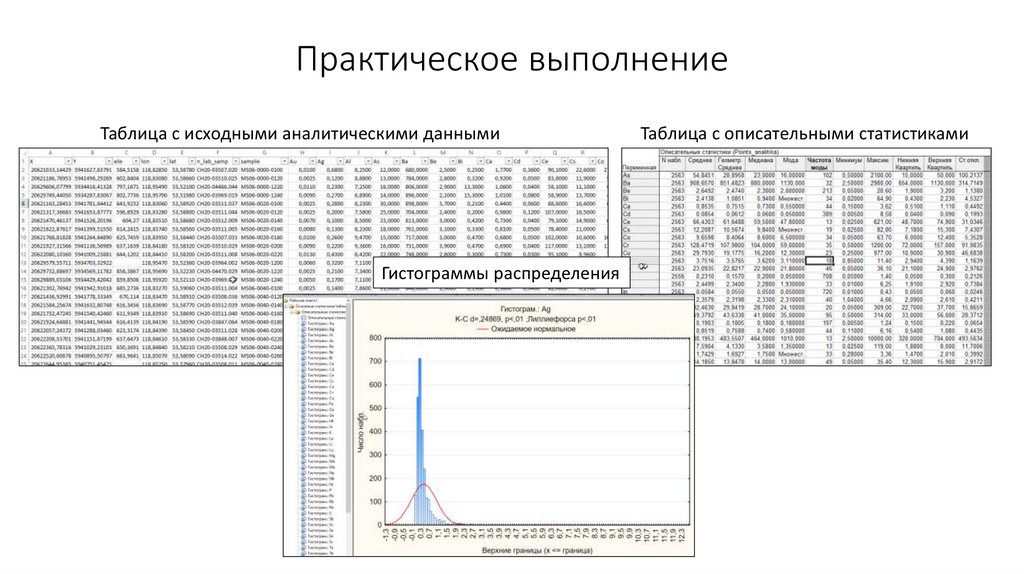
Описательные статистики в программном продукте
STATISTICA
Au. PPM
Ag. PPM
Al. %
As. PPM
Valid
N
3414
3414
3414
3414
Ba. PPM
3414
3412
Be. PPM
Bi. PPM
Ca. %
Cd. PPM
Ce. PPM
Cs. PPM
Co. PPM
3414
3414
3414
3414
3414
3414
3414
3412
3411
3414
3349
3413
3412
3412
Cr. PPM
3414
3413
Cu. PPM
Fe. %
Ga. PPM
Ge. PPM
Hf. PPM
In. PPM
K. %
La. PPM
Li. PPM
Lu. PPM
Mg. %
3414
3414
3414
3407
3414
3414
3414
3414
3414
3414
3414
3405
3414
3412
2406
3414
3412
3414
3413
3412
3412
3414
Mn. PPM
3414
3413
Mo. PPM
Na. %
Nb. PPM
Ni. PPM
P. %
3414
3414
3414
3414
3414
3412
3414
3412
3410
3414
Variable
> NPO
Mean
2626
3366
3414
3402
0,015
0,374
8,299
46,216
921,80
5
2,583
1,921
0,812
0,083
68,237
11,281
9,599
120,53
9
26,703
3,753
22,724
0,244
2,533
0,058
2,353
33,660
46,291
0,201
0,812
564,98
2
6,778
1,763
14,175
22,445
0,063
Задание 1:
Geometri
c
0,008
0,254
8,273
24,671
Mode
Sum
0,0025
0,2300
8,4400
16,0000
1060,000
0
2,0000
0,4300
Multiple
0,0500
114,0000
Multiple
6,6000
52
1276
28332
157783
314704
3
8820
6560
2773
283
232960
38512
32770
0,0025
0,010
4,750
0,500
Maximu
m
1,540
12,600
12,300
2100,000
2,500
4130,000
2,432
0,841
0,710
0,060
63,208
9,463
8,462
Media
n
0,008
0,260
8,310
20,500
895,00
0
2,300
0,620
0,690
0,060
60,900
8,560
8,700
0,050
0,020
0,150
0,005
0,025
0,025
0,050
103,173
97,000
Multiple
411520
17,560
3,589
22,481
0,160
2,420
0,055
2,313
30,852
41,350
0,190
0,730
14,900
3,660
22,400
0,200
2,390
0,060
2,320
29,900
40,000
0,190
0,725
439,00
0
3,280
1,770
13,900
19,000
0,052
Multiple
Multiple
20,9000
0,0500
2,1300
0,0500
2,3100
Multiple
35,0000
0,1900
0,5800
91163
12812
77579
832
8646
199
8032
114916
158036
685
2771
192885
0
23139
6017
48392
76626
216
863,761
463,196
3,814
1,714
13,852
19,169
0,055
Multiple
Multiple
1,8600
Multiple
Multiple
0,0440
Minimum
Std.Dev
.
0,043
0,528
0,651
90,702
Lower
Upper
Variance
20,600
64,900
6,640
8,580
621,000
238,000
63,700
0,005
0,170
7,900
14,000
683,00
0
2,000
0,360
0,480
0,040
49,300
6,380
6,200
0,014
0,400
8,700
39,000
1120,00
0
2,900
1,650
1,050
0,090
78,200
13,800
12,200
0,002
0,279
0,424
8226,796
105778,76
0
1,140
16,169
0,210
0,031
977,785
78,050
25,357
0,500
1200,000
71,000
147,000
6943,596
83,328
0,250
0,850
0,050
0,050
0,010
0,010
1,040
0,050
0,500
0,005
0,110
977,000
11,400
40,000
2,000
45,900
0,430
5,400
309,000
314,000
1,240
6,160
10000,00
0
159,000
3,360
35,400
477,000
0,653
10,400
2,980
20,800
0,050
1,990
0,050
2,070
23,200
32,000
0,160
0,530
307,00
0
1,830
1,490
12,200
13,900
0,039
26,600
4,390
24,400
0,300
2,970
0,060
2,600
39,500
51,000
0,230
1,000
1741,105
1,246
8,462
0,055
1,067
0,001
0,189
262,916
674,596
0,005
0,166
226063,58
4
118,543
0,158
8,442
369,088
0,002
41,727
1,116
2,909
0,234
1,033
0,023
0,435
16,215
25,973
0,069
0,408
2,500
0,025
0,130
0,050
0,250
0,011
670,000
6,780
2,020
15,900
26,600
0,073
1.
Посчитать основные описательные характеристики для всех элементов
2.
Определить закон распределения для всех элементов
325,236
1,068
4,021
0,458
0,176
31,270
8,835
5,036
475,461
10,888
0,397
2,906
19,212
0,044

5.

Описательные статистики в программном продукте
STATISTICA
Исходные данные:
Таблица точек литогеохимического опробования с данными аналитических
исследований.
Таблица, содержащая пределы обнаружения аналитического метода для
каждого элемента

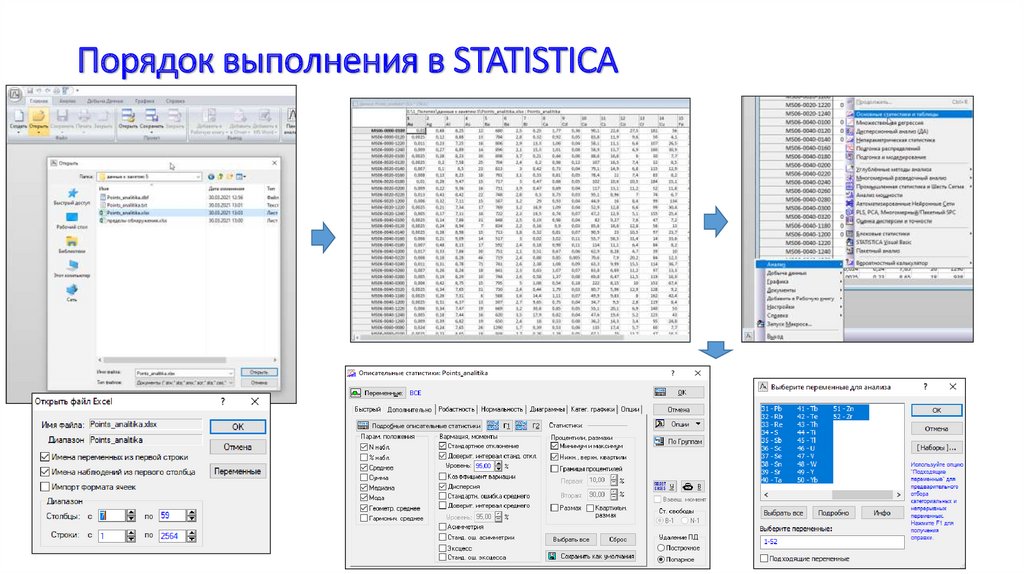
6.

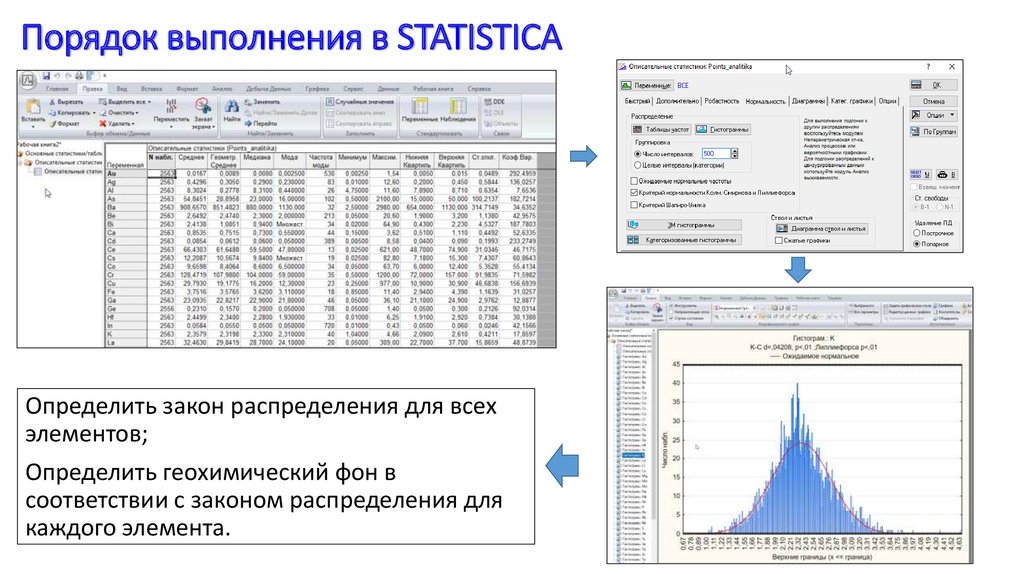
Порядок выполнения в STATISTICA

7.

Порядок выполнения в STATISTICA
Определить закон распределения для всех
элементов;
Определить геохимический фон в
соответствии с законом распределения для
каждого элемента.

8.

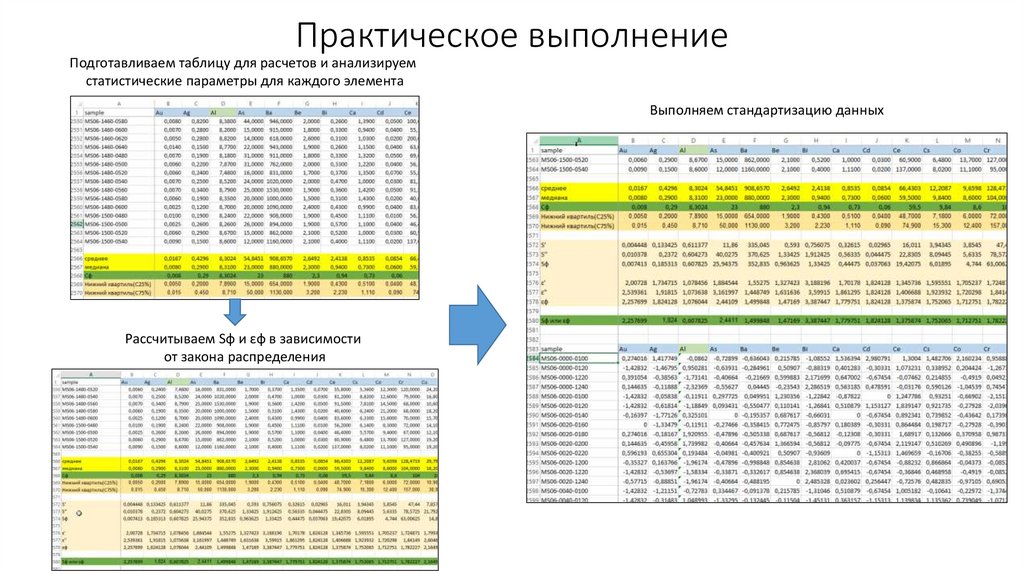
Робастная оценка Sф
Робастная оценка Sф производится по квартилям распределения,
соответствующим 25% (С25%) и 75% (С75%) накопленной частоты.
По левой и правой ветвям центральной части распределения могут быть
вычислены две оценки Sф:
S΄ф = 1.4825 х (Сф-С25%),
S΄΄ф= 1.4825 х (С75%-Сф).
Если оба значения близки по величине, следует взять среднее значение
из них:
Sф = 0.5 х (S΄ф + S΄΄ф).
Если же два значения существенно различаются и есть подозрение, что
какое-то из них определено ненадежно или не вполне соответствует
фоновой совокупности данных, то в качестве Sф лучше взять одно, более
надежное значение.

9.

Робастная оценка εф
Робастная оценка εф по квартилям распределения производится
по формулам:
ε’ф = (Сф/С25%)1.4825
ε’’ф = (С75%/Сф)1.4825
Если оба значения близки по величине, следует взять среднее
геометрическое значение из них: