3D преобразования

1.

3D преобразования
1

2.

Системы координат
• Системы координат используемые в
графике
– Координаты экрана: физическое местоположение
на определенном устройстве вывода
(отображения)
– Координаты окна: экранные координаты
относительно центра окна
– Нормализованные координаты устройства
(NDC): независимая от устройства абстракция
окна экрана
– Мировые координаты: родовая система
координат, которую может использовать любое
приложение, чтобы определить объекты для
показа
2

3.

Экранные координаты
• Физические координаты устройства
– Местоположение пикселей
– Sx Х Sy pixels
• 640x480, 1024x768,
1280x800, 1440x900,
др.
• Изменения трудны для
прикладной программы;
• приводит к зависимому
от устройства коду
3

4.

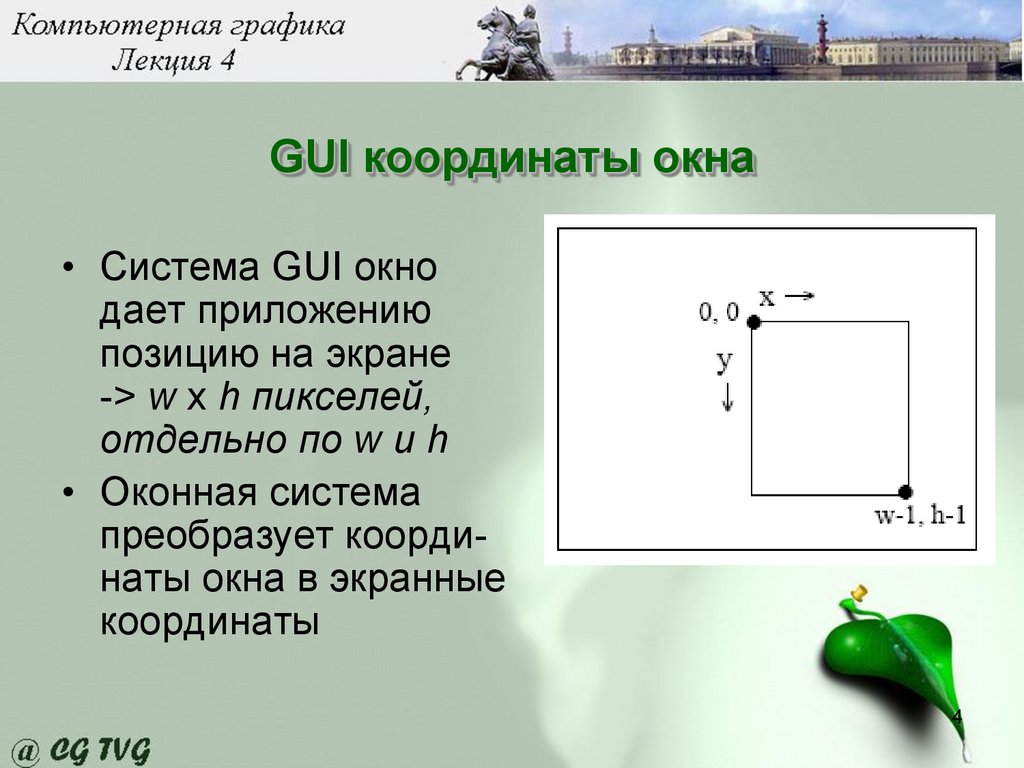
GUI координаты окна
• Система GUI окно
дает приложению
позицию на экране
-> w x h пикселей,
отдельно по w и h
• Оконная система
преобразует координаты окна в экранные
координаты
4

5.

Нормализованные координаты
• Абстракция координат
устройства вывода (экран
и/или GUI окна)
• Значение координат
вещественные с
плавающей запятой
( от 0 до 1)
• Ось Y направлена вверх
5

6.

Мировые координаты
• Приложение должно быть в состоянии
определить объекты в форму, естественную
для области:
– От 0 до 100 м для плана экспозиции дома
– От 0 до 10000 км для карты России
– и т.д.
• Мировые координаты - просто 2 D или 3D
значение с плавающей точкой, которые
могут представить местоположения и
размеры объекта, который будет показан
6

7.

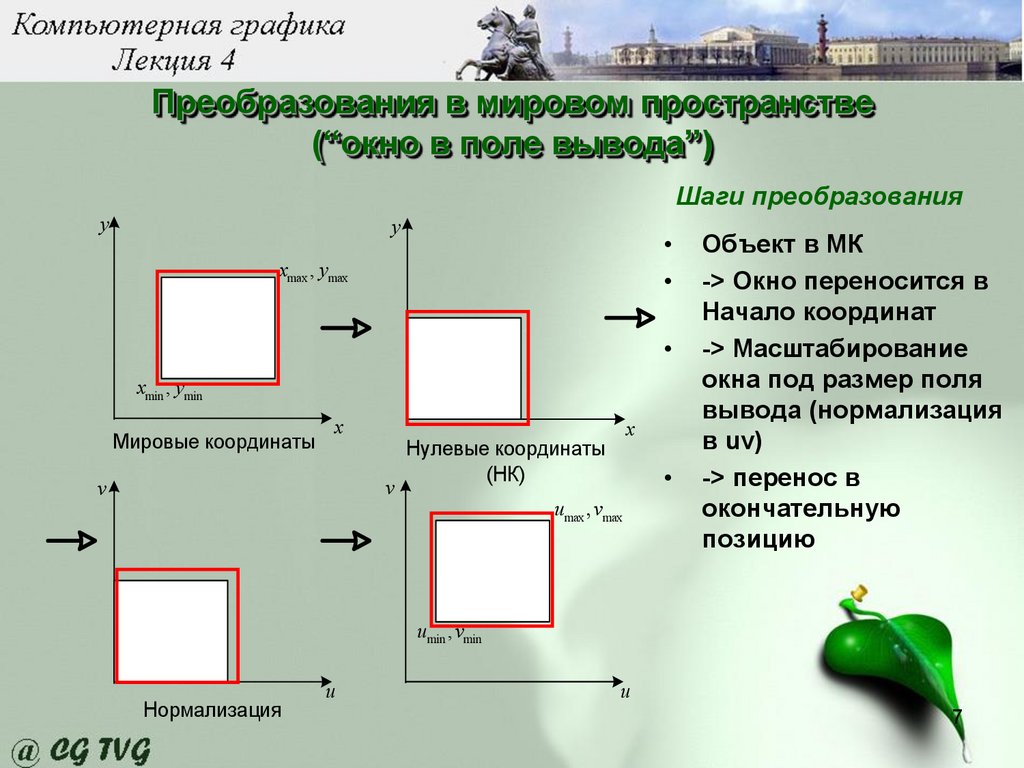
Преобразования в мировом пространстве
(“окно в поле вывода”)
Шаги преобразования
y
y
xmax , ymax
xmin , ymin
Мировые координаты
x
v
v
x
Нулевые координаты
(НК)
umax , vmax
Объект в МК
-> Окно переносится в
Начало координат
-> Масштабирование
окна под размер поля
вывода (нормализация
в uv)
-> перенос в
окончательную
позицию
umin , vmin
Нормализация
u
u
7

8.

Использование нормализованных координат
Подобно тому, как двумерные преобразования описываются матрицами
размером , трехмерные преобразования могут быть представлены матрицами
размером .
Тогда трехмерная точка в трехмерном пространстве P(x, y, z) представится
четырехмерным вектором [x y z 1] или [X Y Z W].
Преобразования из однородных координат описываются соотношениями:
[X Y Z W]=[x y z 1]*Т и [x' y' z' 1]=[X/W Y/W Z/W 1],
где Т- некоторая матрица преобразования. Обобщенная матрица
преобразования 4х4 для трехмерных координат имеет вид
a b
d e
T =
h i
l m
c
f
j
n
p
q
.
r
s
Эта матрица может быть представлена в виде четырех отдельных частей:
3 3 3 1
1 3 1 1
Матрица 3х3 осуществляет линейное преобразование в виде изменения
масштаба, сдвига и вращения. Матрица-строка 1х3 производит
перенос, а матрица-столбец 3х1 – преобразование в перспективе.
Последний скалярный элемент выполняет общее изменение масштаба.
8

9.

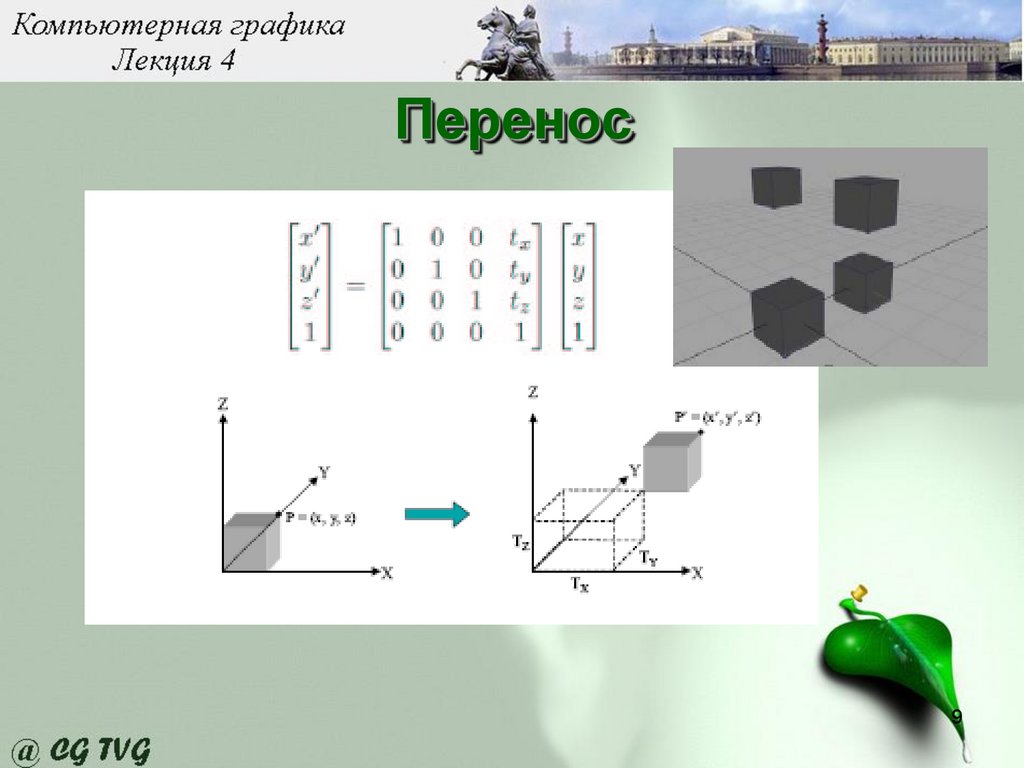
Перенос
9

10.

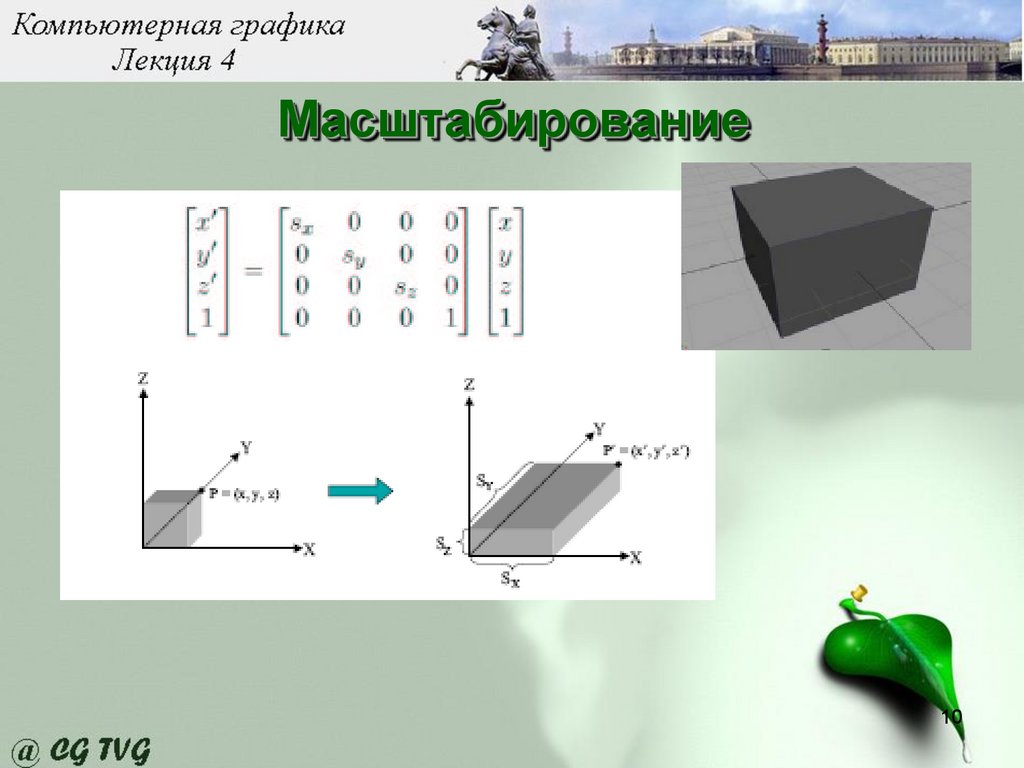
Масштабирование
10

11.

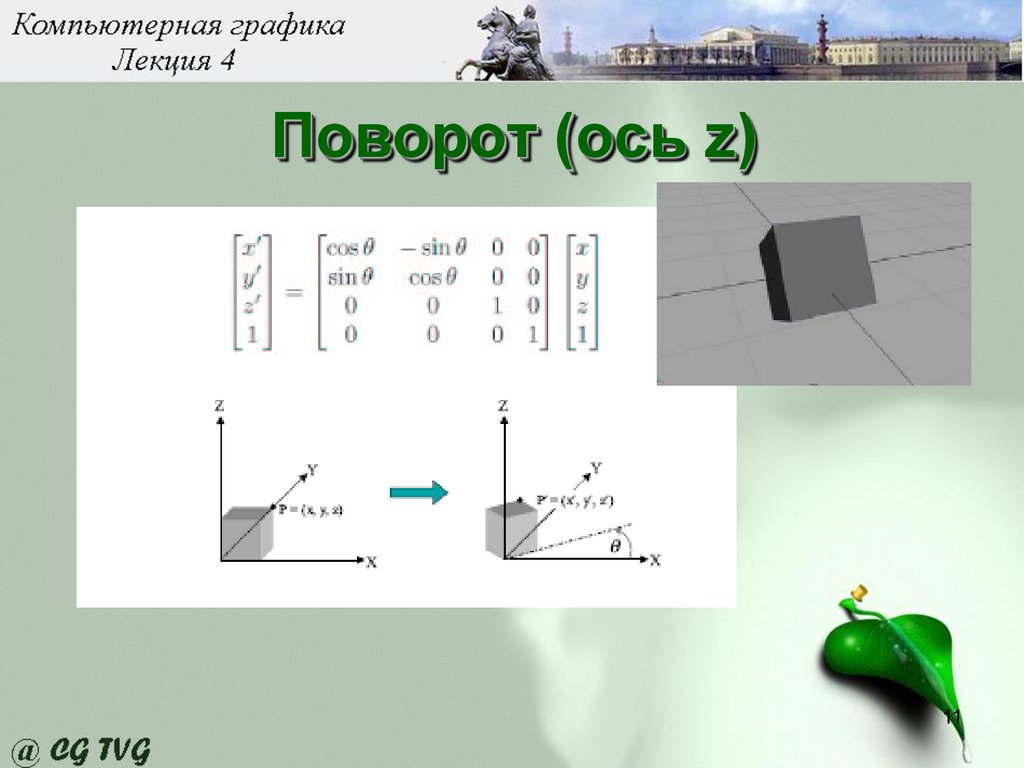
Поворот (ось z)
11

12.

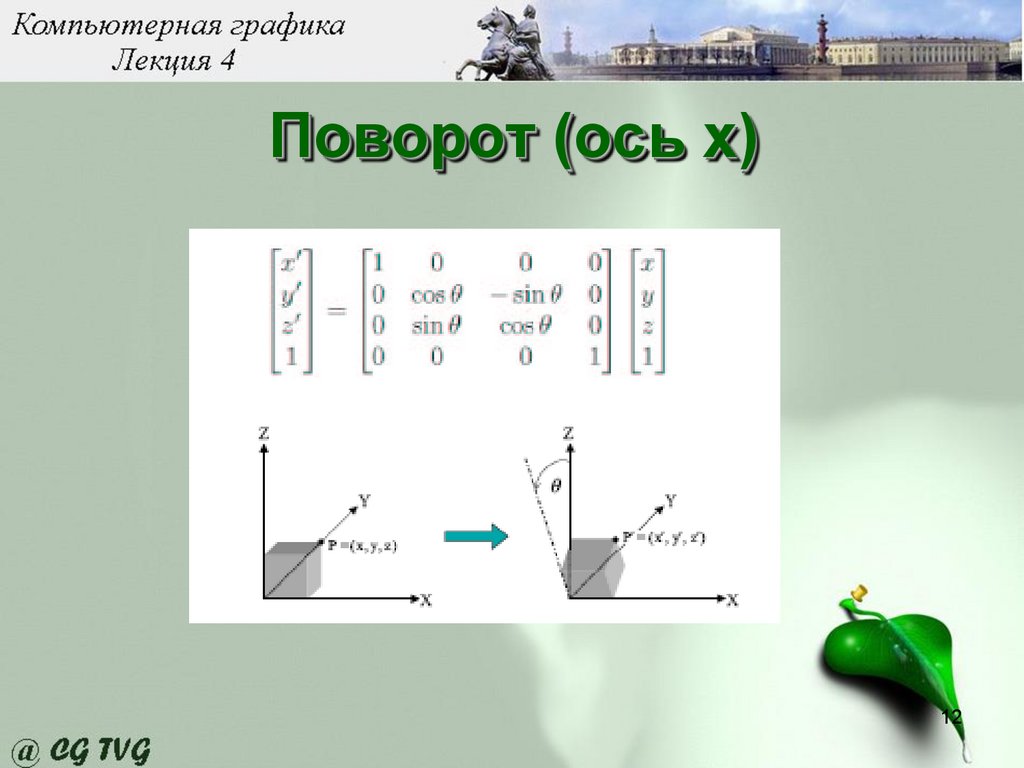
Поворот (ось х)
12

13.

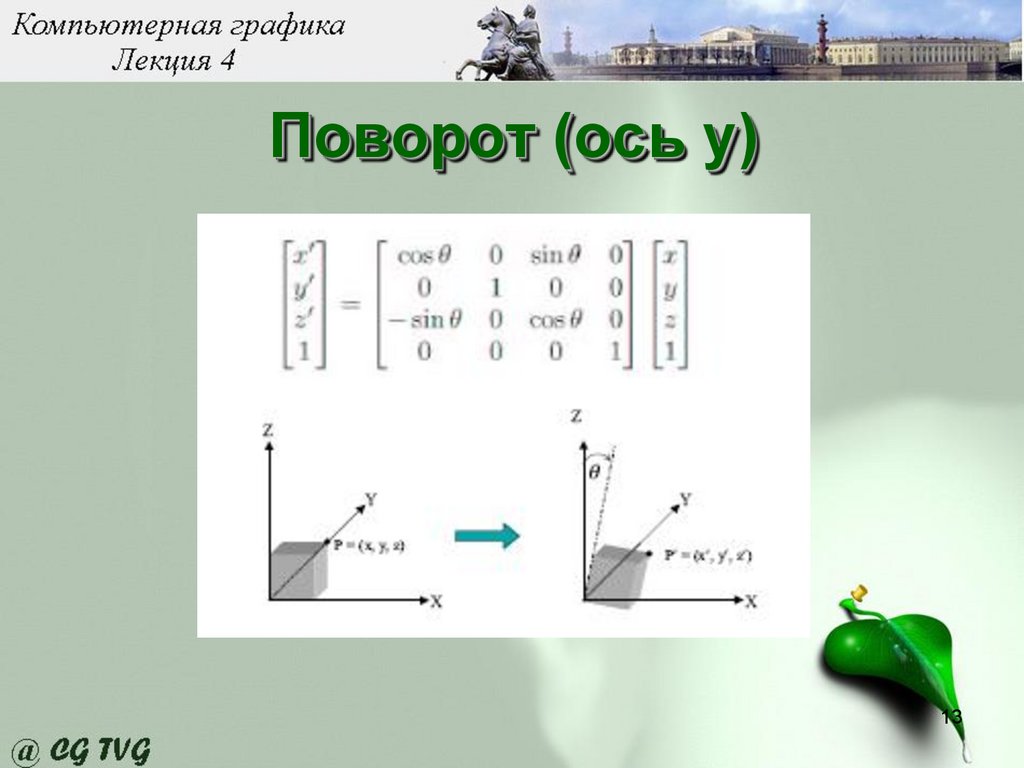
Поворот (ось у)
13

14.

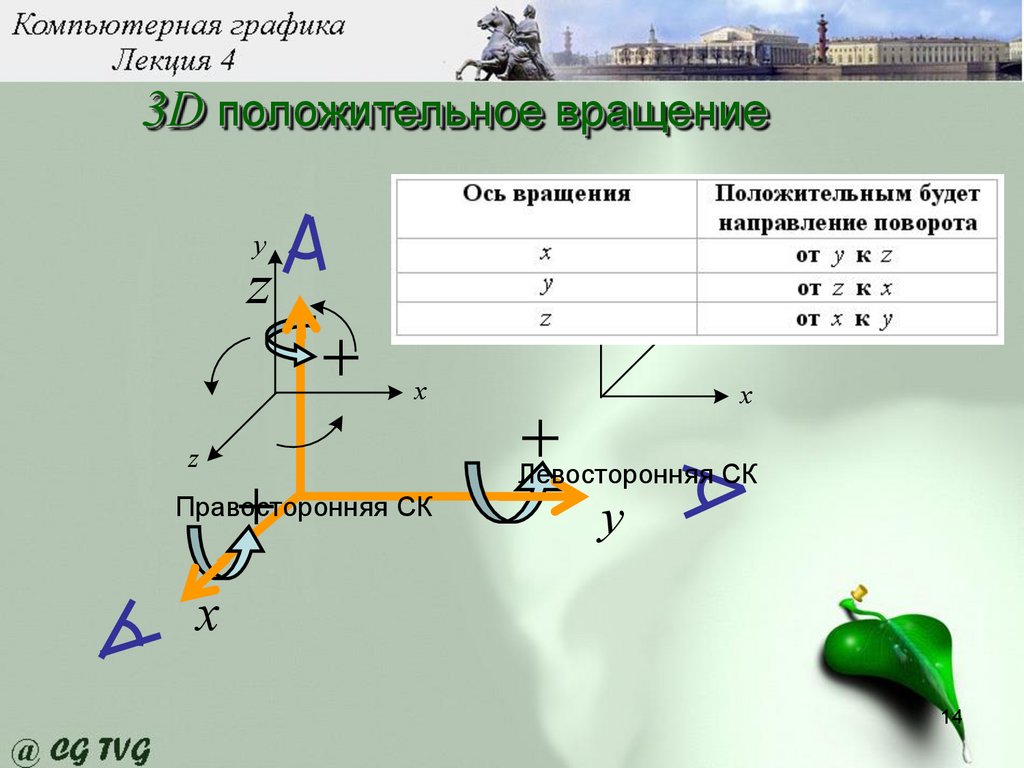
3D положительное вращение
y
z
z
+
y
+
z
x
Правосторонняя СК
+
x
Левосторонняя СК
y
x
14

15.

• Композиция трёхмерных преобразований
1
0
0
0
0
1
0
0
0 dx cos
0 dy sin
1 dz 0
0 1 0
Sx
0
= [ x y z 1]
0
0
0
Sy
0
0
− sin
cos
0
0
0
0
Sz
0
0
0
1
0
0 cos
0 sin
0 0
1 0
0
0
0
1
Sx
0
0
0
0
Sy
0
0
− sin
cos
0
0
0
0
Sz
0
0
0
1
0
0
0
0
1
0
0
0
1
x
y
=
z
1
1
0
0
0
0
1
0
0
0 dx
0 dy
1 dz
0 1
15

16.

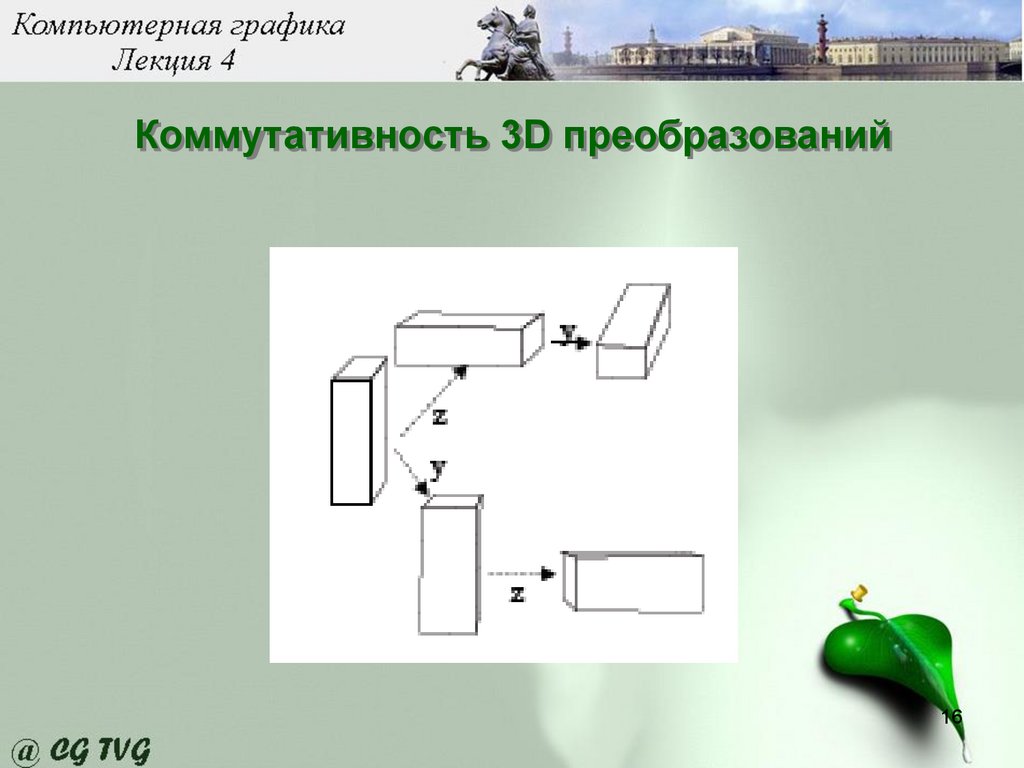
Коммутативность 3D преобразований
16

17.

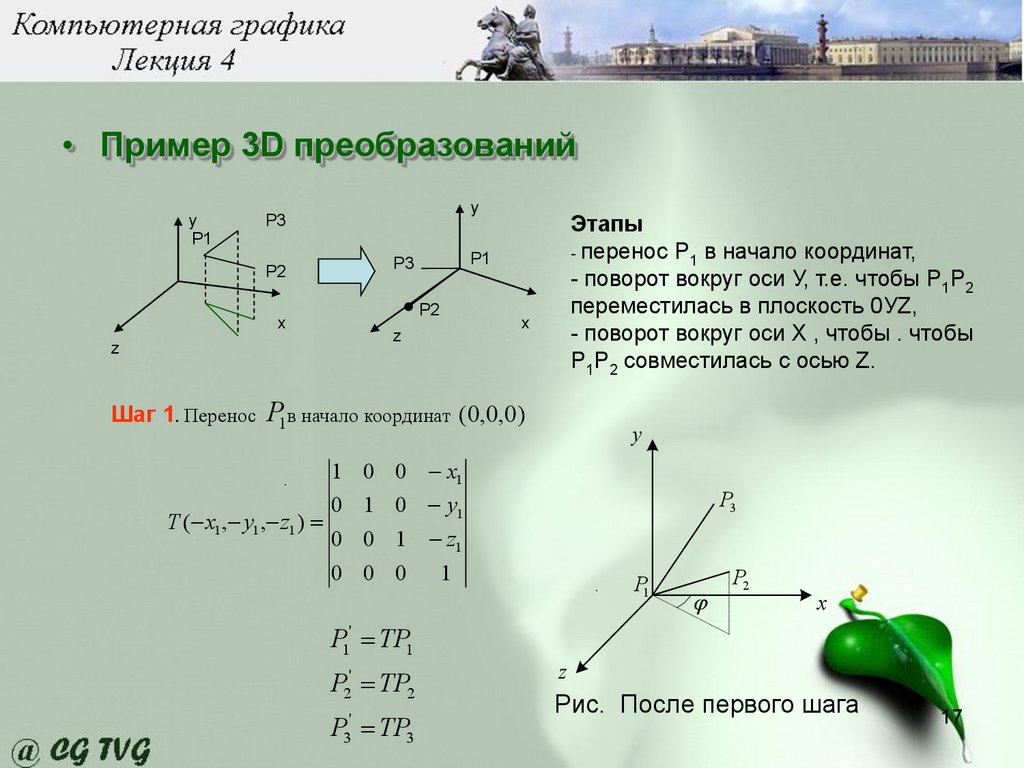
• Пример 3D преобразований
у
P1
у
P3
P2
x
z
z
Шаг 1. Перенос
P1
P3
P2
Этапы
- перенос Р1 в начало координат,
- поворот вокруг оси У, т.е. чтобы Р1Р2
переместилась в плоскость 0УZ,
- поворот вокруг оси Х , чтобы . чтобы
Р1Р2 совместилась с осью Z.
x
P1в начало координат (0,0,0)
1
0
T (− x1 ,− y1 ,− z1 ) =
0
0
0
1
0
0
.
y
0 − x1
0 − y1
1 − z1
0 1
P3
.
P1
P2
x
P1' = TP1
P2' = TP2
P = TP3
'
3
z
Рис. После первого шага
17

18.

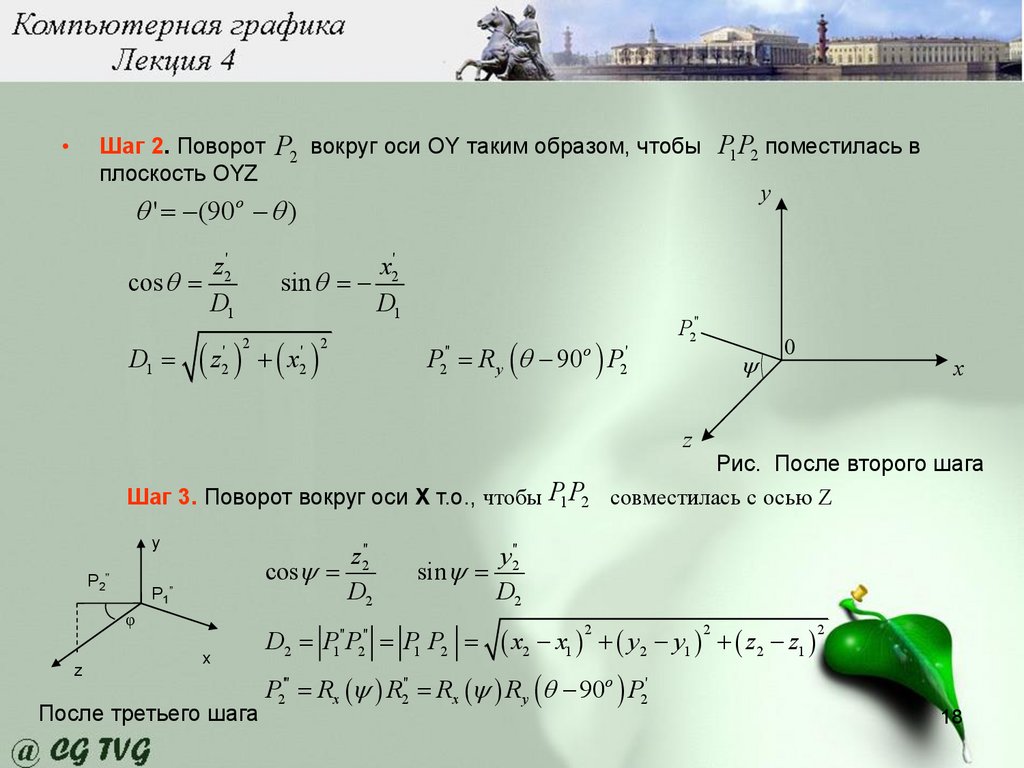
Шаг 2. Поворот
плоскость OYZ
P2
вокруг оси OY таким образом, чтобы
P1P2 поместилась в
y
' = −(90o − )
z2'
cos =
D1
D1 =
x2'
sin = −
D1
( z2' ) + ( x2' )
2
2
P2'' = Ry ( − 90o ) P2'
P2''
0
x
z
Шаг 3. Поворот вокруг оси Х т.о., чтобы
у
P2’’
z2''
cos =
D2
P1”
φ
z
x
После третьего шага
P1P2
Рис. После второго шага
совместилась с осью Z
y2''
sin =
D2
( x2 − x1 ) + ( y2 − y1 ) + ( z2 − z1 )
P2''' = Rx ( ) R2'' = Rx ( ) Ry ( − 90o ) P2'
D2 = P1'' P2'' = P1 P2 =
2
2
2
18

19.

19

20.

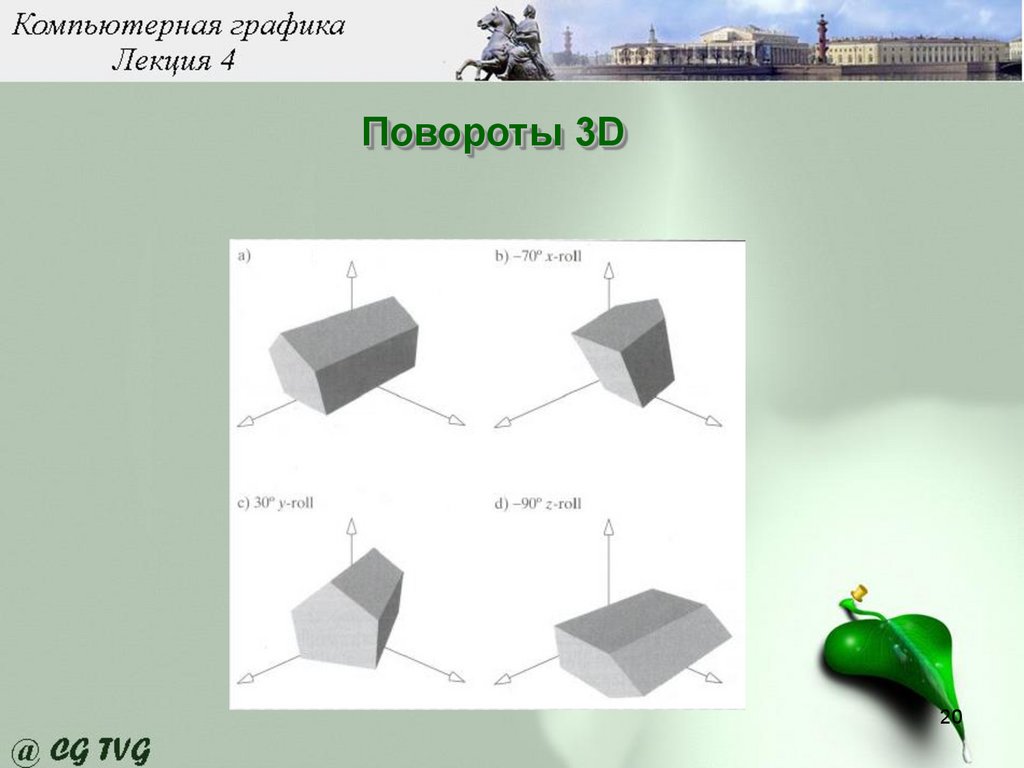
Повороты 3D
20

21.

Трехмерное вращение вокруг произвольной оси
• Классика: используйте
теорему Эйлера
• теорема Эйлера: любая
последовательность
вращений = одно вращение
вокруг некоторой оси
• Наш подход:
– Хотим вращать на β вокруг
оси u через НК и
произвольной точки
– Используем два вращения,
чтобы выровнять u и ось X
– Делаем x-поворот через угол
β
– Два обратных предыдущих
вращения, чтобы девыровнять
u и ось X
Ru(β) = Ry(- )Rz(φ)Rx(β)Rz(-φ)Ry( )
21

22.

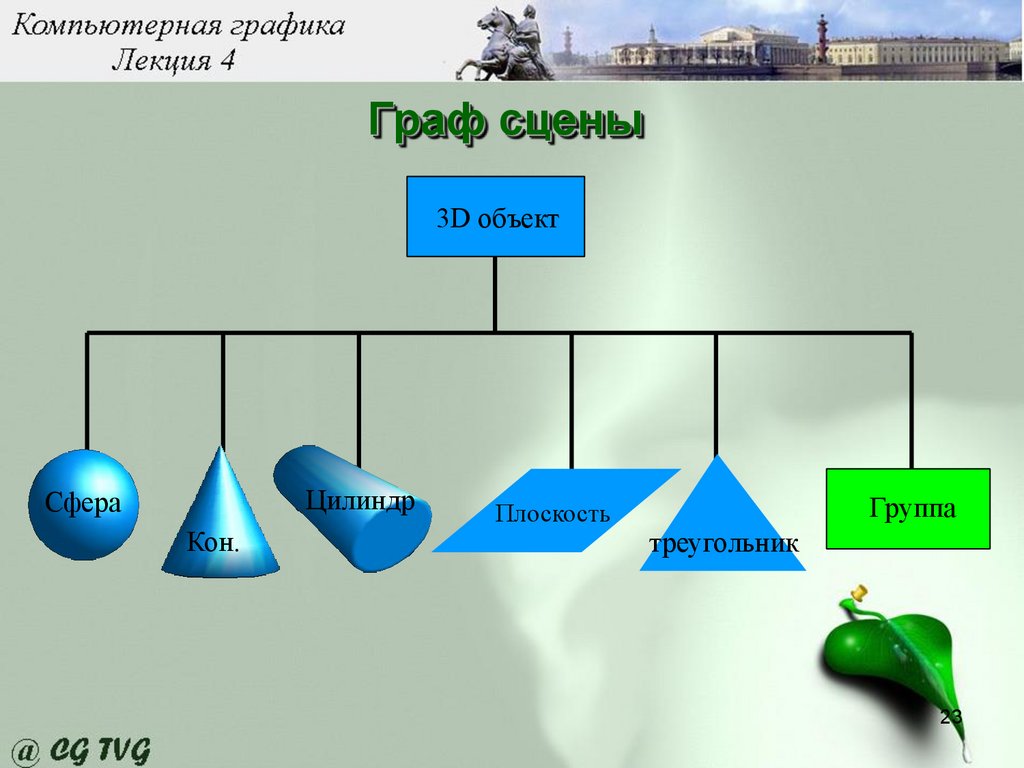
• 3D сцены часто хранятся сохраненный в
направленном ациклическом графе (DAG)
называемый граф сцены
– Open Scene Graph (используемый в Cave)
– Sun’s Java3D™
– X3D ™ (VRML ™ предвестник X3D)
• Обычно граф сцены состоит из:
– oбъекты (кубы, сферы, конусы,
многогранники др.)
– сохраняются как узлы
– aтрибуты (цвет, текстурные карты, др.) и
– преобразования также узлы в графе сцены
22

23.

Граф сцены
3D объект
Цилиндр
Сфера
Кон.
Плоскость
Группа
треугольник
23

24.

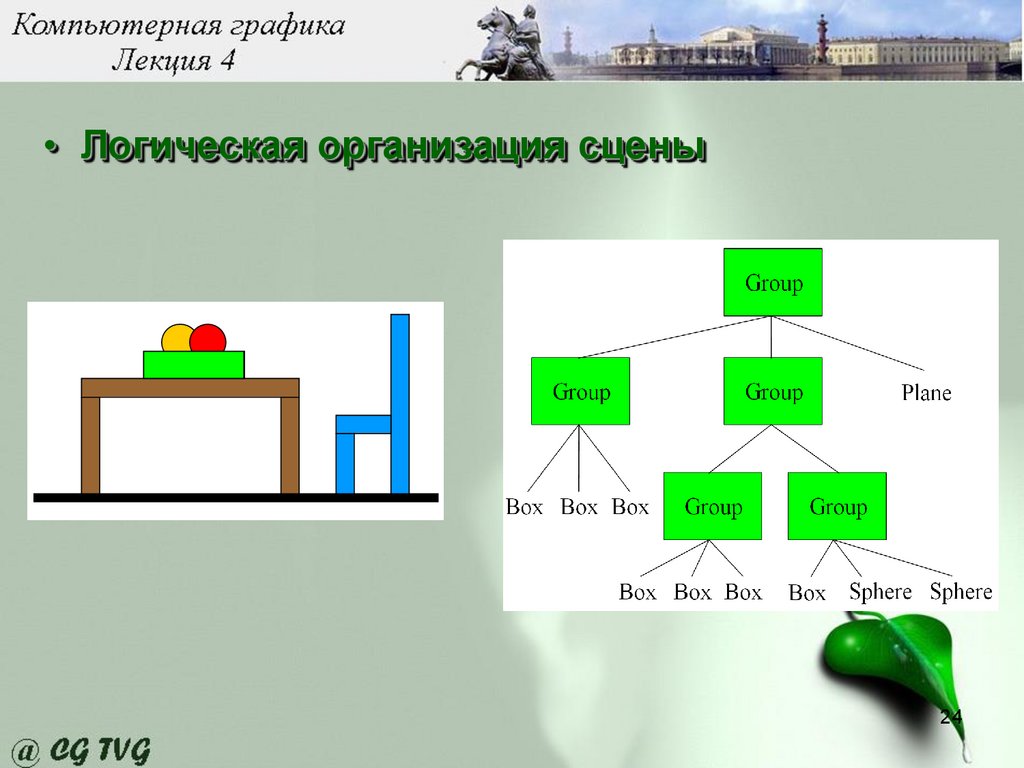
• Логическая организация сцены
24

25.

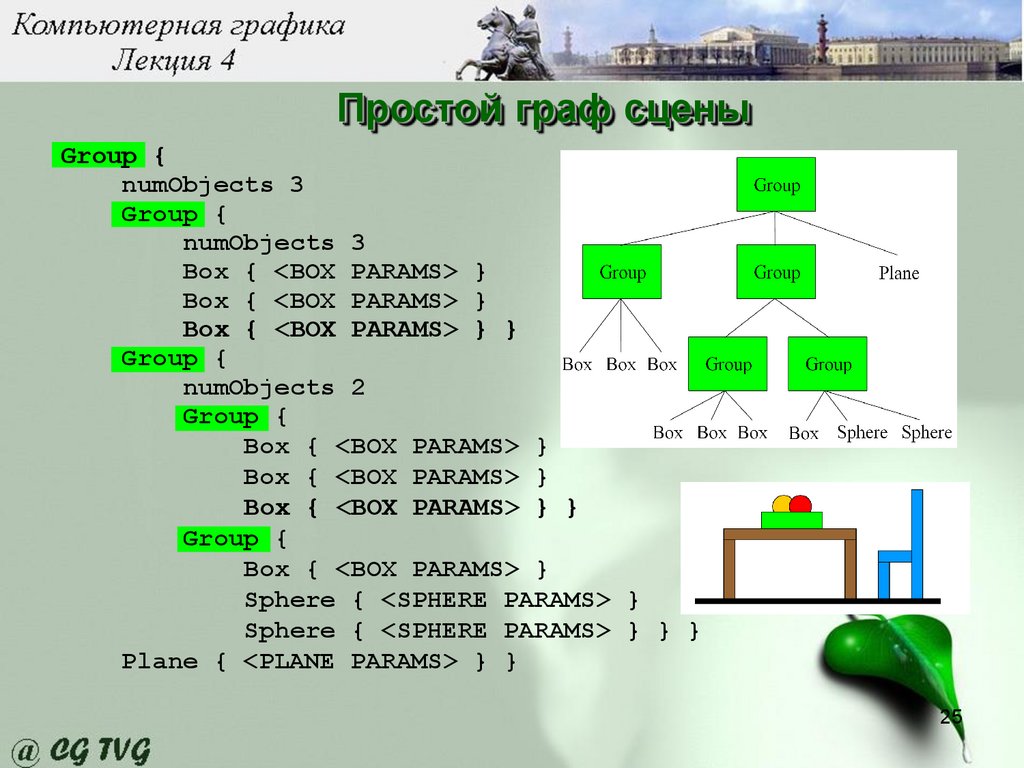
Простой граф сцены
Group {
numObjects 3
Group {
numObjects 3
Box { <BOX PARAMS> }
Box { <BOX PARAMS> }
Box { <BOX PARAMS> } }
Group {
numObjects 2
Group {
Box { <BOX PARAMS> }
Box { <BOX PARAMS> }
Box { <BOX PARAMS> } }
Group {
Box { <BOX PARAMS> }
Sphere { <SPHERE PARAMS> }
Sphere { <SPHERE PARAMS> } } }
Plane { <PLANE PARAMS> } }
25

26.

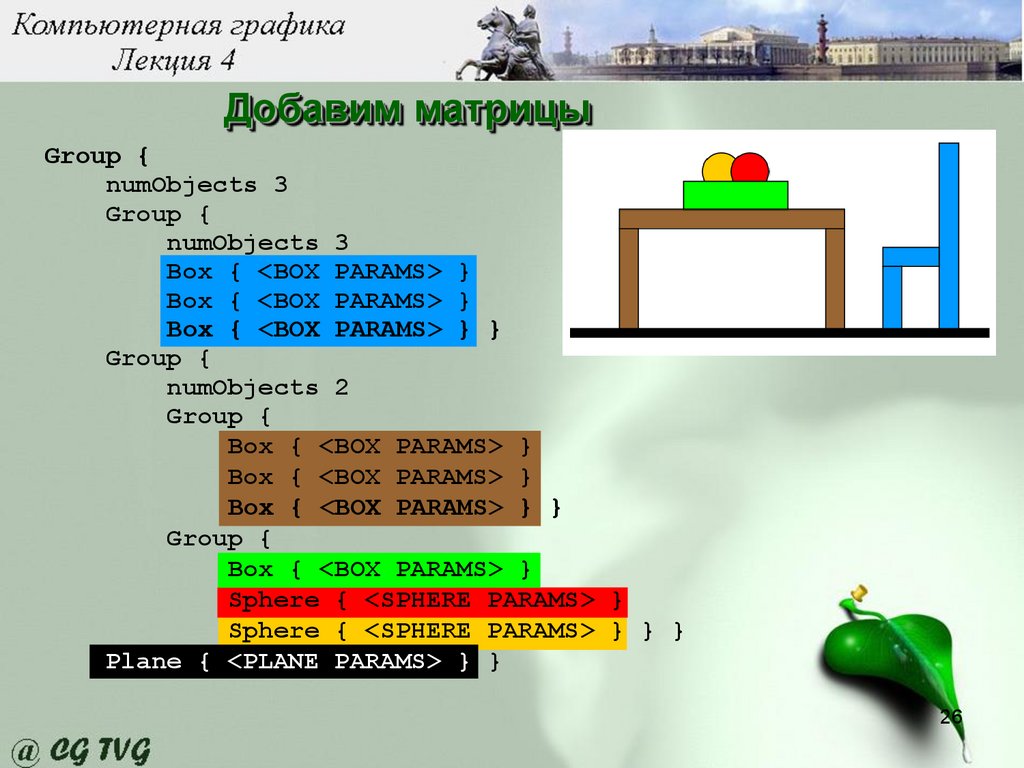
Добавим матрицы
Group {
numObjects 3
Group {
numObjects 3
Box { <BOX PARAMS> }
Box { <BOX PARAMS> }
Box { <BOX PARAMS> } }
Group {
numObjects 2
Group {
Box { <BOX PARAMS> }
Box { <BOX PARAMS> }
Box { <BOX PARAMS> } }
Group {
Box { <BOX PARAMS> }
Sphere { <SPHERE PARAMS> }
Sphere { <SPHERE PARAMS> } } }
Plane { <PLANE PARAMS> } }
26

27.

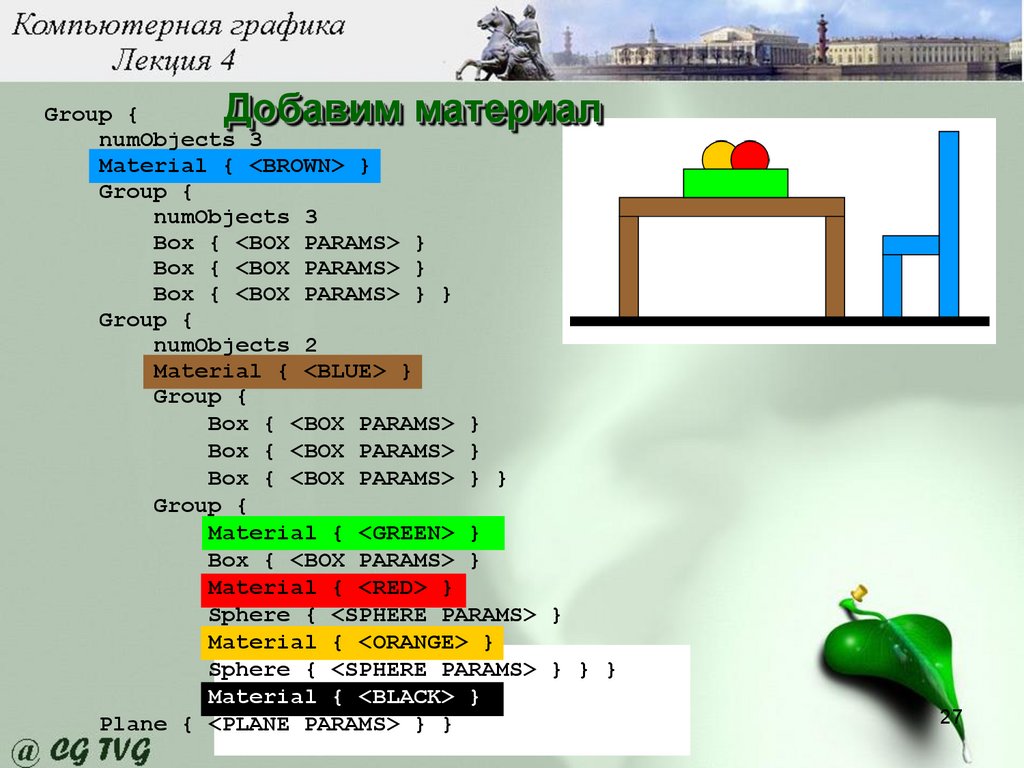
Добавим материал
Group {
numObjects 3
Material { <BROWN> }
Group {
numObjects 3
Box { <BOX PARAMS> }
Box { <BOX PARAMS> }
Box { <BOX PARAMS> } }
Group {
numObjects 2
Material { <BLUE> }
Group {
Box { <BOX PARAMS> }
Box { <BOX PARAMS> }
Box { <BOX PARAMS> } }
Group {
Material { <GREEN> }
Box { <BOX PARAMS> }
Material { <RED> }
Sphere { <SPHERE PARAMS> }
Material { <ORANGE> }
Sphere { <SPHERE PARAMS> } } }
Material { <BLACK> }
Plane { <PLANE PARAMS> } }
27

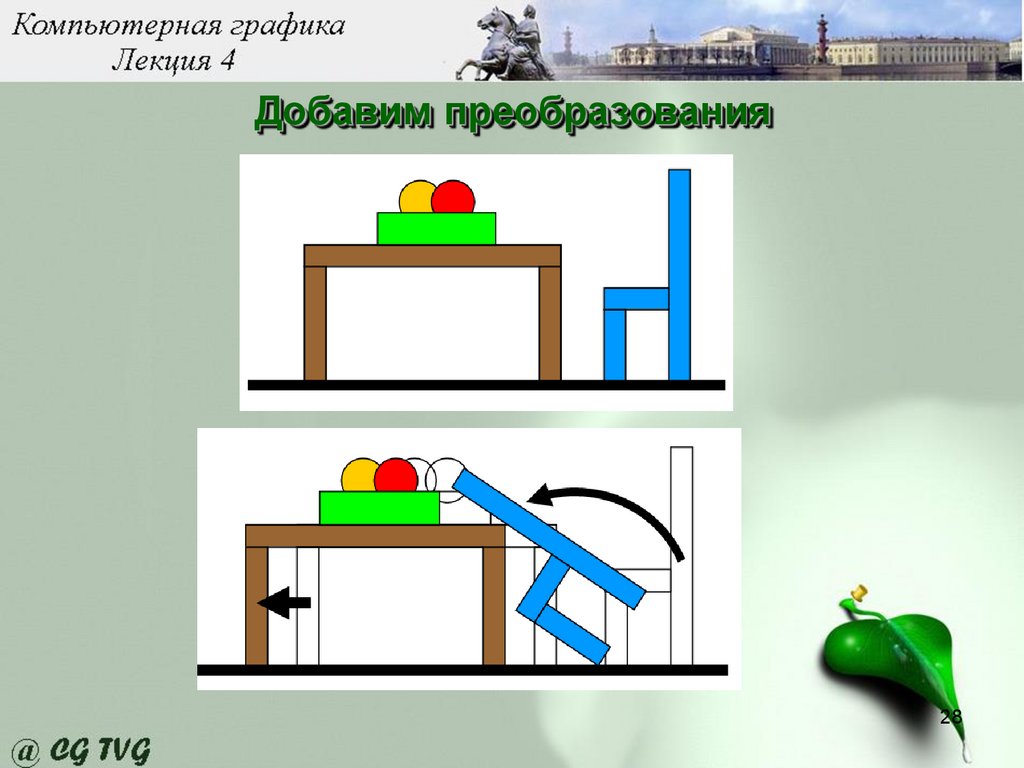
28.

Добавим преобразования
28

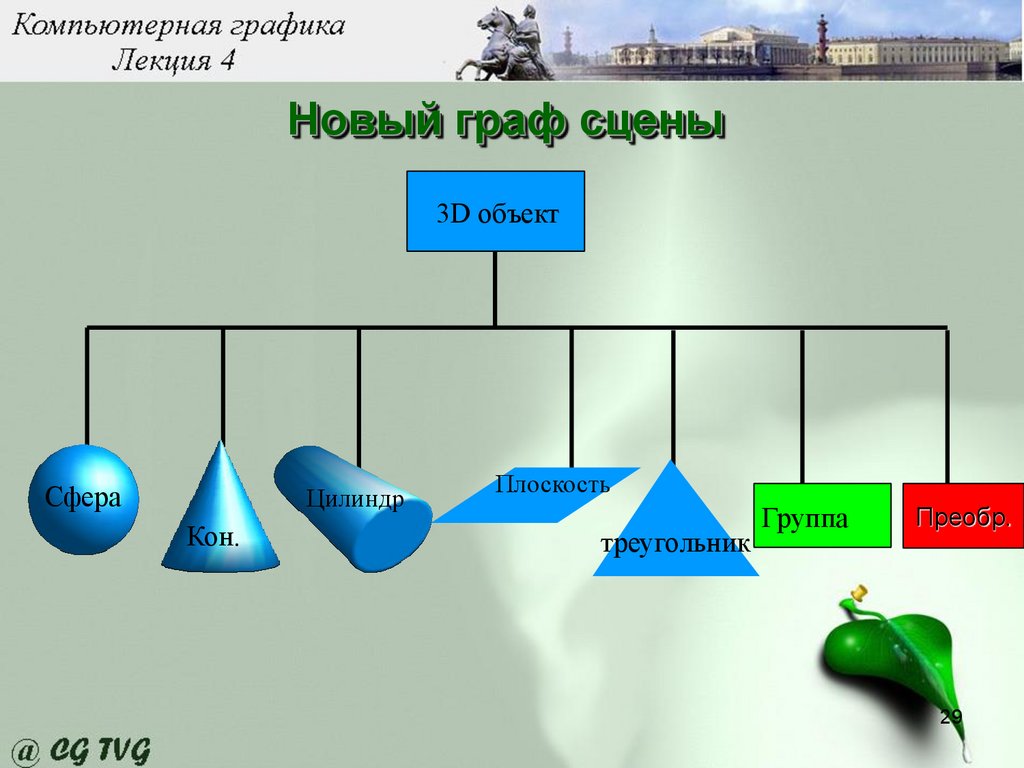
29.

Новый граф сцены
3D объект
Сфера
Цилиндр
Кон.
Плоскость
треугольник
Группа
Преобр.
29

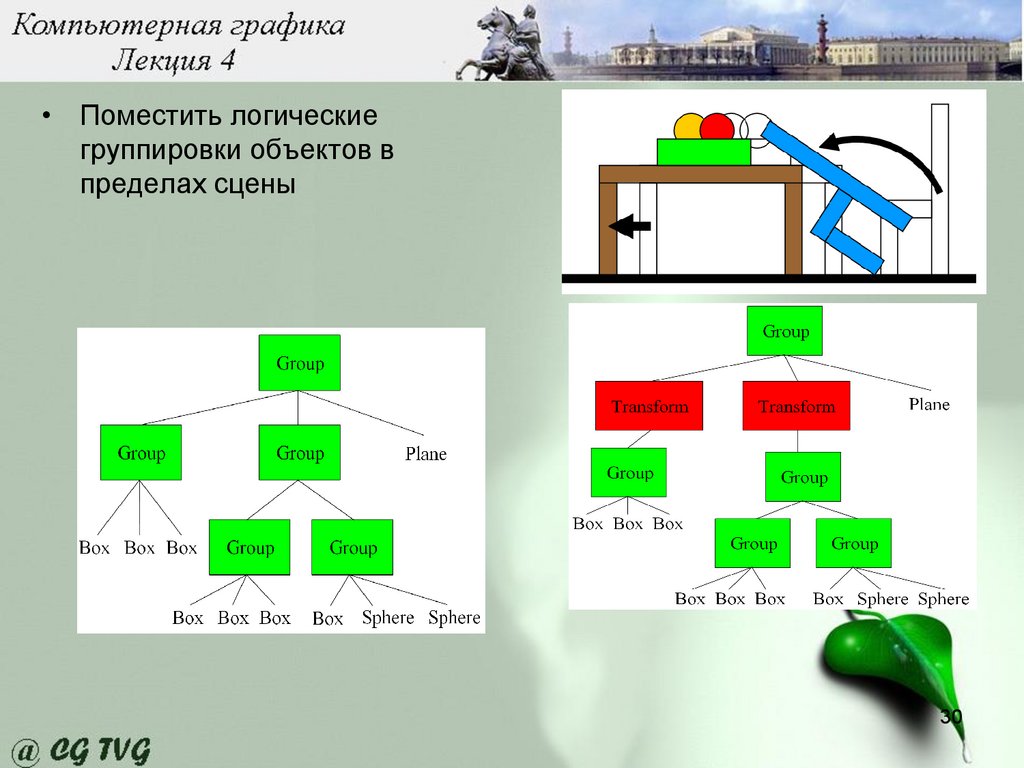
30.

• Поместить логические
группировки объектов в
пределах сцены
30

31.

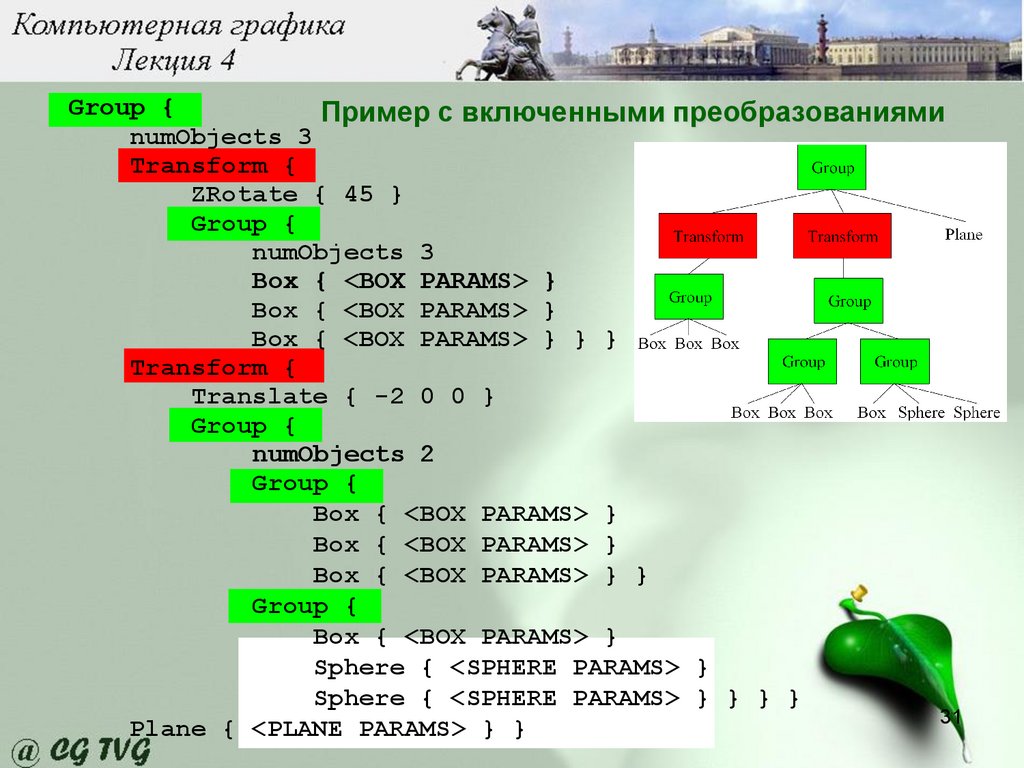
Group {
Пример с включенными преобразованиями
numObjects 3
Transform {
ZRotate { 45 }
Group {
numObjects 3
Box { <BOX PARAMS> }
Box { <BOX PARAMS> }
Box { <BOX PARAMS> } } }
Transform {
Translate { -2 0 0 }
Group {
numObjects 2
Group {
Box { <BOX PARAMS> }
Box { <BOX PARAMS> }
Box { <BOX PARAMS> } }
Group {
Box { <BOX PARAMS> }
Sphere { <SPHERE PARAMS> }
Sphere { <SPHERE PARAMS> } } } }
31
Plane { <PLANE PARAMS> } }

32.

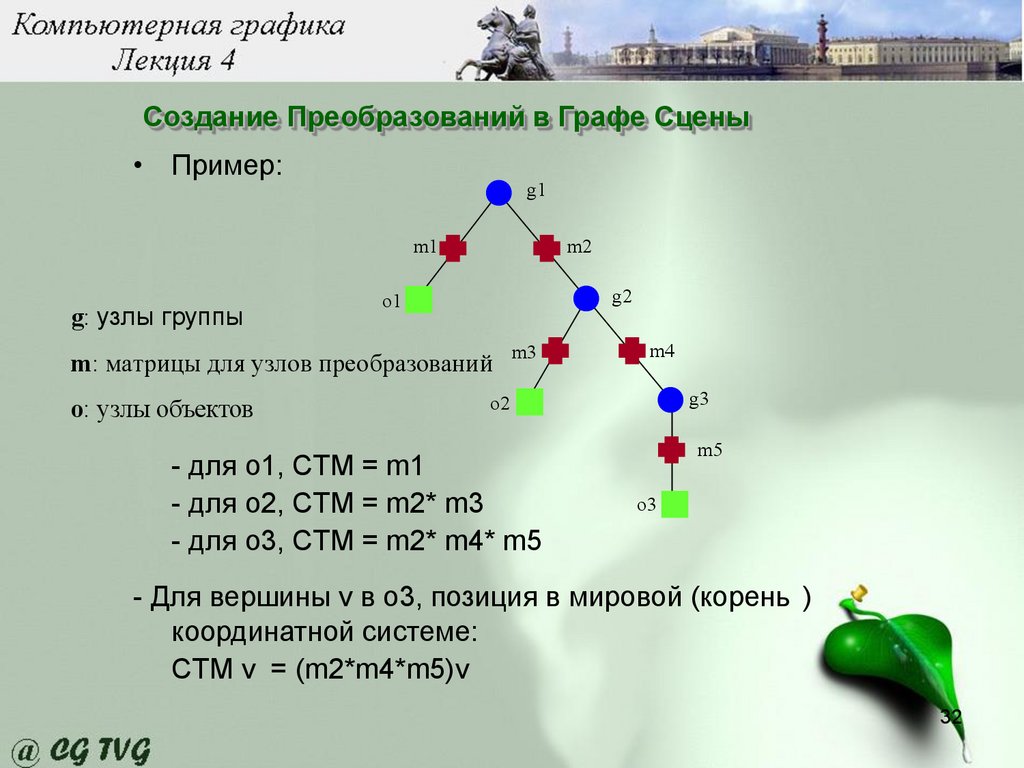
Создание Преобразований в Графе Сцены
• Пример:
g1
m1
g: узлы группы
m2
g2
o1
m: матрицы для узлов преобразований
o: узлы объектов
m3
m4
g3
o2
- для o1, CTM = m1
- для o2, CTM = m2* m3
- для o3, CTM = m2* m4* m5
m5
o3
- Для вершины v в o3, позиция в мировой (корень )
координатной системе:
CTM v = (m2*m4*m5)v
32

33.

• Механизмы не так просто изображаются с помощью
афинных преобразований
http://www.flying-pig.co.uk
33