Комплексные показатели эксплуатационной надежности. Функции распределения

1. Комплексные показатели эксплуатационной надежности. Функции распределения

2. Комплексные показатели эксплуатационной надежности

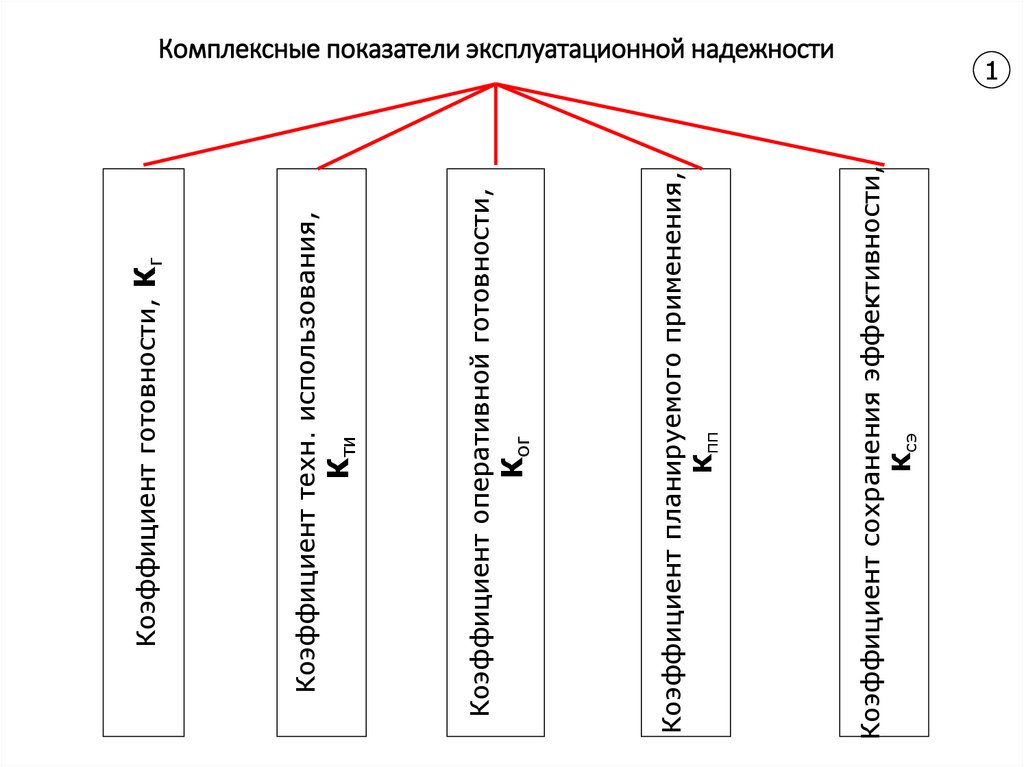
Коэффициент сохранения эффективности,
Ксэ
Коэффициент планируемого применения,
Кпп
Ког
Коэффициент оперативной готовности,
Кти
Коэффициент техн. использования,
Коэффициент готовности, Кг
Комплексные показатели эксплуатационной надежности
1

3.

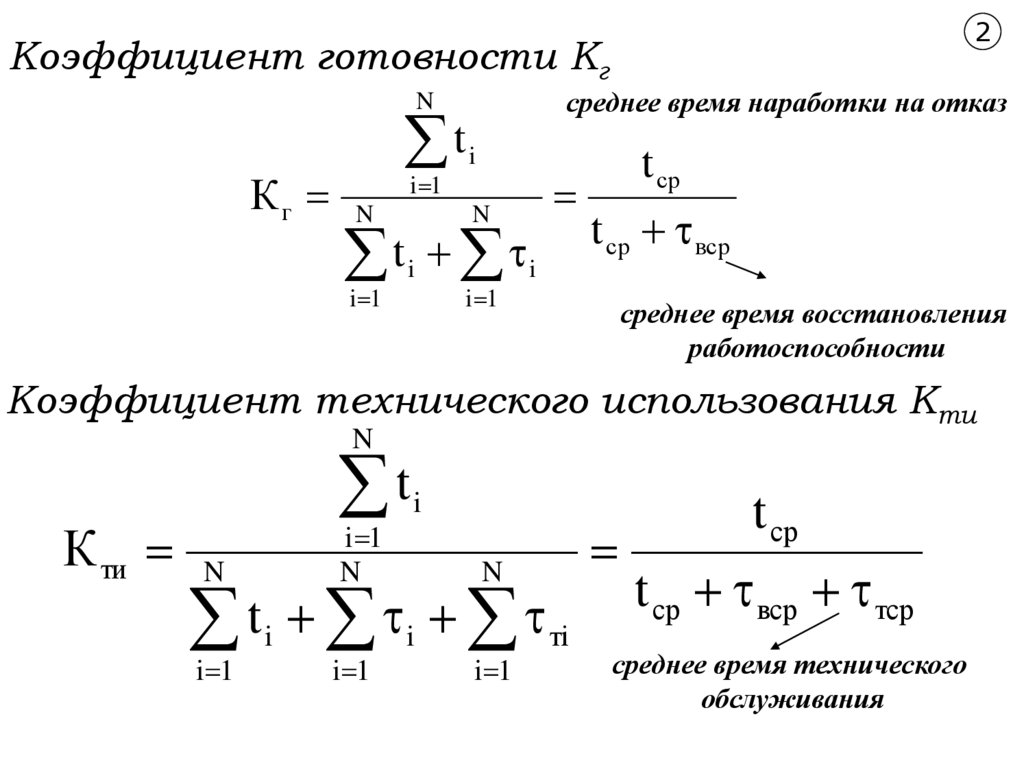
2
Коэффициент готовности Кг
среднее время наработки на отказ
N
Кг
ti
i 1
N
N
i 1
i 1
t i i
t ср
t ср вср
среднее время восстановления
работоспособности
Коэффициент технического использования Кти
N
К ти
ti
N
i 1
N
N
i 1
i 1
i 1
t i i тi
t ср
t ср вср тср
среднее время технического
обслуживания

4.

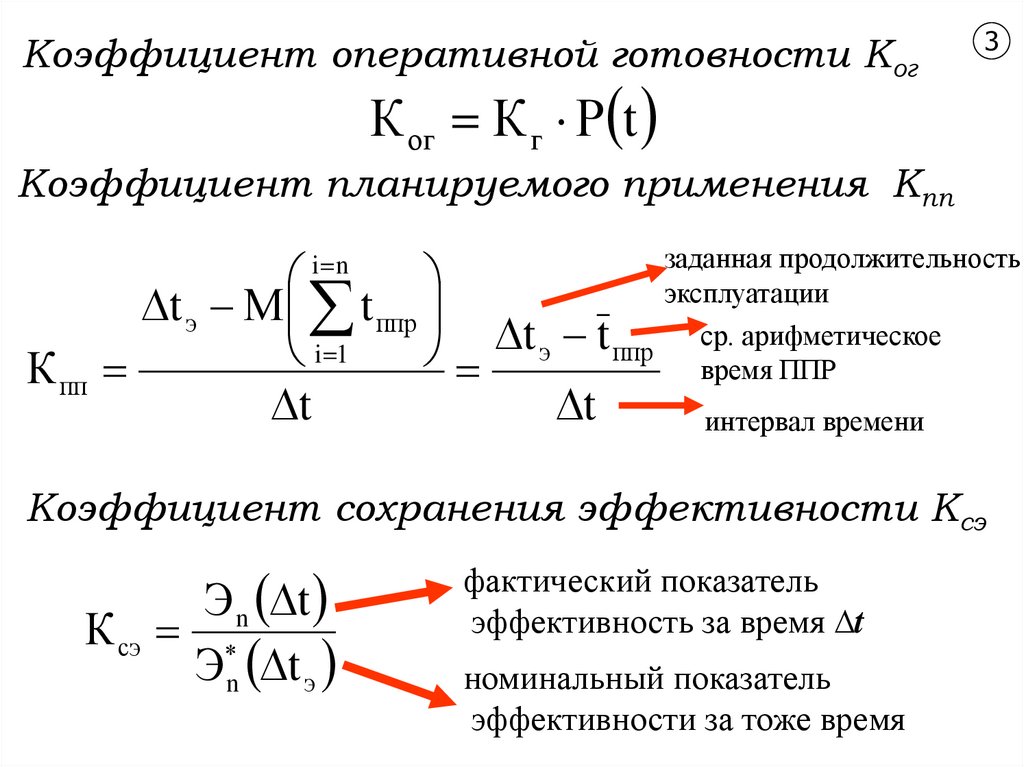
Коэффициент оперативной готовности Ког
3
К ог К г Р t
Коэффициент планируемого применения Кпп
i n
t э М t ппр
t э t
i 1
К пп
t
t
заданная продолжительность
эксплуатации
ср. арифметическое
ппр
время ППР
интервал времени
Коэффициент сохранения эффективности Ксэ
Э n t
К сэ
Э n t э
фактический показатель
эффективность за время ∆t
номинальный показатель
эффективности за тоже время

5. Оценка показателей надежности машин и механизмов

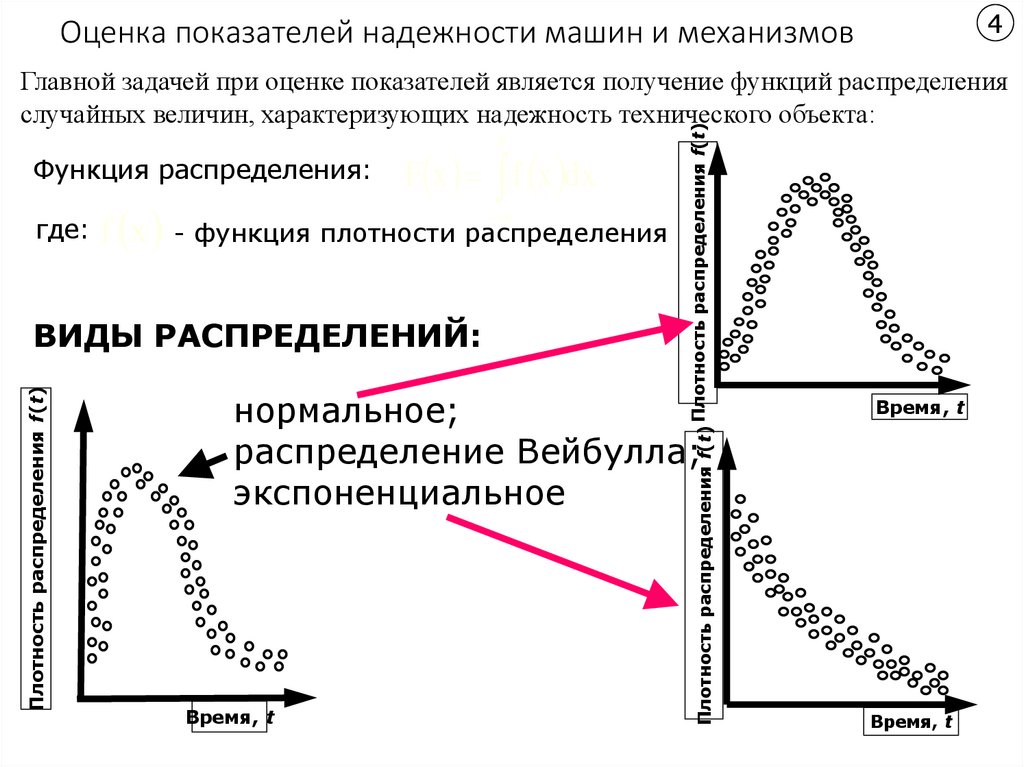
4
Оценка показателей надежности машин и механизмов
x
Функция распределения:
где:
F x f x dx
f x - функция плотности распределения
Плотность распределения f(t)
ВИДЫ РАСПРЕДЕЛЕНИЙ:
Плотность распределения f(t) Плотность распределения f(t)
Главной задачей при оценке показателей является получение функций распределения
случайных величин, характеризующих надежность технического объекта:
нормальное;
распределение Вейбулла;
экспоненциальное
Время, t
Время, t
Время, t

6. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ

5
НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
Задается: плотностью вероятностей двухпараметрической функции
2
1
x a0
f x; а 0 ; 0
exp
2
0 2
2 0
x ; 0 0
а0 и 0 - определяемые (вычисляемые) параметры нормального распределения
Функция нормального распределения имеет вид:
F x
1
0
x a 0
exp
2
2
2 0
x
2
dx
x
Но время t = x принимает только положительные значения

7.

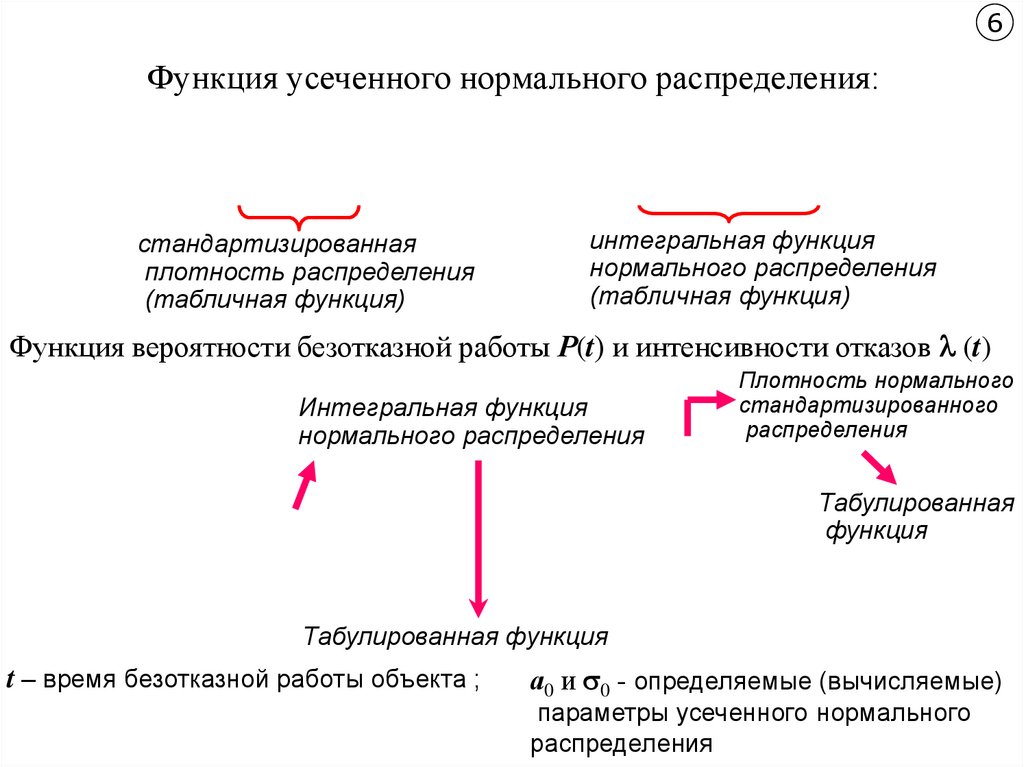
6
Функция усеченного нормального распределения:
1 t a0
f t f 0
0 0
стандартизированная
плотность распределения
(табличная функция)
a0 t
F t 1 F0
0
интегральная функция
нормального распределения
(табличная функция)
Функция вероятности безотказной работы Р(t) и интенсивности отказов (t)
Интегральная функция
нормального распределения
Плотность нормального
стандартизированного
распределения
t a0
Табулированная
f 0
a0 t
0 функция
Р t 1 F t F0
t
0
a0 t
0 F0
Табулированная функция
0
t – время безотказной работы объекта ;
а0 и 0 - определяемые (вычисляемые)
параметры усеченного нормального
распределения

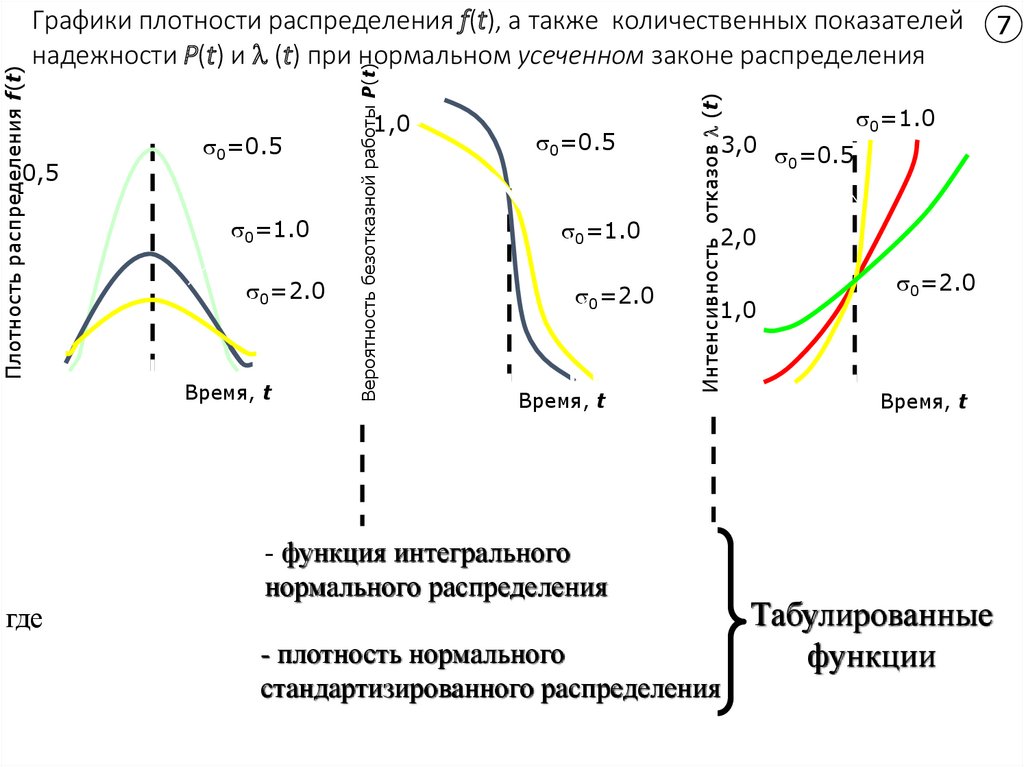
8. Графики плотности распределения f(t), а также количественных показателей надежности Р(t) и  (t) при нормальном усеченном

0=1.0
0=2.0
Время, t
1 t a0
f t; а 0 ; 0 f 0
0 0
t
где
1,0
0=0.5
0=1.0
0=2.0
Время, t
Интенсивность отказов (t)
0,5
0=0.5
Вероятность безотказной работы Р(t)
Плотность распределения f(t)
Графики плотности распределения f(t), а также количественных показателей
надежности Р(t) и (t) при нормальном усеченном законе распределения
3,0 =0.5
0
7
0=1.0
2,0
1,0
а t
P t f t; а 0 ; 0 dt F0 0
0
t
a t - функция интегрального
F0 Z F0 0
0 нормального распределения
t a 0 - плотность нормального
f 0 Z f 0
0 стандартизированного распределения
0=2.0
Время, t
t a0
f 0
f t; a 0 ; 0
t
0
P t
a t
0 F0 0
0
Табулированные
функции