Линейные ДУ

1.

Рассмотрим случай, когда в уравнении
y p( x) y g ( x) y f ( x)
функции p(x) и g(x) – постоянные величины.

2.

Уравнение вида
y p y g y f (x)
называется линейным ДУ с
постоянными коэффициентами
9

3.

Где у – искомая функция, p, g – постоянные
величины.
Если f(х)=0, то уравнение называется
линейным однородным.
Если f (х) не равно 0, то уравнение
называется линейным неоднородным.

4.

Рассмотрим сначала однородное уравнение:
y p y g y 0
10
Будем искать решение этого уравнения в виде
y e
kx
Где k - некоторое число.
Находим производные и подставляем в исходное
уравнение:

5.

y k e
kx
y k e
2
kx
k e p k e g e 0
2
kx
kx
kx
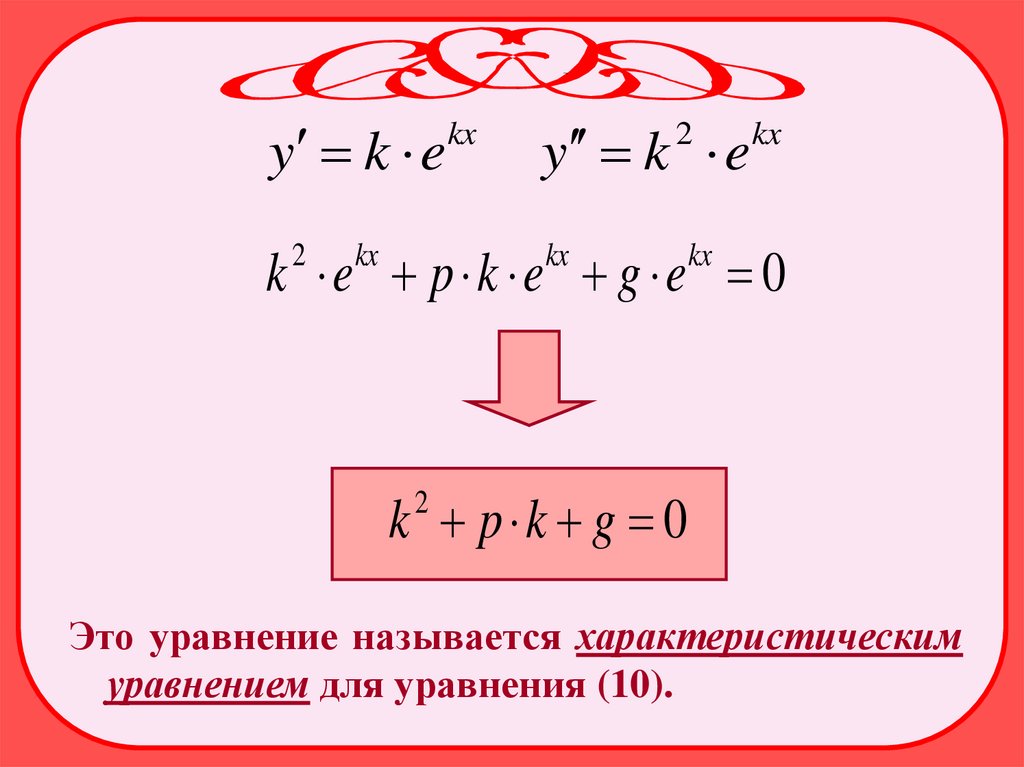
k p k g 0
2
Это уравнение называется характеристическим
уравнением для уравнения (10).

6.

Вид решения линейного однородного ДУ (10)
существенно зависит от того, какие корни
имеет его характеристическое уравнение.
Обозначим эти корни как k1 и k2.

7.

Если корни характеристического
уравнения вещественные и разные
k1 k2
то общее решение однородного
уравнения (9) имеет вид:
y C1e
k1 x
C2e
k2 x

8.

Если корни характеристического
уравнения вещественные и равные
k1 k2 k
то общее решение однородного
уравнения (10) имеет вид:
y C1e C2 x e
kx
kx

9.

Если характеристическое уравнение
не имеет вещественных корней,
то общее решение однородного
уравнения (10) имеет вид:
y C1e cos x C2e sin x
x
где
x
k1 i
k2 i
-комплексные корни
характеристического уравнения.

10.

1
Решить дифференциальное уравнение:
y 5 y 4 y 0

11.

y e
k 5k 4 0
5 3
D 25 16 9 k1, 2
2
k1 4
kx
2
k2 1
Корни вещественные и разные, поэтому общее
решение будет иметь вид:
y C1e C2e
x
4x

12.

2
Решить дифференциальное уравнение:
y 6 y 9 y 0

13.

y e
kx
D 36 36 0
k 6k 9 0
6
k1, 2 3 k
2
2
Корни вещественные и одинаковые, поэтому общее
решение будет иметь вид:
y C1e C2 x e
3x
3x

14.

3
Решить дифференциальное уравнение:
y 2 y 2 y 0

15.

y e
kx
D 4 8 4
k 2k 2 0
2 4
k1, 2
1 i
2
k1 1 i
2
k2 1 i
Корни комплексные, поэтому общее решение будет
иметь вид:
y C1e cos x C2e sin x
x
x