Similar presentations:
Dynamický systém
1.
Základní pojmy:Dynamický systém je systém, který se vyvíjí v čase i bez vnějších podnětů, tzn.
akumuluje některou z forem energie. (např. kinetickou, potenciální, tepelnou,
magnetickou, elektrostatickou, chemickou atd.)
např. jablko na stromě – potenciální energie, padající – kinetická energie
pec, dům , žehlička – tepelná energie
akumulátor (Pb, Li-ion) – chemická energie
elektromotor – elektromagnetická energie v magnetickém obvodu, kinetická
v roztočeném rotoru
solární článek – makroskopicky není dynamický systém (když zanedbáme vliv
teploty)
Teorie řízení je soubor poznatků z technické kybernetiky a aplikované matematiky,
umožňující analýzu a syntézu, tj. návrh takových vhodných regulátorů, aby
zpětnovazební soustava byla stabilní a měla požadované dynamické chováni.
Zpětná vazba: Princip zpětné vazby byl znám již dříve v regulační technice a používal
se při návrhu zpětnovazebních zesilovačů pro účely sdělovací techniky. Zakladatelé
kybernetiky ale rozpoznali, že jde o velmi obecný princip. Je především zásluhou
kybernetiky, že se stal obecně známým a umožnil vysvětlit řadu dějů odehrávajících
se v nejrůznějších dynamických systémech.
2.
Regulované soustavy jsou takové soustavy, v nichž regulátor ovlivňuje stav nebochování regulovaného objektu. Regulovaným objektem jsou obvykle dynamické
soustavy.
Příklady regulovaných soustav:
• regulace teploty pece, regulace vytápěni obytných prostor,
• řízeni otáčivé rychlosti el. pohonu, polohování robotického ramene, CNC stroje
• aktivní tlumeni vibraci a chvěni mechanických soustav (na př. U dopravních
prostředků)
• regulace výkonu turboalternátoru, regulace napěti generátoru
Reálné regulované soustavy se fyzikálně výrazně navzájem liší, přesto mají některé
společné vlastnosti:
• regulované soustavy jsou dynamickými soustavami, tj. akumuluji některou z forem
• energii (kinetickou, potenciální, tepelnou, magnetickou atd.)
• regulované soustavy se vyznačuji neurčitosti některých svých parametrů, které v
řadě případů nemůžeme přesně určit (na př. velikost třeni, včetně závislosti na
rychlosti),nebo které se mohou v čase měnit
• signály získané ze snímačů regulovaných veličin obsahují navíc i šumy.
3.
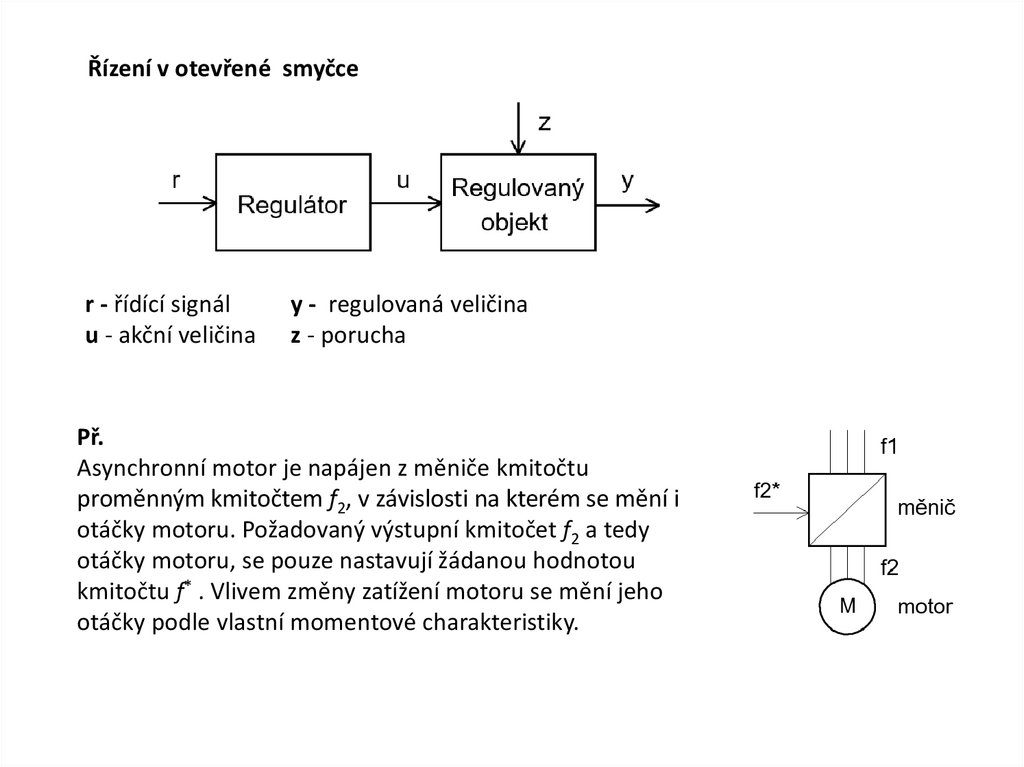
Řízení v otevřené smyčcer - řídící signál
u - akční veličina
y - regulovaná veličina
z - porucha
Př.
Asynchronní motor je napájen z měniče kmitočtu
proměnným kmitočtem f2, v závislosti na kterém se mění i
otáčky motoru. Požadovaný výstupní kmitočet f2 a tedy
otáčky motoru, se pouze nastavují žádanou hodnotou
kmitočtu f* . Vlivem změny zatížení motoru se mění jeho
otáčky podle vlastní momentové charakteristiky.
4.
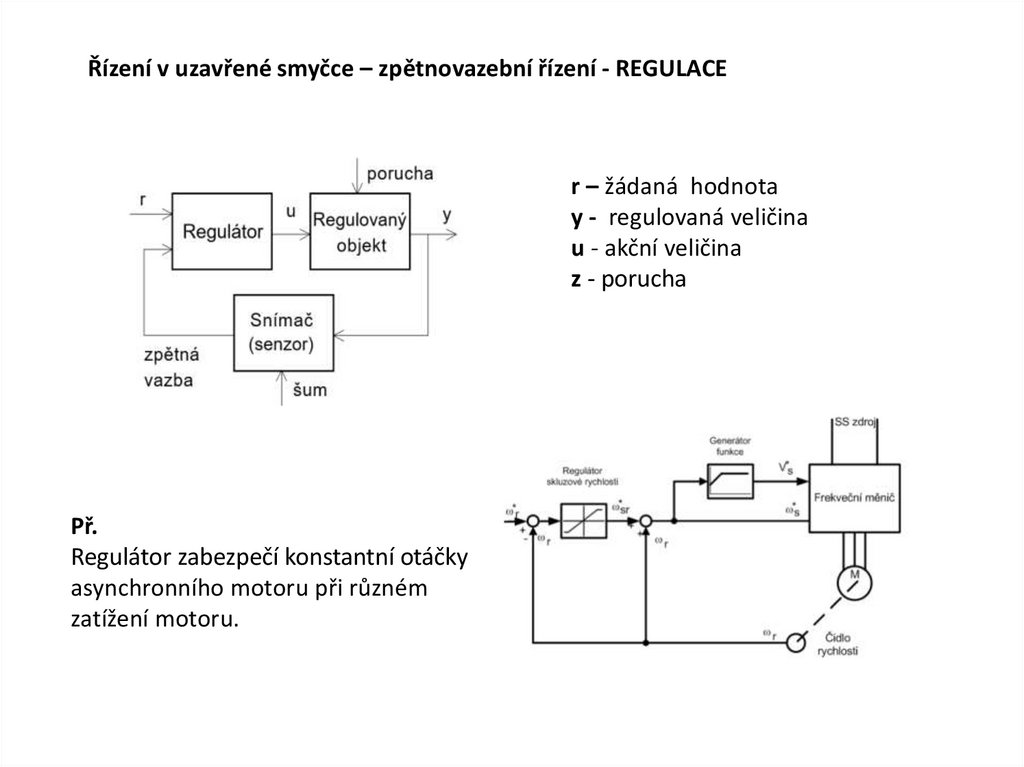
Řízení v uzavřené smyčce – zpětnovazební řízení - REGULACEr – žádaná hodnota
y - regulovaná veličina
u - akční veličina
z - porucha
Př.
Regulátor zabezpečí konstantní otáčky
asynchronního motoru při různém
zatížení motoru.
5.
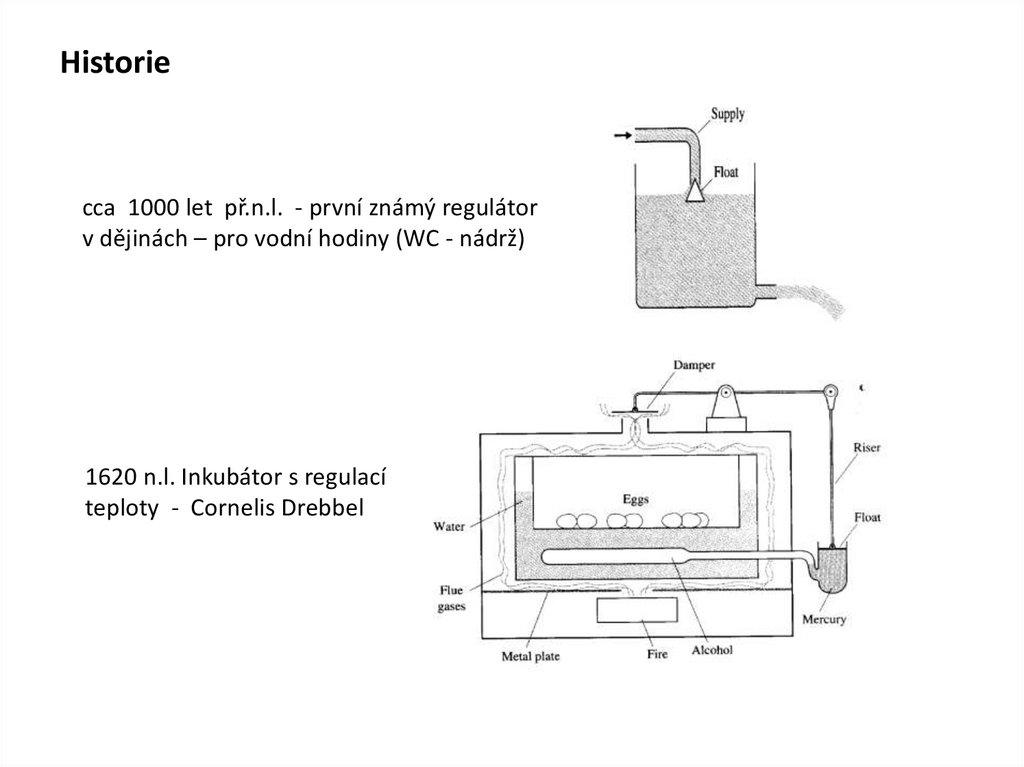
Historiecca 1000 let př.n.l. - první známý regulátor
v dějinách – pro vodní hodiny (WC - nádrž)
1620 n.l. Inkubátor s regulací
teploty - Cornelis Drebbel
6.
Historie1788 n.l.
Odstředivý regulátor otáček parního stroje
J. Watt (1736-1819)
7.
HistoriePočátky teorie řízení:
1. Analýza stability
–
–
–
J. C. Maxwel 1868 (vliv pólů systému)
E .J. Routh
1877 jednoduché kritérium stability i pro vyšší řády
A.M. Lyupanov 1892 obecné (i nelineární systémy)
2. Frekvenční přenos
–
–
H. Nyqust
H. W. Bode
1932 – stabilita zpětnovazebních zesilovačů
1960
3. PID řízení
–
–
Callender
N. Wiener
1936
1948 - Kybernetika aneb Řízení a sdělování u organismů a strojů.
4. Stavová regulace
–
Kalman ,Pontryagin, Bellman a další 1950
8.
Lineární dynamické soustavy – v tomto kurzu výhradněMějme obecnou dynamickou soustavu dle obr. Přivedeme-li na vstup této
soustavy na př. krátký impuls (u reálných soustav to může být impuls síly nebo
napěťový impuls), výstup má již odlišný průběh, závislý na typu soustavy.
Odezva dynamické soustavy
Dynamická soustava je charakterizována proměnnými, které jsou funkcí času.
Příčinou je akumulace některé z forem energií uvnitř soustavy.
Řad dynamické soustavy: je dán počtem akumulátorů energie v soustavě
9.
Lineární dynamické soustavy splňují tzv. princip superpoziceZ toho plynou tyto důležité vlastnosti:
• Chování systému nezávisí na velikosti vstupních signálů a vnitřních proměnných
(počátečních podmínkách) – mění se jen měřítko a počáteční hodnoty
• Vliv více vstupů nebo poruch lze vyšetřovat nezávisle na ostatních (tzn. např. nulových )
• Pro řešení lze využít Laplaceovy transformace
10.
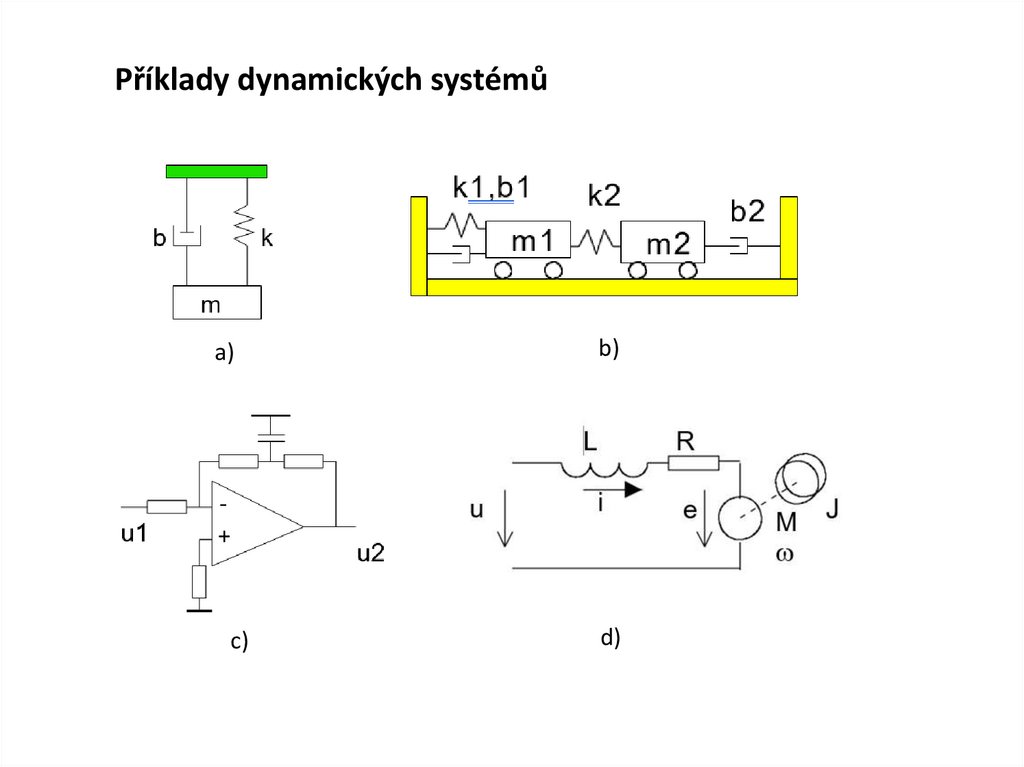
Příklady dynamických systémůa)
b)
+
c)
d)
11.
Matematický popis dynamických soustav:• Diferenciální rovnice n – tého řádu (dle řádu systému)
• Stavové rovnice – n rovnic prvního řádu
• Stavové matice – maticový zápis stavových rovnic (jen lineární systémy)
• Stavový model (grafické znázornění stavových rovnic - Simulink )
• Přenosová funkce – využívá Laplaceovy transformace (jen lineární systémy)
• Frekvenční funkce – přechod od Laplaceovy transformace k Furierově
Grafický popis
• Frekvenční charakteristiky – v komplexní rovině nebo logaritmické (amplituda,fáze)
• Přechodová nebo impulzní charakteristika – časové odezvy na daný vstupní signál
Poznámka: stavové matice, přenosová fce, frekvenční charakteristiky jsou omezeny jen
na lineární systémy
12.
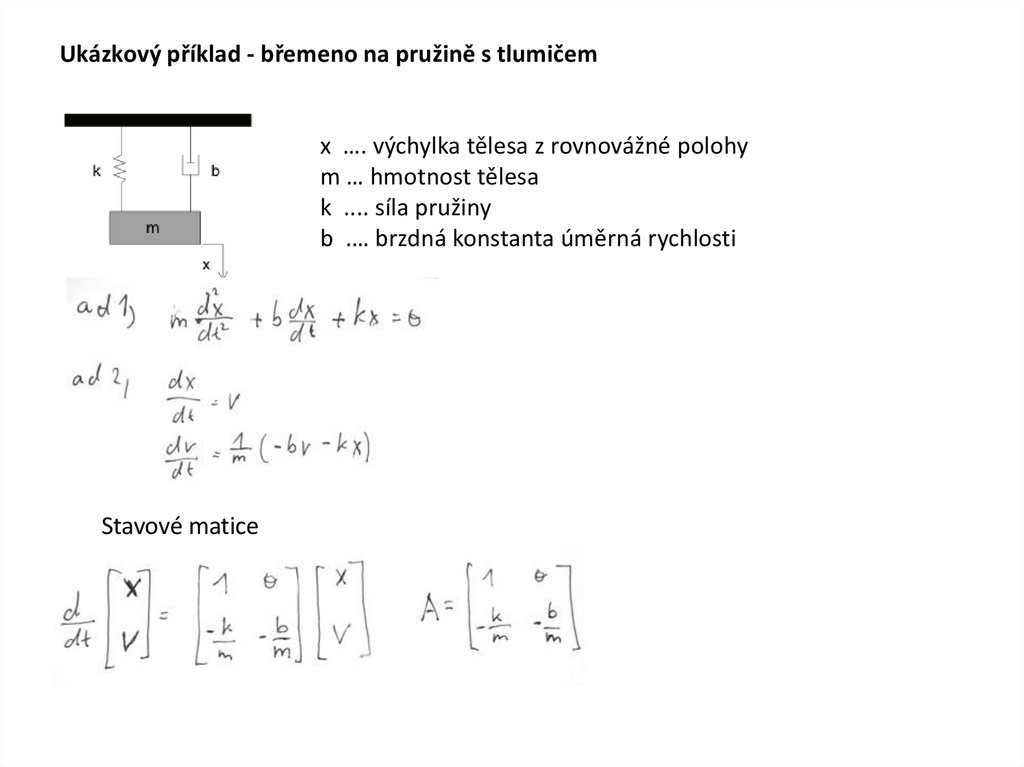
Ukázkový příklad - břemeno na pružině s tlumičemx …. výchylka tělesa z rovnovážné polohy
m … hmotnost tělesa
k .... síla pružiny
b .… brzdná konstanta úměrná rychlosti
Stavové matice
13.
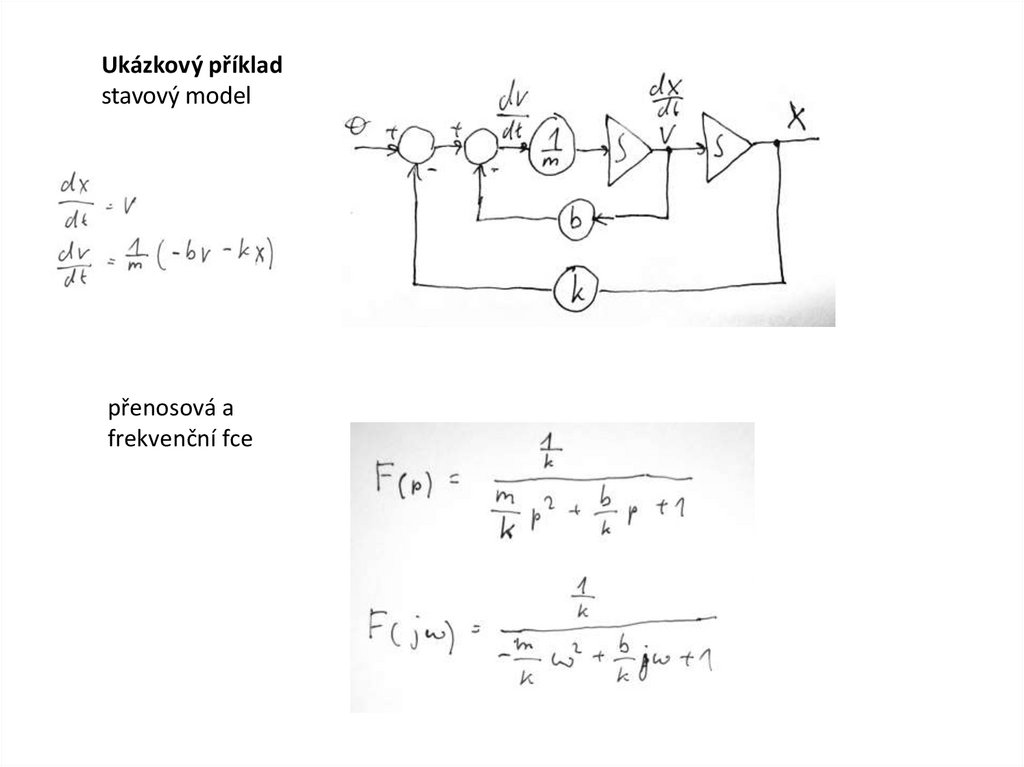
Ukázkový příkladstavový model
přenosová a
frekvenční fce
14.
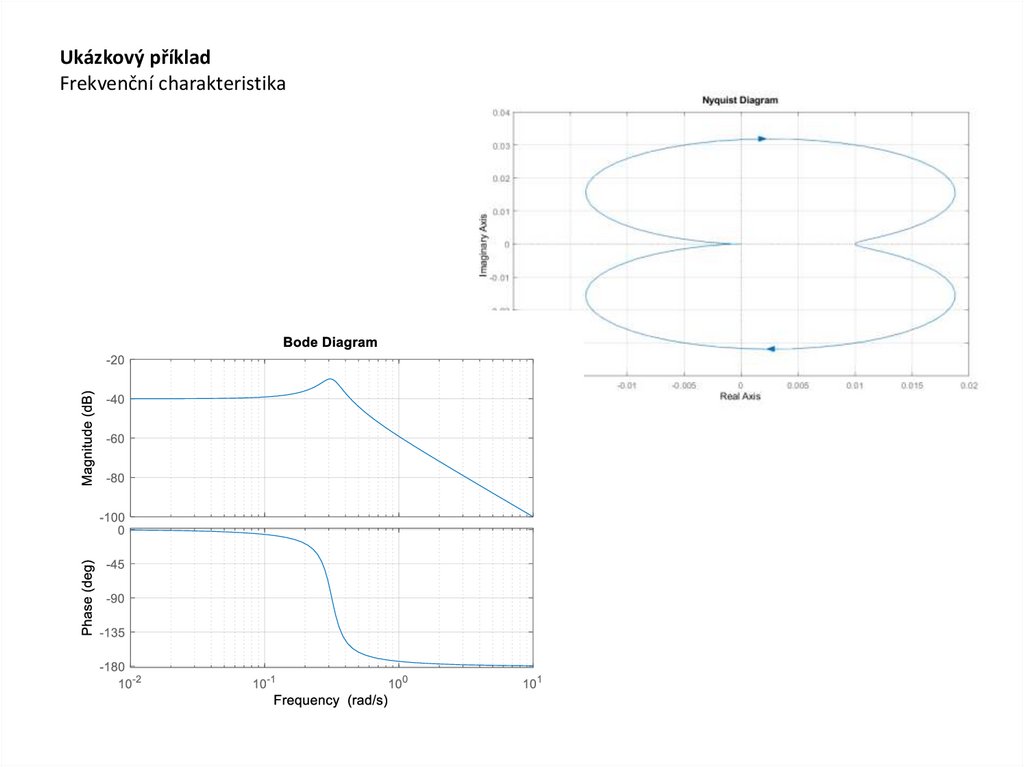
Ukázkový příkladFrekvenční charakteristika
15.
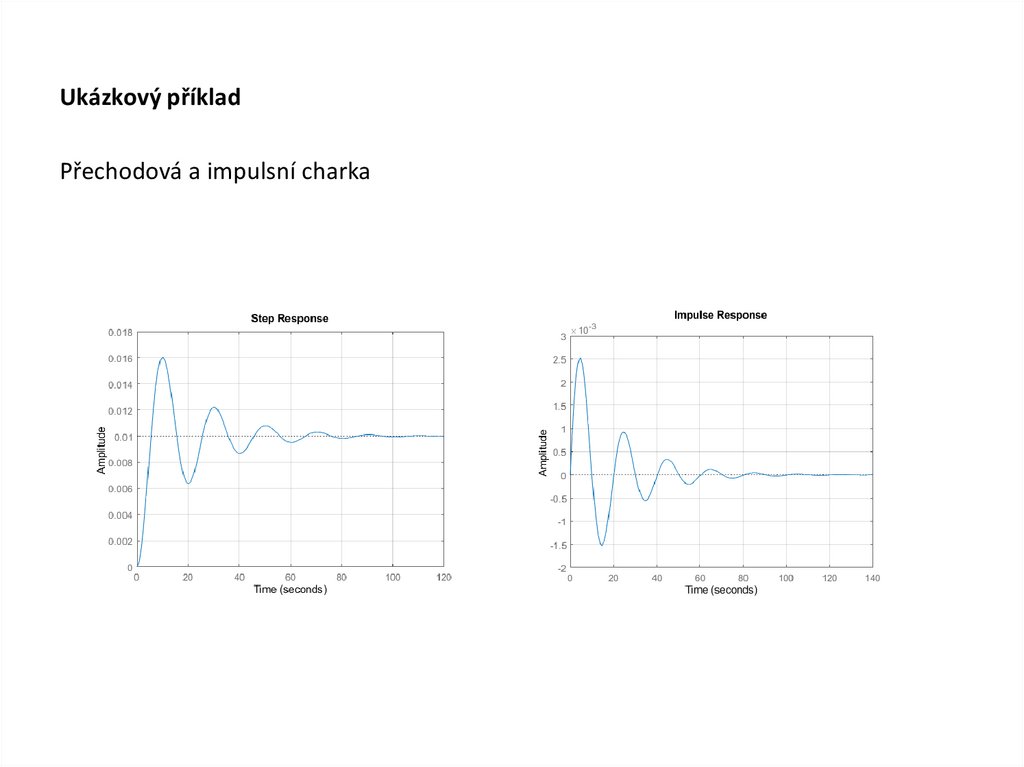
Ukázkový příkladPřechodová a impulsní charka









 physics
physics
