Similar presentations:
ЯМР-спектроскопия. Часть 3
1.
ЯМРСПЕКТРОСКОПИЯ2.
1.3 Возбуждение перехода междуспиновыми состояниями
■ Между двумя рассматриваемыми уровнями возможны
переходы, сопровождающиеся поглощением или
испусканием кванта электромагнитной энергии с
частотой (формула Бора)
= Е/h
(7)
■ Физический смысл переходов: переориентация спина
ядра в магнитном поле Н0.
3.
Основное уравнение ЯМР■ Подставляя выражение Е из уравнения (6) в
соотношение (7), получаем основное уравнение ЯМР,
которое связывает частоту электромагнитного
излучения с напряженностью магнитного поля (условие
резонанса):
γ Η0
ν
2π
(8)
4.
Резонансная частота для протона■ Для протона, находящегося в магнитном поле с индукцией
1,41 Тл, эта частота равна
2,674 108 с 1 Тл 1
ν
1,41 Тл 60 106 с 1 60 МГц
2 3,141
■ Следовательно в данном случае необходимо
радиочастотное поле (60 МГц), что соответствует длине
волны = 5 м, т.е. радиоволнам на границе
радиодиапазона и диапазона СВЧ.
■ Лабораторные магниты создают условия резонанса для
всех магнитных ядер в диапазоне от нескольких
(60 МГц) до сотен (800 МГц) мегагерц.
■ Поэтому ЯМР относят к числу радиоспектроскопических
методов исследования.
5.
1.4 Разность между энергиямиспиновых состояний
■ Основная проблема метода состоит в том, как
заставить протон, сориентированный вдоль
магнитного поля, поглотить электромагнитную
энергию (т.е. переориентировать свой спин и перейти
на более высокий уровень) и как измерить
поглощенную энергию.
■ Энергия, необходимая для перехода протона из
одного спинового состояния в другое, равна
Ε h ν 6,626 10 34 Дж с 60 106 с 1 4 10 26 Дж
■ Отнесенная к 1 моль вещества эта энергия будет
равна
Ε 4 10 26 Дж 6,02 10 23 моль 1 2,4 10 2 Дж/моль
6.
1.5 Физические основы ЯМР■ Пусть имеются множество однотипных ядер
со спином I = 1/2 (например, протонов),
занимающих малый объем в пространстве.
■ Поместим ядра в сильное однородное поле с
напряженностью Н0, направленное вдоль
оси z.
■ Магнитные моменты протонов
ориентируются по полю и против него.
Кроме того, они прецессируют вокруг
направления этого поля (рис.).
■ Ядра оказываются на двух уровнях энергии,
отличающихся на величину Е.
■ Обозначим количество ядер верхнего
энергетического уровня как N и назовем
заселенностью верхнего уровня B1, а для
нижнего энергетического уровня –
соответственно Nα и B2.
z
М
Na
H0
m = +1/2
В2
Nb
В1
m = -1/2
7.
Населенность спиновых состоянийz
■ Многочисленные экспериментальные данные
показывают, что заселенности уровней
подчиняются так называемому статистическому
распределению Больцмана ( Е 0)
М
Na
H0
N / N е
Ε / RT
(9)
m = +1/2
В2
Nb
m = -1/2
В1
■ Для протона
N / N exp[ 0,024 Дж/моль /(8,31 Дж/(моль K) 300 К)] exp( 9,62 10 6 ) 0,9999904
■ Для Н0 = 1,41 Tл ( рез = 60 МГц),
при T = 300 K, N = 0,9999904 Nα
■ Для Н0 = 7,05 Tл ( рез = 300 МГц),
N = 0,99995 Nα (различие растет!)
8.
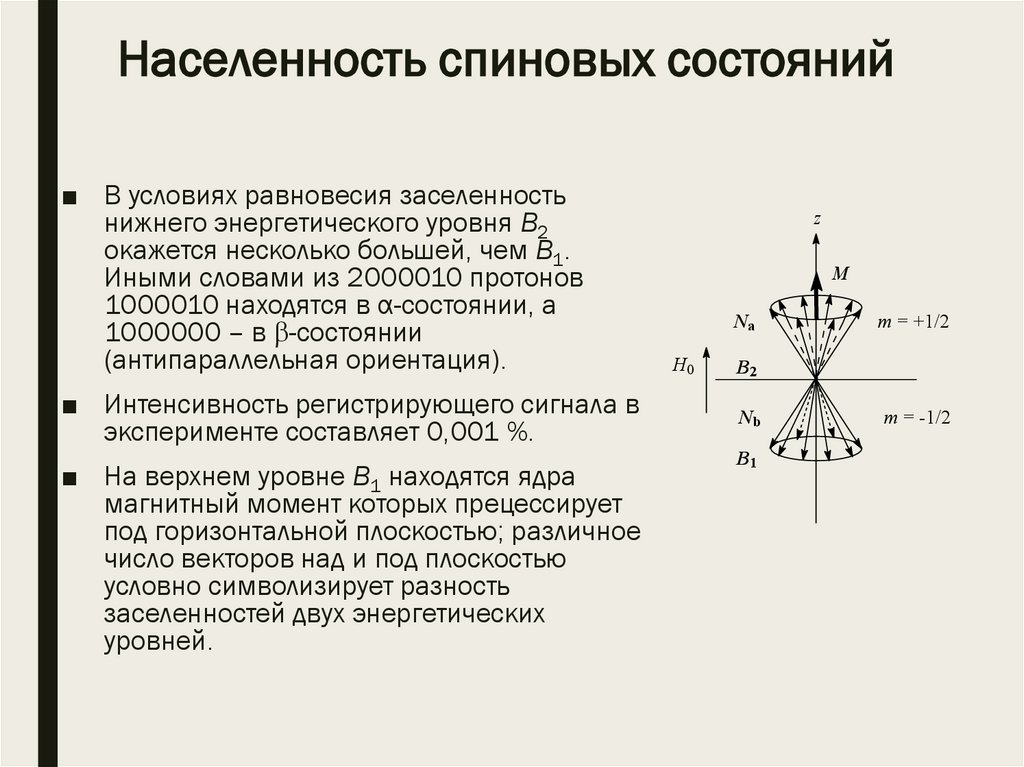
Населенность спиновых состояний■ В условиях равновесия заселенность
нижнего энергетического уровня В2
окажется несколько большей, чем В1.
Иными словами из 2000010 протонов
1000010 находятся в α-состоянии, а
1000000 – в -состоянии
(антипараллельная ориентация).
■ Интенсивность регистрирующего сигнала в
эксперименте составляет 0,001 %.
■ На верхнем уровне В1 находятся ядра
магнитный момент которых прецессирует
под горизонтальной плоскостью; различное
число векторов над и под плоскостью
условно символизирует разность
заселенностей двух энергетических
уровней.
z
М
Na
H0
m = +1/2
В2
Nb
В1
m = -1/2
9.
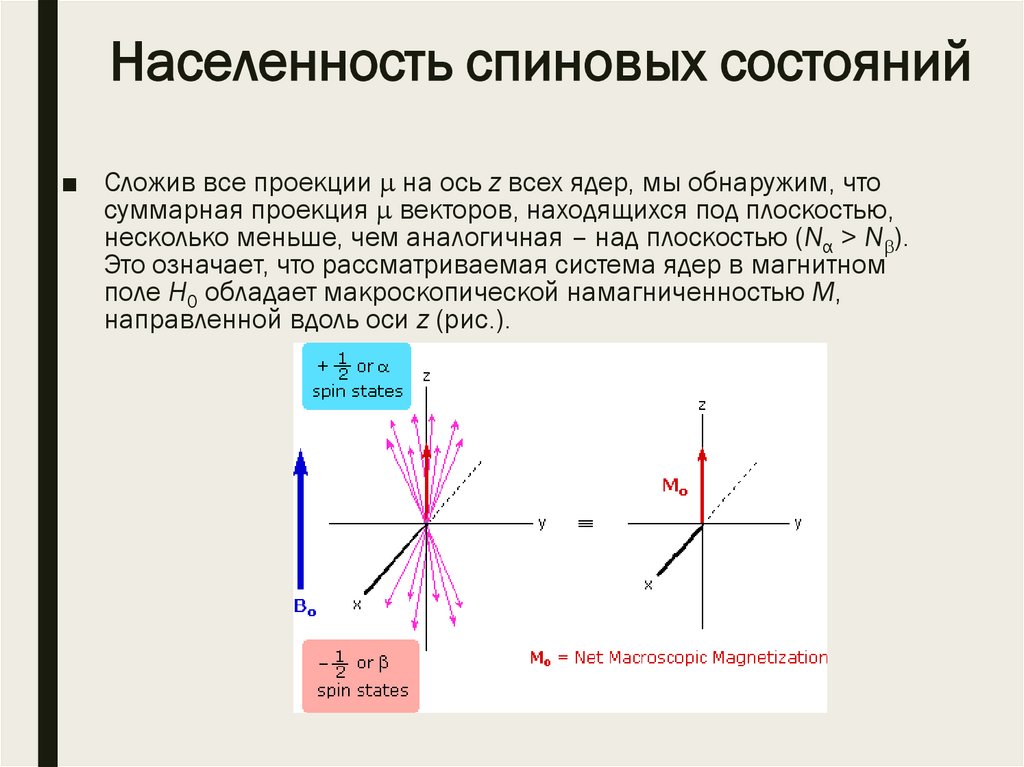
Населенность спиновых состояний■ Сложив все проекции на ось z всех ядер, мы обнаружим, что
суммарная проекция векторов, находящихся под плоскостью,
несколько меньше, чем аналогичная – над плоскостью (Nα > N ).
Это означает, что рассматриваемая система ядер в магнитном
поле Н0 обладает макроскопической намагниченностью М,
направленной вдоль оси z (рис.).
10.
Физические основы ЯМР■ Самопроизвольная, без внешнего
воздействия переориентация спина ядра в
магнитном поле – явление чрезвычайно
маловероятное.
■ Напротив, в условиях взаимодействия с
переменным электромагнитным полем Н1
(менее 1 Вт) небольшой амплитудой
(Н1 << Н0), прецессирующим в
горизонтальной плоскости с частотой 0,
стремящемся отклонить диполь в плоскость
xy, происходит интенсивный обмен
радиочастотными квантами между
источником поля Н1 и системой ядер (рис.)
прецессии
(угол меняется, когда частота
μ
совпадает для и Н1).
z
Ho
y
x
H1
11.
Физические основы ЯМР■ Каждая переориентация вектора магнитного
момента ядер сопровождается испусканием
или поглощением кванта энергии h = .
z
■ Поскольку заселенность верхнего (В1) и
Ho
нижнего (В2) уровня неодинакова, при
равной вероятности перехода с одного
уровня на другой число квантов (как в так и -переходы), поглощаемых системой
ядер, будет несколько больше, чем число
квантов, испускаемых ею.
■ Вследствие этого, плавно меняя частоту 1
переменного поля Н1 вблизи 0, в момент
совпадения частот 1 и 0 мы будем
наблюдать поглощение энергии
радиочастотного поля Н1 системой ядер.
■ Это и есть ядерный магнитный резонанс.
y
x
H1
12.
Чувствительность спектроскопииЯМР 13С и 1Н
■ Если сравнивать чувствительность 13С и 1Н при
одинаковом внешнем магнитном поле Н0, то
заселенность между энергиями спиновых состояний
13С будет меньше.
■ Значит и интенсивность сигнала 13С составит всего
0,016 от интенсивности сигнала протона.
■ С учетом природного содержания изотопа 13С
(1,07 %) – относительная чувствительность
спектроскопии ЯМР 13С и 1Н составляет 0,016 · 0,0107
= 1,71 · 10–4 : 1.
■ Спектроскопия ЯМР 13С в 5848 раз менее
чувствительна, чем спектроскопия ЯМР 1Н.
13.
Чувствительность спектроскопии ЯМР 13С и1Н
■ Наиболее очевидным
путем повышения
интенсивности сигнала
является использование
более сильных
магнитных полей Н0 (до
сверхпроводящих
магнитов порядка 800
МГц) (табл.).
Н0, Tл
1,41
1,88
2,11
2,35
4,70
7,05
9,40
11,74
14,09
Резонансные
частоты, МГц
1
13
Н
С
60
15,1
80
20,1
90
22,63
100
25,15
200
50,3
300
75,4
400
100,6
500
125,7
600
150,9
14.
Чувствительность спектроскопииЯМР 13С и 1Н
■ Многократное сканирование (благодаря
накоплению и усреднению спектров) позволяет
снизить уровень шума. Отношение сигнала (S) к
шуму (N) пропорционально квадратному корню
из числа сканирований спектра n (число
проходов).
S
n
N
(11)
15.
Химический сдвигНинд = ·Н0,
где – коэффициент
пропорциональности, называемый
константой экранирования.
(16)
Теперь напряженность магнитного
поля в месте расположения магнитных
ядер, имеющих одинаковое электронное
окружение, можно выразить
Нэфф = Н0 – Нинд = Н0 (1 – ),
(17)
γ
ν0
(1 σ) Н 0
2π
(18)
16.
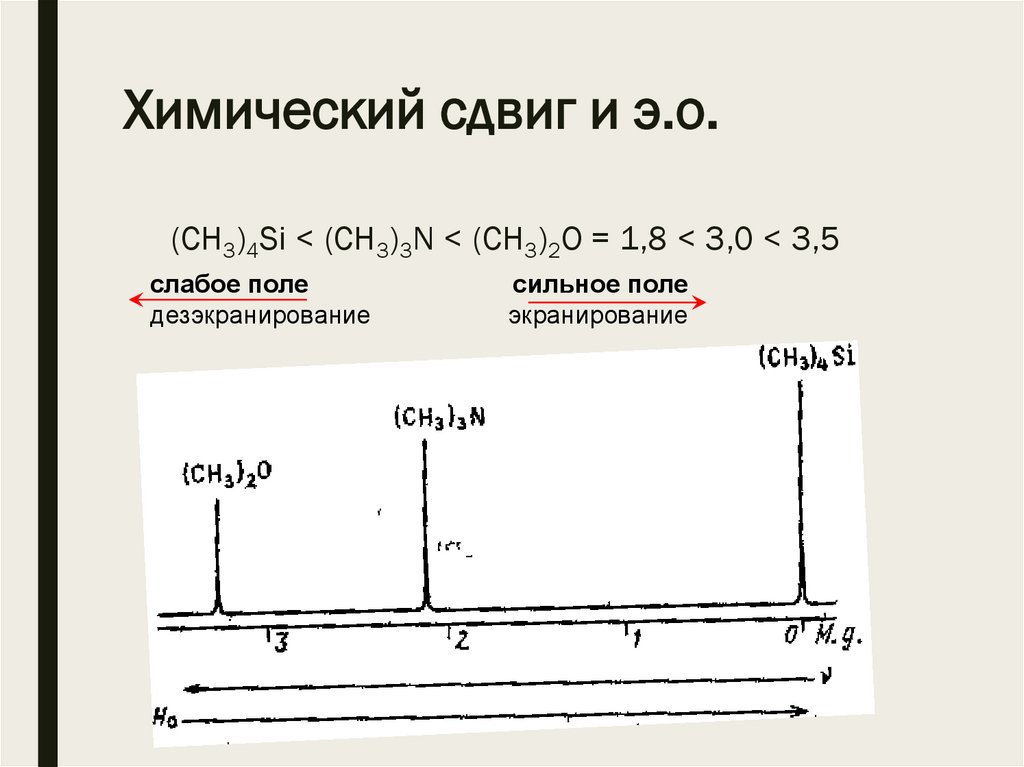
Химический сдвиг и э.о.(CH3)4Si < (CH3)3N < (CH3)2O = 1,8 < 3,0 < 3,5
слабое поле
дезэкранирование
сильное поле
экранирование
17.
Химический сдвиг: м.д. и таушкала■
Химический сдвиг – разность расстояний между двумя линиями в
спектре, выраженная в Гц
ν 01 ν 02
γ
Н 0 (σ 1 σ 2 )
2π
Нобр − Нэт
νобразец − νстандарт
6
δ=
⋅ 10 =
⋅ 106 м. д.
Н0
ν0 (рабочаячастота)
= 10 –
(19)
(20)
18.
Растворители в ЯМРПердейтерированные растворители (внутренний
эталон):
■ CDCl3,
■ ДМСО-d6,
■ бензол-d6,
■ D2O и др.
Для неполярных соединений: CCl4 (внешний
стандарт ТМС).















 physics
physics








