Ременные передачи. Виды, геометрия и кинематика. Расчет ременных передач. Лекция 1

1.

Лекция 1
РЕМЕННЫЕ ПЕРЕДАЧИ. ВИДЫ, ГЕОМЕТРИЯ
И КИНЕМАТИКА.
РАСЧЕТ РЕМЕННЫХ ПЕРЕДАЧ
План лекции:
1. Применение, разновидности, кинематика и
геометрия ременной передачи.
2. Основы расчета ременных передач.
3. Силы и напряжения на ветвях ременной
передачи.

2.

1. Применение, разновидности, кинематика
и геометрия ременной передачи
Принцип действия и классификация. Схема
ременной передачи изображена на рис. 12.1.
Передача состоит
из двух шкивов, закрепленных на валах,
и ремня, охватываРис. 12.1
ющего шкивы.

3.

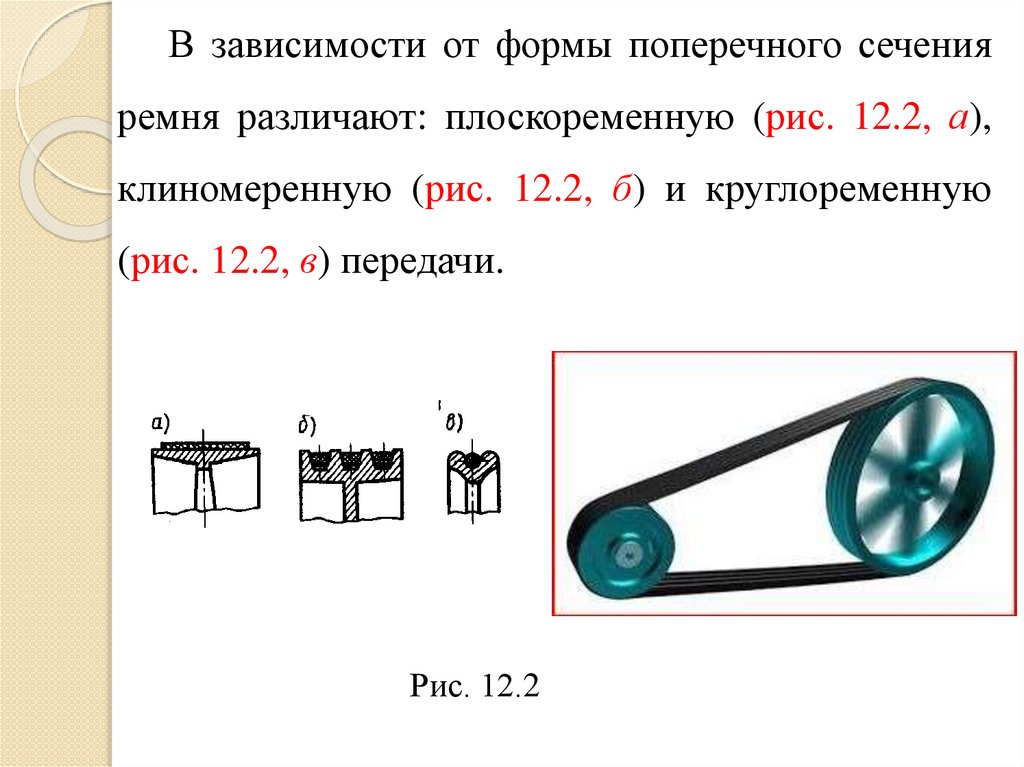
В зависимости от формы поперечного сечения
ремня различают: плоскоременную (рис. 12.2, а),
клиномеренную (рис. 12.2, б) и круглоременную
(рис. 12.2, в) передачи.
Рис. 12.2

4.

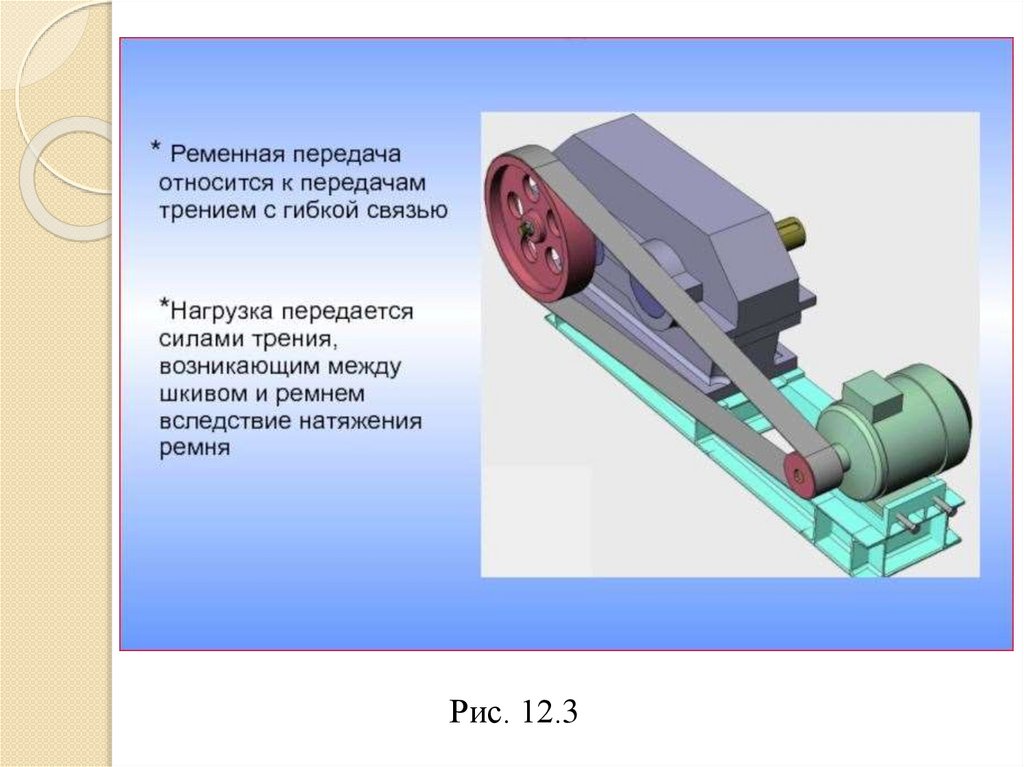
Рис. 12.3

5.

Рис. 12.4

6.

По сравнению с другими типами передач ременная обладает рядом особенностей, которые
определяют целесообразность ее применения.
Для оценки ременной передачи сравним ее с
зубчатой передачей, как наиболее распространенной.
При этом можно отметить следующие основные преимущества ременной передачи:
возможность передачи движения на значительное расстояние (до 15 м и более);

7.

плавность и бесшумность работы, обусловленные эластичностью ремня и позволяющие
работать при высоких скоростях;
предохранение механизмов от резких колебаний нагрузки вследствие упругости ремня;
предохранение механизмов от перегрузки за
счет возможного проскальзывания ремня;
простота конструкции и эксплуатации (передача не требует смазки).

8.

Основными недостатками ременной передачи являются:
повышенные габариты (для одинаковых
условий диаметры шкивов примерно в пять раз
больше диаметров зубчатых колес);
некоторое непостоянство передаточного
отношения, вызванное зависимостью скольжения ремня от нагрузки;
повышенная нагрузка на валы и их опоры,
связанная с большим предварительным натяжением ремня (увеличение нагрузки на валы в 2...3
раза по сравнению с зубчатой передачей);

9.

низкая долговечность ремней (в пределах от
1000 до 5000 ч).
Ременные передачи применяют преимущественно в тех случаях, когда по условиям конструкции валы расположены на значительных
расстояниях. Мощность современных передач не
превышает обычно 50 кВт.
В комбинации с зубчатой передачей ременную
передачу устанавливают обычно на быстроходную ступень, как менее нагруженную.

10.

В современном машиностроении наибольшее
распространение имеют клиновые ремни.
Применение плоских ремней старой конс-
трукции значительно сократилось.
Плоские ремни новой конструкции (пленоч-
ные ремни из пластмасс) получают распространение в высокоскоростных передачах.
Круглые ремни применяют только для малых
мощностей: в приборах, машинах домашнего
обихода и т. п.

11.

2. Основы расчета ременных передач
Теоретические основы расчета являются общими
для всех типов ремней.
Критерии работоспособности и расчета.
Основными критериями работоспособности ременных передач являются: тяговая способность,
определяемая силой трения между ремнем и шкивом, долговечность ремня, которая в условиях
нормальной эксплуатации ограничивается разрушением ремня от усталости.
В настоящее время основным расчетом ременных передач является расчет по тяговой способности.

12.

Кинематические параметры. Окружные скорости на
шкивах
(12.1)
v1 d1 / 60; v2 d 2 / 60.
Учитывая упругое скольжение ремня, можно записать
v2 v1 или
v2 = v1 1
(12.2)
где коэффициент скольжения. При этом передаточное отношение
i= n1 / n2 v1d 2 / v2 d1 d 2 / d1 1
(12.3)
В дальнейшем показано, что величина зависит от нагрузки, поэтому в ременной передаче передаточное отношение не является строго постоянным.

13.

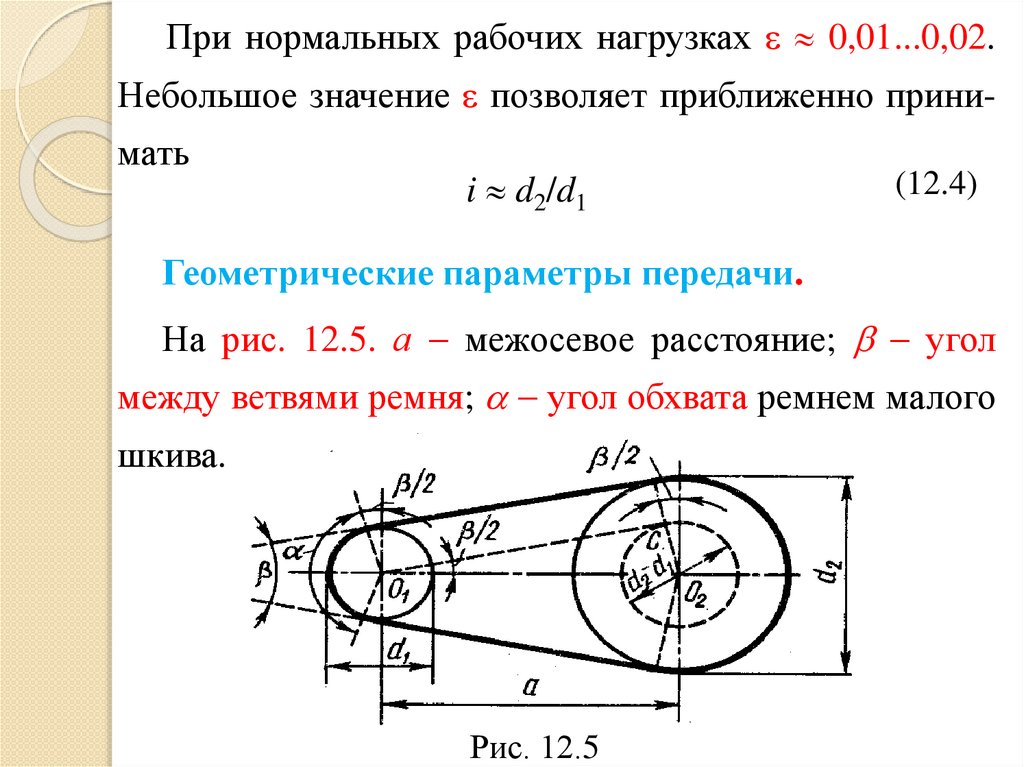
При нормальных рабочих нагрузках 0,01...0,02.
Небольшое значение позволяет приближенно принимать
i d2/d1
(12.4)
Геометрические параметры передачи.
На рис. 12.5. а межосевое расстояние; угол
между ветвями ремня; угол обхвата ремнем малого
шкива.
Рис. 12.5

14.

При геометрическом расчете известными
обычно являются d1, d2, и a, определяют угол и
длину ремня l. Вследствие вытяжки и провисания
ремня значения и не являются точными и определяются приближенно:
180 ; sin 2 d 2 d1 2a
Учитывая, что /2 практически не превышает
15°, приближенно принимаем значение синуса
равным аргументу и запишем

15.

d 2 d1 / a рад 57 d 2 d1 / a
При этом
180 57 d 2 d1 a ,
180 57 d1 i 1 a
или
(12.5)
Длина ремня определяется как сумма прямолинейных
участков и дуг обхвата:
l 2a 0,5 d 2 d1 d 2 d1 4a
2
(12.6)
При заданной длине ремня межосевое расстояние
a
2l d 2 d1
2l d 2 d1 2 8 d 2 d1 2
8
(12 7)

16.

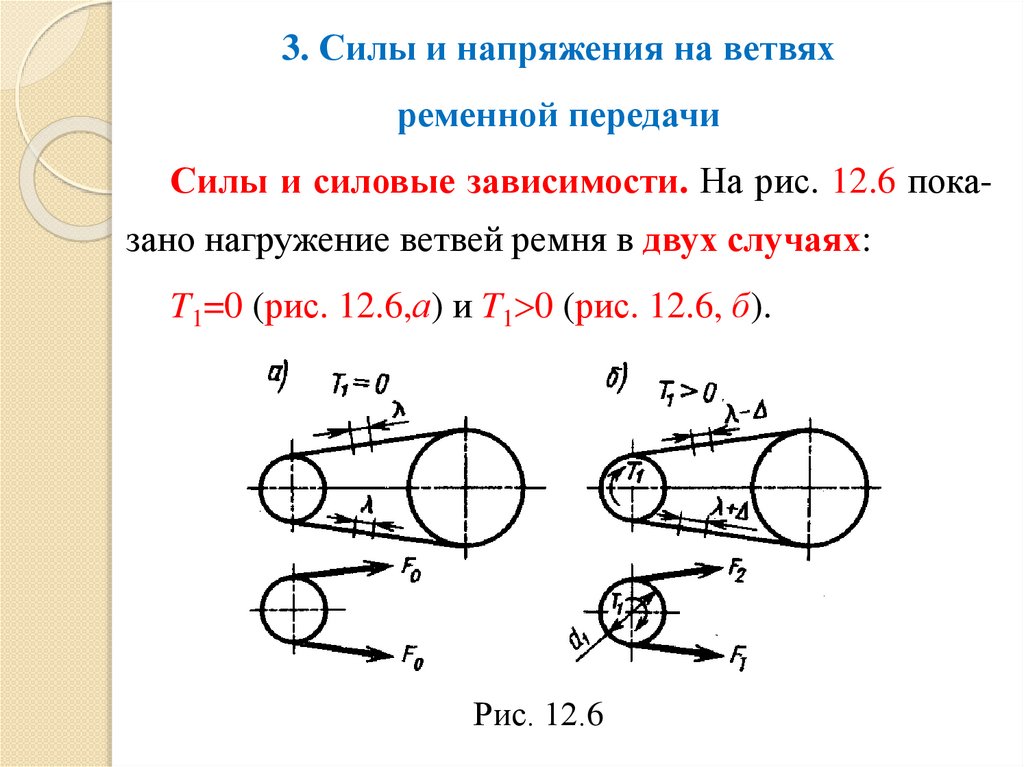
3. Силы и напряжения на ветвях
ременной передачи
Силы и силовые зависимости. На рис. 12.6 пока-
зано нагружение ветвей ремня в двух случаях:
T1=0 (рис. 12.6,а) и T1 0 (рис. 12.6, б).
Рис. 12.6

17.

Здесь обозначено:
F0 предварительное натяжение ремня;
F1 и F2 натяжение ведущей и ведомой ветвей в
нагруженной передаче;
Ft = 2T1/d1 окружная сила передачи.
По условию равновесия шкива имеем
T1 0,5d1 F1 F2
или
F1 F2 Ft
(12.8)
Связь между F0, F1, и F2 можно установить на
основе следующих рассуждений.
Геометрическая длина ремня не зависит от нагрузки [см. формулу (12.6)] и остается неизменной как
в ненагруженной, так и в нагруженной передаче.

18.

Следовательно, дополнительная вытяжка ведущей ветви компенсируется равным сокращением ведомой ветви
(рис. 12.6). Запишем
F1 F0 F , F2 F0 F ,
или
F1 F2 2F0
(12.9)
Из равенств (12.8) и (12.9) следует:
F1 F0 Ft 2 , F2 F0 Ft 2
(12.10)
Получили систему двух уравнений с тремя неизвестными: F0, F1, F2. Эти уравнения устанавливают изменение
натяжений ведущей и ведомой ветвей в зависимости от
нагрузки F1 но не вскрывают способности передавать эту

19.

нагрузку или тяговой способности передачи, которая
связана со значением силы трения между ремнем и
шкивом. Такая связь установлена Эйлером.
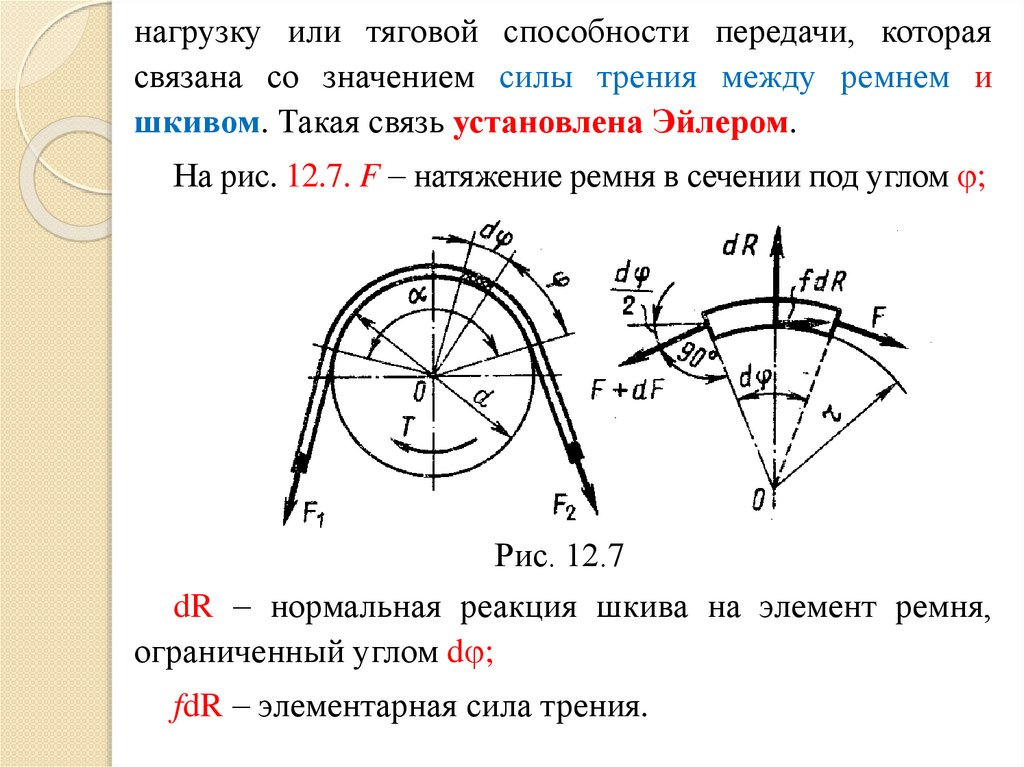
На рис. 12.7. F натяжение ремня в сечении под углом ;
Рис. 12.7
dR нормальная реакция шкива на элемент ремня,
ограниченный углом d ;
fdR элементарная сила трения.

20.

По условиям равновесия,
rF rfdR r F dF 0
(сумма моментов) или fdR = dF;
dR F sin d 2 F dF sin d 2 0
(сумма проекций).
Отбрасывая члены второго порядка малости и принимая sin(d /2) d /2, получаем
dR Fd
Исключая dR находим
dF F fd
Интегрируя, получаем
F1
F1
dF
f
fd
;
In
f
;
e
F F 0
F2
F2
2
F1

21.

или
F1 F2 e f
(12.11)
Решая совместно уравнения (12.8) и (12.11) с учетом
(12.9), находим:
Ft e f 1
e f
1
F1 Ft fa ; F2 Ft f
; F0 f
2 e 1
e 1
e 1
(12.12)
Формулы (12.12) устанавливают связь сил натяжения
ветвей работающей передачи с нагрузкой Ft и факторами
трения f и . Они позволяют также определить минимально необходимое предварительное натяжение ремня
F0, при котором еще возможна передача заданной нагрузки Ft.

22.

Если
F1 e f 1
F0 f
2 e 1
то начнется буксование ремня.
Нетрудно установить [см. формулу (12.12)], что
увеличение значений f и благоприятно отражается
на работе передачи. Эти выводы приняты за основу
при создании конструкций клиноременной передачи и передачи с натяжным роликом.
В первой передаче использован принцип искусственного повышения трения путем заклинивания
ремня в канавках шкива. Во второй увеличивают
угол обхвата установкой натяжного ролика.

23.

Напряжения в ремне. Наибольшие напряжения
создаются в ведущей ветви ремня. Они складываются из 1, v и и:
1 Ft A , F A 2
(12.13)
Учитывая формулу (12.10), напряжение 1 можно
представить в виде
1 F0 A 0,5 Ft A 0 0,5 t
где
t Ft / A
(12.14)
(12.15)
t так называемое полезное напряжение;
0 напряжение от предварительного натяжения.

24.

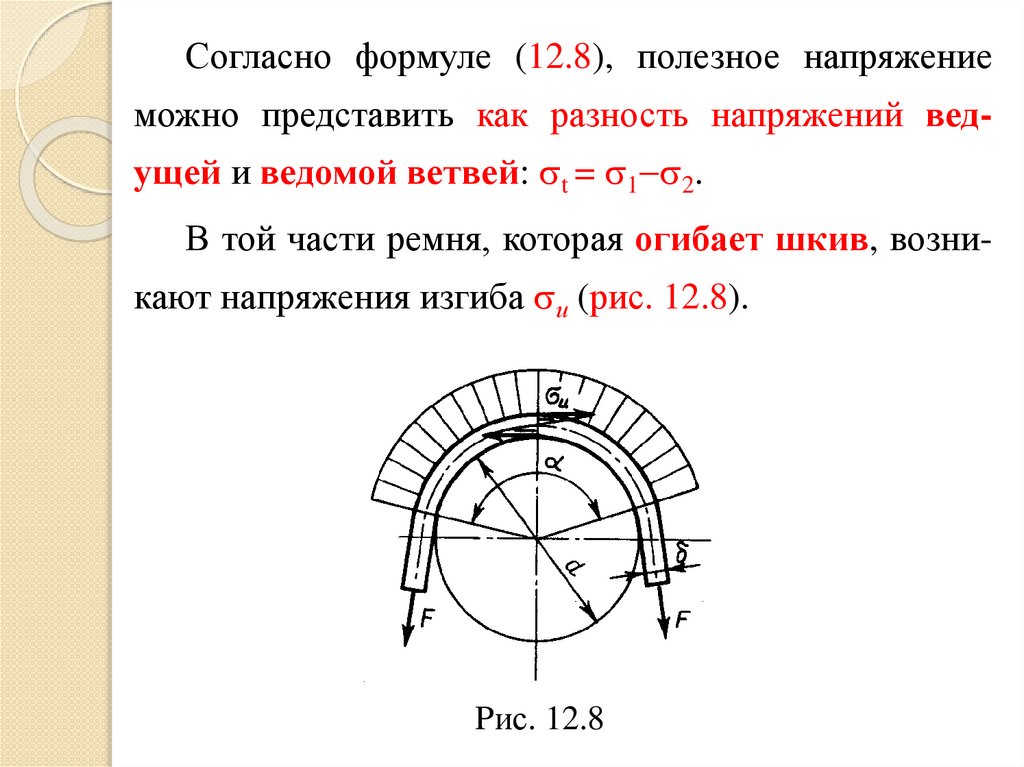
Согласно формуле (12.8), полезное напряжение
можно представить как разность напряжений ведущей и ведомой ветвей: t = 1 2.
В той части ремня, которая огибает шкив, возникают напряжения изгиба и (рис. 12.8).
Pис. 12.8

25.

По закону Гука,
u E
где относительное удлинение, Е модуль упругости. Значение найдем, рассматривая участок дуги ремня,
ограниченный углом d . Длина нейтральной (средней)
линии на этом участке равна (d/2)d , а длина наружней
линии (d/2+ /2)d .
Удлинение наружнего волокна будет
(d/2+ /2)d (d/2)d = /2)d .
Относительное удлинение = ( /2)d /(d/2)d и далее
u E d
(12.16)

26.

Формула (12.16) позволяет отметить, что основным фактором, определяющим значение напряжений
изгиба, является отношение толщины ремня к
диаметру шкива. Чем меньше это отношение, тем
меньше напряжение изгиба в ремне.
Суммарное максимальное напряжение в ведущей
ветви в месте набегания ремня на малый шкив
max 1 u 0 0,5 t u (12.17)
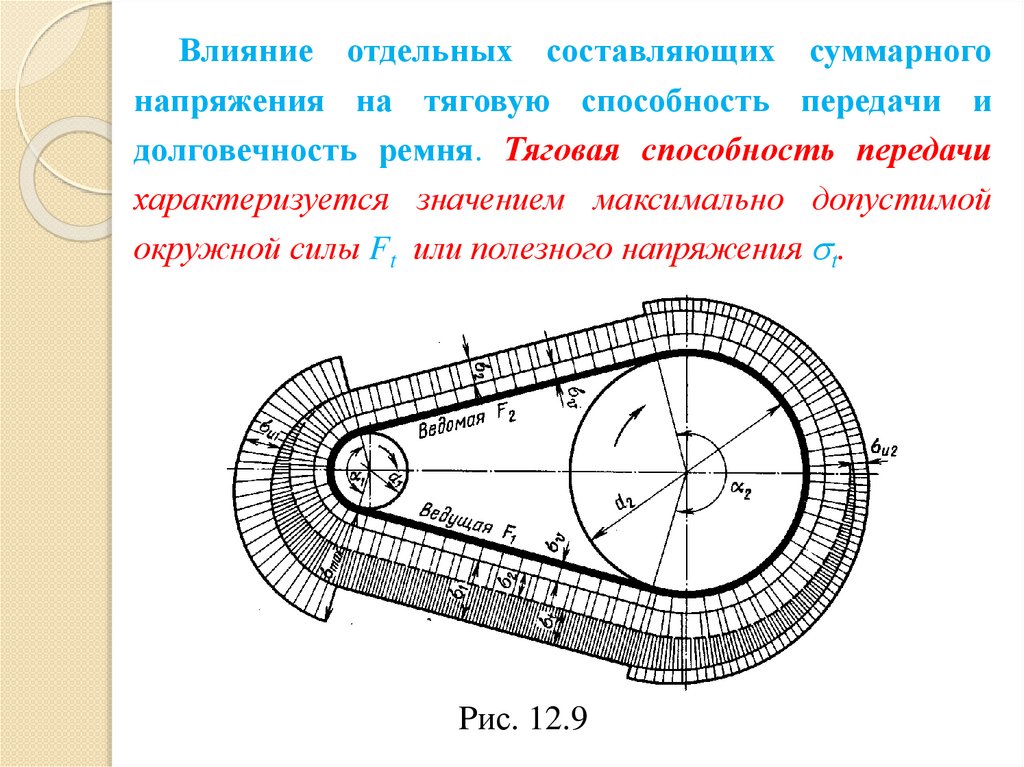
Эпюра распределения напряжений по длине ремня
изображена на рис. 12.9.

27.

Влияние отдельных составляющих суммарного
напряжения на тяговую способность передачи и
долговечность ремня. Тяговая способность передачи
характеризуется значением максимально допустимой
окружной силы Ft или полезного напряжения t.
Pис. 12.9

28.

Учитывая формулу (12.12), нетрудно убедиться, что
допустимое по условию отсутствия буксования t возрастает с увеличением напряжения от предварительного
натяжения 0:
e f 1
t 2 0 f
e 1
(12.18)
Однако практика показывает значительное снижение
долговечности ремня с увеличением 0.
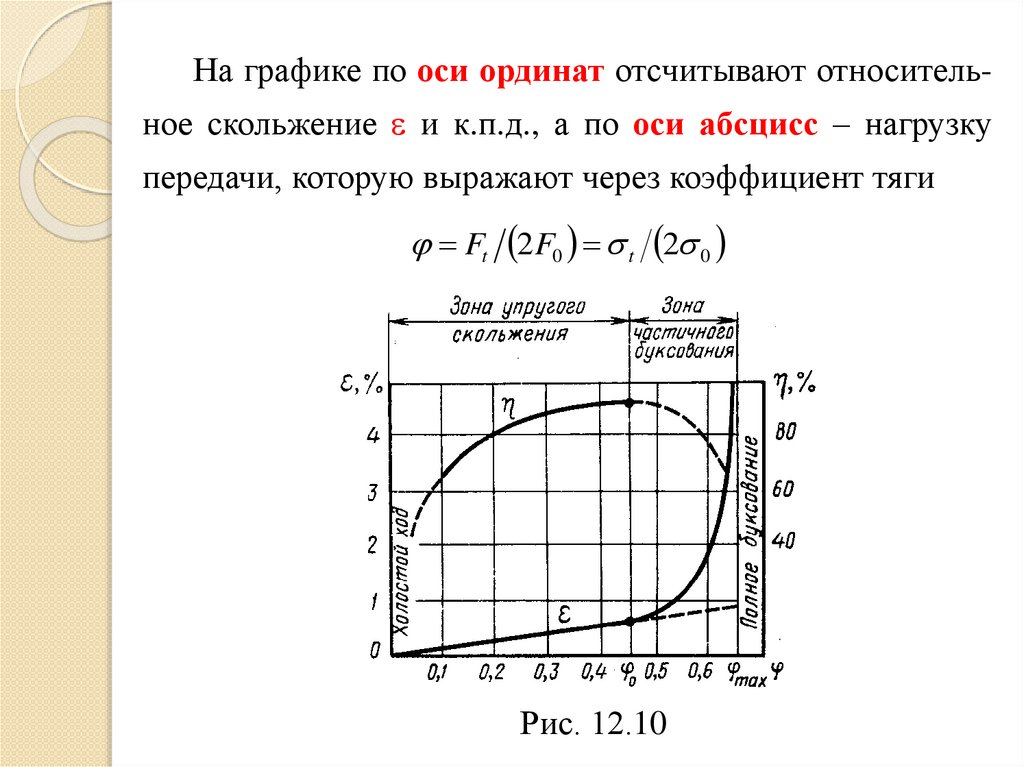
Кривые скольжения и к.п.д. Работоспособность
ременной передачи принято характеризовать кривыми
скольжения и к.п.д (рис. 12.10). Такие кривые являются
результатом испытаний ремней различных типов и
материалов.

29.

На графике по оси ординат отсчитывают относитель-
ное скольжение и к.п.д., а по оси абсцисс – нагрузку
передачи, которую выражают через коэффициент тяги
Ft 2F0 t 2 0
Рис. 12.10

30.

Коэффициент тяги позволяет судить о том, какая
часть предварительного натяжения ремня F0 используется
полезно для передачи нагрузки Ft, т.е. характеризует
степень загруженности передачи. Целесообразность выражения нагрузки передачи через безразмерный коэффициент объясняется тем, что скольжение и к.п.д. связаны
именно со степенью загруженности передачи, а не с абсолютным значением нагрузки.
На начальном участке кривой скольжения от 0 до 0
наблюдается только упругое скольжение. Так как упругие деформации ремня приближенно подчиняются закону Гука, этот участок близок к прямолинейному.

31.

Дальнейшее
увеличение
нагрузки
приводит
к
частичному, а затем и полному буксованию. В зоне
0… max наблюдается как упругое скольжение, так и
буксование. Они разделяются продолжением прямой
штриховой линией.
Рабочую нагрузку рекомендуют выбирать вблизи
критического значения 0 и слева от нее. Этому значению
соответствует также и максимальное значение к.п.д.
Работу в зоне частичного буксования допускают
только при кратковременных перегрузках, например при
пуске. В этой зоне к.п.д. резко снижается вследствие
увеличения потерь на скольжение ремня, а ремень
быстро изнашивается.

32.

Размер зоны частичного буксования характеризует
способность передачи воспринимать кратковременные
перегрузки.
Отношение max/ 0 для ремней:
плоских кожаных и шерстяных 1,35...1,5;
прорезиненных 1,15...1,3;
хлопчатобумажных 1,25... 1,4;
клиновых 1,5...1,6.
Допускаемые полезные напряжения в ремне.
Определив по кривым скольжения 0, находят полезное допускаемое напряжения для испытуемой передачи
(см. предыдущую формулу):

33.

t 0 2 0 0
s
(12.19)
где s 1,2...1,4 запас тяговой способности по
буксованию.
Кривые скольжения получают при испытаниях
ремней на типовых стендах при типовых условиях:
=180°, v = 10 м/с, нагрузка равномерная, передача
горизонтальная.
Переход от значений [ t]0 для типовой передачи к
допускаемым полезным напряжениям [ t] для проектируемой передачи производят с помощью корректирующих коэффициентов:
t t 0 C Cv C p C0
(12.20)

34.

где C коэффициент угла обхвата, учитывающий
снижение тяговой способности передачи с уменьшением
угла обхвата:
, град …150
160
170
180
200
220
C …….…0,91
0,94
0,97
1,0
1,1
1,2
Cv скоростной коэффициент, вводимый только для
передачи без автоматического регулирования натяжения
(см. ниже) и учитывающий уменьшение прижатия ремня
к шкиву под действием центробежных сил:
v, м/с ...... 5
Cv ………1,03
10
15
20
25
30
1,00
0,95
0,88
0,79
0,68

35.

Ср коэффициент режима нагрузки, учитывающий
влияние периодических колебаний нагрузки на долговечность ремня.
Умеренные Значительные
Нагрузка Спокойная
колебания
колебания
Ср
1..0,85
0,9...0,8
0,8. .0,7
Ударная
и резко
переменная
0,7...0,6
Примечание. Меньшие значения для поршневых и других подобных
двигателей.

36.

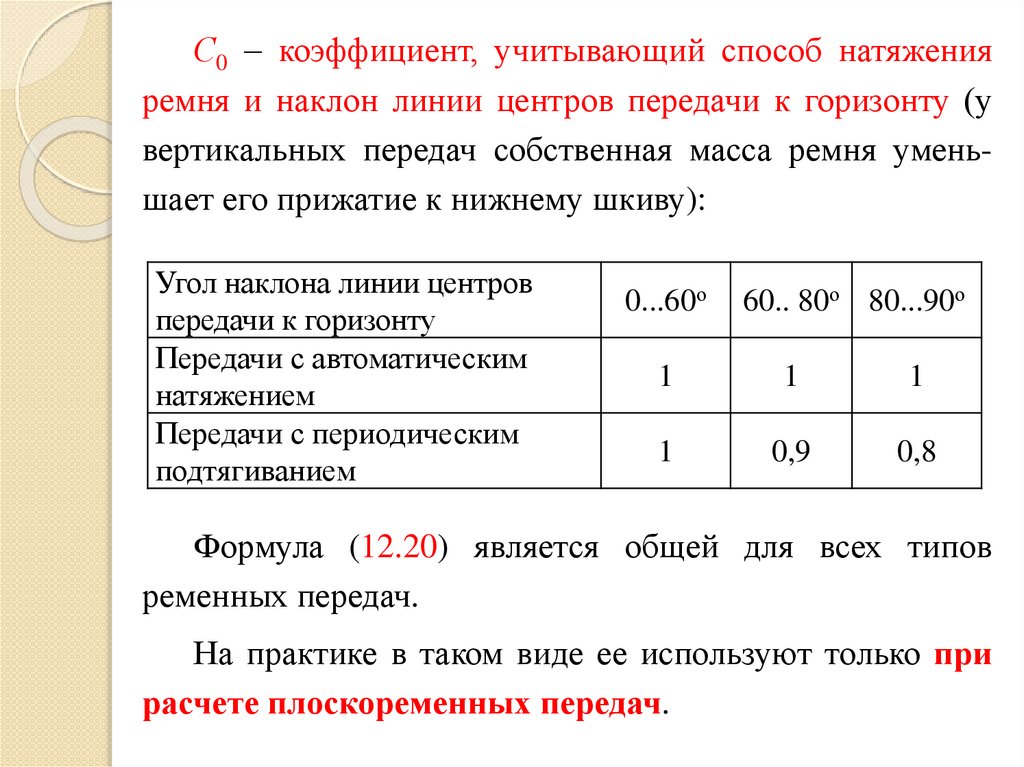
С0 коэффициент, учитывающий способ натяжения
ремня и наклон линии центров передачи к горизонту (у
вертикальных передач собственная масса ремня уменьшает его прижатие к нижнему шкиву):
Угол наклона линии центров
передачи к горизонту
Передачи с автоматическим
натяжением
Передачи с периодическим
подтягиванием
0...60о
60.. 80о 80...90о
1
1
1
1
0,9
0,8
Формула (12.20) является общей для всех типов
ременных передач.
На практике в таком виде ее используют только при
расчете плоскоременных передач.