Цифровая схемотехника

1. Цифровая схемотехника

• Карпов С.Б. Цифровая схемотехника: комбинационные схемы.
Учебно-методическое пособие по спецкурсу
• Калабеков Б.А. Цифровые устройства и микропроцессорные системы
• Угрюмов Е.П. Цифровая схемотехника
• Триггеры: Метод. указания к спецпрактикуму по линейным и
нелинейным системам и к лабораторным работам по цифровой
схемотехнике / Перм.ун-т; Сост. С.И.Гущин, С.Б.Карпов, И.В.Лунегов.
• Счетчики и делители частоты: метод. указания к спецпрактикуму
по линейным и нелинейным системам и к лабораторным работам
по цифровой схемотехнике / Перм.ун-т; Сост. С.И.Гущин,
С.Б.Карпов, И.В.Лунегов.
• Амелина М.А., Амелин С.А. Программа схемотехнического
моделирования Micro-Cap 8

2.

Схемотехника
Схемотехника ‒ занимается проектированием, синтезом и
анализом электронных схем и устройств различного назначения
Операции над сигналами:
‒ Передача
‒ Обработка
‒ Хранение
Аналоговая схемотехника ‒
аналоговые сигналы: напряжение и ток
Цифровая схемотехника ‒
цифровые сигналы: напряжение и ток
2

3.

Аналоговая схемотехника
Аналоговый сигнал ‒ изменяется непрерывно во времени в
определенном диапазоне значений.
+E
Uвых = K * Uвх
Uвых = U1 + U2
3

4.

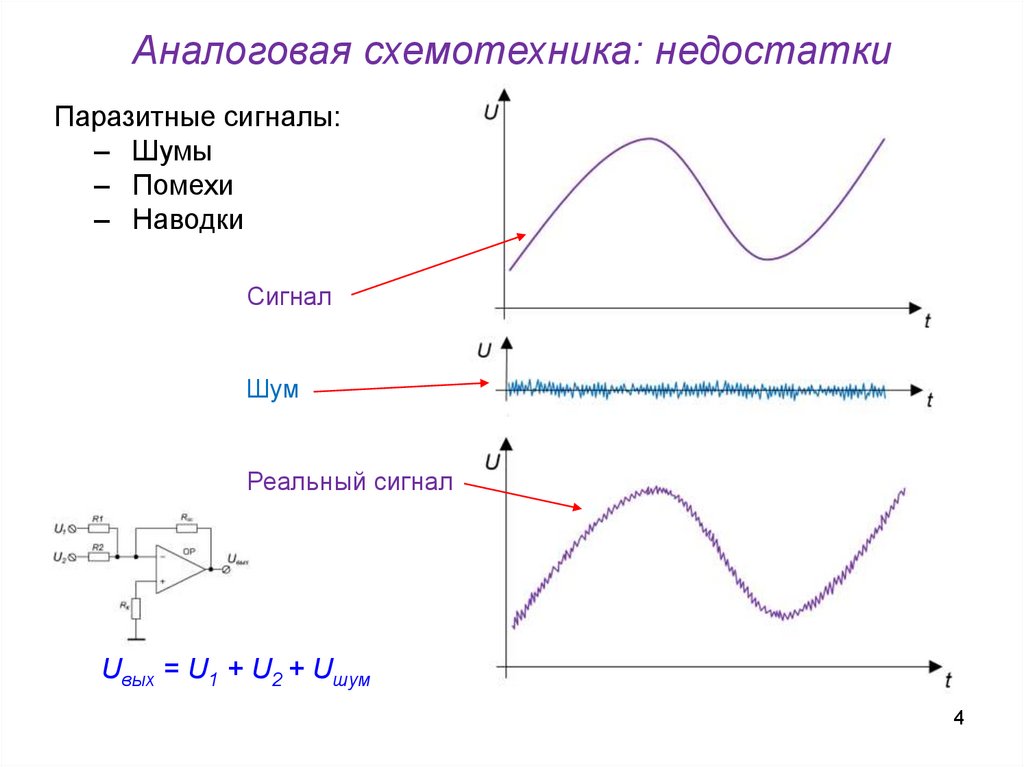
Аналоговая схемотехника: недостатки
Паразитные сигналы:
‒ Шумы
‒ Помехи
‒ Наводки
Сигнал
Шум
Реальный сигнал
Uвых = U1 + U2 + Uшум
4

5.

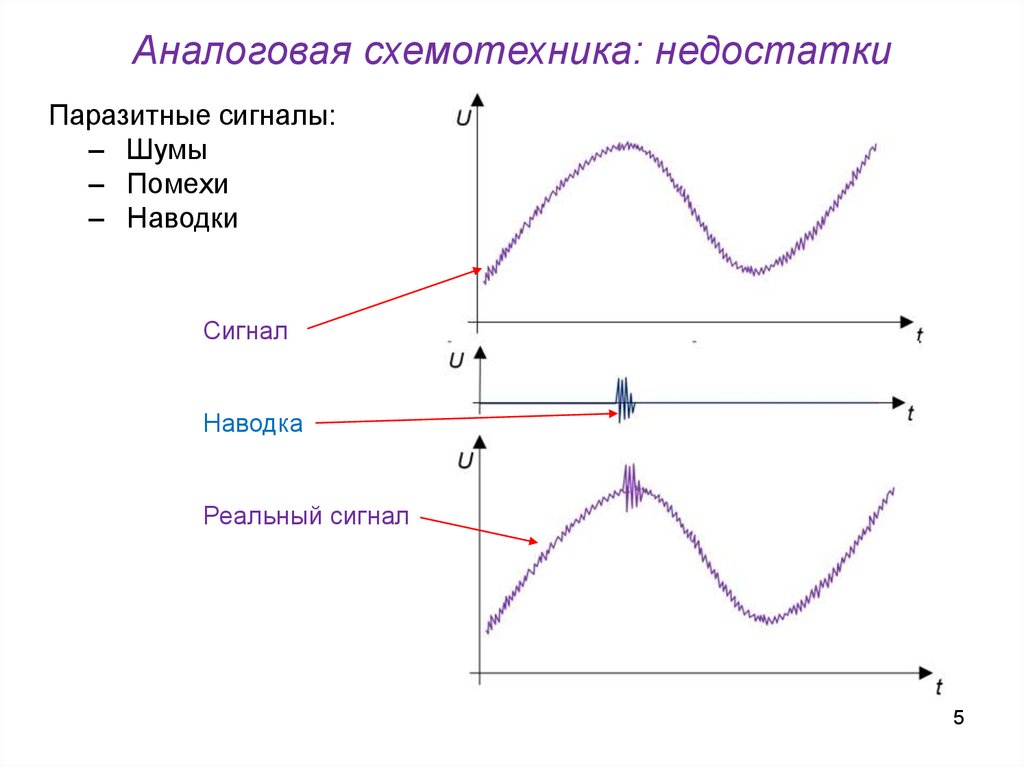
Аналоговая схемотехника: недостатки
Паразитные сигналы:
‒ Шумы
‒ Помехи
‒ Наводки
Сигнал
Наводка
Реальный сигнал
5

6.

Аналоговая схемотехника: недостатки
Ограниченность частотной характеристики
Частотные искажения
Uвых = K * Uвх
Входной сигнал
Выходной сигнал
6

7.

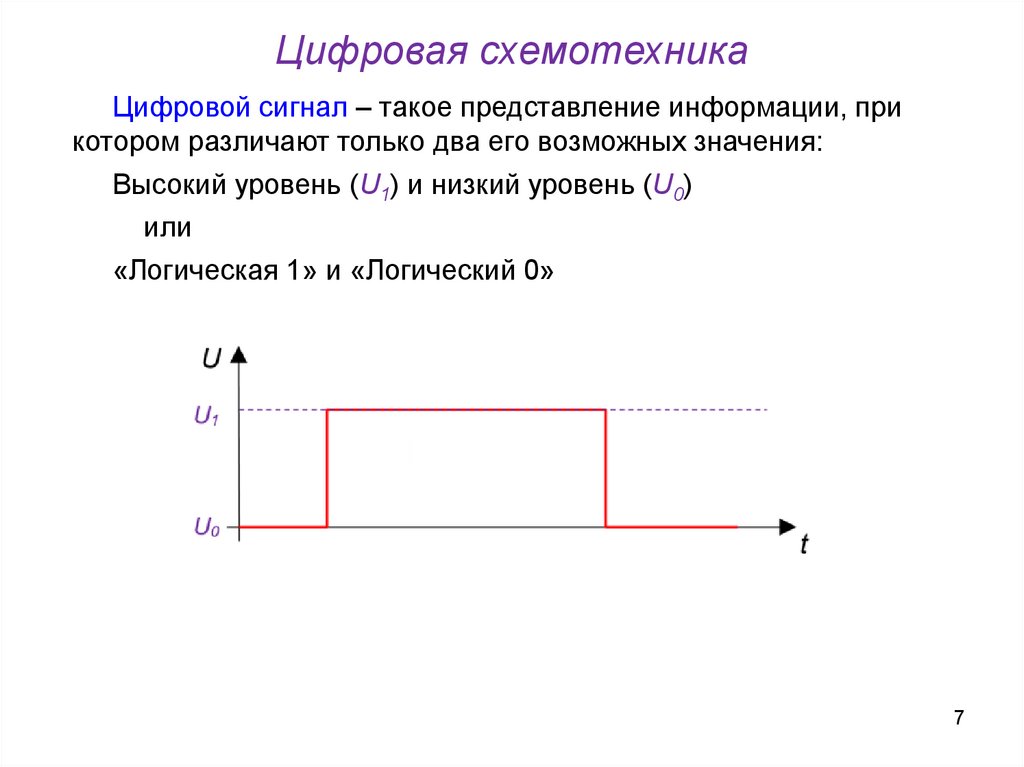
Цифровая схемотехника
Цифровой сигнал – такое представление информации, при
котором различают только два его возможных значения:
Высокий уровень (U1) и низкий уровень (U0)
или
«Логическая 1» и «Логический 0»
7

8.

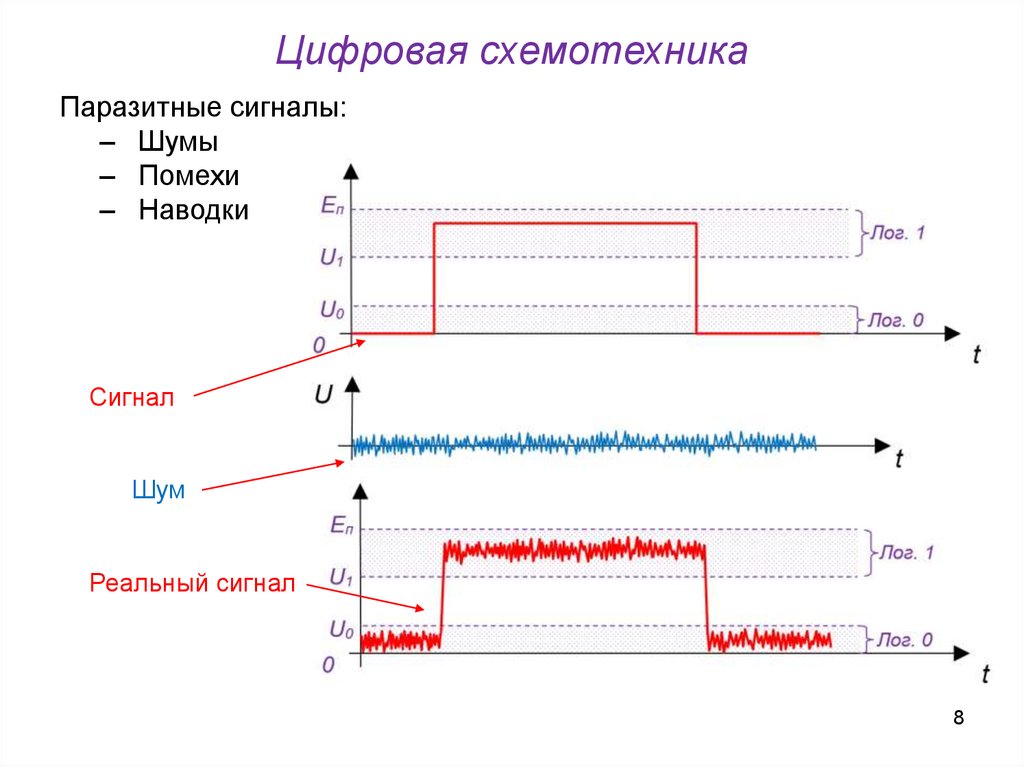
Цифровая схемотехника
Паразитные сигналы:
‒ Шумы
‒ Помехи
‒ Наводки
Сигнал
Шум
Реальный сигнал
8

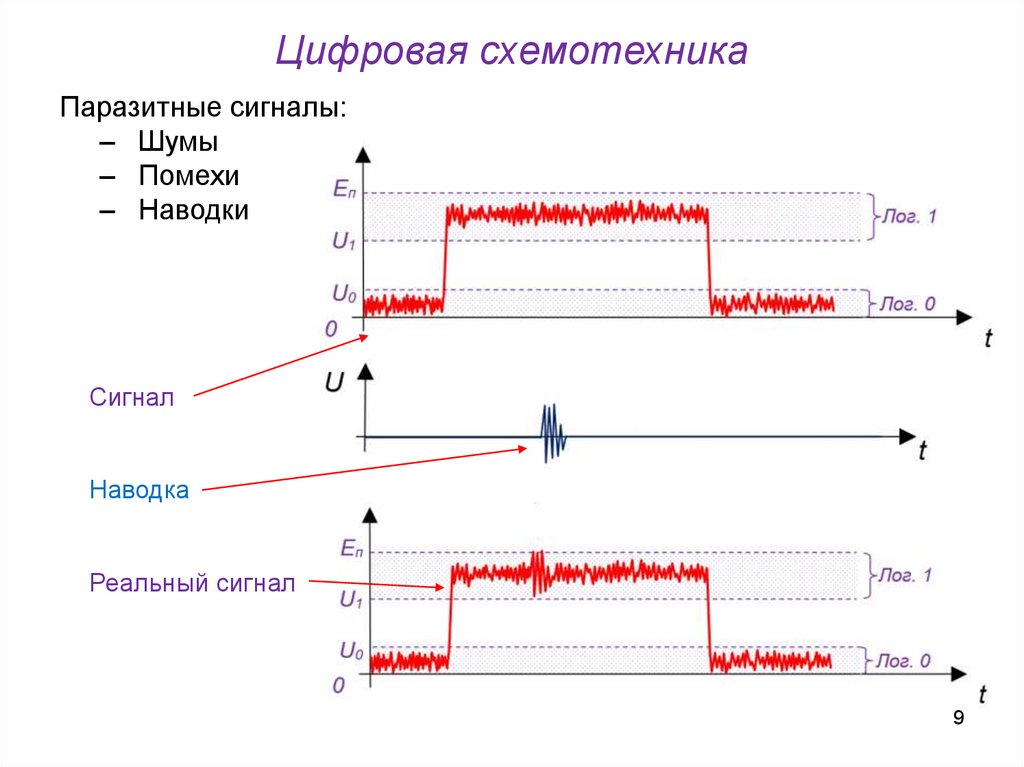
9.

Цифровая схемотехника
Паразитные сигналы:
‒ Шумы
‒ Помехи
‒ Наводки
Сигнал
Наводка
Реальный сигнал
9

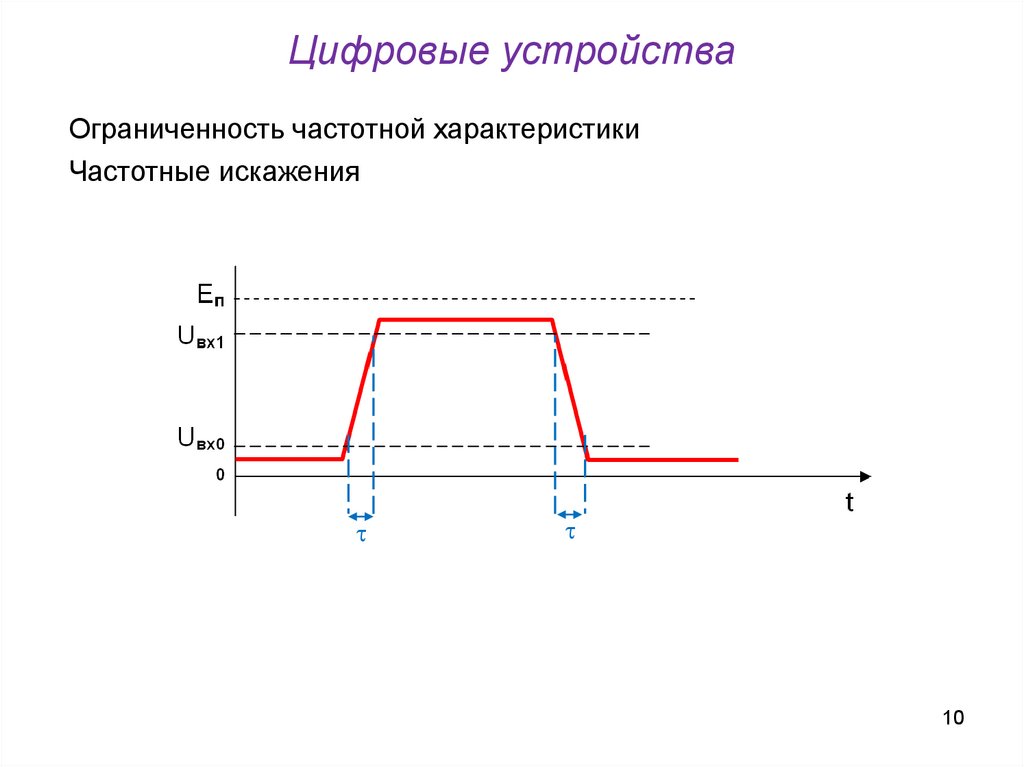
10.

Цифровые устройства
Ограниченность частотной характеристики
Частотные искажения
10

11.

Цифровые устройства
Цифровые устройства предназначены для преобразования
цифровой информации и работают с цифровыми (дискретными,
логическими) сигналами.
Цифровой сигнал – такое представление информации, при
котором различают только два его возможных значения:
«логический 0» и «логическая 1».
Эти сигналы могут быть представлены в виде напряжений
низкого и высокого уровней (или ток НЕ течет и ток
течет).
11

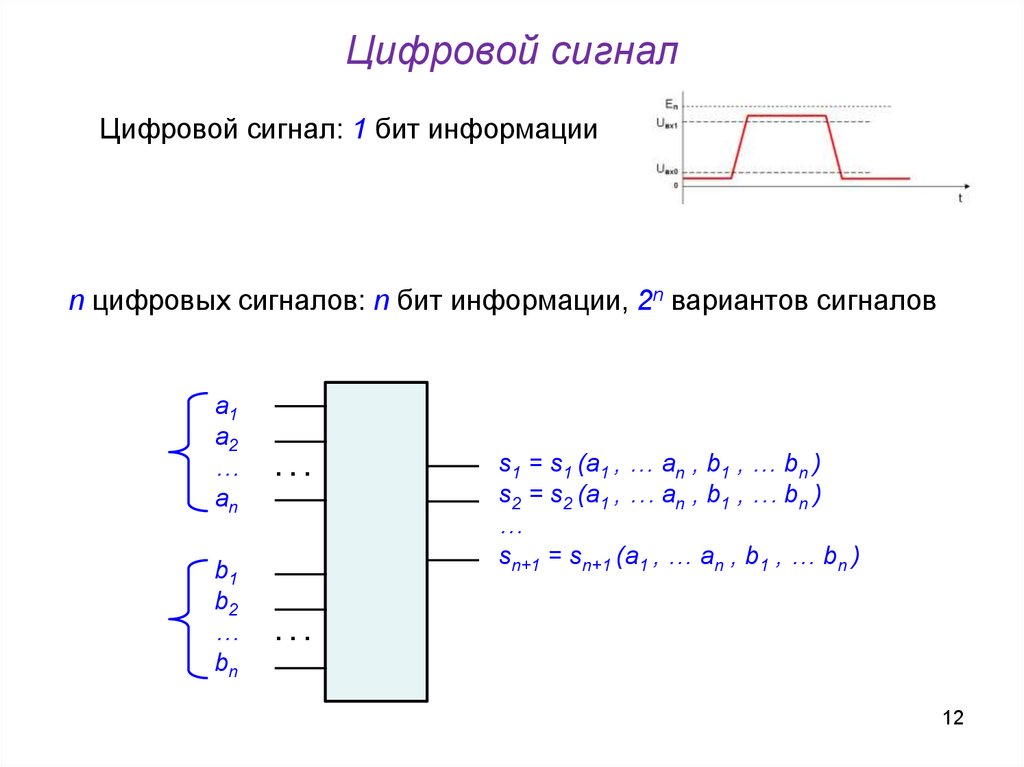
12.

Цифровой сигнал
Цифровой сигнал: 1 бит информации
n цифровых сигналов: n бит информации, 2n вариантов сигналов
a1
a2
…
an
b1
b2
…
bn
...
s1 = s1 (a1 , … an , b1 , … bn )
s2 = s2 (a1 , … an , b1 , … bn )
…
sn+1 = sn+1 (a1 , … an , b1 , … bn )
...
12

13.

Алгебра логики – для описания
логических сигналов
Любой сигнал в цифровой схемотехнике может принимать
только одно из двух возможных значений
Основным понятием алгебры логики является высказывание,
в отношении которого можно сказать истинно оно или ложно.
Это позволяет применить для описания и расчета цифровых
устройств алгебру логики.
В алгебре логики с помощью логических связок из
высказываний можно составлять сложные высказывания, которые
тоже будут истинны или ложны.
Если обозначить высказывания буквами, истинность и
ложность обозначить соответственно 1 и 0 и придумать
обозначения для логических связок, мы получим возможность
записывать сложные высказывания в виде алгебраических
выражений (функций алгебры логики).
13

14. Основы алгебры логики

Основное понятие алгебры логики – высказывание, в
отношении которого можно сказать истинно оно или ложно.
Простые высказывания в алгебре логики будем называть
аргументами, сложные – функциями.
И аргументы и функции принимают лишь одно из двух
возможных значений: «ложь» и «истина», или «логический 0» и
«логическая 1».
В алгебре логики справедлив принцип суперпозиции:
сложные высказывания, могут быть аргументами других, более
сложных высказываний.
14

15. Основы алгебры логики

Аргументы принимают одно из двух возможных значений: 0 или 1.
Ограниченность значений аргументов приводит к тому, что и
область определения любой функции тоже ограничена.
Для функции n аргументов возможно всего 2n разных вариантов
(или наборов) значений аргументов.
Любую функцию можно задать, перечислив все ее возможные
значения на всех наборах аргументов.
Таблица истинности функции двух аргументов
15

16. Основы алгебры логики

Таблица истинности функции двух аргументов
Значения функции
Наборы аргументов
Номер набора
16

17. Таблицы истинности

Таблица истинности функций:
двух аргументов
трех аргументов
Область определения функций ограничена:
2n наборов аргументов
четырех аргументов
17

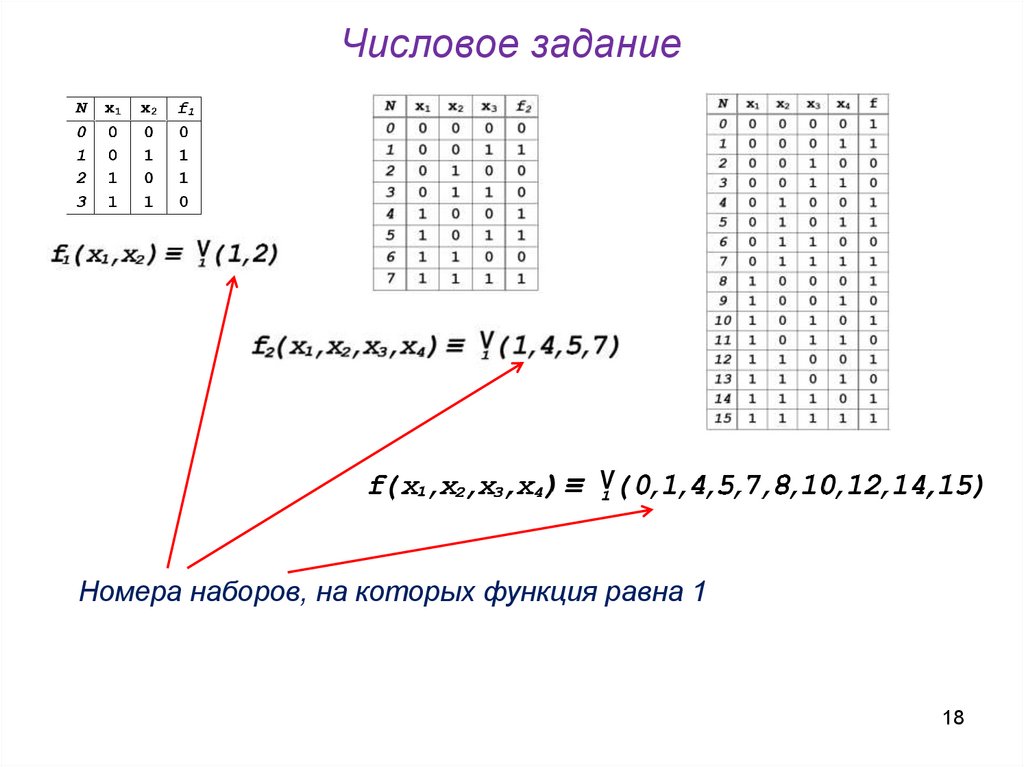
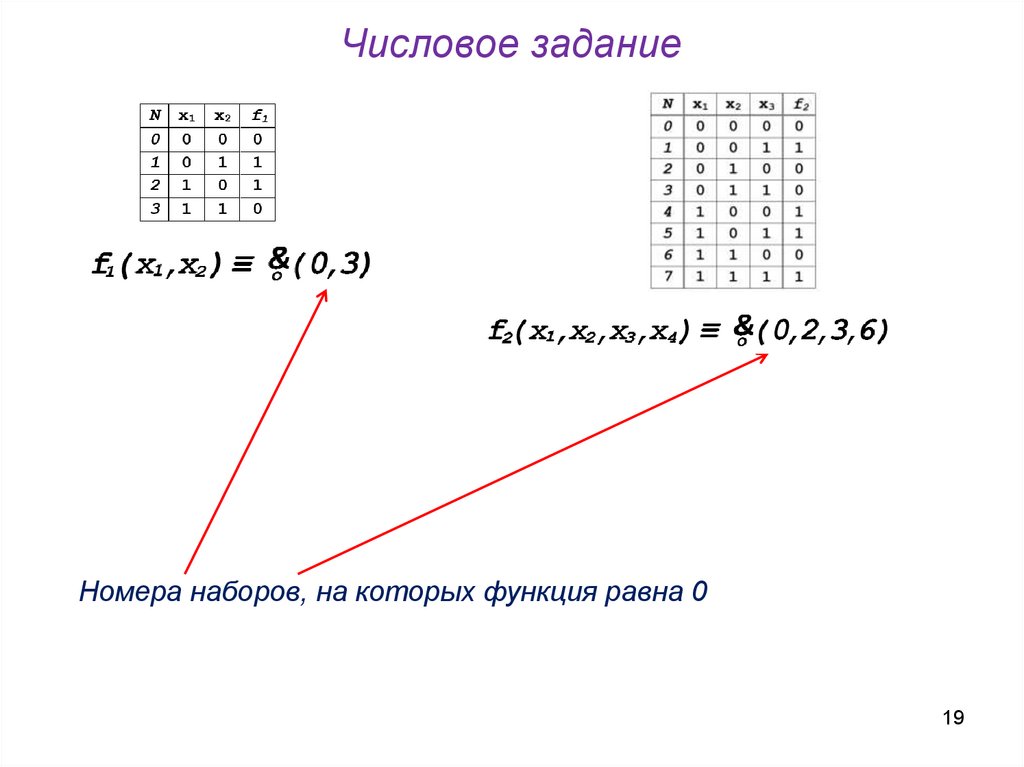
18. Числовое задание

Номера наборов, на которых функция равна 1
18

19. Числовое задание

Номера наборов, на которых функция равна 0
19

20. Основы алгебры логики

Область определения любой функции ограничена.
У функции n аргументов – 2n наборов аргументов.
Число различных функций алгебры логики, зависящих от n
аргументов, равно
.
Равносильные функции – принимают на всех возможных наборах
аргументов одинаковые значения:
20

21. Операции алгебры логики

Унарная операция
Операция отрицание или операция НЕ или инверсия
Обозначение:
21

22. Операции алгебры логики

Определена для двух и более высказываний
Операция дизъюнкция или операция ИЛИ
Обозначение:
Х1 V Х2
22

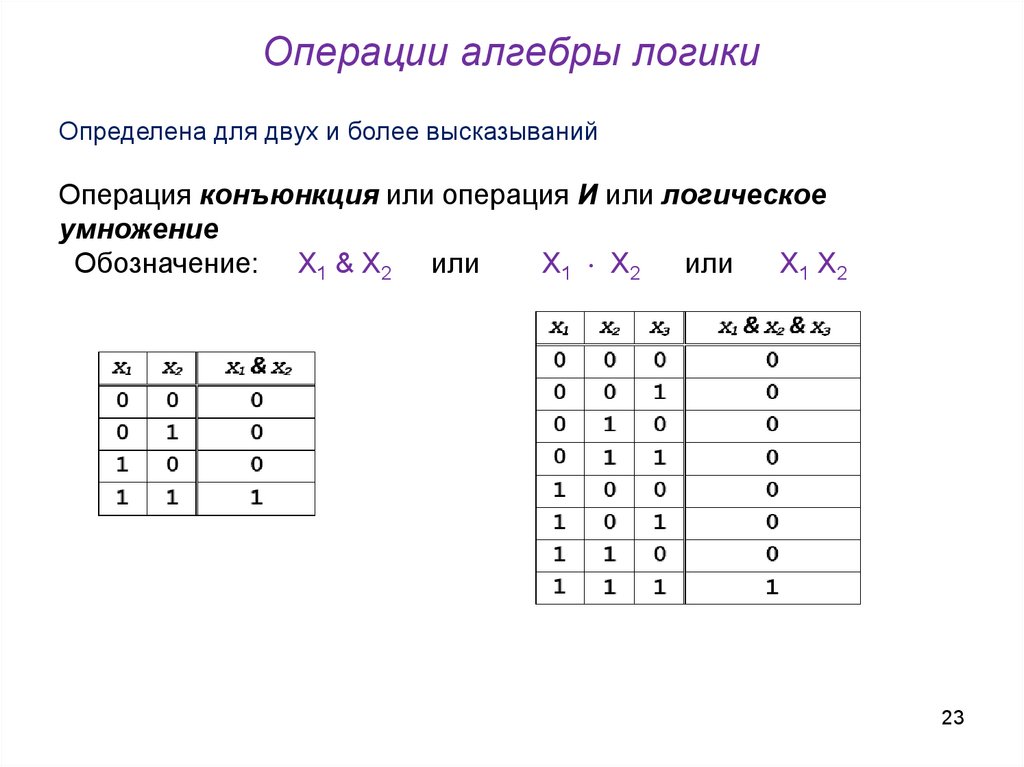
23. Операции алгебры логики

Определена для двух и более высказываний
Операция конъюнкция или операция И или логическое
умножение
Обозначение: Х1 & Х2 или
Х1 Х2
или
Х1 Х2
23

24. Операции алгебры логики

Операции дизъюнкция, конъюнкция и отрицание образуют
базис, т.е. с помощью этих операций можно записать любую,
сколь угодно сложную функцию алгебры логики.
24

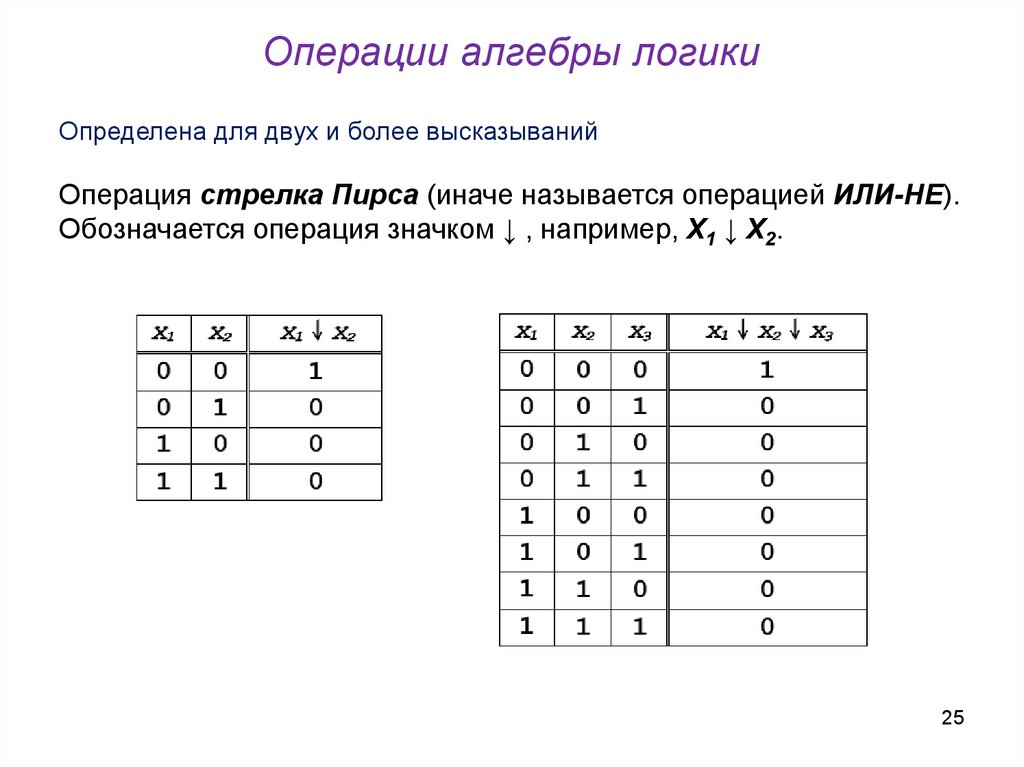
25. Операции алгебры логики

Определена для двух и более высказываний
Операция стрелка Пирса (иначе называется операцией ИЛИ-НЕ).
Обозначается операция значком ↓ , например, Х1 ↓ Х2.
25

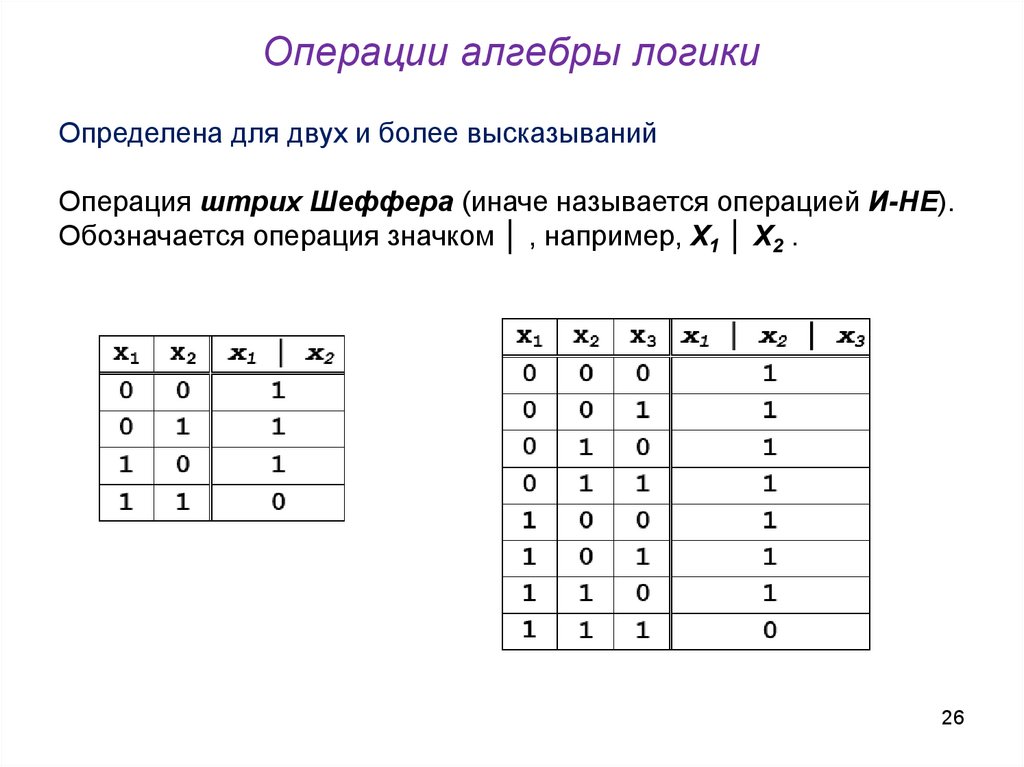
26. Операции алгебры логики

Определена для двух и более высказываний
Операция штрих Шеффера (иначе называется операцией И-НЕ).
Обозначается операция значком │ , например, Х1 │ Х2 .
26

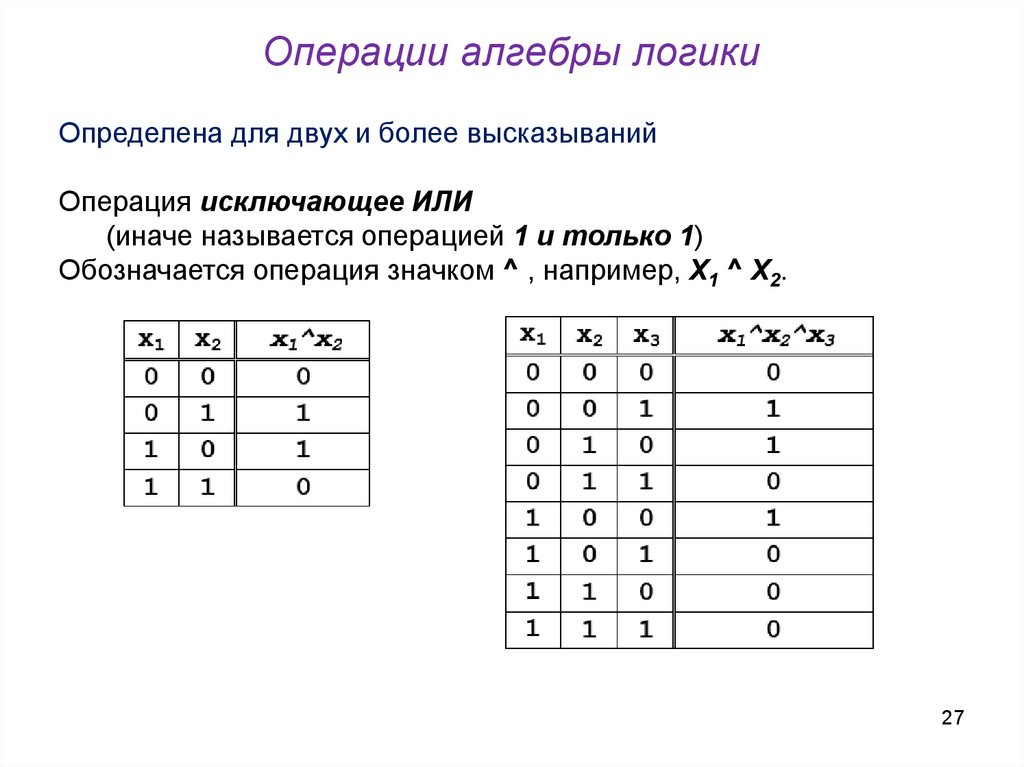
27. Операции алгебры логики

Определена для двух и более высказываний
Операция исключающее ИЛИ
(иначе называется операцией 1 и только 1)
Обозначается операция значком ^ , например, Х1 ^ Х2.
27

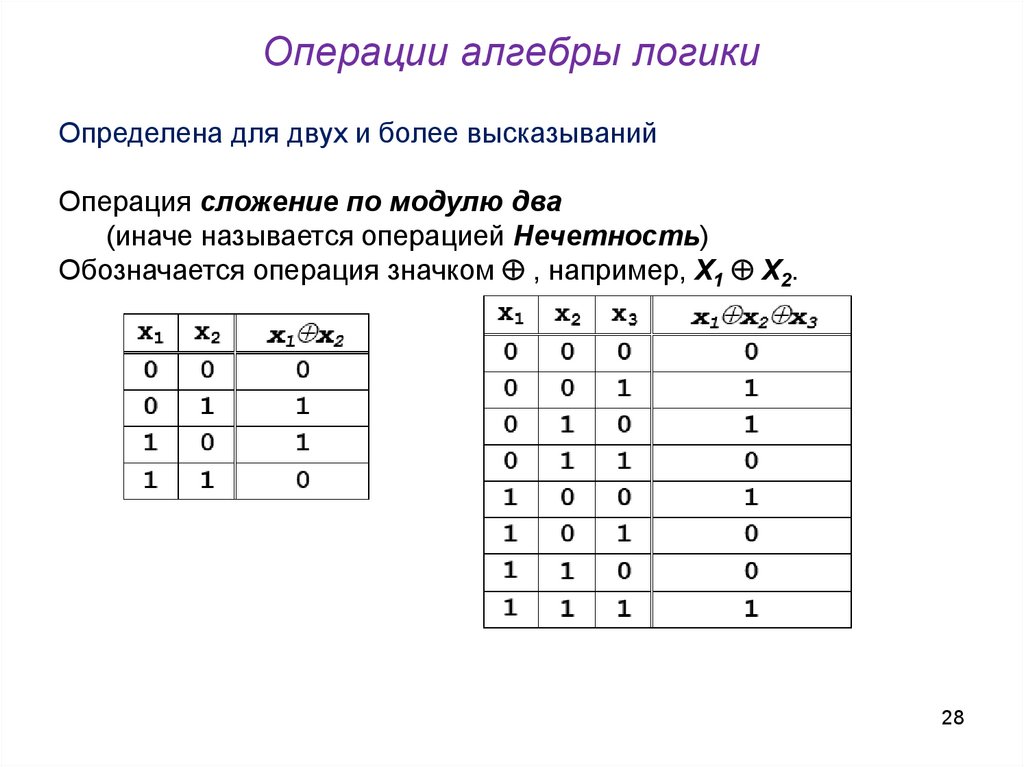
28. Операции алгебры логики

Определена для двух и более высказываний
Операция сложение по модулю два
(иначе называется операцией Нечетность)
Обозначается операция значком , например, Х1 Х2.
28

29. Операции алгебры логики

Определена для двух и более высказываний
Операция эквиваленция (или равнозначность).
Обозначается операция значком ~ , например, Х1 ~ Х2.
29

30. Операции алгебры логики

Определена только для двух высказываний
Операция импликация.
Обозначается операция значком → , например, Х1 → Х2
(читается Х1 имплицирует Х2).
30

31. Операции алгебры логики

Определена только для двух высказываний
Операция запрет.
Обозначается операция значком ← , например, Х2 ← Х1
(читается справа налево: Х1 запрещает Х2).
31

32. Операции алгебры логики

Операция N и только N для m высказываний, где N < m.
Результат операции истинен, когда истинно N и только N из
входящих в него высказываний, и ложен в противном случае.
Например, два и только два для трех высказываний.
32

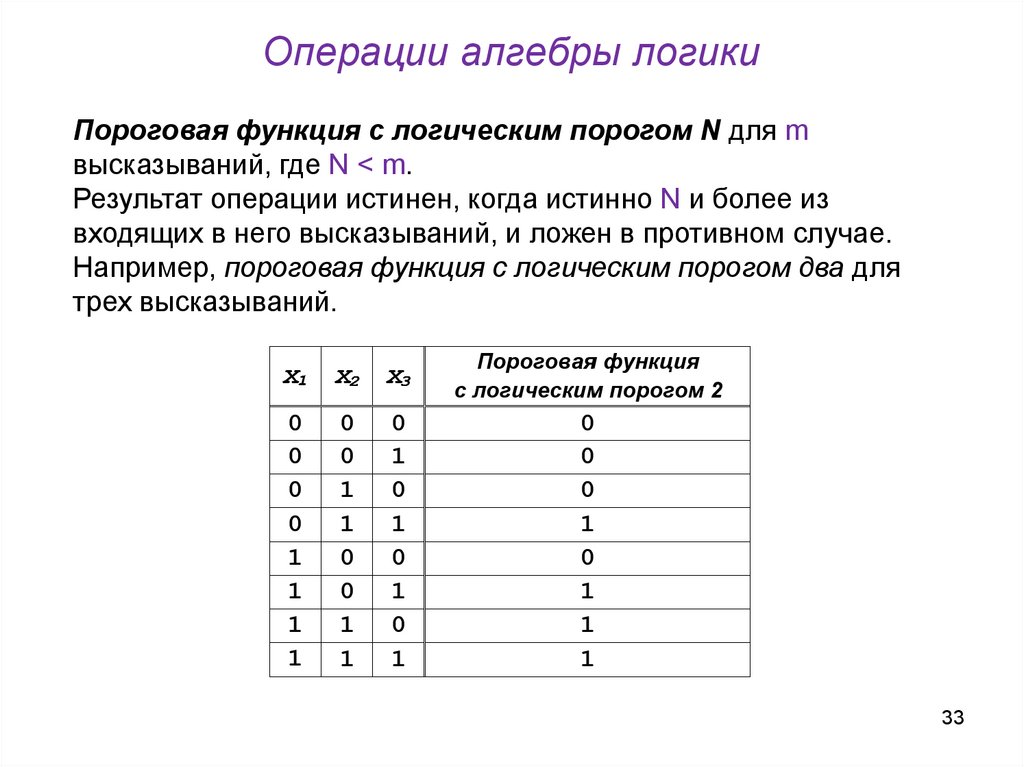
33. Операции алгебры логики

Пороговая функция с логическим порогом N для m
высказываний, где N < m.
Результат операции истинен, когда истинно N и более из
входящих в него высказываний, и ложен в противном случае.
Например, пороговая функция с логическим порогом два для
трех высказываний.
33

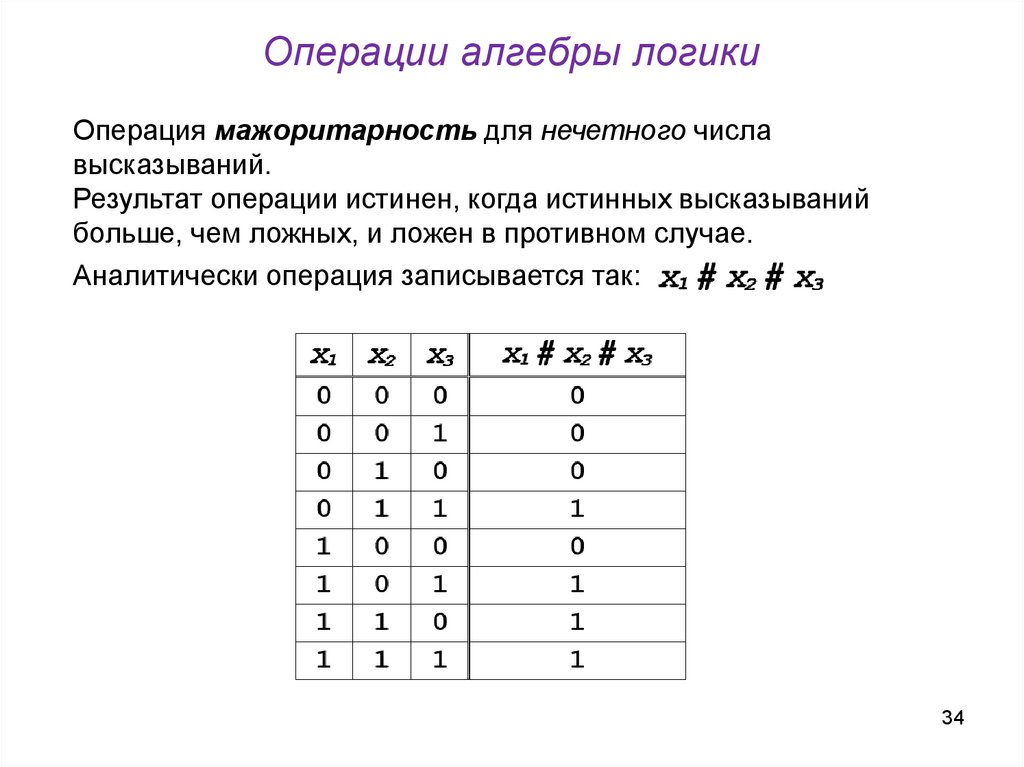
34. Операции алгебры логики

Операция мажоритарность для нечетного числа
высказываний.
Результат операции истинен, когда истинных высказываний
больше, чем ложных, и ложен в противном случае.
Аналитически операция записывается так:
34

35. Операции алгебры логики

Число функций для n аргументов ограничено,
например, в случае n=2 получается всего 16 функций
35

36.

Цифровые устройства
Простейшие схемы, работа которых может быть описана с
помощью основных операций алгебры логики, называются
логическими элементами.
Знак инверсии
36

37. Нормально разомкнутый контакт

Реализация логических элементов
на реле
a=1
0
Нормально разомкнутый контакт
a=0
1
Нормально замкнутый контакт
37

38. Логический элемент Повторитель

Реализация логического элемента
на реле
a=0
1
Логический элемент Повторитель
a
y
0
1
0
1
38

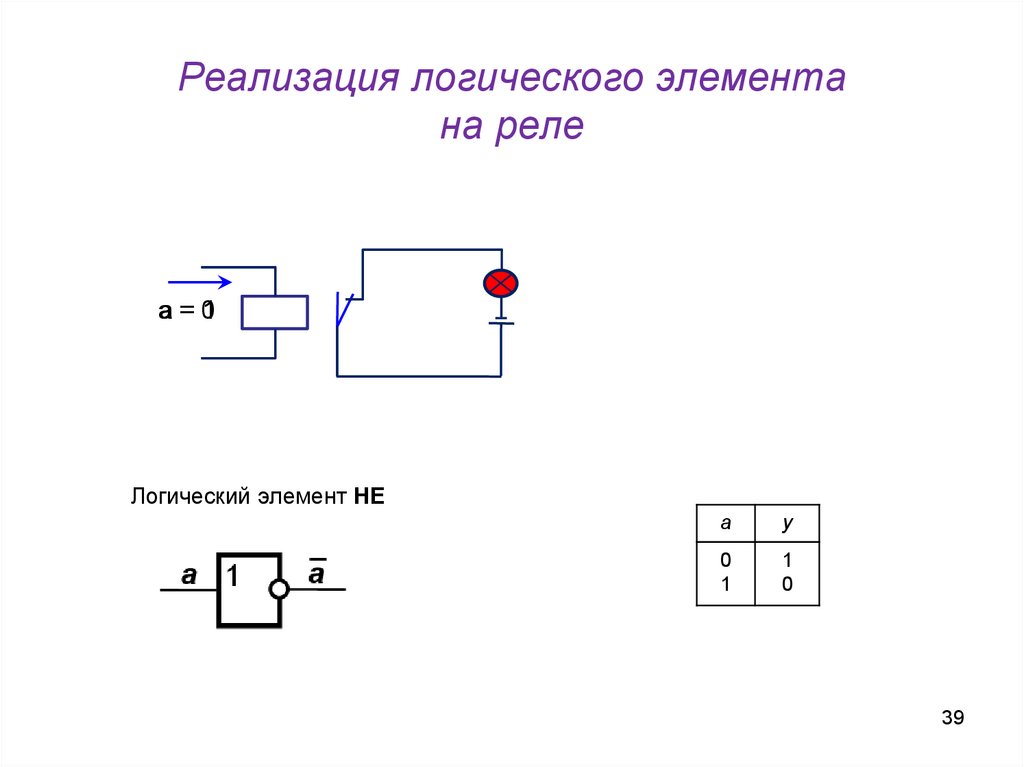
39. Логический элемент НЕ

Реализация логического элемента
на реле
a=0
1
Логический элемент НЕ
a
y
0
1
1
0
39

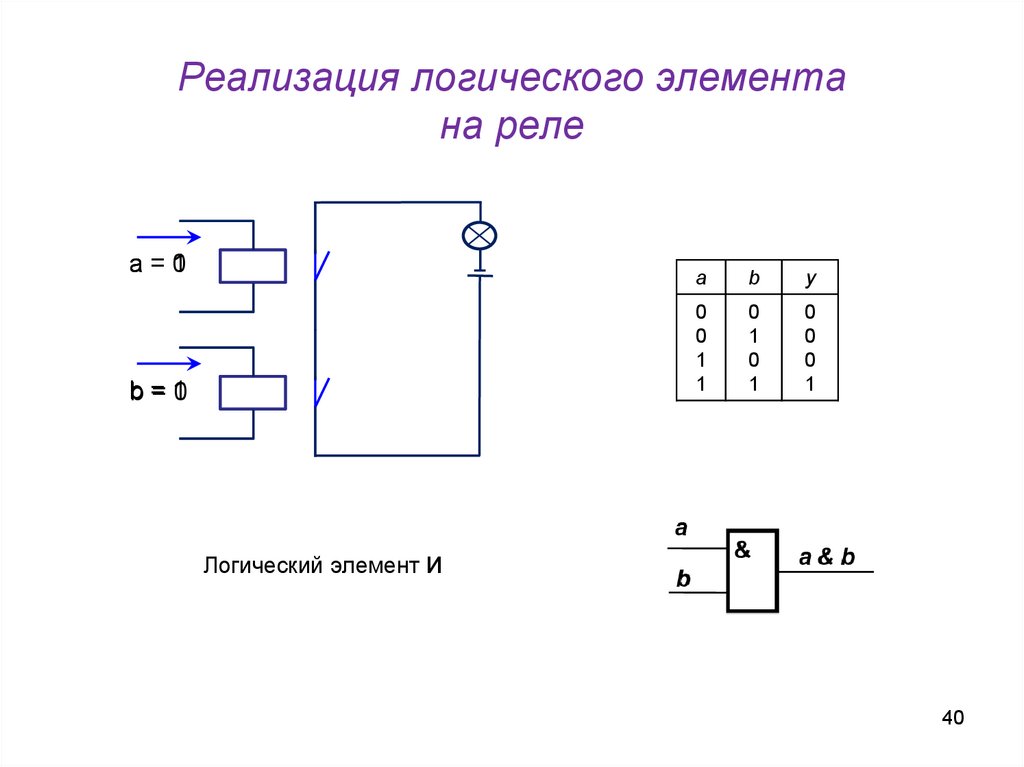
40. Логический элемент И

Реализация логического элемента
на реле
a=0
1
b=1
0
a
b
y
0
0
1
1
0
1
0
1
0
0
0
1
Логический элемент И
40

41. Логический элемент ИЛИ

Реализация логического элемента
на реле
a
b
a
b
y
0
0
1
1
0
1
0
1
0
1
1
1
Логический элемент ИЛИ
41

42.

Реализация логического элемента И
на диодах
+E
Ua
R
R >> Rд пр
Ub
U
Uaa =
=E
E
U
Ubb =
=E
0
a
b
I = E / (R + Rд пр) Uy
y
Uy = E
Uy = I * Rд пр = E * Rд пр / (R + Rд пр) 0
t
Логический элемент И
a
b
y
0
0
1
1
0
1
0
1
0
0
0
1
42

43. Логический элемент ИЛИ

Реализация логического элемента ИЛИ
на диодах
a
Ua
y
b
Ub
R
Uy
t
Логический элемент ИЛИ
a
b
y
0
0
1
1
0
1
0
1
0
1
1
1
43

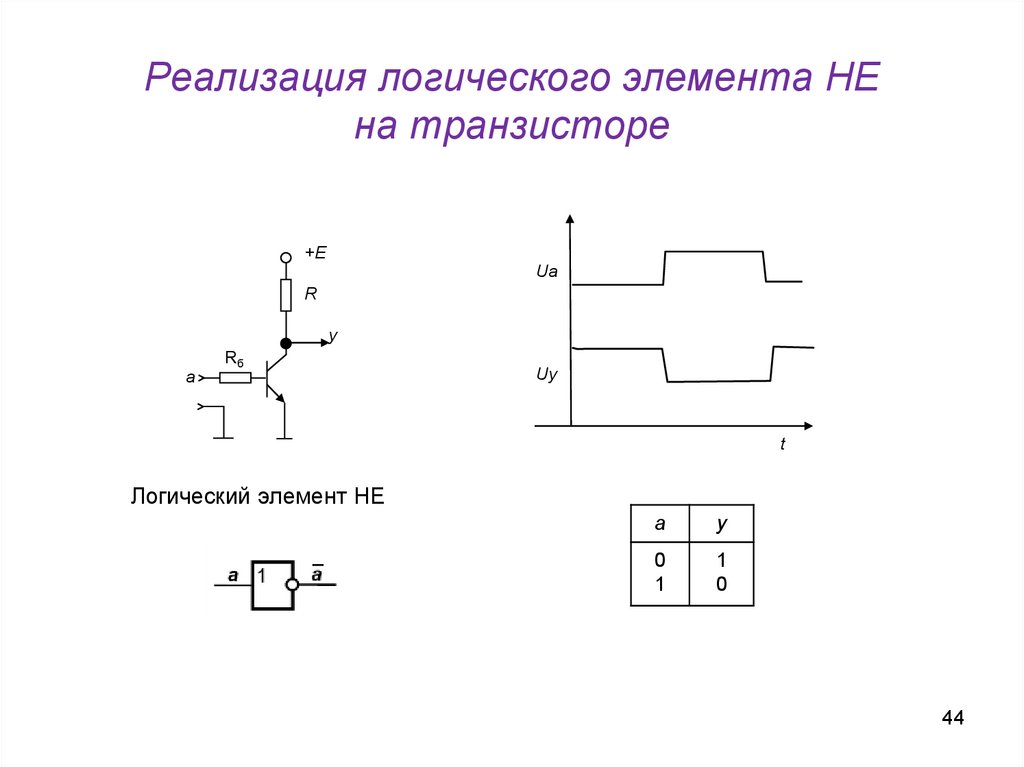
44. Логический элемент НЕ

Реализация логического элемента НЕ
на транзисторе
+E
Ua
R
y
Rб
a
Uy
t
Логический элемент НЕ
a
y
0
1
1
0
44

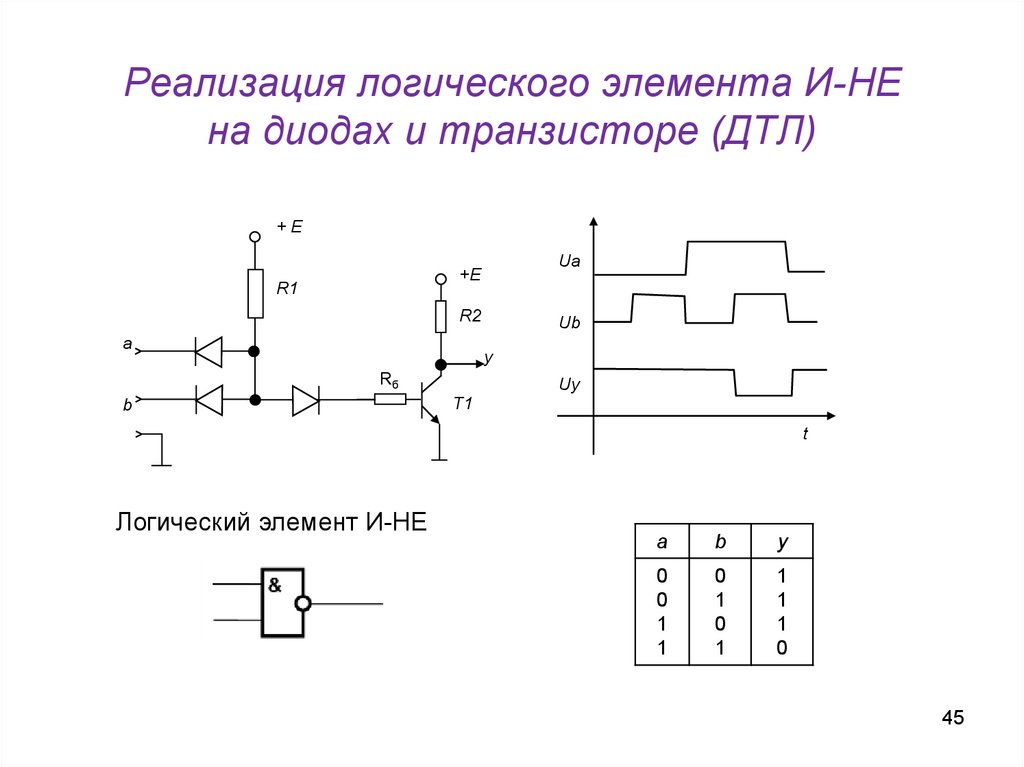
45.

Реализация логического элемента И-НЕ
на диодах и транзисторе (ДТЛ)
+E
Ua
+E
R1
R2
a
Ub
y
Rб
b
Uy
T1
t
Логический элемент И-НЕ
a
b
y
0
0
1
1
0
1
0
1
1
1
1
0
45

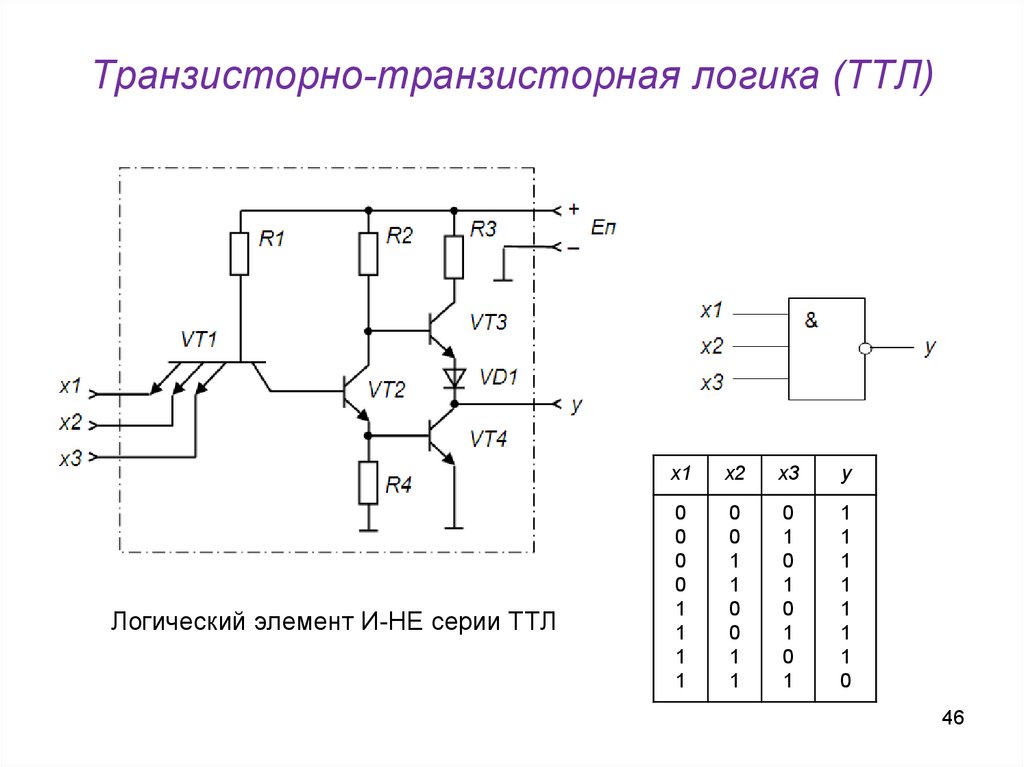
46.

Транзисторно-транзисторная логика (ТТЛ)
Логический элемент И-НЕ серии ТТЛ
x1
x2
x3
y
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
1
1
1
1
1
1
1
0
46

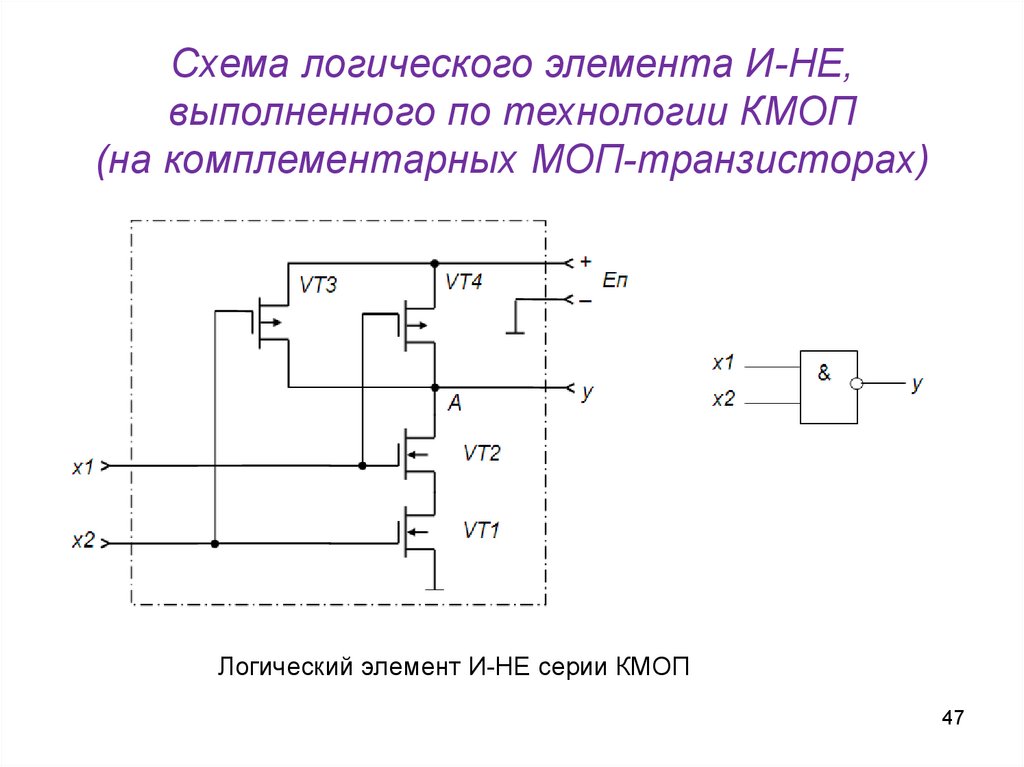
47.

Схема логического элемента И-НЕ,
выполненного по технологии КМОП
(на комплементарных МОП-транзисторах)
Логический элемент И-НЕ серии КМОП
47

48.

Обозначение логических элементов
в системе МЭК
Логический элемент И
Логический элемент ИЛИ
48

49.

Обозначение логических элементов
в системе МЭК
Логический элемент И-НЕ
Логический элемент ИЛИ-НЕ
49

50.

Обозначение логических элементов
в системе МЭК
Логический элемент
Эквивалентор
Логический элемент
Сумматор по модулю 2
50

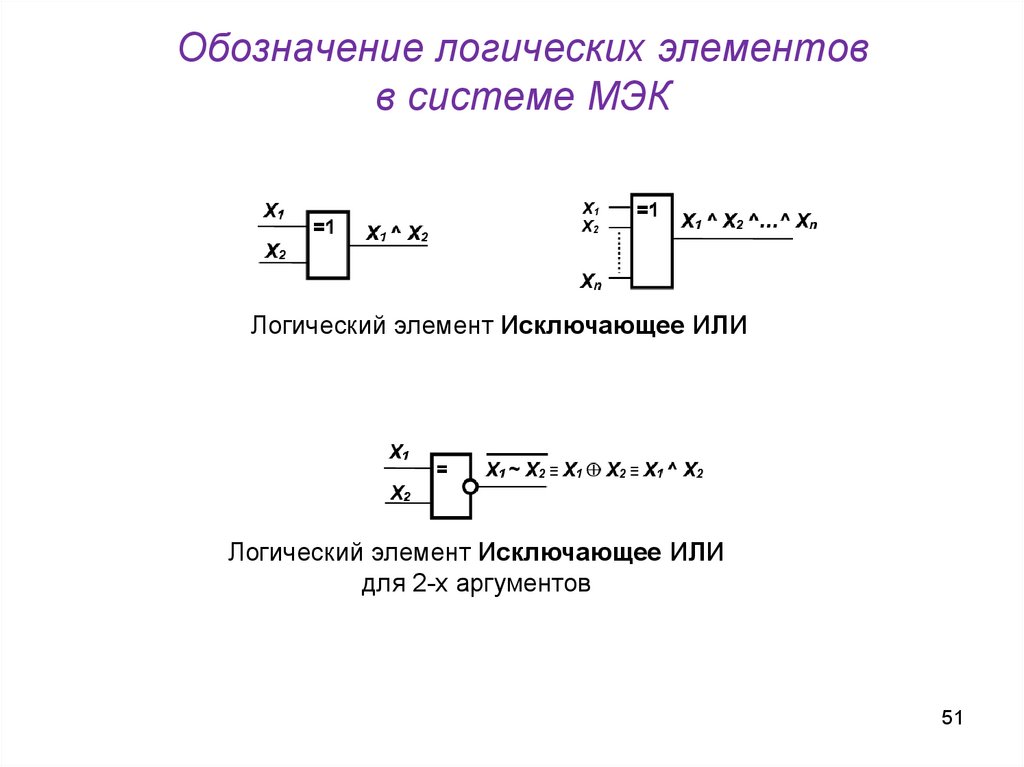
51.

Обозначение логических элементов
в системе МЭК
Логический элемент Исключающее ИЛИ
Логический элемент Исключающее ИЛИ
для 2-х аргументов
51

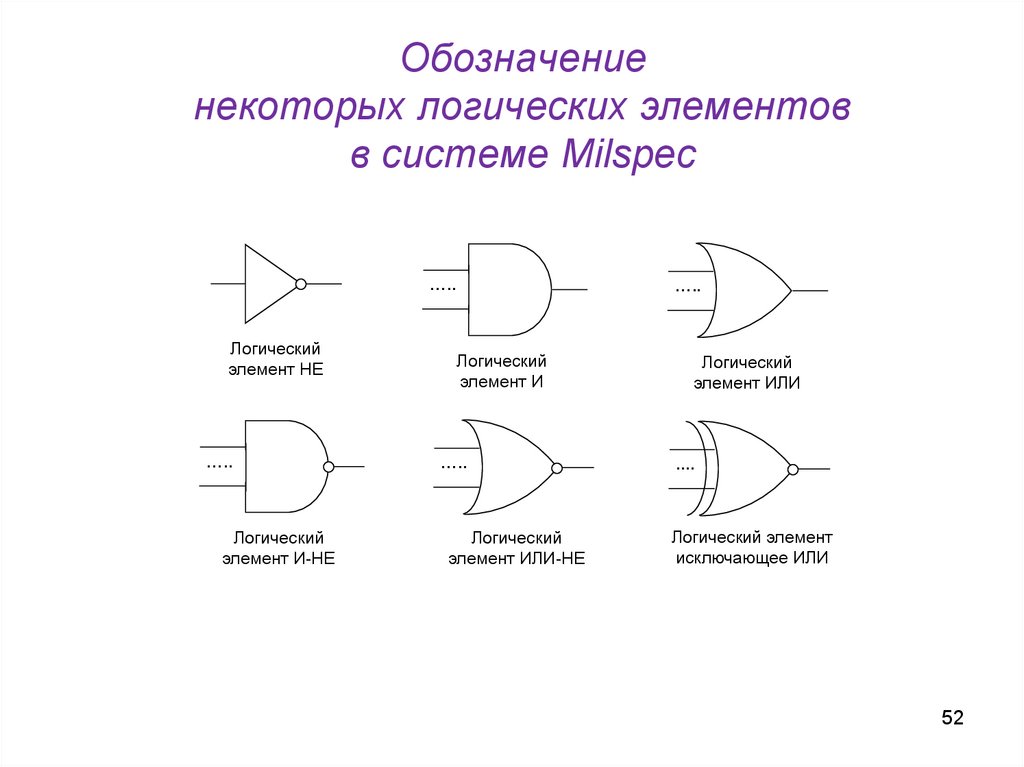
52.

Обозначение
некоторых логических элементов
в системе Milspec
…..
Логический
элемент НЕ
…..
Логический
элемент И-НЕ
…..
Логический
элемент И
…..
Логический
элемент ИЛИ-НЕ
Логический
элемент ИЛИ
....
Логический элемент
исключающее ИЛИ
52

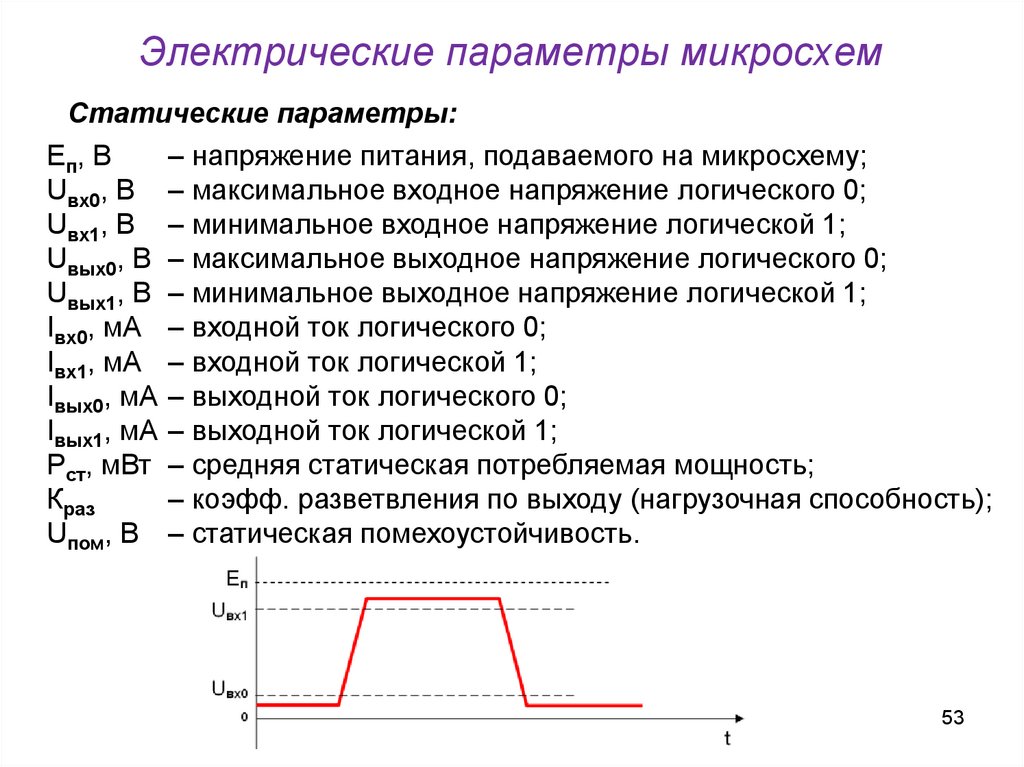
53. Электрические параметры микросхем

Статические параметры:
Еп, В
– напряжение питания, подаваемого на микросхему;
Uвх0, В – максимальное входное напряжение логического 0;
Uвх1, В – минимальное входное напряжение логической 1;
Uвых0, В – максимальное выходное напряжение логического 0;
Uвых1, В – минимальное выходное напряжение логической 1;
Iвх0, мA – входной ток логического 0;
Iвх1, мA – входной ток логической 1;
Iвых0, мA – выходной ток логического 0;
Iвых1, мA – выходной ток логической 1;
Pст, мВт – средняя статическая потребляемая мощность;
Краз
– коэфф. разветвления по выходу (нагрузочная способность);
Uпом, В – статическая помехоустойчивость.
53

54. Электрические параметры микросхем

Динамические параметры:
Тзд 0,1, нсек – время задержки переключения из 0 в 1;
Тзд 1,0, нсек – время задержки переключения из 1 в 0;
Тзд, нсек
– среднее время задержки переключения;
Fмакс, МГц – максимальная частота переключения;
Pд, Вт
– динамическая потребляемая мощность.
Входной сигнал
Выходной сигнал
54

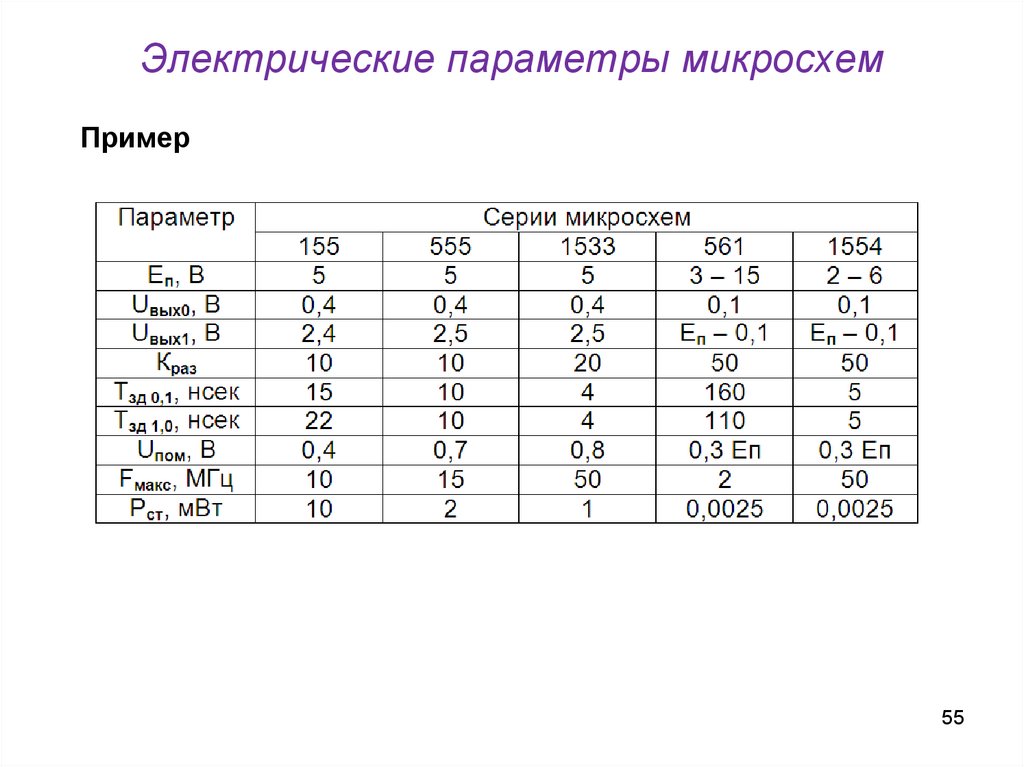
55. Электрические параметры микросхем

Пример
55

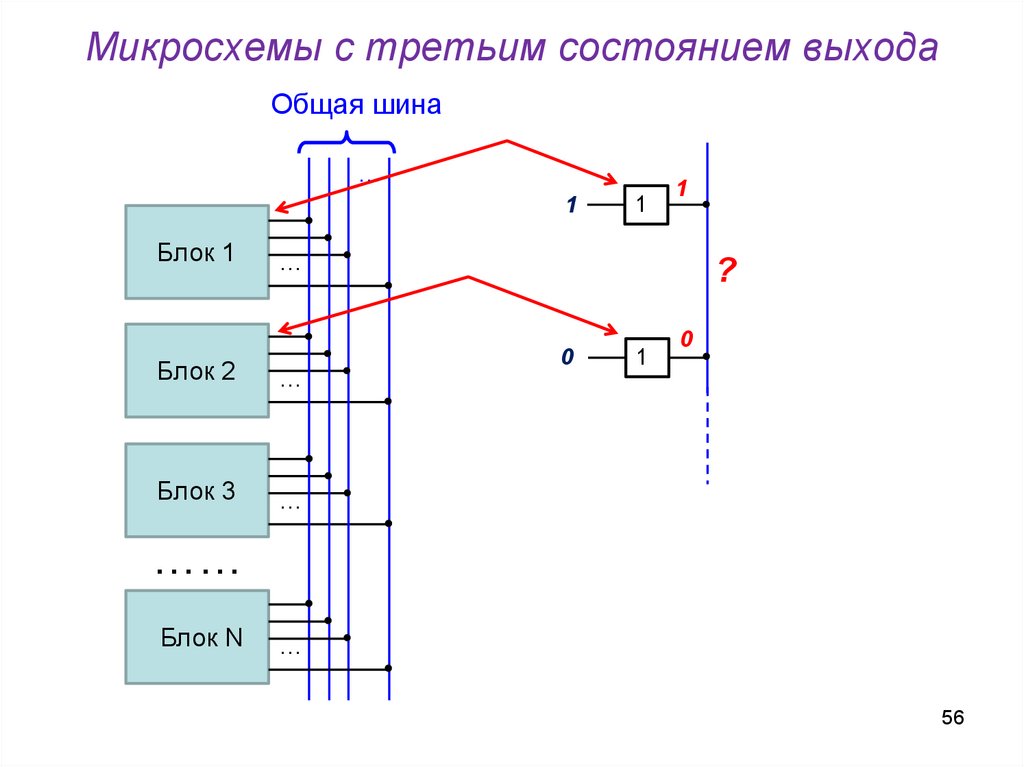
56. Микросхемы с третьим состоянием выхода

Общая шина
…
1
Блок 1
1
1
…
Блок 2
…
Блок 3
…
?
0
1
0
……
Блок N
…
56

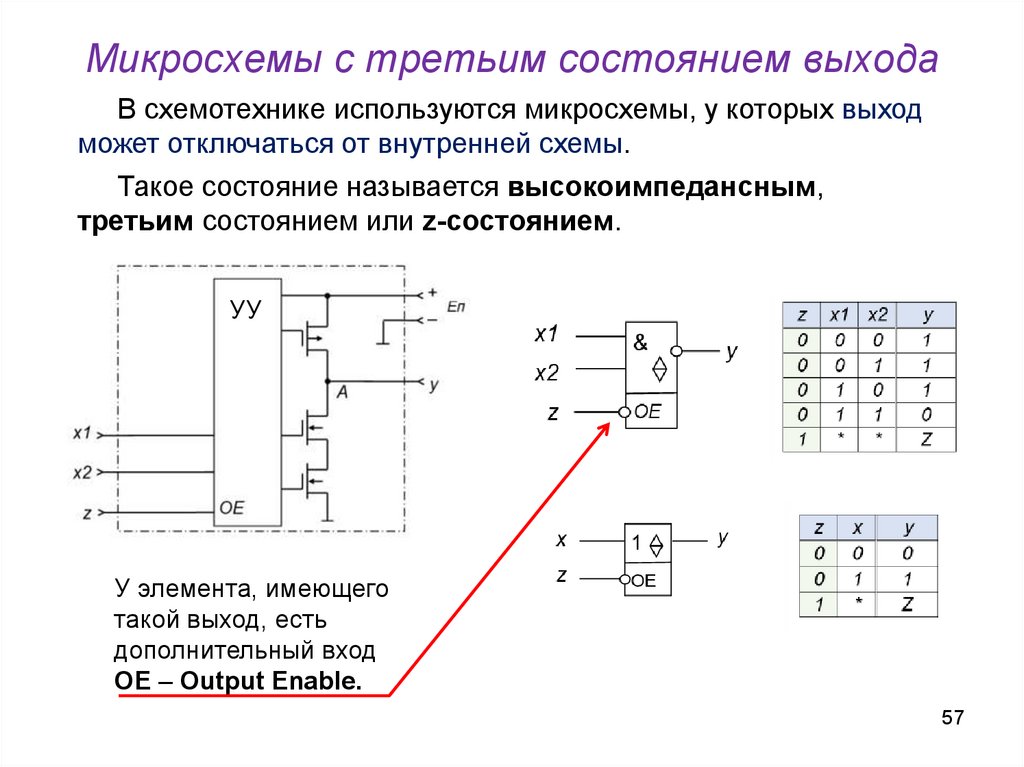
57. Микросхемы с третьим состоянием выхода

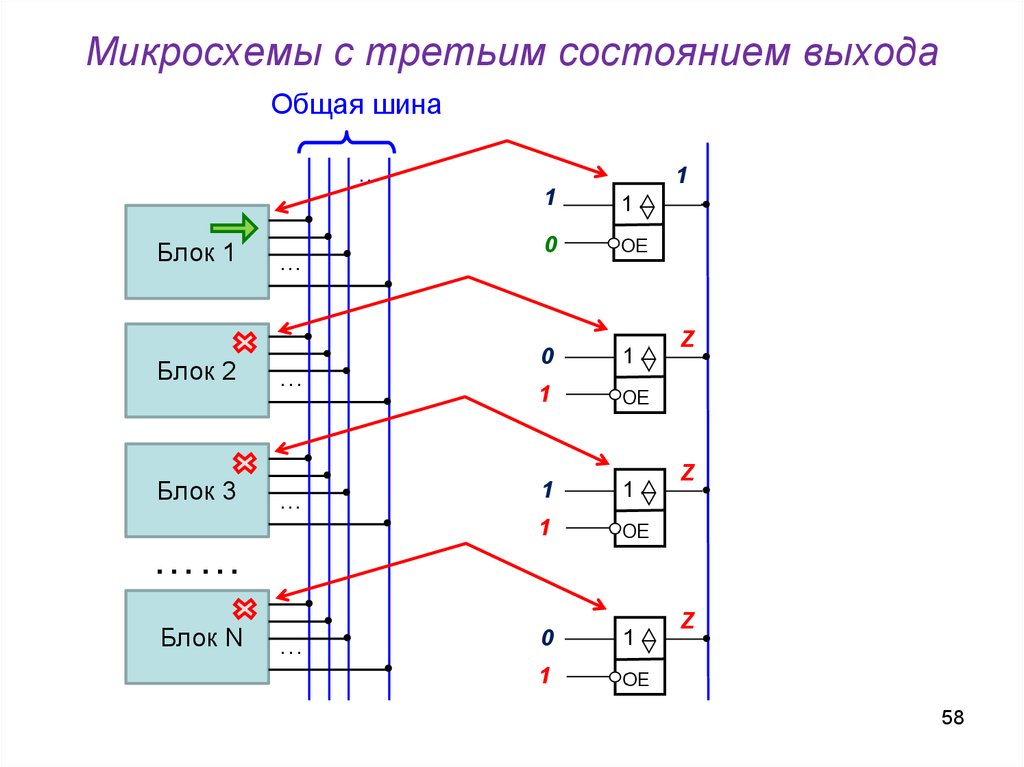
В схемотехнике используются микросхемы, у которых выход
может отключаться от внутренней схемы.
Такое состояние называется высокоимпедансным,
третьим состоянием или z-состоянием.
УУ
У элемента, имеющего
такой выход, есть
дополнительный вход
OE – Output Enable.
57

58. Микросхемы с третьим состоянием выхода

Общая шина
…
1
1
Блок 1
Блок 2
Блок 3
…
…
…
0
Z
1
1
Z
1
……
Блок N
0
…
0
Z
1
58

59. Микросхемы с третьим состоянием выхода

Общая шина
…
Z
1
Блок 1
Блок 2
Блок 3
…
…
…
0
0
0
1
Z
1
……
Блок N
1
…
0
Z
1
59