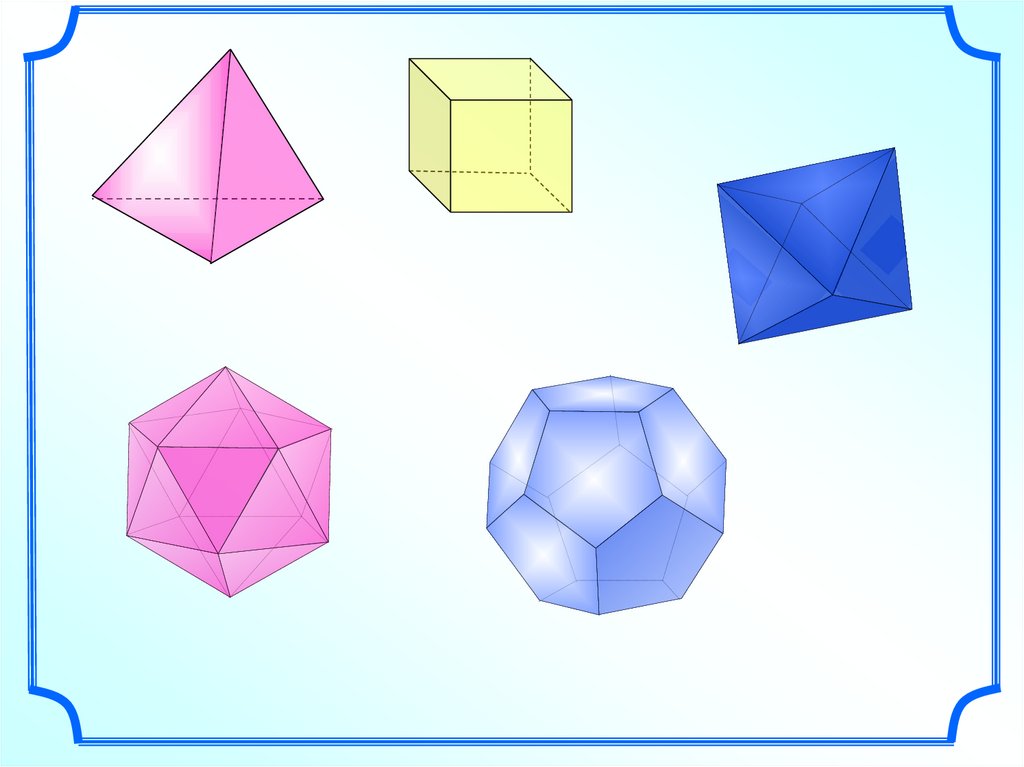
Правильные многогранники

1.

2.

Золото
Апатит

3.

Поваренная
соль
Кальцит (двойник)
Лед

4.

Альмандин
Ставролит (двойник)

5.

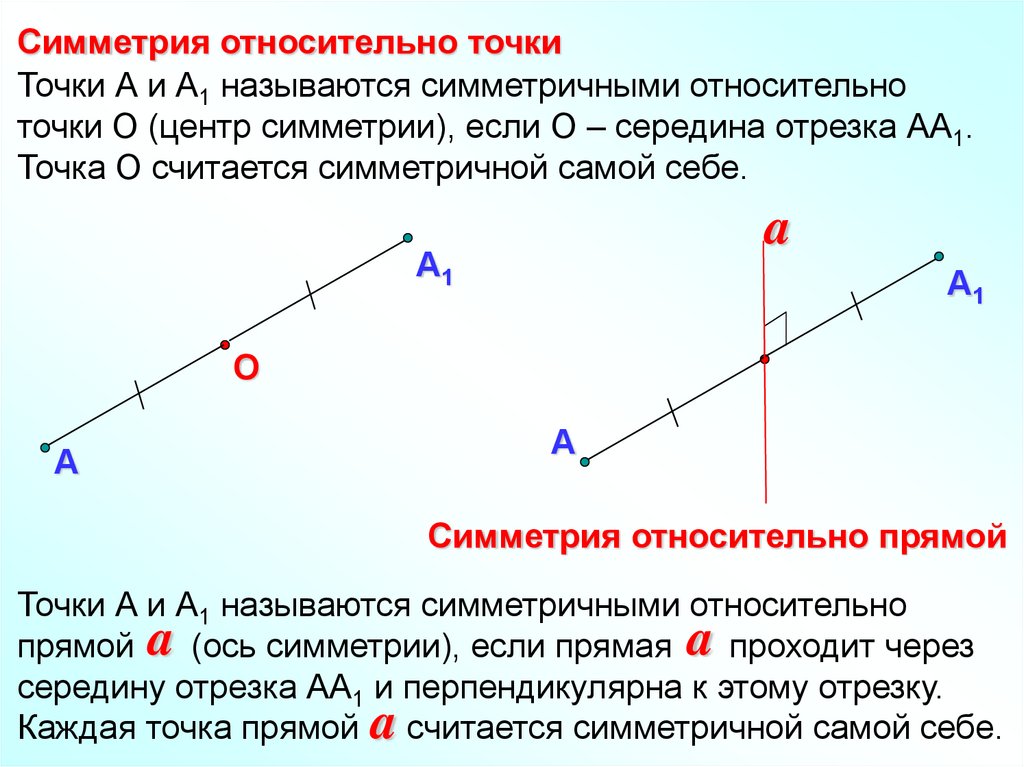
Симметрия относительно точки
Точки А и А1 называются симметричными относительно
точки О (центр симметрии), если О – середина отрезка АА1.
Точка О считается симметричной самой себе.
a
А1
А1
О
А
А
Симметрия относительно прямой
Точки А и А1 называются симметричными относительно
прямой a (ось симметрии), если прямая a проходит через
середину отрезка АА1 и перпендикулярна к этому отрезку.
Каждая точка прямой a считается симметричной самой себе.

6.

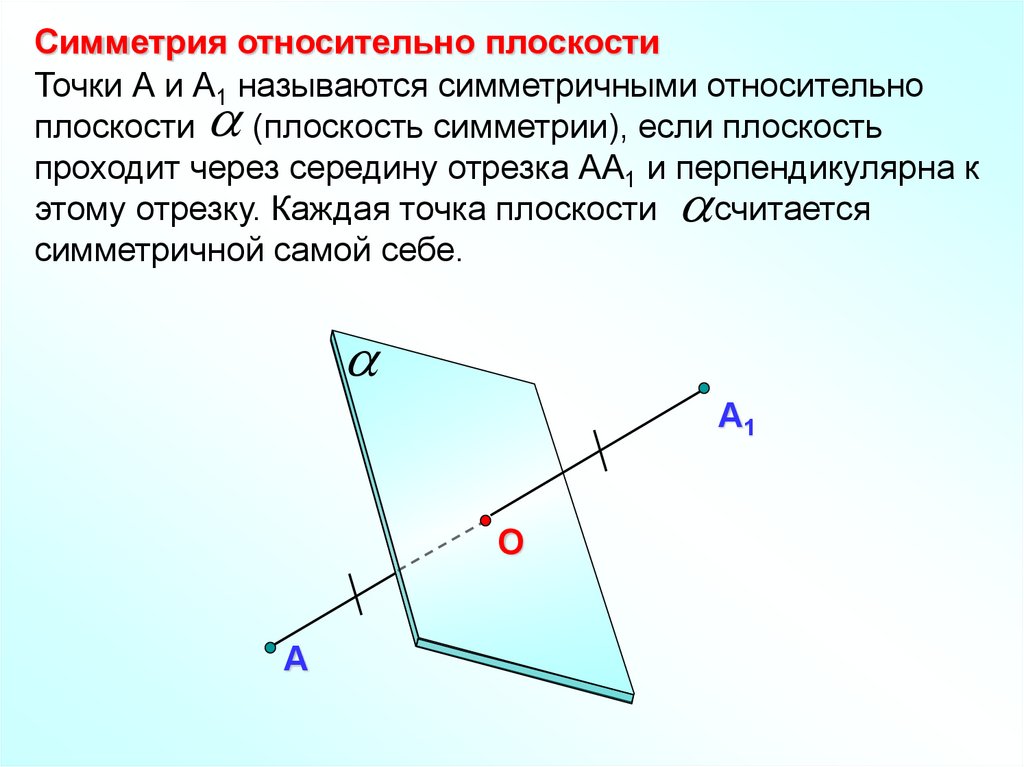
Симметрия относительно плоскости
Точки А и А1 называются симметричными относительно
плоскости
(плоскость симметрии), если плоскость
проходит через середину отрезка АА1 и перпендикулярна к
этому отрезку. Каждая точка плоскости
считается
симметричной самой себе.
А1
О
А

7.

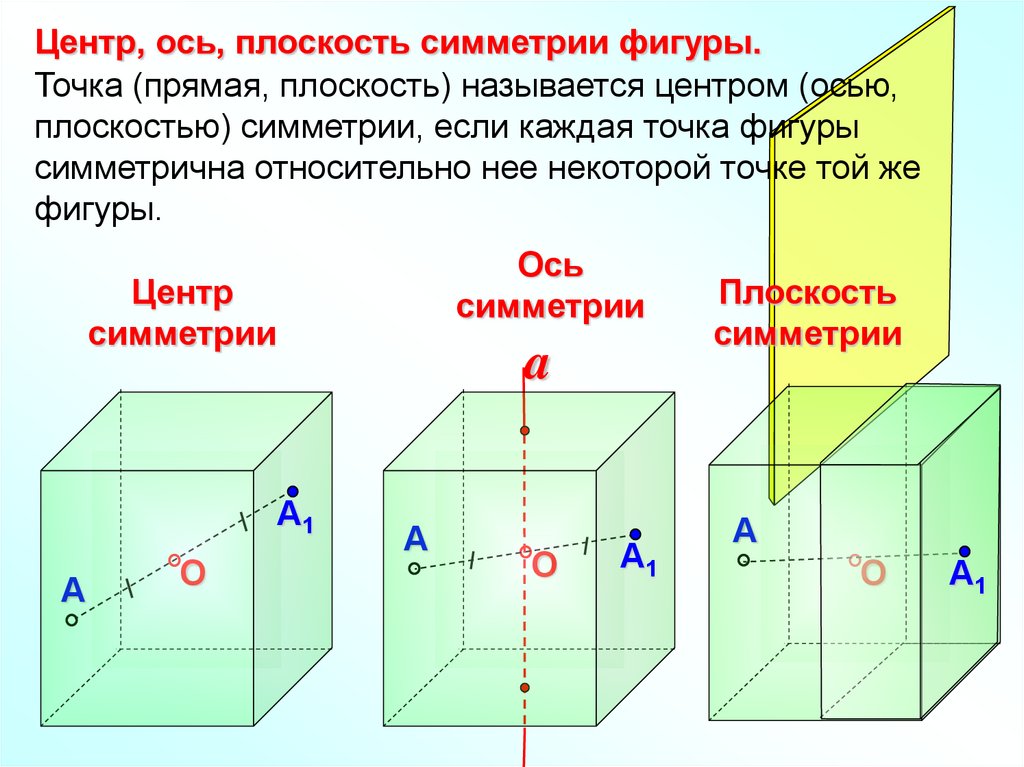
Центр, ось, плоскость симметрии фигуры.
Точка (прямая, плоскость) называется центром (осью,
плоскостью) симметрии, если каждая точка фигуры
симметрична относительно нее некоторой точке той же
фигуры.
Ось
симметрии
Центр
симметрии
a
А1
А
О
А
О
А1
Плоскость
симметрии
А
О
А1

8.

9.

10.

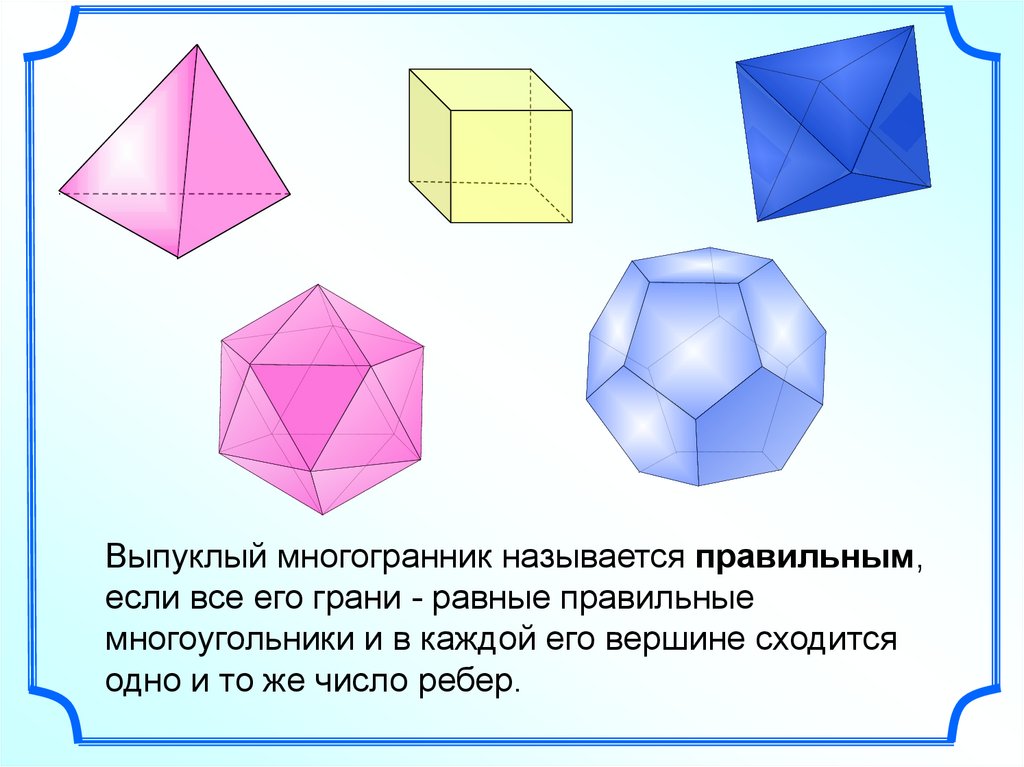
Выпуклый многогранник называется правильным,
если все его грани - равные правильные
многоугольники и в каждой его вершине сходится
одно и то же число ребер.

11.

Первым свойства правильных многогранников описал
древнегреческий ученый Платон. Именно поэтому
правильные многогранники называют также телами Платона.
Платон считал, что мир
строится из четырёх
«стихий» - огня, земли,
воздуха и воды, а атомы этих
«стихий» имеют форму
четырёх правильных
многогранников.
Платон
428 – 348 г. до н.э.

12.

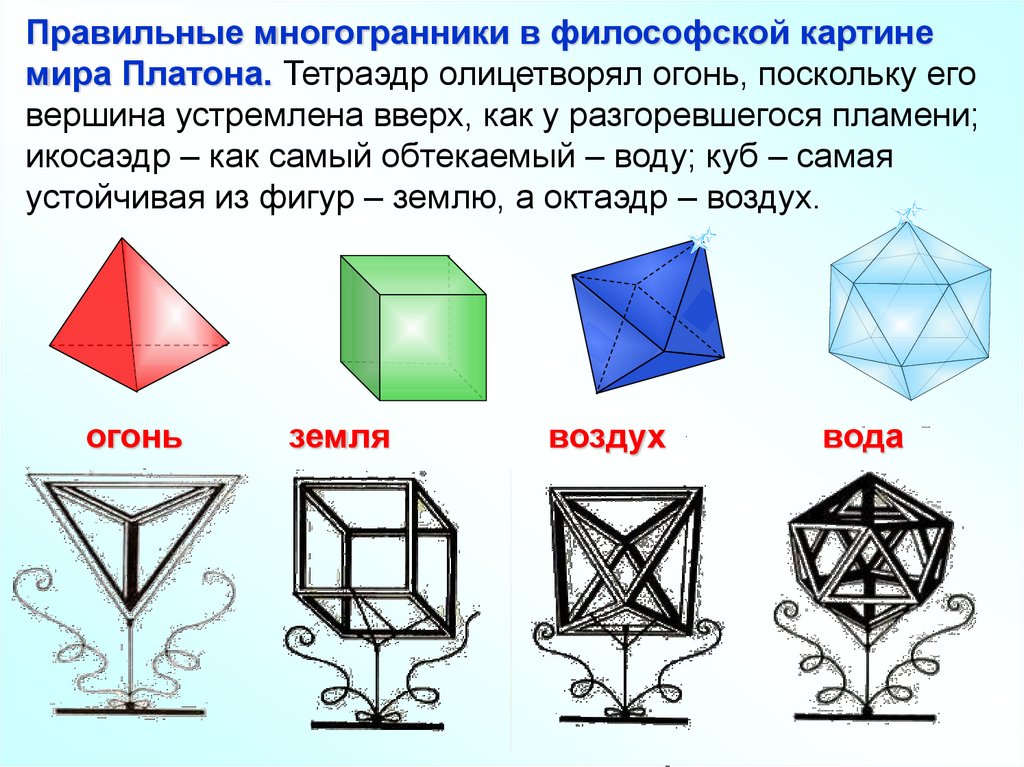
Правильные многогранники в философской картине
мира Платона. Тетраэдр олицетворял огонь, поскольку его
вершина устремлена вверх, как у разгоревшегося пламени;
икосаэдр – как самый обтекаемый – воду; куб – самая
устойчивая из фигур – землю, а октаэдр – воздух.
огонь
земля
воздух
вода

13.

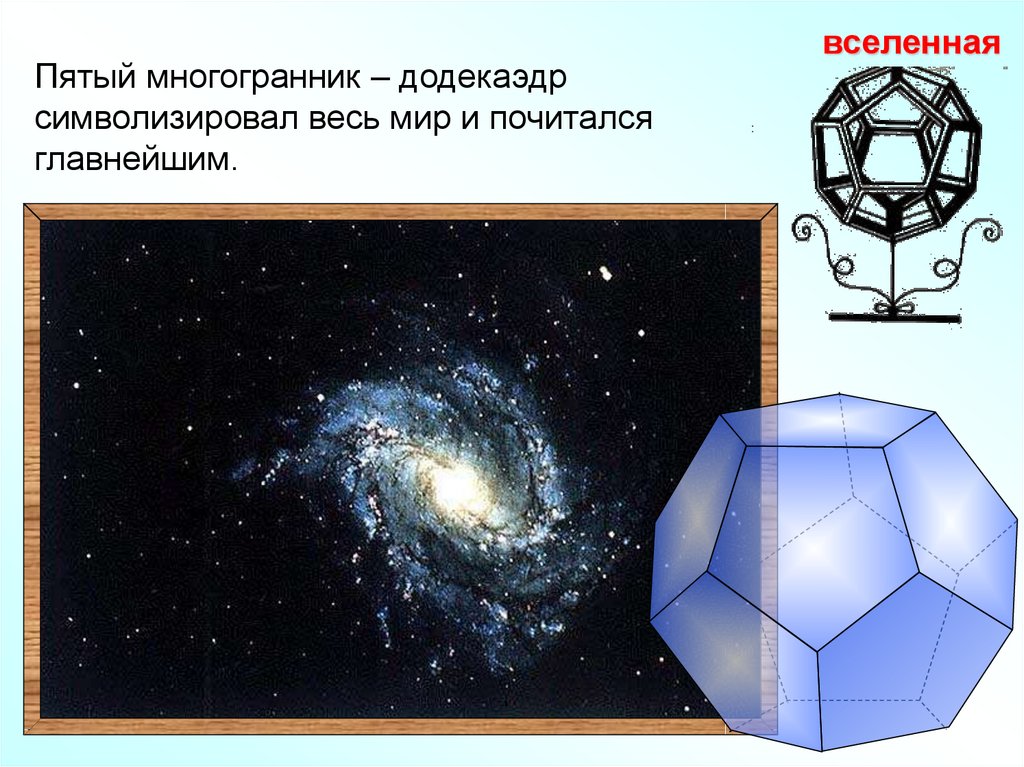
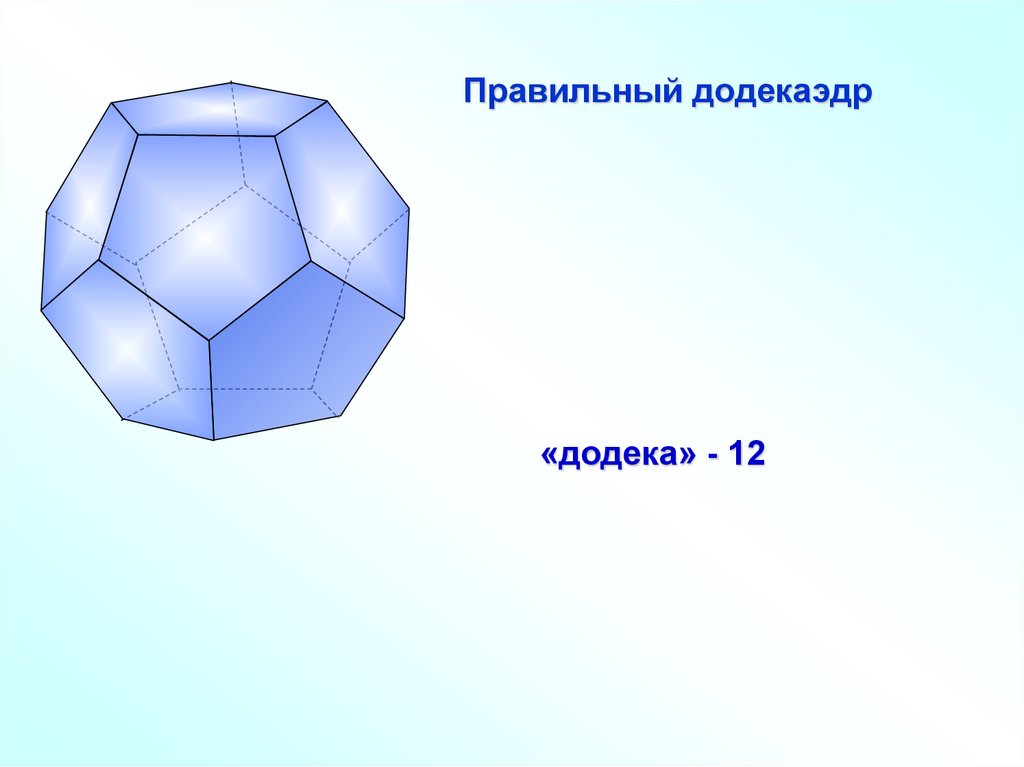
Пятый многогранник – додекаэдр
символизировал весь мир и почитался
главнейшим.
вселенная

14.

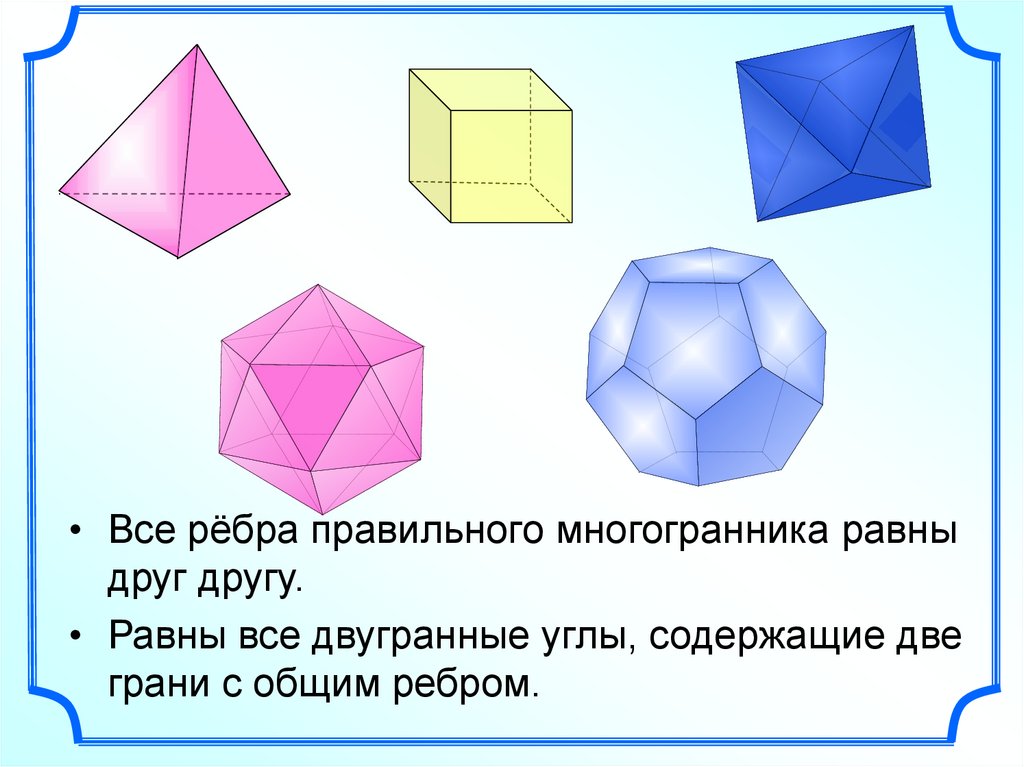
• Все рёбра правильного многогранника равны
друг другу.
• Равны все двугранные углы, содержащие две
грани с общим ребром.

15.

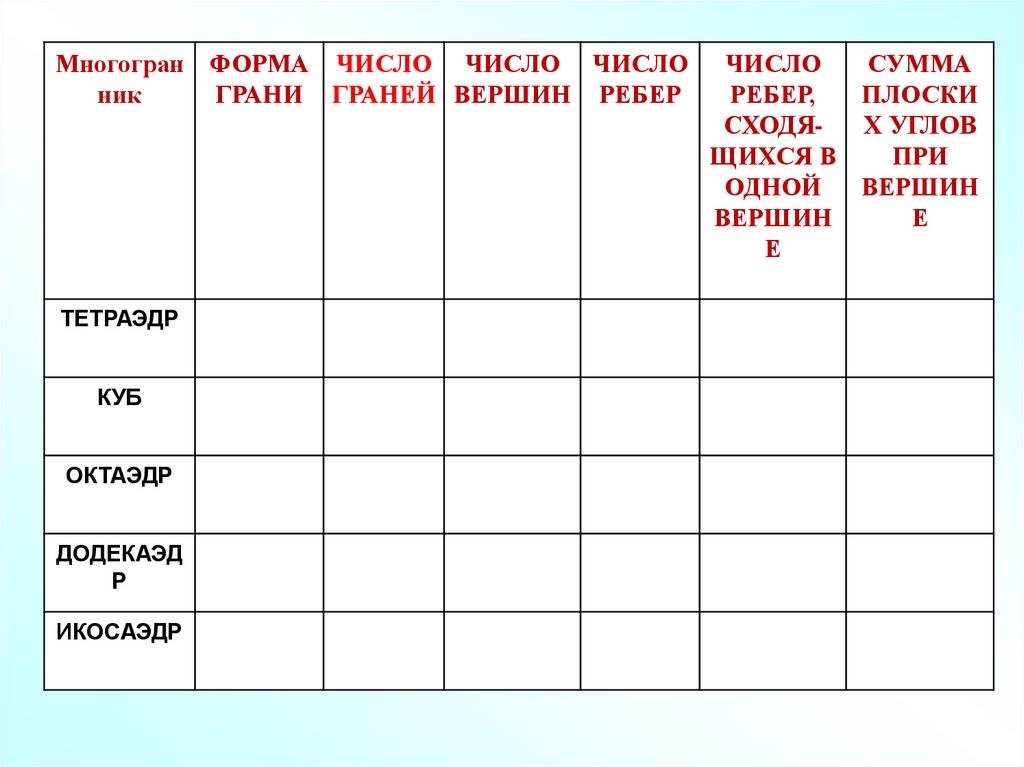
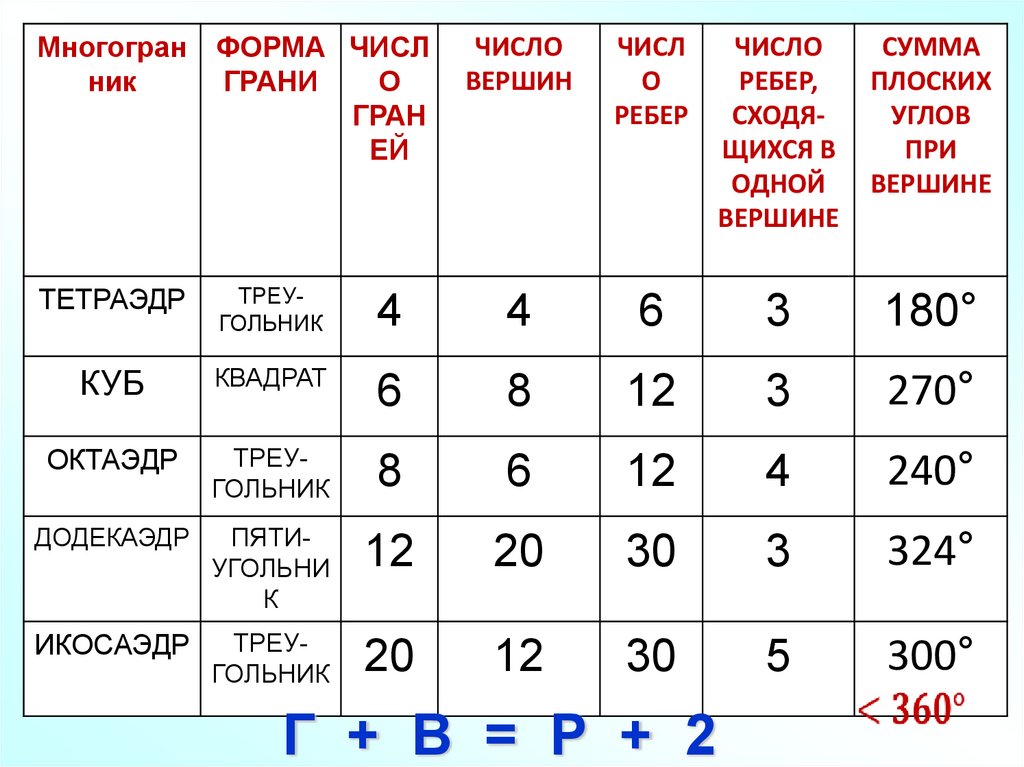
Многогран ФОРМА ЧИСЛО ЧИСЛО ЧИСЛО
ник
ГРАНИ ГРАНЕЙ ВЕРШИН РЕБЕР
ТЕТРАЭДР
КУБ
ОКТАЭДР
ДОДЕКАЭД
Р
ИКОСАЭДР
ЧИСЛО
СУММА
РЕБЕР,
ПЛОСКИ
СХОДЯХ УГЛОВ
ЩИХСЯ В
ПРИ
ОДНОЙ
ВЕРШИН
ВЕРШИН
Е
Е

16.

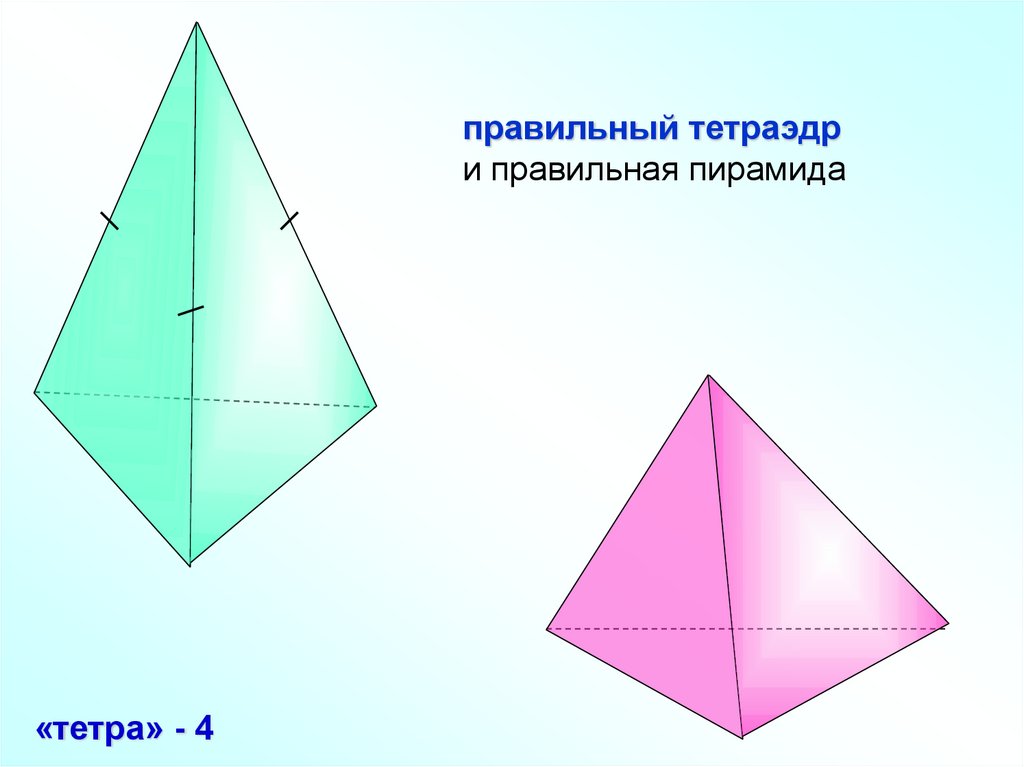
правильный тетраэдр
и правильная пирамида
«тетра» - 4

17.

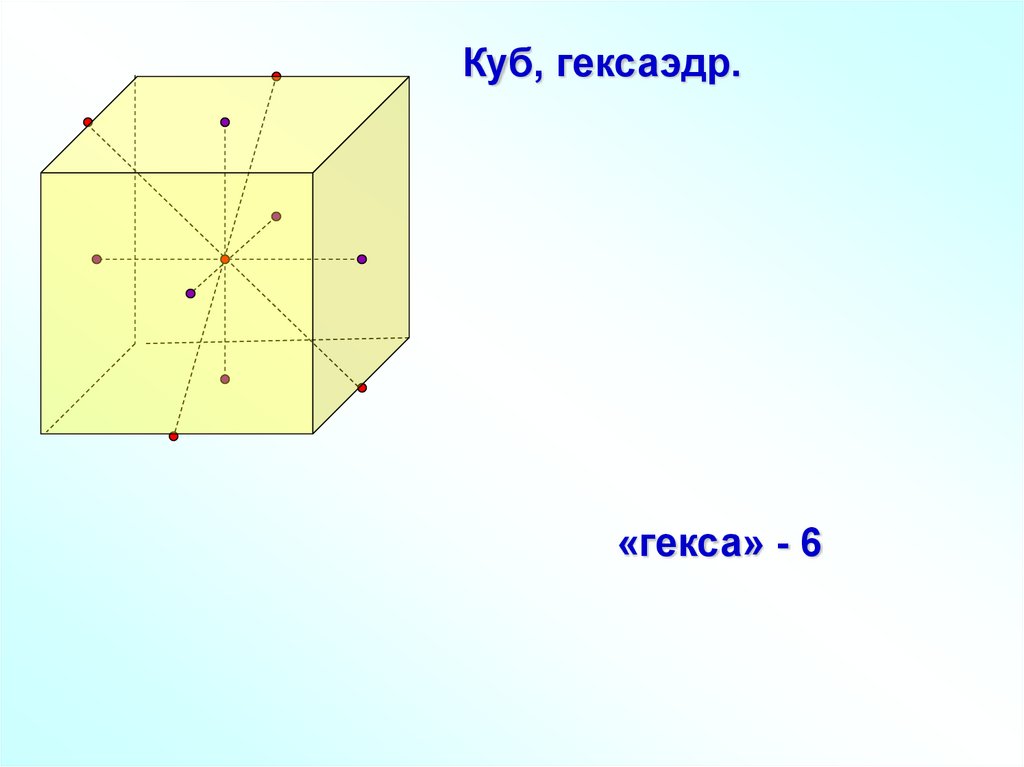
Куб, гексаэдр.
«гекса» - 6

18.

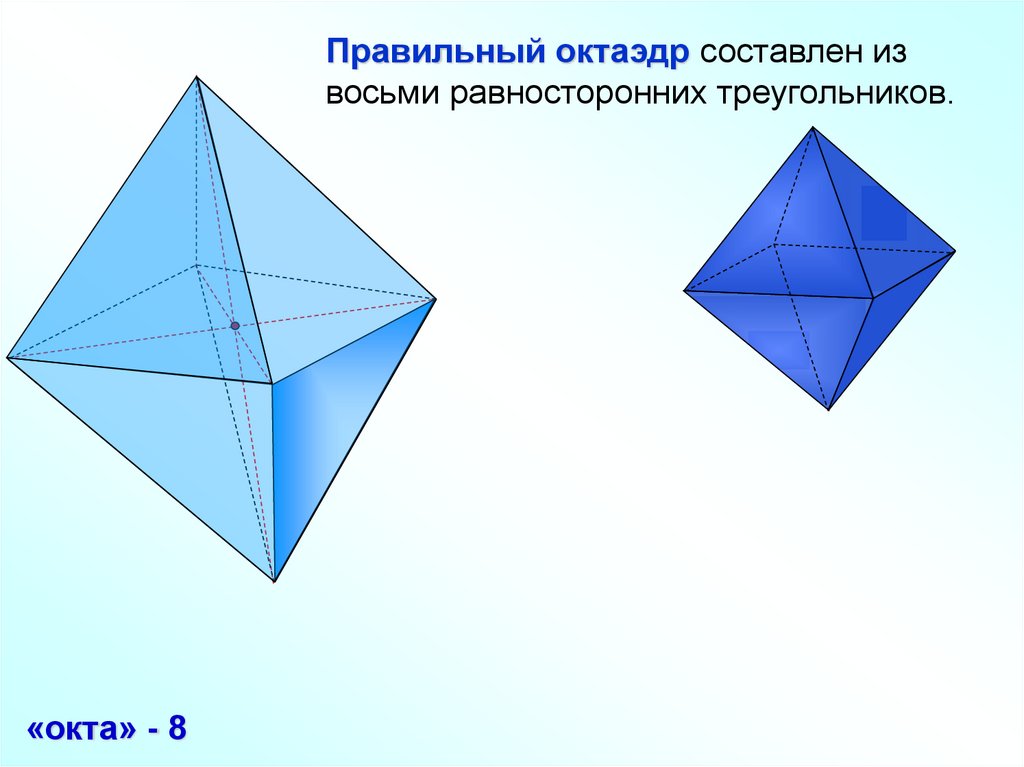
Правильный октаэдр составлен из
восьми равносторонних треугольников.
«окта» - 8

19.

Правильный икосаэдр
«икоса» - 20

20.

Правильный додекаэдр
«додека» - 12

21.

Многогран ФОРМА ЧИСЛ
ник
ГРАНИ
О
ГРАН
ЕЙ
ЧИСЛО
ВЕРШИН
ЧИСЛ
О
РЕБЕР
ЧИСЛО
РЕБЕР,
СХОДЯЩИХСЯ В
ОДНОЙ
ВЕРШИНЕ
СУММА
ПЛОСКИХ
УГЛОВ
ПРИ
ВЕРШИНЕ
ТЕТРАЭДР
ТРЕУГОЛЬНИК
4
4
6
3
180°
КУБ
КВАДРАТ
6
8
12
3
270°
ОКТАЭДР
ТРЕУГОЛЬНИК
8
6
12
4
240°
ДОДЕКАЭДР
ПЯТИУГОЛЬНИ
К
12
20
30
3
324°
ИКОСАЭДР
ТРЕУГОЛЬНИК
20
12
30
5
300°
Г + В = Р + 2

22. Теорема не существования

23.

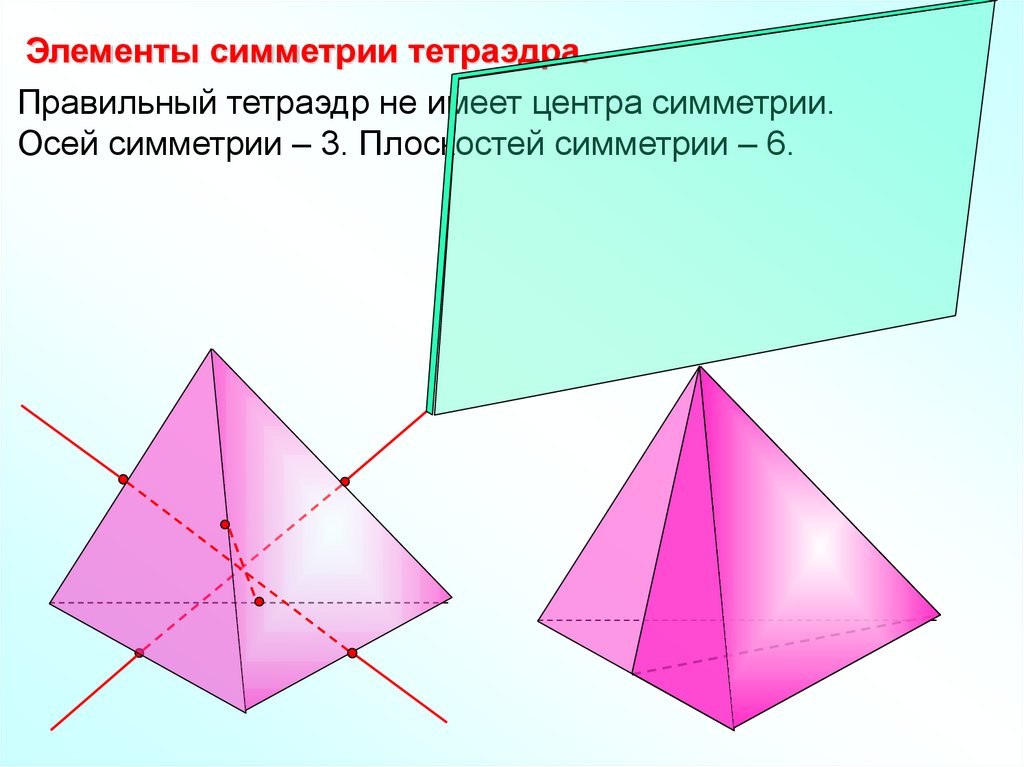
Элементы симметрии тетраэдра.
Правильный тетраэдр не имеет центра симметрии.
Осей симметрии – 3. Плоскостей симметрии – 6.

24.

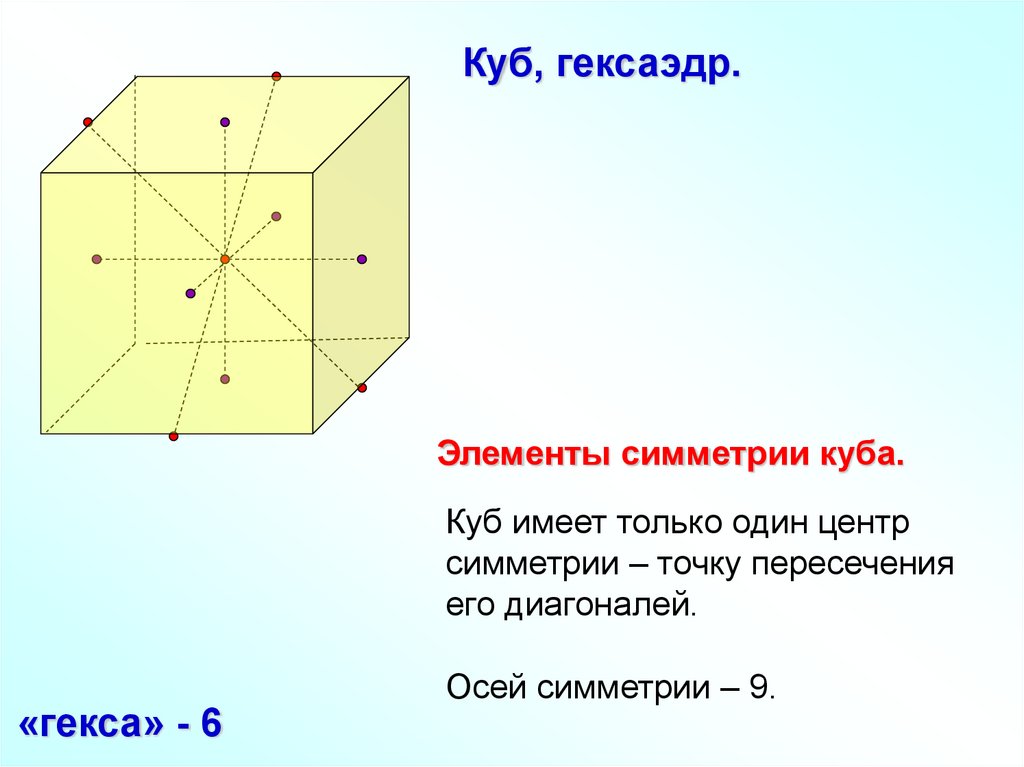
Куб, гексаэдр.
Элементы симметрии куба.
Куб имеет только один центр
симметрии – точку пересечения
его диагоналей.
«гекса» - 6
Осей симметрии – 9.

25.

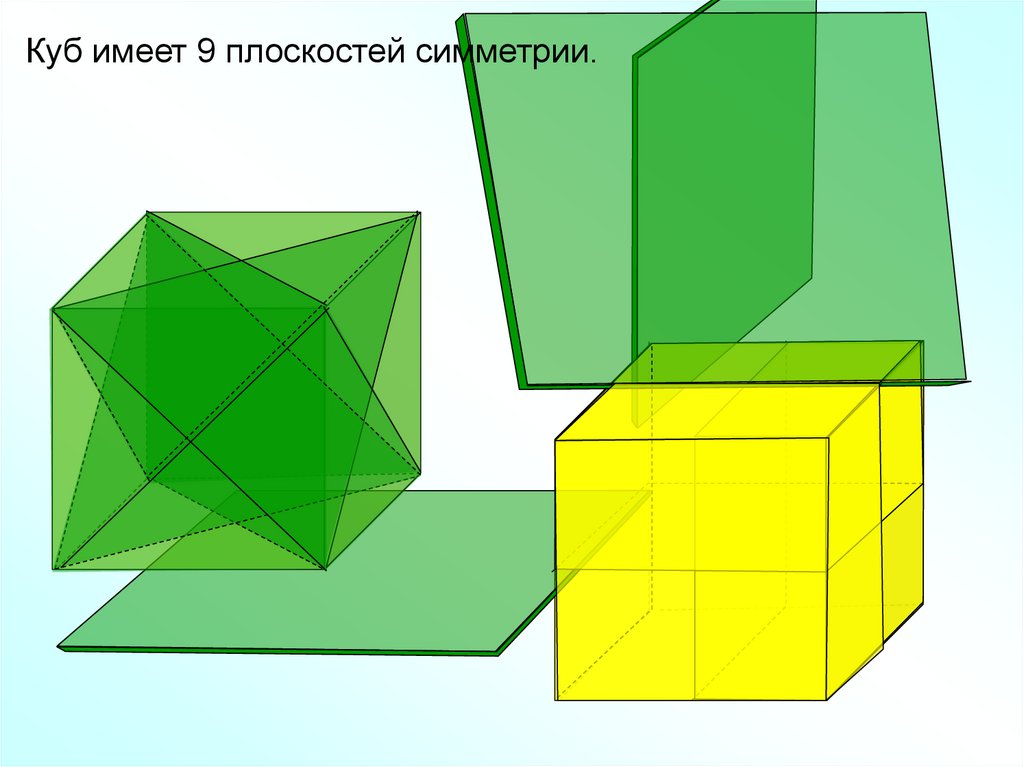
Куб имеет 9 плоскостей симметрии.

26. РЕФЛЕКСИЯ

• 1) Сегодня на уроке я
изучил(а)…
• 2) Я понял(а)…
• 3) На уроке мне…

27. Домашнее задание

• Изготовить из плотной бумаги
правильный многогранник: №271, 272,
273,274, 275,