Предпосылки теории игр. Виды игр

1. 1. Предпосылки теории игр. Виды игр.

Тема 4. Основные понятия теории игр
ПЛАН ЛЕКЦИИ:
1. Предпосылки теории игр. Виды игр.
2. Равновесия в поведении участников
игр.

2. 1. Предпосылки теории игр. Виды игр

1-я
предпосылка:
неприменимость
методов неоклассической теории для
исследования поведения участников
экономик. К этим методам относятся:
А)
полная
рациональность
индивидов;
Б)
единственное
(равновесное)
решение;
В)
экзогенный
(внешний
по

3. 2-я предпосылка:

Необходим анализ ситуаций, в
которых поведение индивидов
взаимообусловлено: решение
каждого из них оказывает влияние
на результат взаимодействия и,
следовательно, на решения
остальных индивидов.

4. 3 предпосылка:

требуется учет разнообразия в
поведении индивидов
(«совершенный калькулятор –
робот»), исключая полную
рациональность.

5. 4-я предпосылка:

взаимодействия индивидов исключают
существование, единственность и
Парето-оптимальность.

6. Основы теории игр:

Дж. Фон Нейман, О. Моргенштерн
«Теория
игр
и
экономическое
поведение» (1944г.)

7. Виды игр:

Кооперативные – возможен обмен
информации между участниками и
формирование коалиций.
Некооперативные – исходный пункт в
анализе – индивид, обмен информацией
и коалиции исключены.

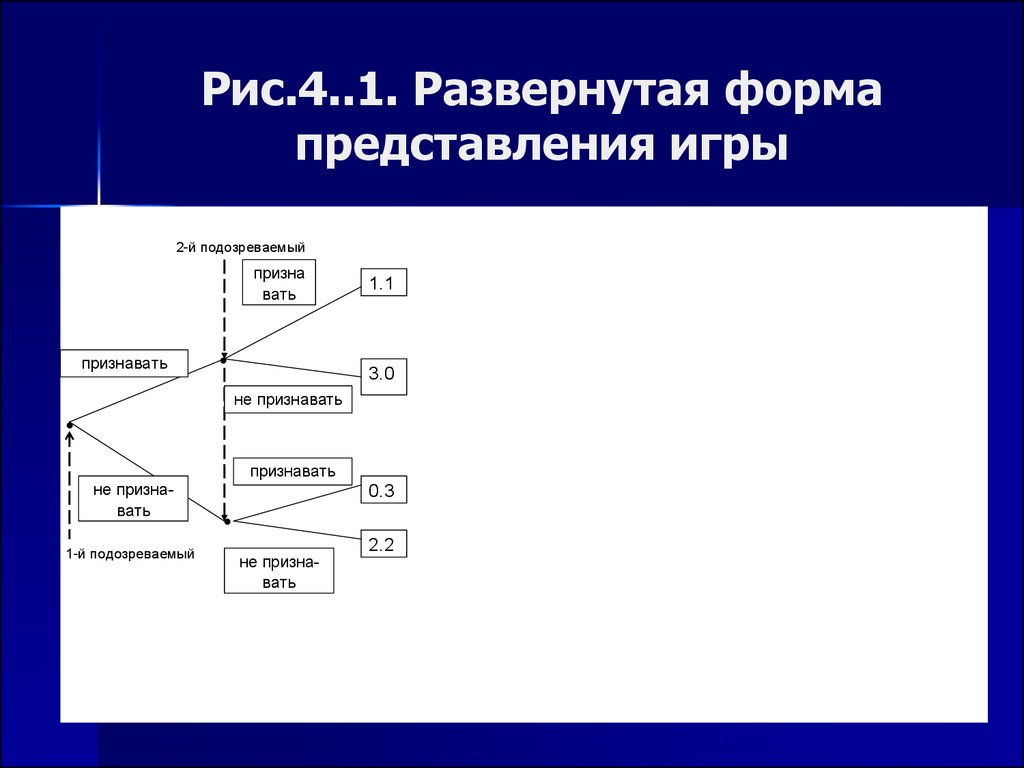
8. Формы представления игр.

А) развернутая (алгоритм) (см. Рис.4.1)

9. Рис.4..1. Развернутая форма представления игры

2-й подозреваемый
призна
вать
признавать
1.1
3.0
не признавать
признавать
не признавать
1-й подозреваемый
0.3
не признавать
2.2

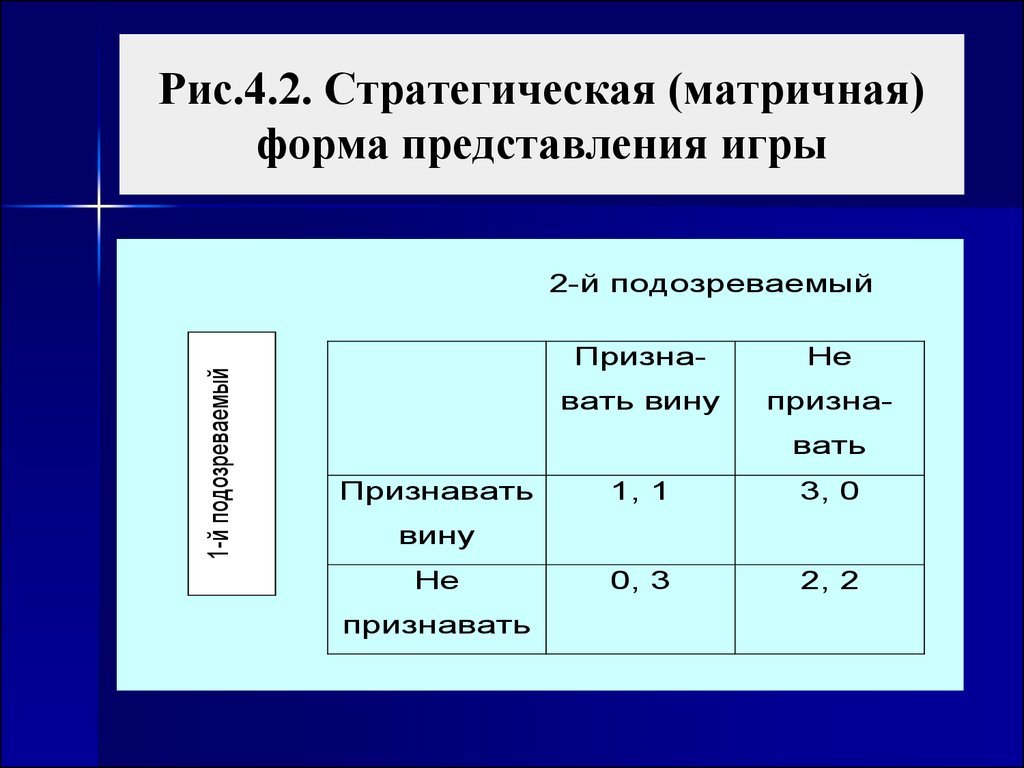
10. Рис.4.2. Стратегическая (матричная) форма представления игры

1-й подозреваемый
2-й подозреваемый
Призна-
Не
вать вину
признавать
Признавать
1, 1
3, 0
0, 3
2, 2
вину
Не
признавать

11. Первые цифры отражают полезность 1-го участника, вторые – 2-го. «Полезность» различных сроков осуждения – обратно пропорциональна их велич

Первые цифры отражают
полезность 1-го участника, вторые
– 2-го. «Полезность» различных
сроков осуждения – обратно
пропорциональна их величине.

12. 2. Равновесия в поведении участников игр

1) Равновесие доминирующих стратегий –
такой план действий, который
обеспечивает участнику максимальную
полезность вне зависимости от действий
другого участника.

13. 2-й тип равновесия:

равновесие по Нэшу – ситуация, в которой
ни один из игроков не может увеличить
свой выигрыш в одностороннем порядке,
меняя свой план действий

14. 3-й тип:

Равновесие по Штакельбергу –
ситуация, когда ни один из игроков не
может увеличить свой выигрыш в
одностороннем порядке, а решения
принимаются сначала одним игроком
и становятся известными второму
игроку.

15. 4-й тип:

Равновесие по Парето – ситуация,
когда нельзя улучшить положение
ни одного из игроков, не ухудшая
при том положения другого и не
снижая суммарного выигрыша
игроков.

16. Типовые модели равновесия.

1) Модель выбора студентами места
встречи: каждого из них при
желании можно найти либо в
буфете, либо в библиотеке. Если оба
хорошо знают друг друга, то местом
встречи будет буфет.

17. 2-я модель:

«Конфликт между супругами в
жесткой форме»: решение о
проведении вечера (жена желает
идти на концерт, муж – на
футбольный матч). У каждого есть
доминирующая стратегия.

18. 3-я модель:

«дилемма заключенных» - признавать
или не признавать вину каждым.

19. 4-я модель:

«конфликт между супругами в
мягкой форме» - высокая оценка
совместно проведенного вечера,
отсутствие доминирующих
стратегий.

20. 5-я модель:

«проблема разоружения» - одна
страна решает, развязывать войну в
отношении другой страны или нет, а
другая
страна
выбирает,
вооружаться или разоружаться.

21. 6-я модель:

Просмотр фильма (моральный
выбор) – смотреть или не
смотреть.

22. 7-я модель:

На угадывание денег в коробке –
взять половину или выбросить.

23. 8-я модель:

Взаимоотношения инвестора и
государства:
Решение инвестора о вложении денег;
Решение государства о введении
налогов на инвестиции.

24. Проблемы в ходе игр:

-
-
Проблема координации – решается
с
помощью
введения
институциональных условий;
Проблема
совместимости
(роль
институтов как ограничителей);
- Проблема кооперации (единственное
решение);

25. Проблема справедливости:

– если единственное равновесие по Нэшу
характеризуется
асимметричным,
несправедливым распределением выигрыша
между
участниками
взаимодействия
(создание норм).