Similar presentations:
Математическое моделирование
1.
МДК 02.03Математическое
моделирование
Задание:
1) Составьте конспект в тетради
2) прислать фото на почту shanenkova75@mail.ru
следующим студентам: Гулиев, Давлетбаев, Ершов,
Заельский, Захаров, Ишдавлетов, Калужин
3) Остальные предоставляют конспект на очной
паре
4) Обратите внимание на решение задач (§2, §3)
2.
Математическое моделирование§1. Математическое моделирование
§2. Примеры линейных моделей
§3. Примеры оптимизационных моделей
2
3.
Трусов Пётр Валентиновичроссийский учёный-физик, д.ф.-м.н.,
специалист в области механики сплошных
сред. Автор учебных пособий для студентов
ВУЗов по механике сплошных сред, теории
определяющих соотношений и
математическому моделированию.
3
4.
§1. Математическое моделированиеКлассификация математических моделей
в зависимости от:
❑Сложности объекта моделирования;
❑Оператора модели;
❑Входных и выходных параметров;
❑Способа исследования модели;
❑Цели моделирования.
4
5.
§1. Математическое моделированиеКлассификация математических моделей в зависимости от:
❑Сложности объекта моделирования;
❑Оператора модели;
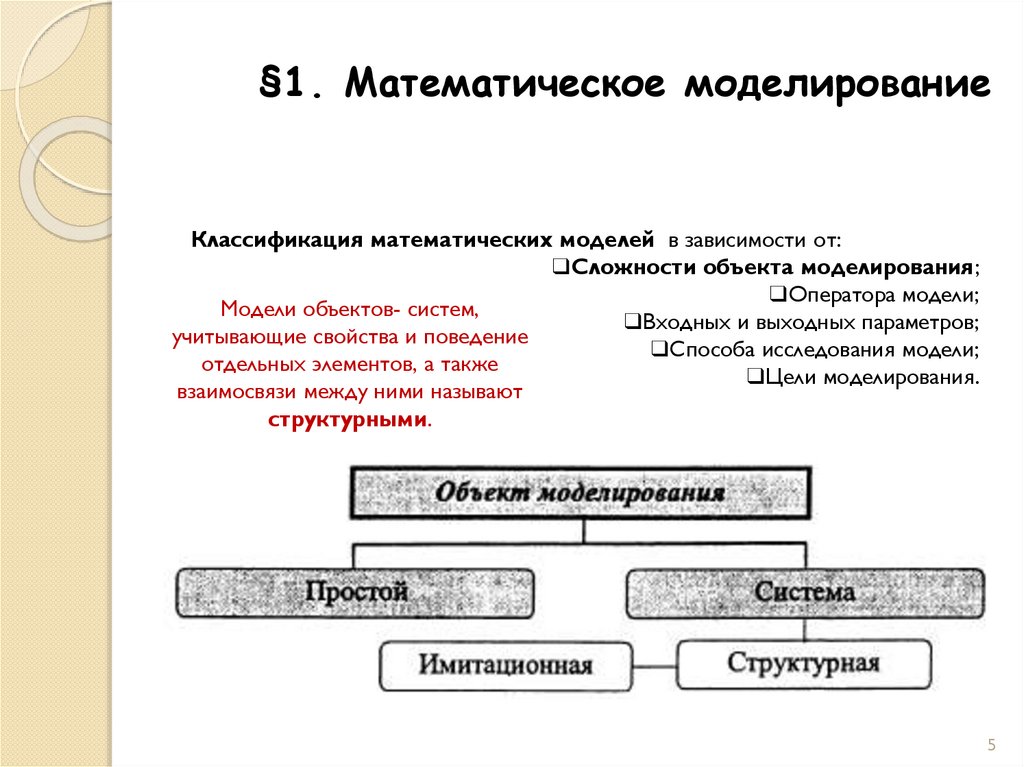
Модели объектов- систем,
❑Входных и выходных параметров;
учитывающие свойства и поведение
❑Способа исследования модели;
отдельных элементов, а также
❑Цели моделирования.
взаимосвязи между ними называют
структурными.
5
6.
§1. Математическое моделированиеКлассификация математических моделей в зависимости от:
❑Сложности объекта моделирования;
❑Оператора модели;
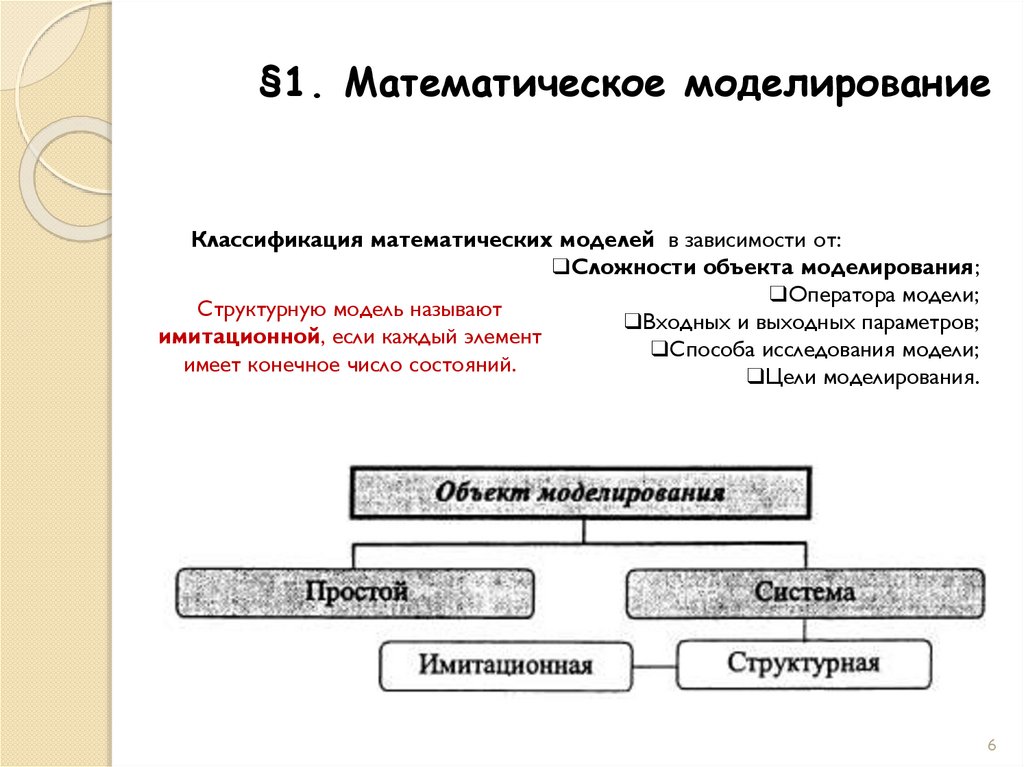
Структурную модель называют
❑Входных и выходных параметров;
имитационной, если каждый элемент
❑Способа исследования модели;
имеет конечное число состояний.
❑Цели моделирования.
6
7.
§1. Математическое моделированиеКлассификация математических моделей в зависимости от:
❑Сложности объекта моделирования;
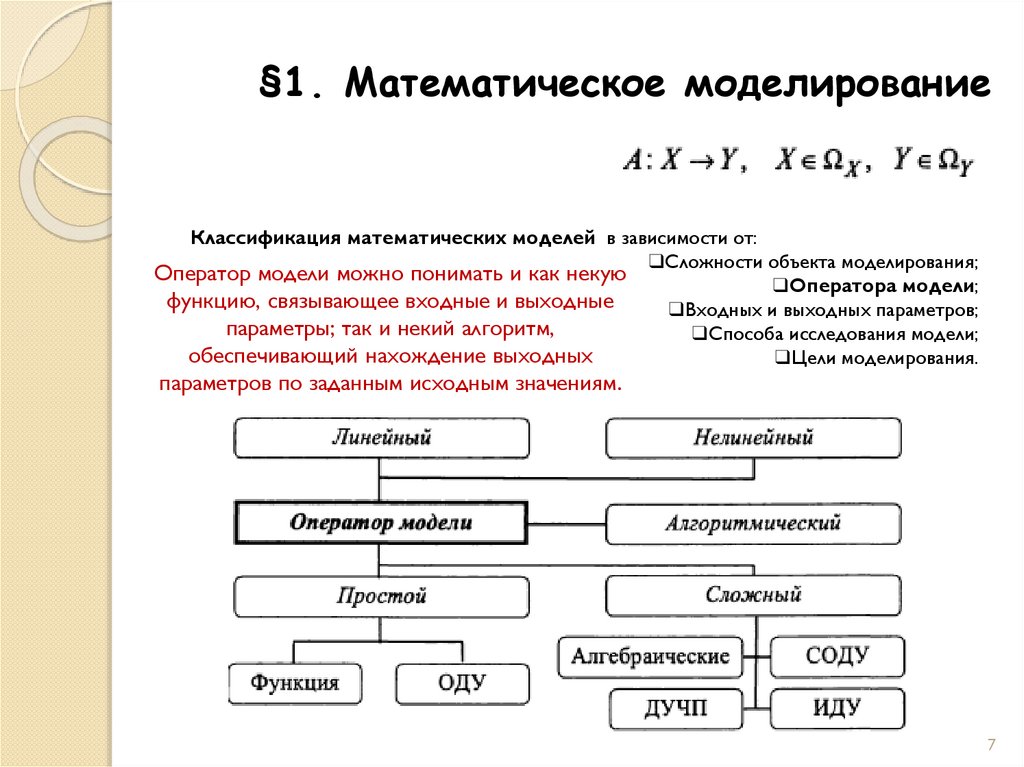
Оператор модели можно понимать и как некую
❑Оператора модели;
функцию, связывающее входные и выходные
❑Входных и выходных параметров;
параметры; так и некий алгоритм,
❑Способа исследования модели;
обеспечивающий нахождение выходных
❑Цели моделирования.
параметров по заданным исходным значениям.
7
8.
§1. Математическое моделированиеКлассификация математических моделей в зависимости от:
❑Сложности объекта моделирования;
❑Оператора модели;
❑Входных и выходных параметров;
❑Способа исследования модели;
❑Цели моделирования.
8
9.
§1. Математическое моделированиеКлассификация математических моделей в зависимости от:
❑Сложности объекта моделирования;
❑Оператора модели;
❑Входных и выходных параметров;
❑Способа исследования модели;
❑Цели моделирования.
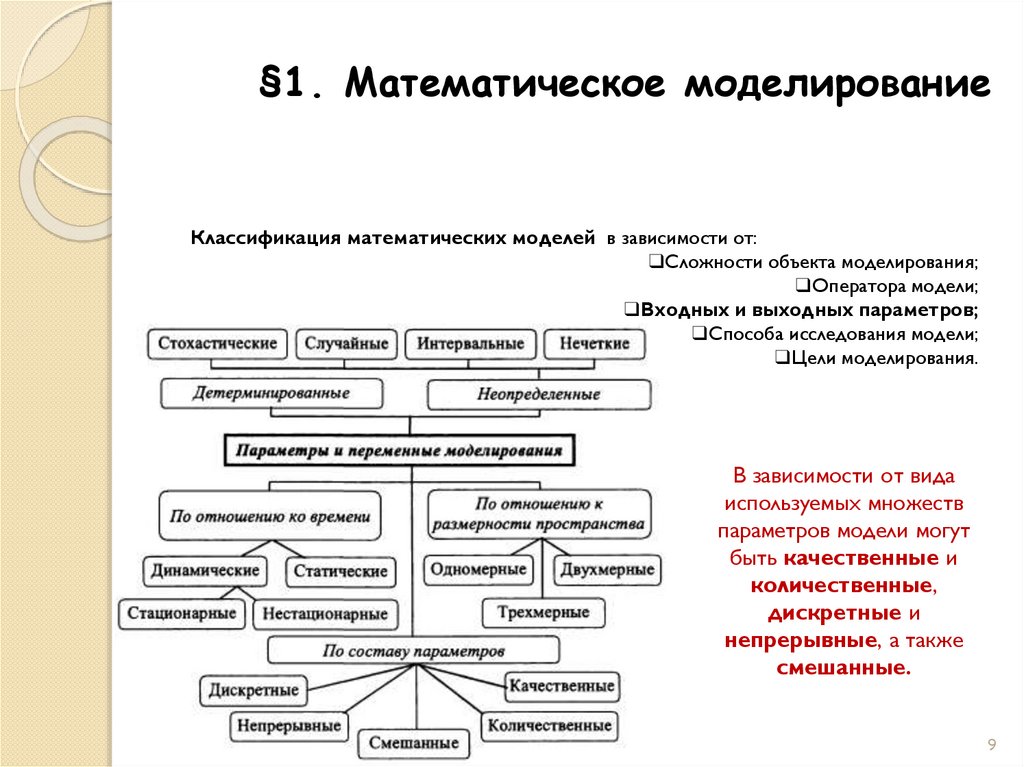
В зависимости от вида
используемых множеств
параметров модели могут
быть качественные и
количественные,
дискретные и
непрерывные, а также
смешанные.
9
10.
§1. Математическое моделированиеКлассификация математических моделей в зависимости от:
❑Сложности объекта моделирования;
❑Оператора модели;
❑Входных и выходных параметров;
❑Способа исследования модели;
❑Цели моделирования.
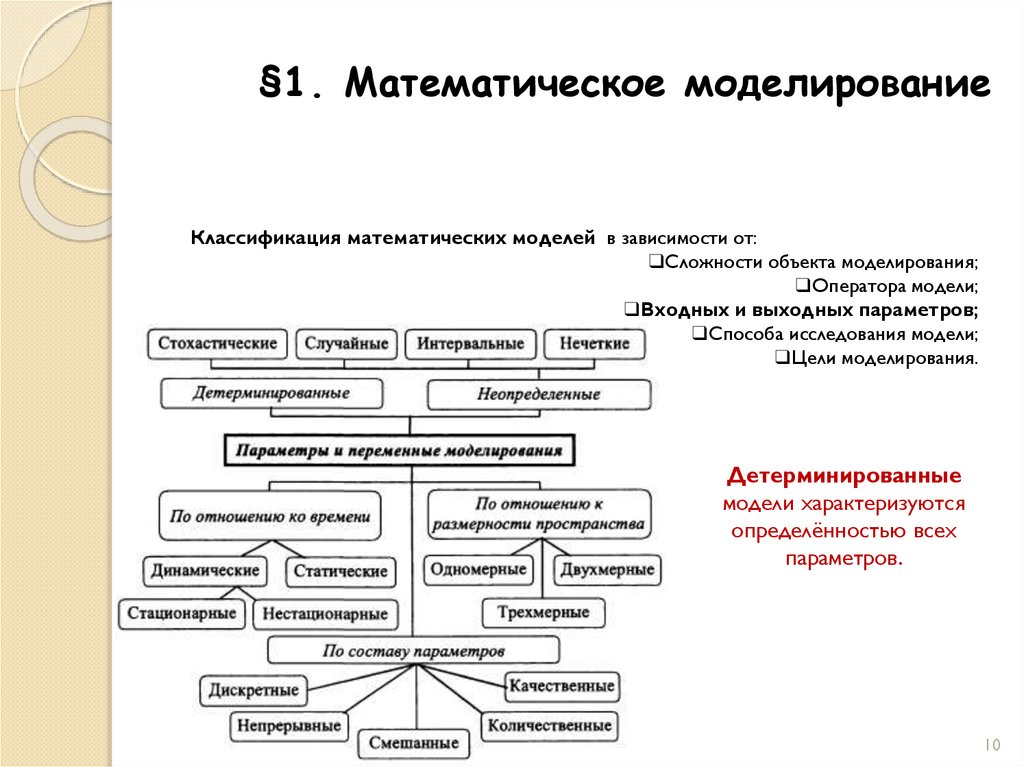
Детерминированные
модели характеризуются
определённостью всех
параметров.
10
11.
§1. Математическое моделированиеКлассификация математических моделей в зависимости от:
❑Сложности объекта моделирования;
❑Оператора модели;
❑Входных и выходных параметров;
❑Способа исследования модели;
❑Цели моделирования.
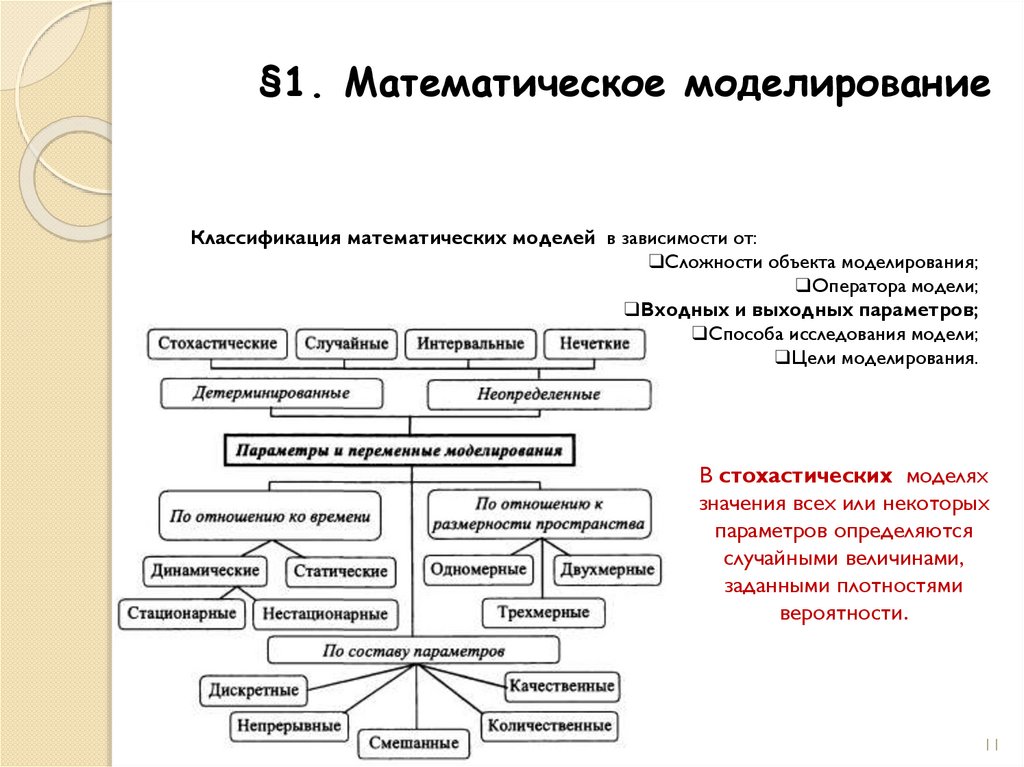
В стохастических моделях
значения всех или некоторых
параметров определяются
случайными величинами,
заданными плотностями
вероятности.
11
12.
§1. Математическое моделированиеКлассификация математических моделей в зависимости от:
❑Сложности объекта моделирования;
❑Оператора модели;
❑Входных и выходных параметров;
❑Способа исследования модели;
❑Цели моделирования.
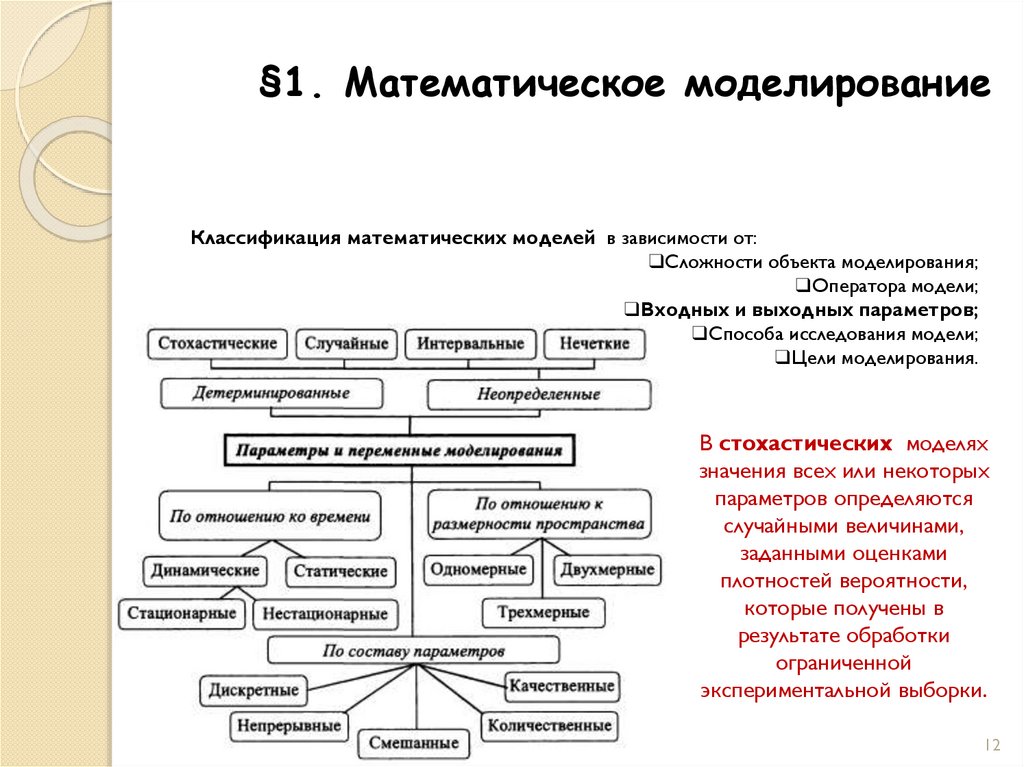
В стохастических моделях
значения всех или некоторых
параметров определяются
случайными величинами,
заданными оценками
плотностей вероятности,
которые получены в
результате обработки
ограниченной
экспериментальной выборки.
12
13.
§1. Математическое моделированиеКлассификация математических моделей в зависимости от:
❑Сложности объекта моделирования;
❑Оператора модели;
❑Входных и выходных параметров;
❑Способа исследования модели;
❑Цели моделирования.
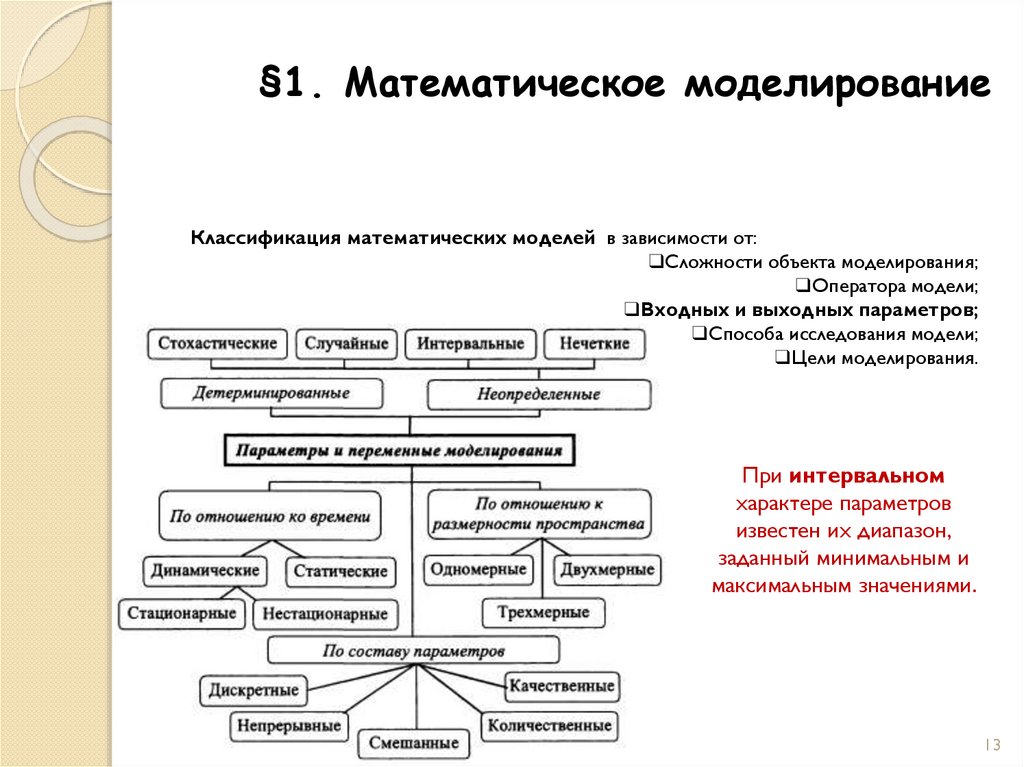
При интервальном
характере параметров
известен их диапазон,
заданный минимальным и
максимальным значениями.
13
14.
§1. Математическое моделированиеКлассификация математических моделей в зависимости от:
❑Сложности объекта моделирования;
❑Оператора модели;
❑Входных и выходных параметров;
❑Способа исследования модели;
❑Цели моделирования.
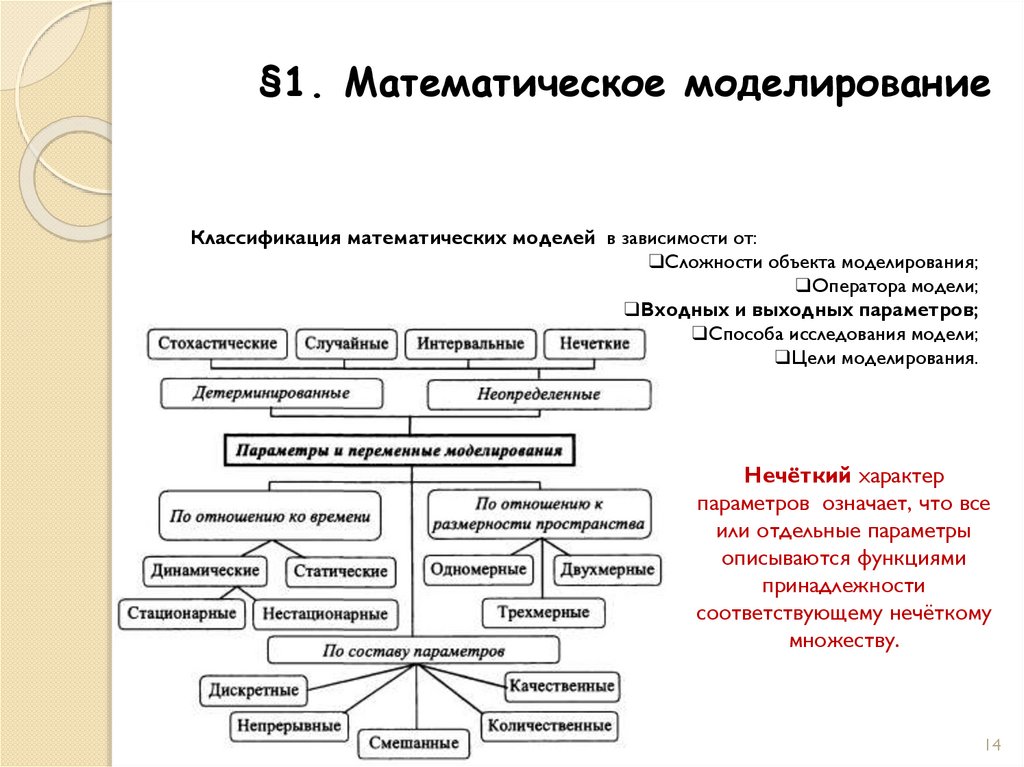
Нечёткий характер
параметров означает, что все
или отдельные параметры
описываются функциями
принадлежности
соответствующему нечёткому
множеству.
14
15.
§1. Математическое моделированиеКлассификация математических моделей в зависимости от:
❑Сложности объекта моделирования;
❑Оператора модели;
❑Входных и выходных параметров;
❑Способа исследования модели;
❑Цели моделирования.
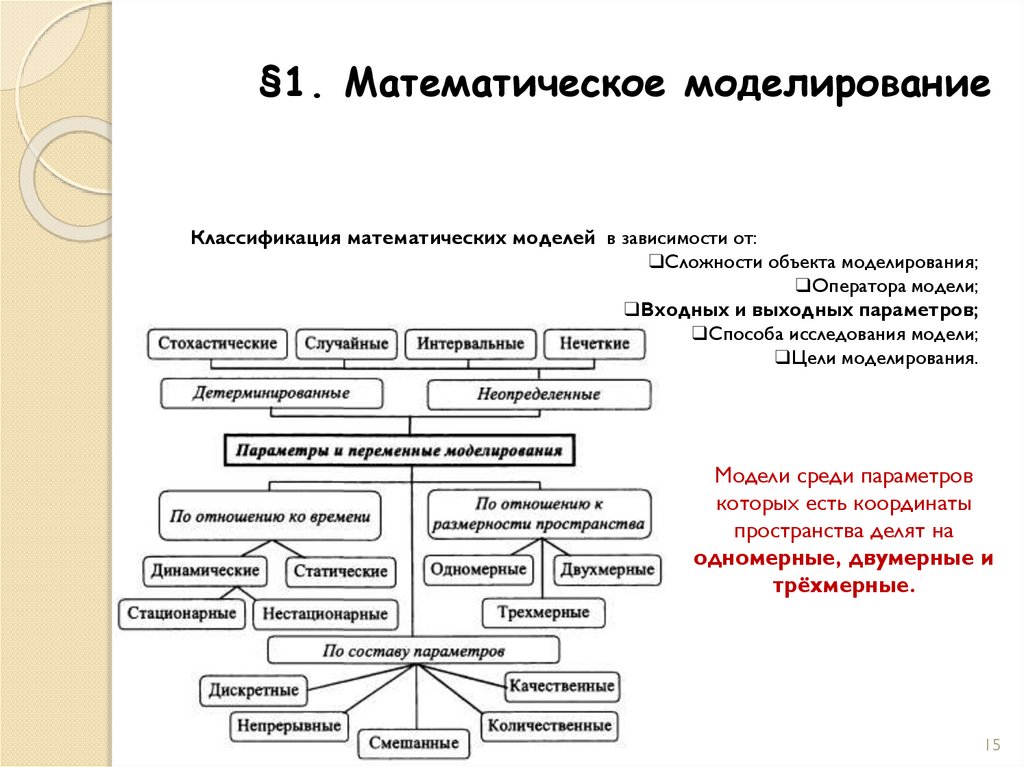
Модели среди параметров
которых есть координаты
пространства делят на
одномерные, двумерные и
трёхмерные.
15
16.
§1. Математическое моделированиеКлассификация математических моделей в зависимости от:
❑Сложности объекта моделирования;
❑Оператора модели;
❑Входных и выходных параметров;
❑Способа исследования модели;
❑Цели моделирования.
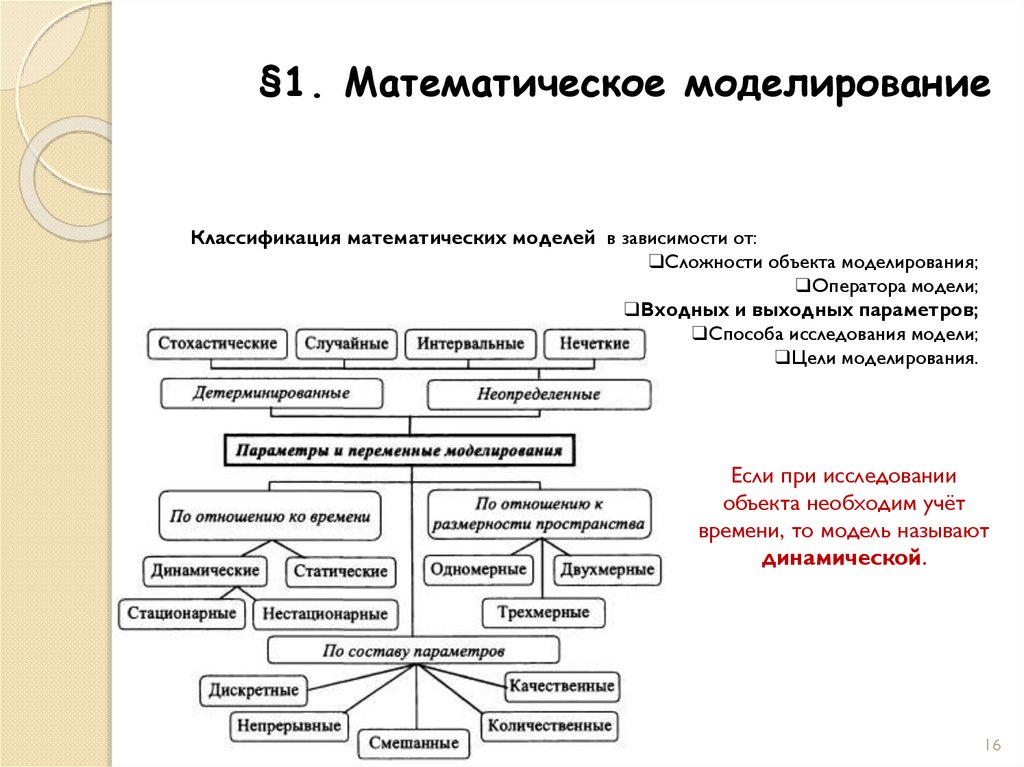
Если при исследовании
объекта необходим учёт
времени, то модель называют
динамической.
16
17.
§1. Математическое моделированиеКлассификация математических моделей в зависимости от:
❑Сложности объекта моделирования;
❑Оператора модели;
❑Входных и выходных параметров;
❑Способа исследования модели;
❑Цели моделирования.
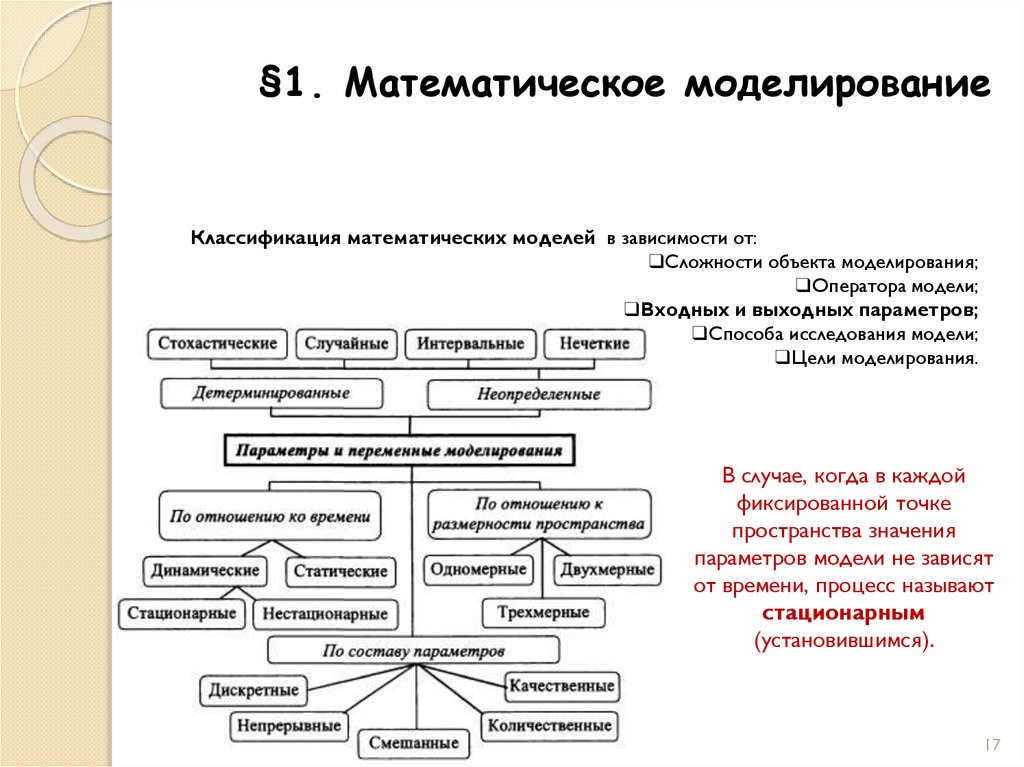
В случае, когда в каждой
фиксированной точке
пространства значения
параметров модели не зависят
от времени, процесс называют
стационарным
(установившимся).
17
18.
§1. Математическое моделированиеКлассификация математических моделей в зависимости от:
❑Сложности объекта моделирования;
❑Оператора модели;
❑Входных и выходных параметров;
❑Способа исследования модели;
❑Цели моделирования.
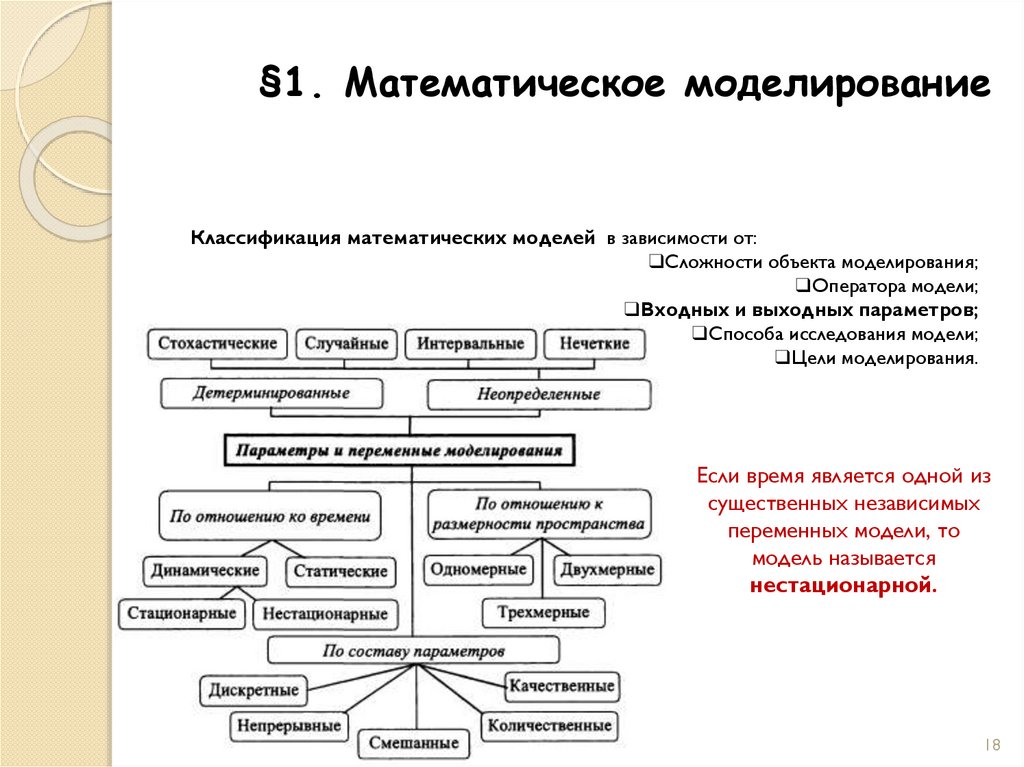
Если время является одной из
существенных независимых
переменных модели, то
модель называется
нестационарной.
18
19.
§1. Математическое моделированиеКлассификация математических моделей в зависимости от:
❑Сложности объекта моделирования;
❑Оператора модели;
❑Входных и выходных параметров;
❑Способа исследования модели;
❑Цели моделирования.
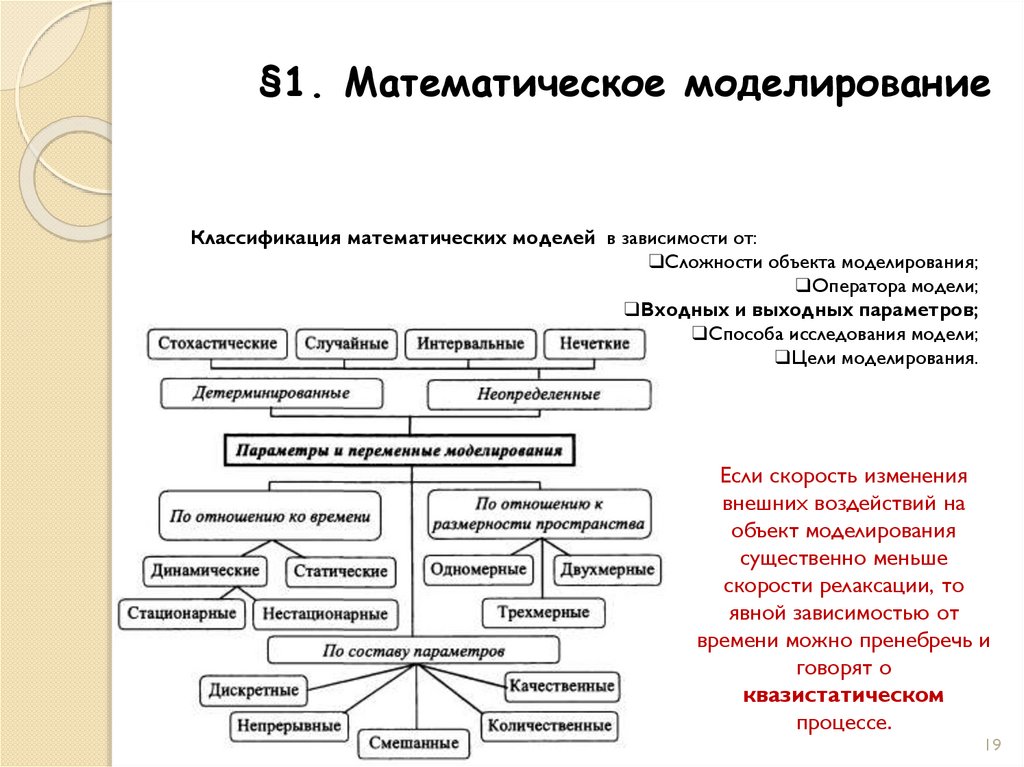
Если скорость изменения
внешних воздействий на
объект моделирования
существенно меньше
скорости релаксации, то
явной зависимостью от
времени можно пренебречь и
говорят о
квазистатическом
процессе.
19
20.
§1. Математическое моделированиеКлассификация математических моделей в зависимости от:
❑Сложности объекта моделирования;
❑Оператора модели;
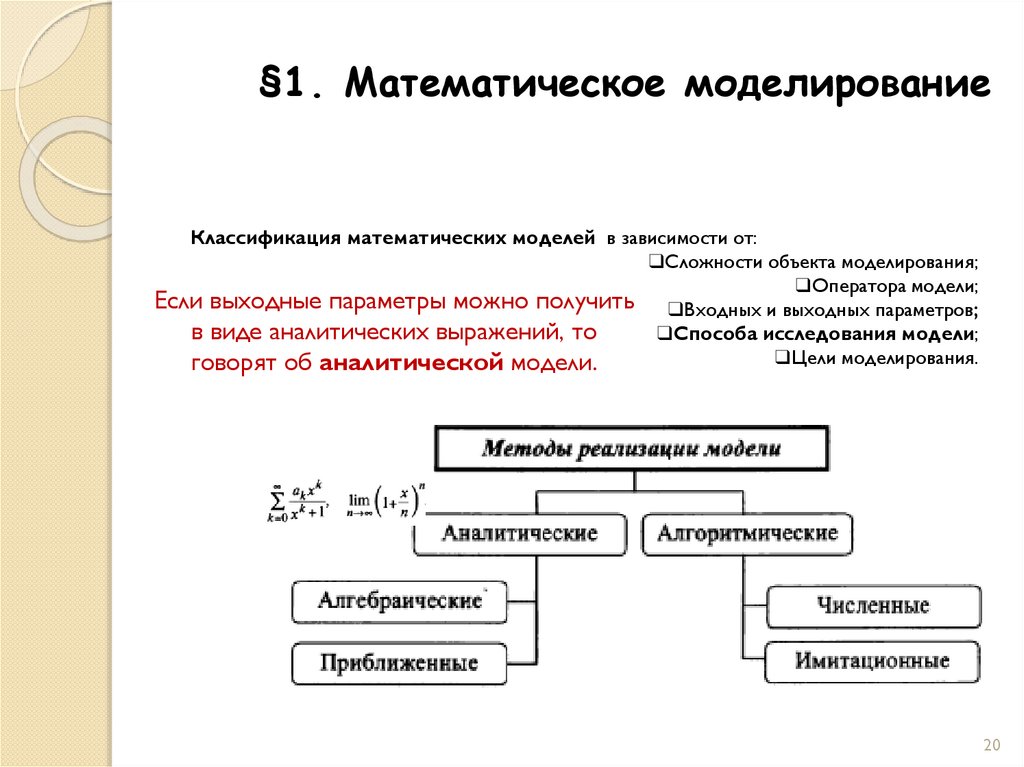
Если выходные параметры можно получить ❑Входных и выходных параметров;
в виде аналитических выражений, то
❑Способа исследования модели;
❑Цели моделирования.
говорят об аналитической модели.
20
21.
§1. Математическое моделированиеКлассификация математических моделей в зависимости от:
❑Сложности объекта моделирования;
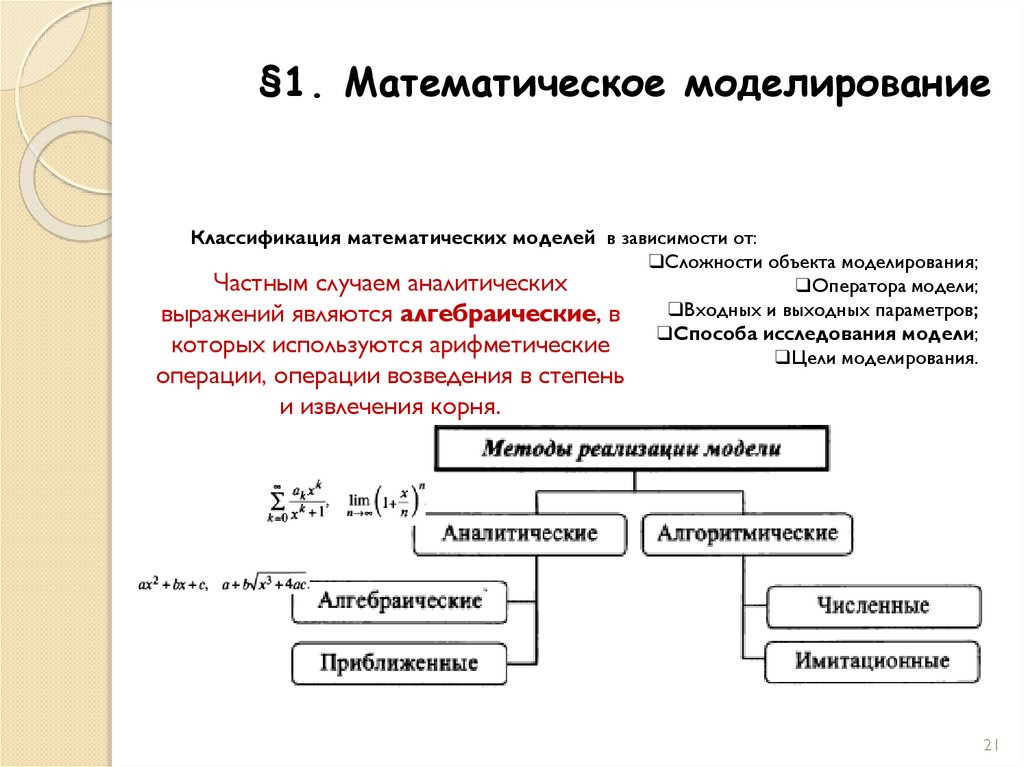
Частным случаем аналитических
❑Оператора модели;
❑Входных и выходных параметров;
выражений являются алгебраические, в
❑Способа исследования модели;
которых используются арифметические
❑Цели моделирования.
операции, операции возведения в степень
и извлечения корня.
21
22.
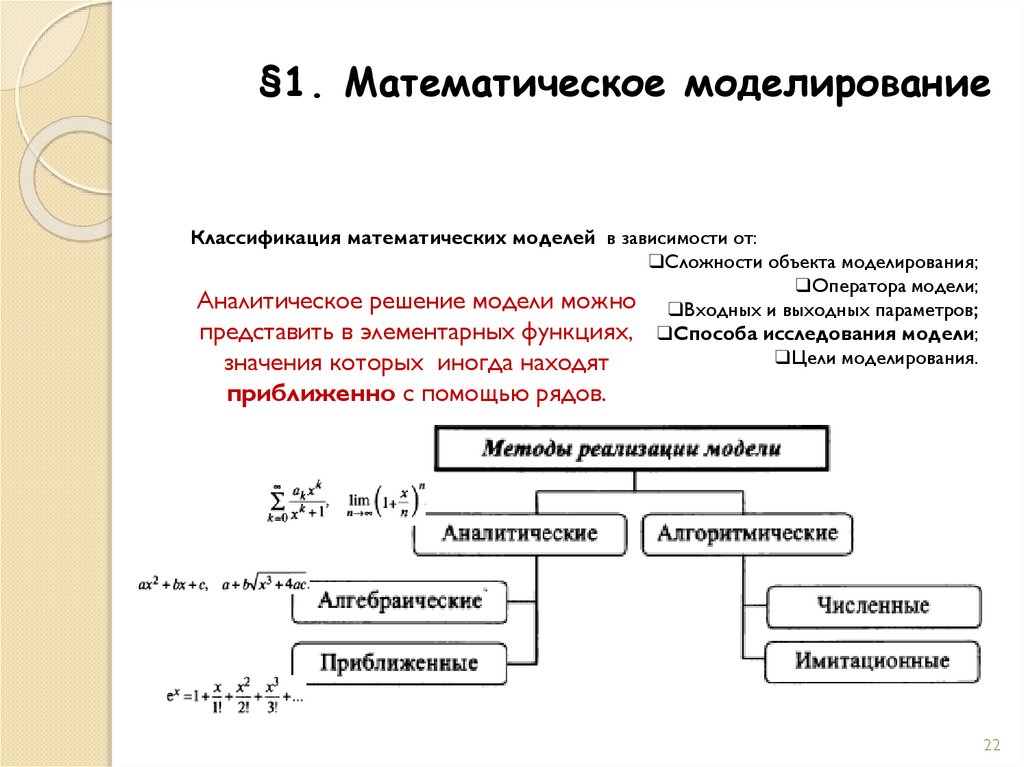
§1. Математическое моделированиеКлассификация математических моделей в зависимости от:
❑Сложности объекта моделирования;
❑Оператора модели;
Аналитическое решение модели можно ❑Входных и выходных параметров;
представить в элементарных функциях, ❑Способа исследования модели;
❑Цели моделирования.
значения которых иногда находят
приближенно с помощью рядов.
22
23.
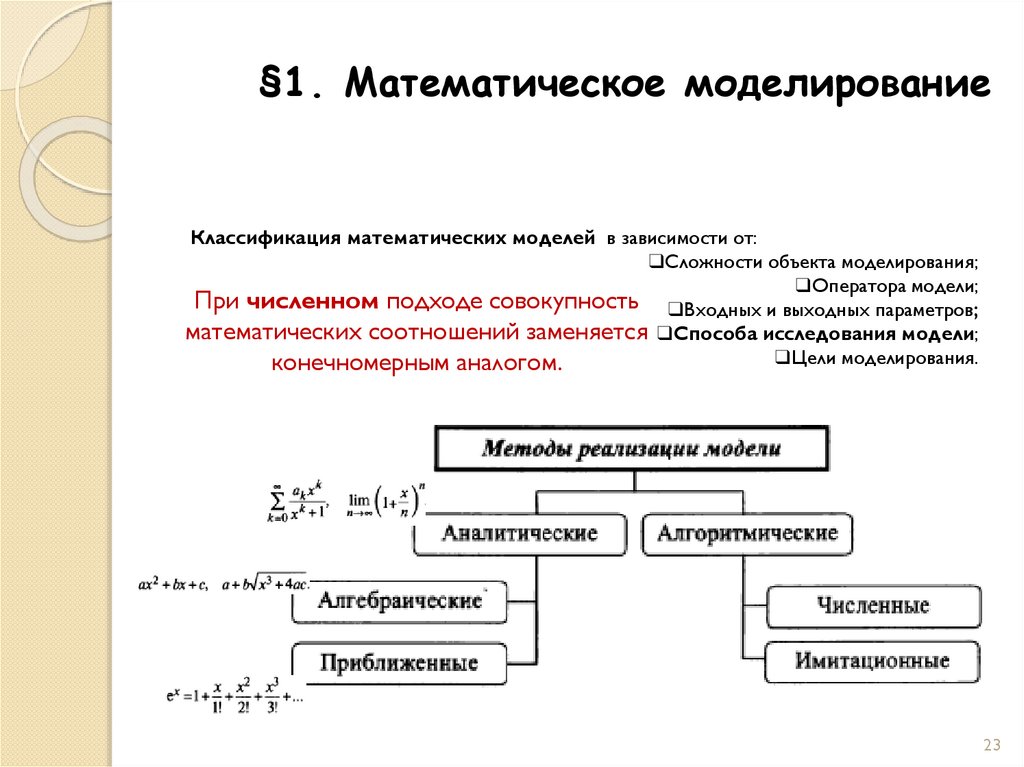
§1. Математическое моделированиеКлассификация математических моделей в зависимости от:
❑Сложности объекта моделирования;
❑Оператора модели;
При численном подходе совокупность ❑Входных и выходных параметров;
математических соотношений заменяется ❑Способа исследования модели;
❑Цели моделирования.
конечномерным аналогом.
23
24.
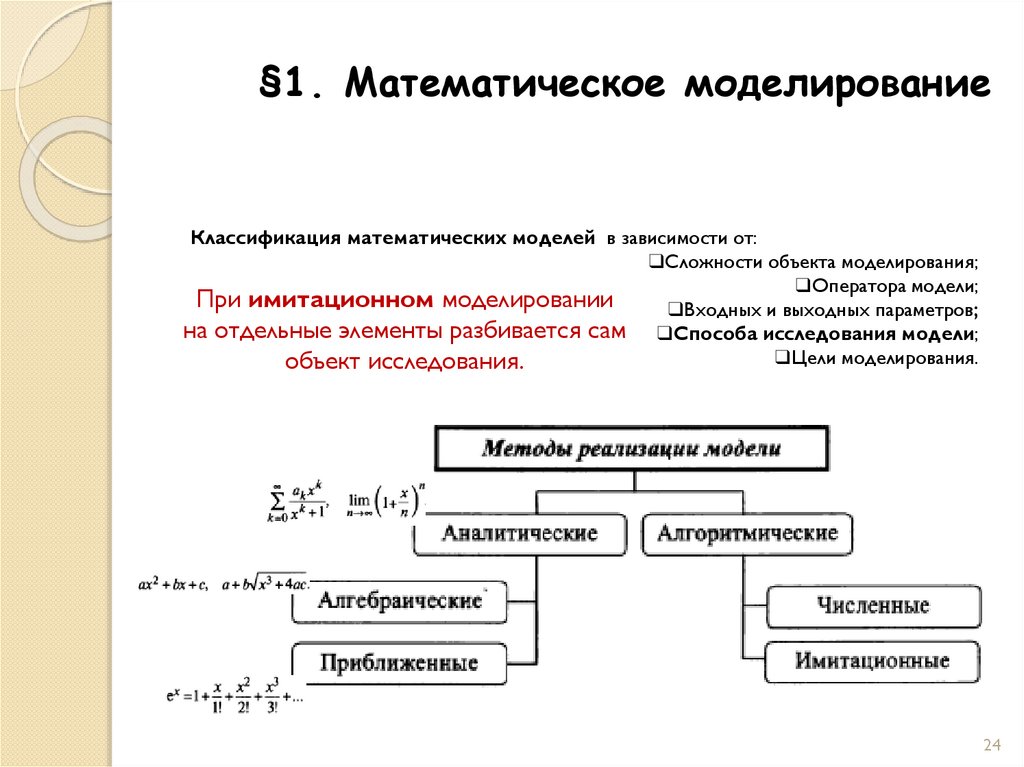
§1. Математическое моделированиеКлассификация математических моделей в зависимости от:
❑Сложности объекта моделирования;
❑Оператора модели;
При имитационном моделировании
❑Входных и выходных параметров;
на отдельные элементы разбивается сам ❑Способа исследования модели;
❑Цели моделирования.
объект исследования.
24
25.
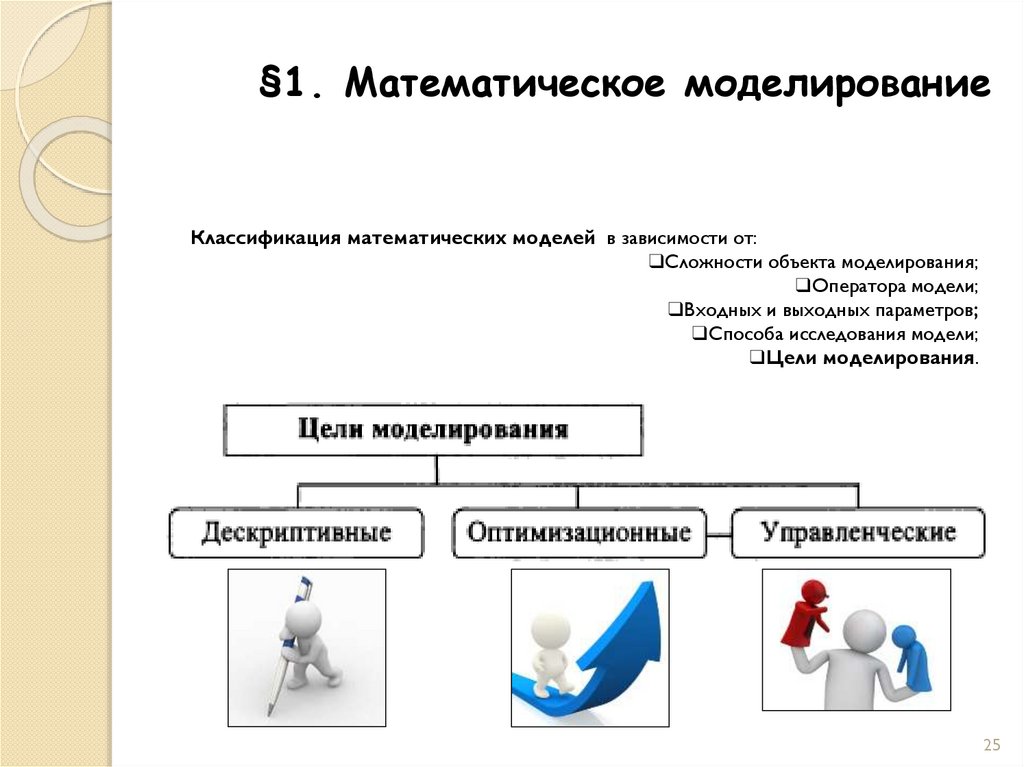
§1. Математическое моделированиеКлассификация математических моделей в зависимости от:
❑Сложности объекта моделирования;
❑Оператора модели;
❑Входных и выходных параметров;
❑Способа исследования модели;
❑Цели моделирования.
25
26.
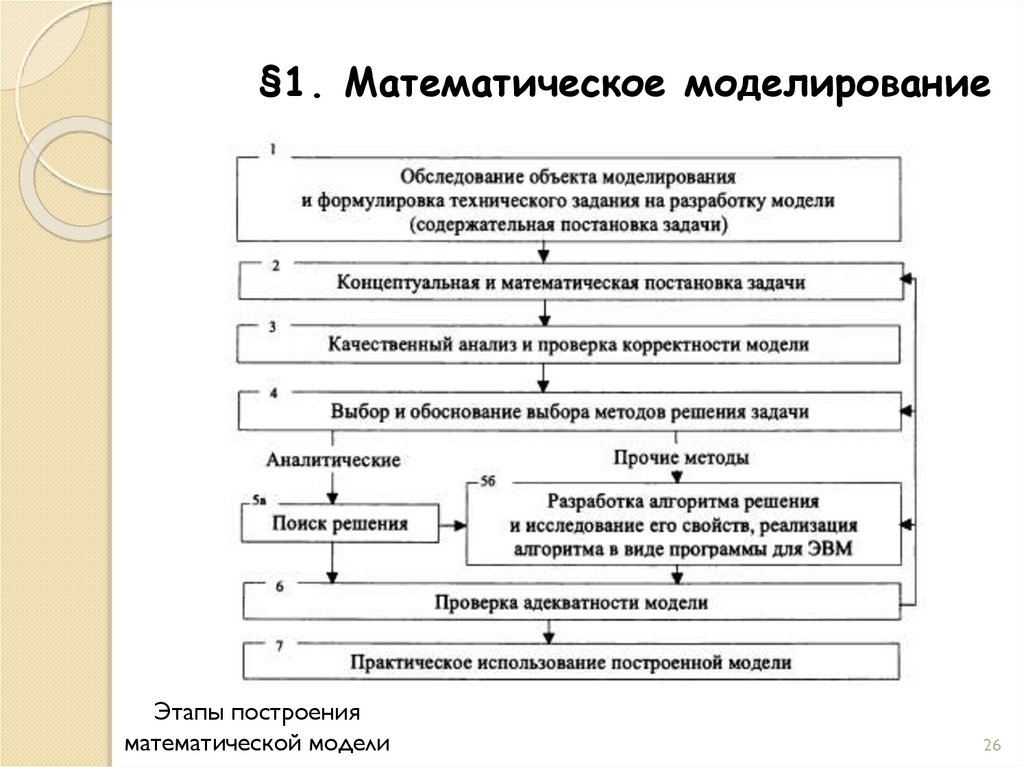
§1. Математическое моделированиеЭтапы построения
математической модели
26
27.
§1. Математическое моделированиеЭтапы построения
математической модели
27
28.
§1. Математическое моделированиеЭтапы построения
математической модели
28
29.
§1. Математическое моделированиеЭтапы построения
математической модели
29
30.
§1. Математическое моделированиеЭтапы построения
математической модели
30
31.
§1. Математическое моделированиеЭтапы построения
математической модели
31
32.
§1. Математическое моделированиеЭтапы построения
математической модели
32
33.
§1. Математическое моделированиеЭтапы построения
математической модели
33
34.
§1. Математическое моделированиеЭтапы построения
математической модели
34
35.
§1. Математическое моделированиеЭтапы построения
математической модели
35
36.
§1. Математическое моделированиеЭтапы построения
математической модели
36
37.
§1. Математическое моделированиеЭтапы построения
математической модели
37
38.
§1. Математическое моделированиеЭтапы построения
математической модели
38
39.
§1. Математическое моделированиеЭтапы построения
математической модели
39
40.
§2. Примеры линейных моделейАбатурова Вера Сергеевна
к.п.н.; зав. отделом образовательных и
информационных технологий Южного
математического института Владикавказского
научного центра РАН;
директор ВЦНМО
40
41.
§2. Примеры линейных моделейСистема уравнений
а - количество единиц травы, которое
было на лугу первоначально;
b - количество единиц травы, которое
ежедневно вырастает на лугу;
с - количество единиц травы, которое
ежедневно съедает одна корова.
Ответ: 20 коров.
41
42.
§2. Примеры линейных моделейСистема уравнений
а - количество единиц травы, которое
было на лугу первоначально;
b - количество единиц травы, которое
ежедневно вырастает на лугу;
с - количество единиц травы, которое
ежедневно съедает одна корова.
Ответ: 20 коров.
1. Выбор переменных.
2. Запись ограничений на
переменные.
3. Формулировка
требований задачи на
языке математики (с
помощью переменных).
4. Решение математической
задачи.
5. Интерпретация
результатов. Запись ответа.
42
43.
§2. Примеры линейных моделейСистема неравенств
х – вес купленных слив (кг);
у – вес купленных яблок (кг).
43
44.
§2. Примеры линейных моделейСистема неравенств
х – вес купленных слив (кг);
у – вес купленных яблок (кг).
44
45.
§3. Примеры оптимизационных моделейЛинейное программирование
45
46.
§3. Примеры оптимизационных моделейЛинейное программирование
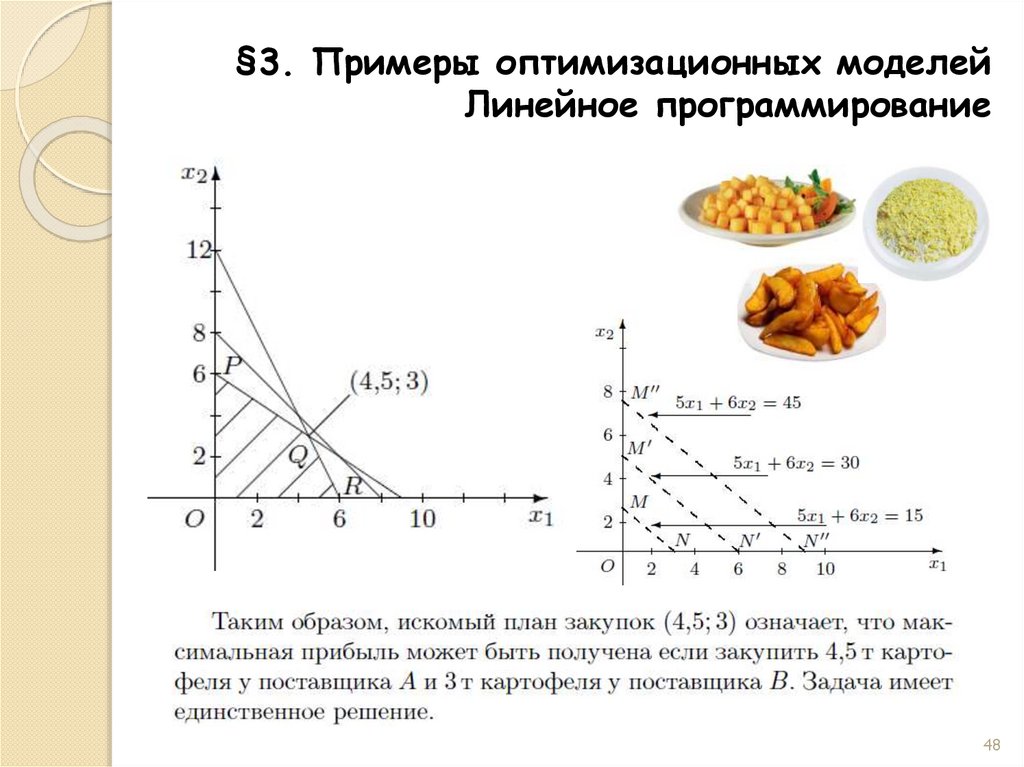
х1 – вес картофеля, который покупается у
поставщика А (т);
х2 – вес картофеля, который покупается у
поставщика В (т).
целевая функция
46
47.
§3. Примеры оптимизационных моделейЛинейное программирование
47
48.
§3. Примеры оптимизационных моделейЛинейное программирование
48
49.
§3. Примеры оптимизационных моделейБрахистохрона
Брахистохрона – кривая
наискорейшего спуска
Оптико—механическая аналогия:
в задаче о преломлении света и в
данной задаче минимизируется
«взвешенная» сумма длин.
49



























 mathematics
mathematics








