Параллельность плоскостей

1.

2.

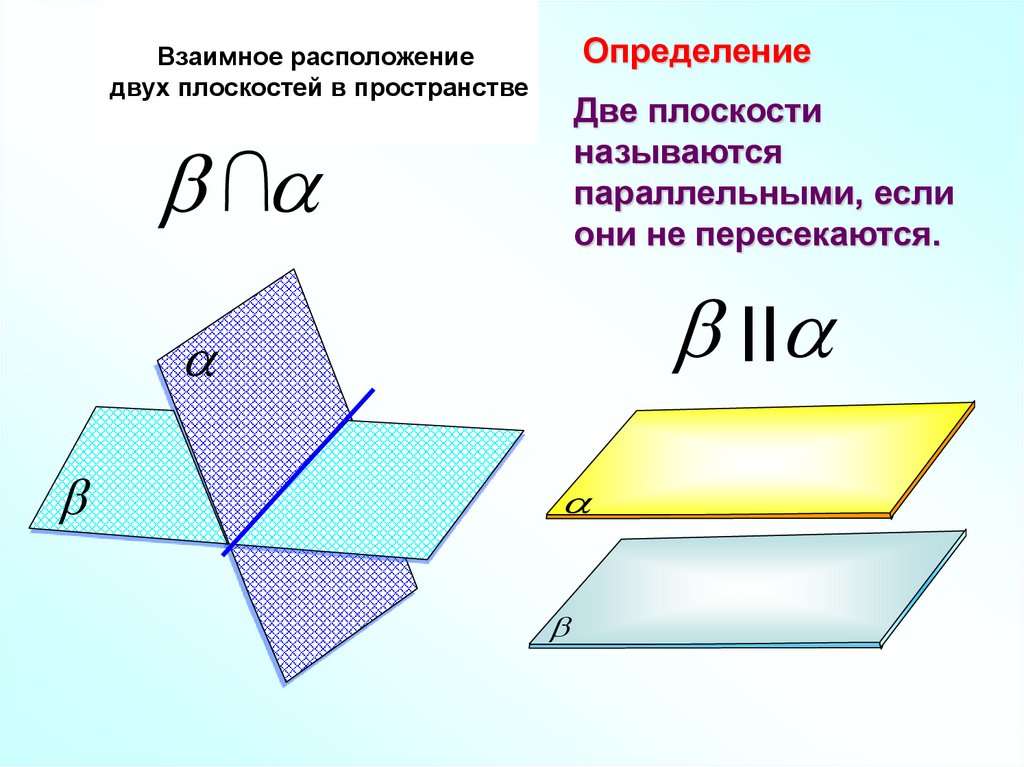
Определение
Взаимное расположение
двух плоскостей в пространстве
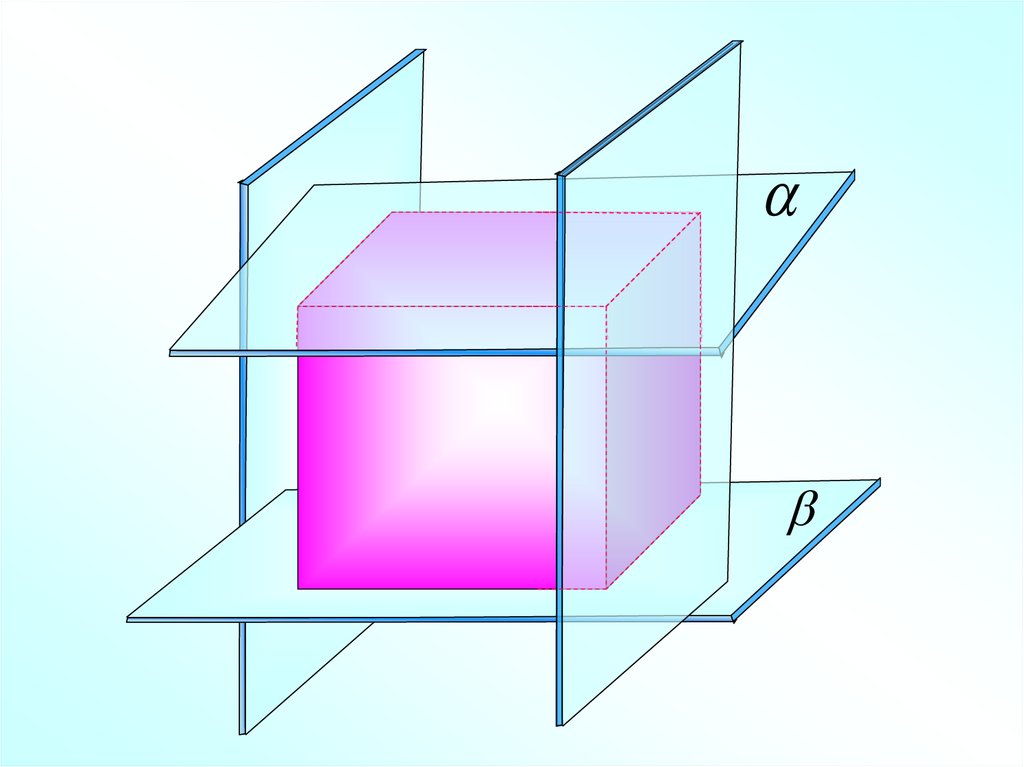
Две плоскости
называются
параллельными, если
они не пересекаются.
II

3.

4.

5.

6.

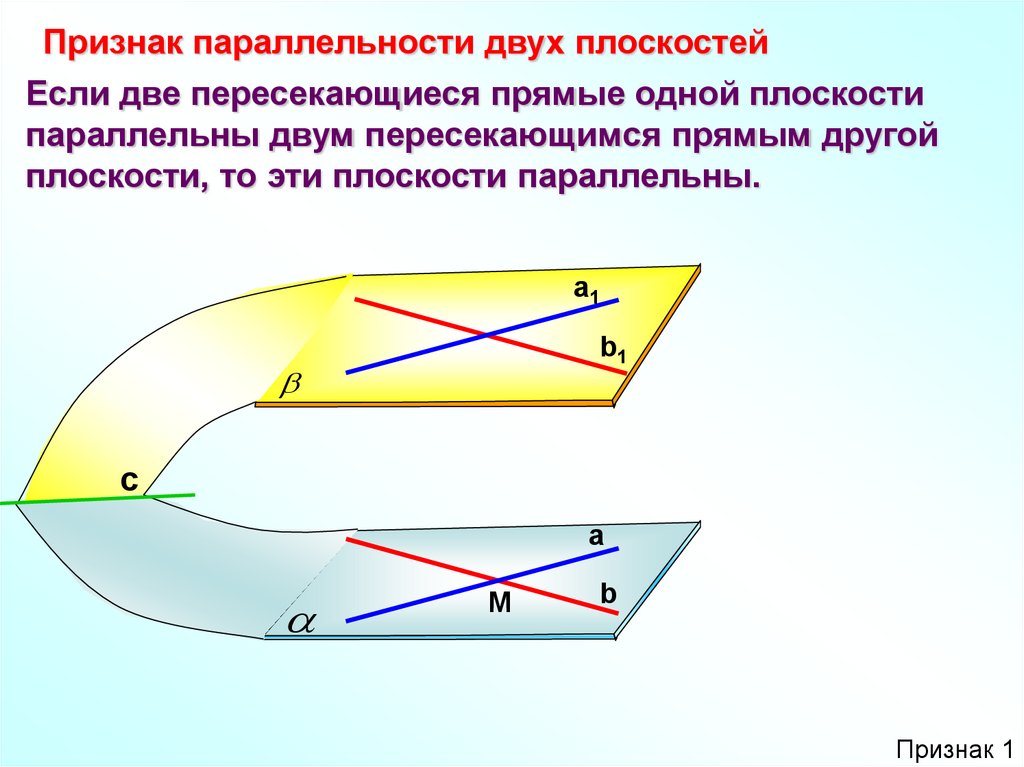
Признак параллельности двух плоскостей
Если две пересекающиеся прямые одной плоскости
параллельны двум пересекающимся прямым другой
плоскости, то эти плоскости параллельны.
а1
b1
с
а
M
b
Признак 1

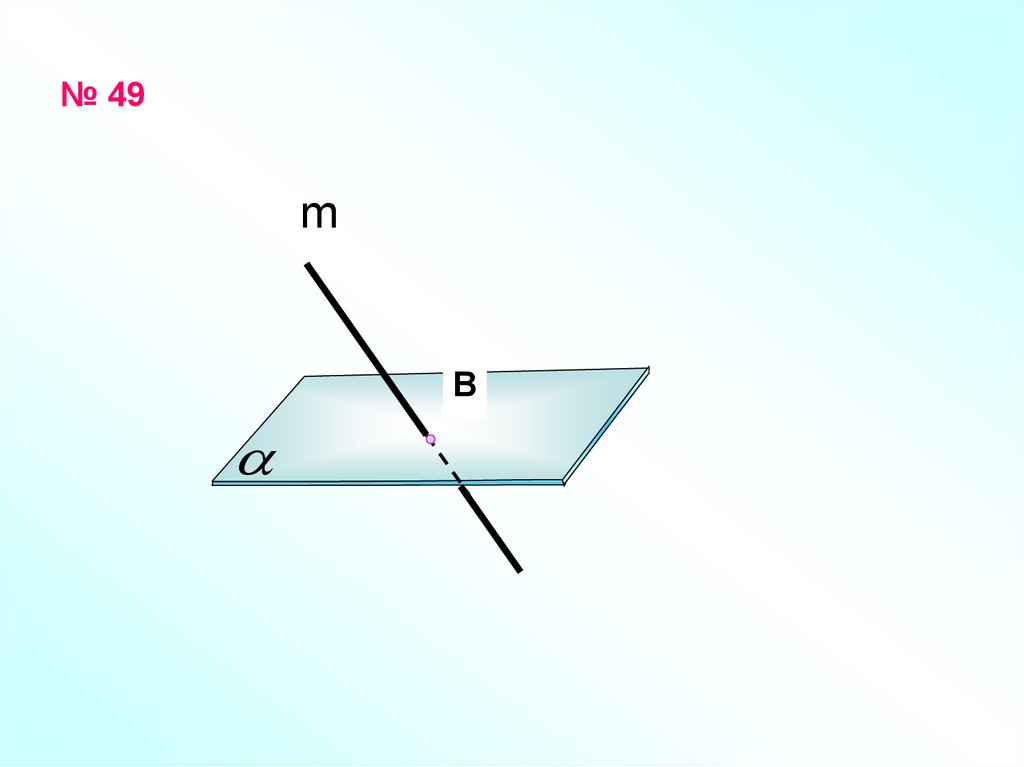
7. № 49

m
В

8.

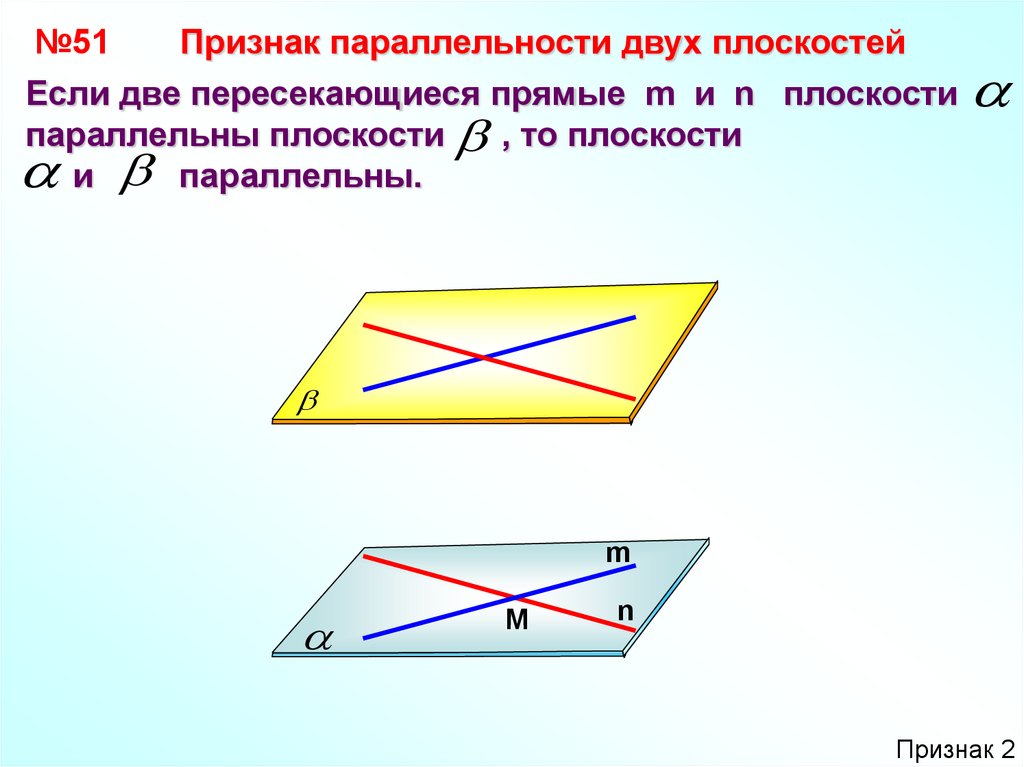
№51
Признак параллельности двух плоскостей
Если две пересекающиеся прямые m и n плоскости
параллельны плоскости , то плоскости
и параллельны.
m
M
n
Признак 2

9.

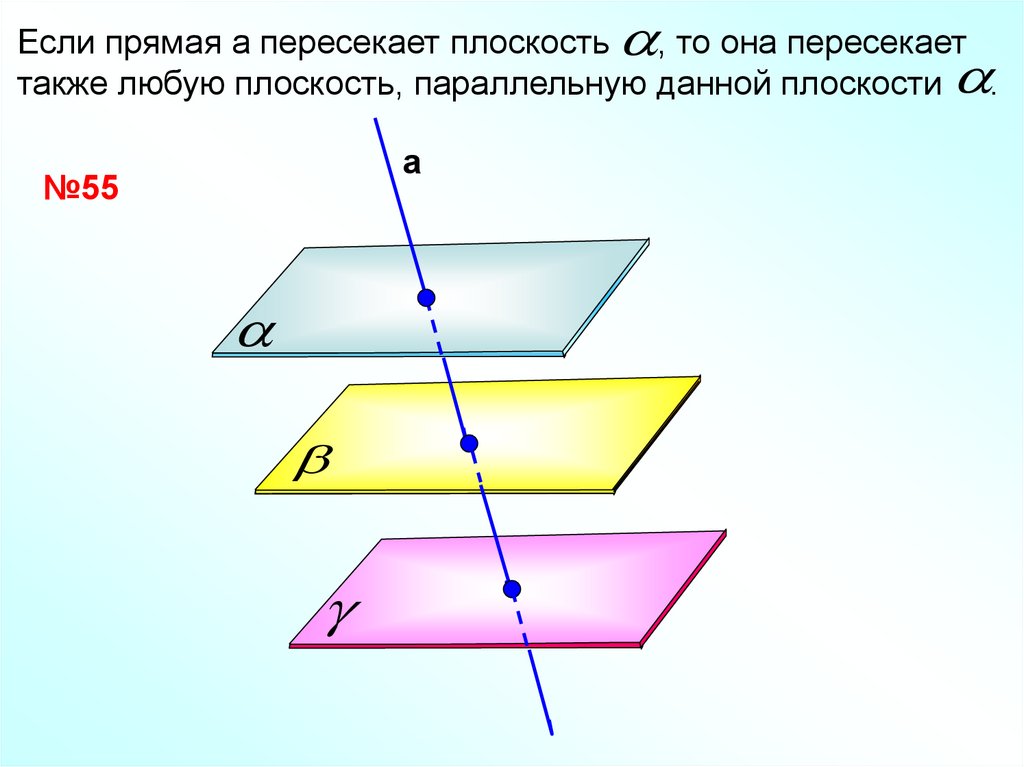
Если прямая а пересекает плоскость , то она пересекает
также любую плоскость, параллельную данной плоскости .
а
№55

10.

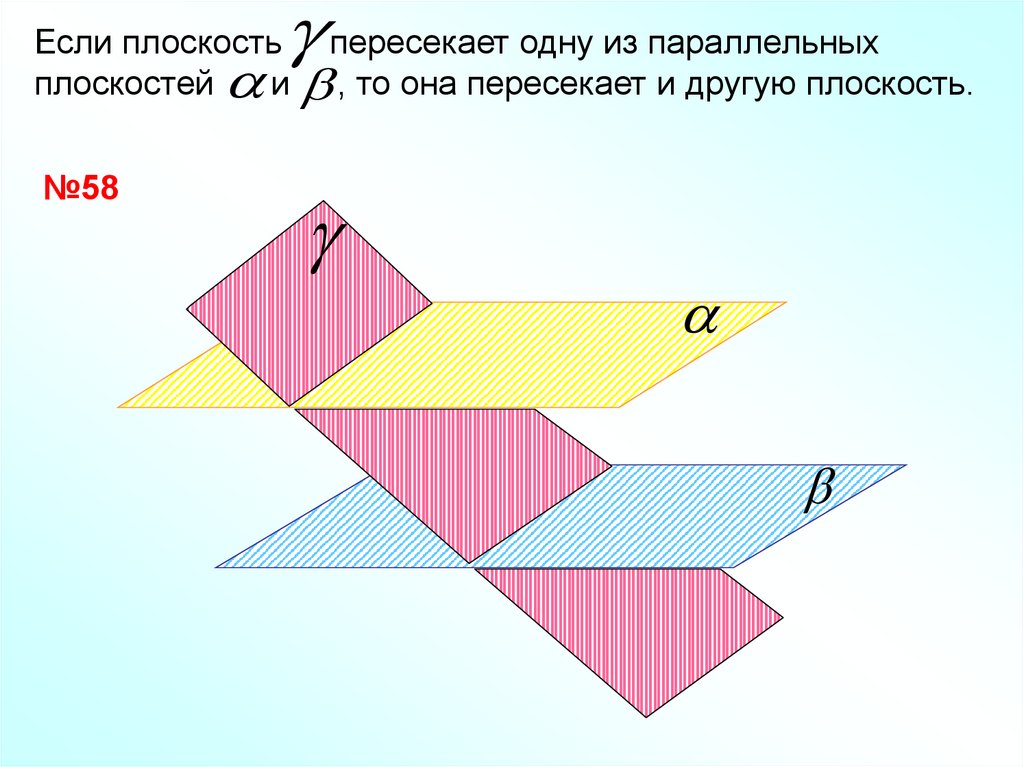
Если плоскость пересекает одну из параллельных
плоскостей
и , то она пересекает и другую плоскость.
№58

11.

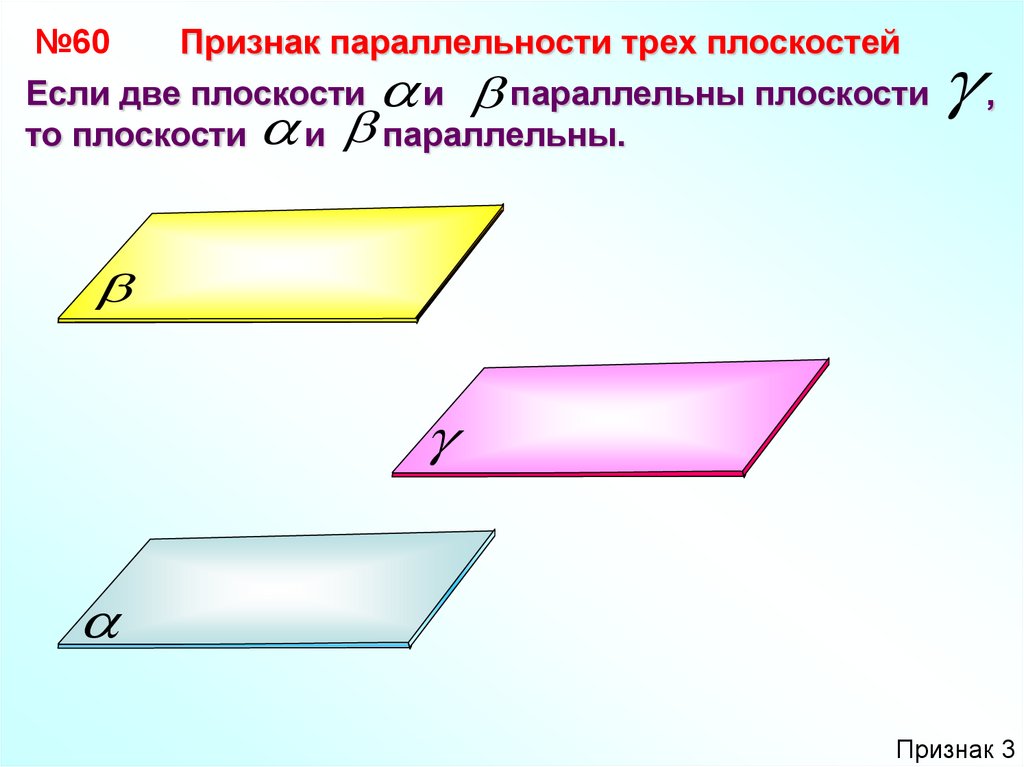
№60
Признак параллельности трех плоскостей
Если две плоскости
и параллельны плоскости
то плоскости
и параллельны.
,
Признак 3

12.

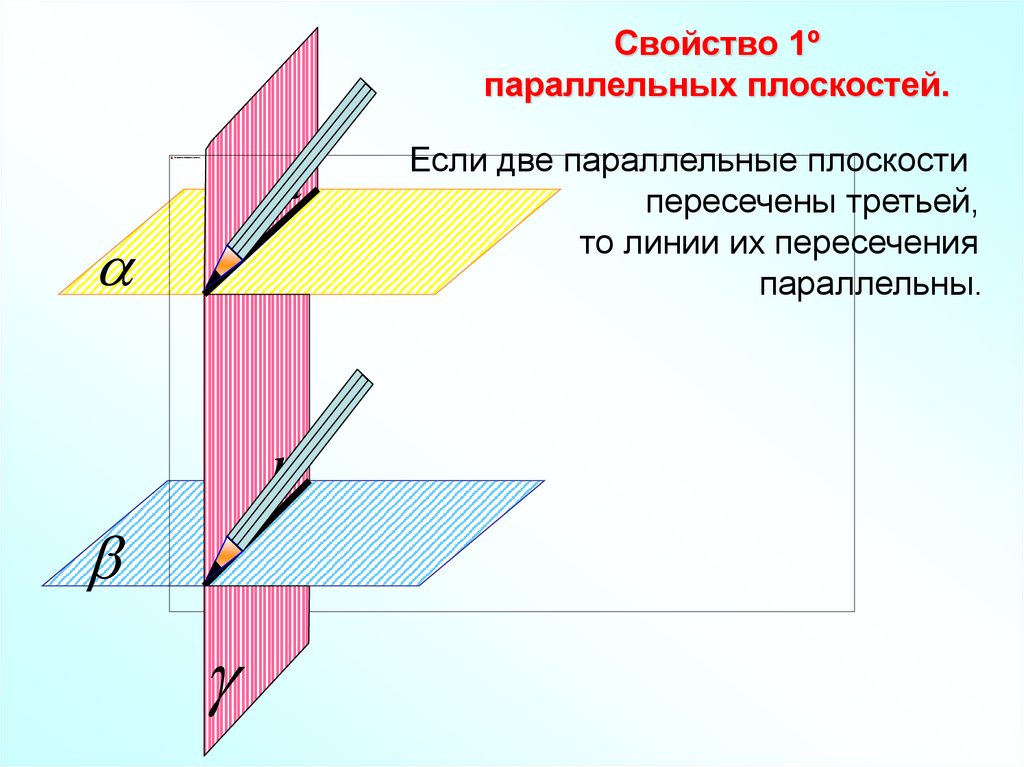
Свойство 1º
параллельных плоскостей.
а
b
Если две параллельные плоскости
пересечены третьей,
то линии их пересечения
параллельны.

13.

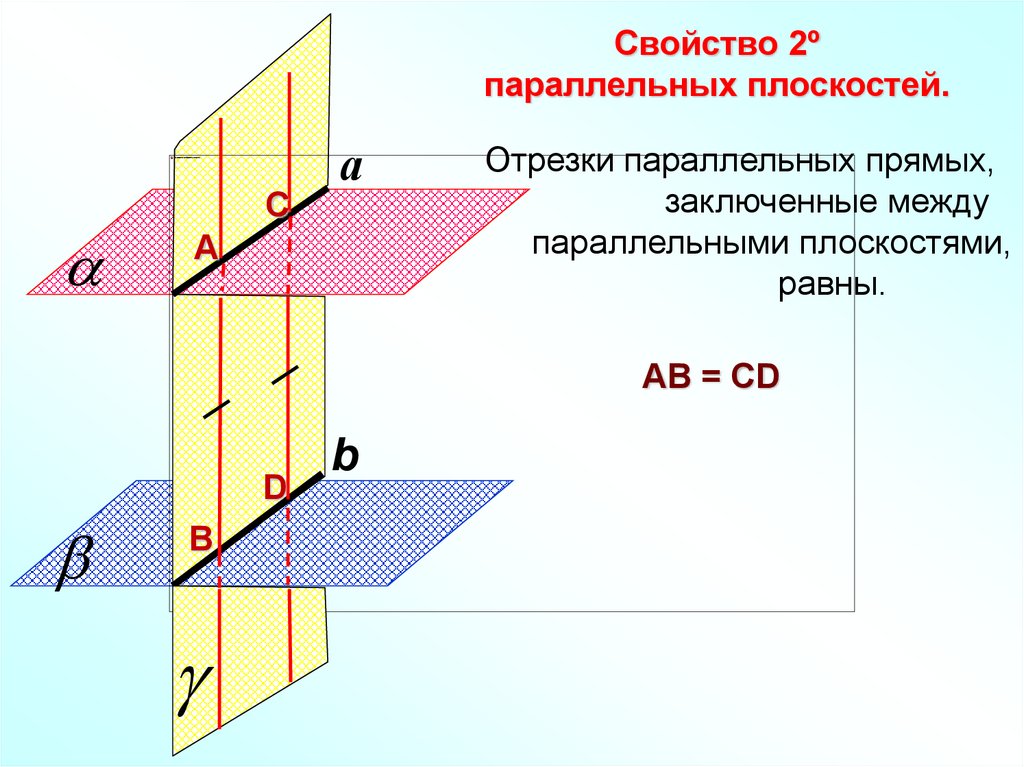
Свойство 2º
параллельных плоскостей.
С
а
А
Отрезки параллельных прямых,
заключенные между
параллельными плоскостями,
равны.
АВ = СD
D
В
b

14. Тетраэдр и параллелепипед

• Тетраэдр
• Параллелепипед
• Свойства параллелепипеда