Similar presentations:
Использование приема обобщения в процессе развития мышления учащихся
1.
2.
В настоящее время большое внимание уделяетсяактивизации познавательной деятельности
учащихся. Многие учителя используют в своей
практике различные приёмы, способствующие
активности учащихся на уроке.
Одной из основных и важнейших операций
логического мышления младшего школьника
является обобщение. В процессе обучения
школьник, путем обобщения, получает возможность
суммировать полученные в школе знания и делать
обобщающие выводы.
Изучение математики сталкивает детей с
необходимостью выделять существенные свойства,
которые присущи нескольким предметам и
явлениям, и обобщать их, формируя определенные
понятия.
3.
Процессобобщения
выступает
приемом
осуществления
учащимися
учебнопознавательной
деятельности.
Данная операция приводит учащихся к новым обобщенным знаниям,
способам действий, т.е. обеспечивает овладение ими основами наук,
которые становятся средствами решения конкретных задач и
дальнейшего овладения математикой;
Таким образом, математика играет важную роль в процессе
формирования процесса обобщения.
Этот процесс начинается в начальной школе. Такие авторы, как А. К.
Артемов, Н. А. Менчинская, М. И. Моро и Г. И. Минская пишут о
необходимости и особенностях формирования вышеназванной
умственной операции. Младший школьник, определяя понятия,
указывает преимущественно наглядные, конкретные и единичные
предметы и явления, их признаки и свойства. Это объясняется
недостатком знаний, а также слабым развитием мыслительной
операции обобщения у детей младшего школьного возраста.
4.
Необходимоиметь в виду,
что обобщения
могут быть
более или менее
широкие.
Например, правило прибавления числа к сумме –
обобщение. Овладение им учащимися
составляют одну из учебных задач в 1 классе.
В 3 классе учащиеся узнают, что при сложении
любые два или несколько слагаемых можно
заменить их суммой. Это также обобщение, но
более широко охватывающее изученное ранее
правило.
В обучении математике процессы обобщения
могут быть организованы по-разному, что влияет
на выбор методики обучения.
5.
В основеобобщения
лежат
приемы:
анализа,
синтеза,
сравнения,
абстрагирование,
конкретизация.
6.
Приёмы логического анализа, синтеза, сравнения,обобщения и классификации необходимы учащимся уже
в 1 классе, без овладения ими не происходит полноценного
усвоения учебного материала.
Эти данные показывают, что именно в младшем
школьном возрасте необходимо проводить
целенаправленную работу по обучению детей основным
приёмам мыслительной деятельности.
Предметы и явления объективного мира находятся между собой в
разнообразных связях и отношениях. Познание и обобщение этих
связей и отношений является одной из важнейших функций
мышления.
7.
Еще С. Л. Рубинштейн писал:«Мышление внутренне связанно с обобщениями – оно
совершенствуется в них и ведет к обобщениям более
высокого порядка»
8.
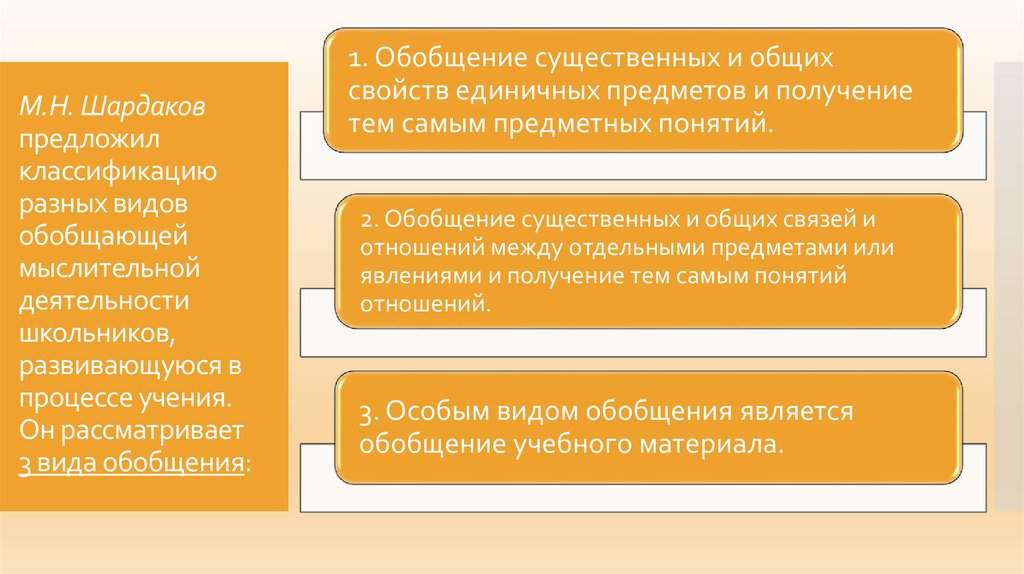
М.Н. Шардаковпредложил
классификацию
разных видов
обобщающей
мыслительной
деятельности
школьников,
развивающуюся в
процессе учения.
Он рассматривает
3 вида обобщения:
1. Обобщение существенных и общих
свойств единичных предметов и получение
тем самым предметных понятий.
2. Обобщение существенных и общих связей и
отношений между отдельными предметами или
явлениями и получение тем самым понятий
отношений.
3. Особым видом обобщения является
обобщение учебного материала.
9.
Таким образом,Обобщение – это нахождение общего в
предметах и явлениях. Нахождение
общего включает в себя сопоставление
предметов, вычленение общих
признаков в каждом из данных
предметов и объединение последних по
этим признакам.
10.
Точно так же каждое явление возникает перед нами всущественных и несущественных связях и отношениях.
Предметы или явления одного рода имеют существенные
признаки или связи, которые всегда общие.
Каждый предмет
имеет
существенные и
несущественные
признаки и
свойства.
Существенные признаки – это признаки
постоянные, устойчивые, сохраняющиеся у данной
группы предметов при вариации несущественных.
При помощи существенных признаков предмет может быть
легко отличен от предметов, которые даже сходны с ним, но
не точно совпадающие с тем предметом, о котором идет
речь.
11.
Успешностьовладения
операцией
обобщения
Сравнивая предметы и явления, мы находим сначала
их общие свойства, а потом объединяем их по общим
существенным признакам. Это объединение
возможно, так как мы отвлекаемся от несущественных
признаков.
Успешность овладения операцией обобщения зависит,
во-первых, от наличия у человека тех знаний,
которыми он должен воспользоваться для решения
поставленной задачи, во-вторых, он должен владеть
специальными умениями, т.е. способами выполнения
умственных действий – анализа, синтеза, сравнения.
Различают результат и процесс обобщения.
Результат фиксируется в понятии, суждении, правилах.
Примером обобщения является любое правило.
12.
А.К. Артемовпредложил
4 вида
организации
процесса
обобщения:
1. Обобщенные знания как способы действий сообщаются
ученикам в готовом виде;
2. Обобщенные знания проявляются как логический вывод из
ранее установленных обобщений.
Здесь процесс обобщения проявляется как процесс рассуж
дения, приводящих к общему выводу;
3. Процесс обобщения представлен путем сравнения одного
или более объектов по существенным признакам;
4. Процесс обобщения характеризуется тем,
что с самого начала путем анализа одного математического
объекта выявляются существенные его особенности,
отражающие общие признаки всех объектов из данной обл
асти (темы, разделы). Это суть теоретического обобщения.
13.
Процессобобщения
может быть
организован
по - разному.
14.
Но прежде чем раскрыть сутьэмпирического и теоретического
обобщения, начать стоит с
подготовительного этапа.
Подготовительный
этап
Подготовительный этап к формированию
обобщения знаний вводится еще в
дошкольный период и продолжается в 1
классе. К нему относятся дидактические
упражнения и игры без математических
понятий.
Содержание обучения на этом этапе во
многом совпадает с тем, с чем дети
познакомились в детском саду. Как
правило, сюда включаются темы:
сравнение и счет предметов; множества
и действия над ними, пространственные
и временные отношения.
15.
Подготовка киспользованию
данного приема
эмпирического
обобщения
начинается с 1
класса, где
используются
упражнения с
предметами вида:
выяви
закономер
ность…
продолжи
ряд…
найди
ошибку…
заполни
пропуски…
16.
Рассмотримна
конкретных
примерах:
Игры,
которые можно
использовать
на
подготовитель
ном этапе.
17.
Условие: Юра разложил перед Клапаном картинки вопределённом порядке (в соответствии с
закономерностью).
Последовательность
в картинках
Задание: Помоги Клапану выбрать следующую картинку.
18.
Цели: Развитие мыслительных операций: классификации,обобщения; развитие мелкой моторики рук; формирование умения
выполнять инструкцию.
Оборудование: Картинки с изображением предметов (объектов)
(по 8), относящимся к определенным обобщающим понятиям,
шнурки по числу участников.
Дидактическая
игра с флажками
Описание вариантов игры:
Вариант 1.
У каждого участника –шнурок с флажками, объединенными общим
понятием, но в ряду допущена ошибка. Нужно убрать лишний флажок,
который не подходит данному понятию.
Вариант 2
У участников шнурок с 3 флажками, на которых изображены предметы
определенной группы. Участникам нужно дополнить свою группу еще
несколькими флажками, выбрав их из остальных флажков.
19.
Раскрасьдорожки для
зайчика и
белочки,
сохраняя
закономерность.
Решение: Белочка и зайчик бегут по разным дорожкам. У
каждой дорожки есть своя закономерность. У зайчика
повторяется 3 цвета на дорожке: красный, голубой,
жёлтый, а у белочки 4: зеленый, коричневый, фиолетовый,
жёлтый.
В этом задании можно обратить внимание на то, что обе
дорожки состоят из 12 кругов. Но количество
повторяющихся цветов разное.
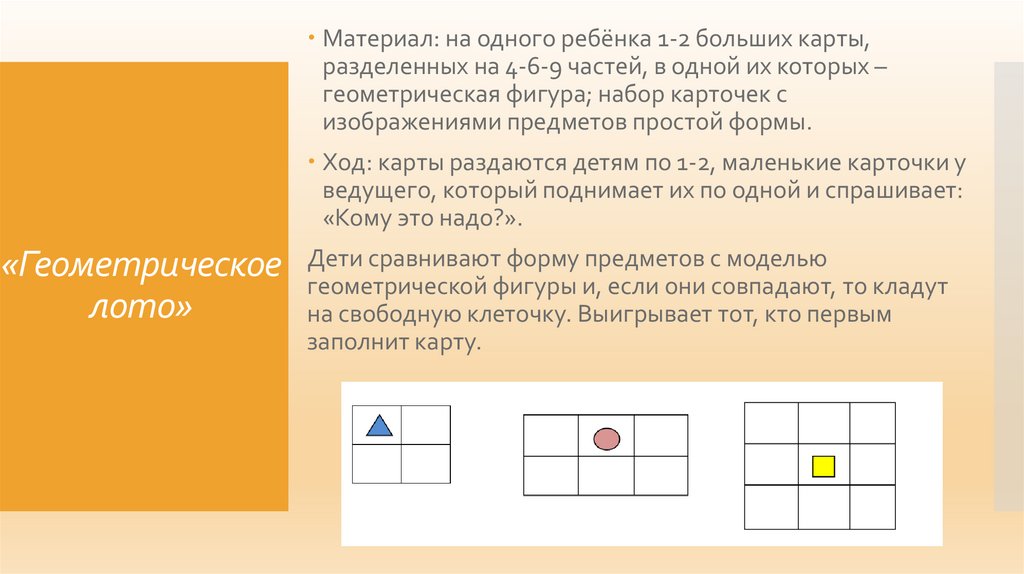
20.
Материал: на одного ребёнка 1-2 больших карты,разделенных на 4-6-9 частей, в одной их которых –
геометрическая фигура; набор карточек с
изображениями предметов простой формы.
Ход: карты раздаются детям по 1-2, маленькие карточки у
ведущего, который поднимает их по одной и спрашивает:
«Кому это надо?».
«Геометрическое
лото»
Дети сравнивают форму предметов с моделью
геометрической фигуры и, если они совпадают, то кладут
на свободную клеточку. Выигрывает тот, кто первым
заполнит карту.
21.
Задание налогику:
22.
В поезде едутгеометрические
фигуры.
Нарисуйте
фигуры, в
четвёртом
вагоне, соблюдая
закономерность
их расположения.
Решение: В поезде едут геометрические фигуры:
квадрат, треугольник, прямоугольник и круг. В трёх
вагонах все места заняты фигурами, в определённом
порядке. Расставим их и в четвертом вагоне: Круг в нём
будет располагаться в нижнем левом углу, квадрат в
верхнем левом, треугольник поедет в правом нижнем, а
прямоугольник – в левом верхнем углу.
23.
Цель: Учить детей совершать мыслительныеоперации: продолжать ряды геометрических фигур по образцу;
закреплять знания геометрических фигур.
Потребуются математические карточки и большое количество
плоскостных геометрических фигур разных цветов, которые дети могут
использовать для продолжения ряда.
«Продолжи
ряд»
На карточках изображены геометрические ряды, которые не
повторяются. Дети должны выбрать карточку, внимательно
рассмотреть нарисованный на ней ряд фигур и продолжить его,
используя раздаточный материал.
24.
Найди ошибкув бусах
Решение: В первых бусах повторяются квадрат и круг,
значит лишний шестой круг.
Во вторых бусах, повторяется закономерность: круг, два
треугольника, два круга, лишний – восьмой, по счету,
круг.
25.
Рассмотримна
конкретных
примерах:
Дидактические
упражнения
из разных
учебных
программ:
26.
УМК «Школа 2100»Авторы: Т. Е.
Демидова и д.р.
27.
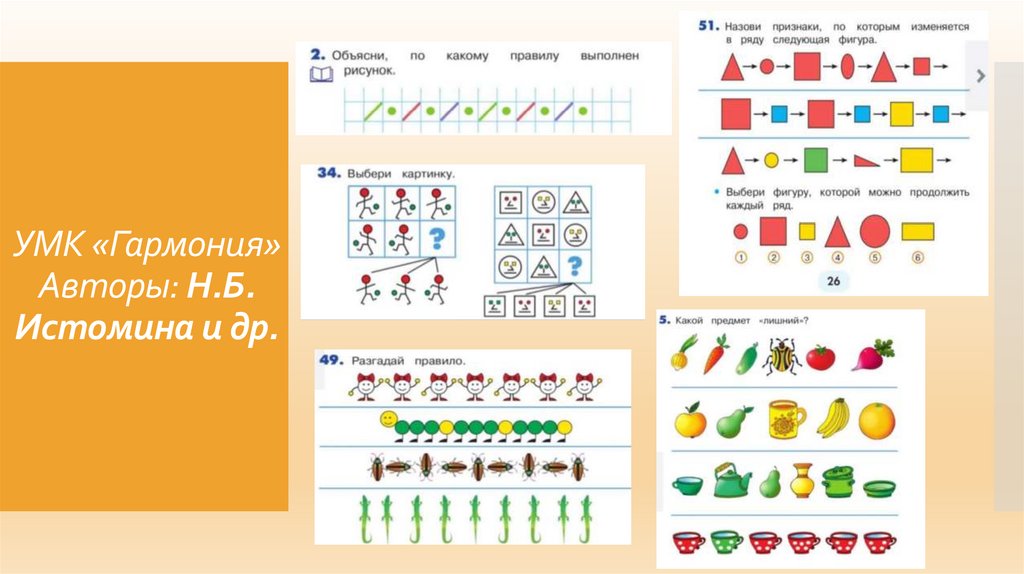
УМК «Гармония»Авторы: Н.Б.
Истомина и др.
28.
УМК «СистемаЛ.В.Занкова»
Авторы:
Аргинская И.И. и
др.
29.
УМК«Перспектива»
Авторы: Л. Г.
Петерсон и др.
30.
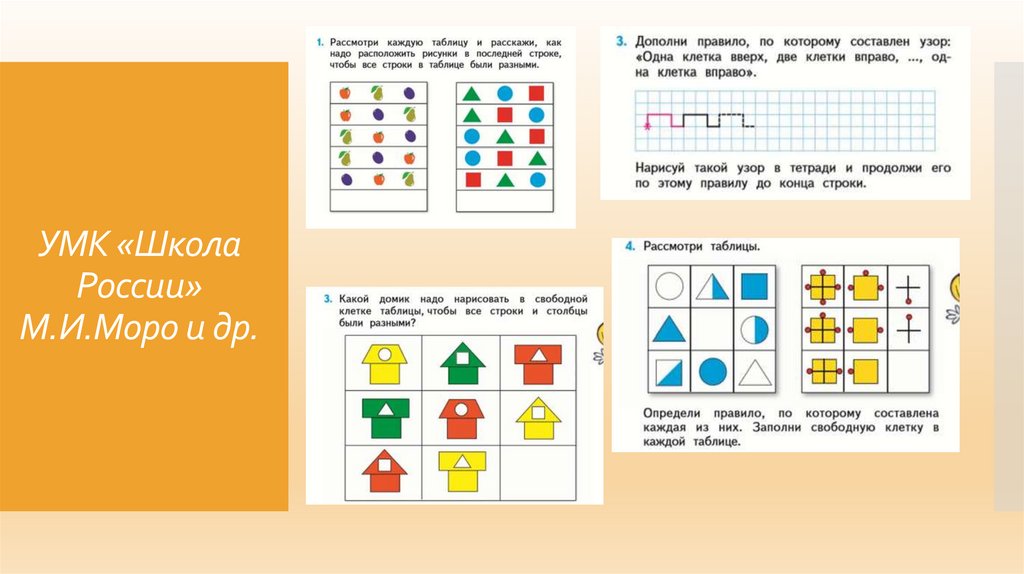
УМК «ШколаРоссии»
М.И.Моро и др.
31.
В системе Д. Б.Эльконина — В. В.
Давыдова
(авторы В. В.
Давыдов, С. Ф.
Горбов и другие)
дочисловой
(подготовительн
ый) период
обучения
построен на иных
основаниях
Его цель подготовка к введению понятия «число —
мера величины», вследствие чего формирование
представлений о величинах и способах их
сравнения образует основное содержание
подготовительного периода обучения.
Если первоначально площади, длины, объемы,
массы сравниваются способом наложения, а
результат сравнения фиксируется словами
«одинаковые», «неодинаковые», то в дальнейшем
результат сравнения обозначается отрезками так,
что большая величина обозначается большим
отрезком.
32.
Необходимым условием осуществленияправильного обобщения на уроках
математики является использование в
обучении методики, учитывающей
особенности умения обобщать у учащихся.
При формировании правильных обобщений
особое место необходимо уделять
варьированию несущественных признаков.
33.
Умениеанализировать
математическ
ие объекты –
одно из
основных
условий
правильного
обобщения,
поэтому его нужно специально
формировать.
С этой целью необходимо строго
продумывать характер вопросов и заданий,
активизирующих мысль детей,
направленную на поиск главного,
существенного в заданном объекте.
В процессе анализа накапливается знание
конкретных фактов, составляющих основу
для формирования последующих
обобщений.
34.
Дляформирования
правильного
обобщения на
уроках
математики и
предотвращения
ошибок учащихся
необходимо
уделять внимание
многим факторам:
35.
Умениянеобходимые
для овладения
приёма
обобщения:
Относить конкретный объект к заданному
взрослым классу и, наоборот, конкретизировать
общее понятие через единичные (действие
отнесения)
Группировать объекта на основе
самостоятельно найденных общих признаков и
обозначать образованную группу словом
(действия обобщения и обозначения)
группировку в уме.
Учащиеся мысленно объединяют предметы и явления в
группы по тем общим и существенным признакам,
которые выделяются в процессе абстрагирования.
36.
Способностьк обобщению
связана с
уровнем
развития у
человека
таких
умений, как:
Умение выделять признаки объектов;
Умение отделять существенные признаки от
несущественных;
Умение правильно выполнять обобщение и
объяснять, как оно выполнено;
Умение выделять операции, входящие в прием,
и раскрывать их последовательность.
Поэтому развитие данных умений будет
способствовать повышению уровня обобщения у
учащихся.
37.
Эмпирическоеобобщение
При изучении математики в начальных классах
обычно используют эмпирическое обобщение.
В этом случае вывод получается на основе
индуктивных умозаключений (от частного к
общему).
Индукция – это наведение, т.е. учитель как бы
ведет учеников к цели.
Для построения такого вывода
рассматривается несколько объектов, в
которых наблюдают проявление данного
свойства или правила, после чего делают
общий вывод.
38.
Дляполучения
правильного
обобщения
индуктивным
способом
необходимо
учитывать
следующее:
(Как отмечает А.Б. Истомина)
1. Главное, чтобы учитель продумал подбор
математических объектов и
последовательность их рассмотрения для
целенаправленного наблюдения и сравнения;
2. Рассмотреть как можно больше частных
случаев, в которых проявляется
закономерность;
3. Варьировать виды частных объектов, используя
и действия с предметами, и схемы, и таблицы;
4. Помогать ученикам формулировать вывод с
помощью наводящих вопросов.
39.
Рассмотрим на конкретномпримере, как можно реализовать
приведенные рекомендации.
Для того, чтобы подвести учащихся
к формулировке
переместительного свойства
умножения, учитель предлагает им
такие задания:
40.
Рассмотритерисунок и
попробуйте
быстро
подсчитать,
сколько окон в
доме.
Дети могут предложить следующие способы:
3+3+3+3, 4+4+4 или 3*4=12; 4*3=12.
Учитель предлагает сравнить полученные
равенства, т. е. выявить их сходство и различие.
Отмечается, что оба произведения одинаковые, а
множители переставлены.
41.
2.Аналогичное задание учащиеся выполняют спрямоугольником, который разбит на квадраты.
Рассмотрите
рисунок и
выполните
задание
аналогичное
предыдущему
В результате получают 9*3=27; 3*9=27 и словесно
описывают те сходства и различия, которые
существуют между записанными равенствами.
Приходят к тому же, что и в задании 1, выводу.
42.
Найти значения следующих выражений, заменивумножение сложением:
3.Ученикам
предлагается
самостоятельная
работа
3*2, 4*2, 3*6, 4*5, 5*3, 8*4
2*3, 2*4, 6*3, 5*4, 3*5, 4*8
Выясняется, чем похожи и чем отличаются
равенства в каждом столбике. Ответы могут быть
такими: «Множители одинаковые, они
переставлены», «Произведения одинаковые» или
«Множители одинаковые, они переставлены,
произведения одинаковые».
43.
4. Учитель помогает сформулироватьсвойство с помощью наводящего
вопроса:
«Если множители переставить, то
что можно сказать о произведении?»
Вывод: «Если множители переставить,
то произведение не изменится» или «От
перестановки множителей значение
произведения не изменится».
44.
Примеры эмпирического обобщения в разных учебныхпрограммах:
45.
Истомина Н.Б. 2 классПримером
эмпирического
обобщения
является,
например,
выведение
сочетательного
свойства
сложения
Так как сначала
предлагается задание
для самостоятельного
решения,
т.е. создание проблемной
ситуации, благодаря
которой учащиеся
самостоятельно, путем
решений, приходят к
новому правилу.
46.
Истомина Н.Б. 3 классПримером
эмпирическог
о обобщения
является,
например,
выведение
сравнения
площадей
фигур.
Учащиеся
выполняют задание
самостоятельно,
затем сверяют свои
догадки с
рассуждениями
Маши и Миши и
приходят к общему
выводу.
47.
Истомина Н.Б. 4 классПримером
эмпирического
обобщения
является,
например,
выведение
выполнения
деления с
остатком.
Сначала учащимся предлагается
решить ряд примеров, но в
некоторых у них не получается
найти результат. Пробуют
ответить на вопрос, в чем же
проблема. Только потом им
предлагается прочитать
рассуждение о данном вопросе в
учебнике и разобрать данное
правило с учителем.
48.
Примеромэмпирического
обобщения
является,
например,
выведение
правила о
параллельных
прямых
Также, например, по
программе Петерсона Л.Г.
во 2 классе учащиеся
сначала выполняют
задания, связанные с
пересечением (или нет)
прямых, пробуют сами
объяснить свои
домыслы/ответы, а только
потом переходят на
правило о параллельных
прямых.
49.
Петерсон Л.Г. 3 классПримером
эмпирического
обобщения
является,
например,
выведение
правила
умножения числа
на 10,100,1000…
Учащиеся сначала вспоминают известные правила умножения,
затем пробуют выполнить предложенное задание, отвечая на
наводящие вопросы, пробуют сделать вывод и прийти к
новому правилу.
50.
Петерсон Л.Г. 4 классПримером
эмпирического
обобщения
является,
например,
выведение
правила
сложения дробей
с одинаковым
знаменетелем.
Прежде чем ввести правило, сначала предлагается
учащимся самим догадаться, как можно сложить дроби,
с помощью раскрашивания картинки.
51.
Аргинская И.И. 2 классПримером
эмпирического
обобщения
является,
например,
выведение
понятия
уравнение и
способ его
решения.
Учащимся дается задание
на анализ и сравнение
картинок, с помощью
которых нужно составить
математический рассказ и
записать это действие.
Далее предлагается
альтернативная запись,
подходящая под
картинки. Задача
учащихся самостоятельно
догадаться, почему такую
запись можно
использовать и как это
объяснить. А только после
дается правило.
52.
Примеромэмпирического
обобщения
является,
например,
выведение
понятия
единичного
отрезка
В программе
И.И.Аргинской в 3
классе учащиеся
самостоятельно
выполняют
задание на
построение
числового луча с
помощью мерок,
отвечая на
вопросы, пробуют
самостоятельно
выйти на новое
понятие, а только
потом оно дается в
учебнике.
53.
Аргинская И.И. 4 классПримером
эмпирического
обобщения
является,
например,
выведение
последовательности
выполнения
действий при
умножении на
двузначное число.
Учащиеся выполняют
известное им умножение в
столбик на однозначное
число. Далее пробуют
выполнить умножение в
столбик на двузначное число,
если у них возникает
проблема, предлагается
рассмотреть образец
умножения и, отвечая на
наводящие вопросы,
осознать
последовательность
действий. Затем, путем
полученного опыта,
самостоятельно получить
порядок действий (алгоритм)
при умножении в столбик на
двузначное число.
54.
Демидова Т.Е. 2 классПримером
эмпирического
обобщения
является,
например,
выведение
правила
упрощения
вычислений.
В данной программе,
аналогично, сначала
задается проблемная
ситуация,
предлагается
сравнение
выражений, задаются
наводящие вопросы,
предлагаются
задание на
самостоятельное
изменение
выражений, чтобы
учащиеся пришли к
правилу об
упрощении
вычислений.
55.
Демидова Т.Е. 3 классПримером
эмпирического
обобщения
является,
например,
выведение
сочетательного
свойства
умножения
Учащимся
предлагается
рассмотреть
рассуждения Дениса
и Костика,
попробовать
объяснить их
решение. Далее
выполняют
сравнение рисунков и
выражений, пробуя
самостоятельно
прийти к выводу и
сформулировать
правило нового
свойства умножения.
56.
Демидова Т.Е. 4 классПримером
эмпирического
обобщения
является,
например,
выведение
понятия
скорости
удаления в
решении задач.
Учащимся
предлагается
задача, решение
которой вызывает у
детей затруднение.
В помощь
предлагается
(картинка) схема и
таблица. С
помощью
наводящих
вопросов,
заполняют таблицу
и пробуют
самостоятельно
прийти к выводу.
Только потом детям
озвучивается новое
правило с
понятием.
57.
Моро М.И. 2 классПримером
эмпирического
обобщения
является,
например,
выведение
взаимосвязи
компонентов.
Учащимся
предлагается
сначала самим
попробовать
выполнить
действия над
равенствами и
сделать вывод, а
только потом
дается правило.
По программе «Школа России» эмпирическое обобщение проявляется
в неявной форме, поэтому сложно найти примеры, т.к. чаще всего
сначала дается правило, а потом на его основе разбирается материал.
58.
Моро М.И. 3 классПримером
эмпирического
обобщения
является,
например,
выведение
правила
порядка
действий в
числовых
выражениях.
Учащимся
предлагается
сначала самим
сравнить данные
выражения и
указать, в каком
порядке будут
выполнять
действия.
А потом уже дается
правило на
порядок действия.
59.
Формируя у младших школьниковумение обобщать наблюдаемые факты
индуктивным способом, полезно
предлагать задания, при выполнении
которых они могут сделать неверные
обобщения.
60.
1) Сравнивыражения,
найди общее
в полученных
неравенствах
и сделай
соответствую
щие выводы:
2+3 ...2*3
4+5...4*5
3+4...3*4
5+6...5*6
Сравнив данные выражения и отметив
закономерности: слева записана сумма, справа
произведение двух последовательных чисел; сумма
всегда меньше произведения, большинство детей
делают вывод: «сумма двух последовательных чисел
всегда меньше произведения».
Но высказанное обобщение ошибочно, так как не
учтены случаи:
61.
0+1 ...0*11+2... 1*2
Можно попытаться сделать правильное
обобщение, в котором будут учтены
определенные условия: «сумма двух
последовательных чисел, начиная с числа 2,
всегда меньше произведения этих же чисел».
62.
2) Найдисумму.
Сравни ее с
каждым
слагаемым.
Сделай
соответствую
щий вывод
Слагаемое 1
2
3
4
5
6
Слагаемое 4
4
4
4
4
4
Сумма
На основе анализа рассмотренных частных случаев
учащиеся приходят к выводу, что: «сумма всегда
больше каждого из слагаемых».
Но его можно опровергнуть, так как: 1+0=1, 2+0=2.
В этих случаях сумма равна одному из слагаемых.
63.
(2+4):2=3 (4+4):2=4 (6+2):2=4 (6+8):2=7 (8+10):2=93) Проверь,
будет ли
делиться
каждое
слагаемое на
число 2, и
сделай вывод.
Анализируя предложенные частные случаи,
дети могут прийти к заключению, что: «если
сумма чисел делится на 2, то каждое
слагаемое этой суммы делится на 2».
Но этот вывод ошибочный, так как его можно
опровергнуть: (1+3):2.
Здесь сумма делится на 2, каждое слагаемое
не делится.
64.
Методбеседы.
При ознакомлении учащихся с
математическими понятиями (число,
арифметическое действие и др.), с
теоретическими знаниями типа
закономерностей (свойства
арифметических действий, связи между
компонентами и результатами действий
и т.п.) чаще всего используется метод
беседы.
65.
Система упражнений в этом случаедолжна вести детей от частных фактов к
общему выводу, к «открытию» той или
иной закономерности, т. е. здесь
целесообразна эвристическая беседа,
обеспечивающая индуктивный путь
рассуждения.
66.
При ознакомлении с новымматериалом индуктивным
путем учитель, проводя беседу,
предлагает учащимся ряд
упражнений. Учащиеся
выполняют их, затем,
анализируя, выделяют
существенные стороны
формируемого знания, в
результате чего делают
соответствующий вывод, т.е.
приходят к обобщению.
67.
К системеупражнений
предъявляется
ряд
требований:
1. Система упражнений должна
обеспечивать наглядную основу
формируемого знания.
2. Упражнения надо подбирать так,
чтобы, анализируя их, учащиеся
смогли бы выделить все существенные
стороны формируемого знания.
Для этого подбираются упражнения так, чтобы
сохранялись существенные стороны, а
несущественные изменялись.
68.
Пример использования эмпирического обобщения на уроке. (фрагмент конспекта)Деятельность учителя
Деятельность учащихся
- Посмотрите на доску и составьте по данному рисунку пример на
умножение.
- Дети составляют пример.
4·2=8
4 – первый множитель
2 – второй множитель
8 – произведение
Произведение чисел 4 и 2 равно 8.
- Второй пример: произведение разделили на
первый множитель и получился второй
множитель.
- Третий пример: произведение разделили
на второй множитель и
получился первый множитель.
4·2=8
- Прочитайте пример с использованием терминологии.
- Я напишу под примером, который вы составили еще два примера.
Объясните, как получили второй и третий примеры из первого.
4·2=8
8:4=2
8:2=4
- Аналогично объясните, как получены второе и третье равенства из
первого в следующем случае. (на доске)
2·3=6
6:2=3
6:3=2
- Сделаем вывод. Я начну, а вы закончите фразу: «Если произведение двух
множителей разделить на один из них, то …»
- Проверим наш вывод, открыв правило в учебнике на стр.72
- Второй пример: произведение разделили на
первый множитель и получился второй
множитель.
- Третий пример: произведение разделили на
второй множитель и получился первый
множитель.
- «Если произведение двух множителей
разделить на один из них, то получится
другой множитель».
69.
Второй вид обобщения – это теоретическоеобобщение.
Теоретическое
обобщение.
Если при организации эмпирического
обобщения анализируют большое количество
частных объектов и при этом ориентируются на
их внешние существенные признаки, то при
организации теоретического обобщения
осуществляется анализ какого – то одного
объекта с целью выявления его существенных
внутренних связей.
Эти связи фиксируются абстрактно, т.е.
теоретически с помощью знаков и схем и
становятся основой для выполнения частных
конкретных действий.
70.
Такимобразом,
Теоретическое обобщение – это
обобщение по типам межпредметных
отношений и связей, которые лежат в
основе способов построения их решения,
а не по внешнему сходству данных,
представленных в условиях.
71.
С.Л. Рубинштейн1. оно выполняется при таком анализе
какого-либо одного конкретного факта
(события, задачи), который
обнаруживает внутреннюю связь его
частных проявлений;
выделил две
характерные
черты
теоретического 2. исходя из знания этой связи, ученик
затем сразу может обобщить все другие
обобщения:
факты (события, задачи) данного круга.
72.
Необходимое условие формирования у младших школьниковспособности к теоретическому обобщению - направленность
обучения на формирование общих способов деятельности.
Для выполнения этого условия нужно продумать такие действия
с математическими объектами, в результате которых дети смогут
сами «открывать» существенные свойства изучаемых понятий и
общих способов действий с ними.
73.
нарефлексии
которая состоит в
рассмотрении
учащимися
оснований
собственных
действий и их
соответствия
условиям задачи
Также
теоретическое
обобщение
строится:
на анализе
содержания
задачи с целью
выделения
принципа или
всеобщего
способа ее
решения
74.
Разработка данного вопроса наметодическом уровне представляет
определенную сложность.
В настоящее время - это одна из самых
актуальных проблем начального обучения,
решение которой связано как с изменением
содержания, так и с изменением организации
учебной деятельности младших школьников,
направленной на его усвоение.
75.
Необходимым условием формирования умладших школьников способности к
теоретическому обобщению является
направленность обучения на формирование
общих способов действий. Это одна из
актуальных проблем начальной школы сегодня.
Вариант решения этой проблемы представлен в
курсе математики В.В. Давыдова.
76.
Курсматематики
В.В. Давыдова
В курс начальной математики (В.В. Давыдова), целью
которого является развитие у детей способности к
теоретическому обобщению, внесены существенные
изменения. Они касаются и его содержания, и способов
организации деятельности.
Основу теоретических обобщений в этом курсе
составляют предметные действия с величинами (длина,
объем), а также различные приемы моделирования этих
действий с помощью геометрических фигур и символов.
Это создает определенные условия для выполнения
теоретических обобщений.
77.
Пример:В этом курсе после введения понятия «измерение
величин» детей учат измерять величины, используя
различные мерки. Измерить, значит узнать, сколько
мерок поместилось в величине. После того как мерки
уложили, подсчитываем их количество.
После серии уроков – закрепление: предлагаем
ситуацию, когда величина большая, а мерка
маленькая, следовательно, ей пользоваться
неудобно, значит, мерку нужно укрупнить. Для этого
соединяем несколько мелких мерок в одну более
крупную и рассуждаем, что соединить можно по 2
мерки или по 3, 4…по 10, 11…и т.д.
Это создает основу для введения двоичной, троичной
и т.д. системы счисления, с которыми знакомят
учащихся по данной программе, т.е. анализ одной
ситуации – укрупнение мерки дает возможность
делать некоторые обобщения.
78.
Примерызаданий с
мерками:
79.
Примерформирования
понятия
«больше на».
Рассмотрим конкретную ситуацию, которая связана с
формированием понятия «больше на». Учащимся
предлагаются две банки.
В одну (первую) налита вода, другая (вторая) пустая.
Учитель предлагает найти способ решения
следующей проблемы: как сделать так, чтобы во
второй банке воды было бы вот на этот стаканчик
(показывает стаканчик с водой) больше, чем в
первой?
80.
Примерформирования
понятия
«больше на».
В результате обсуждения различных
предложений делается вывод: нужно перелить
воду из первой банки во вторую, т. е. налить во
вторую столько же воды, сколько ее налито в
первую банку, и затем вылить во вторую еще
стаканчик воды.
Созданная ситуация позволяет детям самим найти
необходимый способ действия, а учителю
сосредоточить внимание на существенном
признаке понятия «больше на»,
т. е. нацелить учеников на овладение общим
способом действия: «столько же и еще».
81.
Или, например, при введении смысласложения и вычитания опираемся на
сравнение величин и ставим проблему
- как их можно уравнять?
Для этого нужно к меньшей величине
добавить некую часть, либо от
большей величины убрать часть. В это
время еще не введены числа и
результаты, рассуждения
записываются в общем виде с
помощью букв, если
А>Б, то А=Б+В или Б=А-В.
82.
Использование величин дляформирования у школьников
обобщенных способов действий один из возможных вариантов
построения начального курса
математики. Но эту же задачу
можно решать, выполняя
различные действия и с
множествами предметов.
Примеры таких ситуаций нашли
отражение в статьях Г.Г.
Микулиной.
83.
Она советует для формирования понятия«больше на» использовать ситуацию с
множествами предметов: детям предлагается
пачка красных карточек.
Нужно сложить пачку из зеленых карточек так,
чтобы в ней было вот на столько (показывается
пачка синих карточек) больше, чем в пачке
красных.
Условие: карточки пересчитывать нельзя.
Пользуясь способом установления взаимнооднозначного соответствия, учащиеся
выкладывают в зеленой пачке столько же
карточек, сколько их в красной. И добавляют к
ней еще третью пачку (из синих карточек).
84.
Как уже было сказано, при теоретическом обобщениипроводится:
Анализ
предметов
Анализ явлений
Анализ содержания
учебного материала
но при этом выявляются скрытые, незаметные для глаз, общие
признаки, после чего делается вывод.
Рассмотрим пример теоретического обобщения в развивающей
системе обучения Л.В. Занкова.
85.
Например, взадании 212
(Аргинская И.И.
Математика – 3
кл, 1 часть
стр.109.)
предлагается
сравнить
произведения
каждой строки:
и определить, как с помощью последнего
произведения каждого столбика найти значение
двух других произведений.
Учащиеся рассуждают так:
1 единицу умножили на 2, получили 2 единицы,
значит 1 десяток умножим на 2, получим 2
десятка и т.д.
86.
Сходство этих 2 примеров скрыто от учащихся, что затрудняет сделатьобобщение.
Запишем так, как рассуждаем при вычислении:
1 ед * 3,
1 дес * 3,
1 сот * 3
и ставим вопрос: "Чем похожи эти примеры?"
Учитель должен добиться ответа: разрядные числа в пределах 1000
умножаются так же, как и однозначные числа в таблице умножения.
Происходит обобщение, чему способствует реконструкция записи.
87.
Например,изучая
транзитивность
равенства:
(Давыдов В.В. и др.
Математика 1
кл., 1997, с. 40)
Если А=К, а К=Р, то А=Р
сначала сравнивают две планки по длине и
записывают равенство А=К.
Планка А прячется, К сравнивается с новой планкой Р
и дети записывают К=Р. После выясняют, какими могут
быть планки А и Р.
Делают вывод, что А=Р и проверяют результат
непосредственным соизмерением. Далее, при работе
с рисунком учебника к упражнению 1 (К=А, А=Б, К...Б)
выясняют, можно ли, не кладя на весы яблоко и лимон,
установить отношение их масс.
После обсуждения делается вывод (К=Б).
В данной ситуации основой обобщения являются
действия с моделью длины и моделирование этих
действий с помощью рисунка.
88.
На сравнение предметов по разным признакамПримеры
упражнений по
программе
В.В. Давыдова:
89.
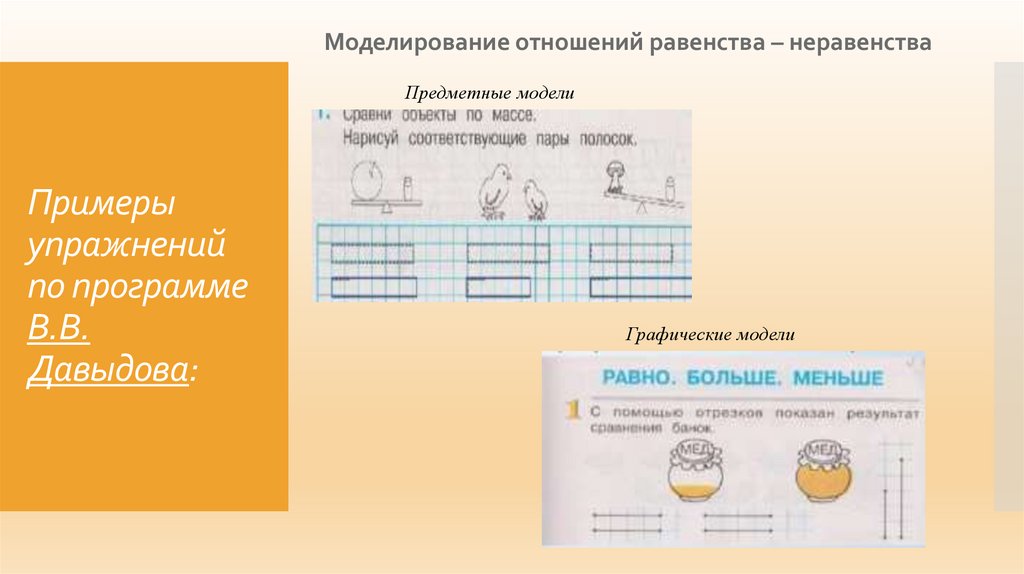
Моделирование отношений равенства – неравенстваПредметные модели
Примеры
упражнений
по программе
В.В.
Давыдова:
Графические модели
90.
Знаковые модели (буквы и знаки «=», «≠», «»)Примеры
упражнений
по программе
В.В.
Давыдова:
91.
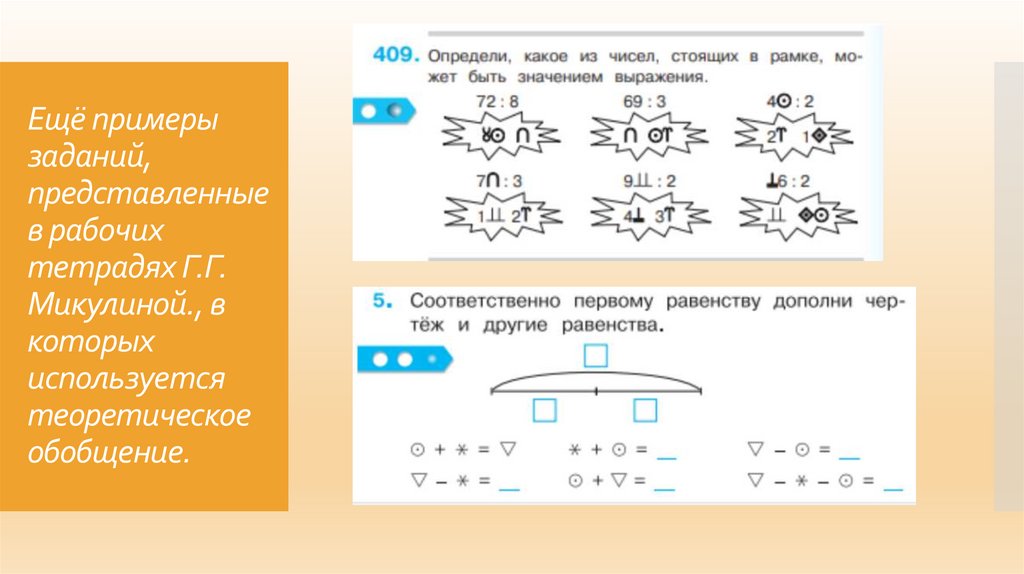
Ещё примерызаданий,
представленные
в рабочих
тетрадях Г.Г.
Микулиной., в
которых
используется
теоретическое
обобщение.
92.
Единицы времени. ЧасПримеры
ситуаций
(Г.Г.
Микулина):
Воспроизводятся единицы времени. Называется
самая маленькая из них и следующая (секунда и
минута).
Далее предлагается оценить протяженность часа.
Для этого называются некоторые занятия, которые
растягиваются на один час или немного больше
(меньше).
Так, урок вместе с большой переменой — это один
час. Длится ли один час телепередача «Спокойной
ночи, малыши»?
Сколько времени длится футбольный матч — больше
часа или меньше?
Далее учитель показывает какую-либо детскую книгу
и сообщает, сколько страниц в ней сможет прочитать
хороший ученик за 1 минуту и за 1 час.
93.
ОбобщениясоглашенияНаряду с эмпирическим и теоретическим
обобщениями в курсе математики имеют
место обобщения-соглашения. Примерами
таких обобщений являются правила
умножения на 1 и на 0, справедливые для
любого числа.
Их обычно сопровождают пояснениями:
«в математике договорились...», «в
математике принято считать...».
94.
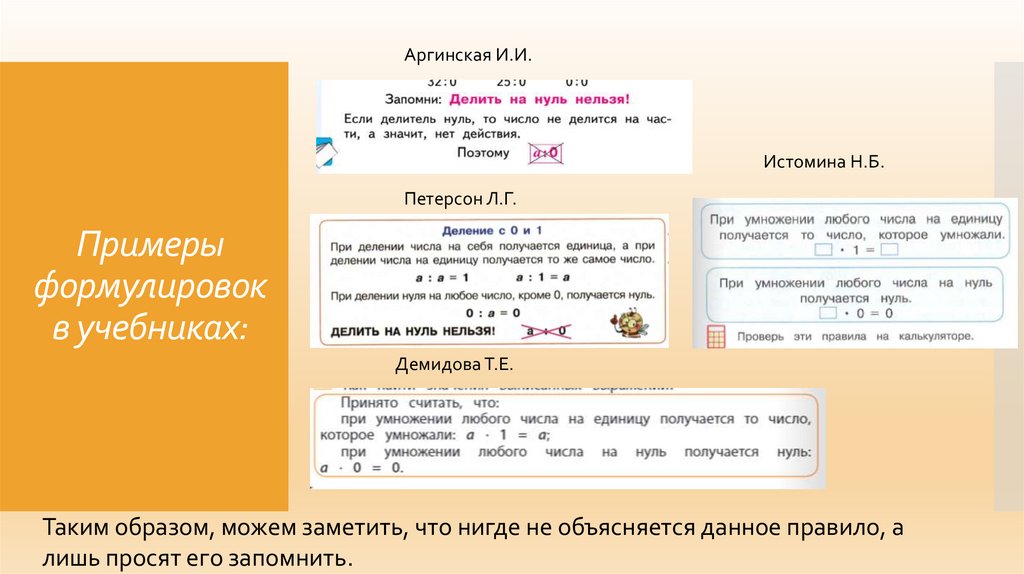
Аргинская И.И.Истомина Н.Б.
Петерсон Л.Г.
Примеры
формулировок
в учебниках:
Демидова Т.Е.
Таким образом, можем заметить, что нигде не объясняется данное правило, а
лишь просят его запомнить.
95.
1) Имеют разные механизмы формирования иразвития:
Эмпирические и
теоретические
понятия могут
быть
противопоставлены
по множеству
существенных
оснований (которые
можно заметить из
вышесказанного):
- Эмпирические обобщения (понятия) вырабатываются
при непосредствен-но-чувственном сравнении
объектов и представлений, что обеспечивает
выделение в них одинаковых свойств.
- Теоретические обобщения (понятия) вырабатываются
на основе анализа, выделения и фиксирования
некоторых межпредметных отношений, которые
выполняют определенную роль, функцию внутри
целостной системы объектов, и служат генетически
исходной основой определенного диапазона явлений
(такие отношения в психологии часто фиксируются в
терминах: «исходная единица анализа», «единицаклеточка»).
96.
2) В результате формирования понятийфиксируются различные результаты
познавательной деятельности:
- В результате эмпирических обобщений
выделяется формально общее наглядное
свойство или признак, что позволяет относить
объекты и явления к определенному классу
(классификация).
- В результате теоретических обобщений
выделяется такое реальное и особенное
отношение, которое служит генетической
основой для развертывания системы понятий,
которые фиксируют сущность (причины
происхождения) определенного диапазона
явлений.
97.
3) Обобщения (понятия) фиксируетразличное содержание:
- Эмпирические обобщения (понятия)
фиксируют внешние наглядные свойства
предметов.
- Теоретические обобщения (понятия)
возникают на основе преобразования
предметов, фиксируют их внутренние
отношения и связи (сущность явлений),
выходят за пределы чувственных
представлений.
98.
4) Различаются способы конкретизацийобобщений (понятий):
- Конкретизация эмпирических понятий
заключается в указании на внешние наглядные
свойства объектов, в подборе словесных
иллюстраций и изображений, которые наглядно
представляют свойства, фиксированные в
обобщении.
- Конкретизация теоретических понятий
заключается в превращении теоретического
знания в развитую теорию путем выведения
(объяснения) фактов и явлений из общих
теоретических оснований через промежуточные
уровни абстракций.
99.
5) Различаются средства фиксированияобобщений:
- Средством фиксирования эмпирических
обобщений (понятий) выступает слово-термин.
- Средством фиксирования теоретических
обобщений (понятий) выступает система знаков и
терминов, фиксирующих способы умственной
деятельности, которые обеспечивают
теоретическое дедуктивное выведение и
объяснение явлений из определенной системы
существенных, чувственно недоступных
отношений и связей (из «единицы-клеточки»)
100.
Обобщение - одна из основных инаиболее значимых форм мышления.
Не умея обобщать, невозможно
Из всего
формировать понятия и законы, делать
вышесказанного выводы.
можно
Необходимо развивать операцию
обобщения у детей с раннего возраста и
сделать
уделять этому вопросу больше внимания.
Но обобщение нельзя формировать
обособленно, изолированно, вне связи с
другими операциями мышления.

























































































 education
education








