Колебательный контур. Превращения энергии в колебательном контуре

1.

Колебательный контур.
Превращения энергии в
колебательном контуре.

2.

Цель обучения: 11.4.2.1-описывать
условия возникновения свободных и
вынужденных колебаний

3.

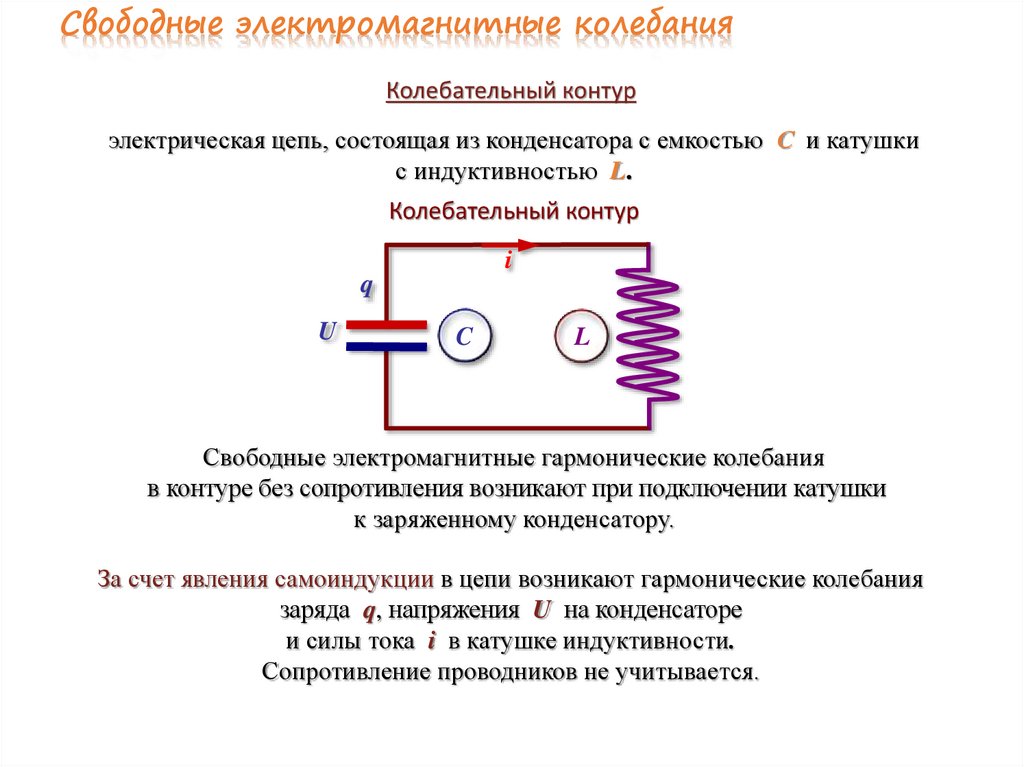
Свободные электромагнитные колебания
Колебательный контур
электрическая цепь, состоящая из конденсатора с емкостью С и катушки
с индуктивностью L.
Колебательный контур
i
q
U
C
L
Свободные электромагнитные гармонические колебания
в контуре без сопротивления возникают при подключении катушки
к заряженному конденсатору.
За счет явления самоиндукции в цепи возникают гармонические колебания
заряда q, напряжения U на конденсаторе
и силы тока i в катушке индуктивности.
Сопротивление проводников не учитывается.

4.

Электроёмкость
физическая величина, равная
отношению заряда проводника к
разности потенциалов между этим
проводником и соседним.
Обозначение: C
Единица измерения: Ф

5.

6.

Энергия заряженного
конденсатора

7.

Индуктивность
•Индуктивность проводника – это скалярная
физическая величина численно равная
отношению магнитного потока, созданного
током в соленоиде к силе тока в нем
L
I

8.

Условия возникновения
электромагнитных колебаний:
•1. Наличие колебательного
контура
•2. Электрическое сопротивление
должно быть очень маленьким.
•3. Зарядить конденсатор (вывести
систему из равновесия).

9.

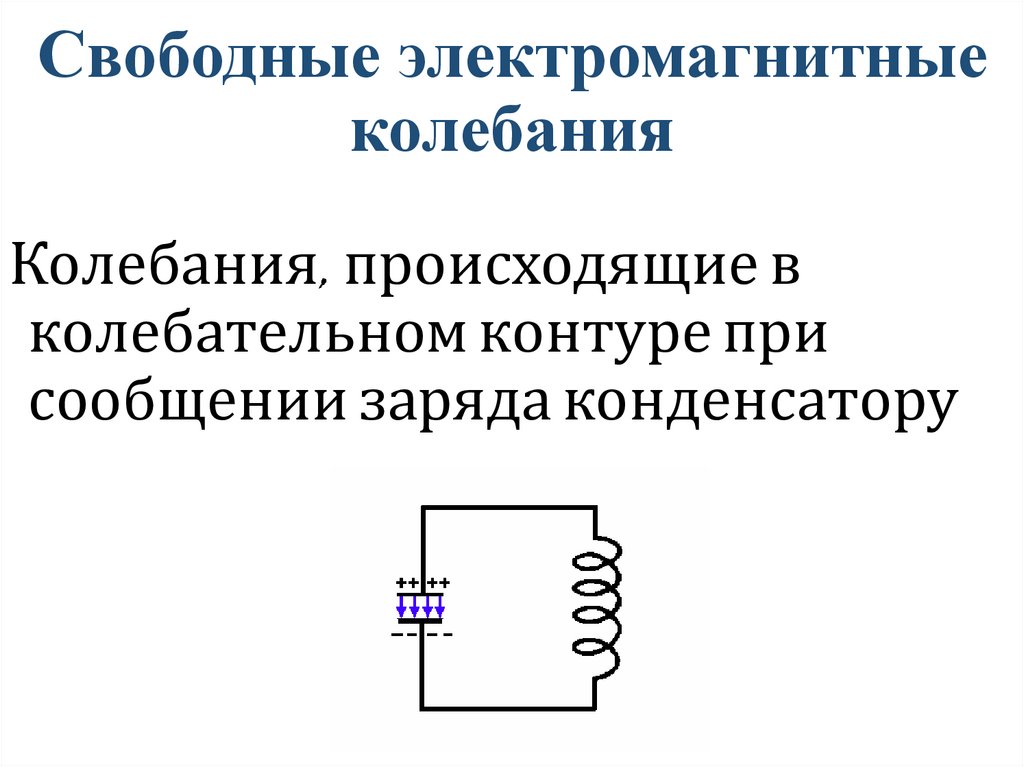
Свободные электромагнитные
колебания
Колебания, происходящие в
колебательном контуре при
сообщении заряда конденсатору

10.

R≠ 0
R=0
колебания затухающие
идеальный колебательный контур

11.

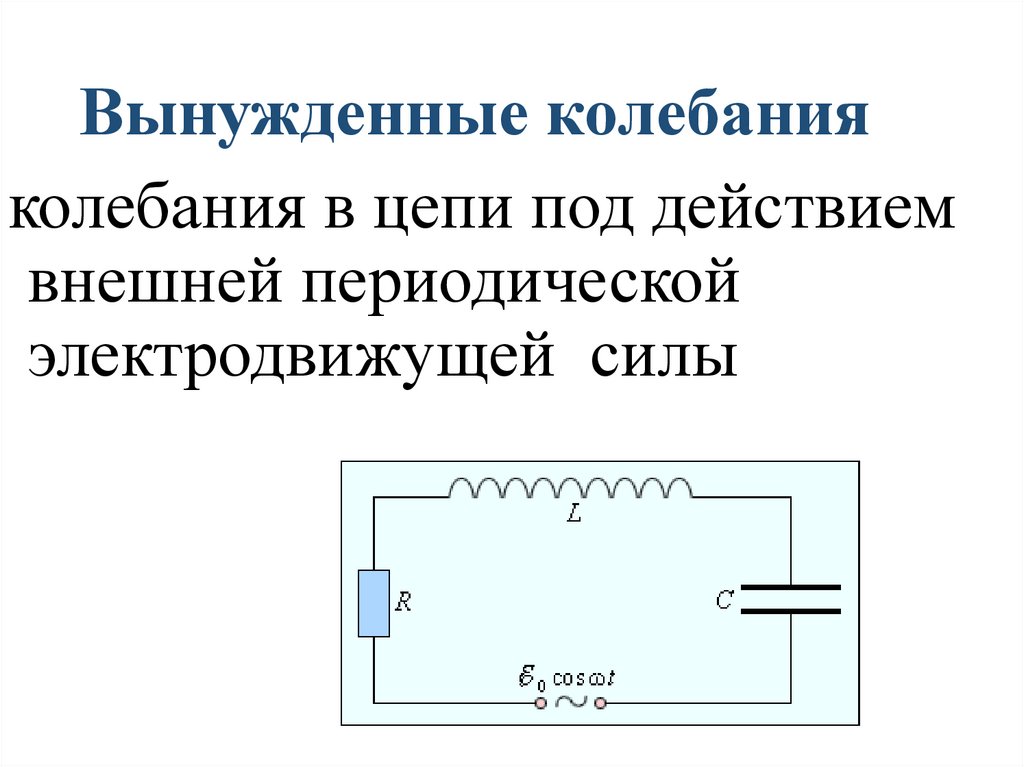
Вынужденные колебания
колебания в цепи под действием
внешней периодической
электродвижущей силы

12.

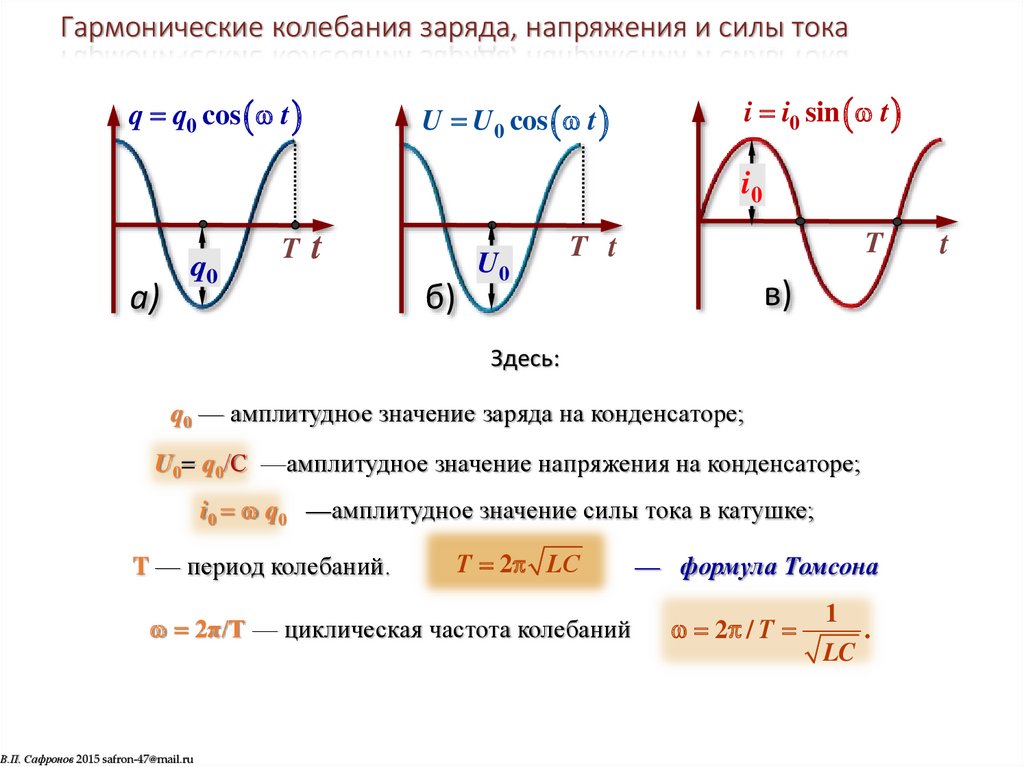
Гармонические колебания заряда, напряжения и силы тока
q q0 cos t
U U 0 cos t
i i0 sin t
i0
а)
q0
T
t
б)
U0
T
T t
в)
Здесь:
q0 — амплитудное значение заряда на конденсаторе;
U0= q0/С —амплитудное значение напряжения на конденсаторе;
i0 q0 —амплитудное значение силы тока в катушке;
T — период колебаний.
Т 2 LC
2π/Т — циклическая частота колебаний
В.П. Сафронов 2015 [email protected]
— формула Томсона
2 / Т
1
.
LC
t

13.

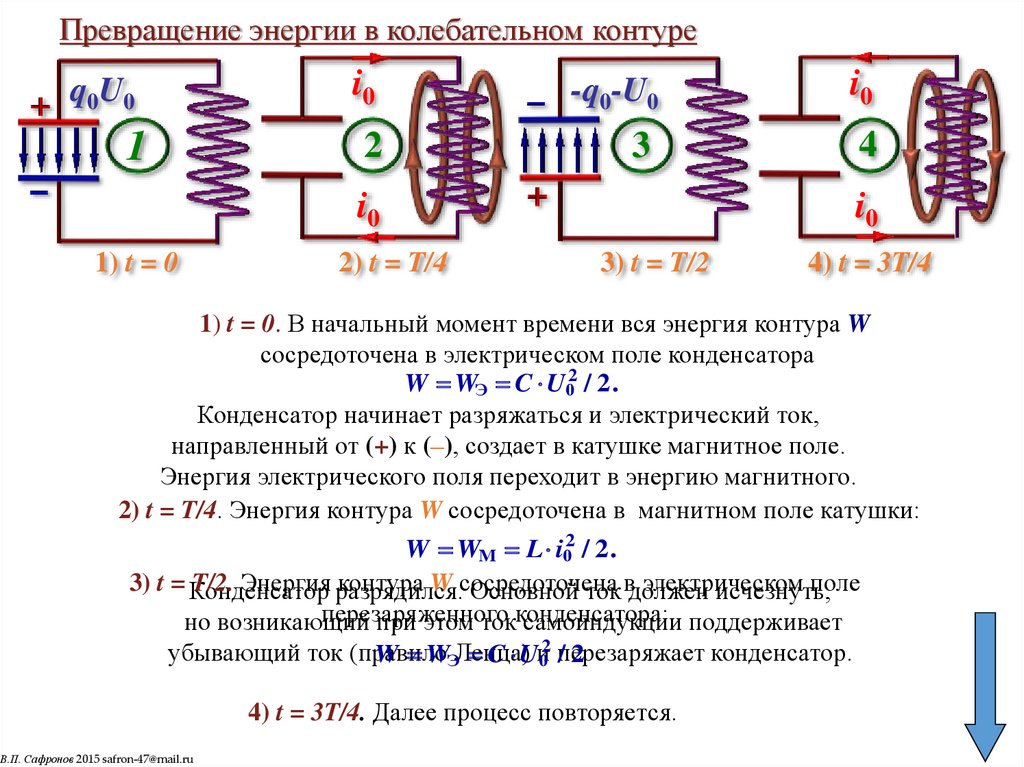
Превращение энергии в колебательном контуре
q0U0
1
i0
-q0-U0
i0
2
3
4
i0
1) t = 0
2) t = T/4
i0
3) t = T/2
4) t = 3T/4
1) t = 0. В начальный момент времени вся энергия контура W
сосредоточена в электрическом поле конденсатора
W WЭ C U02 / 2.
Конденсатор начинает разряжаться и электрический ток,
направленный от (+) к (–), создает в катушке магнитное поле.
Энергия электрического поля переходит в энергию магнитного.
2) t = T/4. Энергия контура W сосредоточена в магнитном поле катушки:
W WМ L i02 / 2.
3) t = Конденсатор
T/2. Энергия разрядился.
контура W сосредоточена
электрическом
поле
Основной ток вдолжен
исчезнуть,
перезаряженного
но возникающий
при этом токконденсатора:
самоиндукции поддерживает
убывающий ток (правило
конденсатор.
W WЭЛенца)
C Uи02 перезаряжает
/2
4) t = 3T/4. Далее процесс повторяется.
В.П. Сафронов 2015 [email protected]

14.

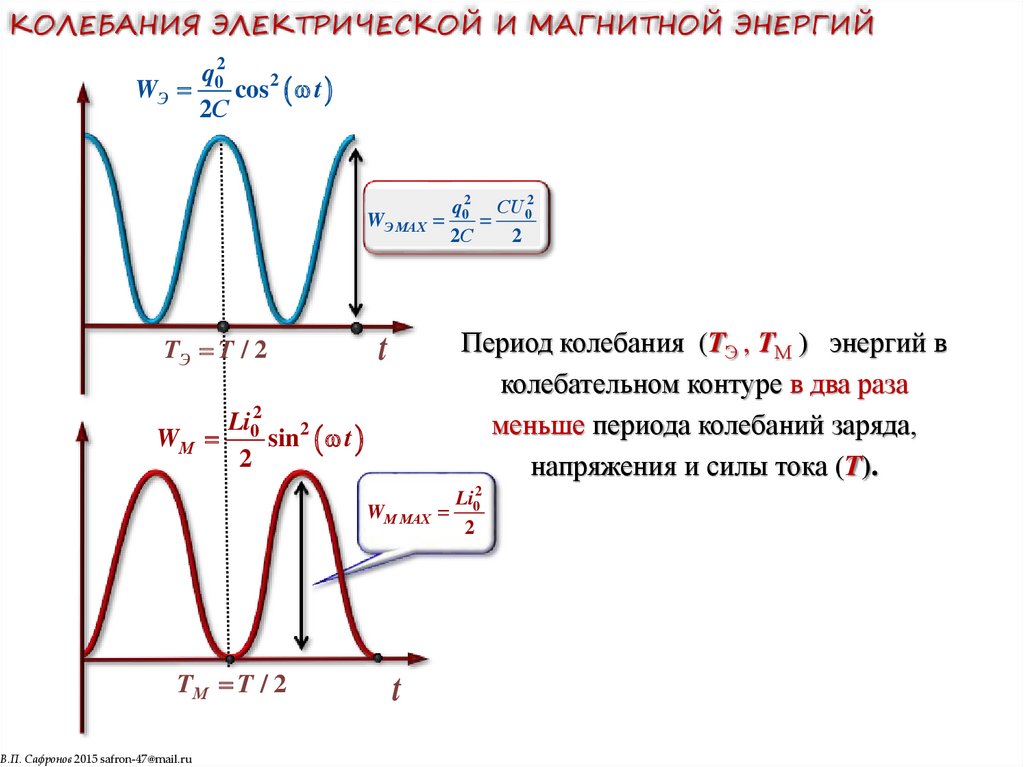
КОЛЕБАНИЯ ЭЛЕКТРИЧЕСКОЙ И МАГНИТНОЙ ЭНЕРГИЙ
q02
WЭ
cos 2 t
2С
WЭ MAX
TЭ T / 2
WМ
Период колебания (TЭ , ТМ ) энергий в
колебательном контуре в два раза
меньше периода колебаний заряда,
напряжения и силы тока (T).
t
Li02
sin 2 t
2
WМ MAX
TМ T / 2
В.П. Сафронов 2015 [email protected]
q02 СU 02
2С
2
t
Li02
2

15.

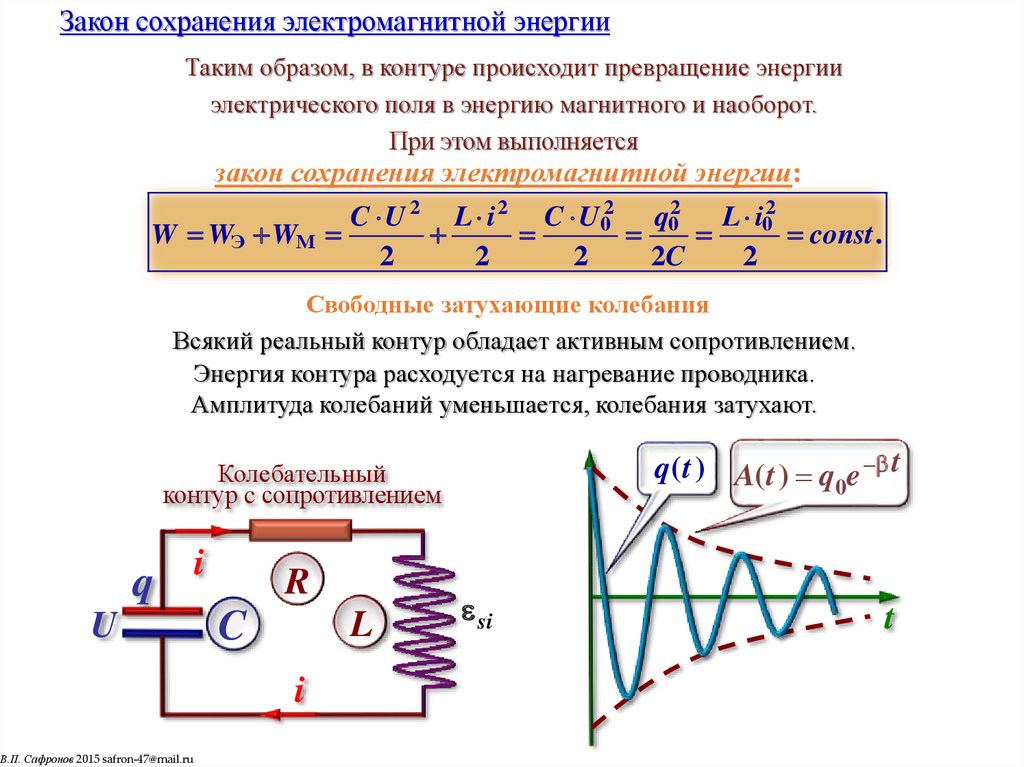
Закон сохранения электромагнитной энергии
Таким образом, в контуре происходит превращение энергии
электрического поля в энергию магнитного и наоборот.
При этом выполняется
закон сохранения электромагнитной энергии:
C U 2 L i 2 C U 02 q02 L i02
W WЭ WМ
const .
2
2
2
2C
2
Свободные затухающие колебания
Всякий реальный контур обладает активным сопротивлением.
Энергия контура расходуется на нагревание проводника.
Амплитуда колебаний уменьшается, колебания затухают.
q( t ) A( t ) q e t
0
Колебательный
контур c сопротивлением
q
U
i
R
C
L
i
В.П. Сафронов 2015 [email protected]
si
t

16.

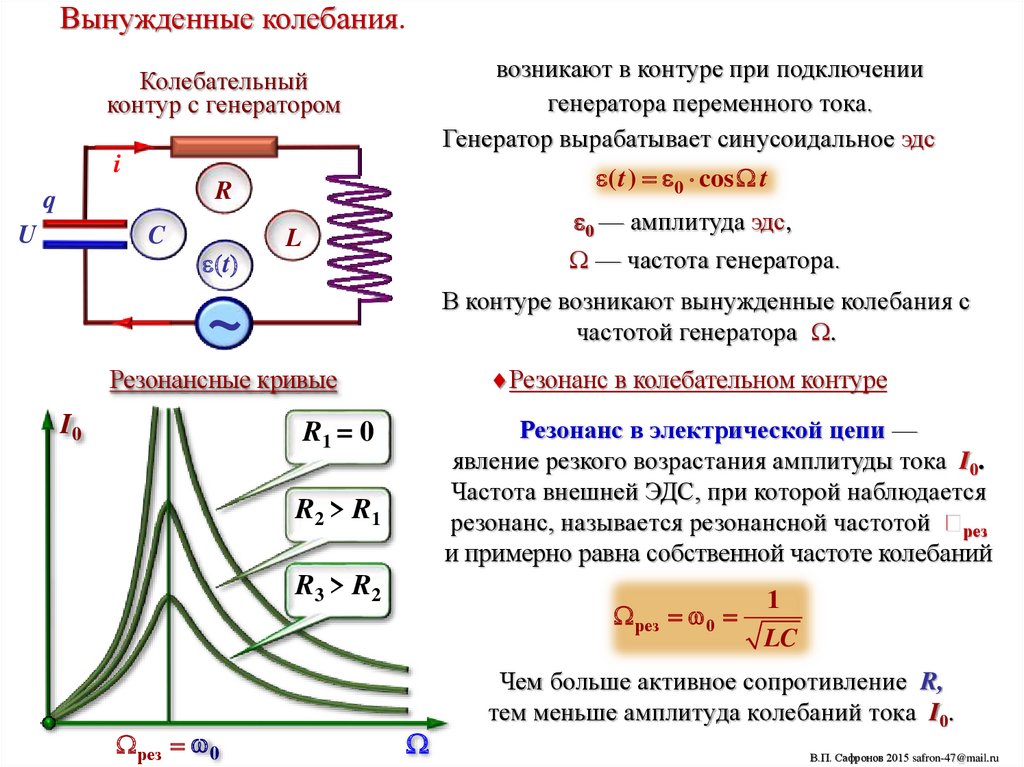
Вынужденные колебания.
возникают в контуре при подключении
генератора переменного тока.
Генератор вырабатывает синусоидальное эдс
Колебательный
контур c генератором
i
( t ) 0 cos t
R
q
U
C
t
0 — амплитуда эдс,
— частота генератора.
L
В контуре возникают вынужденные колебания с
частотой генератора .
~
Резонанс в колебательном контуре
Резонансные кривые
I0
Резонанс в электрической цепи —
явление резкого возрастания амплитуды тока I0.
Частота внешней ЭДС, при которой наблюдается
резонанс, называется резонансной частотой рез
и примерно равна собственной частоте колебаний
R1 = 0
R2 > R1
R3 > R2
рез 0
рез 0
1
LC
Чем больше активное сопротивление R,
тем меньше амплитуда колебаний тока I0.
В.П. Сафронов 2015 [email protected]

17.

Задача 1.
Колебательный контур содержит конденсатор емкостью 800 пФ и
катушку индуктивности индуктивностью 2 мкГн. Каков период
собственных колебаний контура?
3 балла

18.

Задача 2.
Колебательный
контур состоит из конденсатора емкостью С и катушки
.
индуктивности индуктивностью L. Как изменится период свободных
электромагнитных колебаний в этом контуре, если электроемкость
конденсатора и индуктивность катушки увеличить в 3р.
4 балла

19.

Задача 3.
Амплитуда силы тока при свободных колебаниях в колебательном контуре
100 мА. Какова амплитуда напряжения на конденсаторе колебательного
контура, если емкость этого конденсатора 1 мкФ, а индуктивность катушки 1
Гн? Активным сопротивлением пренебречь.
5 баллов

20.

Цель обучения: 11.4.2.1-описывать
условия возникновения свободных и
вынужденных колебаний