Закон сохранения энергии для небесно-механических систем

1.

Закон сохранения энергии
для небесно-механических
систем

2.

Введение
Уравнения 2-го закона Ньютона, закона всемирного тяготения и
центростремительного ускорения вместе с формулой длины окружности
позволяют полностью описать все случаи движения небесных тел друг
вокруг друга в случае круговых орбит. Однако, довольно многие тела
двигаются не по круговым орбитам, а по эллиптическим, при чём
существенно эллиптическим. В этом случае этих уравнений оказывается
недостаточно.

3.

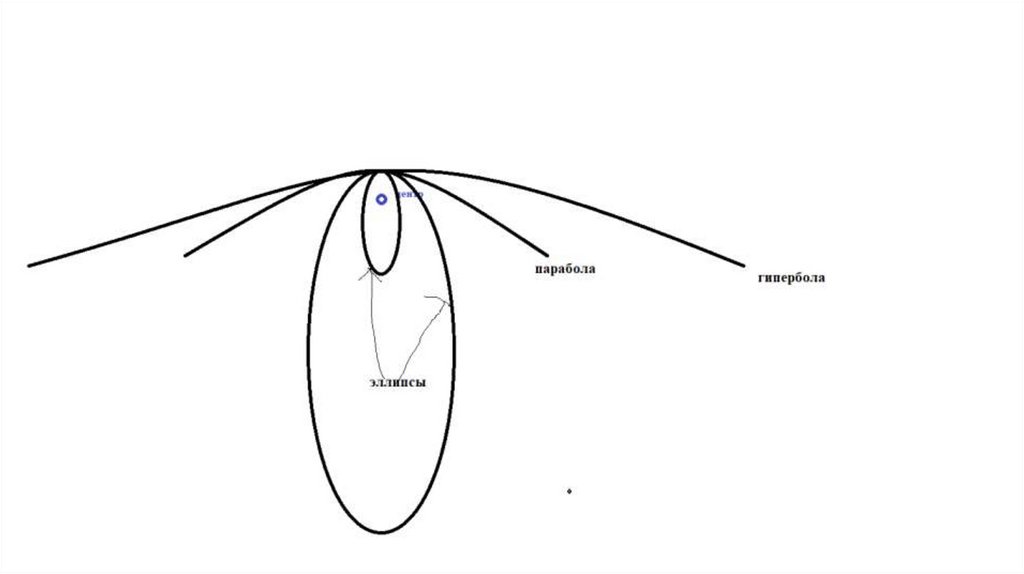
Три типа орбит
Представим себе ситуацию: космическому аппарату, находящемуся
вблизи от некоторого притягивающего центра (Земли, другой планеты,
Солнца) придали некоторую начальную скорость (большую первой
космической), после чего аппарат полностью предоставили самому себе,
двигатели не включали. Какова будет форма траектории аппарата. Есть три
варианта:
1. В случае если скорость не очень велика, орбита будет
эллиптической (овальной). При чём чем больше скорость, тем более
вытянут эллипс.
2. Если скорость примет некоторое пограничное значение, орбита будет
параболической. В этом случае тело сможет уйти бесконечно далеко от
центра.
3. Если скорость станет больше предельной, то орбита примет форму

4.

5.

Типы орбит
Эллиптическая орбита замкнута - то есть аппарат будет вновь и
вновь возвращаться в начальную точку и никогда не покинет её (если не
произойдёт внешнего вмешательства). Пример очень сильно вытянутых
эллиптических орбит могут быть орбиты комет - в самой дальней точке
(афелии) они могут быть в несколько десятков, а то и сотен раз дальше от
Солнца, чем в самой ближней (перигелии). Но однако, они возвращаются в
перигелий снова и снова.
Параболические и гиперболические орбиты не замкнуты - тело,
попавшее на них, покидает центр навсегда, и в дальнейшем будет только
удаляться от него. При устремлении времени к бесконечности тело на таких
орбитах тоже станет бесконечно удалено.

6.

Типы орбит
Различие между параболой и гиперболой может быть для вас
неочевидно - обе орбиты незамкнуты. Хоть вы и строили графики парабол и
гипербол в курсе математики, геометрическое различие этих фигур
неочевидно.
С точки зрения астрономии, нас интересует прежде всего
следующее:
1. Параболическая орбита - пограничная. То есть это некая граница
между очень вытянутым эллипсом и очень сжатой гиперболой.
2. При движении по параболической орбите тело на бесконечности
останавливается (скорость стремится к нулю при расстоянии, стремящимся к
бесконечности). На гиперболической орбите у тела сохраняется некая
ненулевая скорость даже при очень большом удалении.

7.

Закон сохранения энергии
Как известно из курса, физики в случае отсутствия
неконсервативных сил суммарная механическая энергия системы
сохраняется.
Космос - это тот редкий случай, когда трение действительно
отсутствует. Вообще, единственная сила, действующая между нашими
телами - это сила всемирного тяготения, которая является консервативной.
Значит, мы можем записать выражение:
EК+EП=С
,где С - некая постоянная, общая механическая энергия системы.

8.

Потенциальная энергия силы тяготения
Конечно же, формула mgh в данном случае не может работать, потому что
она работает только в том случае, если g постоянно, тогда как ускорение
свободного падения при удалении от центра меняется весьма значительно.
Для притягивающихся тел работает следующая формула (в рамках данного
курса принимаем без доказательства):
EП = -GMm/R
где G - гравитационная постоянная, M - масса центрального тела, m - масса
пробного тела (планеты, косм.аппарата), R - расстояние между ними.

9.

Потенциальная энергия силы тяготения
Хотелось бы отметить, что вообще для потенциальной энергии
важно не само её значение, а разность его значения между двумя точками. В
качестве нуля можно выбрать любую точку. Так, когда мы пользуемся
известной ещё с 7 класса формулой EП=mgh мы можем считать высоту и от
уровня моря, и от уровня поверхности земли, и от уровня пола 10-го этажа.
В формуле, представленной на предыдущем слайде, в качестве
нулевого уровня мы взяли бесконечность. То есть формулу подобрали
таким образом, чтобы энергия взаимодействия тел, бесконечно удалённых
друг от друга была нулевой. Так как при приближении тел потенц.энергия
тяготения уменьшается, получается, что она всегда отрицательна.

10.

Закон сохранения энергии
mV2/2 - GMm/R = C
Это выражение можно поделить на m, и записать C/m в виде C( и то, и то просто обозначение некой константы - свойства данной системы). После
этого мы получим некий закон сохранения “удельной” энергии (энергии на
единицу массы):
V2/2 - GM/R = C
Именно это выражение будет нашим основным уравнением для работы с
небесными телами.

11.

Три случая полной энергии
Рассмотрим три основных случая для значения C.
1. С < 0. Попробуем представить, что наше тело ушло на бесконечность от
центра. В этом случае у нас пот.энергия превратилась в ноль, вся
перешла в кинетическую. EК=С<0. Но кин.энергия пропорциональна
квадрату скорости. Значит, это невозможно. То есть при C < 0 тело не
может улететь на бесконечность. Это случай эллиптических орбит.
2. С = 0. Если тело удалилось на бесконечность, Ek=0, v =0. Пограничный
случай. Это случай параболической орбиты. Тело сможет улететь сколь
угодно далеко, но на бесконечности оно остановится.
3. С > 0. Работая по аналогии, получим, что при удалении на
бесконечность у тела сохранится какая-то энергия и скорость. А значит,
это случай гиперболических орбит.

12.

Параболическая скорость
Вычислим формулу для параболической скорости, скорости
пограничного значения.
C=0
V2/2 - GM/R = 0
V^2 = 2GM/R
V = квадр.корень (2GM/R)
Эту скорость также называют второй космической. Её значение
для земли примерно равно 11,2 км/с.

13.

Вторая космическая скорость
Вторая космическая скорость - это минимальная скорость, необходимая
для того, чтобы полностью покинуть окрестности некоторого небесного тела
и удалиться от него бесконечно далеко.
Заметим, что вторая и первая космические скорости связаны между собой
простым соотношением:
V2 = V1√2
Для Земли:
V2 = 11,2 км/с

14.

Эллиптические орбиты
Рассмотрим поподробнее случай движения небесных тел по
эллиптическим орбитам. Прежде всего, будем рассматривать орбиты
гелиоцентрические (т.е. в качестве центра принимаем Солнце), хотя все эти
законы применимы и для движения вокруг любого другого тела
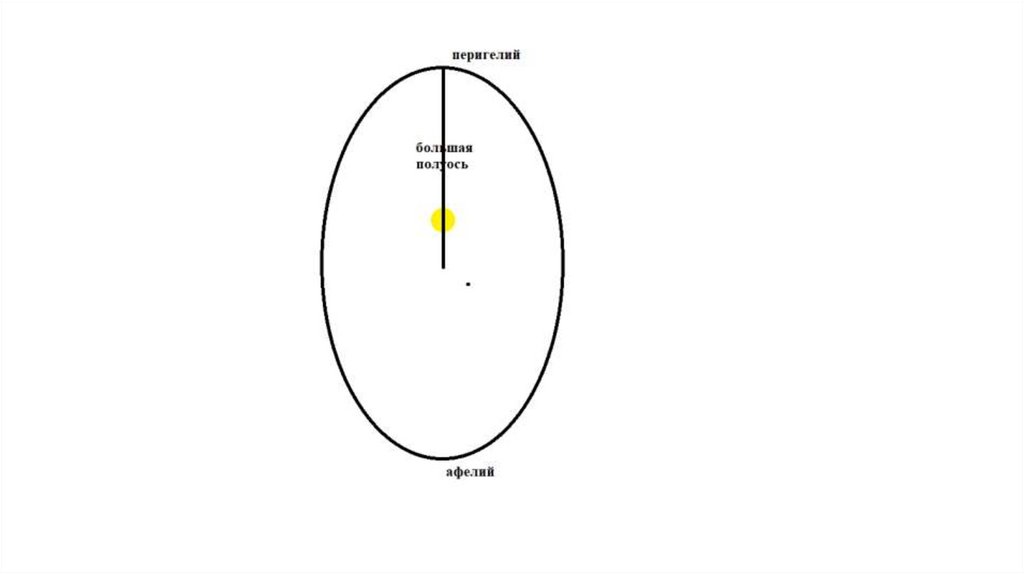
Для начала введём две особые точки:
афелий - наиболее удалённая от Солнца точка орбиты (если
вращение вокруг другого центра, говорят апоцентр).
перигелий - наиболее приближенная к Солнцу точка орбиты (для
произвольной орбиты - перицентр).

15.

16.

Большая полуось
Средним расстоянием от небесного тела до Солнца считается
большая полуось, среднее арифметическое между максимальным (RА) и
минимальным (RП) расстоянием.
Геометрический смысл большой полуоси обозначен на рисунке на
слайде 16. То есть большая ось - это самая длинная ось эллипса
(ЛОГИЧНО!). А полуось - это её половина. Традиционно принято обозначать
большую полуось орбиты (да и любого эллипса) буквой a.
a = (RA+RП)/2
То есть, длина большой полуоси есть среднее арифметическое
между расстояниями от тела до Солнца в перигелии и в афелии.

17.

Общая энергия
Одним из следствий ЗВТ, доказательство которого мы здесь
приводить не будем, является то, что все тела, двигающихся на орбитах с
одинаковой большой полуосью, имеют одинаковую удельную энергию. То
есть, если два тела двигаются вдоль эллипсов с одинаковой “a”, то вне
зависимости от того, насколько вытянута эта орбита - является ли они
“почти” кругом или “почти” параболой - общая энергия “С” у них будет
одинаковой.
Можно посчитать значение этой энергии, в качестве примера взяв
круговую орбиту радиуса a.

18.

Общая энергия
С = V2/2 - GM/R
Мы знаем, что при движении по круговой орбите:
V2=GM/R
С = (GM/2R) - (GM/2R) = -GM/2R
Заменим R на a (радиус окружности = большая полуось)
C = -GM/2a

19.

ЗСЭ. Случай эллипса.
V2/2 - GM/R = -GM/2a
где:
V - скорость тела
M - масса притягивающего центра (обычно Солнца)
R - текущее расстояние от тела до Солнца
a - среднее расстояние от тела до Солнца. Большая полуось орбиты.
Примечание. если вывод на последних слайдах показался сложным, можно
просто пользоваться этой формулой.

20.

ЗСЭ. Решение задач.
Афелий орбиты некоторого небесного тела расположен на расстоянии 10
а.е. от Солнца, перигелий - на 2 а.е. Определите его скорость в перигелии и
афелии.
1 а.е. - это среднее расстояние от Земли до Солнца, примерно 150 млн. км.
Масса Солнца - 2 * 1030 кг
Гравитационная постоянная 6,7 * 10-11Н*м2/кг2.

21.

Решение
1. Заметим, что перигелий орбиты - 2 а.е, афелий - 10 а.е. Значит, большая полуось:
a = (RA+RП)/2 = 6 а.е.
2. Найдём скорость в перигелии:
V2/2 - GM/RП = -GM/2a
V2 =2GM(1/RП-1/2a)
V2 = 2 * 6,7 * 10-11 * 2*1030(1/(2*1,5*1011)-1/(2*6*1,5*1011)
V2 = 26,8 * 1019 * (10-11 * (1/3 - 1/18)) = 7,44 * 108
Извлекаем квадратный корень:
V = 2,7 * 104 = 27 км/с
3. Аналогичным образом можно найти и скорость в афелии

22.

Система единиц
Можно очень сильно упростить себе жизнь, если при решении задач
пользоваться так называемой “астрономической” системой единиц
измерения.
В ней масса измеряется в массах Солнца, расстояние - в
астрономических единицах (среднее расстояние от Земли до Солнца).
Гравитационную постоянную принимаем равной единице, тогда скорость
оказывается измеряемой в орбитальных скоростях Земли (примерно 30
км/с).

23.

Решение задачи в новой системе единиц
В новой системе единиц M=1, G =1, RА = 10, RП = 2.
Тогда:
VА=2GM(1/RА - 1/2a)
VА = 2 * 1 * 1 (1/10 - 1/(2*6)) = 2 * (1/10 - 1/12) = 2 * (1/60) = 1/30
Осталось перейти к нормальным единицам. Вспомним, что орбитальная
скорость Земли - 30 км/с. Получаем:
VА = 1/30 * 30 = 1 км/с
Ответ: скорость в афелии составляет 1 км/с

24.

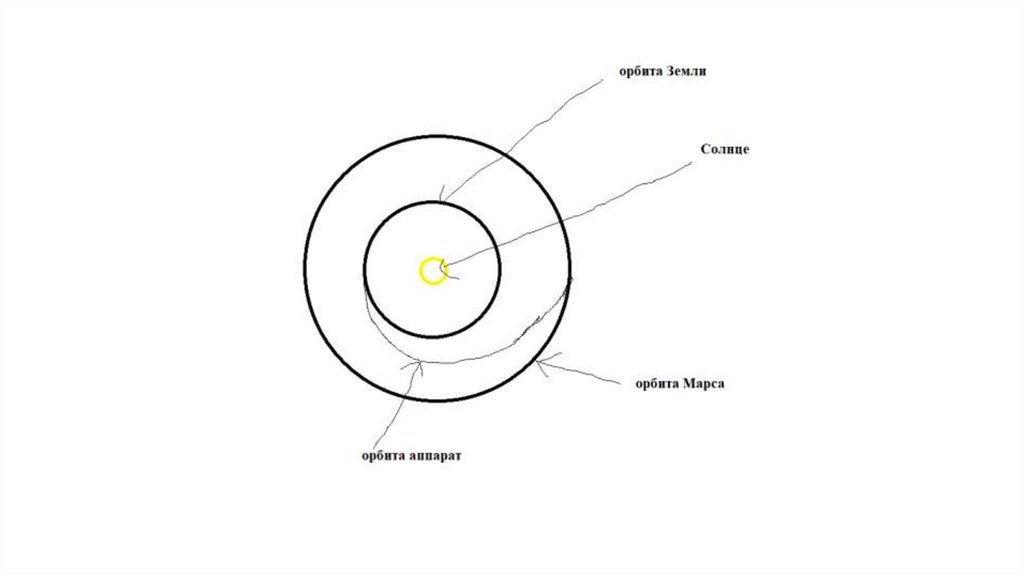
Движение космических аппаратов
При полёте космических аппаратов к другим планетам, например, к
Марсу, наиболее экономично лететь по эллиптической орбите, направленной
по касательной к земной и марсианской, то есть такой орбите, у которой
перигелий равен радиусу земной (1 а.е), а афелий - радиусу марсианской
(1,5 а.е.,хотя марсианская орбита не так уж близка к круговой).

25.

26.

Решение задач. Примеры.
Расчитайте скорость, которую нужно иметь космическому аппарату на
земной орбите, чтобы долететь до Марса наиболее экономичным способом
(по такой орбите, перигелий которой совпадает с земной, а афелий - с
марсианской).

27.

Решение задач. Примеры.
Решение.
1. Вычислим большую полуось нашей орбиты.
a = (RA+RП)/2 = (1 + 1,5)/2 = 1,25 а.е.
2. Запишем закон сохранения энергии
V2/2 - GM/R = -GM/2a
V2 = 2GM (1/R - 1/2a)
Воспользуемся нашей любимой астрономической системой единиц
V2 = 2 * 1 * 1 * (1/1 - 1/(2 * 1,25)) = 2 * (1 - 0,4) = 1,2
V = 1,09VЗ
Домножим на орбитальную скорость Земли
V = 1,09 * 30 = 32,7 км/с
Ответ: 32,7 км/с

28.

СПАСИБО ЗА ВНИМАНИЕ!