Similar presentations:
Уравнение касательной к графику функции
1.
ТЕМА УРОКА:«Уравнение касательной к
графику функции»
1.Задания со слайда 3 и 4
решить, используя формулы со
слайда 2
2.Написать конспект :слайды 59,12
3.Написать примеры с
решениями: слайды 10,11,13,14
2.
Таблица производныхУмеете лиn вы дифференцировать?
f(x)
C
x
f /(x)
0
nxn-1
x
1
2 x
sin x cos x tg x ctg x
cos x -sin x
1
1
2
2
sin
x
cos x
Правила дифференцирования
(u v) u v
(uv) u v v u
(Cu) Cu
(u(v(x)) ) u v
u u v v u
2
v
v
3.
1. Используя формулы и правиладифференцирования, найдите производные
следующих функций:
1. у 2 х10
2. у 4 х
3. у 7 х 4
5
4. у tgx
x
5. у х 3 sin x
х2
6. у
3 4х
4.
Отгадайте фамилию учёногоf(x)
х2 – 3х+4
А
f / (x)
Г
Ж
2x 2x - 3 2
1
sin x
3
слово
Л
А
Г
Р
Л
5tg x
2x – 3
Н
Р
2x
А
2
3
x
Н
Ж
5.
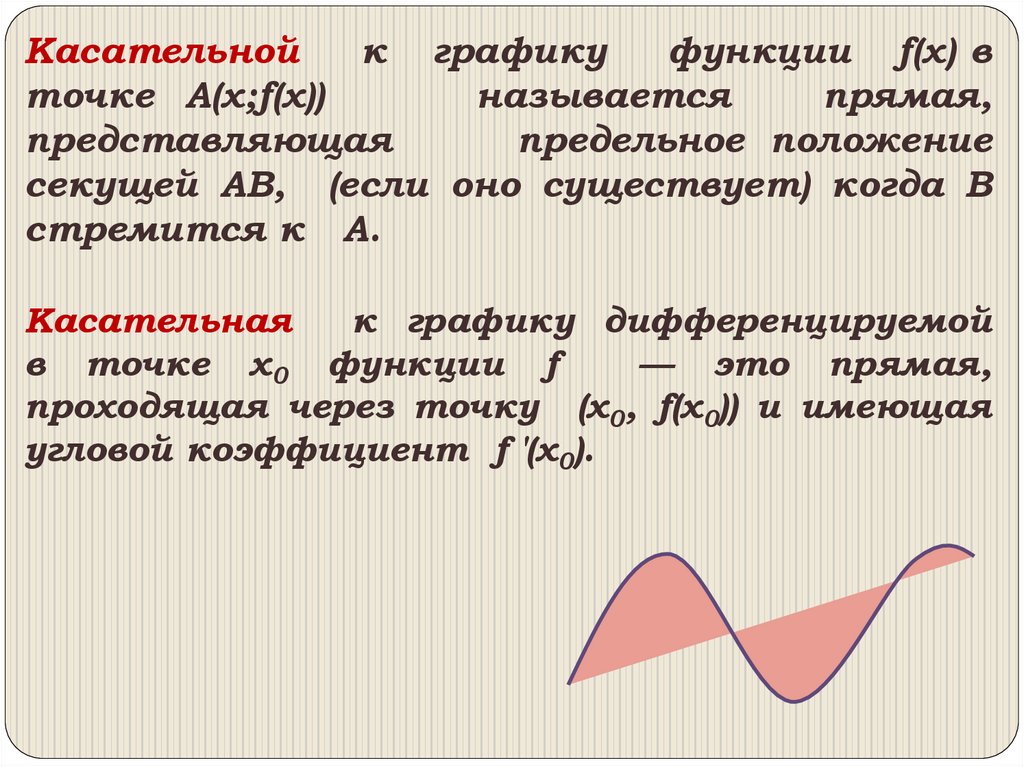
Касательнойк графику
функции f(x) в
точке А(х;f(х))
называется
прямая,
представляющая
предельное положение
секущей АВ, (если оно существует) когда В
стремится к А.
Касательная
к графику дифференцируемой
в точке х0 функции f
— это прямая,
проходящая через точку (x0, f(x0)) и имеющая
угловой коэффициент f '(х0).
6.
By = f(х)
y
A
В
T
x
О
угол TAВ → 0, если
АВ → АТ,
f
f ( x0 ) , если Δх → 0
x
7.
Геометрический смысл производнойЗначение производной функции y= f(x) в точке
касания х0
равно угловому
коэффициенту
касательной
к графику функции
y=f(x)
в
точке х0.
k f ( x0 )
/
k tg
tg f ( x0 )
8.
Геометрический смысл производнойПричем, если :
.
9.
Пусть в точке А ( х0 ; у 0 ) проведена касательная.Уравнение любой
прямой проходящей через
данную точку имеет вид
у у 0 k ( x x0 )
y0 f ( x0 )
k f ( x0 )
/
y y0 f ( x0 )( x x0 )
y к f ( x0 ) f ( x0 )( x x0 )
10.
1. Составить уравнение касательной к графикуфункции f ( x) x 2 в точке M 1;1
f (1) 12 1
f ( x) 2 x
'
f (1) 2 1 2
'
y f (a ) f (a )( x a )
'
y 1 2 ( x 1)
y 1 2x 2
y 2x 1
11.
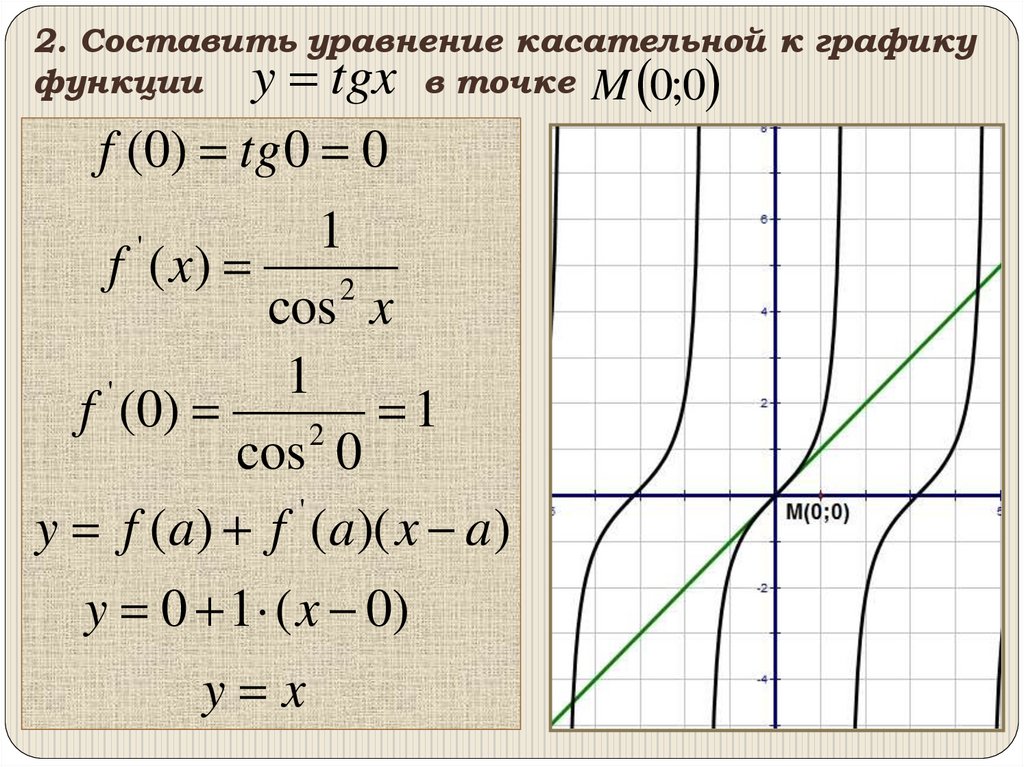
2. Составить уравнение касательной к графикуфункции y tgx в точке M 0;0
f (0) tg 0 0
1
f ( x)
2
cos x
1
'
f ( 0)
1
2
cos 0
'
y f (a ) f (a )( x a )
'
y 0 1 ( x 0)
y x
12.
Алгоритмнахождения
уравнения
касательной к графику функции y=f(x).
1.Обозначим абсциссу точки касания
буквой x0.
2.Вычислим
.
3.Найдем
и
.
4.Подставим найденные числа x0,
и
в формулу
13.
3. Составить уравнение касательной к графикуфункции f ( x)
1
в точке
x
1) a 1
2) f (a) f (1) 1
1
3) f ( x) 2
x
'
1
f (a ) f (1) 2 1
1
'
'
4) y 1 ( x 1)
y 2 x
Ответ: y 2 x
x 1
14.
4. К графику функцииx3
y
3
провести
касательную так, чтобы она была параллельна
прямой y 4 x 5
kкас 4, k кас f ' ( x) f ' ( x) 4
x
f ( x)
3
'
1
3 x 2 x 2
3
f ' (a) a 2 a 2 4,
3
'
.
1) a1 2, a2 2
3
(
2
)
8
2 8 , f (a )
2) f (a1 )
2
3
3
3 3
3
3) f (a1 ) f (a2 ) 4
'
'
16
16
4) y 4 x
, y 4x
3
3
,












 mathematics
mathematics








