Статистика в НМД 1. Описательная статистика

1.

Статистика в НМД 1
Описательная статистика

2.

• Статистика - отрасль знаний, в которой излагаются общие
вопросы сбора, измерения и анализа массовых
статистических (количественных или качественных) данных;
изучение количественной стороны массовых явлений в
числовой форме.
• Математическая статистика – наука о математических
методах систематизации, обработки и использования
статистических данных для научных и практических
выводов.
• Вариационная статистика (от лат. variatio - изменение) раздел математической статистики, изучающий
распределение варьирующих количеств, признаков в
совокупностях объектов (исследуемых группах).
2

3.

• Статистической совокупностью называют группу статистических данных (величин,
вариант, единиц наблюдения, переменных), объединенных в хотя бы одним
статистическим признаком. Число данных в статистической совокупности называют
ее объемом и обозначают n.
Генеральные и выборочные совокупности
• Генеральная совокупность - совокупность всех единиц наблюдения интересующих
исследователя при изучении конкретной проблемы. Состоит из всех объектов,
которые имеют свойства, интересующие исследователя (например, все школьники
младшего возраста определённого региона).
• Выборочная совокупность – достаточно небольшая часть единиц наблюдения,
выбранная из генеральной совокупности по определённым правилам.
• Виды отбора единиц наблюдения в выборочную совокупность:
случайный (по жребию),
механический (например, каждый второй),
серийный (выбор не отдельных единиц, а например, самых типичных серий),
основного массива (выбор объектов, в которых сосредоточено большинство изучаемых
явлений),
• направленный (выбор только тех единицы наблюдения, которые позволяют выявить
влияние неизвестных факторов при устранении влияния известных) и др.
3

4.

Типовые этапы и задачи статистического
анализа полученных данных
Этапы
Описание
данных
Изучение сходства/
различия
Задачи
Компактное
Установление
описание
совпадений/
данных
различий данных 2-х
Определение
выборок
объёма выборки
Методы
Описательная
статистика
Определение
объёма выборки
Статистические
критерии
Исследование
зависимостей
Установление
наличия/отсутствия
зависимости между
показателями и
количественное
описание этих
зависимостей.
Корреляционный,
дисперсный,
регрессионный анализ
4

5.

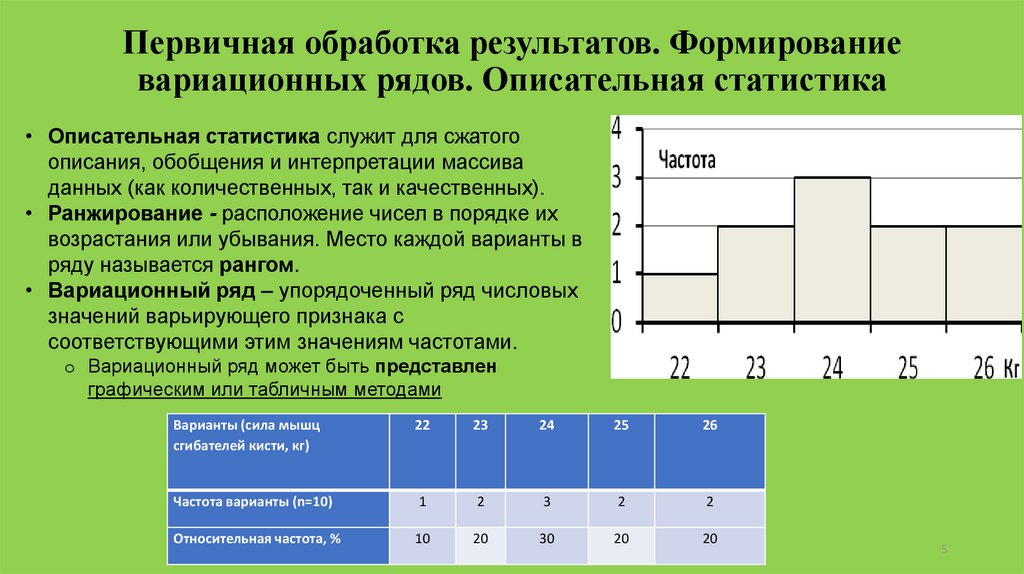
Первичная обработка результатов. Формирование
вариационных рядов. Описательная статистика
• Описательная статистика служит для сжатого
описания, обобщения и интерпретации массива
данных (как количественных, так и качественных).
• Ранжирование - расположение чисел в порядке их
возрастания или убывания. Место каждой варианты в
ряду называется рангом.
• Вариационный ряд – упорядоченный ряд числовых
значений варьирующего признака с
соответствующими этим значениям частотами.
o Вариационный ряд может быть представлен
графическим или табличным методами
Варианты (сила мышц
сгибателей кисти, кг)
22
23
24
25
26
Частота варианты (n=10)
1
2
3
2
2
Относительная частота, %
10
20
30
20
20
5

6.

6

7.

Оценка центральной тенденции
(положения) вариационного ряда
Мода
o Значение, которое наиболее часто
встречается в ряду распределения.
Следует обратить внимание, что мода –
это наиболее частое значение, а не
частота этого значения.
o На
гистограмме
вероятностного
распределения
значению
моды
соответствует
наибольший
подъём
графика.
• Медиана
o Варианта,
находящаяся
посередине
ранжированного ряда данных и делящая
этот ряд на две равные по количеству
членов части.
Среднее арифметическое
o Показатель среднего уровня, самого
типичного и характерного для всего ряда.
7

8.

Квантиль - точка на числовой оси признака, которая заданная случайная величина не
превышает с фиксированной вероятностью.
Процентили (Р) делят упорядоченное по возрастанию множество наблюдений на 100
равных по численности частей.
Децили (D) делят выборку на десять равных частей. Так, первый дециль отделяет 10 %
наименьших величин от 90 % наибольших величин.
Квартили (Q) - это 3 значения признака (Q1, Q2, Q3), которые делят упорядоченное по
возрастанию множество наблюдений на 4 равные по численности части.
8

9.

Показатели рассеивания вариационного ряда
Размах
o Разница между максимальным и минимальным значениями варианты
(исключающий размах).
Интерквартильный размах
o Разность между 3 и 1 квартилями; включает центральные 50% данных.
Дисперсия выборки (D, σ2)
o Пропорциональная сумме квадратов отклонений всех измеренных значений
от их арифметического среднего.
o Указывает на варьирование, т.е. рассеивание (разброс) всех измеренных
метрических данных относительно средней арифметической величины.
9

10.

Среднеквадратическое отклонение (σ – сигма) или стандартное отклонение
o Определяется как положительный квадратный корень из дисперсии (поэтому и
называется «средним квадратичным отклонением»).
o Характеризует степень отклонения результатов от среднего значения конкретной
выборки в абсолютных единицах (в тех же единицах, что и варианты ряда).
o Является основной мерой изменчивости признака у членов совокупности,
имеющей нормальный тип распределения.
Коэффициент вариации
o Является относительной характеристикой однородности наблюдений. Даёт
представление о величине разброса данных, независимо от масштаба измерений.
o Определяется как отношение среднего квадратического отклонения к среднему
арифметическому, выраженное в процентах:
• V = δ/Х * 100%
10

11.

Стандартная ошибка средней величины (выборки) или ошибка
репрезентативности
Не является описательной статистикой и не должна использоваться в таком
качестве.
Является оценкой возможного отличия между значением среднего в
анализируемой выборке и истинным средним во всей популяции. Следует
использовать для оценки среднего генеральной совокупности.
Определяется по формуле: m = σ / √n
Отличие «m» от «σ» заключается в том, что «σ» характеризует варьирование
отдельных вариант вокруг средней величины конкретного вариационного ряда, а
«m» – варьирование средних величин отдельных выборок вокруг средней величины
генеральной совокупности, т.е. стандартная ошибка отражает точность оценки.
11

12.

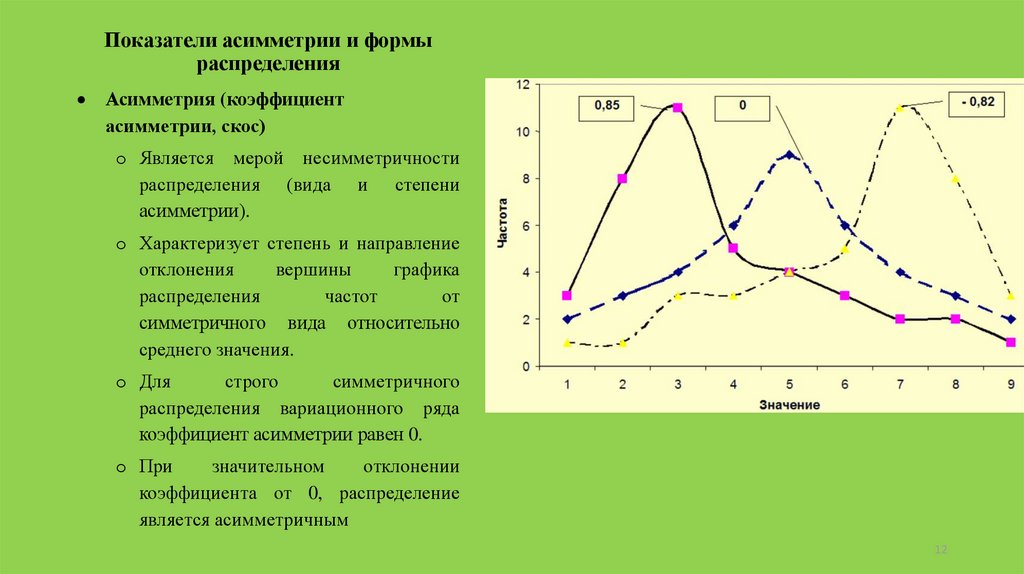
Показатели асимметрии и формы
распределения
Асимметрия (коэффициент
асимметрии, скос)
o Является мерой несимметричности
распределения (вида и степени
асимметрии).
o Характеризует степень и направление
отклонения
вершины
графика
распределения
частот
от
симметричного вида относительно
среднего значения.
o Для
строго
симметричного
распределения вариационного ряда
коэффициент асимметрии равен 0.
o При
значительном
отклонении
коэффициента от 0, распределение
является асимметричным
12

13.

Эксцесс, или коэффициент эксцесса
измеряет остроту пика распределения
o
Является
показателем
«островершинности»
распределения;
показывает,
насколько ярко выражена вершина
распределения.
o
Интерпретация: эксцесс > 0 –
острый пик (по сравнению с
нормальным
распределением);
эксцесс < 0 – плосковершинная
форма.
Гистограммы, полигоны – дают
визуальное
представление
о
симметричности
и
форме
распределения данных.
13

14.

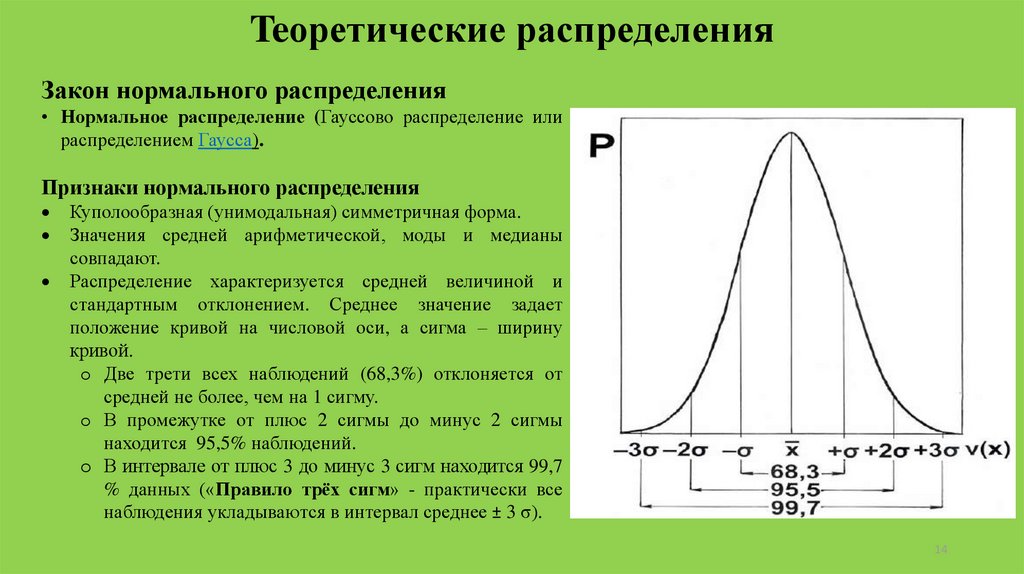
Teоретические распределения
Закон нормального распределения
• Нормальное распределение (Гауссово распределение или
распределением Гаусса).
Признаки нормального распределения
Куполообразная (унимодальная) симметричная форма.
Значения средней арифметической, моды и медианы
совпадают.
Распределение характеризуется средней величиной и
стандартным отклонением. Среднее значение задает
положение кривой на числовой оси, а сигма – ширину
кривой.
o Две трети всех наблюдений (68,3%) отклоняется от
средней не более, чем на 1 сигму.
o В промежутке от плюс 2 сигмы до минус 2 сигмы
находится 95,5% наблюдений.
o В интервале от плюс 3 до минус 3 сигм находится 99,7
% данных («Правило трёх сигм» - практически все
наблюдения укладываются в интервал среднее ± 3 σ).
14

15.

Представление данных и статистик
Табличное представление данных и статистик
Функции таблиц
Уплотнить или суммировать данные.
Организовать и показать данные более ясно и кратко, чем словами.
Сравнить значения или группы значений.
Улучшить лёгкость и скорость нахождения и понимания информации.
Облегчить вычисления.
Принципы построения таблиц
Наличие цели, которая должна определять её структуру.
Самодостаточность - название и данные понятны независимо от
текста, наличие терминов, используемых в тексте, а также единиц
измерения.
Интегрированность с текстом, но отсутствие дублирования данных,
представленных в тексте или на рисунках.
Удобный формат, помогающий в поиске, визуализации и запоминании
информации. Размещение сравниваемых данных рядом, выделение
важных значений.
Округление чисел до 2 значащих цифр, если не требуется большей
точности.
Включение в таблицу строк и столбцов с итоговыми/вычисляемыми
статистиками, доверительных интервалов и т.д.
Таблица 4.3.
Динамика гемодинамических показателей группы
студенток специальной медицинской группы в ходе
исследования, средние значения и средние квадратичные
отклонения в скобках.
Показатели
ЧСС, уд/мин.
САД, мм.рт.ст.
ДАД, мм.рт.ст.
Исходные
данные
88,6 (2,4)
128,0 (2,1)
82,5 (1,7)
Конечные данные
78,0 (2,6)*
110,8 (2,1)**
71,6 (1,2)*
Примечание: * – статистически значимое изменение по
отношению к исходным данным р <0,05; **–
статистически значимое изменение по отношению к
исходным данным р < 0,01.
15

16.

Графическое представление данных
Функции рисунков
Показать структуру данных способами, которые невозможны в тексте или
таблицах.
Представить данные более кратко и ясно, чем это возможно в таблицах и
тексте.
Уплотнить и суммировать большие массивы данных.
Облегчить и ускорить понимание и поиск информации.
16

17.

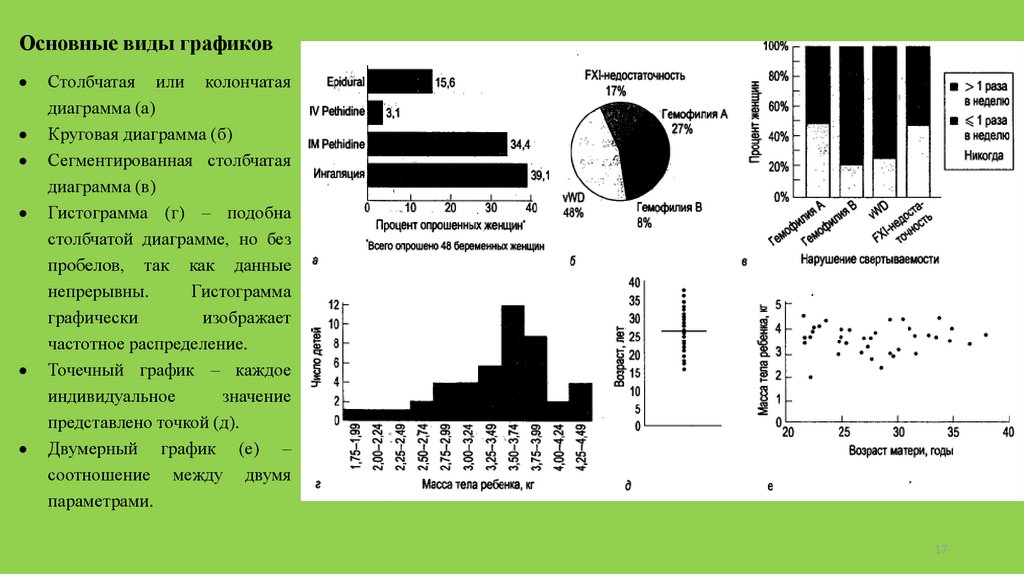
Основные виды графиков
Столбчатая или колончатая
диаграмма (а)
Круговая диаграмма (б)
Сегментированная столбчатая
диаграмма (в)
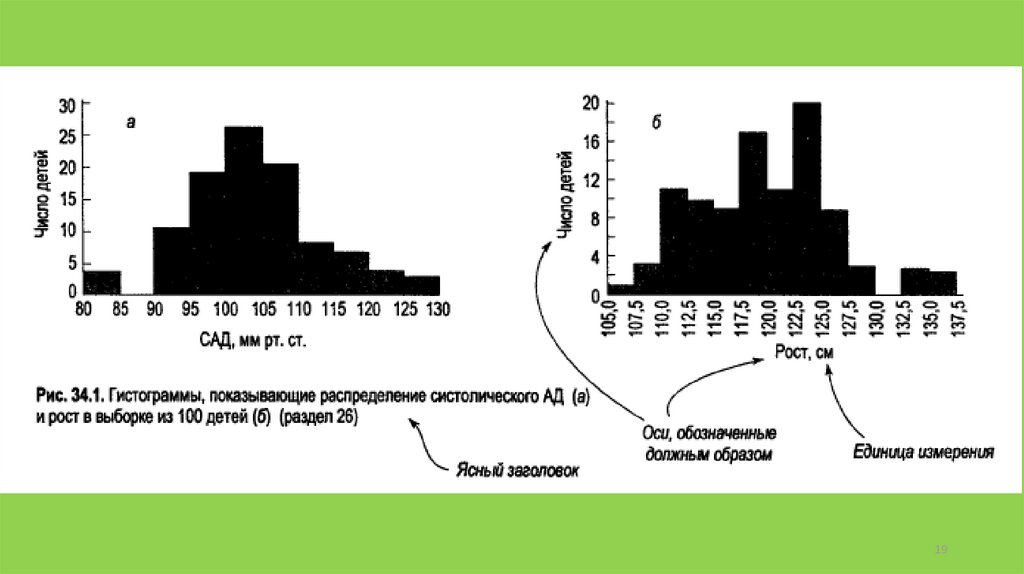
Гистограмма (г) – подобна
столбчатой диаграмме, но без
пробелов, так как данные
непрерывны.
Гистограмма
графически
изображает
частотное распределение.
Точечный график – каждое
индивидуальное
значение
представлено точкой (д).
Двумерный график (е) –
соотношение между двумя
параметрами.
17

18.

Рекомендации по построению графиков
• Рисунки и графики, которые автоматически формируются стандартными программами
редко подходят для представления данных в научных публикациях. Электронные графики
часто нуждаются в пере- или до-оформлении.
Наличие чёткой цели, интегрированность с основным текстом, отсутствие дублирования
данных текста или таблиц.
Самодостаточность (понятен «сам по себе»), наличие всех необходимых обозначений
(названия осей, единицы измерения и т.д.).
Соответствие подписи (как правило, ставится под рисунками) данным.
Краткость представления, наличие только необходимых элементов, отсутствие ненужных
«украшений».
Соответствие принципам психологии восприятия. Каждое значение на графике должно
быть визуально отличным.
Наличие точек отсчёта на осях и главных интервалов.
18

19.

19

20.

Правила представления числовых результатов
Разумная степенью точности чисел, наличие единиц измерения.
Указание объёма выборки (например, n = 28).
Статистические показатели центральной тенденции вариационного ряда (среднее, мода, медиана)
следует указывать с показателями разброса (стандартное отклонение, дисперсия, процентильный
разброс).
o При нормальном распределении непрерывных данных лучше указывать среднее значение и
стандартное отклонение. Не следует использовать символ «±» при указании среднего
арифметического и стандартного отклонения..
o Распределения, заметно отличающиеся от нормального: медиана (50-й перцентиль) и размах
или интерквартильная широта (фактически – значения 25-го и 75-го процентилей).
o Не следует применять стандартную ошибку среднего в качестве показателя разброса.
Стандартная ошибка характеризует точность оценки среднего, а не разброс данных.
20

21.

Сравнение рассеяния двух и более множеств нормально
распределенных.
Вместо
стандартного
отклонения
лучше
использовать коэффициент вариации (особенно при различных
единицах измерения). Коэффициент вариации удобен тем, что
объединят среднее и сигму в один показатель.
Малые выборки. Уместно приводить все имеющиеся данные.
Среднее и сигма могут давать неадекватное представление малых
множеств данных.
Для описания дискретных данных (по определению не
подчиняются
нормальному
распределению)
используется
представление данных в виде пропорций (доли, процента). При этом
относительные частоты (%) указываются с числом знаков после
запятой не более 1. При объёме выборки менее 20 – указываются не
%, а числовые данные.
21

22.

Статистические методы обработки результатов измерений
Теория оценивания и теория проверки гипотез
Элементы теории вероятности
• В основе теории вероятности лежит случайное явление, которое, при
определённых обстоятельствах, может произойти, а может нет.
• Вероятность (P):
измеряет неопределённость или возможность того или иного события.
является положительным числом, которое находится в интервале между 0 и 1
(0 ≤ Р ≤ 1).
o Р=0 - события быть не может (невозможное событие).
o Р=1 – событие обязательно должно произойти (достоверное событие).
• Поскольку в статистическом оценивании, базирующемся на теории
вероятностей, нет ни P=1, ни P=0, а всегда 0<P<1, ни достоверность, ни
невозможность посчитать нельзя.
22

23.

Статистические гипотезы
Статистическая гипотеза в теории проверки гипотез - положение,
которое будет приято или отклонено (поддержано или нет) на основании
результатов исследования.
• Виды статистических гипотез
Нулевая гипотеза (Но) – предполагает отсутствие различия между
сравниваемыми выборками или отсутствие влияния исследуемых
факторов на исследуемую величину – опровергает эффект (случайность
результата). Она противоположна тому, в чём желает убедиться
исследователь.
Альтернативная гипотеза (На) – предполагает наличие различия между
группами. Принимается, если нулевая гипотеза не верна.
23

24.

Статистические ошибки при принятии решений
• Выдвинутая статистическая гипотеза проверяется статистическими методами. При этом
возможно 2 вида ошибок.
Статистическая ошибка первого рода (Type I Error, альфа) – ошибка обнаружить
различия или связи, которые на самом деле не существуют. Истинная Но отклоняется.
Вероятность совершить ошибку первого рода называется уровнем статистической
значимости.
Статистическая ошибка второго рода (Type II Error, бетта) – ошибка не обнаружить
различия или связи, которые на самом деле существуют. Ложная Но не может быть
отклонена. Характеризует мощность теста. Важна для определения объёма выборки для
исследования.
o Более «критичной» ошибкой считается статистическая ошибка первого рода.
«Судебная» аналогия: Вердикт «Не виновен» или «Виновен». Ошибка первого рода невинный обвинен. Ошибка второго рода - виновный освобожден.
o Для принятия решения какую статистическую гипотезу принять используют
специальные статистические методы – статистические критерии. Критерием
называется как сам метод, так и результат его применения.
24

25.

Статистическая значимость
• Статистическая значимость в теории проверки гипотез
вероятность
того, что найденные различия, основанные не на
случайности.
ассоциирована
с р-значением – вероятностным значением:
вероятностью того, что исход (результат) мог бы иметь место случайно.
При условии, что р-значение равно или ниже заданного критического
уровня значимости, указывает, что случайность, вероятно, не является
объяснением разности.
В статистике величину называют статистически значимой, если мала
вероятность её случайного возникновения. Разница называется
«статистически значимой», если появление имеющихся данных было бы
маловероятно, если предположить, что эта разница отсутствует.
25

26.

Критический уровень статистической значимости
• Всякое статистическое решение, принимаемое на основе
ограниченного ряда наблюдений, неизбежно сопровождается
вероятностью ошибочного заключения.
Понятие критического уровня статистической значимости
o Заданное значение верхнего предела вероятности ошибки первого
рода.
o Пороговая (критическая, максимально допускаемая) вероятность
ошибки, заключающейся в отклонении нулевой гипотезы, когда она
верна. Другими словами, это допустимая (с точки зрения
исследователя) вероятность совершения статистической ошибки
первого рода.
Обозначение – альфа, α.
26

27.

Принятие в практике уровни статистической значимости
Альфа = 0,05
o низший уровень статистической значимости, рекомендован для небольших
выборок.
o допускается не более чем 5%-ая вероятность ошибки первого рода (вероятность
случайного возникновения обнаруженного различия) при проверке
статистической гипотезы – 5 шансов из 100. p-уровень < 0,05 или р ≤ 0,05.
o Если данный уровень значимости не достигается (вероятность ошибки выше
5%) - разница может быть случайной и поэтому нельзя отклонить Но на взятом
уровне альфа. Не отвергая Но, можно заявить, что результаты не значимы на 5%
уровне.
Альфа = 0,01 (p<0,01 или р ≤ 0,01). Допускается 1% уровень вероятности
совершения ошибки. В данном случае можно написать.
Альфа = 0,001 (p<0,001 или р ≤ 0,001). Допускается 0,1% уровень вероятности
совершения ошибки.
27

28.

Достигнутый уровень статистической значимости (р)
Достигнутый p-уровень значимости (p-value) - рассчитанное в ходе
статистического теста значение.
Если p < α, Но отклоняется и различия считаются статистически
значимыми. Чем меньше значение р, тем сильнее аргументы против Но и
более значима тестовая статистика.
Определение результата только как значимого на определенном уровне
граничного значения (например 0, 05) может ввести в заблуждение.
Рекомендуется всегда указывать точное значение р, получаемое путем
компьютерного анализа.
р – это величина, получаемая в эксперименте, альфа – это теоретическая
граница, используемая для оценки р.
28