Similar presentations:
Законы логики
1. Законы логики
2. I. Законы формальной логики
• Наиболее простые и необходимыеистинные связи между мыслями
выражаются в основных законах
формальной логики. Эти законы
являются основными потому, что в
логике они играют особо важную роль,
являются наиболее общими. Они
позволяют упрощать логические
выражения и строить умозаключения и
доказательства
3. I. Законы формальной логики
1. Закон тождества: в процессеопределённого рассуждения всякое
понятие и суждение должны быть
тождественны самим себе.
Аристотель
4. I. Законы формальной логики
2. Закон непротиворечия: невозможно,чтобы одно и то же в одно то же время
было и не было присуще одному и
тому же в одном и том же отношении.
То есть невозможно что-либо
одновременно утверждать и отрицать.
Аристотель
5. I. Законы формальной логики
3. Закон исключённого третьего: из двухпротиворечащих суждения одно
истинно, другое ложно, а третьего не
дано.
Аристотель
6.
Закон достаточногооснования:
всякая истинная мысль должна быть
достаточно обоснована.
7. I. Законы формальной логики
4.Закон достаточного основания: всякая истинная мысль
должна быть достаточно обоснована.
Г. Лейбниц
Другими словами, доказательство чего-либо предполагает обоснование
истинных и только истинных мыслей. Ложные же мысли доказать
нельзя.
«Ошибаться свойственно всякому человеку, но настаивать на
ошибке свойственно только глупцу».
латинская пословица
Формулы этого закона нет, так как он имеет только содержательный
характер. В качестве аргументов для подтверждения истинной мысли
могут быть использованы истинные суждения, цифровой материал,
статистические данные, законы науки, аксиомы, теоремы.
8. Законы алгебры высказываний
• В алгебре логики имеется ряд законов,позволяющих производить
равносильные преобразования формул.
• Законы алгебры высказываний – это
тавтологии. Иногда эти законы
называются теоремами.
9.
Закон тождества:в процессе определенного рассуждения
всякое понятие и суждение должны
быть тождественны самим себе.
А=А
10. Основные законы алгебры высказываний:
1. Закон тождества: А = А.Всякая мысль тождественна самой себе.
Данный закон означает, что в процессе
рассуждения нельзя подменять одну
мысль другой, одно понятие другим. При
нарушении этого закона возможны
логические ошибки.
11.
Закон непротиворечия:невозможно, чтобы одно и тоже в
одно и тоже время было и не было
присуще одному и тому же в одном и
том же отношении. То есть
невозможно что-то одновременно
утверждать и отрицать.
А*Ā=0
12.
Закон исключениятретьего:
из двух противоречащих суждений
одно истинно, другое ложно, а
третьего не дано.
А+Ā=1
13. Основные законы алгебры высказываний:
14.
Закон двойногоотрицания:
если отрицать дважды некоторое
высказывание, то в результате
получается исходное высказывание.
А =А
15. Основные законы алгебры высказываний:
16.
Свойства констант:отрицание
лжи есть
истина.
0=1
отрицание
истины
есть ложь.
1=0
А+0=А
А*0=0
А+1=1
А*1=A
17.
Закон идемпотентности:А+А=А
А*А=A
Например, сколько бы раз мы ни повторяли: телевизор включен или телевизор
включен или телевизор включен….значение высказывания не изменится.
18.
Законы коммутативности(сочетательные законы):
операнды А и В в операциях
дизъюнкции и конъюнкции можно
менять местами.
А+В=В+А
А*В=В*А
19.
Законы ассоциативности(распределительные законы):
если в выражении используется только
операция дизъюнкции или только операция
конъюнкции, то можно пренебрегать
скобками или произвольно их расставлять.
А + (В + C) = (А + В) + C
А * (В * C) = (А * В) * C
20.
Законы дистрибутивности:А + (В * C) = (А + В) * (А + C)
А * (В + C) = (А * В) + (А * C)
21. Внимание:
Закон ассоциативности аналогичензакону алгебры чисел, а закон
дистрибутивности справедлив
только в алгебре логики.
22.
Законы поглощения:А * (В + B) = А или
А * (А + В) = А или
(А + B) * B = А * B
А + В * B = А или
А + (А * В) = А или
(А * B) + B = А +B
23.
Законы де Моргана:отрицание дизъюнкции есть конъюнкция
отрицаний. Отрицание конъюнкции есть
дизъюнкция отрицаний.
А + В = А * В или
А+B=А*B
А * В = А + В или
А*B=А+B
24.
25.
Правило замены операцииимпликации:
А В =А+В
26.
Правило замены операцииэквивалентности:
А В =В А
А В = (А + В) * (А + B)
А В = (А * В) + (А * B)
А В = (А В) * (B A)
27.
28. Тождества
логического сложения1) А + 0 = А
2) А + 1 = 1
3) А + А = А
4) А + А = 1
(ИЗ ДВУХ
ПРОТИВОПОЛОЖНЫХ
ВЫСКАЗЫВАНИЙ ХОТЯ
БЫ ОДНО ИСТИННО)
1.
2.
3.
4.
логического
умножения
А*0=0
А*1=А
А*А=А
А*А=0
(НЕВОЗМОЖНО, ЧТОБЫ
ОДНОВРЕМЕННО ДВА
ПРОТИВОПОЛОЖНЫХ
ВЫСКАЗЫВАНИЯ БЫЛИ
ИСТИННЫ)
А = А (ДВОЙНОЕ ОТРИЦАНИЕ)
28
29. Законы алгебры логики
Переместительный законА+В=В+А
А·В=В·А
Сочетательный закон
(А + В) + С = А + (В + С) (А · В) · С = А · (В · С)
Распределительный закон
(А + В)·С = А·С + В·С
А·В + С = (А + С)·(В + С)
Закон де Моргана (закон отрицания)
A+B=A•B
A•B=A+B
A→B=B→A=A+B
A ↔ B = AB + AB = (A + B) ( A + B)
29
30.
X=X&1- по свойствам констант;
X=Xv0
1=АvA
- по закону исключения третьего;
0=Z&Z
- по закону исключения третьего;
B=BvB=BvBvBvB
C=C&C=C&C&C&C
E=E
- по законам
идемпотентности;
- по закону двойного отрицания.
























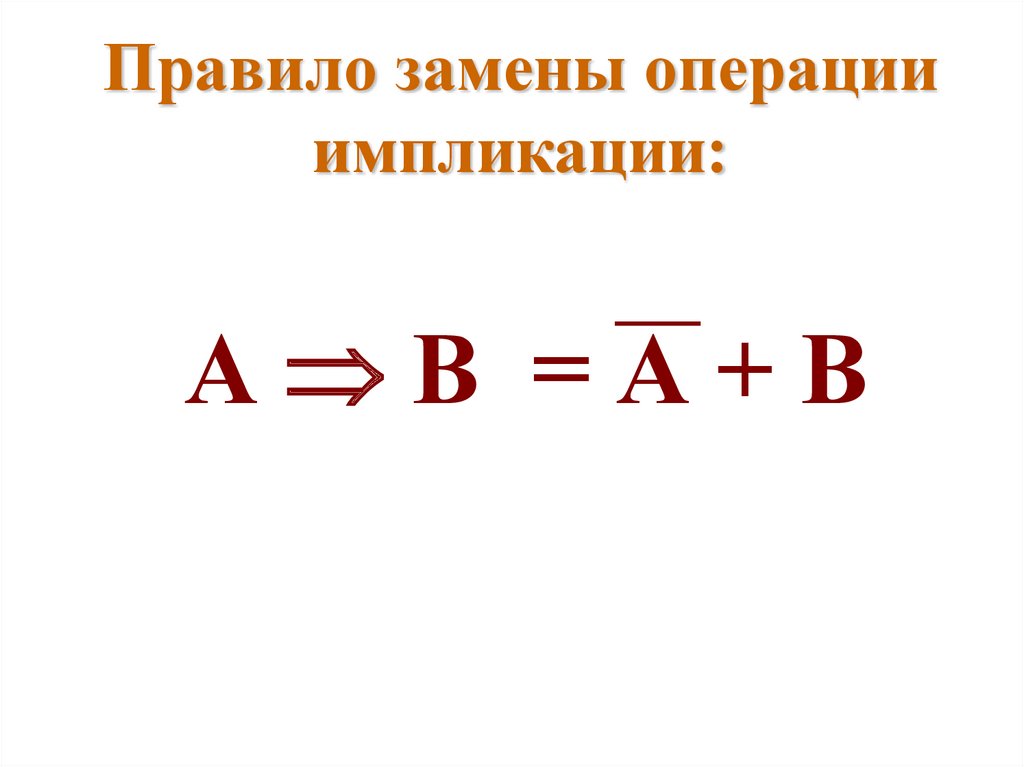





 informatics
informatics








