Динамическое программирование и его задачи

1.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФГБОУ ВО
«МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ
(НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ)»
ДОКЛАД
ПО КУРСУ: «ТЕОРИЯ СИСТЕМ И СИСТЕМНЫЙ АНАЛИЗ»
ТЕМА: «ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ И ЕГО ЗАДАЧИ»
Подготовили: студенты гр.М4О-311Б-19
Уланов О.О. и Кандауров В.А.
Принял: Агринский Н.М.

2.

Предпосылки к появлению DP
DP - математический аппарат, используемый для решения некоторого класса задач
путем их разложения на небольшие и менее сложные задачи.
■ Необходимость поиска оптимального
решения экономической задачи.
■ «Разделяй и властвуй»
■ Формулировка принципа
оптимальности Ричардом Беллманом
Ричард Эрнст Беллман

3.

Постановка задачи и особенности DP
■ Требуется определить такое управление Х*, переводящее систему из начального
состояния S0 в конечное состояние Sn, при котором целевая функция принимает
наибольшее (наименьшее) значение F(S0, X*) → extr.
1) Задача оптимизации – конечный многошаговый процесс управления;
2) Выигрыш F = ∑ Fk (Sk−1, x k ) → extremum ;
3) Нет обратной связи;
4) Отсутствие последействия, уравнение состояния: Sk= fk (Sk-1, хk), k = 1, n;
5) хk зависит от конечного числа управляющих переменных, а состояние системы
Sk зависит от конечного числа параметров;
6)Оптимальное управление - собой вектор X*, X = (х*1, х*2, …, х*k, …, х*n), число которых
и определяет количество шагов задачи.

4.

Общий принцип работы метода DP
Задачи динамического программирования являются многоэтапными или
многошаговыми. При использовании этого метода задача разбивается
на количество шагов по числу неизвестных.
На каждом шаге решается задача оптимизации только по одной
переменной.
Таким образом, процесс нахождения оптимального плана многомерной
задачи распадается на ряд более простых одномерных задач
оптимизации.
Принимая решение на i-ом шаге надо учитывать его влияние на будущее,
т.е. учитывать влияние принимаемого решения на эффективность
последующих шагов.

5.

Функциональное уравнение Беллмана
функциональное
уравнение Беллмана для последнего n-го шага
функциональное уравнение Беллмана для (n-1)-го шага
функциональное уравнение Беллмана для k-го шага (в общем виде)

6.

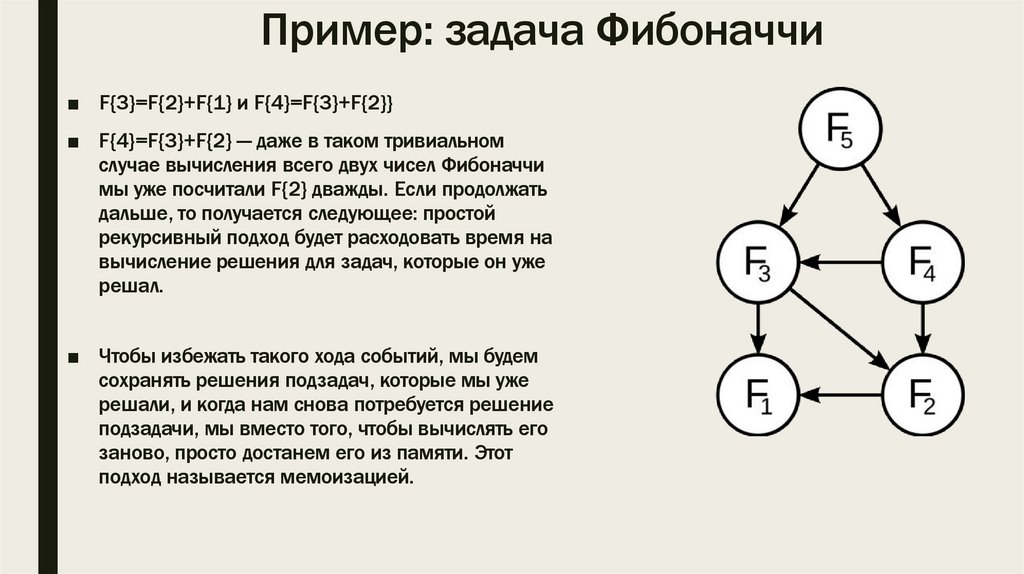
Пример: задача Фибоначчи
■ F{3}=F{2}+F{1} и F{4}=F{3}+F{2}}
■ F{4}=F{3}+F{2} — даже в таком тривиальном
случае вычисления всего двух чисел Фибоначчи
мы уже посчитали F{2} дважды. Если продолжать
дальше, то получается следующее: простой
рекурсивный подход будет расходовать время на
вычисление решения для задач, которые он уже
решал.
■ Чтобы избежать такого хода событий, мы будем
сохранять решения подзадач, которые мы уже
решали, и когда нам снова потребуется решение
подзадачи, мы вместо того, чтобы вычислять его
заново, просто достанем его из памяти. Этот
подход называется мемоизацией.

7.

Достоинства и недостатки
ПРЕИМУЩЕСТВА
НЕДОСТАТКИ
■ На каждом этапе решается задача
поиска экстремума лишь по части
переменных, следовательно,
размерность этих задач по сравнению с
исходной значительно ниже. Это
позволяет упростить поиск оптимальных
значений искомых переменных.
■ Отсутствие универсального алгоритма, который
был бы пригоден для решения всех задач
рассматриваемого класса. Алгоритмы ДП
объединены лишь общей идеей, и в каждом
конкретном случае должны формироваться
применительно к специфике прикладной
задачи.
■ Решение задач, которые не могут быть
решены другими методами.
■ При большой размерности исходной задачи эти
алгоритмы требуют значительных ресурсов
ЭВМ.
■ Простая реализация на ЭВМ.

8.

Классические и практические задачи
динамического программирования
Практические:
Задача распределения средств
между предприятиями
Задача распределения ресурсов
Задача замены оборудования
Складская задача
Задача найма работников на
предприятие и т.д.
Классические:
Задача о вычислении чисел
Фибоначчи
Задача о редакционном расстоянии
Задача о порядке перемножения
матриц
Задача о «рюкзаке» и т.д.

9.

Классификация DP по порядку действий
Нисходящее: задача разбивается на подзадачи меньшего размера, они
решаются, и затем комбинируются для решения исходной задачи.
Восходящее: все подзадачи, которые впоследствии понадобятся для
решения исходной задачи, просчитываются заранее и затем
используются для построения решения исходной задачи. Восходящее
DP экономит время решения задачи.

10.

Вывод
Таким образом, динамическое программирование является
методом математического решения задач, при помощи которого
можно найти оптимальное решение экономических и
технических задач. Как и любой вид программирования он имеет
свои достоинства и недостатки, а также широко используется при
решении различных задач.

11.

Спасибо за внимание