Similar presentations:
Распределения Бозе-Эйнштейна и Ферми-Дирака. Фазовое пространство. Плотность распределения. Лекция 19
1.
Лекция 19Распределения Бозе-Эйнштейна и ФермиДирака.
Фазовое пространство. Плотность
распределения.
Микроканонический и канонический ансамбли
Гиббса.
Статистические суммы по состояниям Z и Q.
2.
Лекция 18Термодинамическая вероятность.
Метод ячеек Больцмана. Распределение Больцмана.
Фазовое пространство. Плотность вероятности в
фазовом пространстве.
3.
Выберите правильные утверждения2 балла
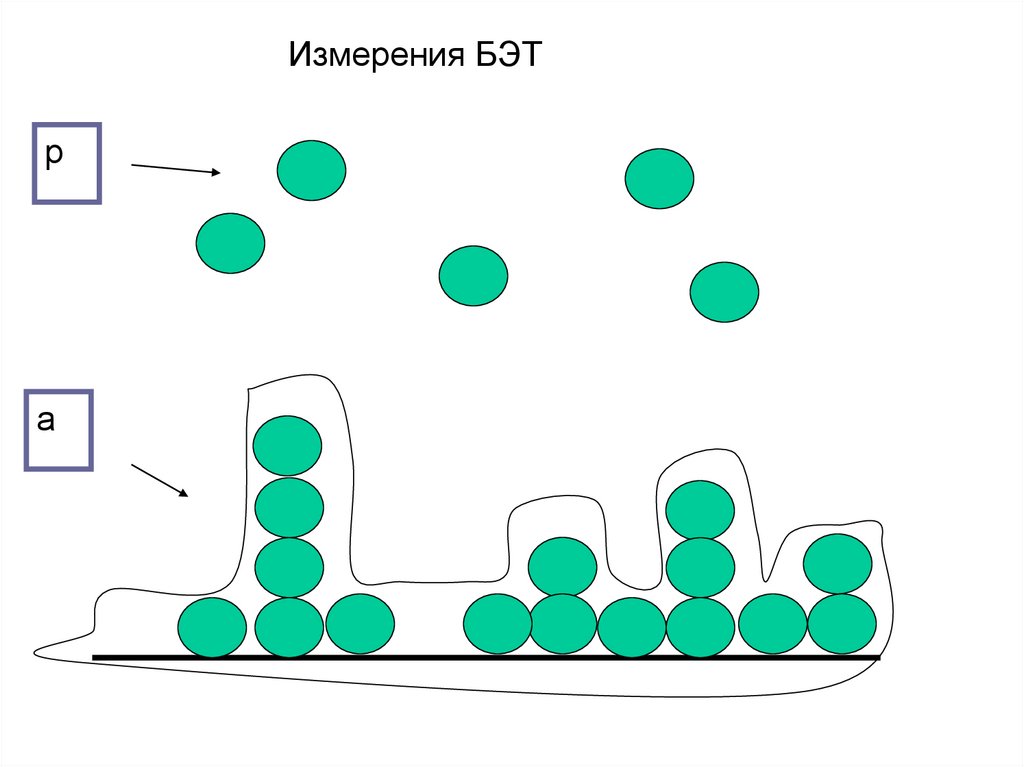
1. Модель БЭТ предполагает, что поверхность адсорбента
последовательно заполняется слоями адсорбата.
2. Во всех слоях, кроме первого, центрами адсорбции служат
молекулы адсорбированного вещества.
3. В модели БЭТ три параметра: К1 ,К2 и am .
4. Чтобы определить площадь поверхности образца по БЭТ,
нужно знать радиус сорбированной молекулы.
5. Модель БЭТ работает как для идеального, так и для реального
газа.
4.
Измерения БЭТр
a
5.
1p
1
a
ps
1
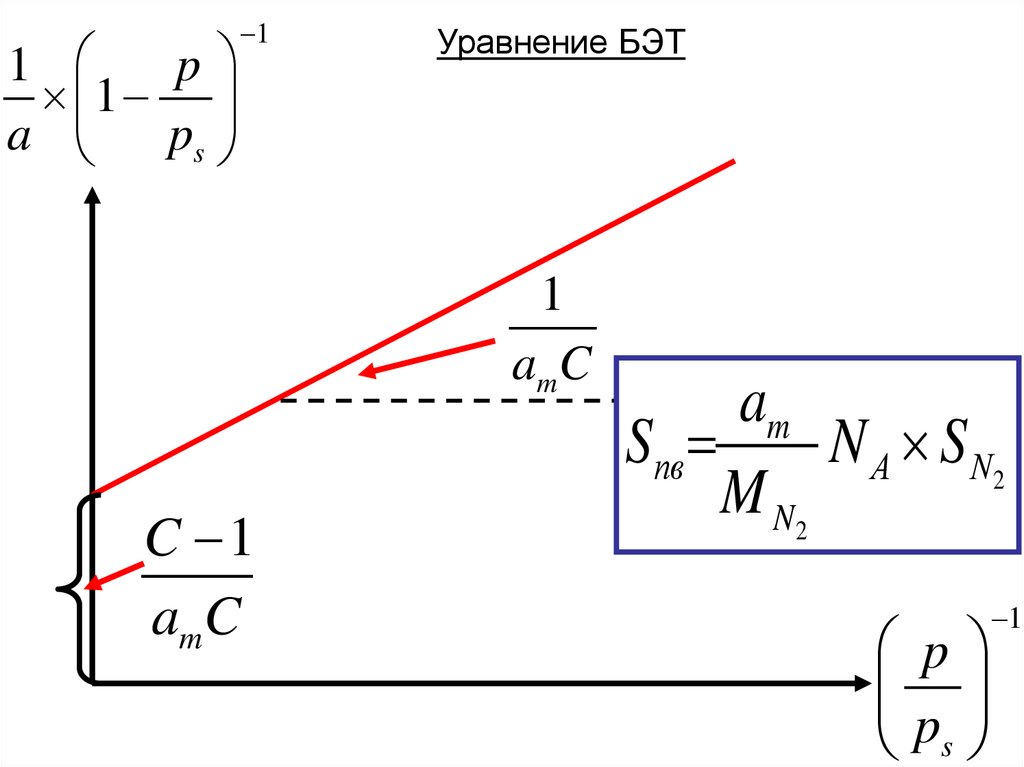
Уравнение БЭТ
1
am C
C 1
amC
am
Sпв
N A S N2
M N2
p
ps
1
6.
Выберите правильные утверждения2 балла
1. Константа равновесия любой химической реакции
зависит только от температуры.
2. Константа равновесия химической реакции с участием
реальных газов зависит от температуры и давления
3. Константа равновесия химической реакции определяется
выбором стандартных химпотенциалов продуктов и
реагентов.
4. Если хотя бы для одного участника реакции выбран
стандартный потенциал μᴓ, константа равновесия будет
меняться при смене растворителя.
d ln p Н
dT
RT 2
5. Уравнение Клаузиуса – Клайперона – это
7.
Уравнение Клаузиуса - Клапейронаd ln p Н
dT
RT 2
??
Только равновесия с участием
идеальных газов !
dp
Н ( II ) Н ( I )
S ( II ) S ( I )
( II )
!!
( II )
(I )
(I )
dT T V V V V
Равновесия: газ-жд.; газ-тв.; жд.-тв. тв.-тв.; жд.-жд.
8.
Химический потенциал компонента в однокомпонентнойсистеме обладает следующими свойствами
2 балла
Укажите правильный ответ !
1. Убывает с температурой при постоянном давлении.
2. Постоянен при постоянной температуре.
3. Возрастает с температурой при постоянном давлении.
4. В точке фазового перехода первого рода наблюдается скачок
химпотенциала.
5. Является парциальной мольной энтальпией.
9.
1баллаКонстанта равновесия реакции А+В =АВ в растворе
зависит от ….
Отметьте неправильное утверждение !!
1. температуры,
2. растворителя,
3. внешнего давления на раствор,
4. концентрации реагентов и продуктов,
5. выбора стандартных хим.потенциалов для продуктов и
реагентов.
10.
1 баллаТермодинамическая вероятность, W, по Больцману, это
1. Кинетическая энергия системы
2. Число микросостояний системы
3. Число макросостояний системы
4. Максимальное число микросостояний, доступных
системе при данных условиях (E,N – const)
5. Вероятность попасть в данное микросостояние.
11.
Сумма по состояниям частицы, Q, это:1 балла
1.
W
2.
i
n ln n n
i
i
i
5.
ze
i
i
i
i
i
3.
z e
i
i
i
N!
4.
i ni !
12.
Модель ячеек Больцмана.Расчет W
13.
Модель БольцманаN - общее число частиц; nr -число частиц на уровне r;
Ɛr - энергия частицы на уровне r
N n1 n2 n3 ...nr const
U E n1 1 n2 2 n3 3 ...nr r const
V const ; ni заданы, частицы различимы
N!
W
n1 ! n2 ! n3 !...nr !
14.
Модель БольцманаМетод неопределенных множителей Лагранжа
/ / d ni 0 ;
N const
i
/ / i dni 0;
U E const
i
ln ni dni dni ln zi dni 0
i
i
i
ln z1 ln n1 dn1 ....... ln zi ln ni dni ..
ln z1 1 ln n1 dn1 ln z2 2 ln n2 dn2
..... ln zi i ln ni dni 0
ln ni i ln zi 0;
ni zi e i
15.
Критика модели БольцманаРазличимость частиц
Формула Стирлинга
ln(N!) ≈ NlnN - N
Описание системы невзаимодействующих частиц?
16.
Статистика Бозе – Эйнштейнаи
Ферми-Дирака
17.
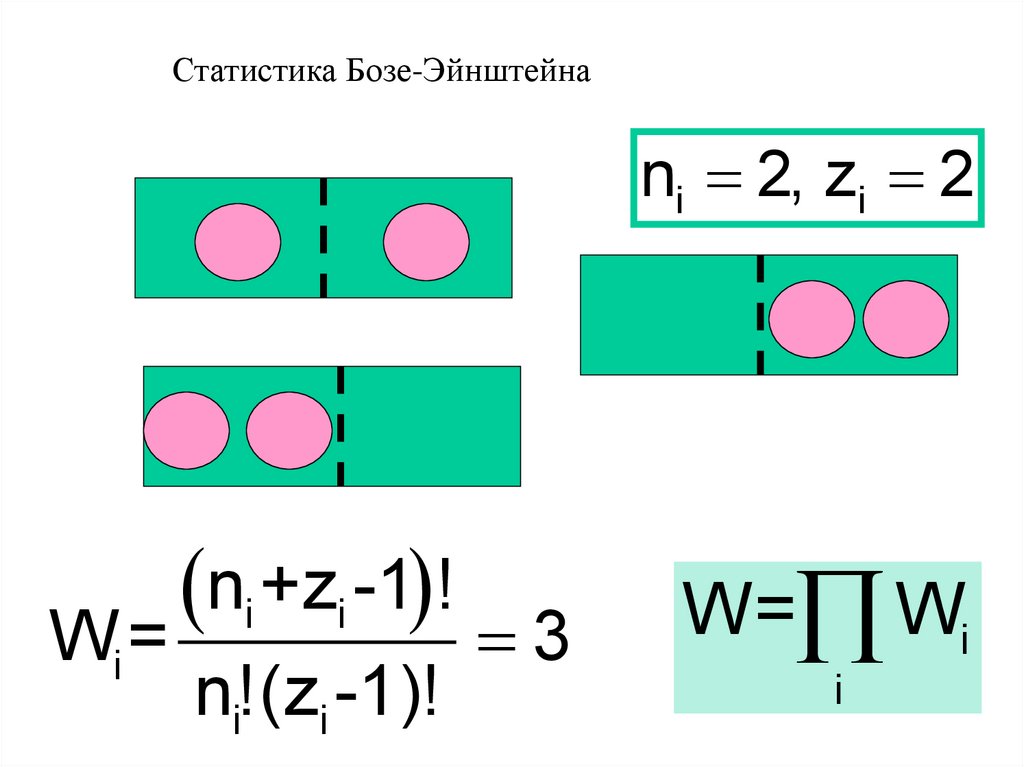
Статистика Бозе-Эйнштейнаni 2, zi 2
ni +zi -1 !
W=
3
i
n!(z
i
i -1)!
W= Wi
i
18.
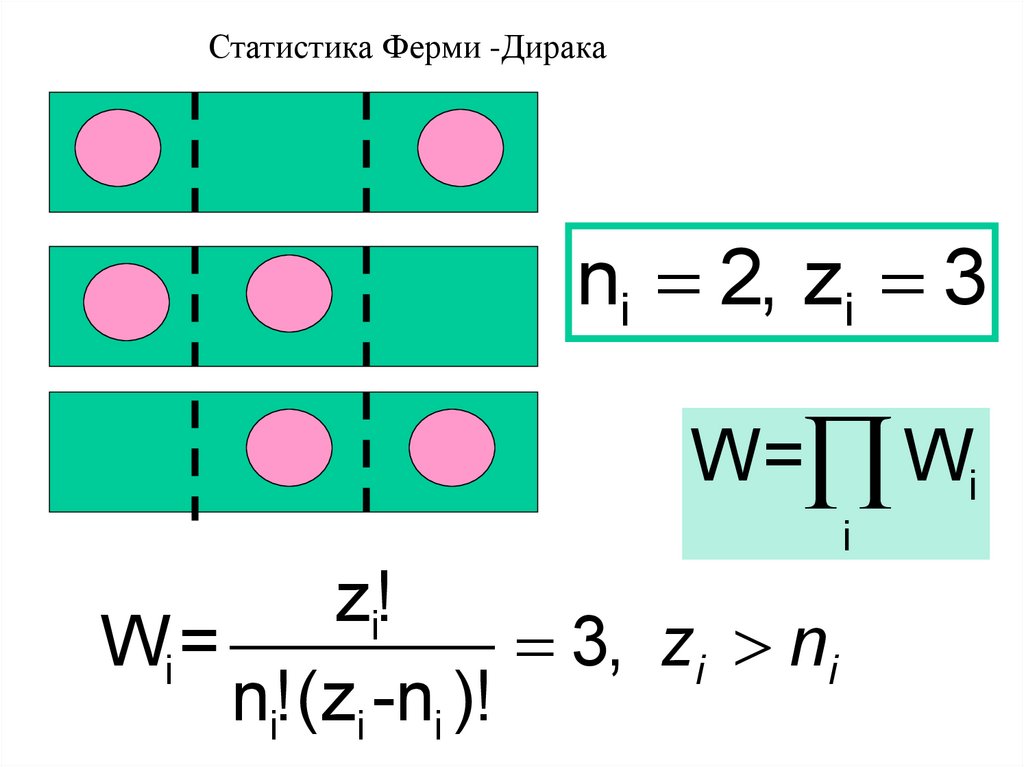
Статистика Ферми -Диракаni 2, zi 3
W= Wi
i
z!i
Wi =
3, zi ni
n!(z
i
i -ni )!
19.
БольцманБозе -Эйнштейн
Ферми-Дирак
ni
zi
i
e
ni
ni
zi
i
e
1
zi
i
e
1
20.
Фазовое пространство и ансамбли Гиббса21.
Микросостояния системы – это её «фазы»dw = ρ(p,q) dΓ
22.
Фазовое пространство….Пространство размерности (6+2f) NA
Координаты Г пространства:
(3+f) NA координат и (3+f) NA импульсов
Каждая точка фазового пространства –
микросостояние системы.
23.
Фазовое пространство….dw =ρ(p,q) dpdq
24.
Фазовое пространство…..dw =ρ(p,q) dpdq
dw =dn/N
25.
Фазовые пространства, плотность вероятности26.
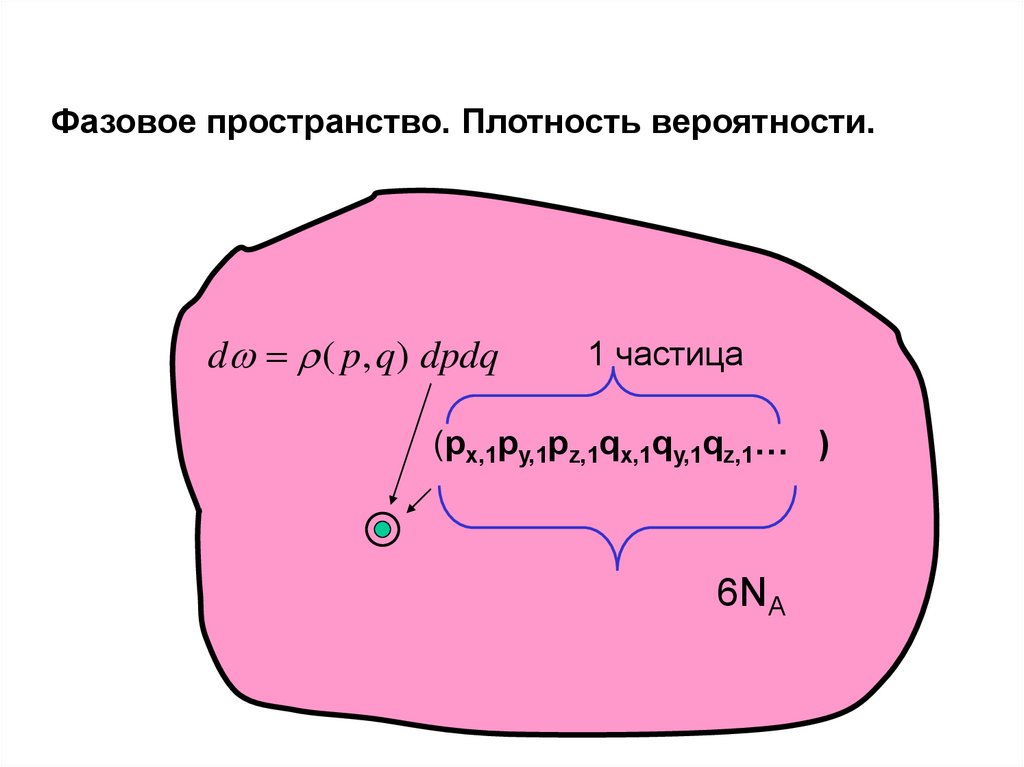
Фазовое пространство. Плотность вероятности.d ( p, q) dpdq
1 частица
(px,1py,1pz,1qx,1qy,1qz,1… )
6NA
27.
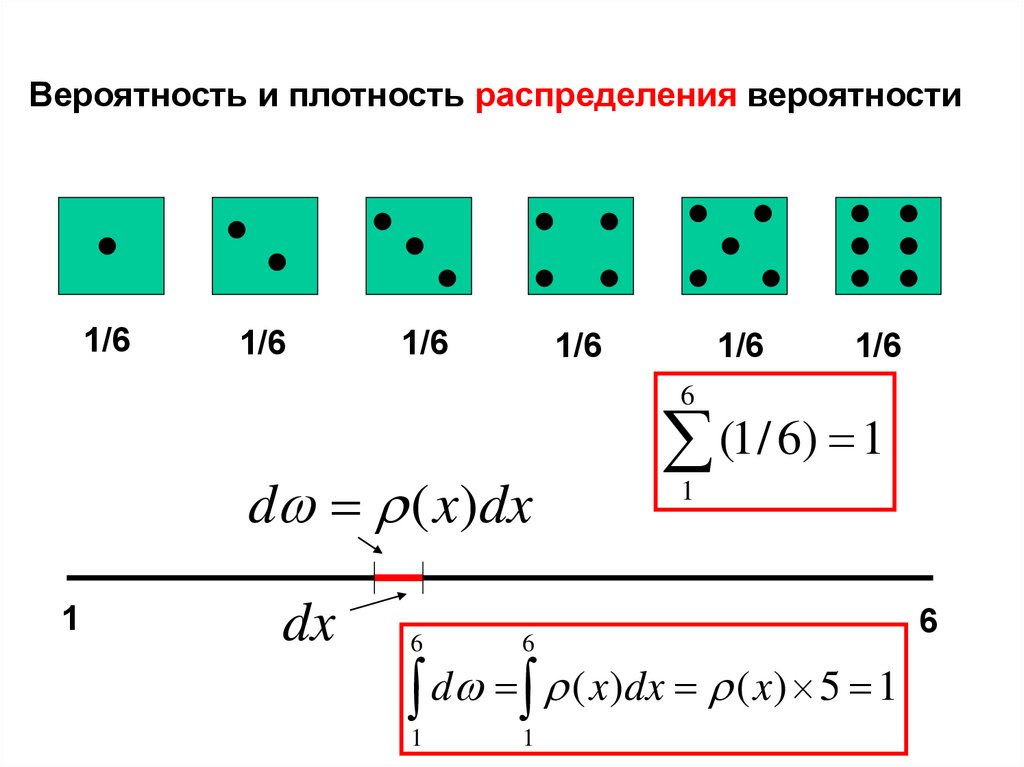
Вероятность и плотность распределения вероятности1/6
1/6
1/6
1/6
1/6
1/6
6
d ( x)dx
1
dx
6
6
1
1
(1/ 6) 1
1
d ( x)dx ( x) 5 1
6
28.
Свойства плотности вероятностиdw ( p, q )dpdq
( p, q) 0,
( p, q)dpdq 1
Г
q пространственные координаты, (3 f ) N
p mv импульсы, (3 f ) N
f внутренние координаты (колебания, вращение внутри молекулы)
29.
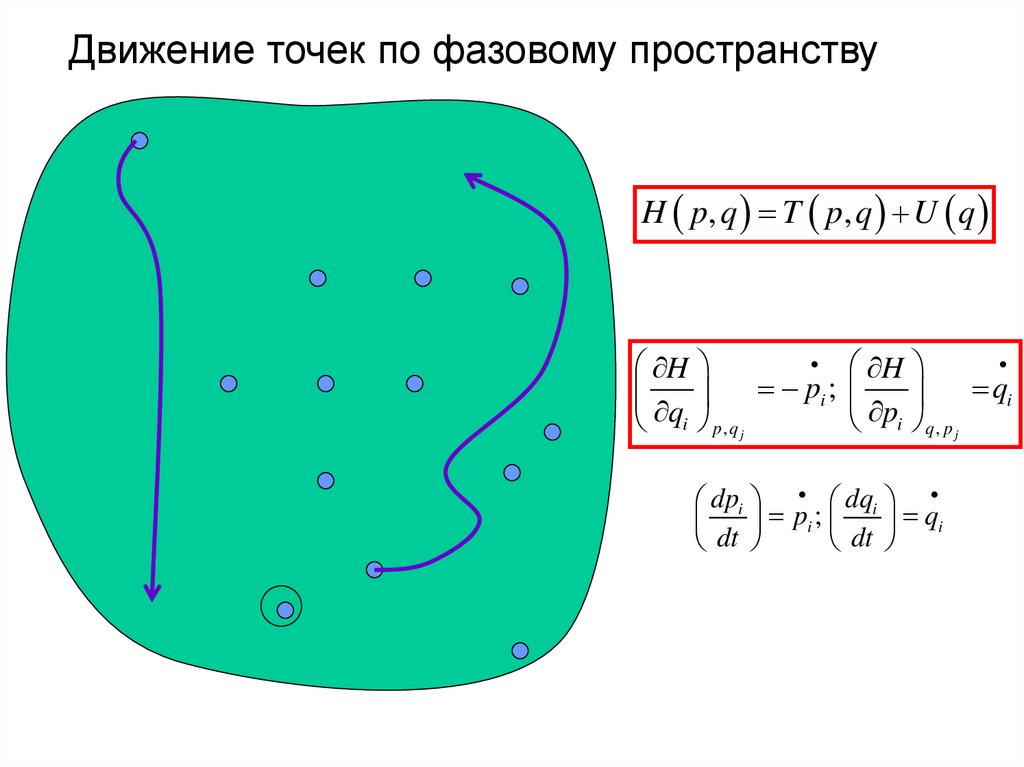
Движение точек по фазовому пространствуH p, q T p, q U q
H
H
pi ;
qi
qi p , q j
pi q , p j
dpi dqi
pi ;
qi
dt
dt
30.
В наших записях H(p,q) = E(p,q) !!31.
Плотность вероятности в фазовомпространстве.
( p, q, t ) 0
Е p, q теорема Лиувилля
0
t p ,q
32.
y f sin x ;y ( x)
( E p , q ) p , q
33.
( р, q ) Е p, qМикросостояния с равной энергией равновероятны.
Плотность вероятности в точках фазового пространства
с равной энергии одинакова.
Вероятность обнаружить систему в микросостояниях
с равной энергией одинакова.
34.
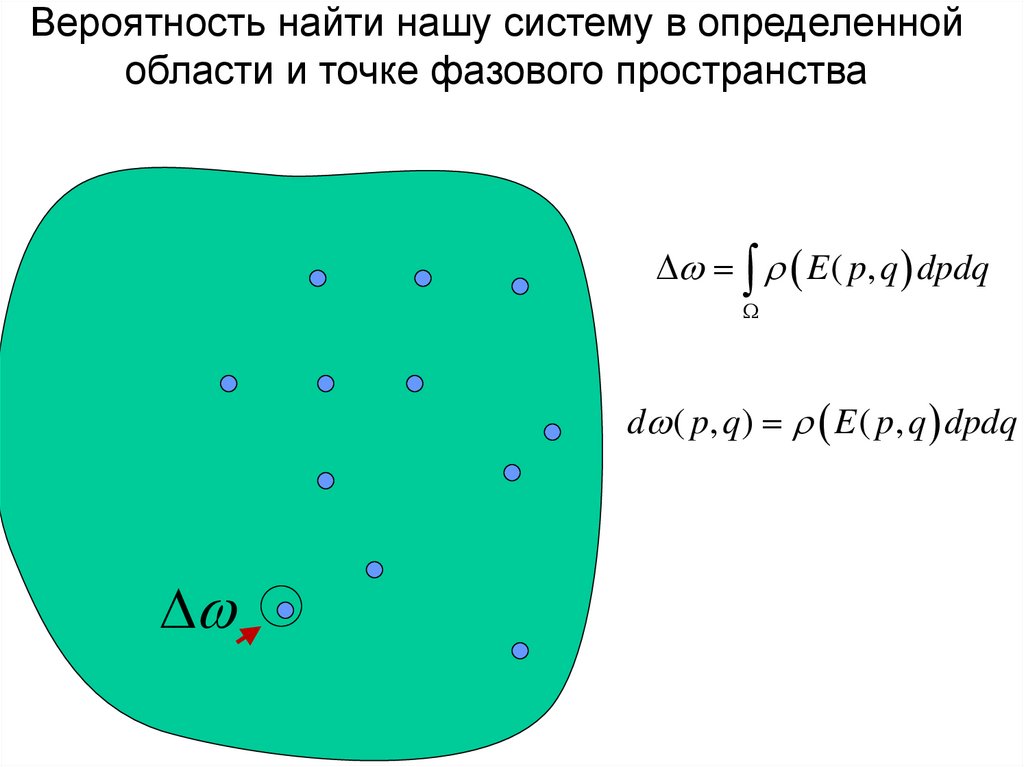
Вероятность найти нашу систему в определеннойобласти и точке фазового пространства
E ( p, q dpdq
d ( p, q ) E ( p, q dpdq
35.
Средние величиныF
i
Средняя по времени :
i
ni
F
Средняя по ансамблю : F F ( p, q ) ( p, q ) dpdq
Г
36.
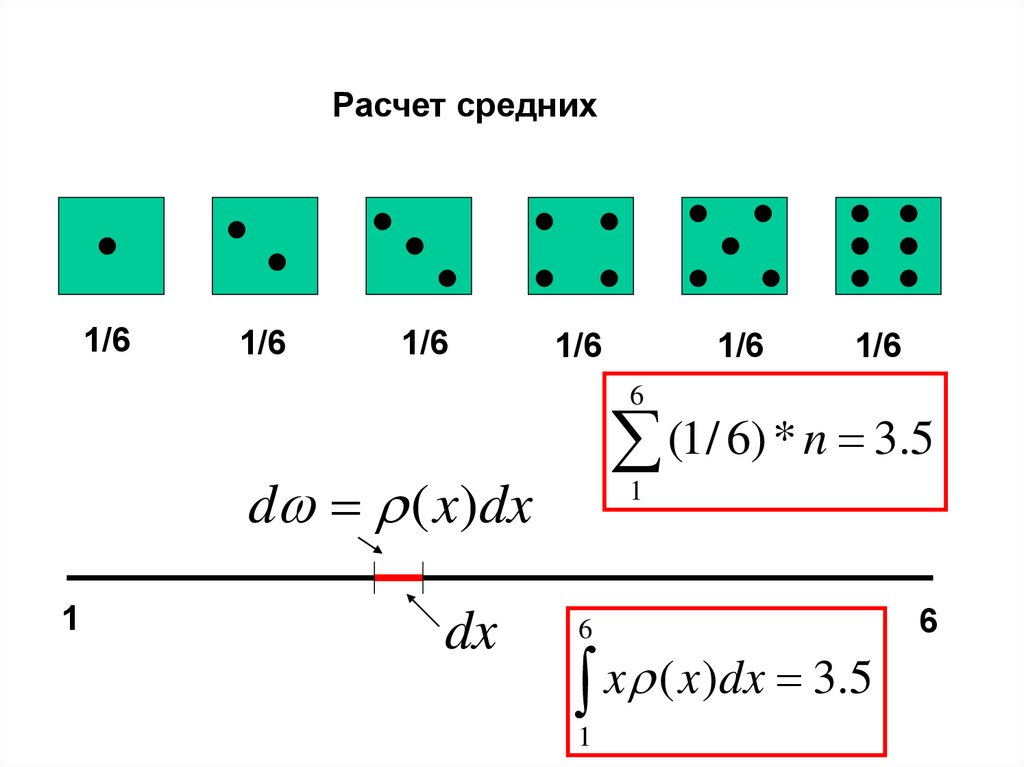
Расчет средних1/6
1/6
1/6
1/6
1/6
1/6
6
(1/ 6) * n 3.5
d ( x)dx
1
dx
1
6
x ( x)dx 3.5
1
6
37.
Эргоидная гипотеза.Среднее по времени для системы
равняется среднему по ансамблю систем.
38.
Эргоидная гипотеза.Среднее по времени для системы
равняется среднему по ансамблю систем.
Система
Ансамбль систем
j
0
t
C
1
j
t C0
t C0
Студ.
t C 0 (Студ.) d Cтуд.
39.
Квазиклассическое выражение для плотности вероятности40.
Квазиклассическое приближениеdpdq
общее число микросостояний ??
p,q
{dp1dq1 , dp2 dq2 ............dp7 dq7 }..................{dp7 dq7 , dp2 dq2 ............dp1dq1}
1
dpdq общее число микросостояний
N! N!
41.
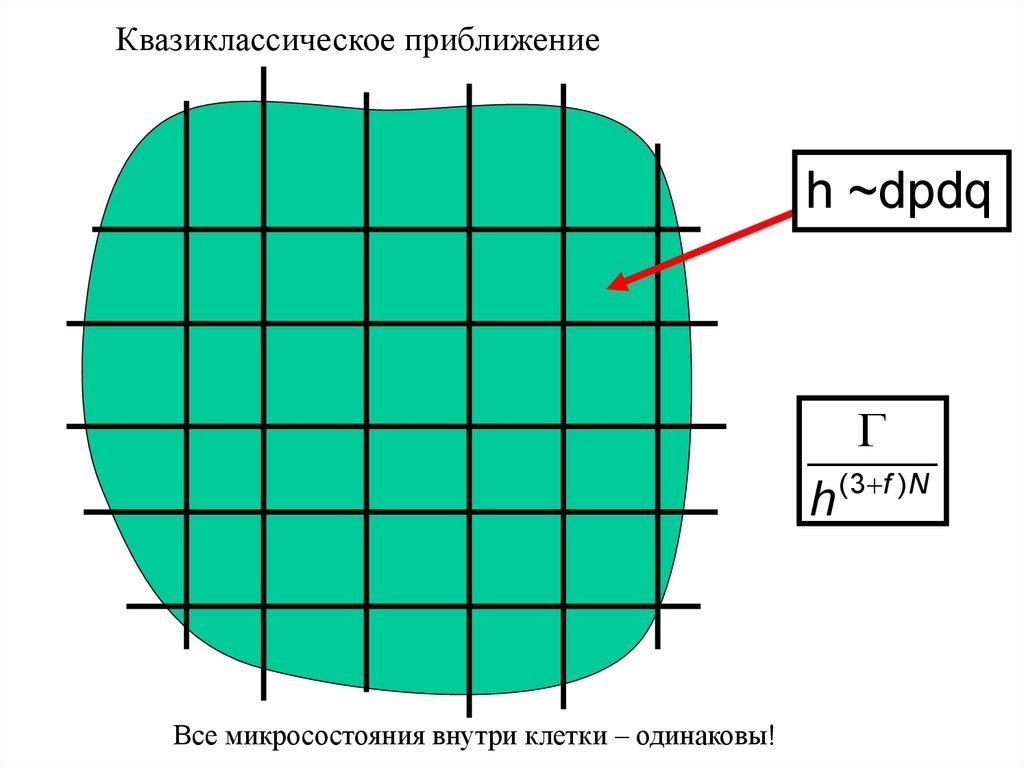
Квазиклассическое приближениеh ~dpdq
h
Все микросостояния внутри клетки – одинаковы!
(3 f )N
42.
Квазиклассическое приближениеdpdq
d
N (3 f ) d
N (3 f )
h
N! h
N!
N (3 f )
N (3 f )
dqdp
h
i 1
Вероятность попасть в клетку {p,q}
dw( p, q ) c d N !h N (3 f ) c
dpdq
dpdq
cc d
cc
N (3 f )
N (3 f )
N !h
N !h
N !h c ( E ( p, q )) cc ( E ( p, q ))
Nf
43.
АнсамблиАнсамбль – это фазовое пространство
с заданной плотностью вероятности ρ(E(p,q)
44.
Микроканонический ансамбль( p, q) ( E0 E ( p, q) E0 E ) const
( p , q ) d 1 ( p, q ) d ( p , q )
p,q
p,q
S k ln W k ln k ln ( E ( p, q ))
Система с одинаковой энергией во всех микросостояниях
45.
Каноническое распределениеE ( p, q ) e
E p,q
Простейшее… для системы, состоящей из
невзаимодействующих частей, каждая часть
будет распределена по такому же закону.
…служит основой для установления связей с
термодинамикой
46.
Что такое канонический ансамбль?47.
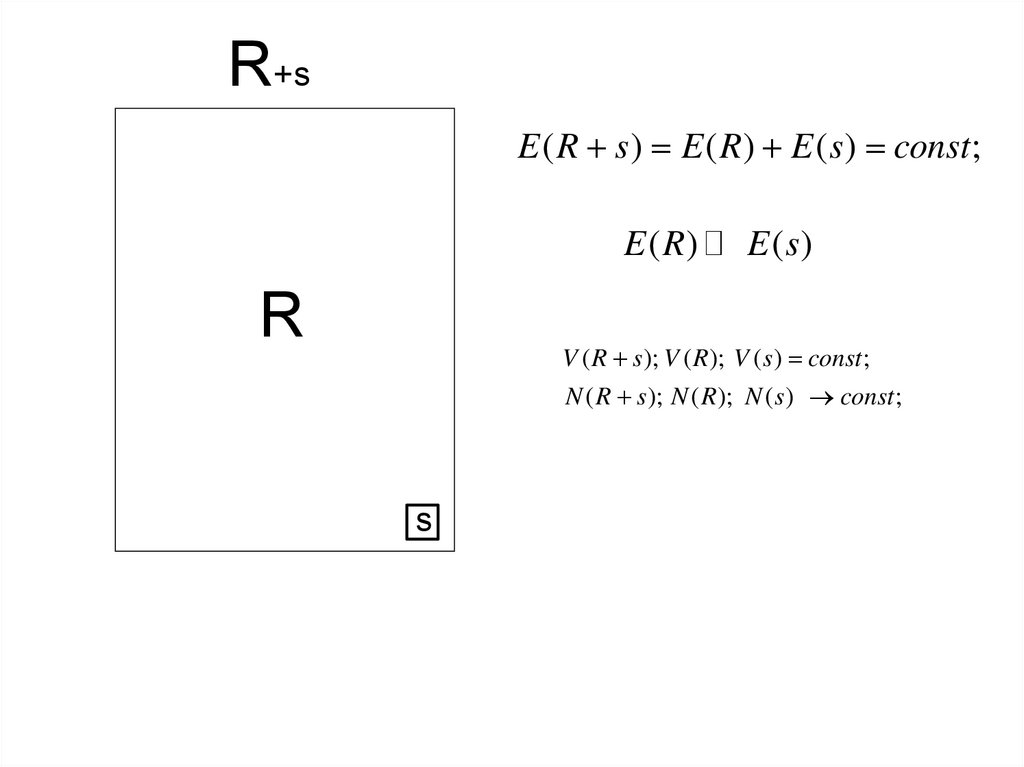
R+sE ( R s ) E ( R ) E ( s ) const ;
E ( R)
R
E (s)
V ( R s ); V ( R ); V ( s ) const ;
N ( R s ); N ( R ); N ( s ) const ;
s
48.
Канонический ансамбльE ( p, q ) E ( p1 , q1 ) E ( p2 , q2 ) const ;
dE ( p, q ) dE ( p1 , q1 ) dE ( p2 , q2 ) 0;
dE ( p1 , q1 ) dE ( p2 , q2 )
( E ( p, q)) ( E ( p1 , q1 )) ( E ( p2 , q2 ))
ln ( E ( p, q)) ln ( E ( p1 , q1 )) ln ( E ( p2 , q2 ))
d ln E p, q
dE
dE
d ln E p1 , q1
d ln E p1 , q1
dE p1 , q1
dE p1 , q1
dE p1 , q1
d ln E p2 , q2
dE p2 , q2
d ln E ( p, q ) E p2 , q2
dE p1 , q1
dE p2 , q2 0
d ln E p2 , q2
ln E p2 , q2 E p2 , q2
dE p2 , q2
49.
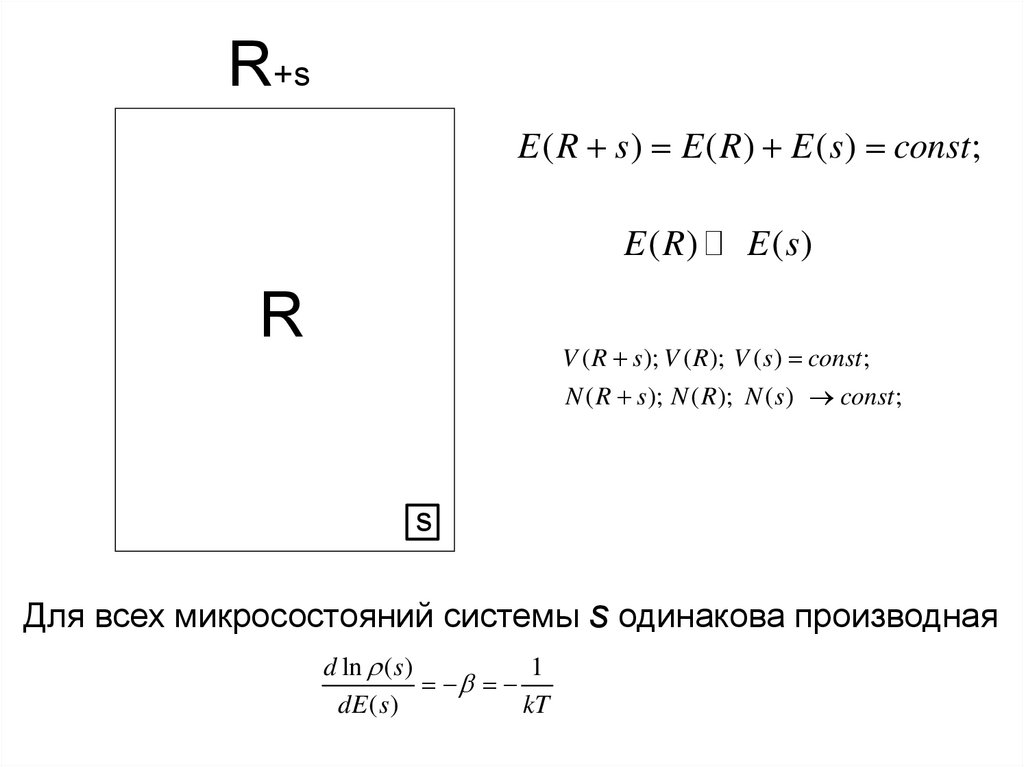
R+sE ( R s ) E ( R ) E ( s ) const ;
E ( R)
R
E (s)
V ( R s ); V ( R ); V ( s ) const ;
N ( R s ); N ( R ); N ( s ) const ;
s
Для всех микросостояний системы s одинакова производная
d ln ( s )
1
dE ( s )
kT
50.
Канонический ансамбльln E ( p, q ) E ( p, q)
Е ( p, q ) e E ( p , q )
E ( p , q )
Е
(
p
,
q
)
d
1
e
d
1 e
e
E ( p ,q )
1
d ; e e E ( p ,q ) d Z
e
Z e E ( p ,q ) d
Q zi e i
51.
Канонический ансамбльE ( p , q ) e e E ( p , q ) ;
Z e e
E ( p,q)
d
1 E ( p,q)
p, q e
; ln p, q ln Z E ( p, q )
Z
52.
Канонический ансамбльS k ln ( E0 ( p, q ))
микроканонический ансамбль
S k ln ( p, q ) k ln p, q p, q d
ln p, q ln Z E ( p, q )
S k ln
1
p, q d k ln e E ( p ,q ) p, q d
Z
k ln Z k E ( p, q ) p, q d k ln Z k E ( p, q )
S k ln ( p, q ) k ln Z k E ( p, q )
53.
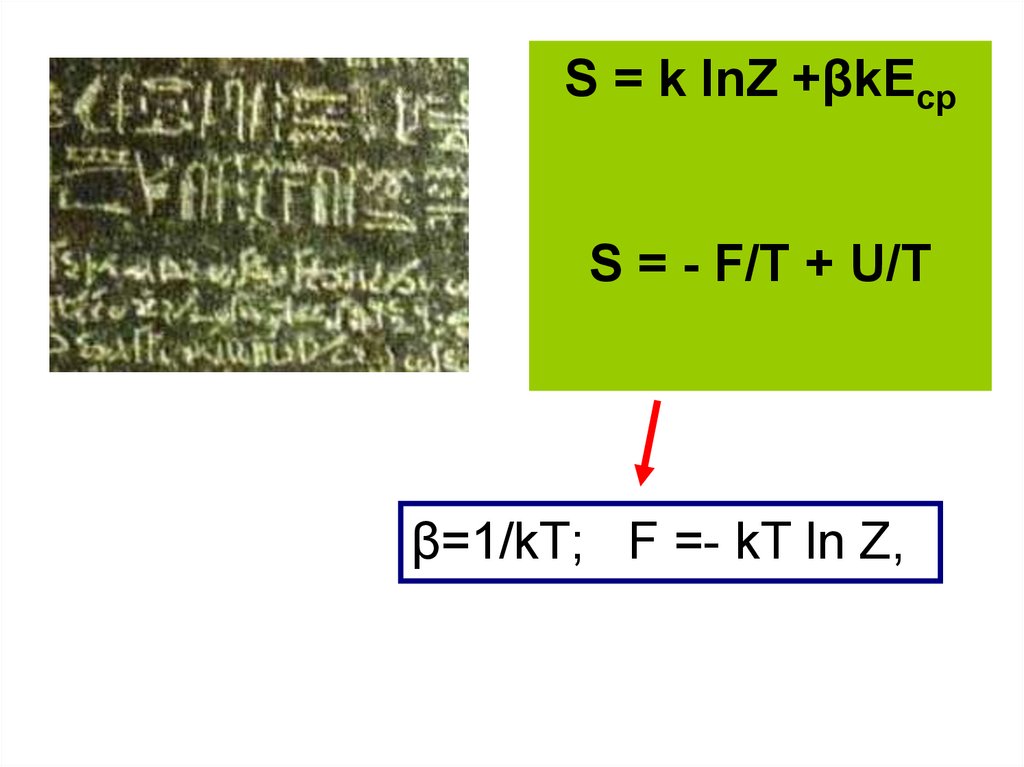
S = k lnZ +βkEсрS = - F/T + U/T
β=1/kT; F =- kT ln Z,
54.
Канонический ансамбльS k ln ( p, q ) k ln Z k E ( p, q );
k ln Z S kU
F U TS ;
F
U
S
T
T
F kT ln Z ;
1
( p, q ) e
Z
1
kT
E ( p,q)
kT
55.
Канонический ансамбльF kT ln Z ;
1
kT
F
kT ln Z
ln Z
S
k ln Z kT
T V , n T V , n
T V , n
ln Z
2 ln Z
U F TS kT ln Z kT ln Z kT
kT
T
T
V , n
V , n
2
2
U
ln Z
2 ln Z
сv
2kT
kT
2
T
T
T
V , n
V , n
V , n














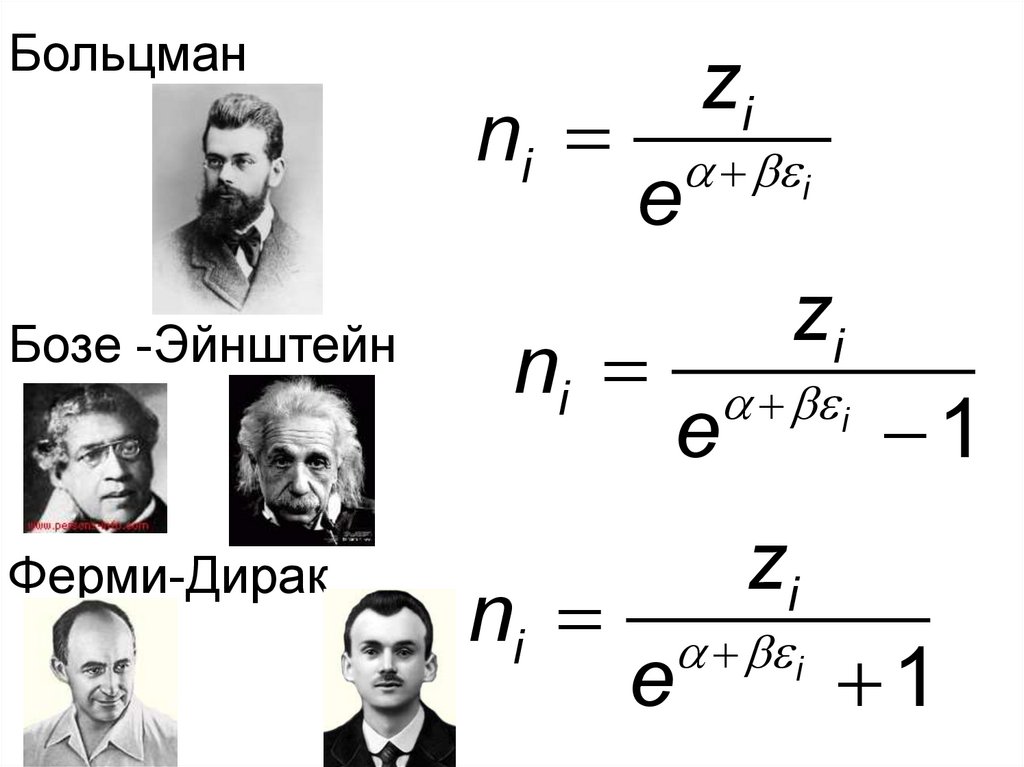









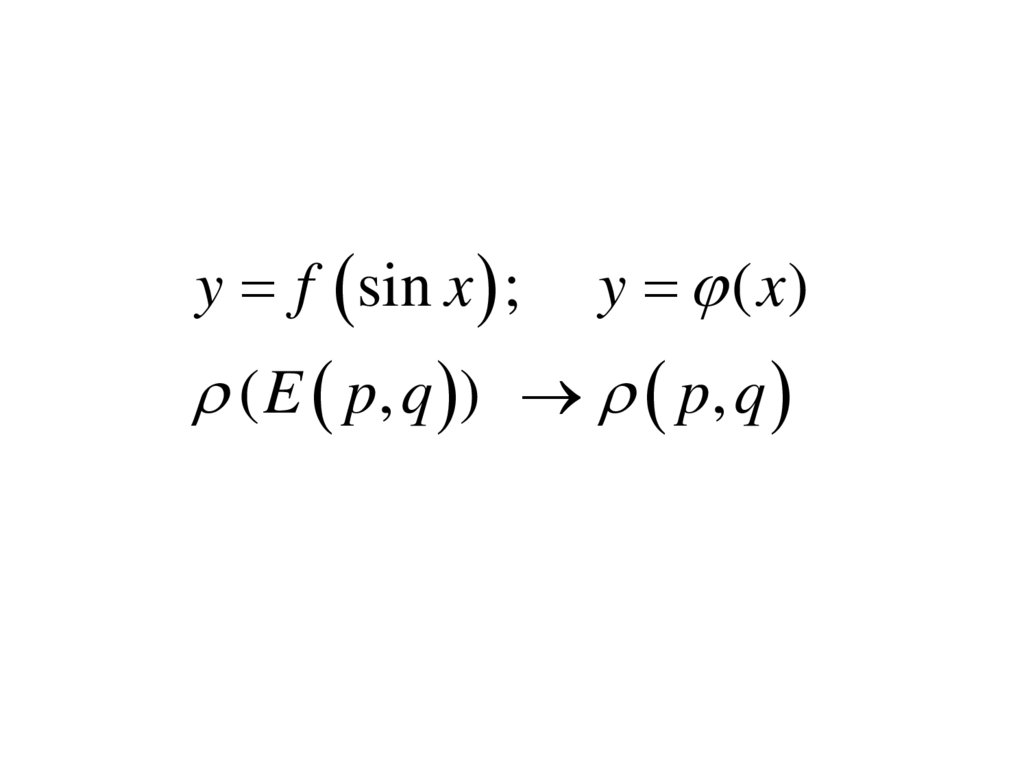

















 physics
physics








