Similar presentations:
Декодирование линейных групповых кодов
1. Декодирование линейных групповых кодов
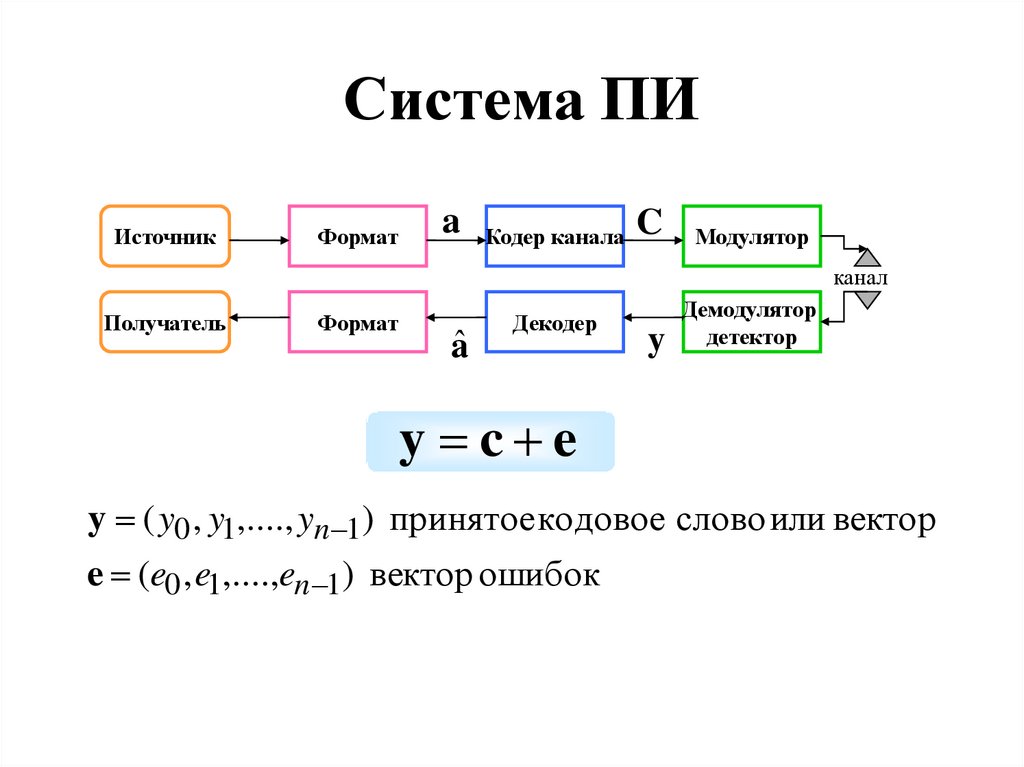
2. Система ПИ
ИсточникФормат
a
Кодер канала
C
Модулятор
канал
Получатель
Формат
â
Декодер
y
Демодулятор
детектор
y c e
y ( y0 , y1,...., yn 1) принятое кодовое слово или вектор
e (e0 , e1,....,en 1) вектор ошибок
3. Декодирование по смежным классам
Нулевое
Кодовое слово
Таблица смежных классов
n k
- Для строк i 1,2,...,q
1 находим ранее не
использованный вектор из Vn минимального веса.
- Обозначим такой вектор как e i вектор-ошибок и образуем на
его основе i-ю строку – смежный класс
c0
c1
e1
e1 c1
c k
2 1
e1 c k
2 1
Смежный класс
e n k
e n k c1 e n k c k
2
1
2
1
2
1
2 1
Лидеры смежных классов
4. Декодирование по МП
5. Каким образом действует декодер?
Ищет в таблице полученное на выходеканала связи слово y, например, y = (1101)
Принимает решение, что вектор ошибок
e – это лидер класса смежности, содержащего
вектор y, т. е. e = (1000).
Далее вектор y декодируется в вектор
• c = y – e = (1101)+(1000)=(0101)
• и делается вывод, что исходно сообщение
равно a = (01)
6. Синдром
• Синдром (отображение ошибок):– S является синдромом y, соответствующий
отображению вектора ошибок e в H.
T
T
S yH eH
7. Свойства синдрома
• 1 Если проверочная матрица имеет(n – k),то синдром s произвольного вектора y
является вектором длины (n – k).
• 2.Поскольку по определению линейного
кода вектор y является кодовым тогда и
только тогда, когда yHT = 0, то
справедливы следующие утверждения
8. Утверждения
• Утверждение. Синдром s вектора yравен 0 тогда
только тогда, когда
является кодовым вектором
• Утверждение. Для двоичного линейного
кода синдром s принятого вектора y
равен сумме тех столбцов проверочной
матрицы H, где произошли ошибки.
9. Док-во
Док-во
Пусть получен вектор y = c + e.
По определению синдрома
s = yHT = eHT
Пусть e имеет ошибки «1» в координатах с номерами
i1 , i2 ,...,iv
T
v
eH ei j h i j h i1 h i2 ... h iv
j 1
• Тогда имеем
h i j – это ij – столбец матрицы H.
v
s hi j
• Следовательно,
j 1
• синдром выделяет те позиции вектора, где произошли
ошибки.
10. Алгоритм декодирования
Составляются таблицы смежных классов и
синдромов
T
S
yH
1. Вычисляется
2. Находится лидер смежного класса eˆ ei ,
соответствующий S
3. По синдрому вычисляют оценку cˆ y eˆ и
оценку информации â .
– Заметим, что
cˆ y eˆ (c e) eˆ c (e eˆ )
если eˆ e, то ошибка исправляемая.
если eˆ e, появляется не исправляемая ошибка.
11. Пример
• Таблица смежных классов для кода (6,3)Кодовые слова
000000
110100
011010
101110
101001
011101
110011
000111
000001
110101
011011
101111
101000
011100
110010
000110
000010
110111
011000
101100
101011
011111
110001
000101
000100
110011
011100
101010
101101
011010
110111
000110
001000
111100
010000
100100
Смежный класс
100000
010100
010001
100101
Лидеры смежных классов
010110
12. Пример таблица синдромов
Вектора ошибок Синдромc (101110) Кодовоеслово, переданное.
000000
000
000001
101
000010
011
Синдром y вычисляется как :
000100
110
S yH T (001110) HT (100)
001000
001
010000
010
100000
100
Оценка ошибки для этого значения синдрома равна
eˆ (100000)
010001
111
y (001110)
Принятый вектор.
Оценка принятого кодового слова после коррекции
сˆ y eˆ (001110) (100000) (101110)
13. Пример
Все ошибки веса (dmin – 1)/2 имеют уникальный синдромСиндром Лидер см кл
Кодовые слова













 programming
programming








