ЕГЭ-2022. Разбор задания 4 информатика

1.

ЕГЭ-2022
РАЗБОР ЗАДАНИЯ 4
ИНФОРМАТИКА
Кодирование и декодирование информации

2.

Введение
В данном уроке мы рассмотрим такие понятия как «Условие Фано»
и «Префиксный код» , научимся строить бинарные деревья, а так
же рассмотрим разные типы задач на тему «Кодирование и
декодирование информации».

3.

ТЕОРИЯ
Условие Фано и Префиксный код

4.

Условие Фано
Прямое условие Фано.
Неравномерный код может быть однозначно
декодирован, если никакой из кодов не совпадает с
началом (префиксом) какого-либо другого, более
длинного кода.
Такой код называют «префиксным».

5.

Условие Фано
Обратное условие Фано.
Неравномерный код может быть однозначно
декодирован, если никакой из кодов не совпадает с
окончанием (постфиксом) какого-либо другого, более
длинного кода.
Такой код называют «постфиксным».

6.

Префиксный код
Префиксный код— код со словом переменной длины, имеющий такое свойство (выполнение
условия Фано): если в код входит слово a, то для любой непустой строки b слова ab в коде не
существует.
Например, код, состоящий из слов 0, 10 и 11, является префиксным, и сообщение 01001101110 можно
разбить на слова единственным образом:
0 10 0 11 0 11 10
Код, состоящий из слов 0, 10, 11 и 100, префиксным не является, и то же сообщение можно трактовать
несколькими способами.
0 10 0 11 0 11 10
0 100 11 0 11 10

7.

Бинарное дерево
Бинарное дерево— это иерархическая структура данных, в которой каждый
узел имеет значение и ссылки на левого и правого потомка. Узел,
находящийся на самом верхнем уровне называется корнем. Узлы, не
имеющие потомков называются листьями.

8.

Бинарное дерево. Термины
◦ Узел (вершина) — это каждый элемент бинарного дерева;
◦ Ветви — связи между узлами;
◦ Глубина (высота) — наибольший уровень какого-нибудь элемента;
◦ Лист (терминальный узел) — термин применяется, если элемент не имеет потомков;
◦ Внутренние узлы — узлы ветвления;
◦ Степень внутреннего узла — число его потомков (наибольшая степень всех
существующих узлов — это степень всего бинарного дерева);
◦ Длина пути к x — количество ветвей, которые необходимо пройти от корня до текущего
узла x. Длина пути самого корня равна нулю, а узел на уровне i обладает длиной пути,
которая равна i.

9.

Построение
Бинарного
дерева
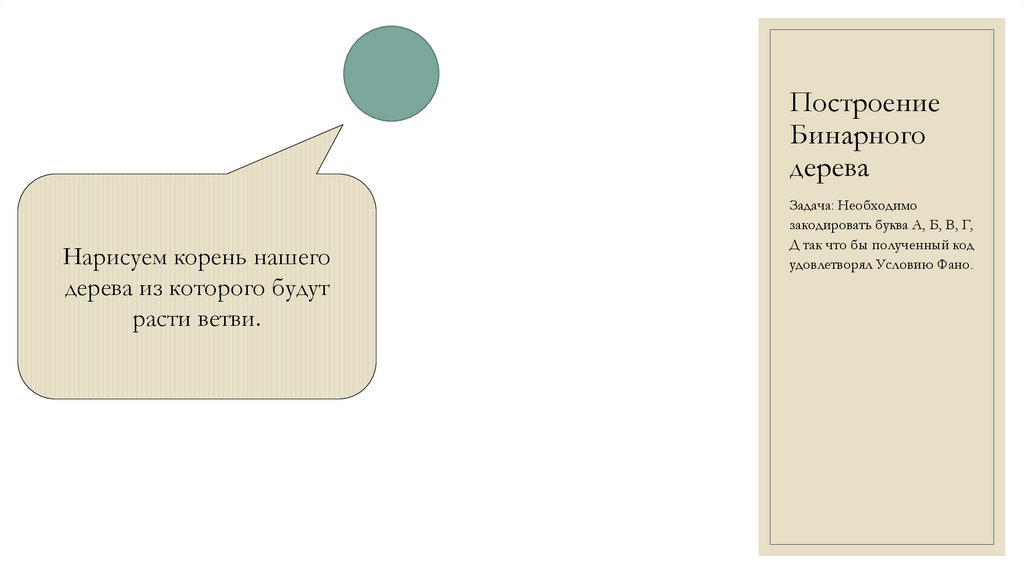
Нарисуем корень нашего
дерева из которого будут
расти ветви.
Задача: Необходимо
закодировать буква А, Б, В, Г,
Д так что бы полученный код
удовлетворял Условию Фано.

10.

Построение
Бинарного
дерева
Задача: Необходимо
закодировать буква А, Б, В, Г,
Д так что бы полученный код
удовлетворял Условию Фано.
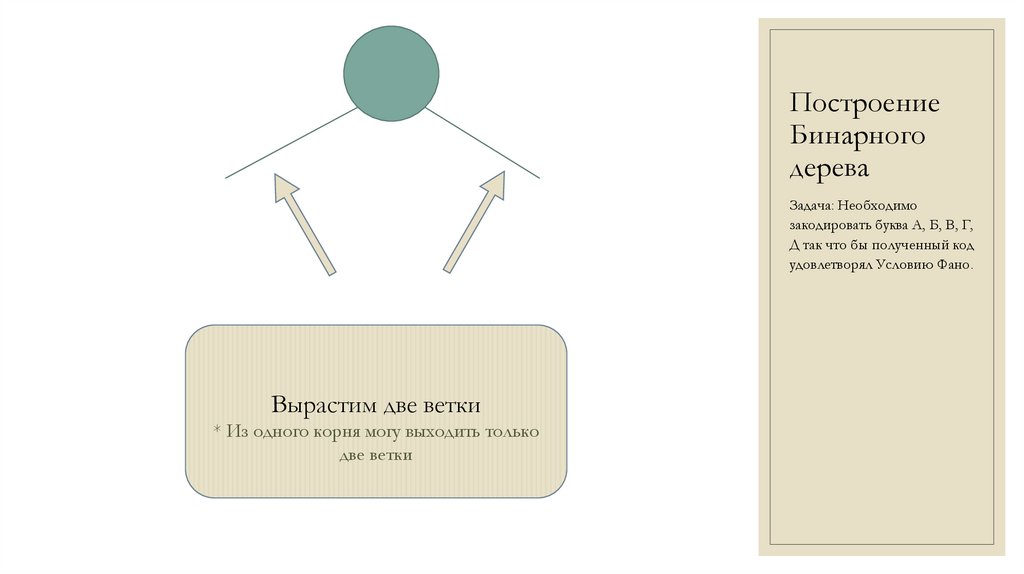
Вырастим две ветки
* Из одного корня могу выходить только
две ветки

11.

0
1
Построение
Бинарного
дерева
Задача: Необходимо
закодировать буква А, Б, В, Г,
Д так что бы полученный код
удовлетворял Условию Фано.
Пронумеруем ветки двоичным
кодом слева → направо

12.

0
1
Построение
Бинарного
дерева
Задача: Необходимо
закодировать буква А, Б, В, Г,
Д так что бы полученный код
удовлетворял Условию Фано.
Вырастим два листика.
В дереве появилось два места
для двух букв.

13.

0
1
Построение
Бинарного
дерева
Задача: Необходимо
закодировать буква А, Б, В, Г,
Д так что бы полученный код
удовлетворял Условию Фано.
Как мы видим место больше нет что
бы добавить листик дерева.
В этом случаем листик превращаем
в узел и растим ещё две ветки.

14.

0
1
Построение
Бинарного
дерева
Задача: Необходимо
закодировать буква А, Б, В, Г,
Д так что бы полученный код
удовлетворял Условию Фано.
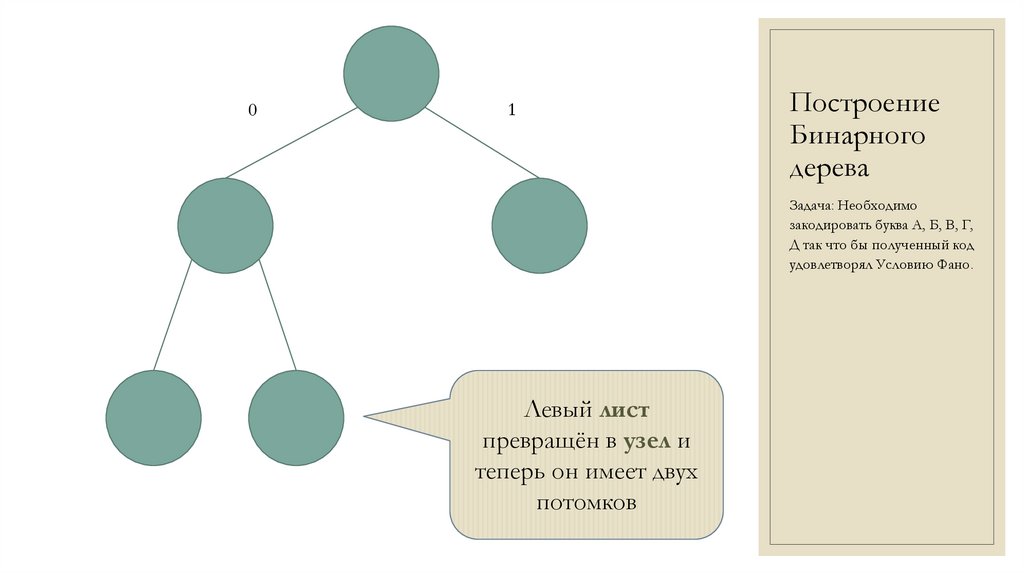
Левый лист
превращён в узел и
теперь он имеет двух
потомков

15.

1
0
Построение
Бинарного
дерева
Задача: Необходимо
закодировать буква А, Б, В, Г,
Д так что бы полученный код
удовлетворял Условию Фано.
0
1
И пронумерую ветки
двоичным кодом
слева → направо

16.

1
0
Построение
Бинарного
дерева
Задача: Необходимо
закодировать буква А, Б, В, Г,
Д так что бы полученный код
удовлетворял Условию Фано.
0
1
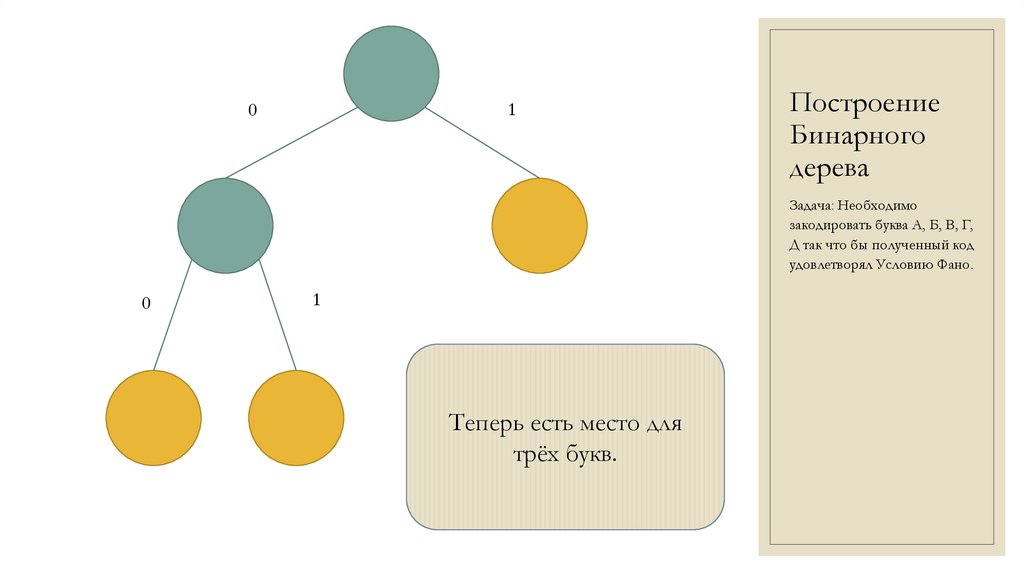
Теперь есть место для
трёх букв.

17.

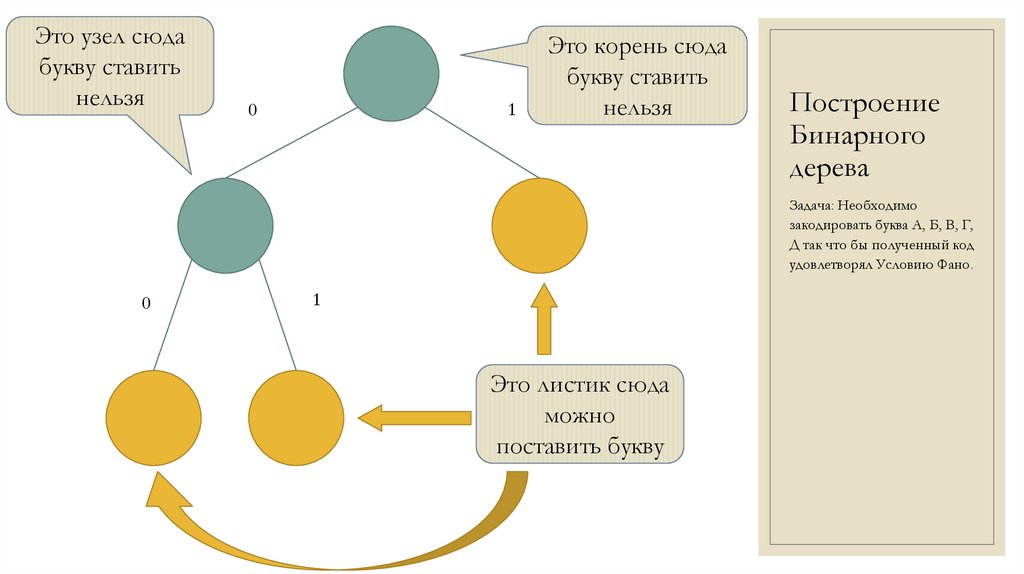
Это узел сюда
букву ставить
нельзя
1
0
Это корень сюда
букву ставить
нельзя
Построение
Бинарного
дерева
Задача: Необходимо
закодировать буква А, Б, В, Г,
Д так что бы полученный код
удовлетворял Условию Фано.
0
1
Это листик сюда
можно
поставить букву

18.

1
0
Построение
Бинарного
дерева
Задача: Необходимо
закодировать буква А, Б, В, Г,
Д так что бы полученный код
удовлетворял Условию Фано.
0
1
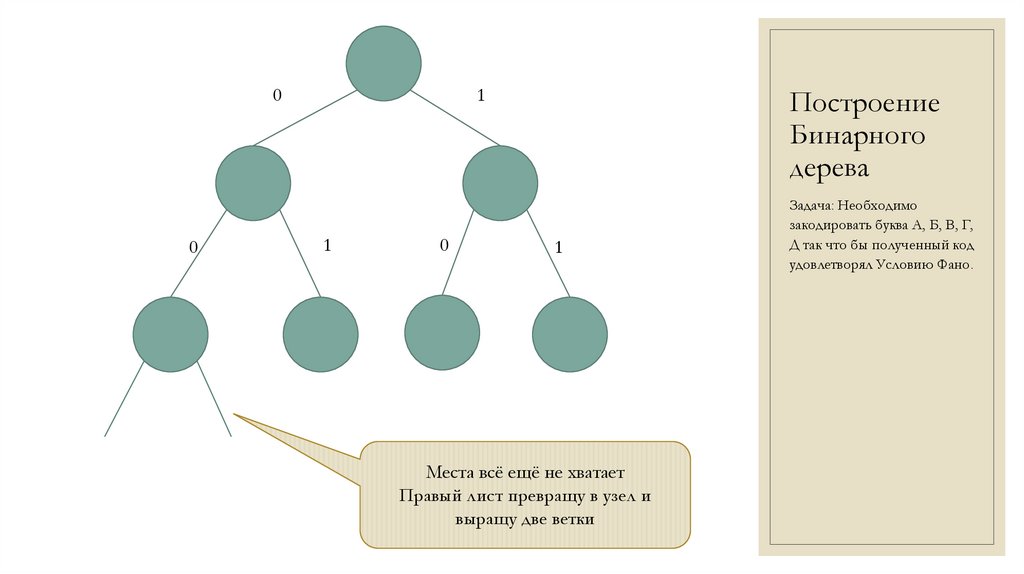
Места всё ещё не хватает
Правый лист превращу в
узел и выращу две ветки.

19.

Построение
Бинарного
дерева
1
0
Задача: Необходимо
закодировать буква А, Б, В, Г,
Д так что бы полученный код
удовлетворял Условию Фано.
0
1
0
1
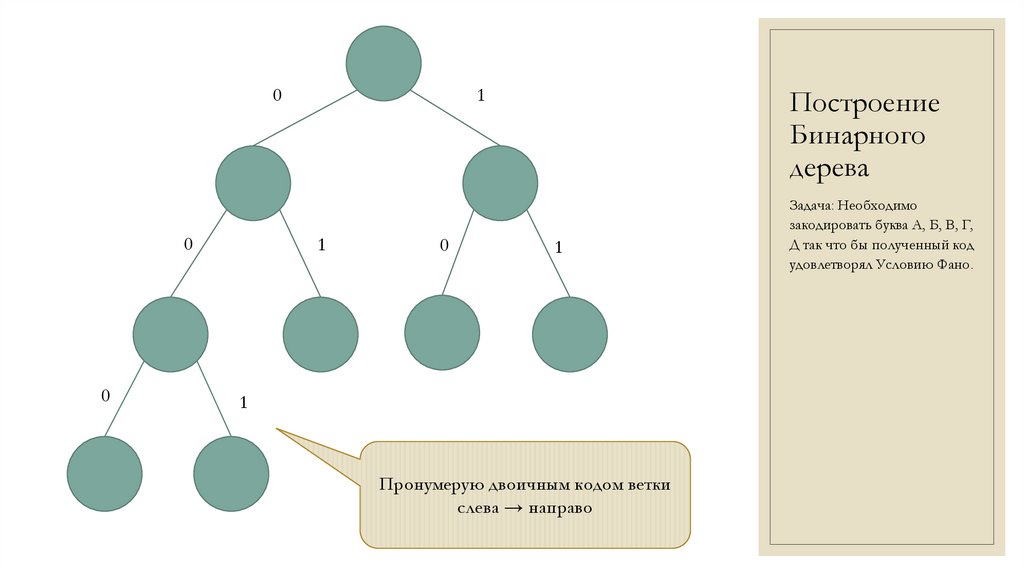
Пронумеруем ветки
двоичным кодом
слева → направо

20.

1
0
Построение
Бинарного
дерева
Задача: Необходимо
закодировать буква А, Б, В, Г,
Д так что бы полученный код
удовлетворял Условию Фано.
0
1
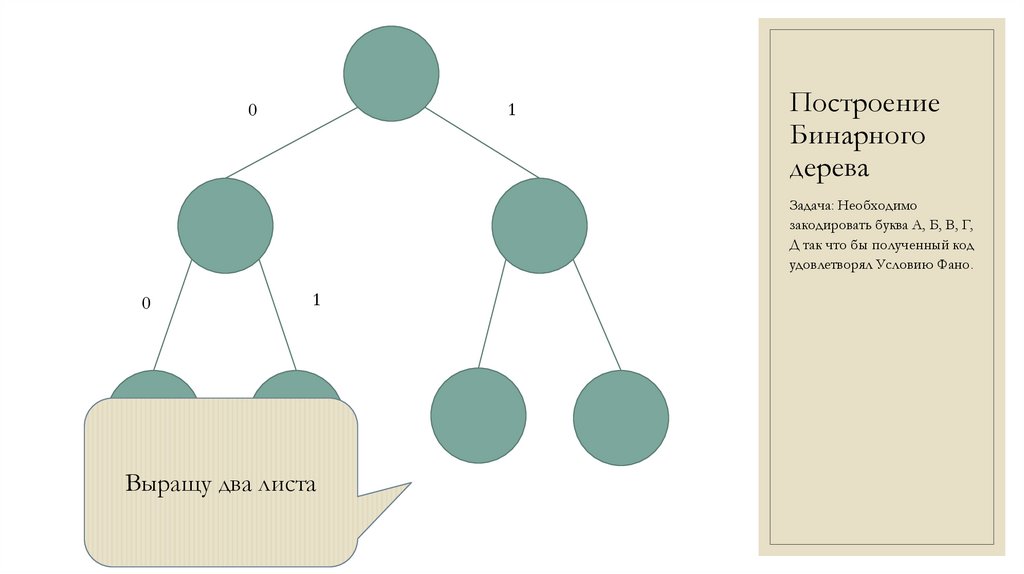
Выращу два листа

21.

Построение
Бинарного
дерева
1
0
Задача: Необходимо
закодировать буква А, Б, В, Г,
Д так что бы полученный код
удовлетворял Условию Фано.
0
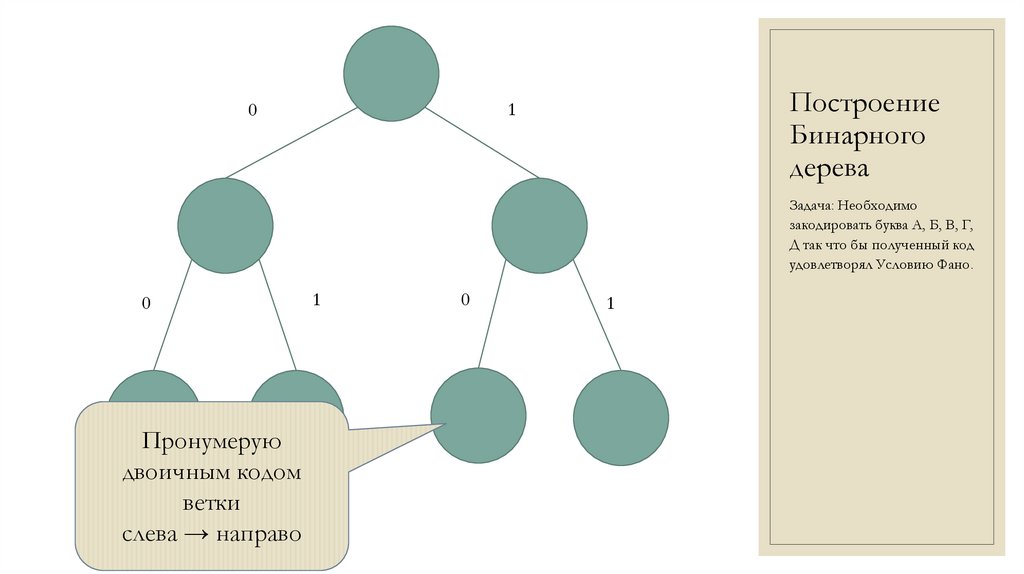
Пронумерую
двоичным кодом
ветки
слева → направо
1
0
1

22.

Построение
Бинарного
дерева
1
0
Задача: Необходимо
закодировать буква А, Б, В, Г,
Д так что бы полученный код
удовлетворял Условию Фано.
0
1
0
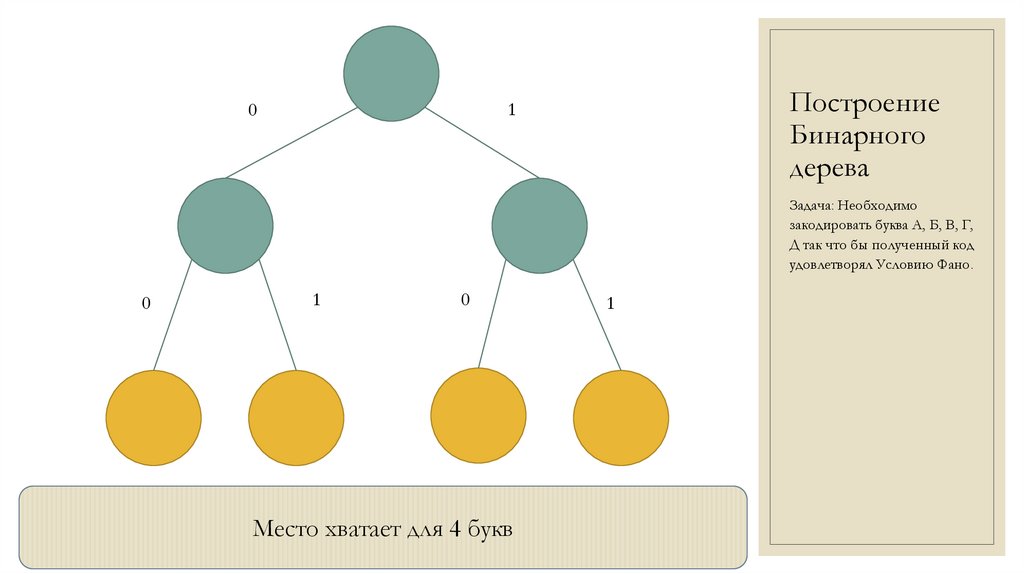
Место хватает для 4 букв
1

23.

1
0
0
1
0
Построение
Бинарного
дерева
1
Места всё ещё не хватает
Правый лист превращу в узел и
выращу две ветки
Задача: Необходимо
закодировать буква А, Б, В, Г,
Д так что бы полученный код
удовлетворял Условию Фано.

24.

1
0
0
0
1
0
Построение
Бинарного
дерева
1
1
Пронумерую двоичным кодом ветки
слева → направо
Задача: Необходимо
закодировать буква А, Б, В, Г,
Д так что бы полученный код
удовлетворял Условию Фано.

25.

1
0
0
0
1
0
Построение
Бинарного
дерева
1
1
Место есть для пяти букв
Задача: Необходимо
закодировать буква А, Б, В, Г,
Д так что бы полученный код
удовлетворял Условию Фано.

26.

1
0
0
0
А
1
0
В
Г
Построение
Бинарного
дерева
1
Д
1
Б
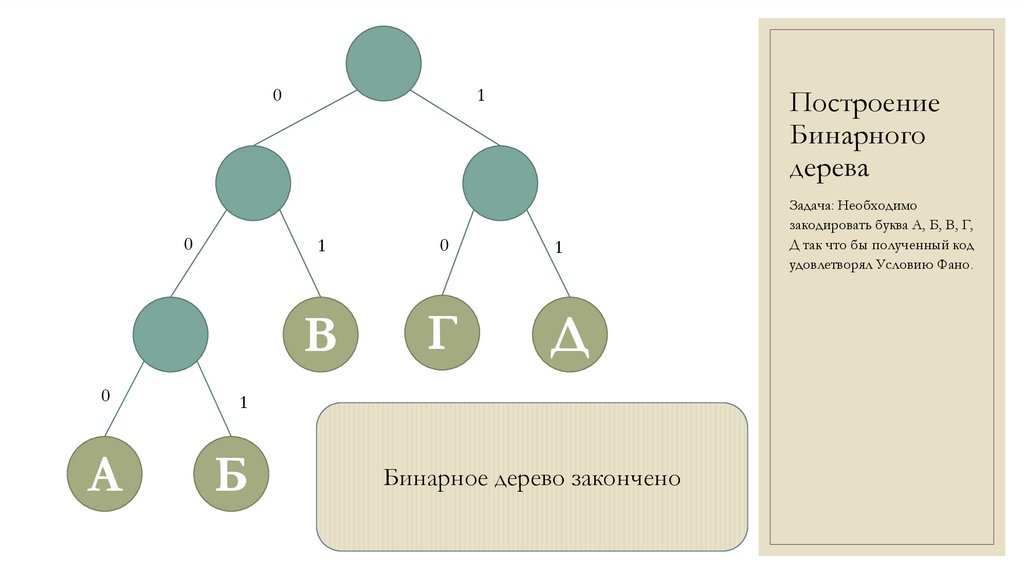
Заполню листья буквами
А, Б, В, Г, Д
Задача: Необходимо
закодировать буква А, Б, В, Г,
Д так что бы полученный код
удовлетворял Условию Фано.

27.

1
0
0
0
А
1
0
В
Г
Построение
Бинарного
дерева
1
Д
1
Б
Бинарное дерево закончено
Задача: Необходимо
закодировать буква А, Б, В, Г,
Д так что бы полученный код
удовлетворял Условию Фано.

28.

НАЙТИ КОД СИМВОЛА С
ПОМОЩЬЮ БИНАРНОГО ДЕРЕВА

29.

Код символа по бинарному дереву
1
0
Для того что бы найти код
символа посмотрим на наш
корень
1
0
В
0
А
1
Б
0
1
Г
Д

30.

Код символа по бинарному дереву
Символ
Код
1
0
1
0
В
Что бы добрать до листика А от
корня – необходимо двигаться по
левой стороне.
0
А
1
Б
0
1
Г
Д

31.

Код символа по бинарному дереву
Символ
А
Код
0
1
0
1
0
В
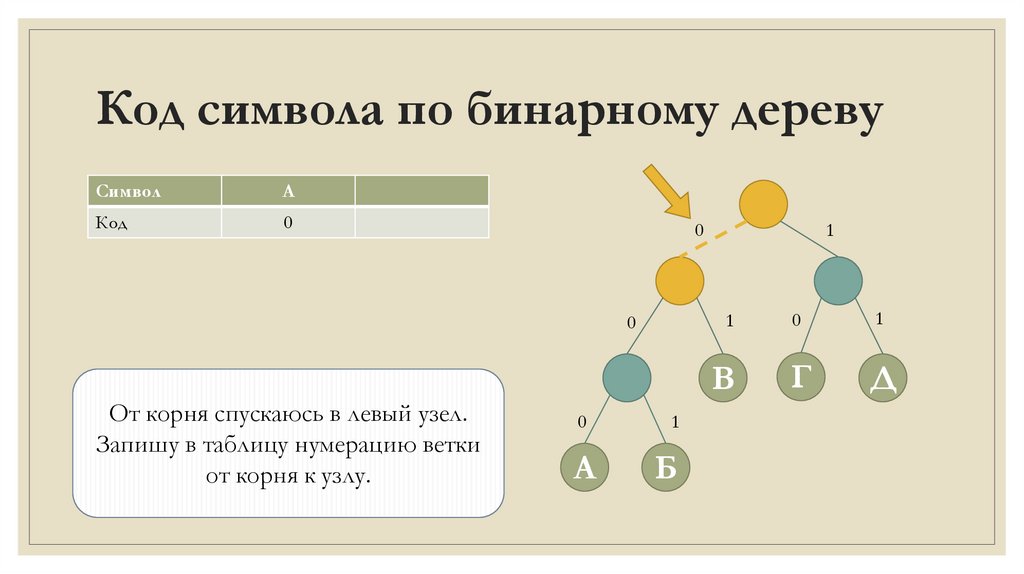
От корня спускаюсь в левый узел.
Запишу в таблицу нумерацию ветки
от корня к узлу.
0
А
1
Б
0
1
Г
Д

32.

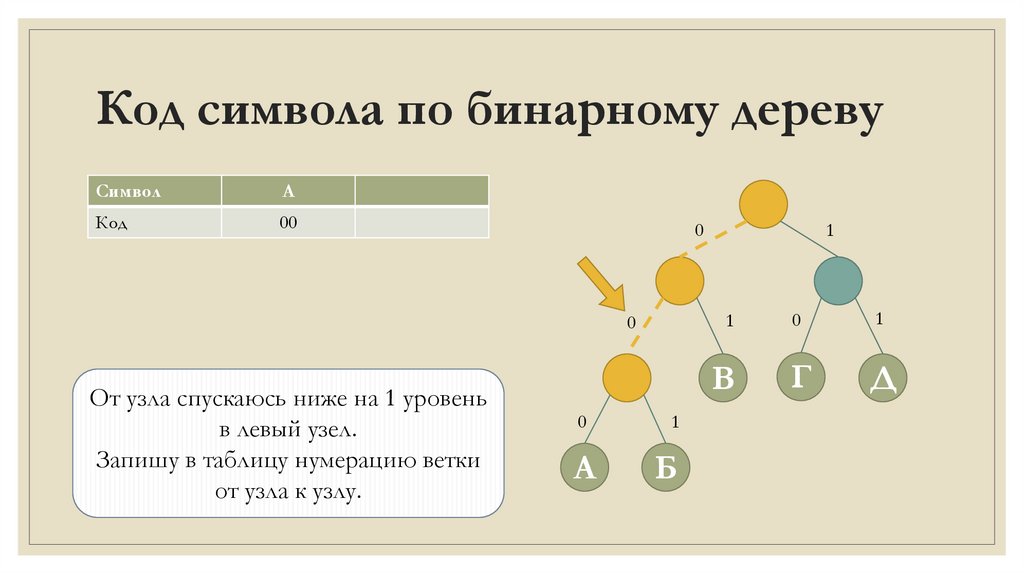
Код символа по бинарному дереву
Символ
А
Код
00
1
0
От узла спускаюсь ниже на 1 уровень
в левый узел.
Запишу в таблицу нумерацию ветки
от узла к узлу.
1
0
В
0
А
1
Б
0
1
Г
Д

33.

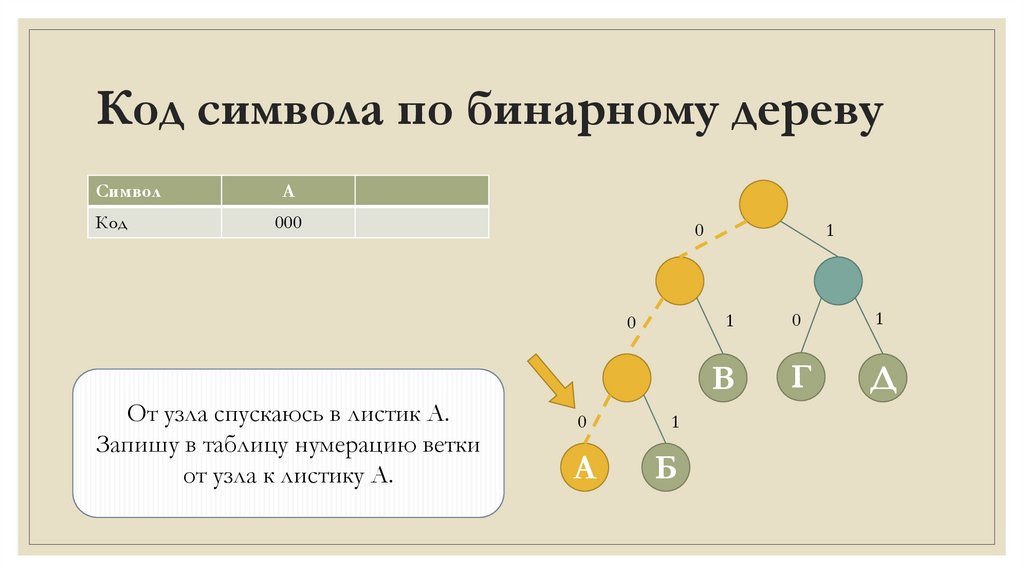
Код символа по бинарному дереву
Символ
Код
А
000
1
0
1
0
В
От узла спускаюсь в листик А.
Запишу в таблицу нумерацию ветки
от узла к листику А.
0
А
1
Б
0
1
Г
Д

34.

Код символа по бинарному дереву
Символ
Код
А
000
1
0
1
0
В
Получился маршрут от корня до
листика А которые равен 000.
0
А
1
Б
0
1
Г
Д

35.

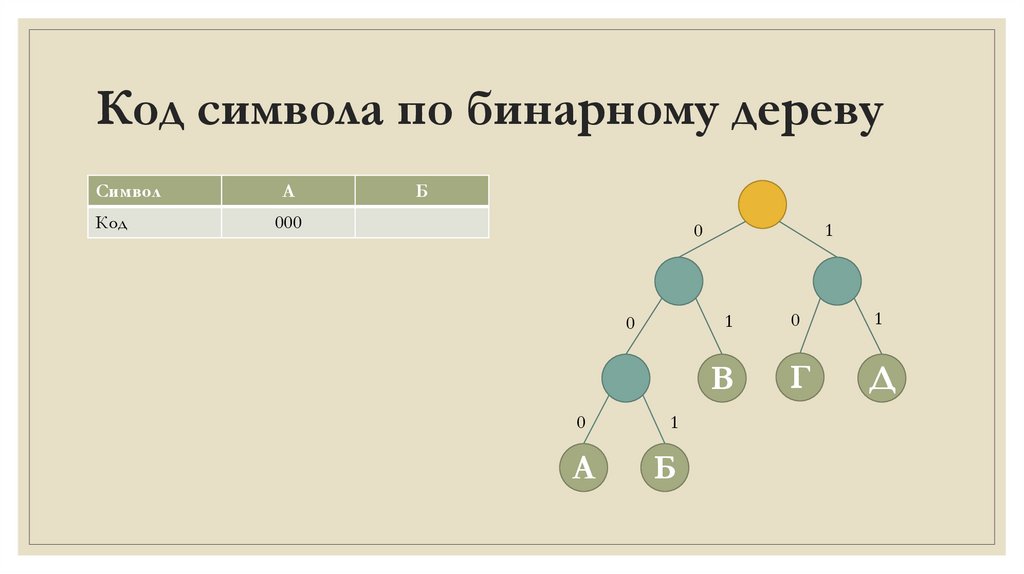
Код символа по бинарному дереву
Символ
Код
А
Б
000
1
0
1
0
В
Аналогично найду код символа Б.
0
А
1
Б
0
1
Г
Д

36.

Код символа по бинарному дереву
Символ
Код
А
Б
000
1
0
1
0
В
0
А
1
Б
0
1
Г
Д

37.

Код символа по бинарному дереву
Символ
Код
А
Б
000
0
1
0
1
0
В
0
А
1
Б
0
1
Г
Д

38.

Код символа по бинарному дереву
Символ
Код
А
Б
000
001
1
0
1
0
В
0
А
1
Б
0
1
Г
Д

39.

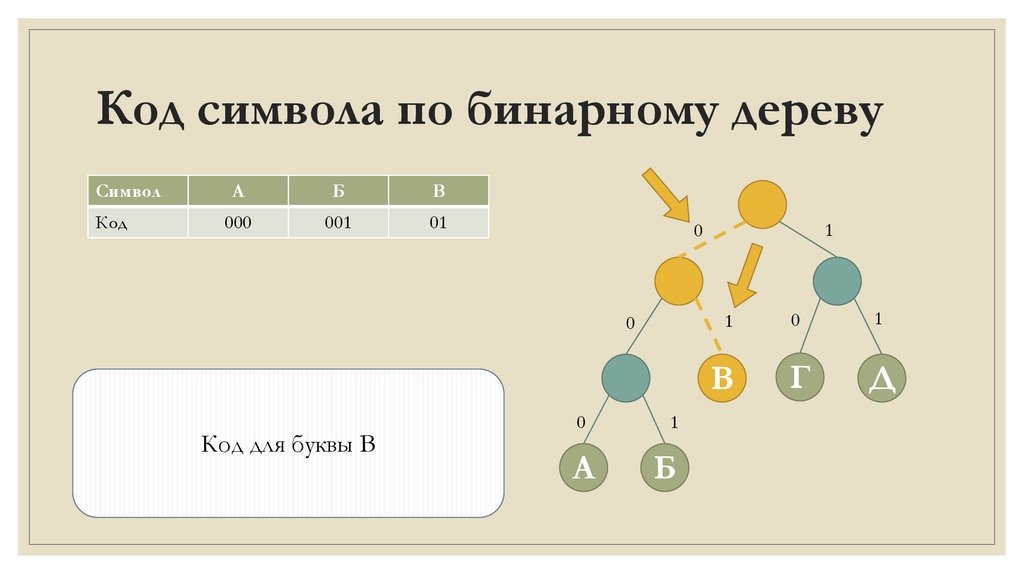
Код символа по бинарному дереву
Символ
Код
А
Б
В
000
001
01
1
0
1
0
В
Код для буквы В
0
А
1
Б
0
1
Г
Д

40.

Код символа по бинарному дереву
Символ
Код
А
Б
В
Г
000
001
01
10
1
0
1
0
В
Код для буквы Г
0
А
1
Б
0
1
Г
Д

41.

Код символа по бинарному дереву
Символ
Код
А
Б
В
Г
Д
000
001
01
10
11
1
0
1
0
В
Код для буквы Г
0
А
1
Б
0
1
Г
Д

42.

Код символа по бинарному дереву
Символ
Код
А
Б
В
Г
Д
000
001
01
10
11

43.

СОКРАЩЕНИЕ
ДВОИЧНОГО КОДА
Тип задачи №1

44.

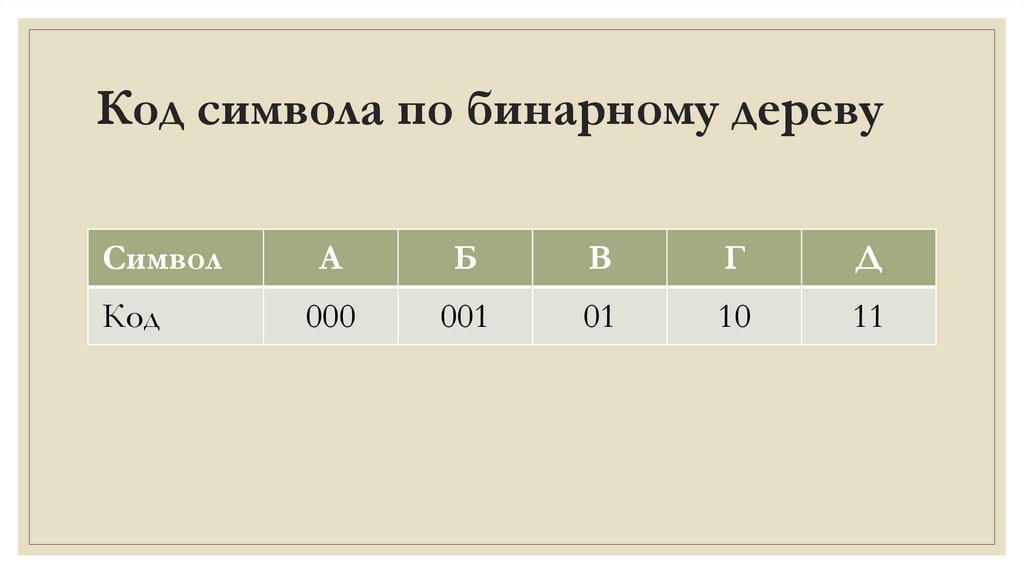
Задача 1
Для кодирования некоторой последовательности, состоящей из букв А, Б,
В, Г и Д, используется неравномерный двоичный код, позволяющий
однозначно декодировать полученную двоичную последовательность.
Вот этот код: А – 10; Б – 11; В – 000; Г – 001; Д – 010.
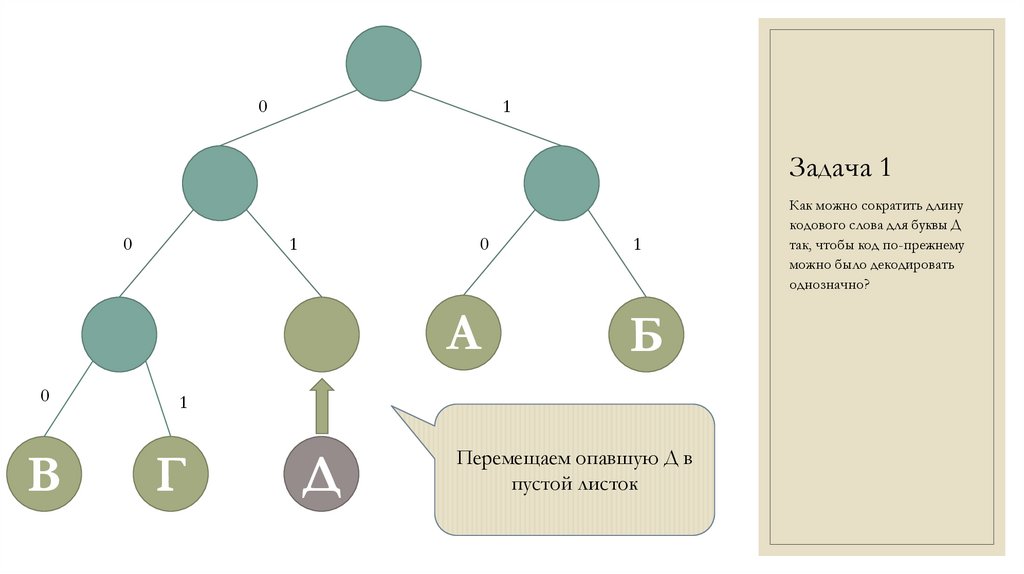
Как можно сократить длину кодового слова для буквы Д так, чтобы код попрежнему можно было декодировать однозначно?
Коды остальных букв меняться не должны. Если есть несколько вариантов,
выберите кодовое слово с минимальным значением.

45.

Задача 1
Построим бинарное
дерево.
Коды листов известны по
условию задачи
Код: А – 10; Б – 11; В – 000; Г
– 001; Д – 010.

46.

0
1
Задача 1
Код:
0
1
0
1
А – 10;
Б – 11;
В – 000;
А
0
В
1
Г
0
Д
1
Б
Г – 001;
Д – 010.

47.

0
1
Задача 1
0
1
0
А
0
В
1
Г
0
Д
1
Б
1
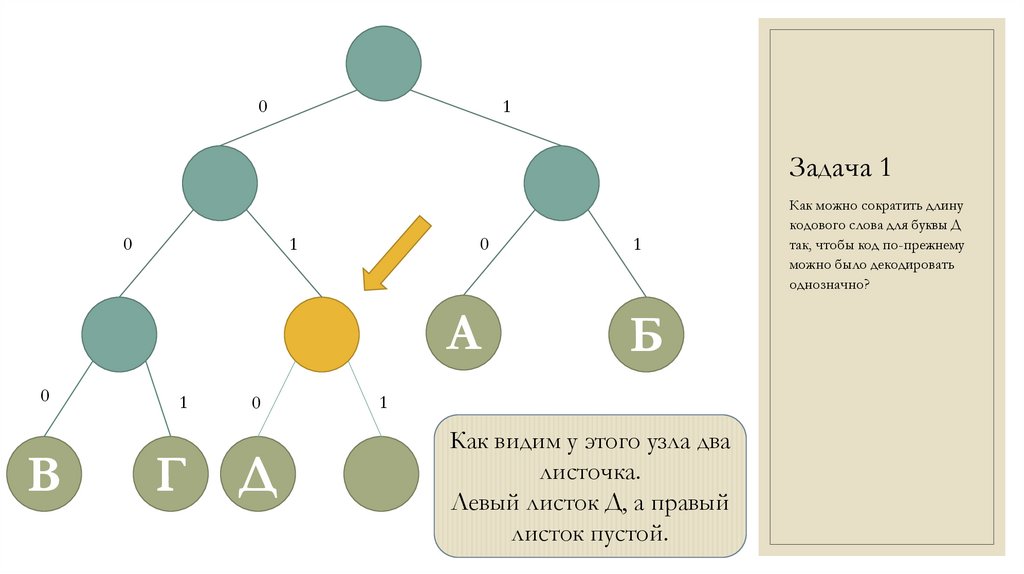
Как видим у этого узла два
листочка.
Левый листок Д, а правый
листок пустой.
Как можно сократить длину
кодового слова для буквы Д
так, чтобы код по-прежнему
можно было декодировать
однозначно?

48.

0
1
Задача 1
0
1
0
А
0
В
1
Г
0
Д
1
Б
1
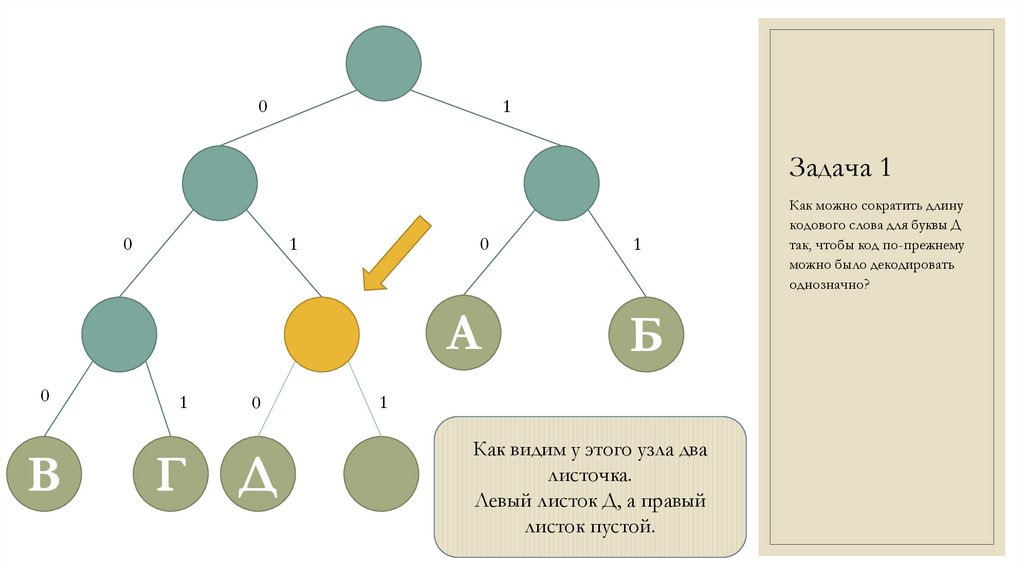
Как видим у этого узла два
листочка.
Левый листок Д, а правый
листок пустой.
Как можно сократить длину
кодового слова для буквы Д
так, чтобы код по-прежнему
можно было декодировать
однозначно?

49.

0
1
Задача 1
0
1
0
А
0
В
1
Г
0
Д
1
Б
1
Пустой листочек мы не
используем в кодирование
сообщений, следовательно
его можно отбросить
Как можно сократить длину
кодового слова для буквы Д
так, чтобы код по-прежнему
можно было декодировать
однозначно?

50.

0
1
Задача 1
0
1
0
А
0
В
1
Г
0
Д
1
1
Б
Как можно сократить длину
кодового слова для буквы Д
так, чтобы код по-прежнему
можно было декодировать
однозначно?

51.

0
1
Задача 1
0
1
0
А
0
В
1
Б
1
Г
Д
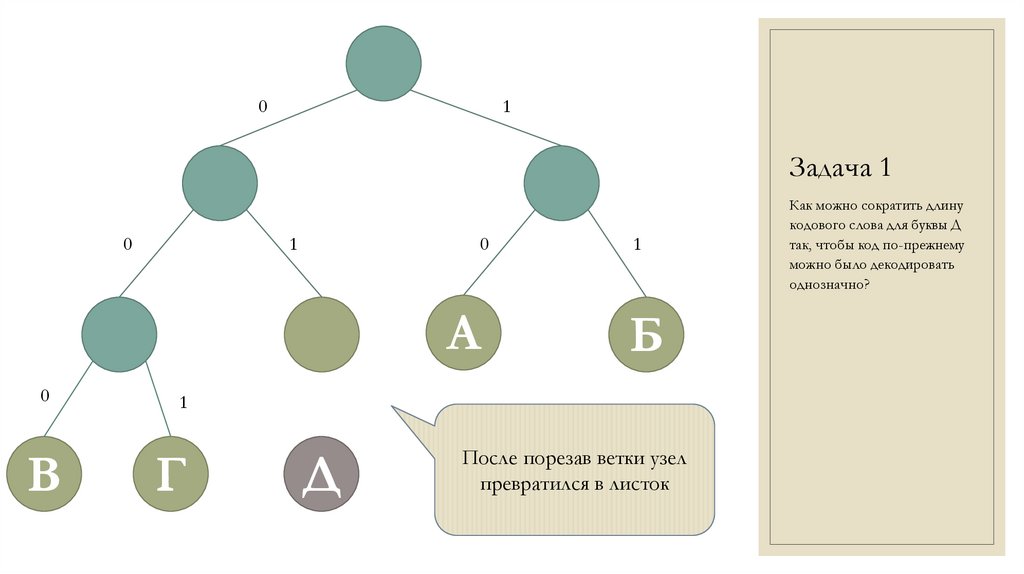
После порезав ветки узел
превратился в листок
Как можно сократить длину
кодового слова для буквы Д
так, чтобы код по-прежнему
можно было декодировать
однозначно?

52.

0
1
Задача 1
0
1
0
А
0
В
1
Б
1
Г
Д
После порезав ветки узел
превратился в листок (одно
свободное место)
Как можно сократить длину
кодового слова для буквы Д
так, чтобы код по-прежнему
можно было декодировать
однозначно?

53.

0
1
Задача 1
0
1
0
А
0
В
1
Б
1
Г
Д
Перемещаем опавшую Д в
пустой листок
Как можно сократить длину
кодового слова для буквы Д
так, чтобы код по-прежнему
можно было декодировать
однозначно?

54.

0
1
Задача 1
0
1
0
Д
0
В
А
1
Б
1
Г
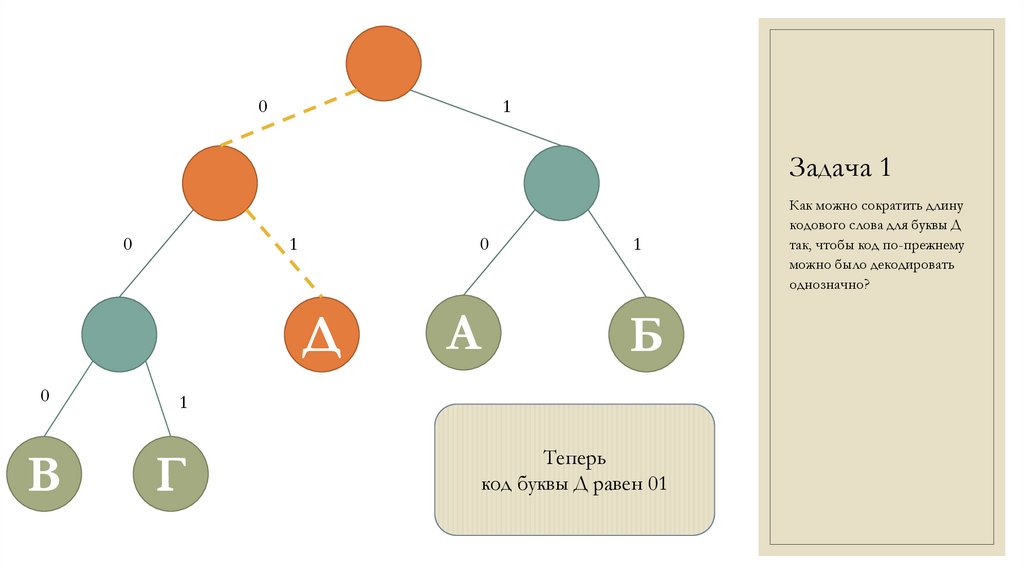
Теперь
код буквы Д равен 01
Как можно сократить длину
кодового слова для буквы Д
так, чтобы код по-прежнему
можно было декодировать
однозначно?

55.

Ответ
Длину кодового слова для буквы Д
можно сократить до 01

56.

ВЫБОР КОДА ДЛЯ
ОДНОЙ БУКВЫ
Тип задачи №2

57.

Задача 2
По каналу связи передаются сообщения, содержащие только шесть букв: У, Р,
А, Е, Г, Э; для передачи используется двоичный код, удовлетворяющий
условию Фано.
Буквы Е, Р, А, Г, У имеют коды 01, 000, 100, 101, 110 соответственно. Укажите
код наименьшей длины для буквы Э.
Если в качестве кода может быть использовано несколько кодов одинаковой
длины, выбрать тот, числовое значение которого меньше.

58.

0
1
Задача 2
0
0
1
Буквы Е, Р, А, Г, У имеют
коды 01, 000, 100, 101, 110
соответственно.
1
Е
0
Р
1
0
А
1
Г
0
У
1

59.

0
1
Букву Э можно
поставить в один из
двух листочков
Задача 2
0
0
1
Укажите код наименьшей
длины для буквы Э.
1
Е
0
Р
1
Э
001
0
А
1
Г
0
У
1
Э
111

60.

Задача 2
Сравним два получившихся числа
Двоичная система счисления
001
111
Десятичная система счисления
1
7
Для удобства можно перевести в десятичную систему счисления
0012 = 110
1112 = 710

61.

Задача 2
Сравним два получившихся числа
Двоичная система счисления
001
111
Десятичная система счисления
1
7
1<7

62.

Задача 2
Сравним два получившихся числа
Двоичная система счисления
001
111
001<111
Десятичная система счисления
1
7
1<7
1 меньше 7, следовательно 001 меньше 111
Ответ: код наименьшей длины для буквы Э - 001

63.

ПОМЕХОУСТОЙЧИВЫЕ
КОДЫ
Тип задачи №3

64.

Задача 3
По каналу связи с помощью равномерного двоичного кода передаются
сообщения, содержащие только 4 буквы: А, Б, В, Г.
Каждой букве соответствует своё кодовое слово, при этом для набора кодовых
слов выполнено такое свойство: любые два слова из набора отличаются не
менее чем в трёх позициях. Это свойство важно для расшифровки
сообщений при наличии помех.
Для кодирования букв Б, В, Г используются 5-битовые кодовые слова: Б –
00001, В – 01111, Г – 10110.
5-битовый код для буквы А начинается с 1 и заканчивается на 0. Определите
кодовое слово для буквы А.

65.

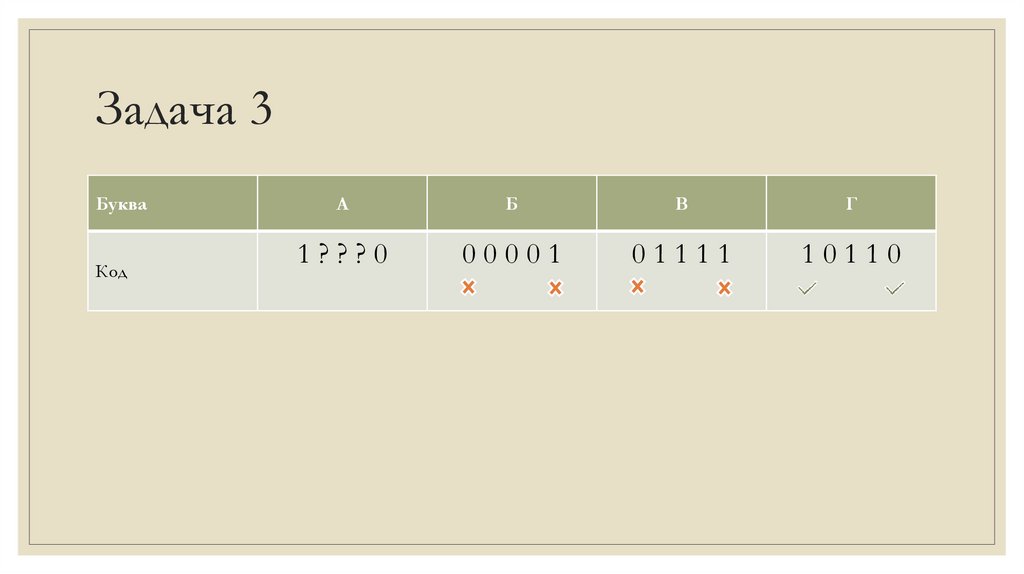
Задача 3
Буква
Код
А
Б
В
Г
1???0
00001
01111
10110
позиция
Пример
00001
кодовое слово

66.

Задача 3
Буква
Код
А
Б
В
Г
1???0
00001
01111
10110
Сравним позиции кодовых слов Б, В, Г с позициями кодового слова А

67.

Задача 3
Буква
Код
А
Б
В
Г
1???0
00001
01111
10110
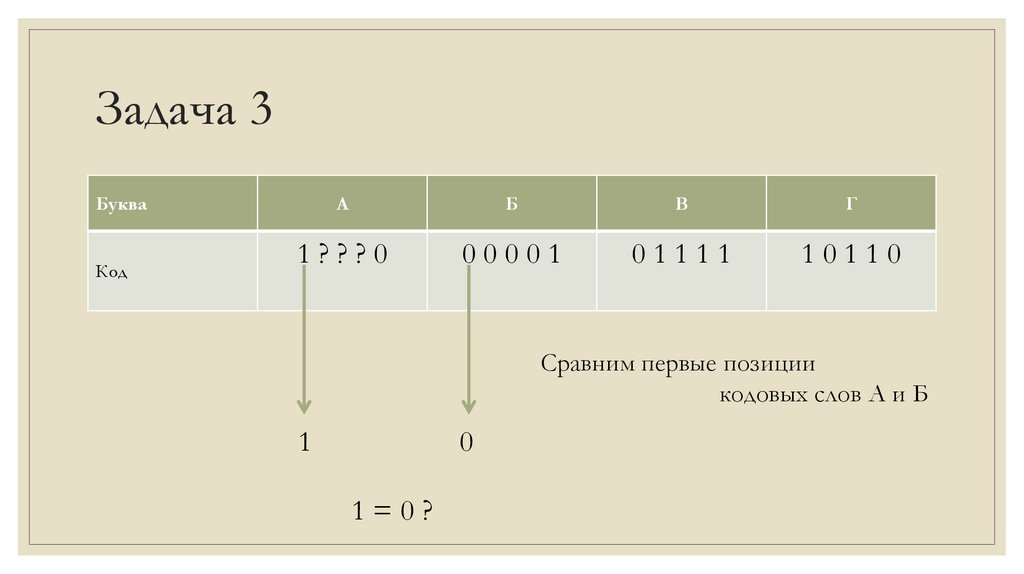
Сравним первые позиции
кодовых слов А и Б
1
0
1=0?

68.

Задача 3
Буква
Код
А
Б
В
Г
1???0
00001
01111
10110
1
1=0?
0
Сравним первые позиции кодовых слов А и В

69.

Задача 3
Буква
Код
А
Б
В
Г
1???0
00001
01111
10110
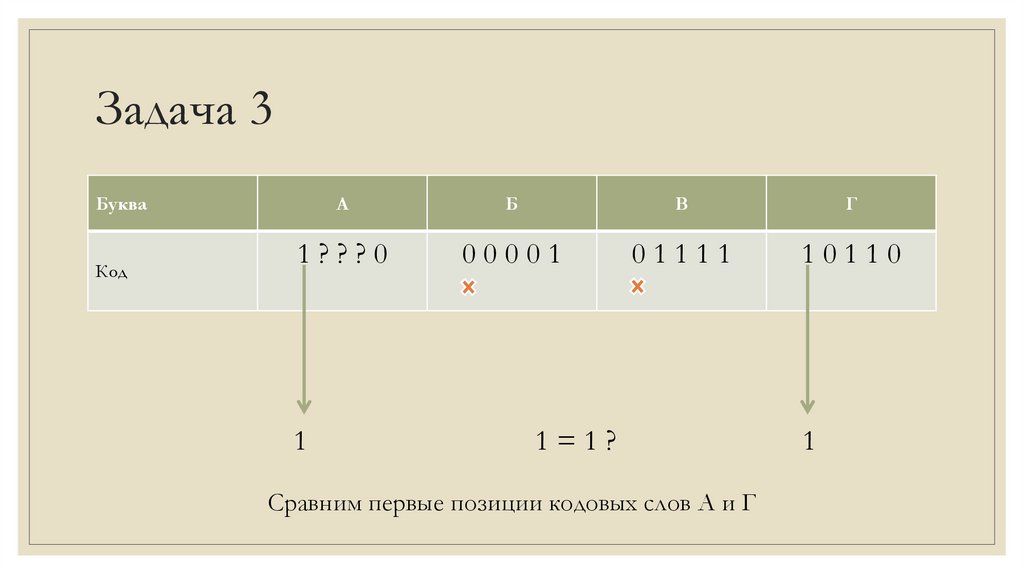
1
1=1?
Сравним первые позиции кодовых слов А и Г
1

70.

Задача 3
Буква
Код
А
Б
В
Г
1???0
00001
01111
10110
Теперь сравниваем последние позиции

71.

Задача 3
Буква
Код
А
Б
В
Г
1???0
00001
01111
10110
0
1
1
0
?
А=Б
0=1
?
А=В
0=1
?
А=Г
0=0

72.

Задача 3
Буква
Код
А
Б
В
Г
1???0
00001
01111
10110

73.

Задача 3
Буква
Код
А
Б
В
Г
1???0
00001
01111
10110
У кодового слова буква Б сошлись две позиции.
По условию: любые два слова из набора отличаются не менее чем
в трёх позициях.
У нас уже есть две одинаковые позиции значит остальные три
должны быть различные.

74.

Задача 3
Буква
Код
А
Б
В
Г
1???0
00001
01111
10110
У кодового слова буква Б сошлись две позиции.
По условию: любые два слова из набора отличаются не менее чем
в трёх позициях.
У нас уже есть две одинаковые позиции значит остальные три
должны быть различные.

75.

Задача 3
Буква
Код
А
Б
В
Г
1???0
00001
01111
10110
¬0 (НЕ 0)
Если вторая позиция у кодового слова Г равна 0, следовательно
вторая позиция у кодового слова А равна НЕ Г (¬ г).

76.

Задача 3
Буква
Код
А
Б
В
Г
11??0
00001
01111
10110
¬0 (НЕ 0)
Если вторая позиция у кодового слова Г равна 0, следовательно
вторая позиция у кодового слова А равна НЕ Г (¬ г).

77.

Задача 3
Буква
Код
А
Б
В
Г
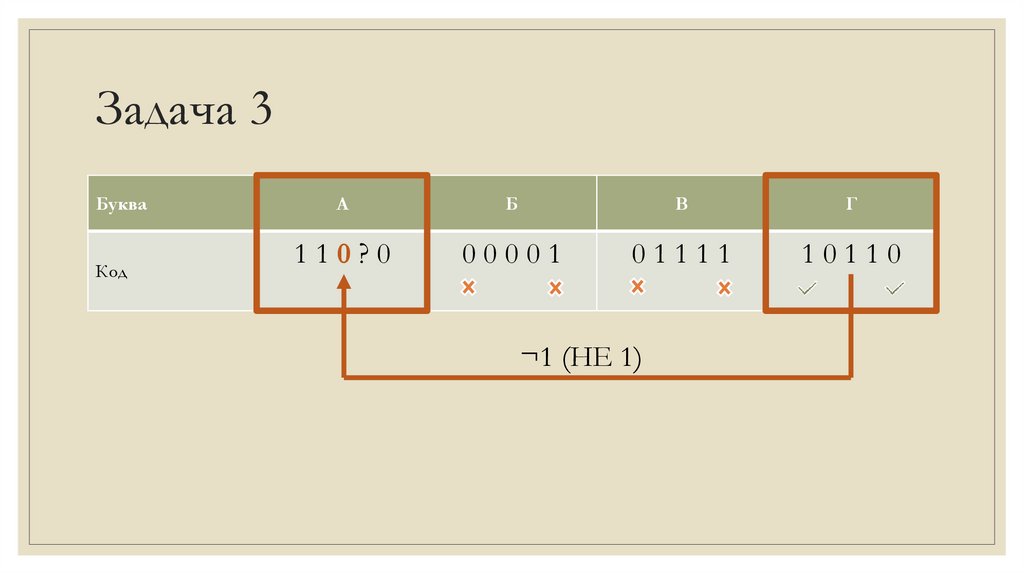
110?0
00001
01111
10110
¬1 (НЕ 1)

78.

Задача 3
Буква
Код
А
Б
В
Г
11000
00001
01111
10110
¬1 (НЕ 1)

79.

Задача 3
Буква
Код
А
Б
В
Г
11000
00001
01111
10110
Ответ: кодовое слово для буквы А равно 11000

80.

ВЫБОР КОДОВ ДЛЯ
НЕСКОЛЬКИХ БУКВ
Тип задачи №4

81.

Задача 4
Для кодирования некоторой последовательности, состоящей из букв П, О, Е,
Х, А, Л, И, решили использовать неравномерный двоичный код,
удовлетворяющий условию Фано.
Для букв О, Е, А, И использовали соответственно кодовые слова 01, 110,
1010, 001.
Найдите наименьшую возможную суммарную длину всех кодовых слов.

82.

0
1
Задача 4
0
1
0
Для букв О, Е, А, И
использовали соответственно
кодовые слова 01, 110, 1010,
001.
1
О
0
1
1
0
0
И
Е
0
А
1
1

83.

0
1
Задача 4
0
1
0
Некоторая
последовательность, состоит
из букв П, О, Е, Х, А, Л, И
1
О
0
П
1
И
1
0
Х
0
А
1
0
1
Е
Л
Для букв П Х Л нет
кода.
Добавим его
самостоятельно.

84.

0
1
Задача 4
0
1
0
Некоторая
последовательность, состоит
из букв П, О, Е, Х, А, Л, И
1
О
0
П
1
И
1
0
Х
0
А
1
0
1
Е
Л
Оставшийся листик
1011 мы не берём т.к
в нём самое большое
количество знаков
чем в остальных

85.

Задача 4
Допишем оставшиеся коды.
П
О
Е
Х
А
Л
И
000
01
110
100
1010
111
001

86.

Задача 4
Подсчитаю количество знаков
П
О
Е
Х
А
Л
И
000
01
110
100
1010
111
001
Индекс
П
П1
0
П2
0
П3
0
Колич
ество
3
Индекс
О1
О
0
О2
1
Колич
ество
2
Индекс
Е
Индекс
Х
Индекс
А
Е1
1
Х1
1
А1
1
А2
0
А3
1
Индекс
Л
Индекс
И
Л1
1
И1
0
Л2
1
И2
0
Е2
1
Х2
0
Е3
0
Х3
0
А4
0
Л3
1
И3
1
Колич
ество
3
Количе
ство
3
Колич
ество
4
Колич
ество
3
Колич
ество
3

87.

Задача 4
Буква
П
О
Е
Х
А
Л
И
Код
000
01
110
100
1010
111
001
Количество
знаков
3
2
3
3
4
3
3
П+О+Е+Х+А+Л+И = 3+2+3+3+4+3+3 = 21
Ответ: наименьшая возможная суммарная длина всех
кодовых слов равна 21

88.

Примечание
◦ Предположим для буквы Л выбрали код 1011
вместо кода 111, тогда
Букв
а
П
О
Е
Х
А
Л
И
Код
000
01
110
100
1010
1011
001
Колич
ество
знаков
3
2
3
3
4
4
1
0
3
П+О+Е+Х+А+Л+И = 3+2+3+3+4+4+3 = 22
0
0
1
1
П И
0
1
О
1
0
0
Х
Е
0
1
А Л
1

89.

ДЕКОДИРОВАНИЕ
Тип задачи №5

90.

Задача 5
Заглавные буквы русского алфавита закодированы неравномерным двоичным
кодом, в котором никакое кодовое слово не является началом другого
кодового слова. Это условие обеспечивает возможность однозначной
расшифровки закодированных сообщений.
Известно, что все кодовые слова содержат не меньше двух и не больше трёх
двоичных знаков, а слову КАПОТ соответствует код 11000111110011. Какой
код соответствует слову ТОК?

91.

Задача 5
Рассмотрим внимательно код 11000111110011
С первого взгляда можно сказать что количество 1
больше чем количество 0, из чего можно сделать
вывод что левая ветка будет иметь минимум
третий уровень, т.к. одна буква шифруется тремя
знаками.
Набрасываем бинарное дерево
1
0
1
0
0
1

92.

Задача 5
Про просмотре кода
11000111110011
В глаза бросается большое скопление 1 в
середине.
1
0
1
0
0
1

93.

Задача 5
Предположим что код 111 - П
11000111110011
Тогда
1
0
1
0
1 1 0 0 0 1 .1 1 1 .1 0 0 1 1
0
* Если 111 листок, следовательно 11 и 1 это узел,
в которых не может быть букв.
1
П

94.

Задача 5
От 111 справа на лево распределим ещё две буквы
под два символа
110.001.111.10011
1
0
Поскольку кодовое слово начинается на К,
то 110 – К, следовательно 001 – А.
0
Дорисовываем дерево.
*Если 110 или 001 листок,
следовательно 11 и 1 это узел, в которых не может
быть букв.
1
0
1
А
1
0
0
1
К
П

95.

Задача 5
0
1
Осталось 5 символов которые можно
разложить на 100 и 11, или на 10 и 011
110.001.111.10011
Листок 100 существует А вот листочка 11
быть не может. Мы уже сказали что это узел,
а в узле не может быть буквы. Это вариант
вычёркиваем.
0
0
1
1
А
0
0
1
1
0
1
К П

96.

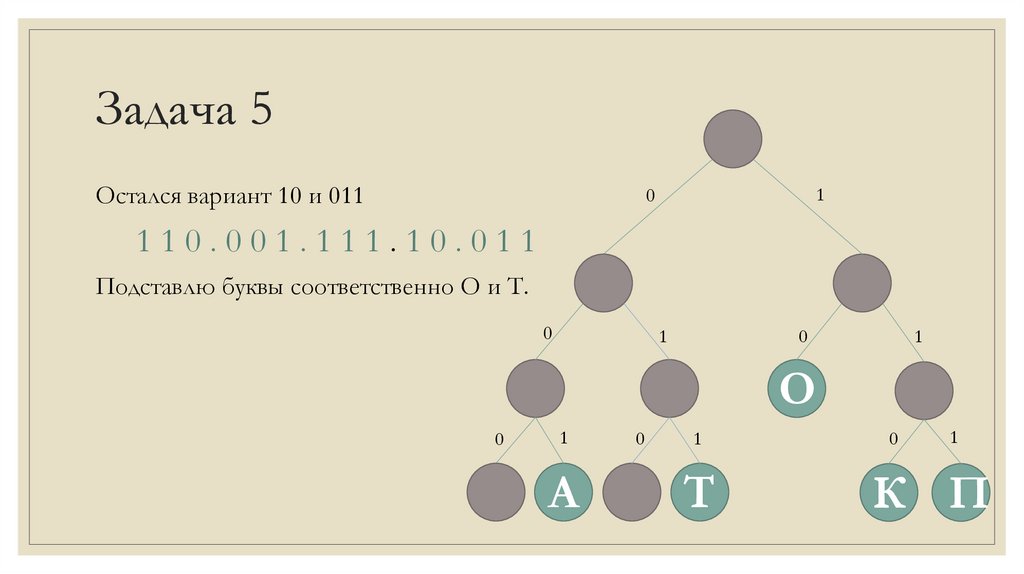
Задача 5
Остался вариант 10 и 011
1
0
110.001.111.10.011
Подставлю буквы соответственно О и Т.
0
1
0
1
О
0
1
А
0
1
Т
0
1
К П

97.

Задача 5
Запишем результат в таблицу
К
111
А
001
П
110
О
10
Т
011

98.

Задача 5
С помощью таблицы закодируем слово ТОК
К
110
А
001
П
111
О
10
Т
011
О
10
К
110
Ответ: слову ТОК соответствует код 01110110
Т
011

99.

СПИСОК
ЛИТЕРАТУРЫ

100.

Список литературы
◦ 1. Учебник для 11 класса : в 2 ч. Ч. 1 / К. Ю. Поляков, Е. А. Ере- мин. — М. : БИНОМ. Лаборатория
знаний, 2020
◦ 2. Богомолова О.Б., Усенков Д.Ю. Фано и его «коллеги»: растим дерево. // компьютерные
инструменты в школе – 2017 – Выпуск №2 - С. 26-31. Режим доступа:
http://ipo.spb.ru/journal/index.php?article/1873/, свободный.
◦ 3. Задачи для подготовки ЕГЭ https://kpolyakov.spb.ru/school/ege/generate.htm