Similar presentations:
Электроемкость. Конденсаторы
1.
2. Электроемкость проводника
Электроемкость - это способностьпроводников или системы из
нескольких проводников
накапливать электрические
заряды, а следовательно, и
электроэнергию, которая в
дальнейшем может быть
использована.
3.
Электроемкость уединенного проводника— физическая величина, равная
отношению электрического заряда
уединенного проводника к его
потенциалу: C q
Электроемкость проводника не зависит
от рода вещества и заряда, но зависит от
его формы и размеров, а также от
наличия вблизи других проводников или
диэлектриков.
4. Электроемкость сферы
Если уединенным проводникомявляется заряженная сфера, то
q
q
C ; ш
ш
4 0 R
Тогда
C 4 0 R
5. ЗАДАЧА №1. Определить электроемкость Земли, считая ее радиус равным 6370 км.
Дано:R 6,37 10 м
6
0 8,85 10
12
Ф
м
C 4 3,14 1 8,85 10
Электроемкость
шара определяется
по формуле:
C 4 0 R
12
6,37 10 710 мкФ
6
6.
Если двум изолированным друг от другапроводникам сообщить заряды q1 и q2, то
между ними возникает некоторая разность
потенциалов Δφ, зависящая от величин
зарядов
и
геометрии
проводников.
Разность потенциалов Δφ между двумя
точками в электрическом поле часто
называют напряжением и обозначают
буквой
U.
Наибольший
практический
интерес представляет случай, когда заряды
проводников одинаковы по модулю и
противоположны по знаку: q1 = – q2 = q. В
этом случае можно ввести понятие
электрической емкости.
7.
Электроемкостьюсистемы
из
двух
проводников
называется
физическая величина, определяемая как
отношение
заряда
q
одного
из
проводников к разности потенциалов Δφ
между ними:
В системе СИ единица
называется фарад (Ф):
электроемкости
8.
Существуюттакие
конфигурации
проводников, при которых электрическое
поле
оказывается
сосредоточенным
(локализованным) лишь в некоторой
области пространства. Такие системы
называются
конденсаторами,
а
проводники, составляющие конденсатор,
называются обкладками.
9. Виды конденсаторов
По геометрии: плоские,сферические, цилиндрические.
По диэлектрику: воздушные,
бумажные, слюдяные,
керамические, электролитические.
По емкости: постоянные,
переменные
10.
Простейший конденсатор – системаиз двух плоских проводящих пластин,
расположенных
параллельно
друг
другу на малом по сравнению с
размерами пластин расстоянии и
разделенных
слоем
диэлектрика.
Такой
конденсатор
называется
плоским.
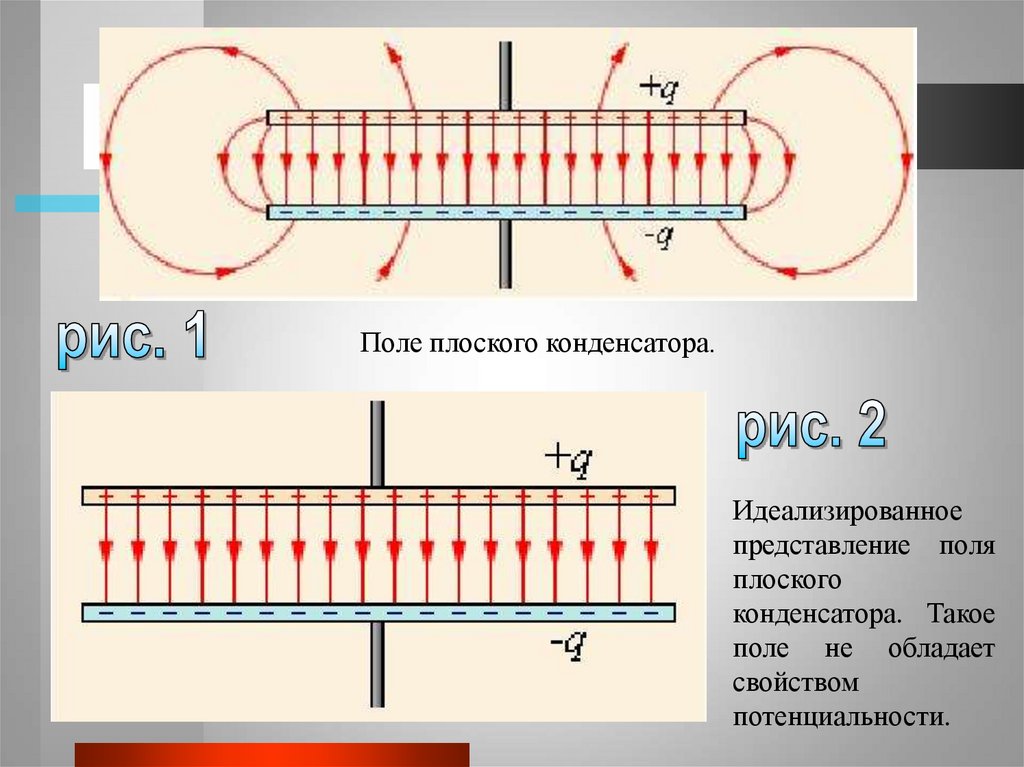
11.
Поле плоского конденсатора.Идеализированное
представление поля
плоского
конденсатора. Такое
поле не обладает
свойством
потенциальности.
12.
Каждая из заряженныхпластин плоского
конденсатора создает
вблизи поверхности
электрическое поле, модуль
напряженности которого
выражается соотношением
13.
В настоящее время широко применяются бумажныеконденсаторы для напряжений в несколько сот вольт и
ёмкостью в несколько микрофарад. В таких конденсаторах
обкладками служат две длинные ленты тонкой металлической
фольги, а изолирующей прокладкой между ними – несколько
более широкая бумажная лента, пропитанная парафином.
Бумажной лентой покрывается одна из обкладок, затем ленты
туго свёртываются в рулон и укладываются в специальный
корпус. Такой конденсатор, имея размеры спичечного коробка,
обладает ёмкостью 10мкФ (металлический шар такой ёмкости
имел бы радиус 90км).
14.
В радиотехнике применяются слюдяные конденсаторынебольшой ёмкости (от десятков до десятков тысяч
пикофарад). В них листки станиоля прокладываются слюдой
так, что все нечётные листки станиоля, соединённые вместе ,
образуют одну обкладку конденсатора, тогда как чётные
листки образуют другую обкладку. Внешний вид и отдельные
части такого конденсатора показаны на рисунке. Эти
конденсаторы могут работать при напряжениях от сотен до
тысяч вольт.
15.
В последнее время слюдяные конденсаторы врадиотехнике начали заменять керамическими.
Диэлектриком в них служит специальная керамика.
Обкладки
керамических
конденсаторов
изготавливаются в виде слоя серебра, нанесённого
на поверхность керамики и защищённого слоем
лака. Керамические конденсаторы изготавливаются
на ёмкости о единиц до сотен пикофарад и на
напряжения от сотен до тысяч вольт.
16.
Широкоераспространение
получили
так
называемые
электролитические
конденсаторы,
диэлектриком в которых служит тончайший окисный
слой на поверхности алюминия или тантала,
находящийся
в
контакте
со
специальным
электролитом. Эти конденсаторы имеют большую
ёмкость (до нескольких тысяч микрофарад) при
небольших размерах.
17.
Часто используются конденсаторы переменнойемкости с воздушным или твёрдым диэлектриком.
Они состоят из двух систем металлических пластин,
изолированных друг от друга. Одна система пластин
неподвижна, вторая может вращаться вокруг оси.
Вращая подвижную систему, плавно изменяют
ёмкость конденсатора.
18.
Электроемкость плоского конденсаторапрямо
пропорциональна
площади
пластин
(обкладок)
и
обратно
пропорциональна
расстоянию
между
ними.
Если
пространство
между
обкладками заполнено диэлектриком,
электроемкость
конденсатора
увеличивается
в
ε
раз:
19. Соединение конденсаторов в батарею
Конденсаторы могут соединятьсямежду собой, образуя батареи
конденсаторов.
20. Параллельное соединение конденсаторов
При параллельномсоединении
конденсаторов
напряжения на
конденсаторах
одинаковы:
U1 = U2 = U, а заряды
равны q1 = С1U и
q2 = С2U
21. ЗАДАЧА № 2. Батарея из двух конденсаторов 20 и 30 мкФ, соединенных параллельно, заряжена до напряжения 220 В. Определите
емкость батареи и заряд каждого конденсатора.Дано:
U 220B
С1 20 мкФ
Так как конденсаторы
соединяются
параллельно, то Сб
U U 1 U 2
С1 С2
С2 30 мкФ
Сб 20 мкФ 30 мкФ 50 мкФ
Сб ?
q1 C1U ; q2 C2U
q1; q2 ?
q1 4,4 мКл; q2 6,6 мКл
22. Последовательное соединение конденсаторов
Припоследовательном
соединении
одинаковыми
оказываются заряды
обоих конденсаторов:
q1 = q2 = q, а
напряжения на них
равны
23. ЗАДАЧА № 3. батарея из двух конденсаторов 4 и 6 мкФ, соединенных последовательно, заряжена до напряжения 220 В. Определить
емкость и заряд батареи конденсаторов.Дано:
С1 4 мкФ
Так как конденсаторы соединяются
последовательно, то
q1 q2 q б
С2 6 мкФ
1
1
1
;
Сб
С1
С2
U 220B
1
1
1
2 3
5
Сб 4 мкФ 6 мкФ 12 мкФ 12 мкФ
Cб ?
qб ?
12 мкФ
Сб
2,4 мкФ
5
q C U 2,4 220 528 мкКл
24.
Формулы для параллельного ипоследовательного
соединения
остаются
справедливыми
при
любом
числе
конденсаторов,
соединенных в батарею.
25. Задача № 3. Определить электроемкость батареи конденсаторов, изображенной на рисунке.
С2С1
С3
Дано:
С1 20 мкФ
С2 80 мкФ
С3 50 мкФ
26. Энергия заряженного конденсатора
Электрическое поле конденсаторасосредоточено между его
обкладками, следовательно и
энергия электрического поля
локализована там же.
qU
CU
W
2
2
2
2
q
2C
27. Задача № 4.Определить емкость конденсатора, если напряжение на его обкладках 100 В, а энергия 2 Дж.
Дано:U=100 В
W=2 Дж
Энергия эл.поля конденсатора
С-?
2 2 Дж
4
С
4
10
400 мкФ
4 2
10 В
CU 2
W
2
2W
С 2
U


























 physics
physics








