Similar presentations:
Решение профессиональных задач в excel: прямая и обратная геодезическая задачи
1. РЕШЕНИЕ ПРОФЕССИОНАЛЬНЫХ ЗАДАЧ В EXCEL: ПРЯМАЯ И ОБРАТНАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧИ
2.
1.2.
3.
1.
2.
3.
4.
5.
ЦЕЛИ ЗАНЯТИЯ
Закрепить знания и умения работы в Excel
Познакомиться с технологией решения профессиональных задач
в Excel на примере задач по геодезии.
Научиться организовывать свою работу от постановки цели и
задач до самооценки выполненной задачи.
ЗАДАЧИ
Повторить термины из курса геодезии.
Познакомиться с решением в Excel прямой геодезической задачи.
Создать программу решения обратной геодезической задачи.
Оценить свою работу - заполнить анкету выходную.
Оформить отчет по практической работе – заполнить бланк
отчета.
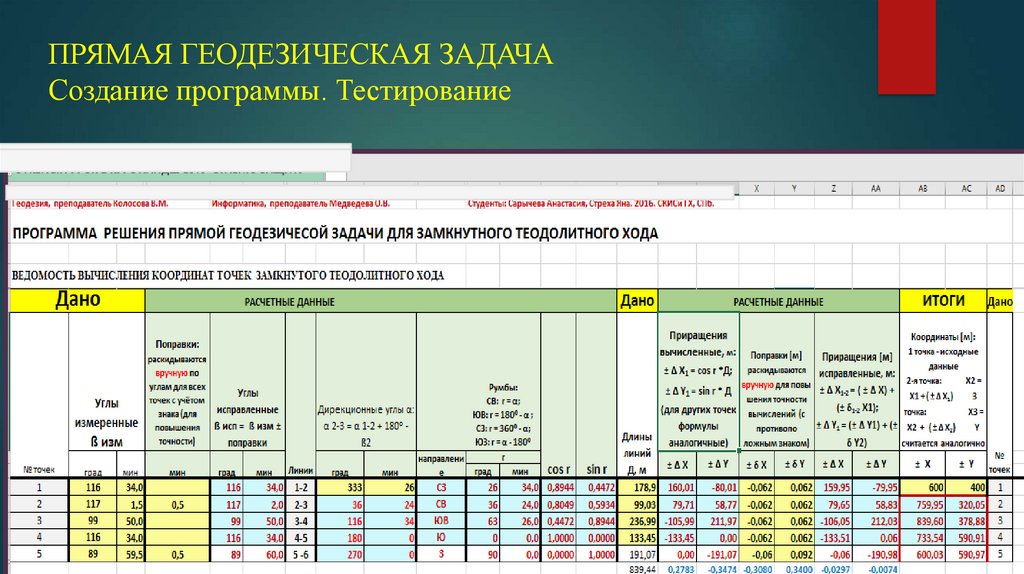
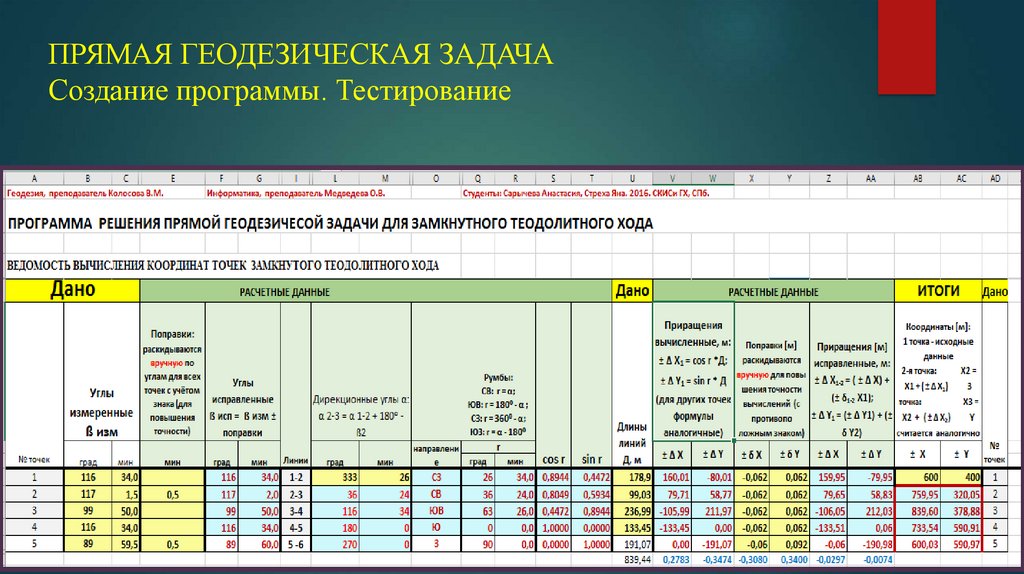
3. ПРЯМАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧА Создание программы. Тестирование
4.
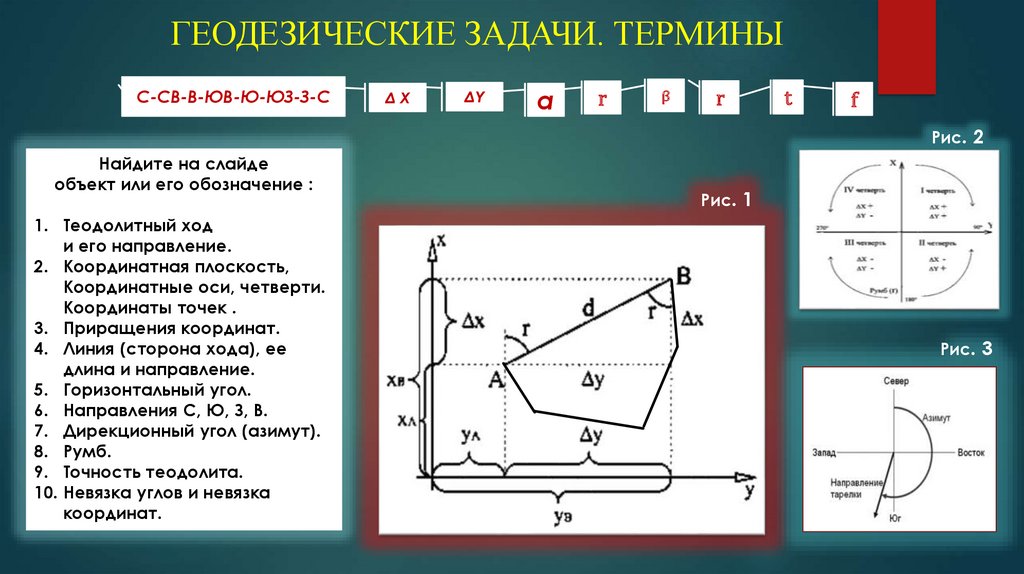
ГЕОДЕЗИЧЕСКИЕ ЗАДАЧИ. ТЕРМИНЫC-СВ-В-ЮВ-Ю-ЮЗ-З-С
ΔX
ΔY
α
r
β
r
t
f
Рис. 2
Найдите на слайде
объект или его обозначение :
1. Теодолитный ход
и его направление.
2. Координатная плоскость,
Координатные оси, четверти.
Координаты точек .
3. Приращения координат.
4. Линия (сторона хода), ее
длина и направление.
5. Горизонтальный угол.
6. Направления С, Ю, З, В.
7. Дирекционный угол (азимут).
8. Румб.
9. Точность теодолита.
10. Невязка углов и невязка
координат.
Рис. 1
Рис. 3
5.
ГЕОДЕЗИЧЕСКИЕ ЗАДАЧИПрямая задача
Дано:
β - измеренные горизонтальные
углы
Обратная задача
Дано:
X,Y - координаты точек
D - длины сторон теодолитного хода
Требуется определить:
α 1-2- дирекционный угол начальной
r -румбы
стороны
X1, Y1 - коррдинаты первой точки
теодолитног хода
Требуется определить: координаты
всех точек теодолитного хода.
Построить теодолитный ход.
α -дирекционные углы для всех
точек
β горизонтальные углы
D -длины сторон хода
6.
ЭТАПЫ РЕШЕНИЯ ЗАДАЧ НА ЭВМПостановка задачи
Создание математической модели
(алгоритм в виде формул)
Создание программы в Excel
Отладка программы.
Тестирование оперативное и
заключительное.
Решение типовой задачи
7.
ПРЯМАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧАМатематическая модель
I шаг . Оценка качества угловых измерений
6) Распределяем измеренную невязку
с обратным знаком в виде поправок и
получим исправленные углы.
7) По формуле α 2-3 = α 1-2 + 180⁰ - ß 2
вычисляем все дирекционные углы.
8) От дирекционных углов переходим к
румбам.
9) Для румбов определяем косинус и
синус.
8.
ПРЯМАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧАМатематическая модель и расчетные формулы
II шаг. Оценка качества линейных измерений
1)Определяем приращение координат
(± Δ X = cos r * Д );
( ± Δ Y = sin r * Д)
3)Расставляем знаки
у приращений координат.
Определяем
Σ ΔХ = f x - невязка по оси «X»;
Σ ΔУ = f y - невязка по оси «Y»;
4)Определяем Р - периметр ( Σ Д).
5) f x и f y распределяем с обратным
знаком в виде поправок и получаем
исправленные
приращения
координат.
6) Вычисляем координаты всех точек
замкнутого теодолитного хода. По
формуле: Х2 =
X1 + ΔХ1-2; Y2 =
Y1+ΔY1-2.
7) Если fотн < 1 / 2000 , то качество
линейных измерений
удовлетворительное.
9.
ПРЯМАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧАМатематическая модель
III шаг.
Строим план теодолитного хода по вычисленным на П–м этапе координатам.
Математическая модель решения прямой задачи готова.
На уроках геодезии все
расчеты и построение теодолитного хода выполнялись вручную.
Данная математическая модель
является алгоритмом для составления программы в Excel
10.
ПРЯМАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧАМатематическая модель - это алгоритм для программы в Excel
II шаг. Оценка качества
линейных измерений
I шаг . Оценка качества
угловых измерений
III шаг.
• Определение
Расчет параметров:
•Невязка f ß изм и ее сравнение
с допустимой
•Распределение невязки
в виде поправки к углам
•Дирекционные углы
с учетом поправки
•Румбы
Расчет параметров:
Приращения координат
Невязки по осям «X»и «Y»
Периметрё
Распределение невязки в виде
поправки приращений по осям
Приращения координат с
поправками
Относительная невязка и ее
сравнение с допустимой.
Вычисление координат точек
координат
• Построение плана
теодолитного хода
по вычисленным на
координатам.
Задача решена.
11. ПРЯМАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧА Создание программы. Тестирование
12.
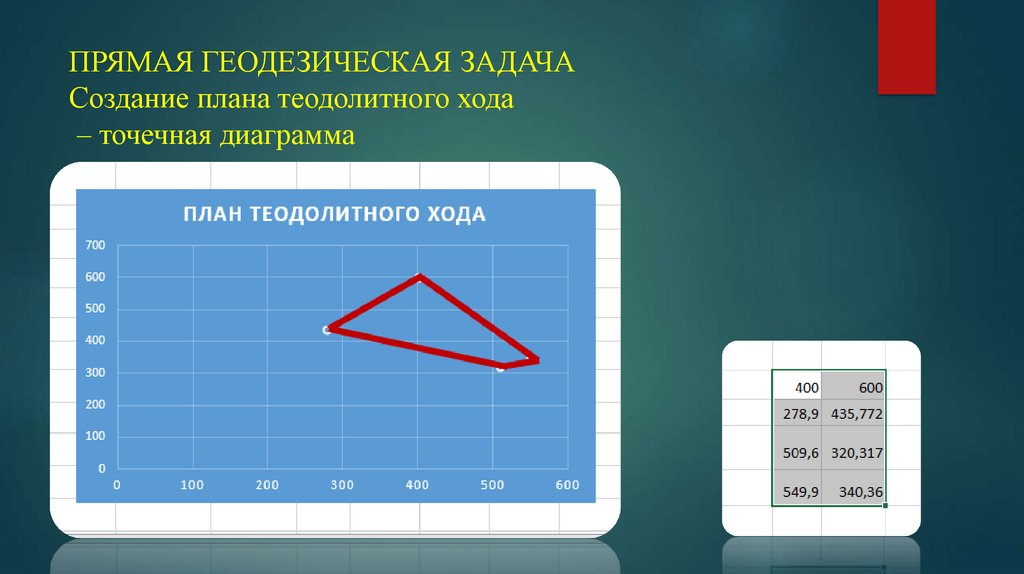
ПРЯМАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧАСоздание плана теодолитного хода
– точечная диаграмма
13. Пример действующей программы для решения прямой геодезической задачи. Проверка ее работоспособности
Кнопка вызова программы14.
САМОСТОЯТЕЛЬНАЯ РАБОТА- решить обратную геодезическую задачу в Excel
Обратная задача
Указания к работе
1.
Составить программу
решения обратной геодезической задачи.
2.
Проверить работоспособность.
Данные для тестирования взять в
методических указаниях к работе.
3.
Построить точечную диаграмму
теодолитного хода.
β горизонтальные углы
4.
Установить защиту программы.
D -длины сторон хода
5.
Сохранить файл в общей папке и а флэшке.
6.
Заполнить анкету и бланк отчета.
Дано:
X,Y - координаты точек
Требуется определить:
r -румбы
α -дирекционные углы для всех
точек
15. Пример действующей программы для решения обратной геодезической задачи. Проверка ее работоспособности
Кнопка вызова программы16.
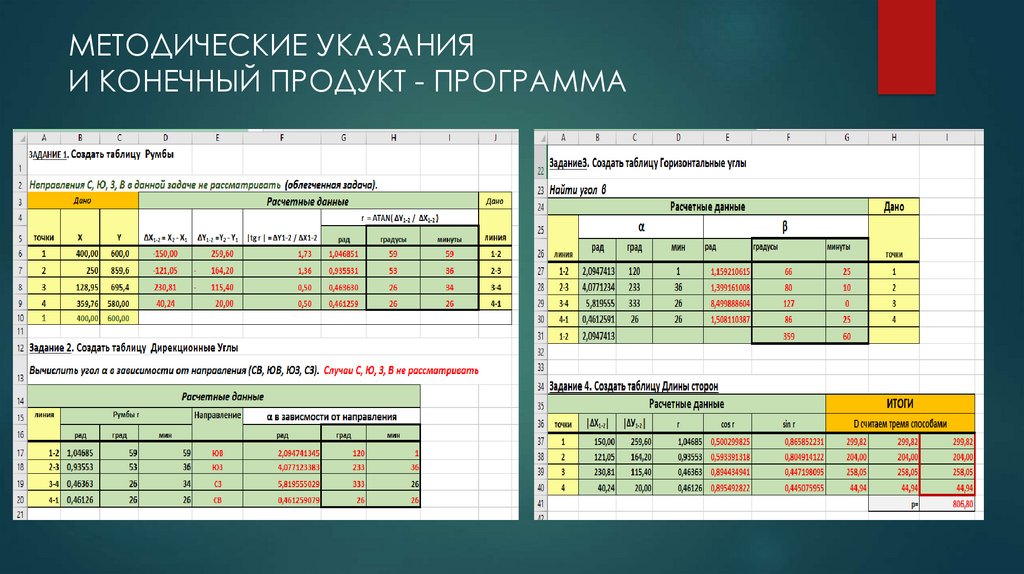
МЕТОДИЧЕСКИЕ УКАЗАНИЯИ КОНЕЧНЫЙ ПРОДУКТ - ПРОГРАММА
17.
КРИТЕТЕРИИ ОЦЕНКИ РАБОТЫ«Удовлетворительно»: созданы все таблицы, протестированы, имеются
1-2 недочета, форматирование выполнено минимально (в виде границ).
Отчет по работе не представлен. Анкета заполнена.
«Хорошо»: все таблицы созданы и протестированы, , имеются недочеты;
форматирование минимально (в виде границ).
Отчет по работе представлен. Анкета заполнена.
«Отлично»: все таблицы созданы и протестированы; форматировано
выполнено полностью и подчеркивает логическую структуру таблицы.
Отчет по работе представлен. Анкета заполнена.
18.
ДОМАШНЕЕ ЗАДАНИЕ1. КАКОЙ ПАРАМЕТР ОБРАТНОЙ ГЕОДЕЗИЧЕСКОЙ ЗАДАЧИ НАХОДИТСЯ
ПО ФОРМУЛЕ:
=ЕСЛИ(N10=0;"С";
ЕСЛИ(И(N10>0;N10<ПИ()/2);"СВ”;
ЕСЛИ(N10=ПИ()/2;"В";
ЕСЛИ(И(N10>ПИ()/2;N10<ПИ());"ЮВ";
ЕСЛИ(N10=ПИ(); «Ю»;
ЕСЛИ(И(N10>ПИ();N10<1,5*ПИ());"ЮЗ";
ЕСЛИ(N10=1,5*ПИ();"З";
ЕСЛИ(И(N10>1,5*ПИ();N10<2*ПИ());"СЗ"))))))))
2. УСОВЕРШЕНСТВОВАТЬ ПРОГРАММУ:
ПОМИМО НАПРАВЛЕНИЙ СВ, ЮВ, ЮЗ, СЗ УЧЕСТЬ
ЕЩЕ ЧЕТЫРЕ ВОЗМОЖНЫХ НАПРАВЛЕНИЯ: С, В, Ю, З.
3. ЗАПОЛНИТЬ БЛАНК ОТЧЕТА ПО ПРАКТИЧЕСКОЙ РАБОТЕ.
19.
Функции, используемые в программах• математические, статистические, логические
1) РАДИАНЫ (угол в градусах)
Действия над углами в Excel
производятся
в радианной мере:
•минуты переводятся в градусы
•суммируются с градусами,
•переводятся в радианы
Пример :
град
116
мин
рад
34,0 2,0344721
D10 =РАДИАНЫ(B10+C10/60)
В ячейке D10 угол в радианах
В ячейке B10 угол в градусах
В ячейке C10 угол в минутах
Аргумент функции всегда заключается в скобки
20.
Функции, используемые в программах• математические, статистические, логические
(продолжение)
2) ГРАДУСЫ (угол в радианах)
• Радианы переводятся в градусы (ГРАДУСЫ)
• Выделяется целая часть градусов (ОТБ)
• Дробная часть угла, выраженная в градусной
мере, переводится в в минуты
( *60)
3) ОТБР (….) – функция, значение которой –
целая часть вещественного числа.
Пример.:
рад
град
0,635300
мин
36
24,0
В градусы:
Q11 =ОТБР(ГРАДУСЫ(P11))
В минуты:
R11 =(ГРАДУСЫ(P11)-Q11)*60
В ячейке P11 угол в радианах
В ячейке Q11 угол в градусах,
нуль минут
В ячейке R угол в минутах
Аргумент функции всегда заключается в скобки
21.
Функции, используемые в программах• математические, статистические, логические
(продолжение)
6) ATAN(…) -
4) КОРЕНЬ(..) -
Возвращает угол по заданному значению его
Извлечение квадратного корня , то же возведение в
тангенса. Используется для перехода от
степень 0,5. тангенса румба к значению румба.
5) Сумм(.. : …) -
автосумма диапазона ячеек
7) ABS (….) –
Абсолютная величина (модуль величины).
Используется для вычисления тангенса рубма.
8) ЕСЛИ (условие; значение функции, если условие
9,10) И, ИЛИ
логические функции для реализации составного
условия
выполняется; значение функции, если условие не
выполняется) логическая функция
для реализации структуры ветвление
Аргумент функции всегда заключается в скобки
22.
ОПЕРАЦИИ, ИСПОЛЬЗУЕМЫЕ В РАБОТЕ1. Ввод формул вручную и с помощью
Мастера функций.
4. Работа с листами
5. Форматирование ячеек:
2. Копирование формул
(с относительными адресами)
‾
‾
‾
‾
‾
3. Вставка символов
объединение ячеек,
изменение направления текста
заливка, оформление границ,
изменение начертания шрифта,
установка индексов
6. Защита ячеек, защита листа, защита документа

















 informatics
informatics








