Метод МО Хюккеля (МОХ)
1.
Метод МОХюккеля
(МОХ)
2.
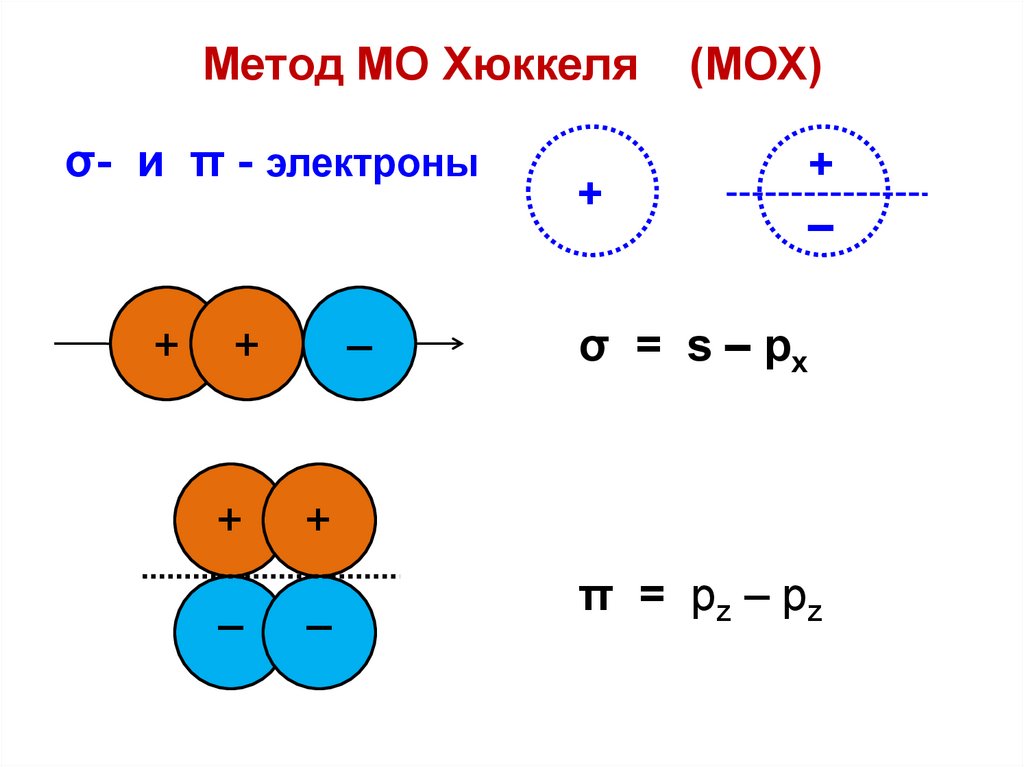
Метод МО Хюккеляσ- и π - электроны
–
+
+
+
–
σ = s – px
+
+
–
–
+
(МОХ)
π = pz – pz
3.
σπ
+
+
–
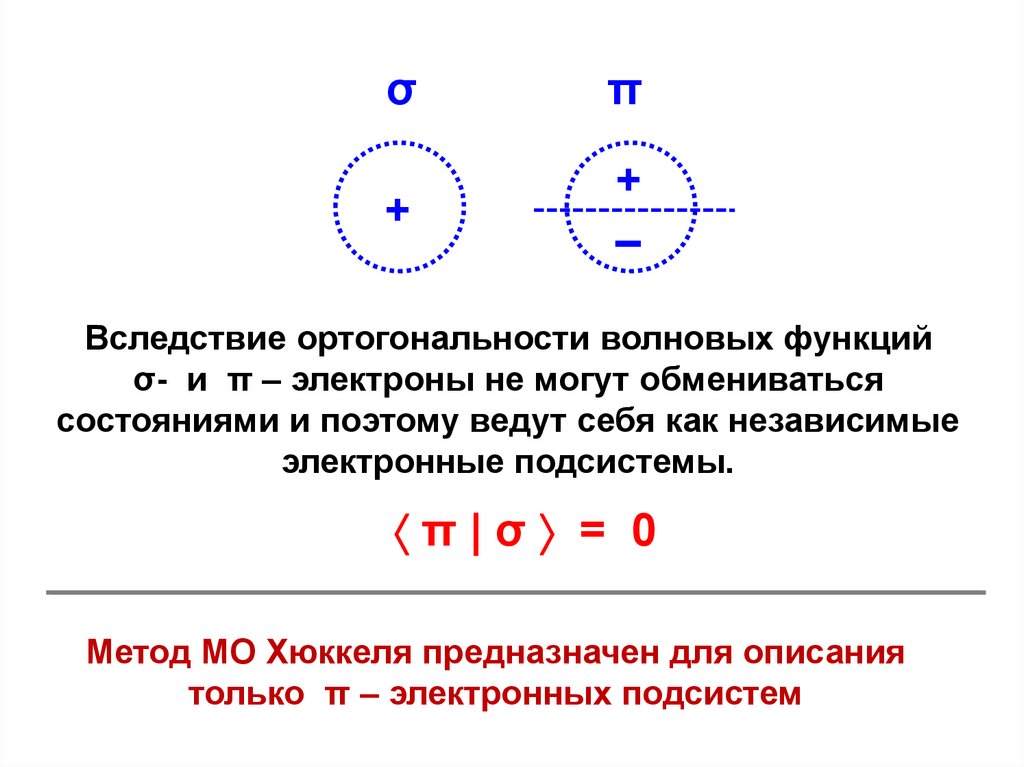
Вследствие ортогональности волновых функций
σ- и π – электроны не могут обмениваться
состояниями и поэтому ведут себя как независимые
электронные подсистемы.
π|σ = 0
Метод МО Хюккеля предназначен для описания
только π – электронных подсистем
4.
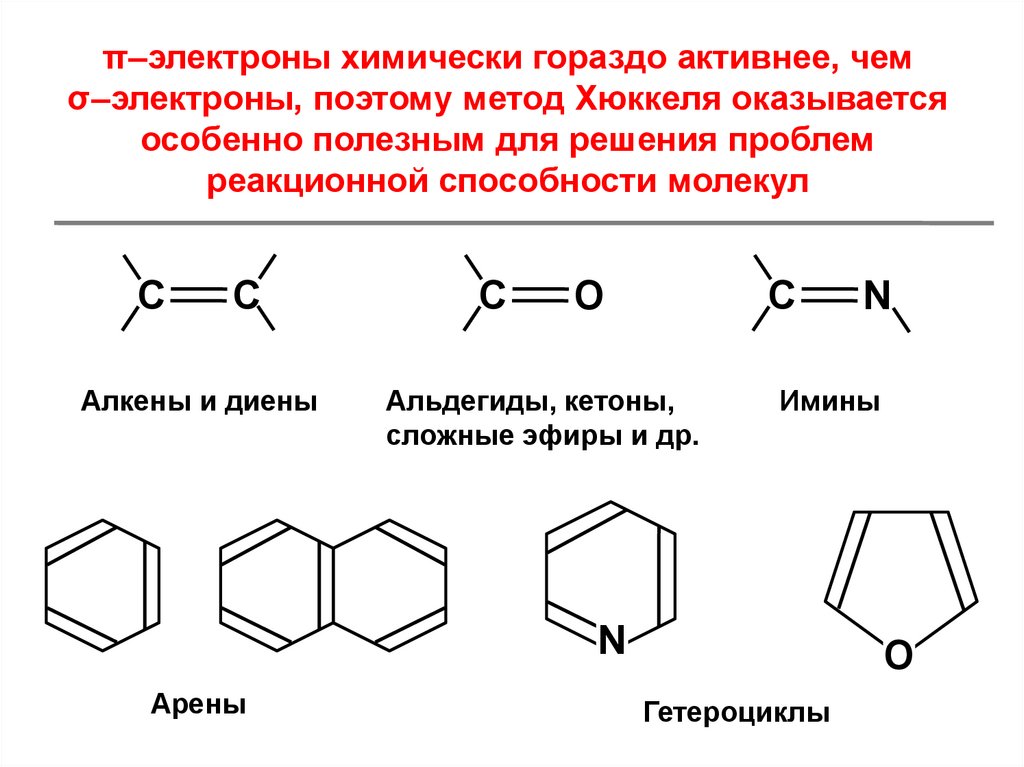
π–электроны химически гораздо активнее, чемσ–электроны, поэтому метод Хюккеля оказывается
особенно полезным для решения проблем
реакционной способности молекул
C
C
Алкены и диены
C
O
C
Альдегиды, кетоны,
сложные эфиры и др.
Имины
N
Арены
N
O
Гетероциклы
5.
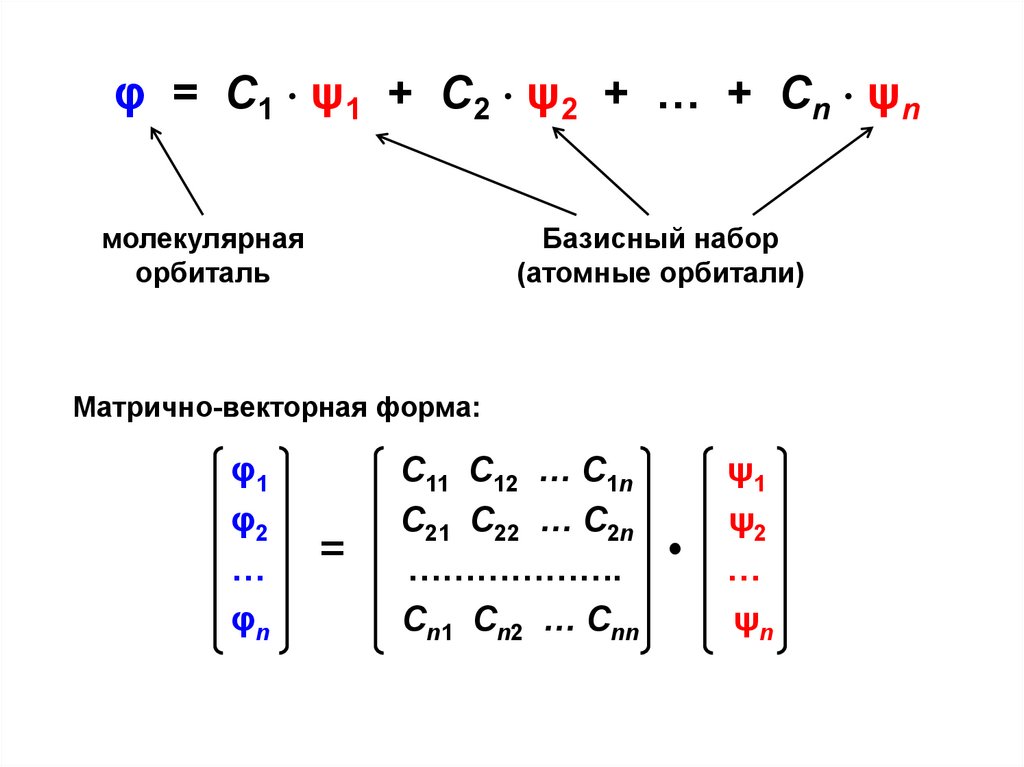
φ = С1 ψ1 + С2 ψ2 + … + Сn ψnмолекулярная
орбиталь
Базисный набор
(атомные орбитали)
Матрично-векторная форма:
φ1
φ2
…
φn
=
С11 С12 … С1n
С21 С22 … С2n
……………….
Сn1 Сn2 … Сnn
ψ1
ψ2
…
ψn
6.
Уравнения Хартри-Фока-РутанаF – S
F – S .
. F n – S n
С
F – S
F – S .
. F n – S n
С
.
.
.
.
.
.
.
.
.
• .
.
.
.
.
.
.
.
.
.
.
Fn – Sn
Fn – Sn .
. Fnn – Snn
= 0
Сn
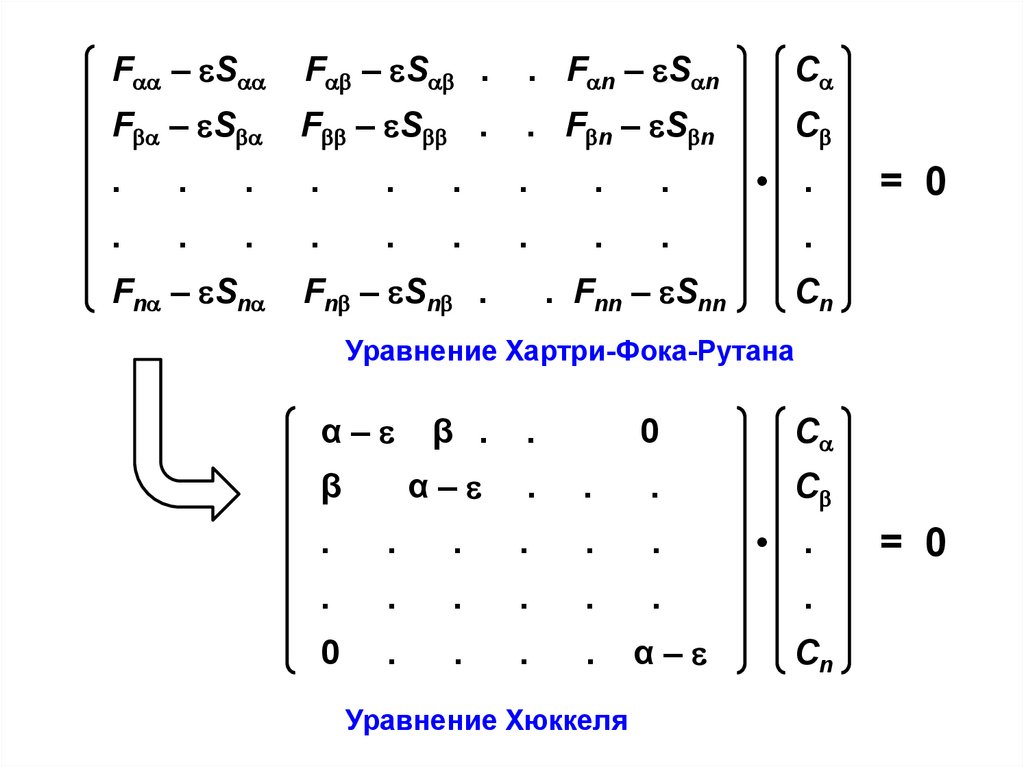
F — матричные элементы оператора Фока, характеризующие
либо энергию электрона в изолированном атоме с
номером (при = ), либо изменение энергии
электрона при его обобществлении двумя атомами с
номерами и (при ),
S — интегралы перекрывания для базисных АО с номерами
и ,
— энергия МО с коэффициентами {С С … Сn }.
7.
Основные проблемы метода МО связаны снеобходимостью процедуры самосогласования,
включающей многократные вычисления
интегралов типа F и S
1. Метод Хюккеля — ПОЛУЭМПИРИЧЕСКИЙ, поскольку ни один
из этих интегралов не вычисляется — они определяются на
основании экспериментальных данных (спектральные,
калориметрические и т.д.).
2. Fii = Fjj =
С
(т.е. предполагается, что молекулы образованы
из одинаковых по природе атомов)
С
С
С
8.
3. Недиагональные интегралы Fij разделяются на два типа.Первый тип относится к парам атомов, соединенных между
собой химическими связями. Для таких пар атомов
принимается следующее условие:
Fij = (резонансный интеграл).
Второй тип относится к парам атомов, которые не связаны
между собой химически; для них
Fij = 0.
Разделение недиагональных интегралов Fij на два типа
(нулевые и ненулевые) осуществляется исключительно на
химической основе — по химической структурной формуле
(т о п о л о г и ч е с к и е варианты метода МО).
4. Приближение нулевого
дифференциального
перекрывания (НДП)
Sij =
1
(i = j)
0
(i ≠ j)
9.
F – SF – S .
. F n – S n
С
F – S
F – S .
. F n – S n
С
.
.
.
.
.
.
.
.
.
• .
.
.
.
.
.
.
.
.
.
.
Fn – Sn
Fn – Sn .
. Fnn – Snn
= 0
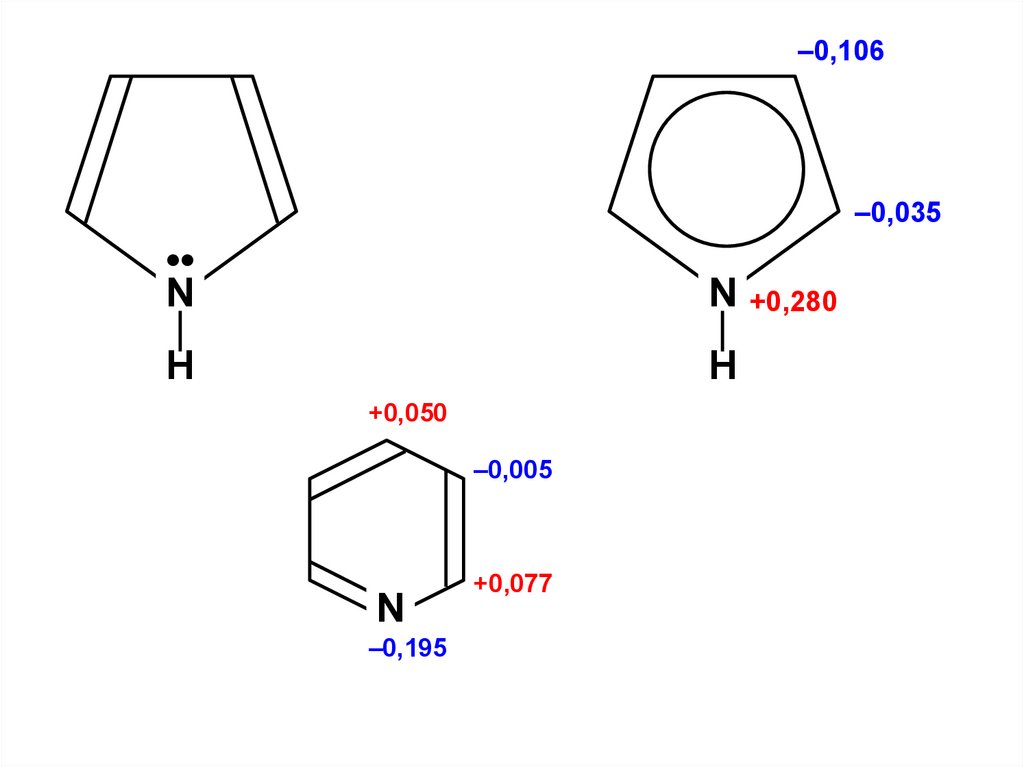
Сn
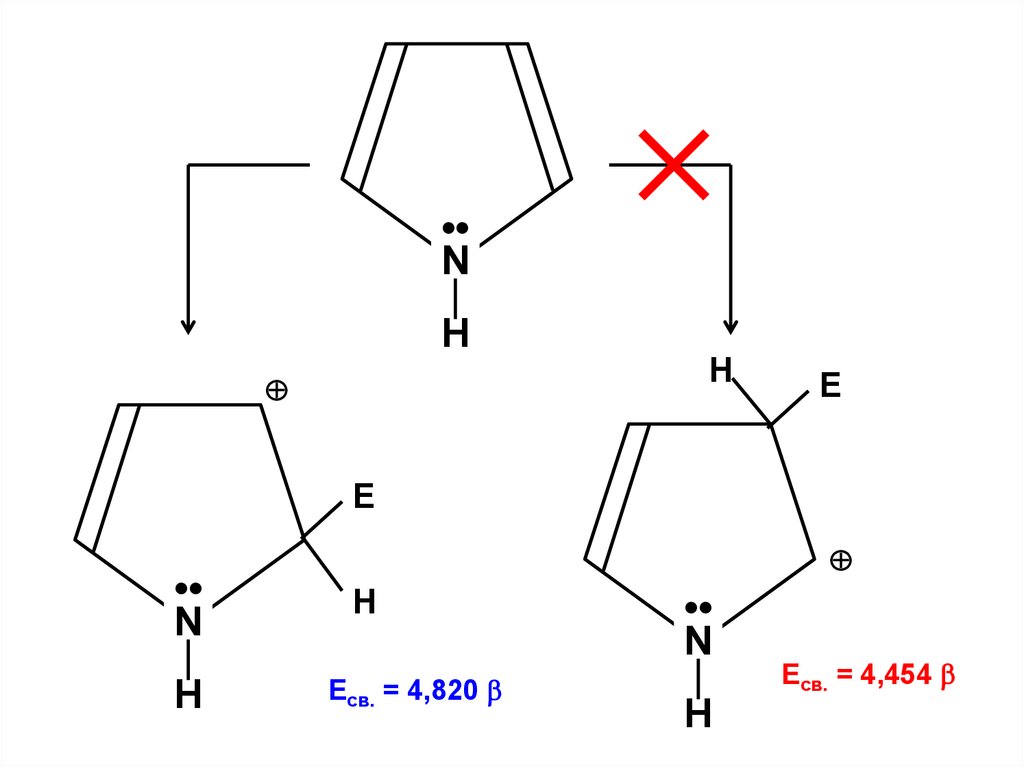
Уравнение Хартри-Фока-Рутана
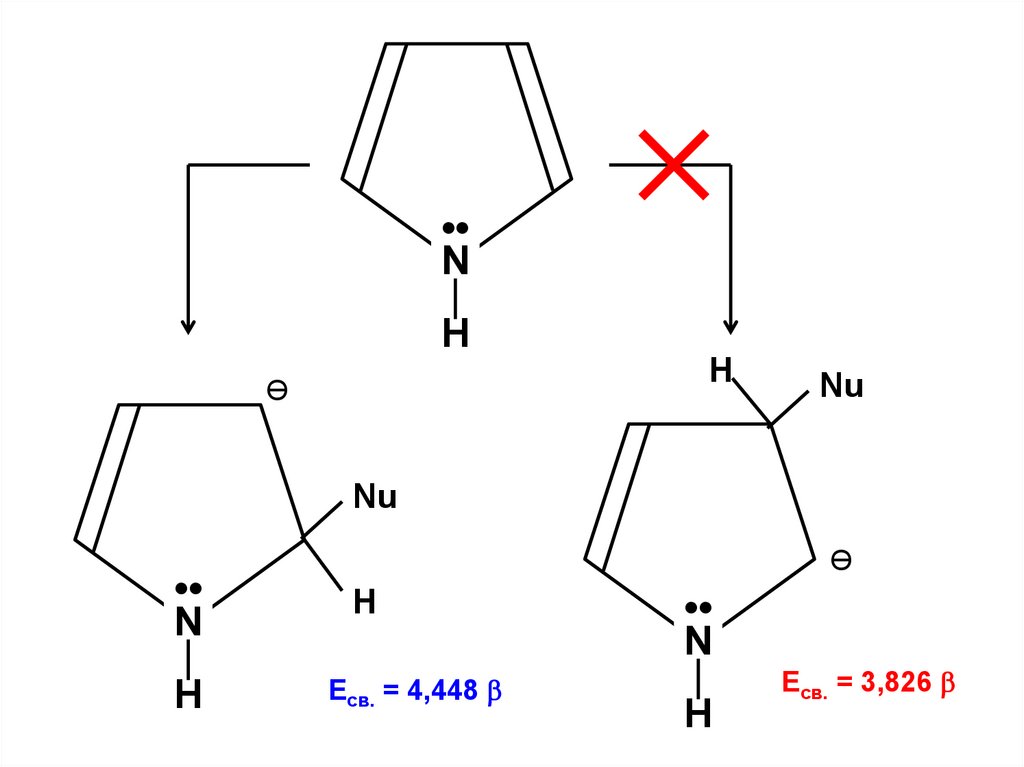
α–
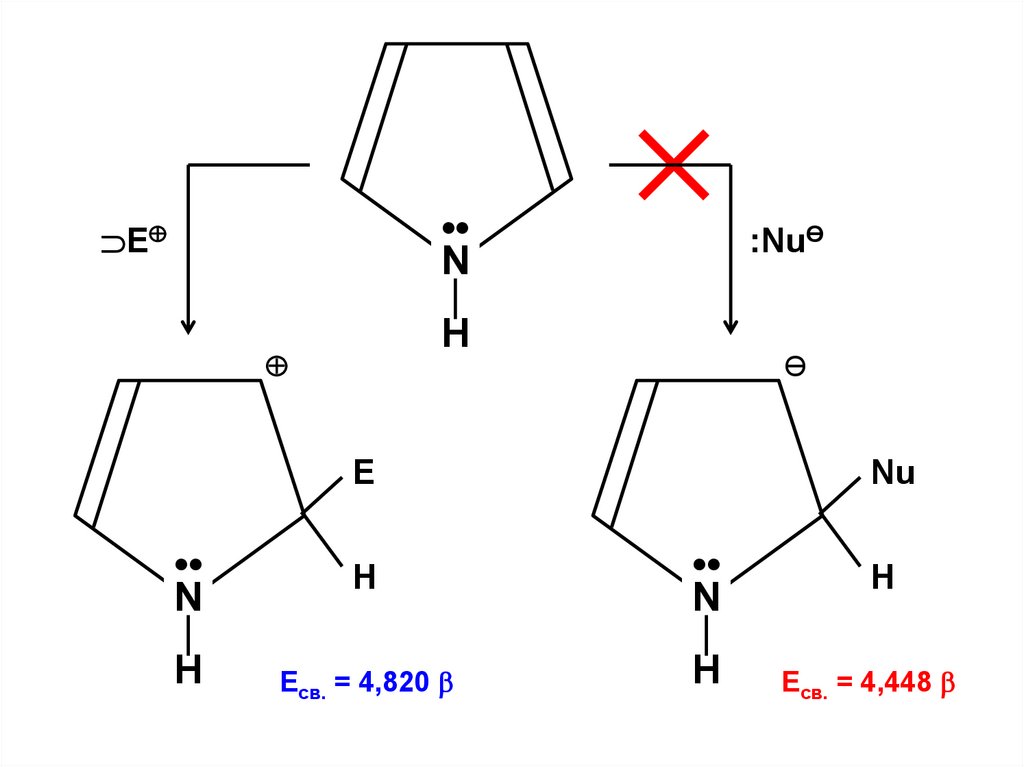
β
β .
.
α–
.
0
С
.
.
С
.
.
.
.
.
.
• .
.
.
.
.
.
.
.
0
.
.
.
.
Уравнение Хюккеля
α–
Сn
= 0
10.
α–1
β
β
β .
.
α–
.
0
С
.
.
С
.
.
.
.
.
.
• .
.
.
.
.
.
.
.
0
.
.
.
.
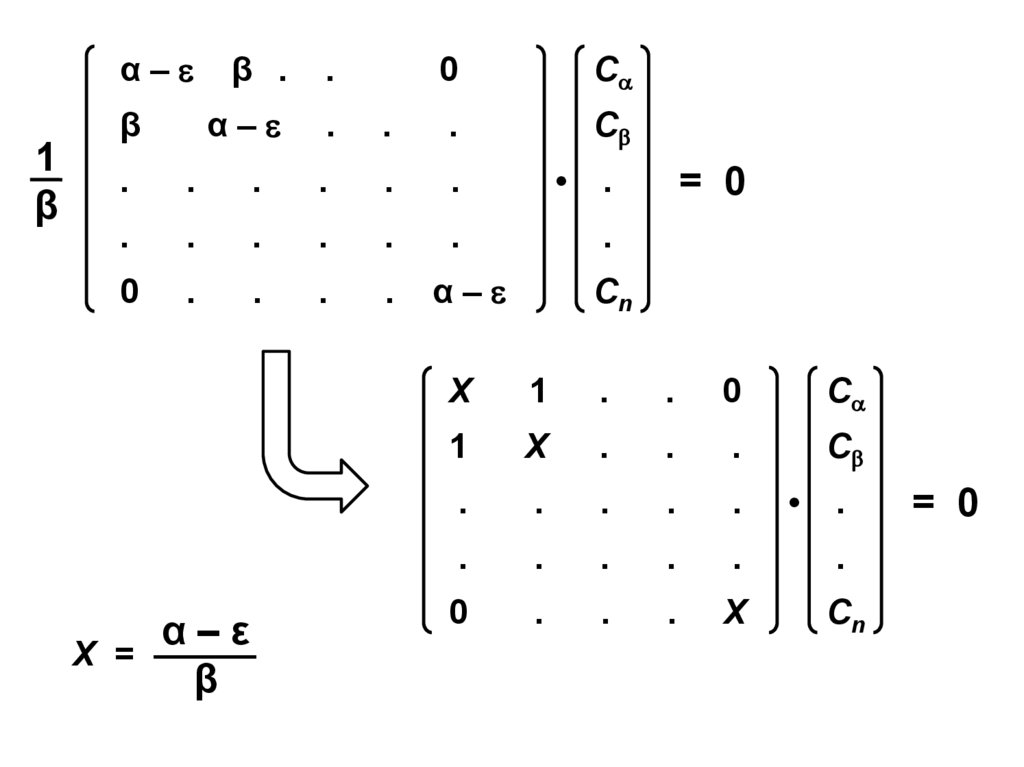
α–ε
β
Х = ———
α–
= 0
Сn
Х
1
.
.
0
С
1
Х
.
.
.
С
.
.
.
.
.
• .
.
.
.
.
.
.
0
.
.
.
Х
Сn
= 0
11.
Х1
.
.
0
С
1
Х
.
.
.
С
.
.
.
.
.
• .
.
.
.
.
.
.
0
.
.
.
Х
Сn
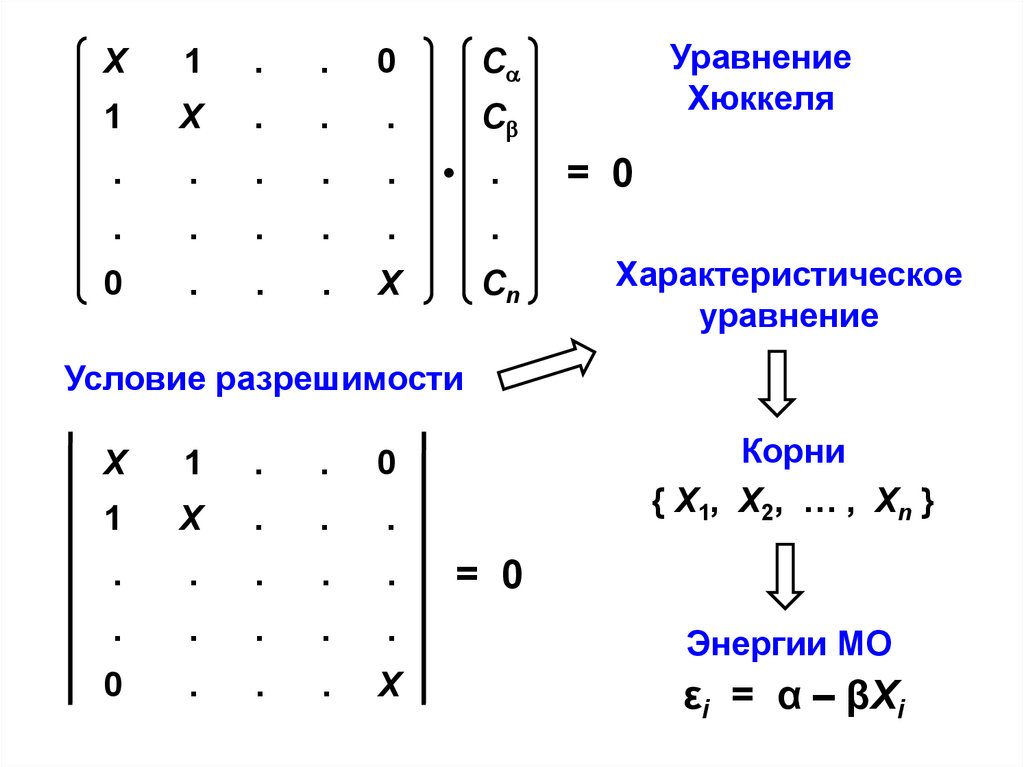
Уравнение
Хюккеля
= 0
Характеристическое
уравнение
Условие разрешимости
Корни
{ X1, X2, … , Xn }
Х
1
.
.
0
1
Х
.
.
.
.
.
.
.
.
.
.
.
.
.
Энергии МО
0
.
.
.
Х
εi = α – βXi
= 0
12.
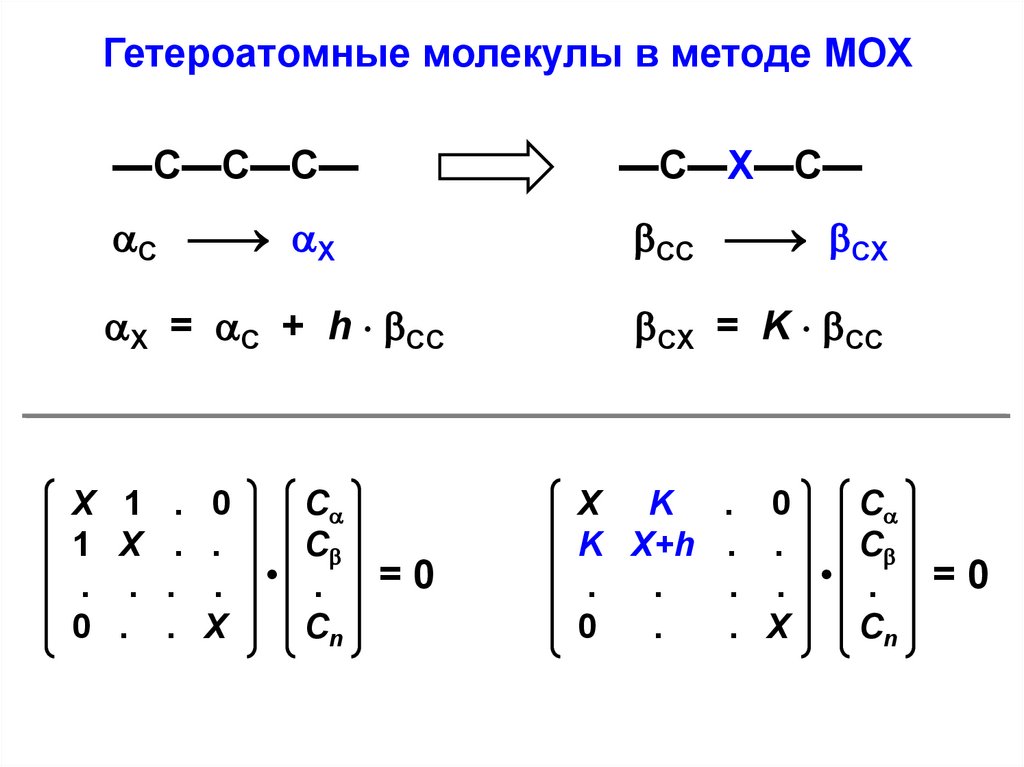
Гетероатомные молекулы в методе МОХ—С—С—С—
Х
1
.
0
—С—Х—С—
С X
CC CX
X = С + h CС
CХ = K CС
1
Х
.
.
.
.
.
.
0
С
.
С
. • .
Х
Сn
=0
Х K . 0
С
K Х+h . .
С
.
.
. . • .
0
.
. Х
Сn
=0
13.
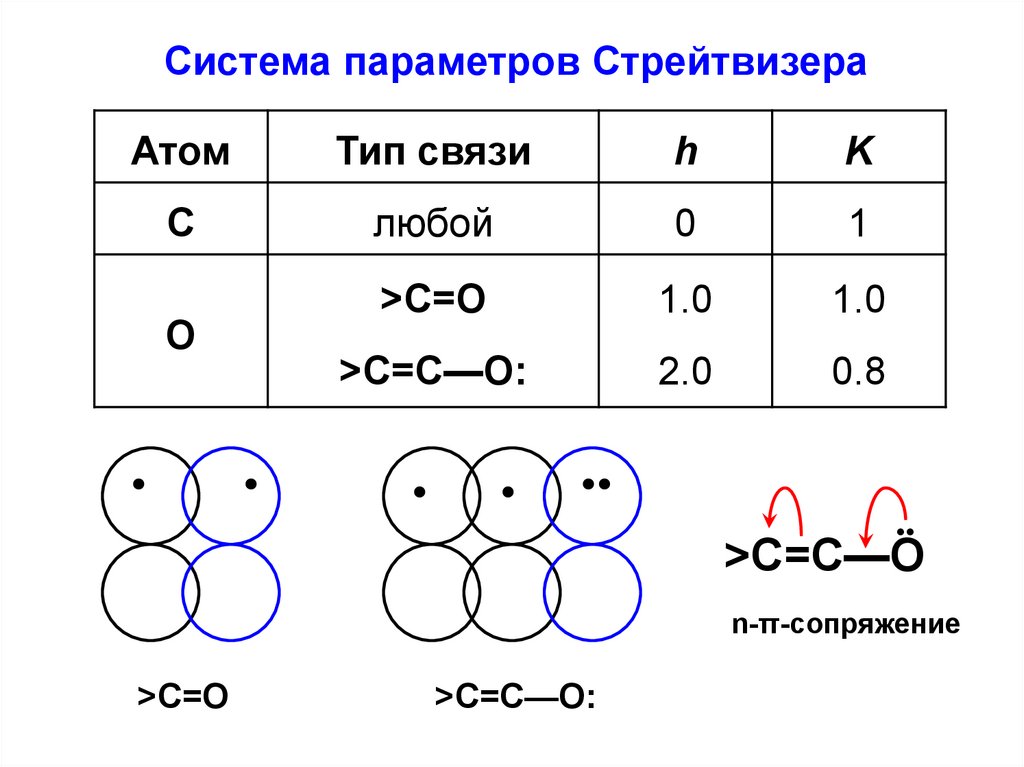
Система параметров СтрейтвизераАтом
Тип связи
h
K
C
любой
0
1
>C=O
1.0
1.0
>C=C—O:
2.0
0.8
O
•
>C=C—O
n-π-сопряжение
>C=O
>C=C—O:
14.
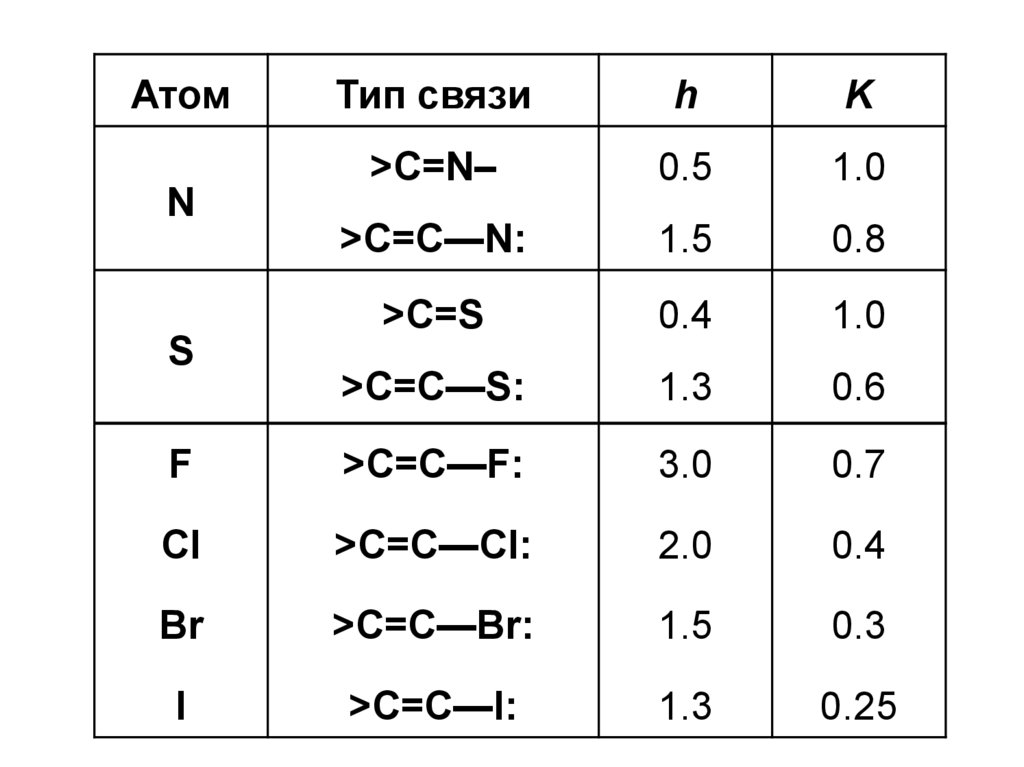
АтомТип связи
h
K
>C=N–
0.5
1.0
>C=C—N:
1.5
0.8
>C=S
0.4
1.0
>C=C—S:
1.3
0.6
F
>C=C—F:
3.0
0.7
Cl
>C=C—Cl:
2.0
0.4
Br
>C=C—Br:
1.5
0.3
I
>C=C—I:
1.3
0.25
N
S
15.
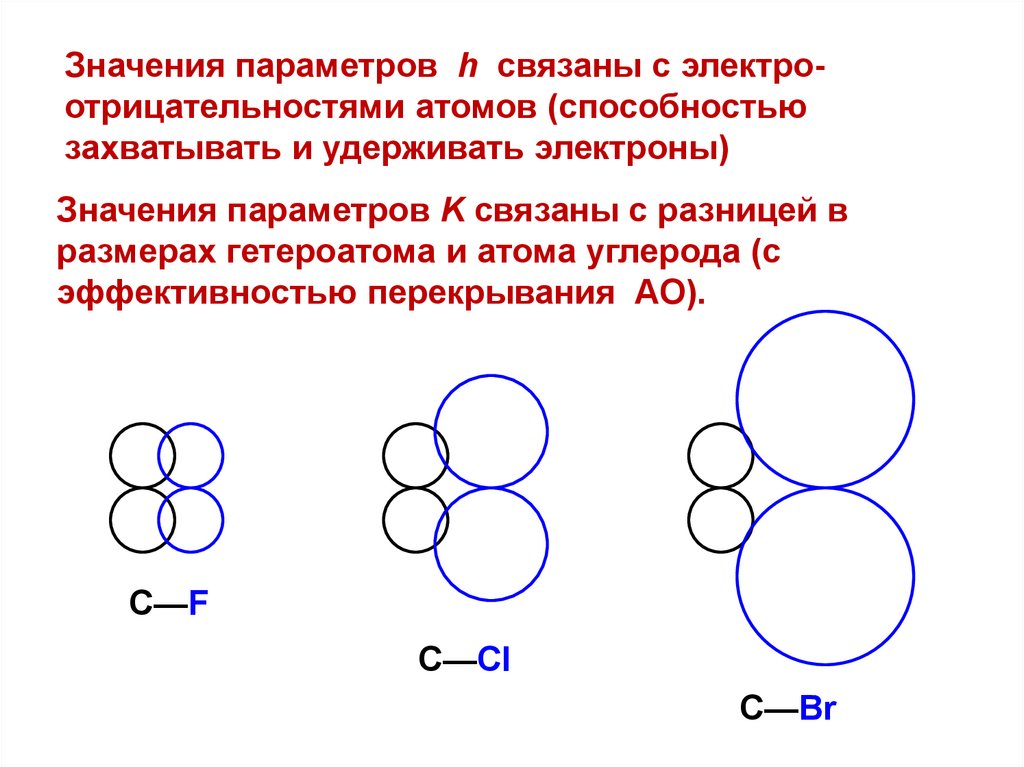
Значения параметров h связаны с электроотрицательностями атомов (способностьюзахватывать и удерживать электроны)
Значения параметров K связаны с разницей в
размерах гетероатома и атома углерода (с
эффективностью перекрывания АО).
С—F
С—Cl
С—Br
16.
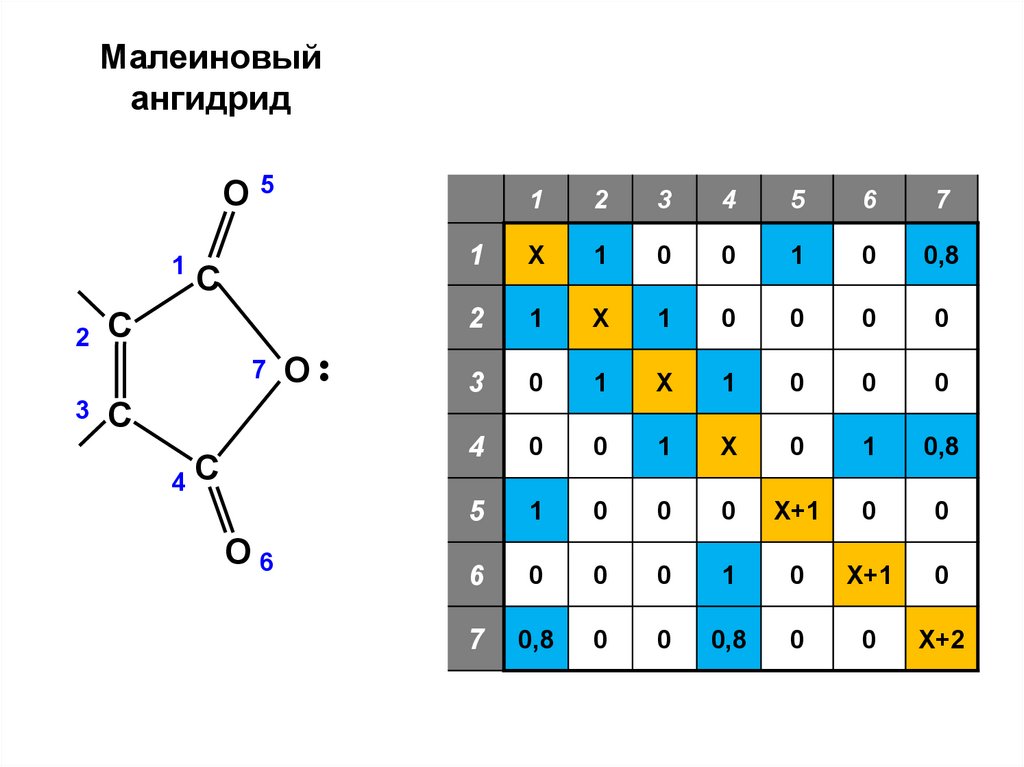
Малеиновыйангидрид
О
1
С
С
7
3
С
4
С
О6
О
•
2
5
1
2
3
4
5
6
7
1
Х
1
0
0
1
0
0,8
2
1
Х
1
0
0
0
0
3
0
1
Х
1
0
0
0
4
0
0
1
Х
0
1
0,8
5
1
0
0
0
Х+1
0
0
6
0
0
0
1
0
Х+1
0
7
0,8
0
0
0,8
0
0
Х+2
17.
Домашнее заданиеЗадача 8.1.
Для указанной молекулы составить матрицу
Хюккеля с учетом поправок Стрейтвизера на
гетероатомы.
18.
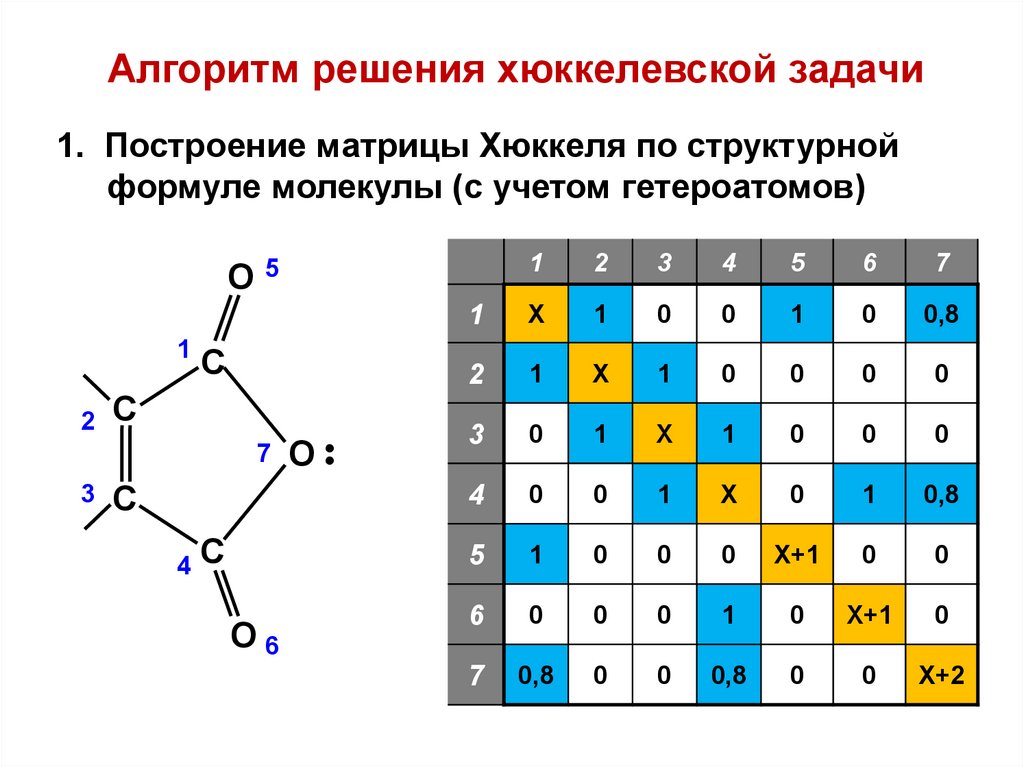
Алгоритм решения хюккелевской задачи1. Построение матрицы Хюккеля по структурной
формуле молекулы (с учетом гетероатомов)
О
1
С
С
7
3
С
4
С
О6
О
•
2
1
2
3
4
5
6
7
1
Х
1
0
0
1
0
0,8
2
1
Х
1
0
0
0
0
3
0
1
Х
1
0
0
0
4
0
0
1
Х
0
1
0,8
5
1
0
0
0
Х+1
0
0
6
0
0
0
1
0
Х+1
0
7
0,8
0
0
0,8
0
0
Х+2
5
19.
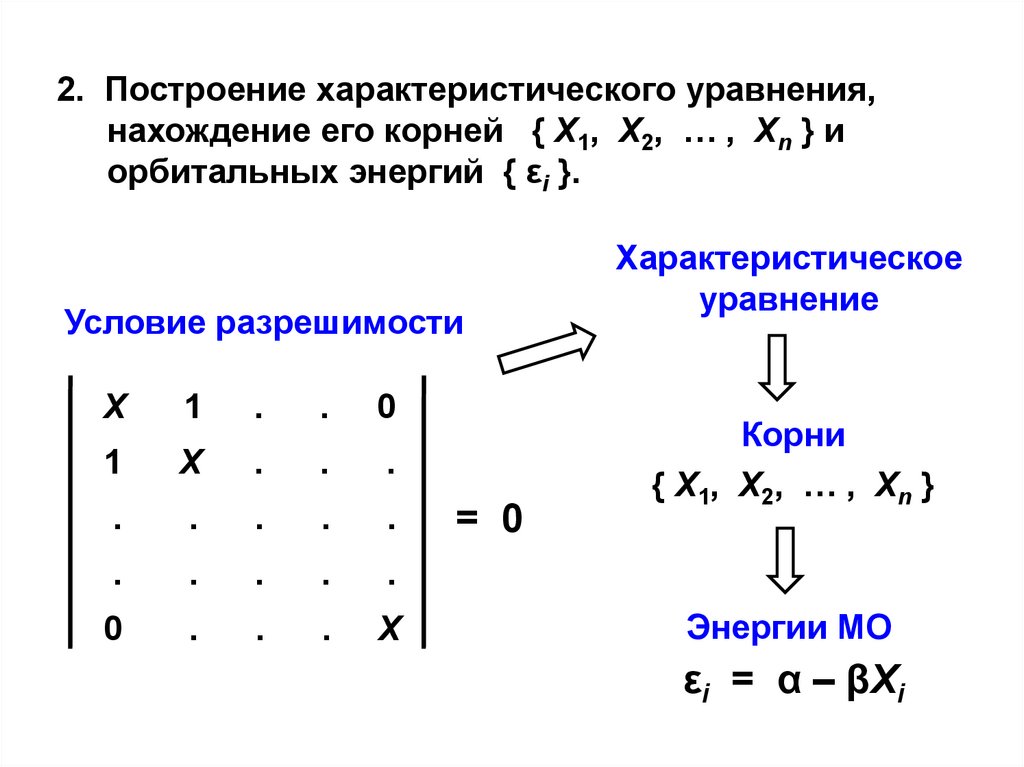
2. Построение характеристического уравнения,нахождение его корней { X1, X2, … , Xn } и
орбитальных энергий { εi }.
Условие разрешимости
Х
1
.
.
0
1
Х
.
.
.
.
.
.
.
.
.
.
.
.
.
0
.
.
.
Х
= 0
Характеристическое
уравнение
Корни
{ X1, X2, … , Xn }
Энергии МО
εi = α – βXi
20.
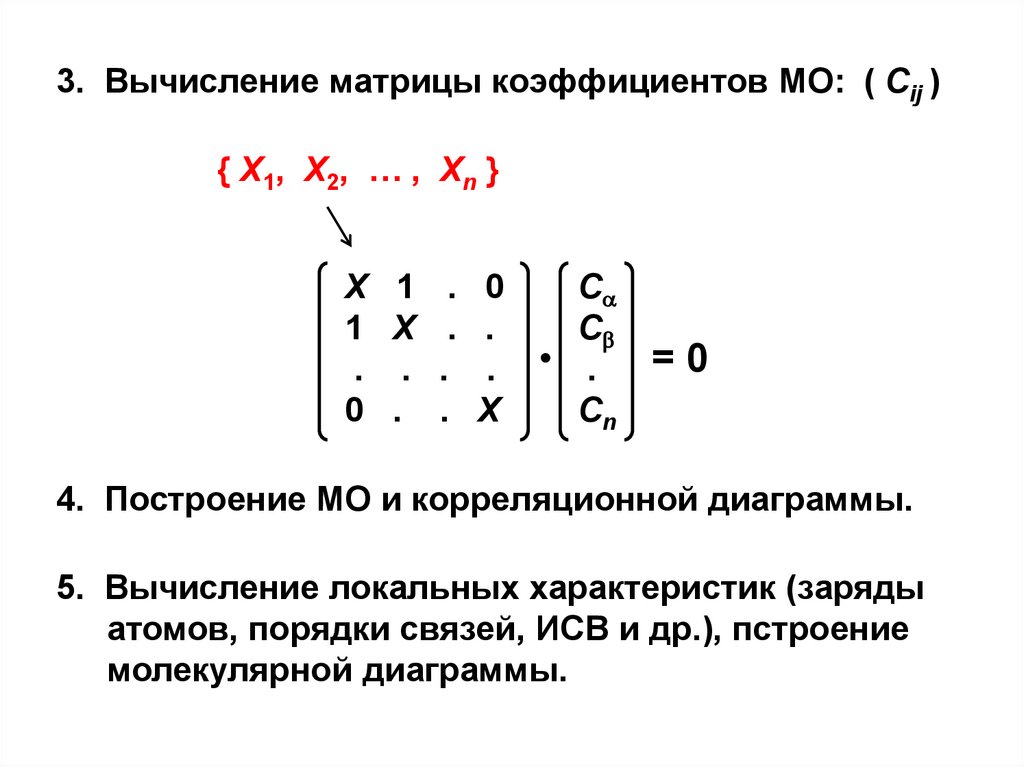
3. Вычисление матрицы коэффициентов МО: ( Сij ){ X1, X2, … , Xn }
Х
1
.
0
1
Х
.
.
.
.
.
.
0
С
.
С
. • .
Х
Сn
=0
4. Построение МО и корреляционной диаграммы.
5. Вычисление локальных характеристик (заряды
атомов, порядки связей, ИСВ и др.), пстроение
молекулярной диаграммы.
21.
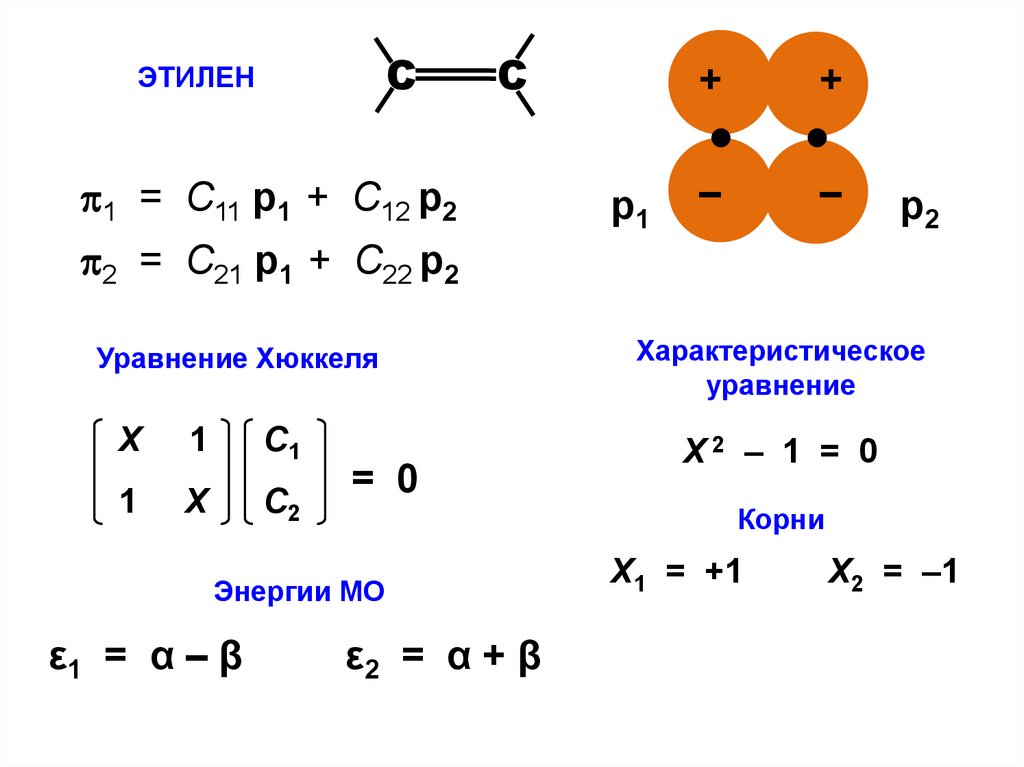
СЭТИЛЕН
С
1 = С11 p1 + C12 p2
2 = С21 p1 + C22 p2
Уравнение Хюккеля
Х
1
С1
1
Х
С2
= 0
+
–
–
р2
Характеристическое
уравнение
Х2 – 1 = 0
Корни
Энергии МО
ε1 = α – β
р1
+
ε2 = α + β
Х1 = +1
Х2 = –1
22.
Уравнение ХюккеляХ
С1
1
Х
1
С2
= 0
При Х = Х1 = +1
С1 Х + С2 = 0
С1 + С2 Х = 0
При Х = Х1 = –1
С1 + С2 = 0
–С1 + С2 = 0
С1 + С2 = 0
С1 – С2 = 0
С1 = –С2
1 =
1
–1
С1 = С2
2 =
1
1
23.
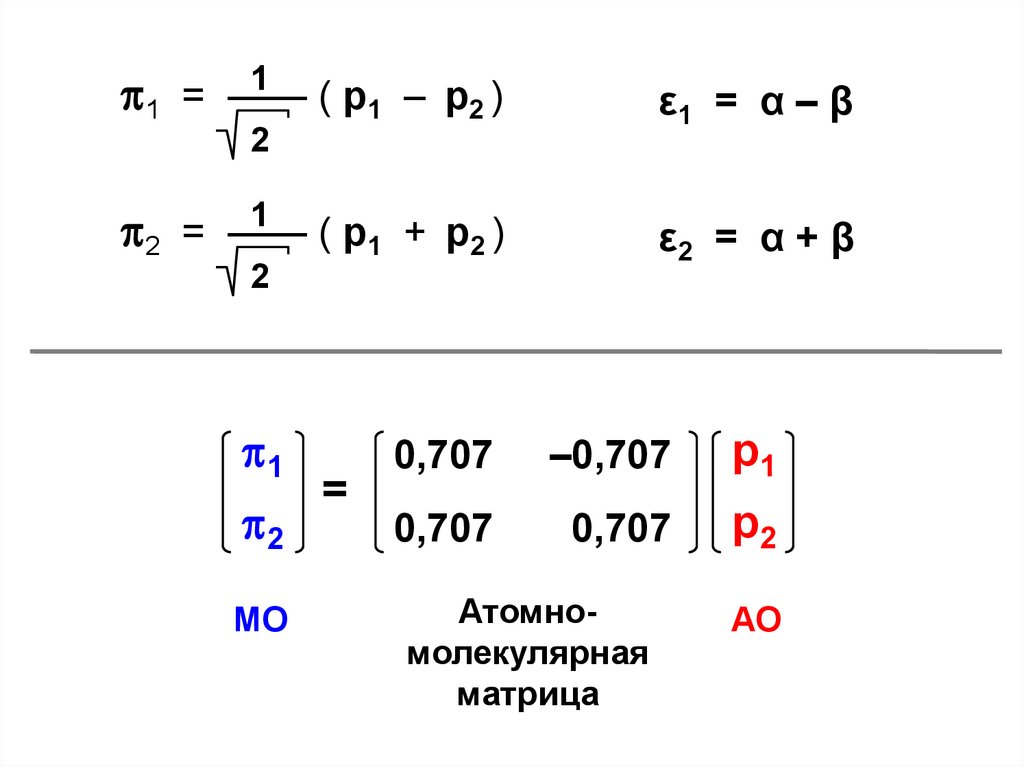
11 = ——
( p1 – p2 )
ε1 = α – β
2
2 = —— ( p1 + p2 )
1
ε2 = α + β
2
1
2
МО
=
0,707
–0,707
р1
0,707
0,707
р2
Атомномолекулярная
матрица
АО
24.
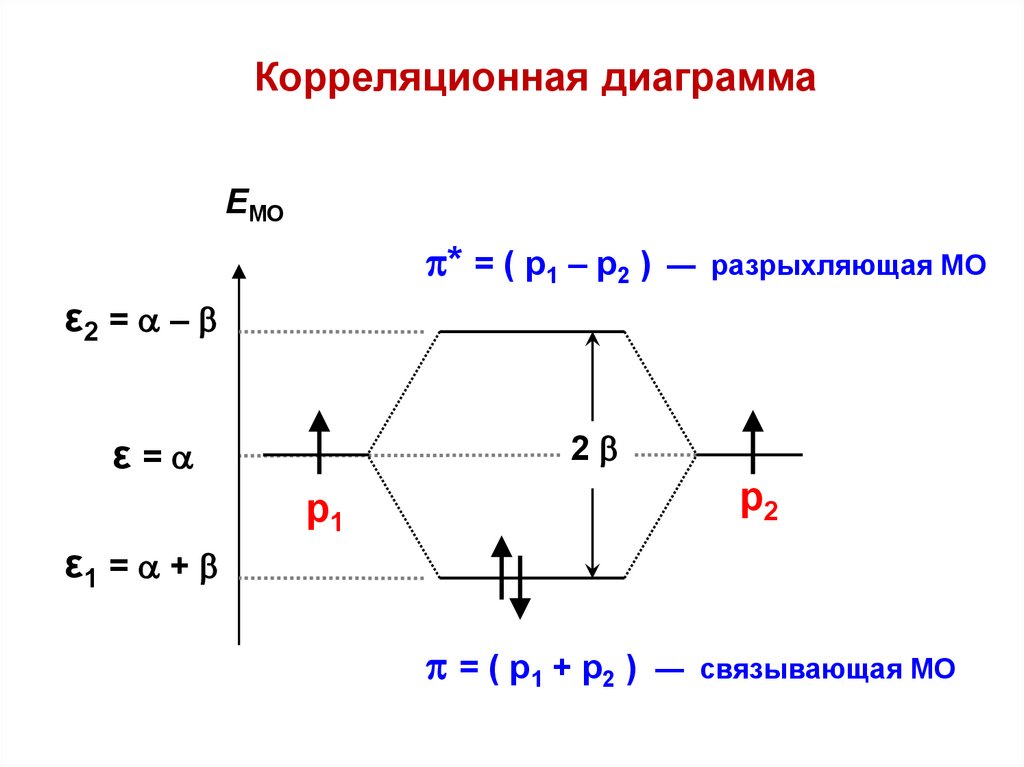
Корреляционная диаграммаEМО
* = ( р1 – р2 )
— разрыхляющая МО
ε2 = –
2
ε=
р2
р1
ε1 = +
= ( р1 + р2 )
— связывающая МО
25.
+–
–
+
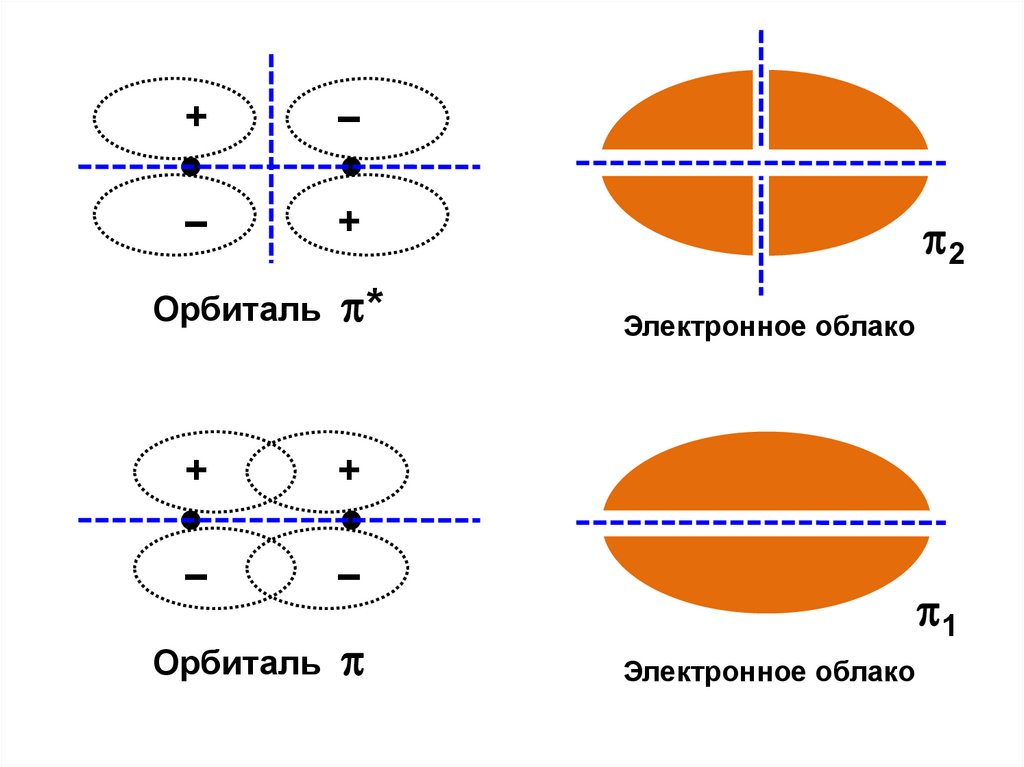
Орбиталь
*
+
+
–
–
Орбиталь
2
Электронное облако
1
Электронное облако
26.
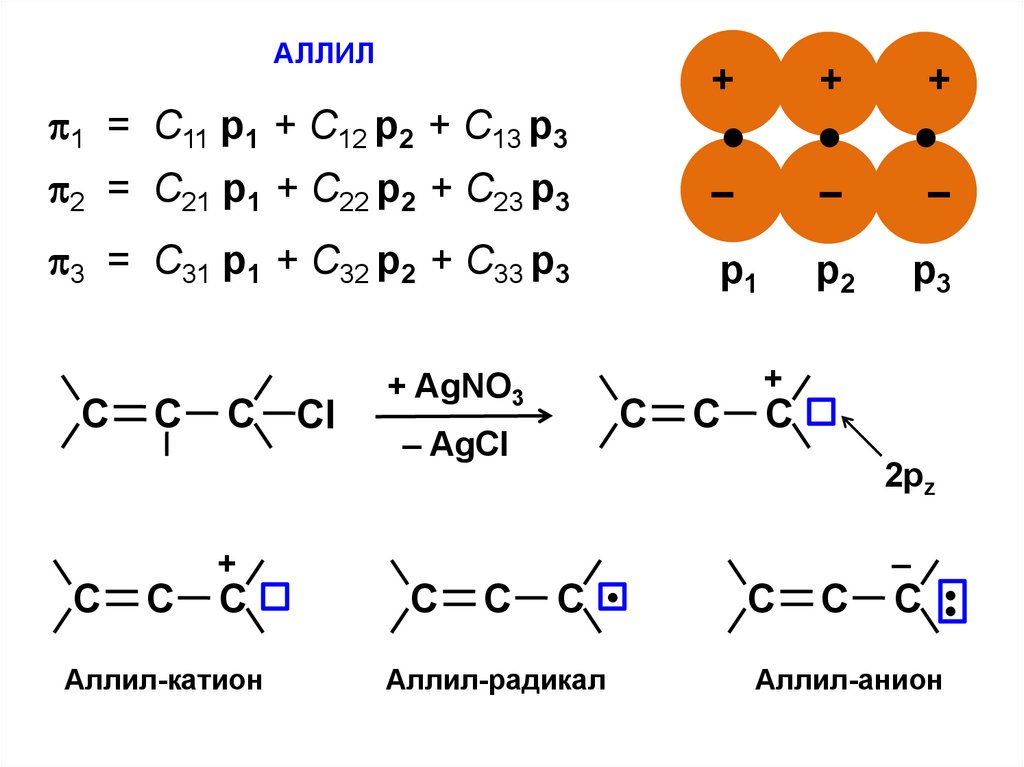
АЛЛИЛ+
+
+
2 = С21 p1 + C22 p2 + C23 p3
–
–
–
3 = С31 p1 + C32 p2 + C33 p3
р1
р2
р3
1 = С11 p1 + C12 p2 + C13 p3
С
С
С
С
С
+
С
Аллил-катион
Сl
+ AgNO3
С
– AgCl
С
С
С
+
С
2pz
С
Аллил-радикал
С
С
–
С •
Аллил-анион
27.
Уравнение ХюккеляХ
1
0
С1
1
Х
1
С2
0
1
Х
С3
Характеристическое
уравнение
= 0
Х(Х 2 – 2) = 0
Энергии МО
Корни
ε3 = α – 2 β
Х3 = + 2
ε2 = α
ε1 = α + 2 β
Х2 = 0
Х1 = – 2
28.
Уравнение ХюккеляХ
1
0
С1
1
Х
1
С2
0
1
Х
С3
С1 Х + С2 + 0
= 0
= 0
С1 + С2 Х + С3 = 0
0 + С2 + С3 Х = 0
Х = + 2
С1 = С3
С2 = –
Х = 0
С1 = –С3
С2 = 0
Х = – 2
С1 = С3
С2 =
2 С1
2 С1
29.
13 = —
( p1 – 2 p2 + р3 )
ε3 = α – 2 β
1
2 = —
( p1 – р3 )
ε2 = α
1
1 = —
( p1 + 2 p2 + р3 )
ε1 = α + 2 β
2
2
2
3
2
1
=
0,500
–0,707
0,500
р1
0,707
0
–0,707
р2
0,500
0,707
0,500
р3
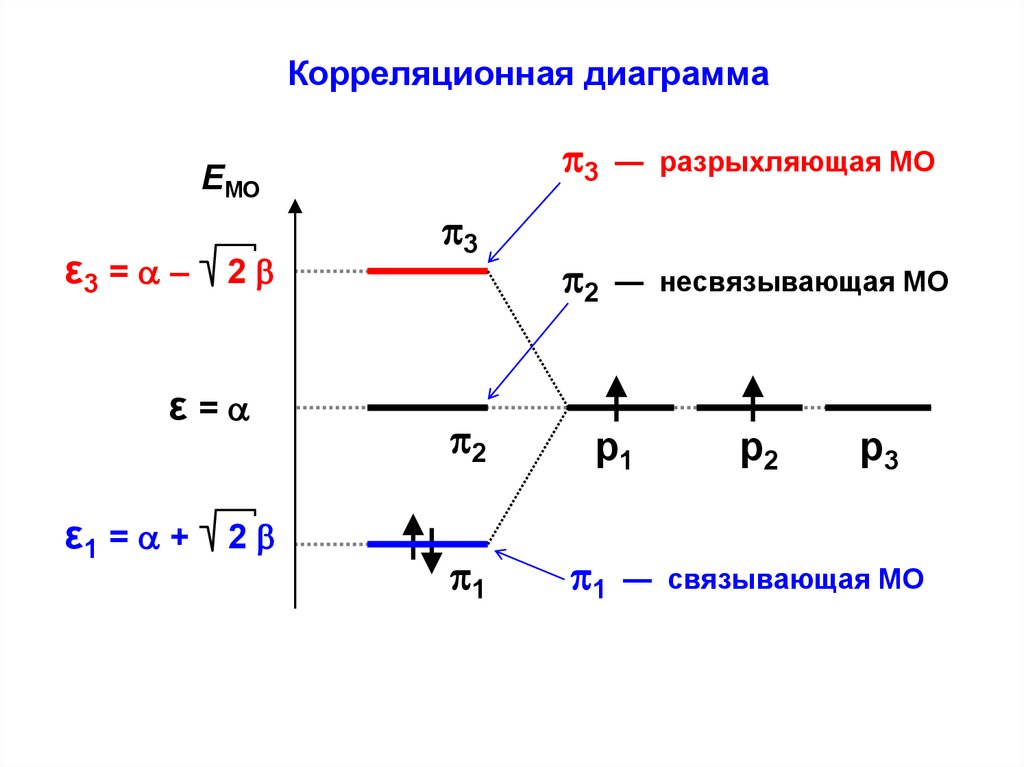
30.
Корреляционная диаграммаEМО
ε3 = – 2
ε=
ε1 = + 2
3
2
1
3
— разрыхляющая МО
2
— несвязывающая МО
р1
1
р2
р3
— связывающая МО
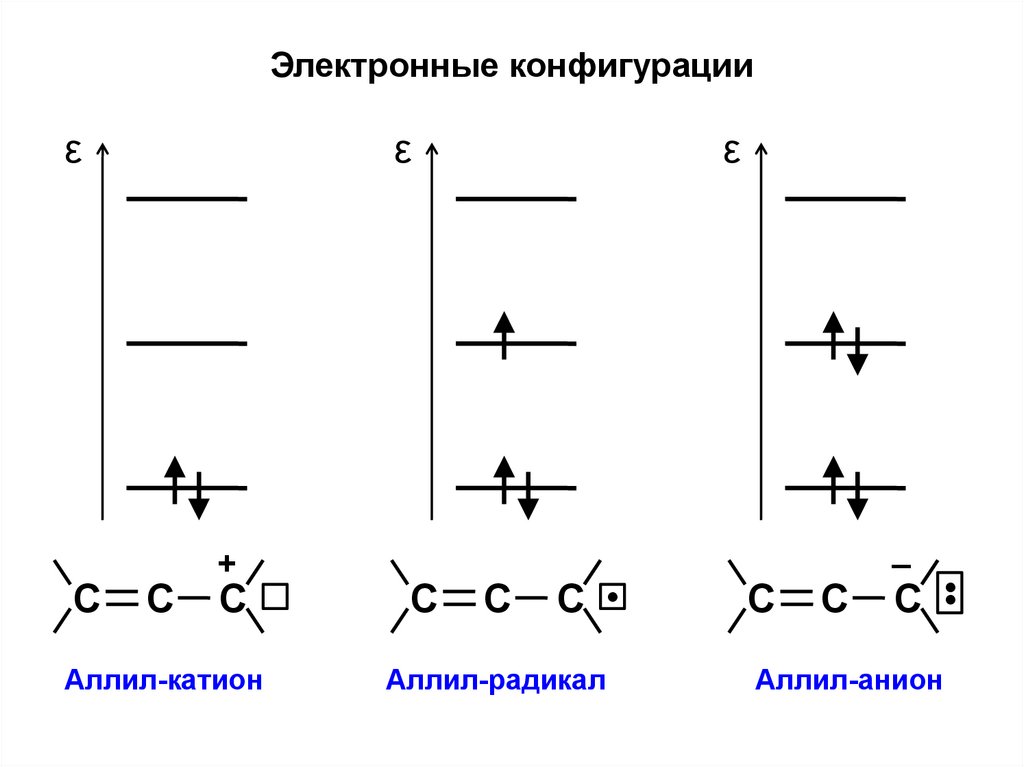
31.
Электронные конфигурацииε
С
ε
С
+
С
Аллил-катион
С
ε
С
С
Аллил-радикал
С
С
–
С •
Аллил-анион
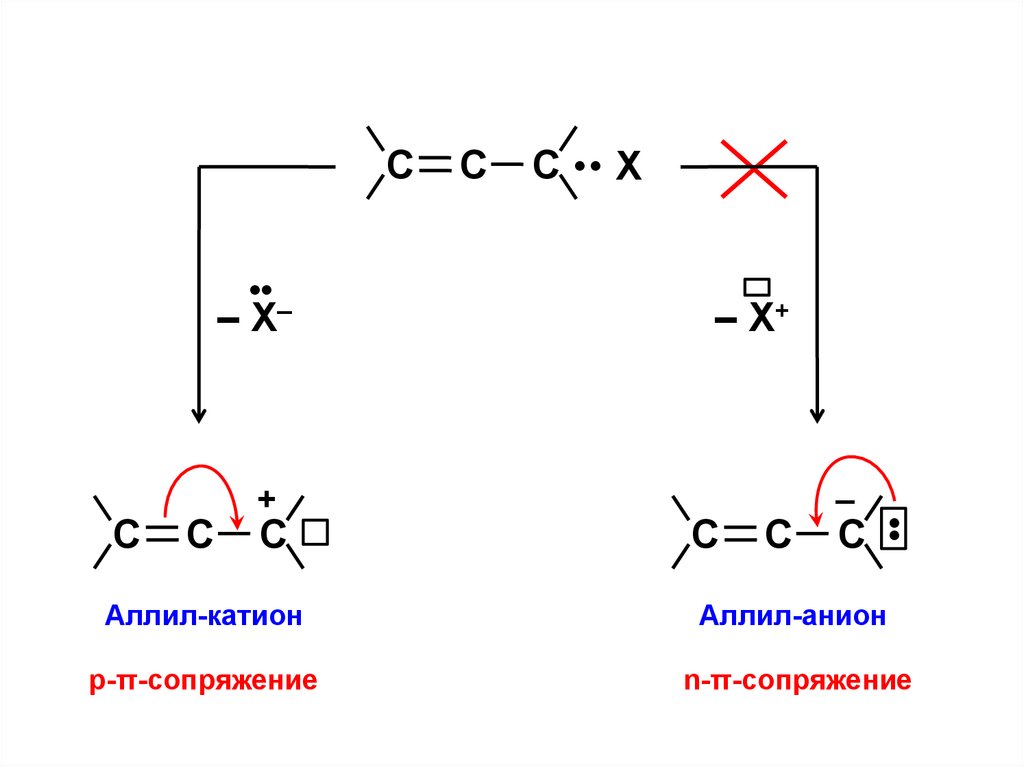
32.
С•
– X–
С
С
+
С
С
С •• X
– X+
С
С
–
С •
Аллил-катион
Аллил-анион
р-π-сопряжение
n-π-сопряжение
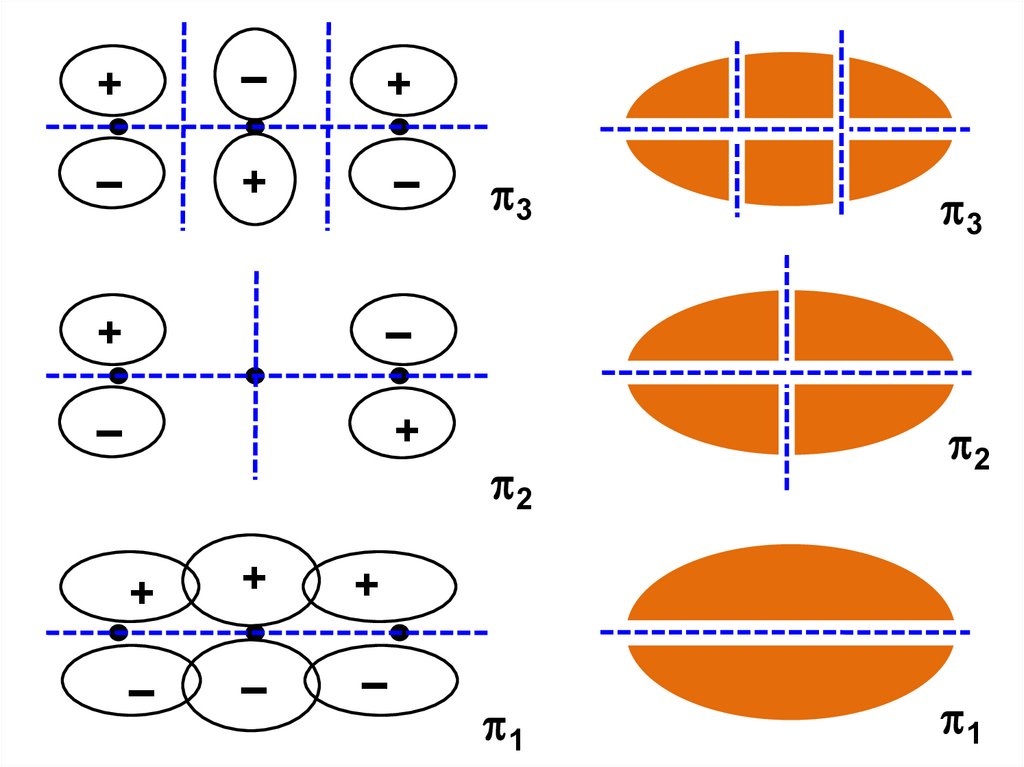
33.
+–
+
–
+
–
+
–
–
+
+
+
+
–
–
–
3
2
1
3
2
1
34.
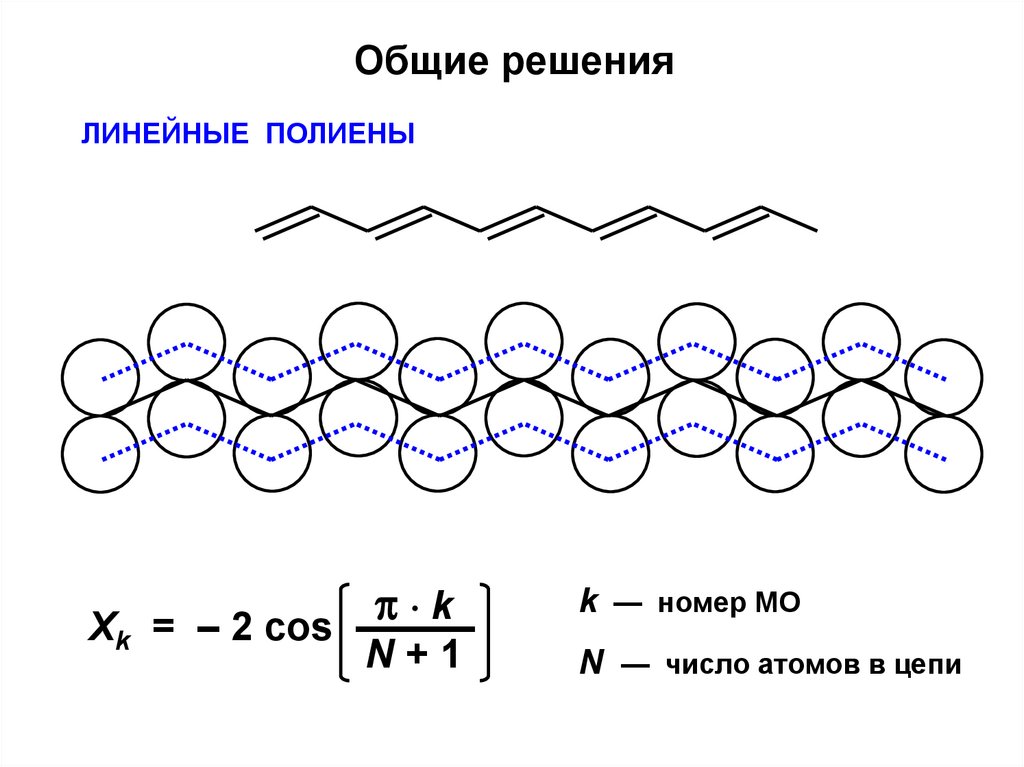
Общие решенияЛИНЕЙНЫЕ ПОЛИЕНЫ
k
Xk = – 2 cos ———
N+1
k — номер МО
N — число атомов в цепи
35.
ХХ
2
+1
Х
1,618
0,618
0
–0,618
–1
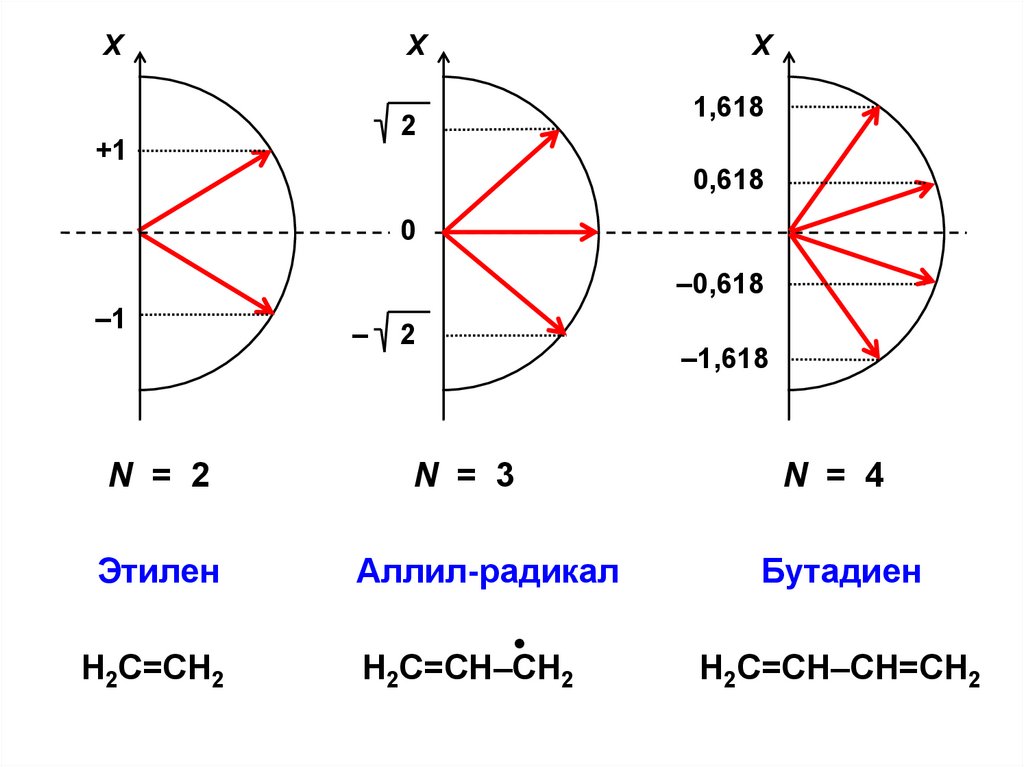
N = 2
Этилен
Н2С=СН2
–
2
N = 3
Аллил-радикал
Н2С=СН–СН2
–1,618
N = 4
Бутадиен
Н2С=СН–СН=СН2
36.
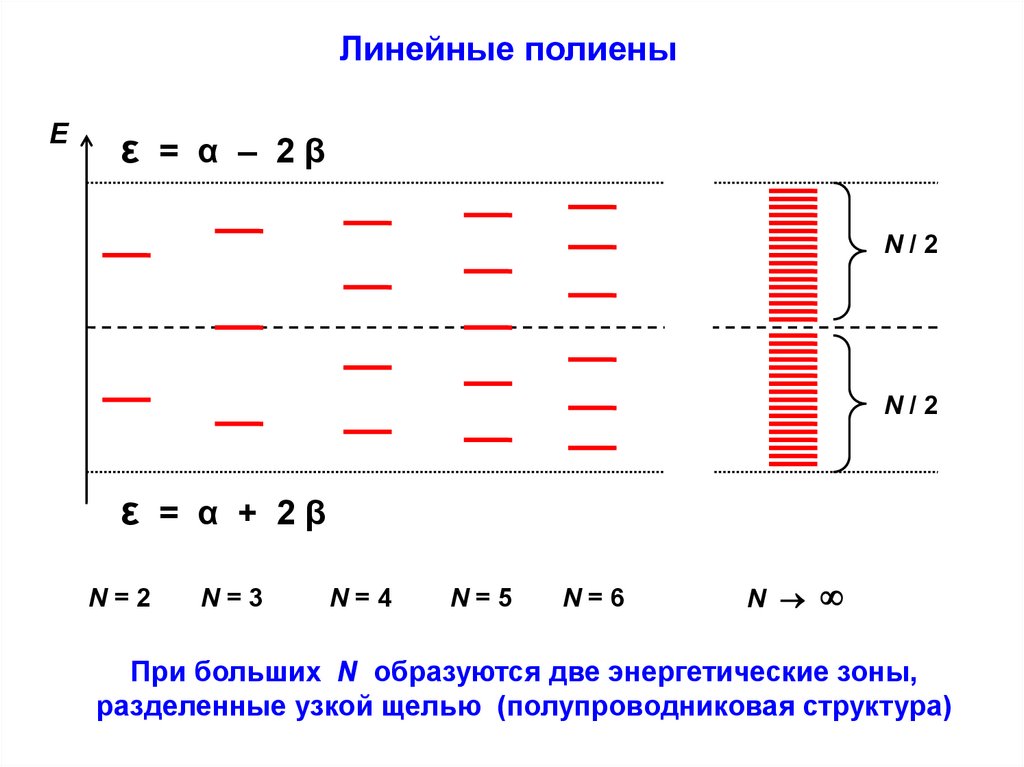
Линейные полиеныЕ
ε = α – 2β
N/2
N/2
ε = α + 2β
N=2
N=3
N=4
N=5
N=6
N
При больших N образуются две энергетические зоны,
разделенные узкой щелью (полупроводниковая структура)
37.
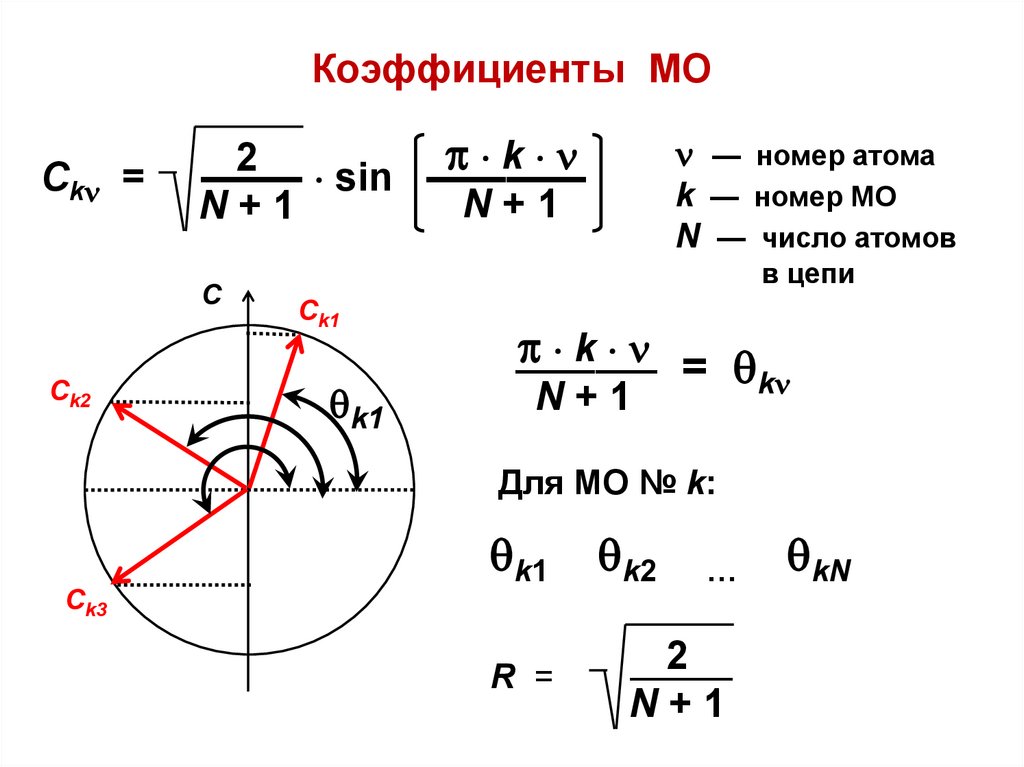
Коэффициенты МОСk =
k
2
——– sin ————
N+1
N+1
С
Сk2
— номер атома
k — номер МО
N — число атомов
в цепи
Сk1
k1
k
———– = k
N+1
Для МО № k:
Сk3
k1
R =
k2
…
2
N+1
———
kN
38.
Сk =k
2
——– sin ————
N+1
N+1
С11 =
2
— sin ( /3) = 0,707
3
С12 =
2 sin (2 /3) = 0,707
—
3
С21 =
2 sin (2 /3) = 0,707
—
3
С22 =
2
— sin (4 /3) = – 0,707
3
Этилен N = 2
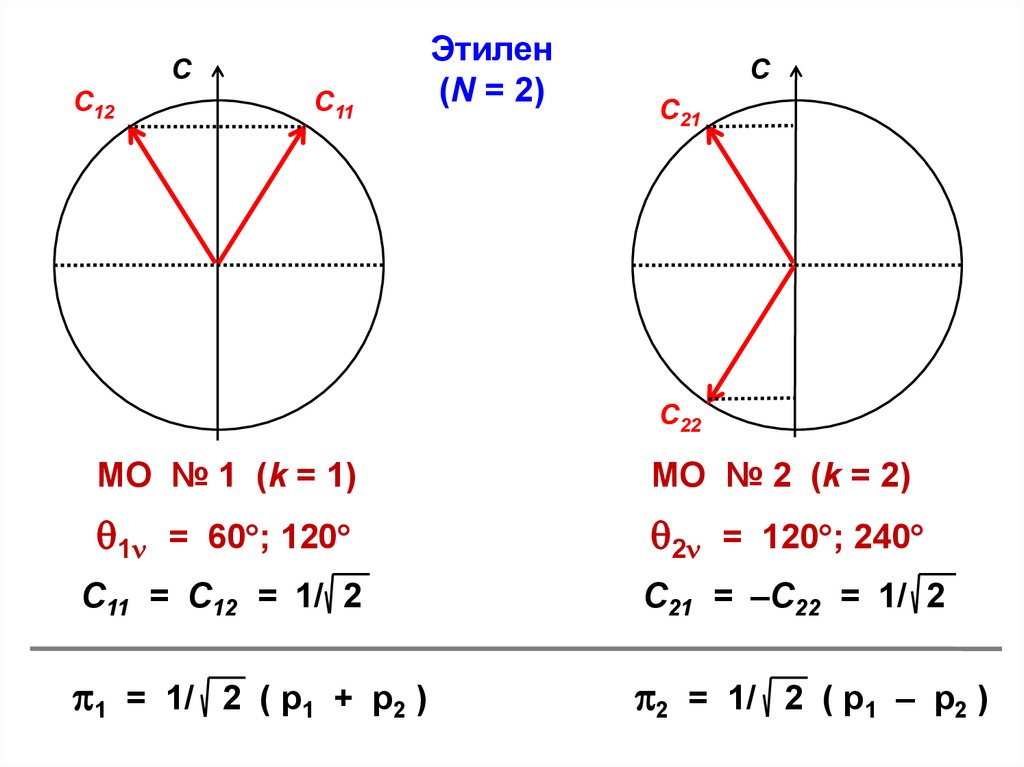
39.
СС12
С11
Этилен
(N = 2)
С
С21
С22
МО № 1 (k = 1)
МО № 2 (k = 2)
1 = 60 ; 120
2 = 120 ; 240
С11 = С12 = 1/ 2
С21 = –С22 = 1/ 2
1 = 1/ 2 ( p1 + p2 )
2 = 1/ 2 ( p1 – p2 )
40.
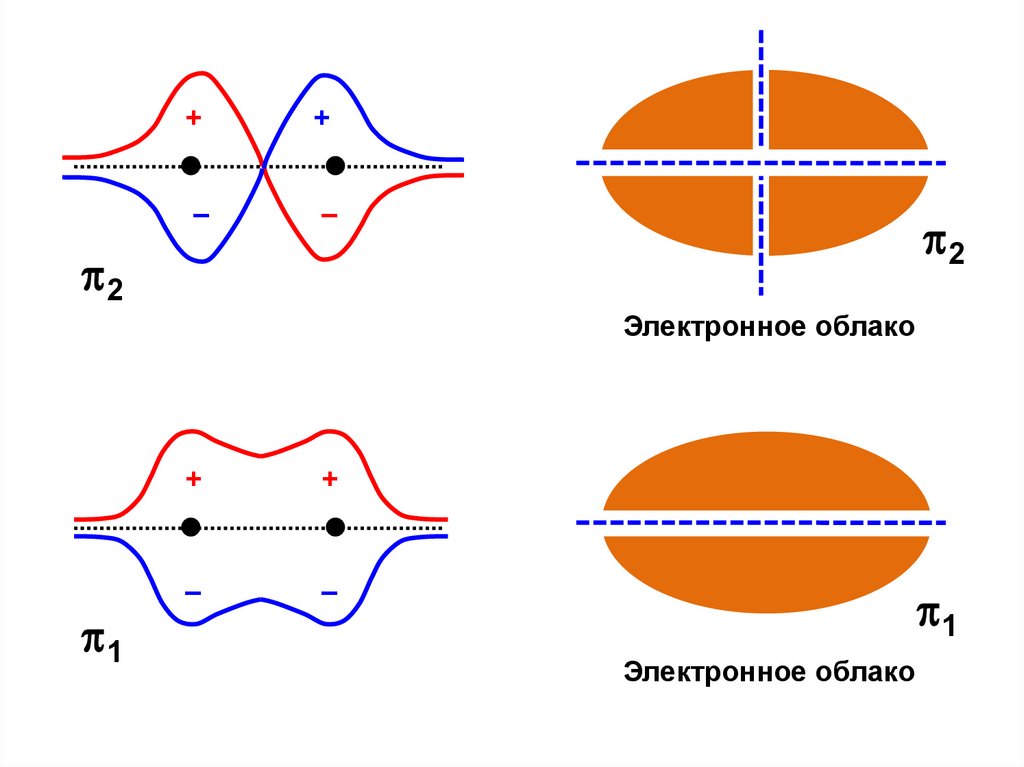
++
–
–
2
2
Электронное облако
1
+
+
–
–
1
Электронное облако
41.
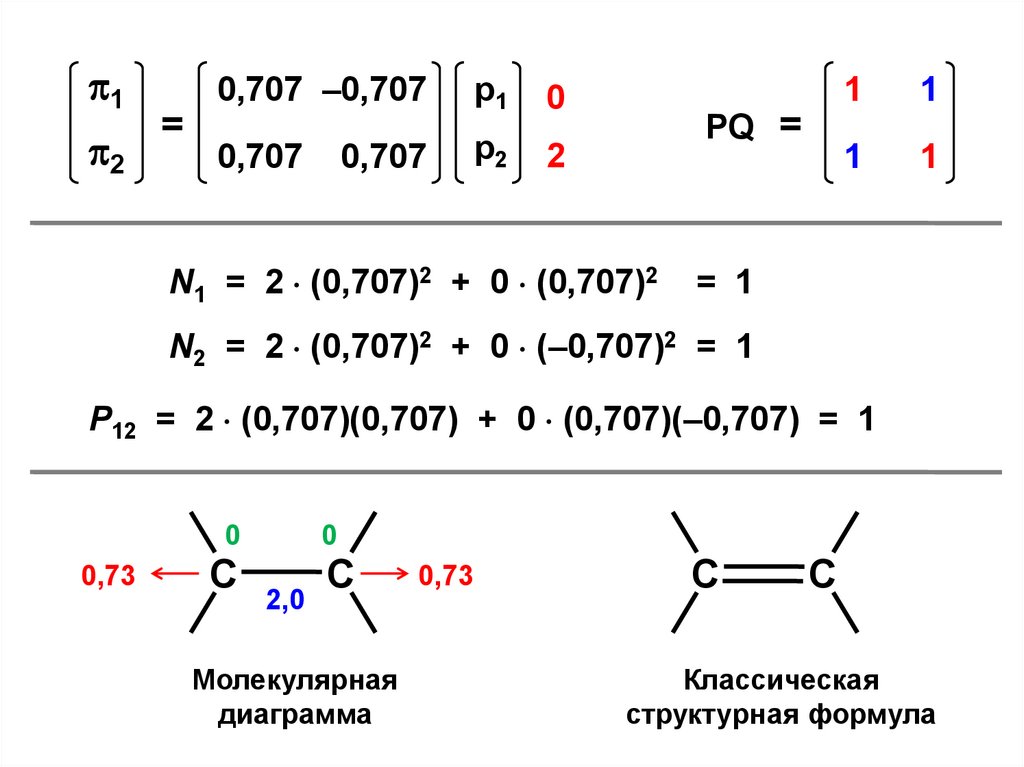
12
0,707 –0,707
=
0,707
0,707
р1
0
р2
2
PQ =
N1 = 2 (0,707)2 + 0 (0,707)2
1
1
1
1
= 1
N2 = 2 (0,707)2 + 0 (–0,707)2 = 1
P12 = 2 (0,707)(0,707) + 0 (0,707)(–0,707) = 1
0
0,73
C
0
2,0
C
Молекулярная
диаграмма
0,73
C
C
Классическая
структурная формула
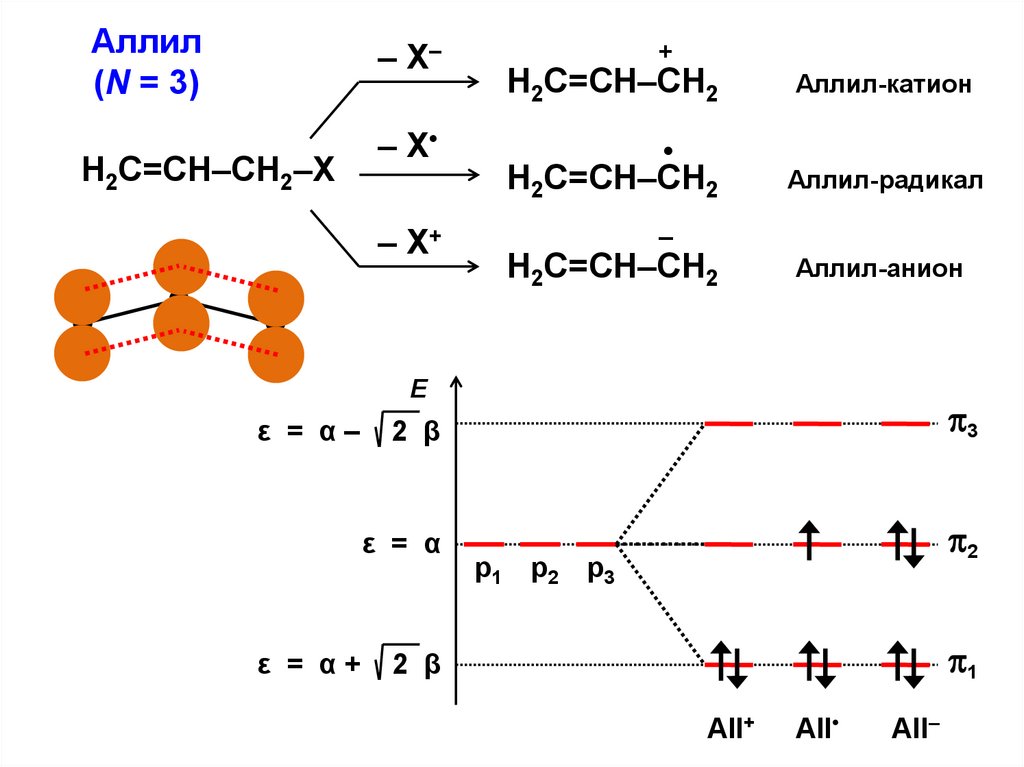
42.
Аллил(N = 3)
– Х–
Н2С=СН–СН2–Х
– Х
– Х+
+
Н2С=СН–СН2
Н2С=СН–СН2
Аллил-катион
Аллил-радикал
–
Н2С=СН–СН2
Аллил-анион
Е
ε = α–
ε = α+
2 β
3
ε = α
2
р1 р2 р3
1
2 β
All+
All
All–
43.
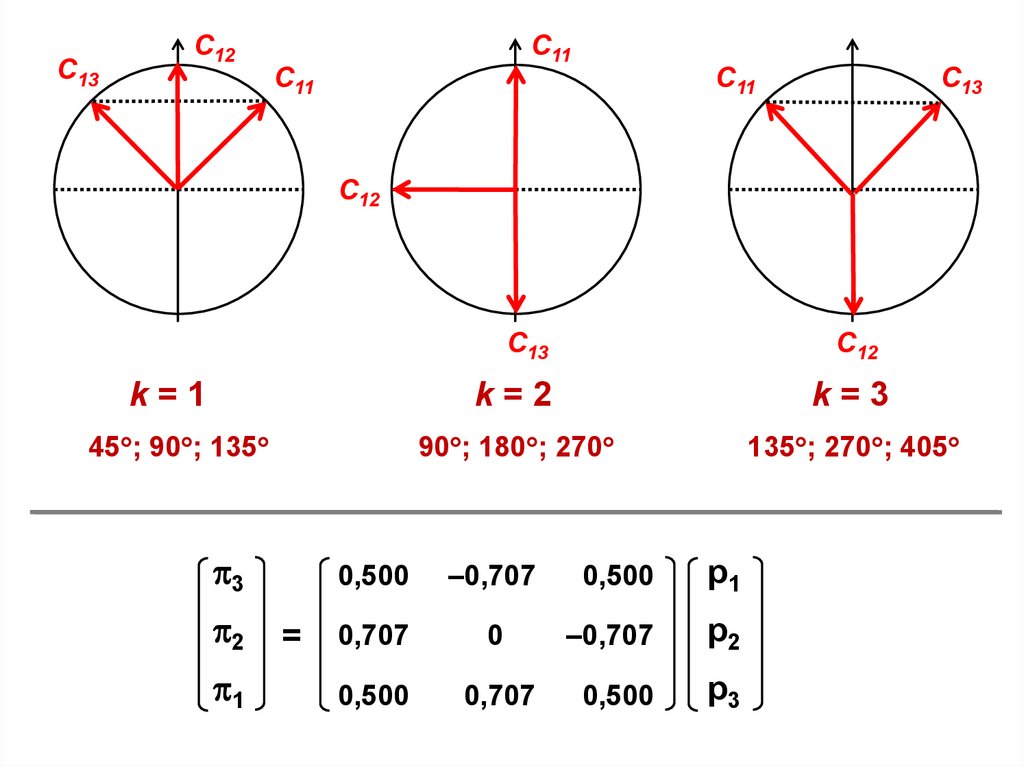
С13С12
С11
С11
С11
С13
С12
С13
k=1
45 ; 90 ; 135
3
2
1
=
С12
k=2
k=3
90 ; 180 ; 270
135 ; 270 ; 405
0,500
–0,707
0,500
р1
0,707
0
–0,707
р2
0,500
0,707
0,500
р3
44.
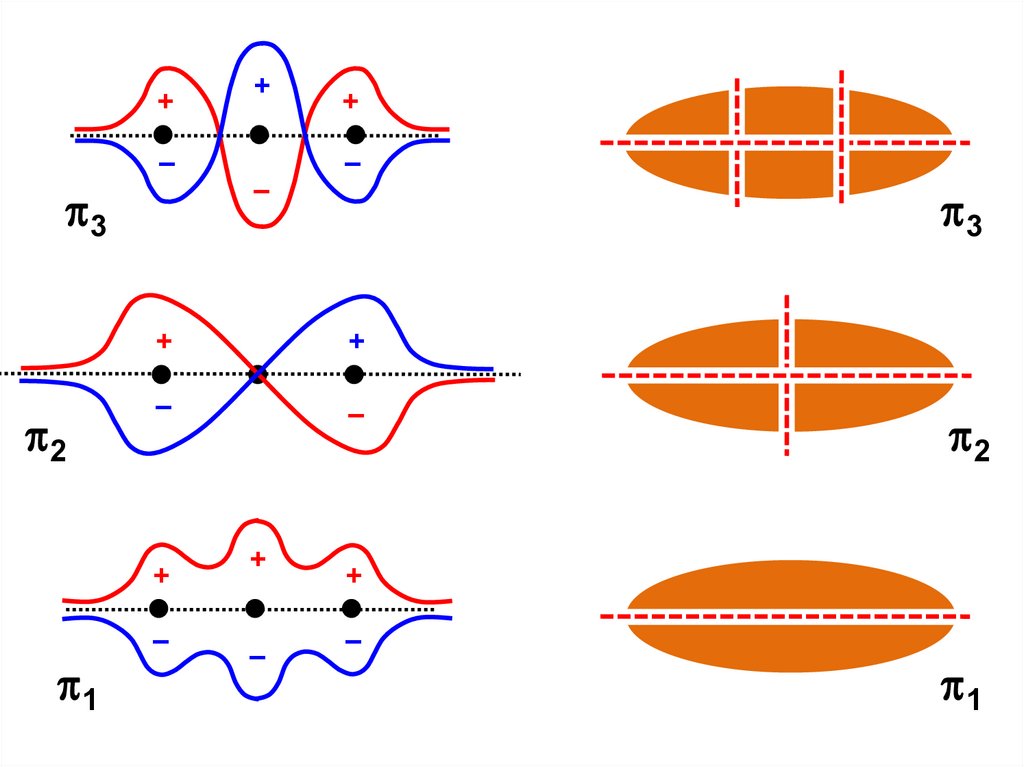
+–
3
2
–
+
–
3
+
+
–
–
+
1
+
–
+
–
2
+
–
1
45.
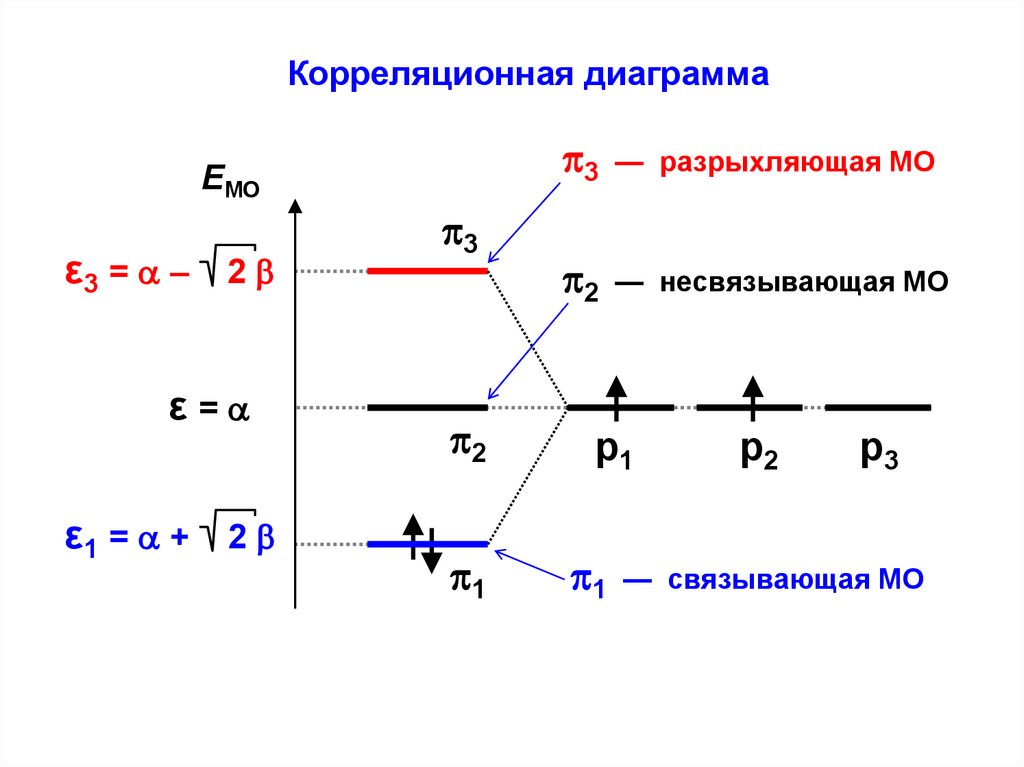
Корреляционная диаграммаEМО
ε3 = – 2
ε=
ε1 = + 2
3
2
1
3
— разрыхляющая МО
2
— несвязывающая МО
р1
1
р2
р3
— связывающая МО
46.
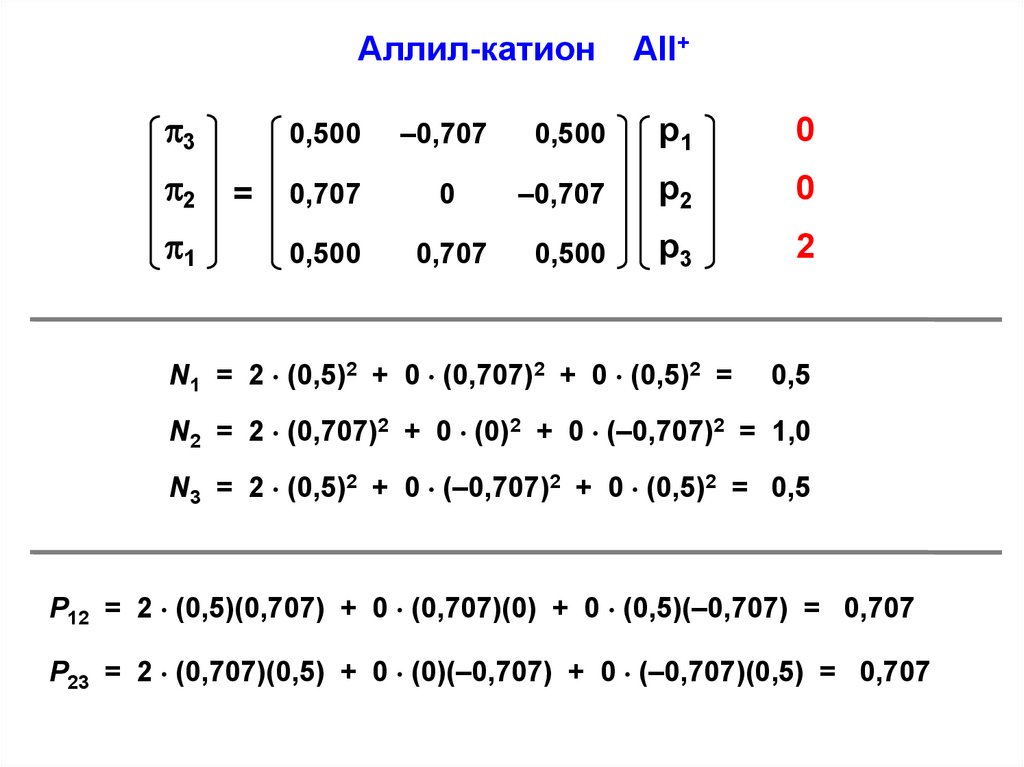
Аллил-катион3
2
1
=
All+
0,500
–0,707
0,500
р1
0
0,707
0
–0,707
р2
0
0,500
0,707
0,500
р3
2
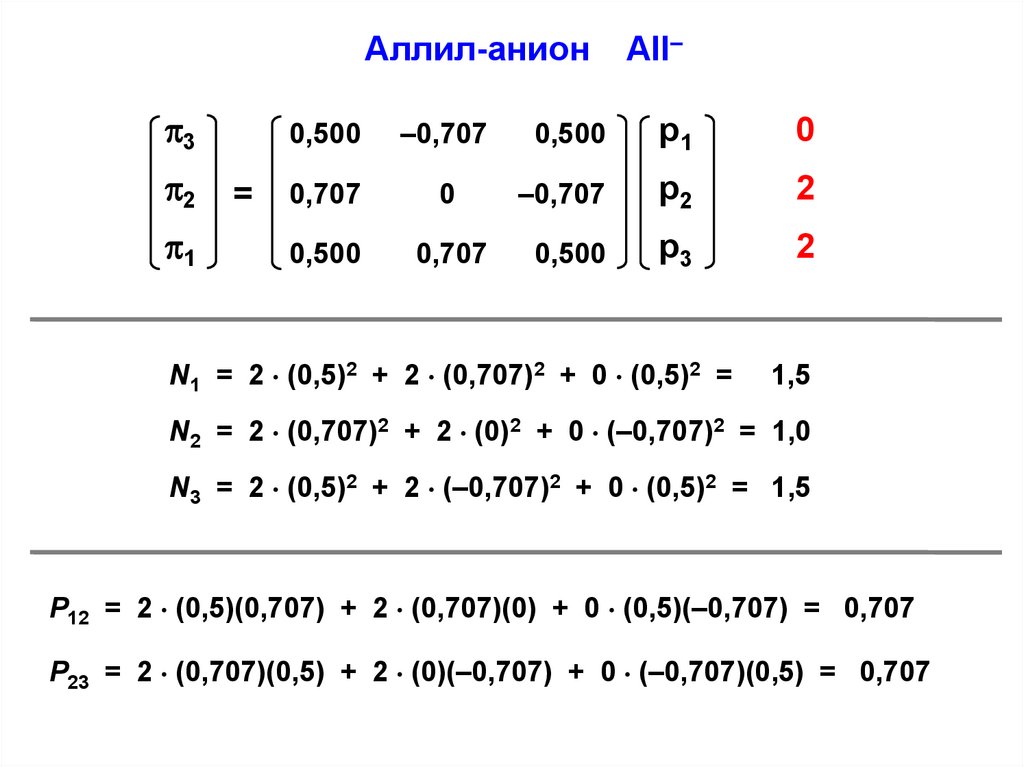
N1 = 2 (0,5)2 + 0 (0,707)2 + 0 (0,5)2 =
0,5
N2 = 2 (0,707)2 + 0 (0)2 + 0 (–0,707)2 = 1,0
N3 = 2 (0,5)2 + 0 (–0,707)2 + 0 (0,5)2 = 0,5
P12 = 2 (0,5)(0,707) + 0 (0,707)(0) + 0 (0,5)(–0,707) = 0,707
P23 = 2 (0,707)(0,5) + 0 (0)(–0,707) + 0 (–0,707)(0,5) = 0,707
47.
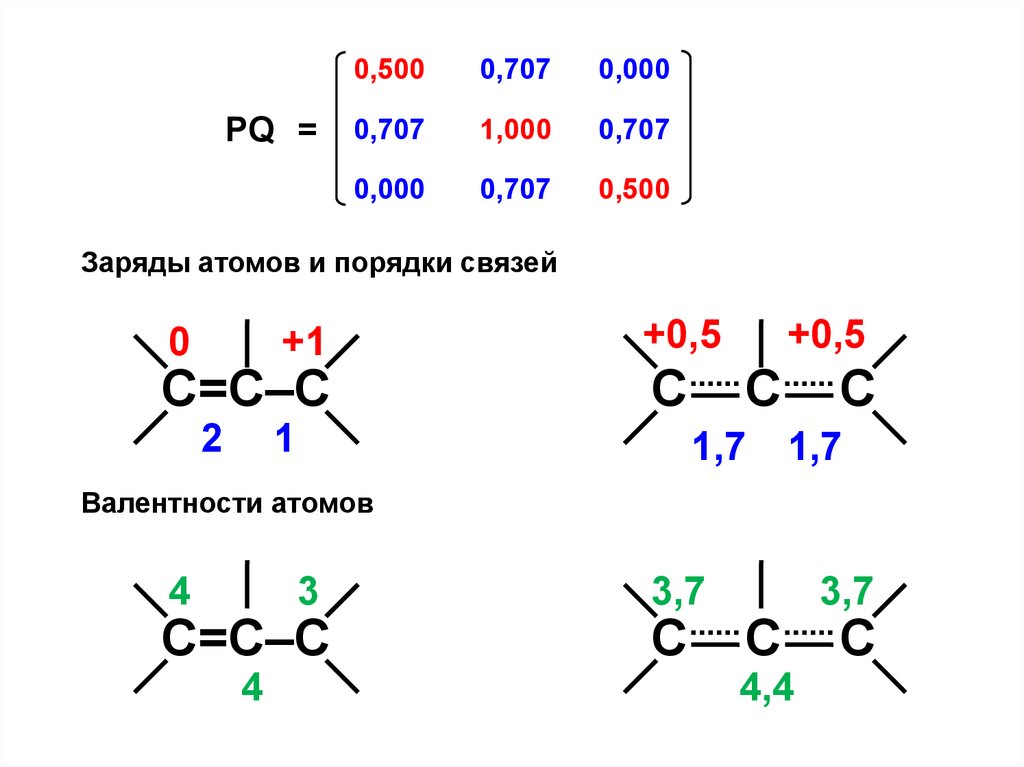
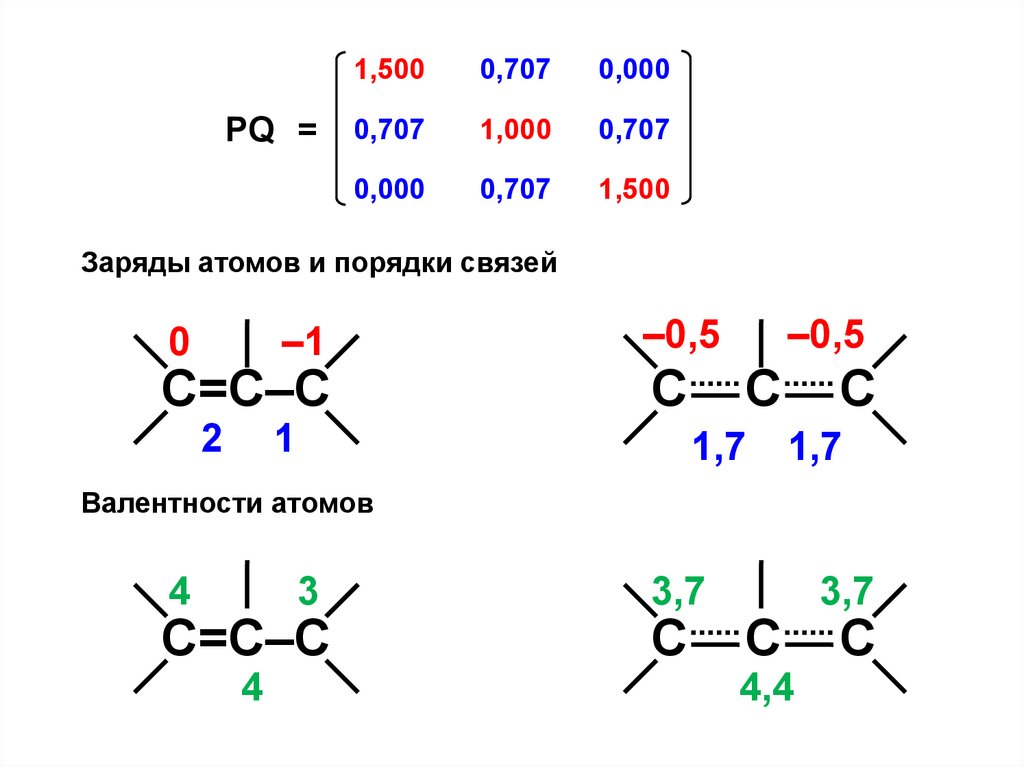
PQ =0,500
0,707
0,000
0,707
1,000
0,707
0,000
0,707
0,500
Заряды атомов и порядки связей
0
+1
С=С–С
2
+0,5
С
1
+0,5
С
1,7
С
1,7
Валентности атомов
4
3
С=С–С
4
3,7
С
С
4,4
3,7
С
48.
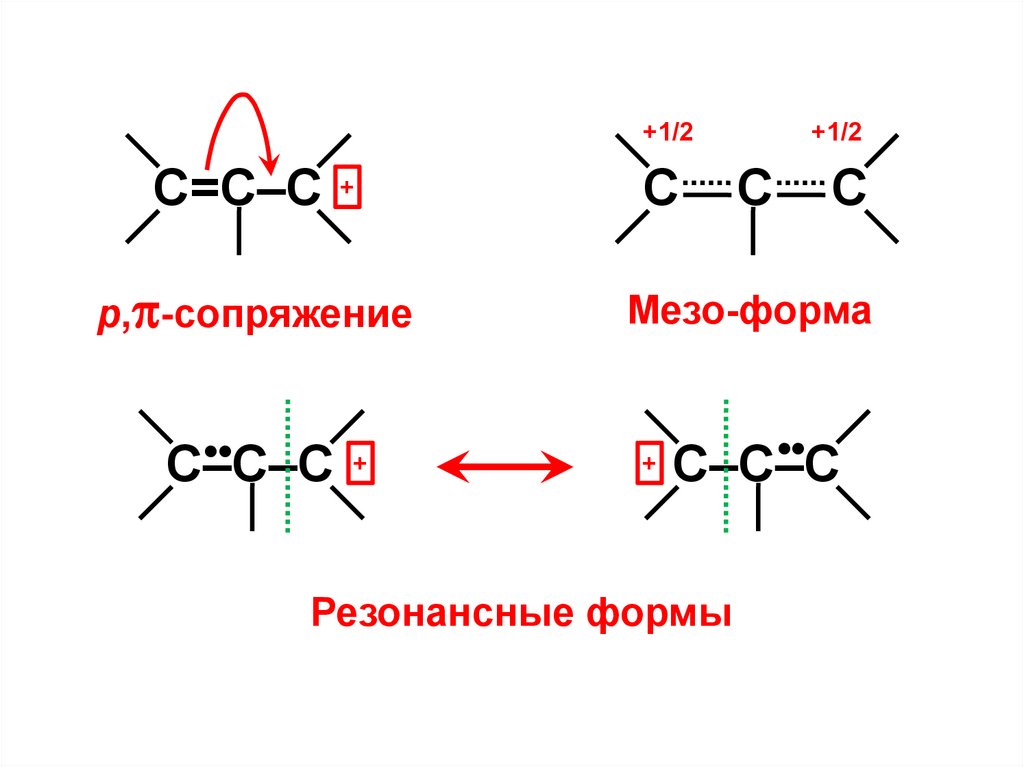
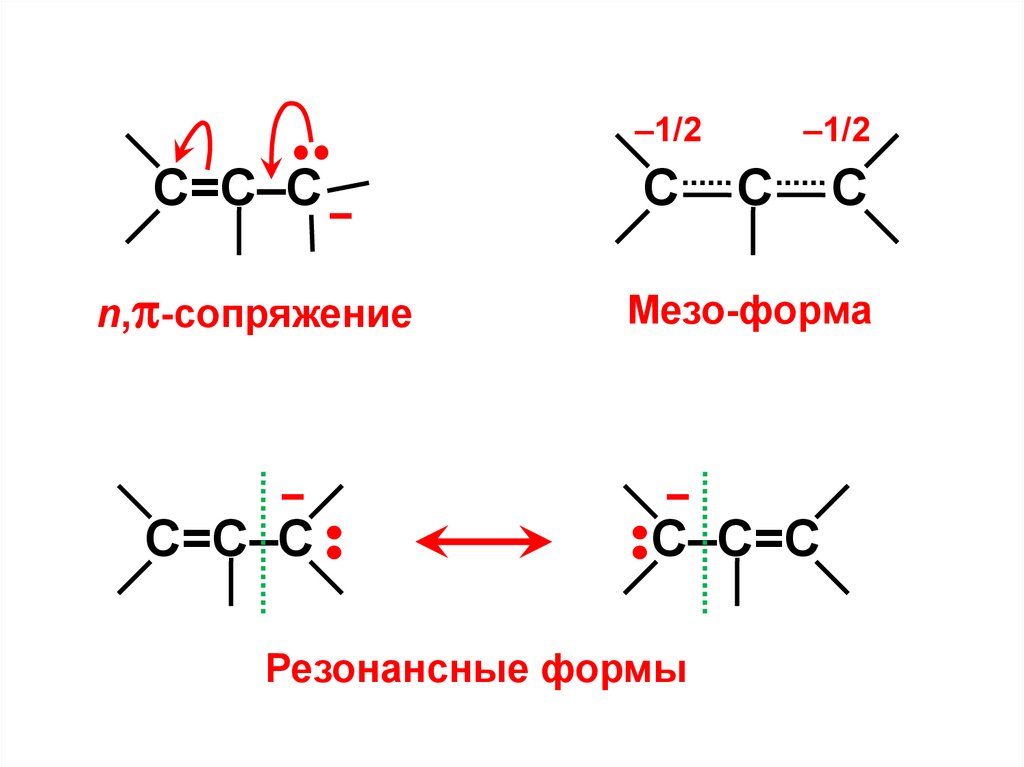
+1/2С=С–С
+
р, -сопряжение
•
С–С–С
+
С
+1/2
С
С
Мезо-форма
+
•
С–С–С
Резонансные формы
49.
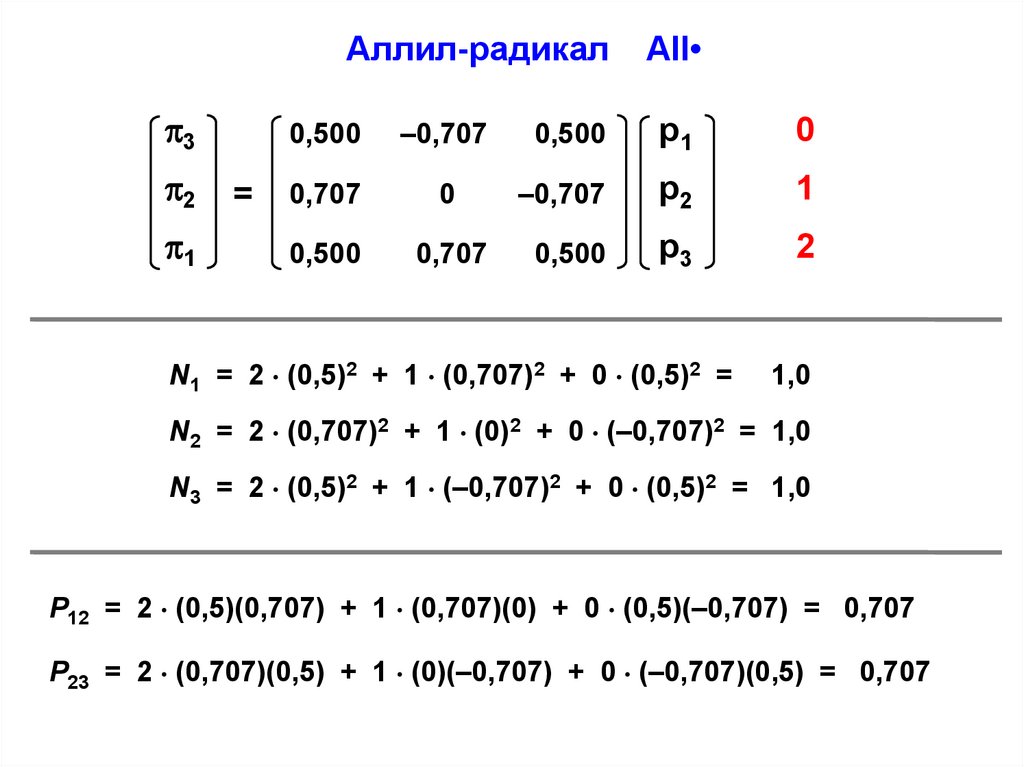
Аллил-радикал3
2
1
=
All
0,500
–0,707
0,500
р1
0
0,707
0
–0,707
р2
1
0,500
0,707
0,500
р3
2
N1 = 2 (0,5)2 + 1 (0,707)2 + 0 (0,5)2 =
1,0
N2 = 2 (0,707)2 + 1 (0)2 + 0 (–0,707)2 = 1,0
N3 = 2 (0,5)2 + 1 (–0,707)2 + 0 (0,5)2 = 1,0
P12 = 2 (0,5)(0,707) + 1 (0,707)(0) + 0 (0,5)(–0,707) = 0,707
P23 = 2 (0,707)(0,5) + 1 (0)(–0,707) + 0 (–0,707)(0,5) = 0,707
50.
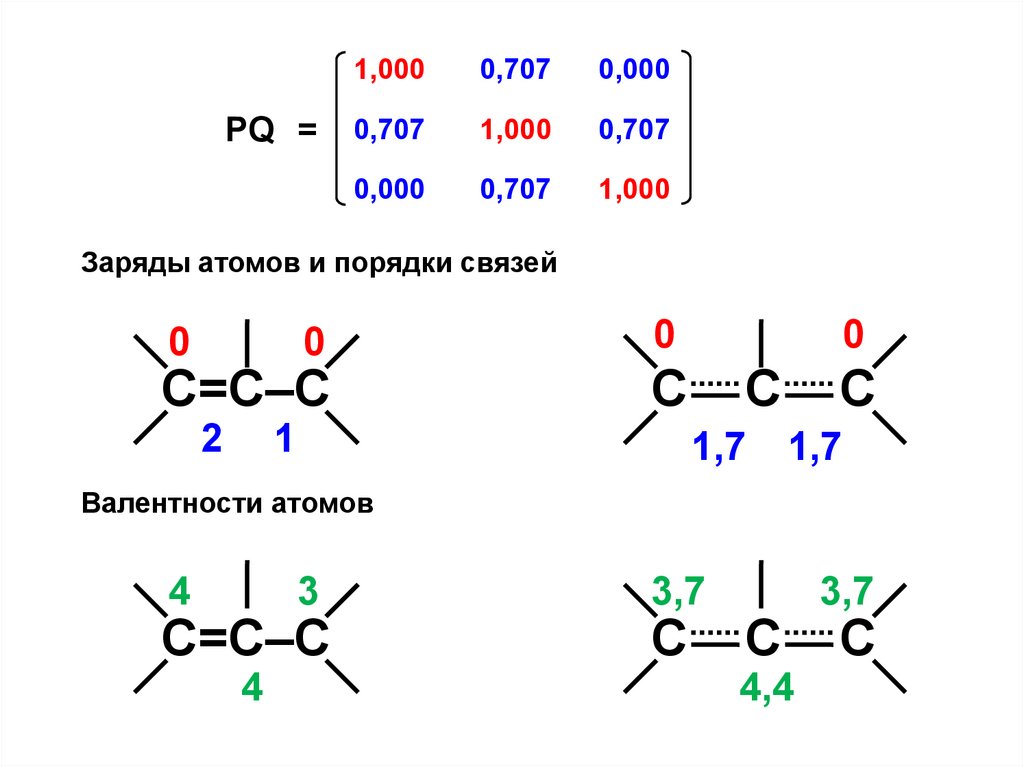
PQ =1,000
0,707
0,000
0,707
1,000
0,707
0,000
0,707
1,000
Заряды атомов и порядки связей
0
0
С=С–С
2
0
0
С
1
С
1,7
С
1,7
Валентности атомов
4
3
С=С–С
4
3,7
С
С
4,4
3,7
С
51.
Аллил-анион3
2
1
=
All–
0,500
–0,707
0,500
р1
0
0,707
0
–0,707
р2
2
0,500
0,707
0,500
р3
2
N1 = 2 (0,5)2 + 2 (0,707)2 + 0 (0,5)2 =
1,5
N2 = 2 (0,707)2 + 2 (0)2 + 0 (–0,707)2 = 1,0
N3 = 2 (0,5)2 + 2 (–0,707)2 + 0 (0,5)2 = 1,5
P12 = 2 (0,5)(0,707) + 2 (0,707)(0) + 0 (0,5)(–0,707) = 0,707
P23 = 2 (0,707)(0,5) + 2 (0)(–0,707) + 0 (–0,707)(0,5) = 0,707
52.
PQ =1,500
0,707
0,000
0,707
1,000
0,707
0,000
0,707
1,500
Заряды атомов и порядки связей
–1
0
С=С–С
2
–0,5
С
1
–0,5
С
1,7
С
1,7
Валентности атомов
4
3
С=С–С
4
3,7
С
С
4,4
3,7
С
53.
•С=С–С –
n, -сопряжение
–
С
–1/2
С
С
Мезо-форма
–
С–С=С
•
•
С=С–С
–1/2
Резонансные формы
54.
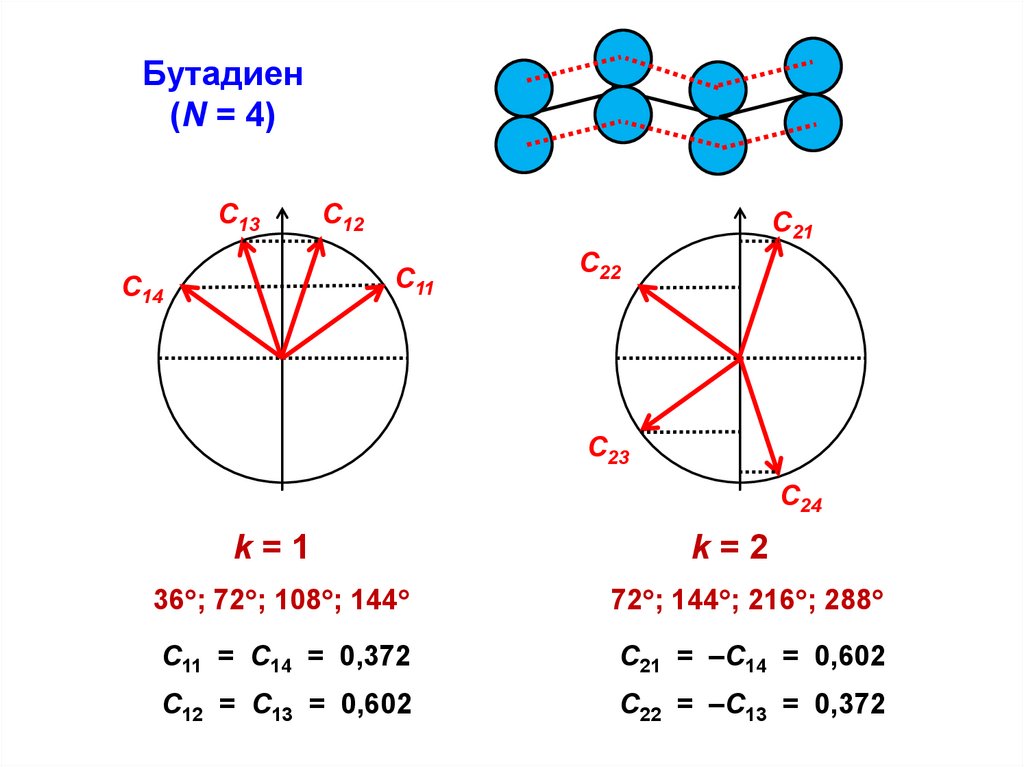
Бутадиен(N = 4)
С13
С12
С21
С11
С14
С22
С23
С24
k=1
k=2
36 ; 72 ; 108 ; 144
72 ; 144 ; 216 ; 288
С11 = С14 = 0,372
С21 = –С14 = 0,602
С12 = С13 = 0,602
С22 = –С13 = 0,372
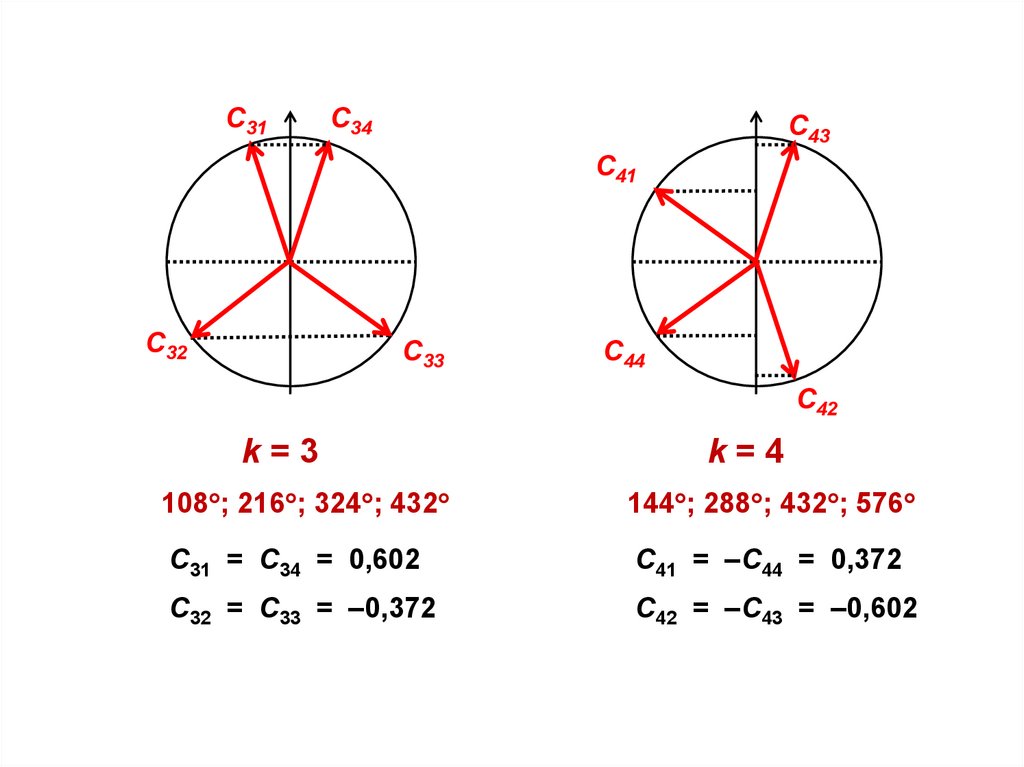
55.
С31С34
С43
С41
С32
С33
С44
С42
k=3
k=4
108 ; 216 ; 324 ; 432
144 ; 288 ; 432 ; 576
С31 = С34 = 0,602
С41 = –С44 = 0,372
С32 = С33 = –0,372
С42 = –С43 = –0,602
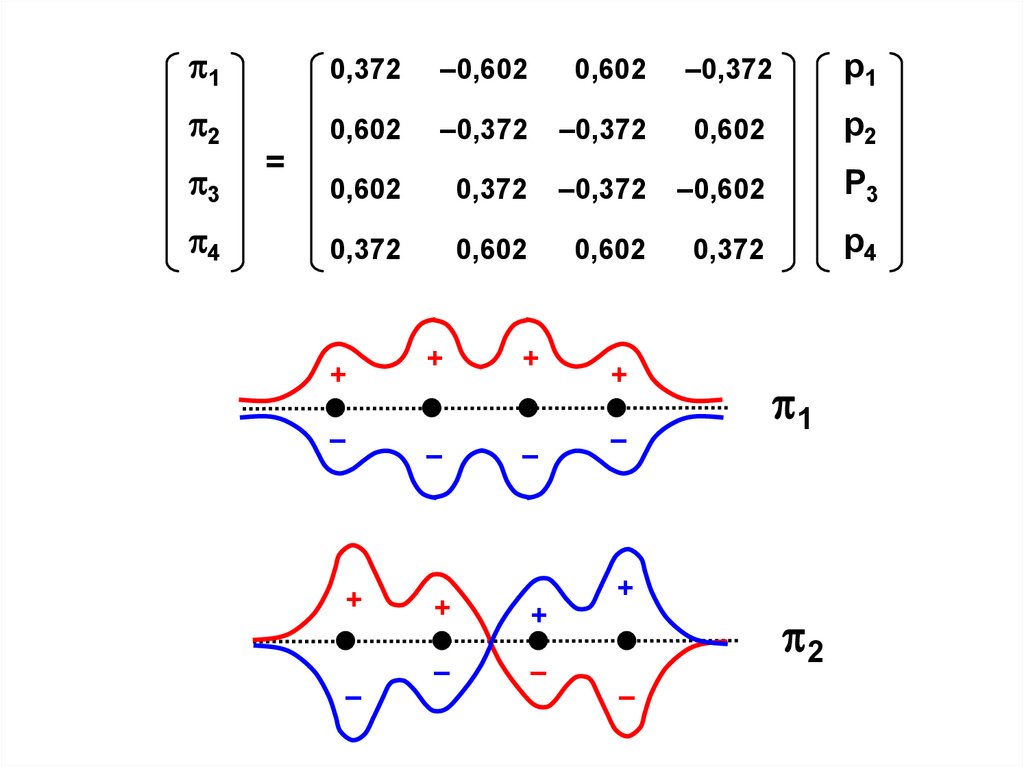
56.
10,372
–0,602
0,602
–0,372
р1
2
0,602
–0,372
–0,372
0,602
р2
0,602
0,372
–0,372
–0,602
Р3
0,372
0,602
0,602
0,372
р4
3
4
=
+
–
+
–
+
+
–
–
+
–
1
+
+
+
–
–
2
–
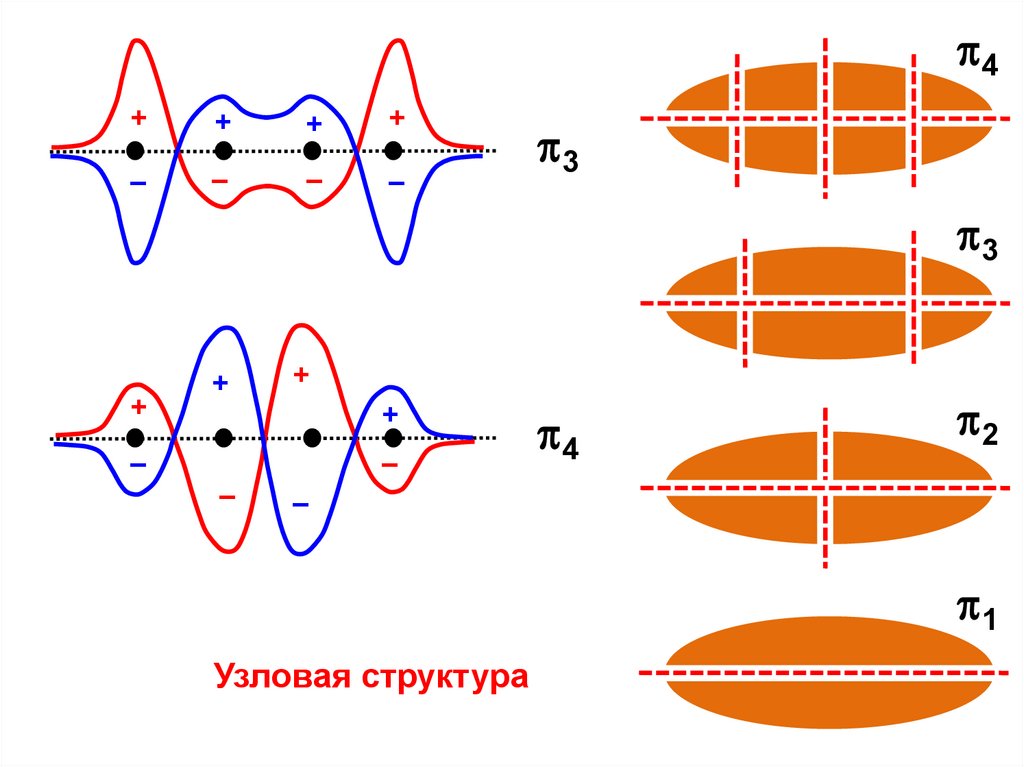
57.
4+
+
+
+
–
–
–
–
3
3
+
+
+
+
–
–
–
4
2
–
1
Узловая структура
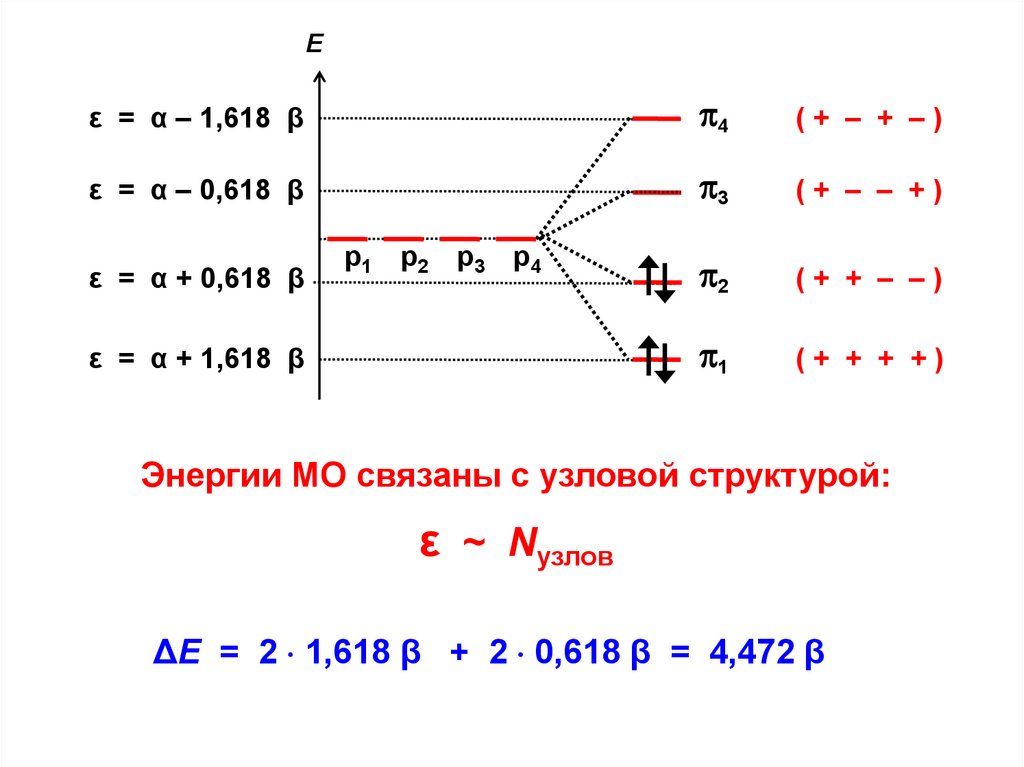
58.
Еε = α – 1,618 β
4
(+ – + –)
ε = α – 0,618 β
3
(+ – – +)
2
(+ + – –)
1
(+ + + +)
ε = α + 0,618 β
р1 р2 р3 р4
ε = α + 1,618 β
Энергии МО связаны с узловой структурой:
ε ~ Nузлов
ΔЕ = 2 1,618 β + 2 0,618 β = 4,472 β
59.
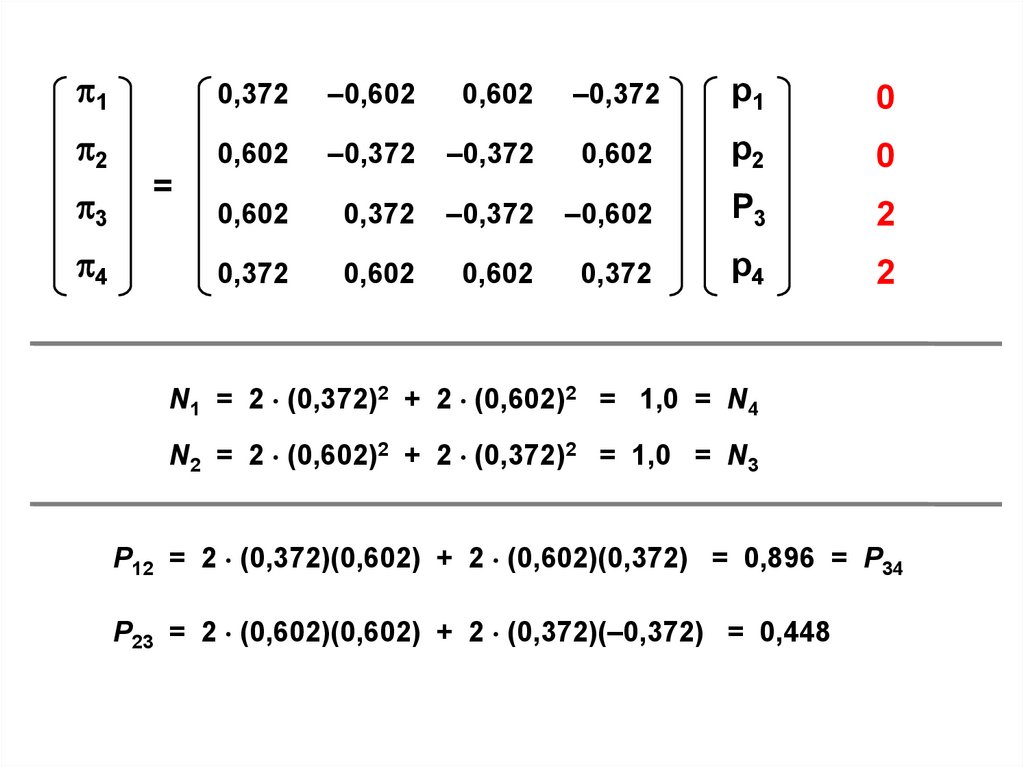
10,372
–0,602
0,602
–0,372
р1
0
2
0,602
–0,372
–0,372
0,602
р2
0
0,602
0,372
–0,372
–0,602
Р3
2
0,372
0,602
0,602
0,372
р4
2
3
4
=
N1 = 2 (0,372)2 + 2 (0,602)2 = 1,0 = N4
N2 = 2 (0,602)2 + 2 (0,372)2 = 1,0 = N3
P12 = 2 (0,372)(0,602) + 2 (0,602)(0,372) = 0,896 = P34
P23 = 2 (0,602)(0,602) + 2 (0,372)(–0,372) = 0,448
60.
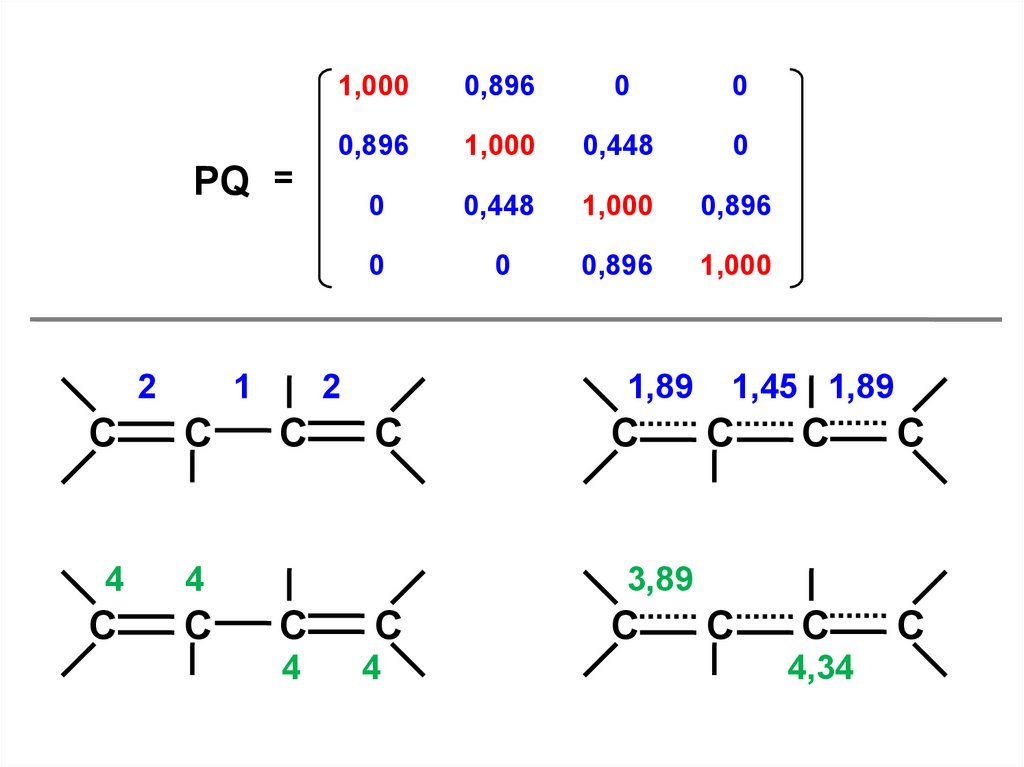
1,0000,896
0
0
0,896
1,000
0,448
0
0
0,448
1,000
0,896
0
0
0,896
1,000
PQ =
2
1
C
C
4
4
C
C
2
C
1,89
C
C
1,45 1,89
C
C
C
C
C
C
3,89
C
4
C
4
C
4,34
61.
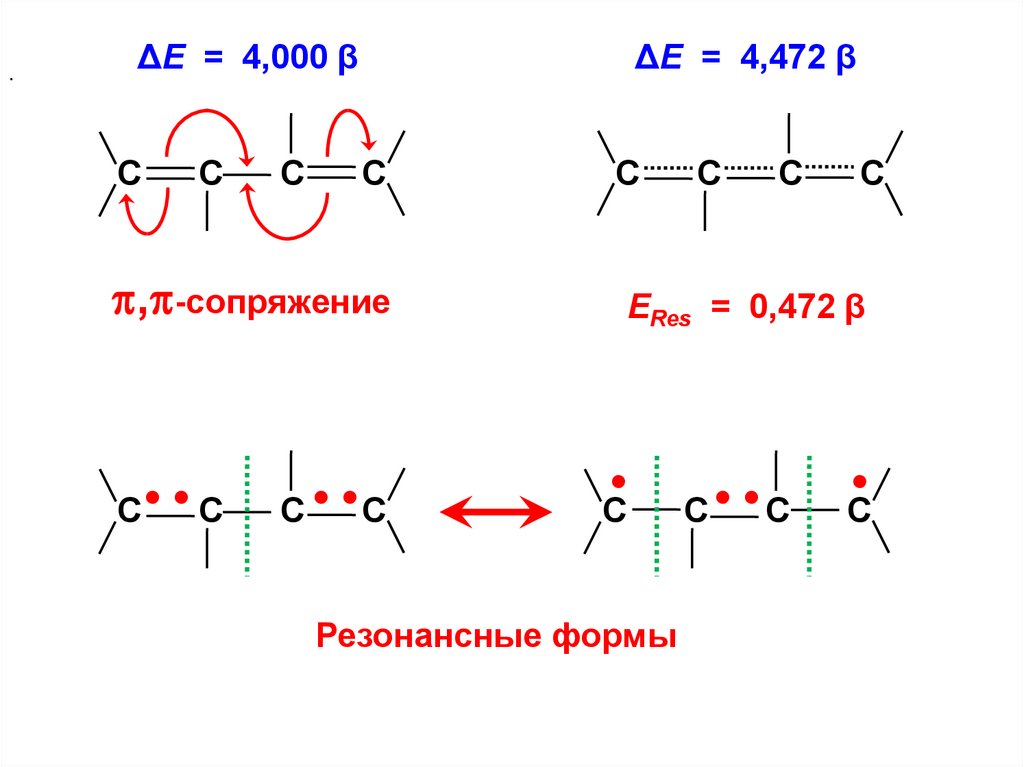
.ΔЕ = 4,000 β
С
С
С
ΔЕ = 4,472 β
С
С
, -сопряжение
С• • С
С • •С
С
С
С
ЕRes = 0,472 β
С
Резонансные формы
С• •С
С
62.
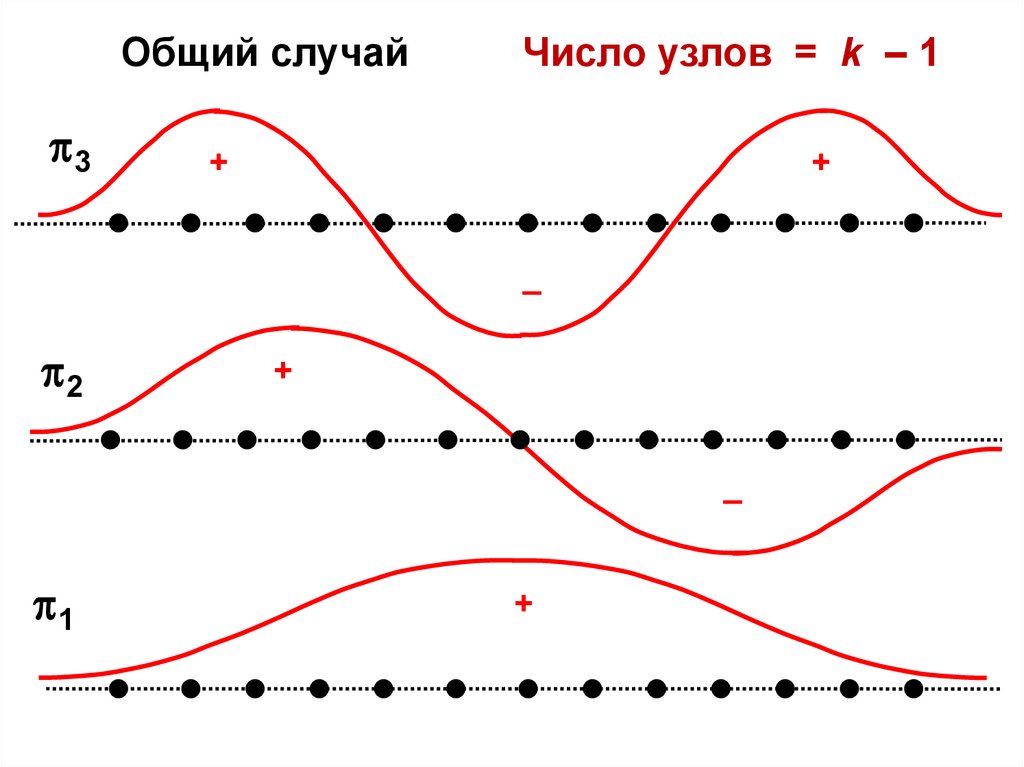
Общий случай3
Число узлов = k – 1
+
+
–
2
+
–
1
+
63.
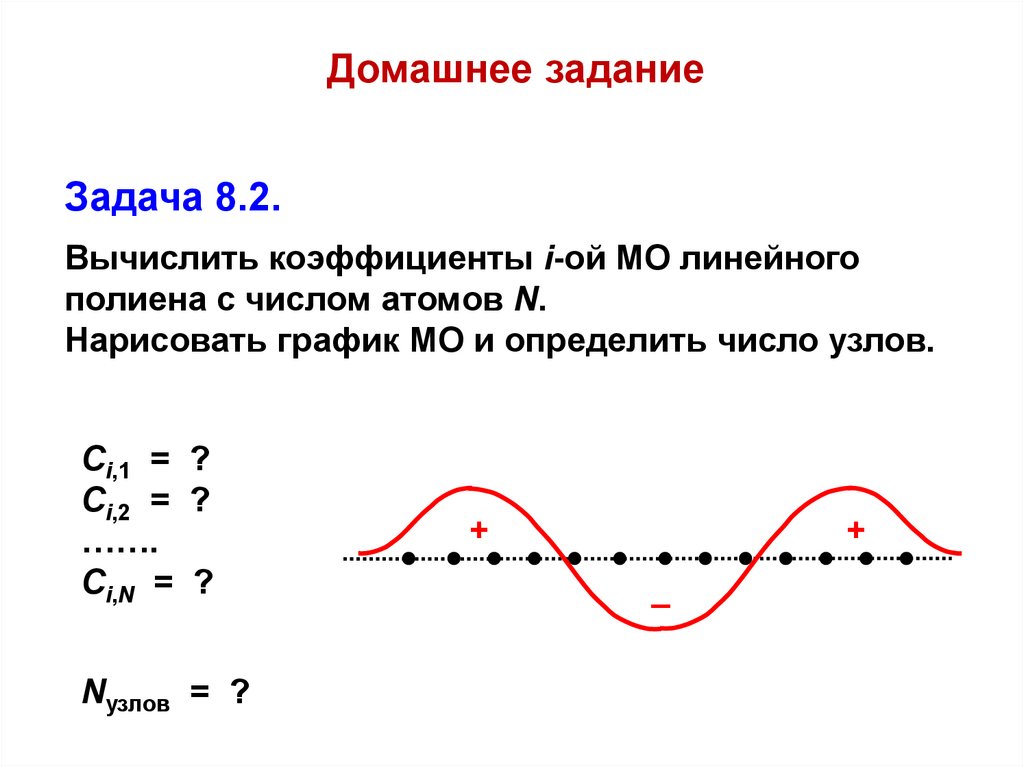
Домашнее заданиеЗадача 8.2.
Вычислить коэффициенты i-ой МО линейного
полиена с числом атомов N.
Нарисовать график МО и определить число узлов.
Сi,1 = ?
Ci,2 = ?
…….
Ci,N = ?
Nузлов = ?
+
+
–
64.
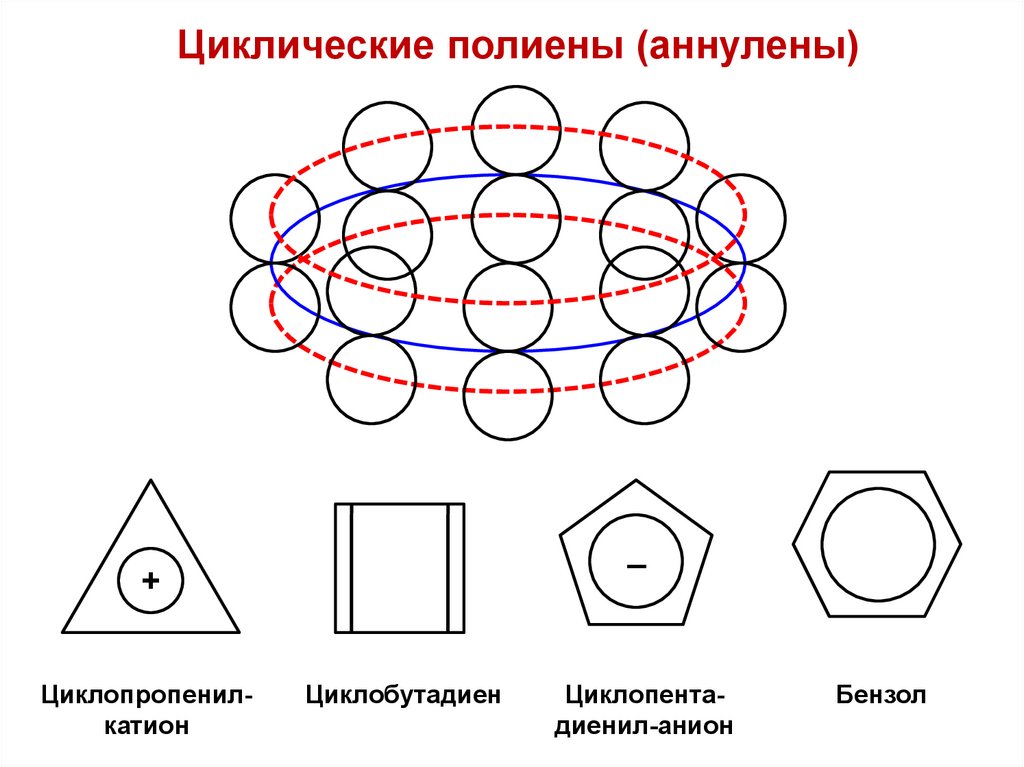
Циклические полиены (аннулены)–
+
Циклопропенилкатион
Циклобутадиен
Циклопентадиенил-анион
Бензол
65.
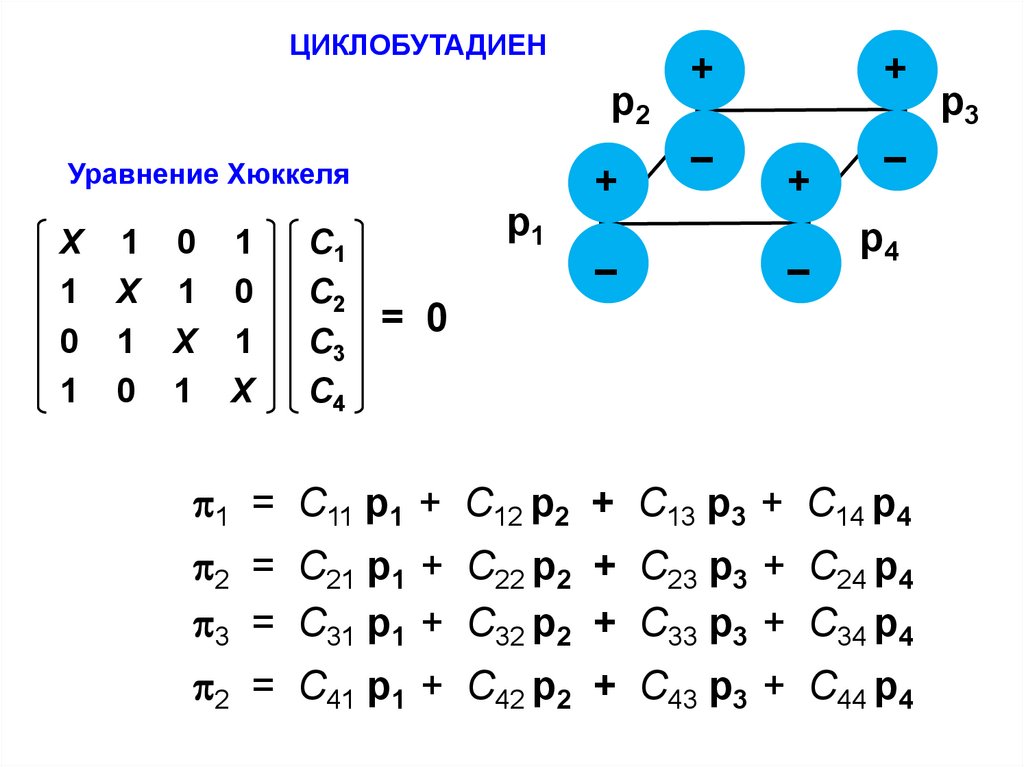
ЦИКЛОБУТАДИЕНр2
Уравнение Хюккеля
Х 1 0 1
1 Х 1 0
0 1 Х 1
1 0 1 Х
С1
С2
С3
С4
р1
+
–
+
+
–
–
+
–
р4
= 0
1 = С11 p1 + C12 p2 + С13 p3 + C14 p4
2 = С21 p1 + C22 p2 + С23 p3 + C24 p4
3 = С31 p1 + C32 p2 + С33 p3 + C34 p4
2 = С41 p1 + C42 p2 + С43 p3 + C44 p4
р3
66.
Характеристическоеуравнение
Х 2(Х 2
– 4) = 0
Корни
Энергии МО
Х1 = –2
Х2 = 0
Х3 = 0
Х4 = +2
ε1 = α + 2β
ε2 = α
ε3 = α
ε4 = α – 2β
Уравнение Хюккеля
Х 1 0 1
1 Х 1 0
0 1 Х 1
1 0 1 Х
С1
С2
С3
С4
= 0
С1 Х + С2 + С4
С1 + С2 Х + С3
С2 + С3 Х + С4
С1 + С3 + С4 Х
=
=
=
=
0
0
0
0
67.
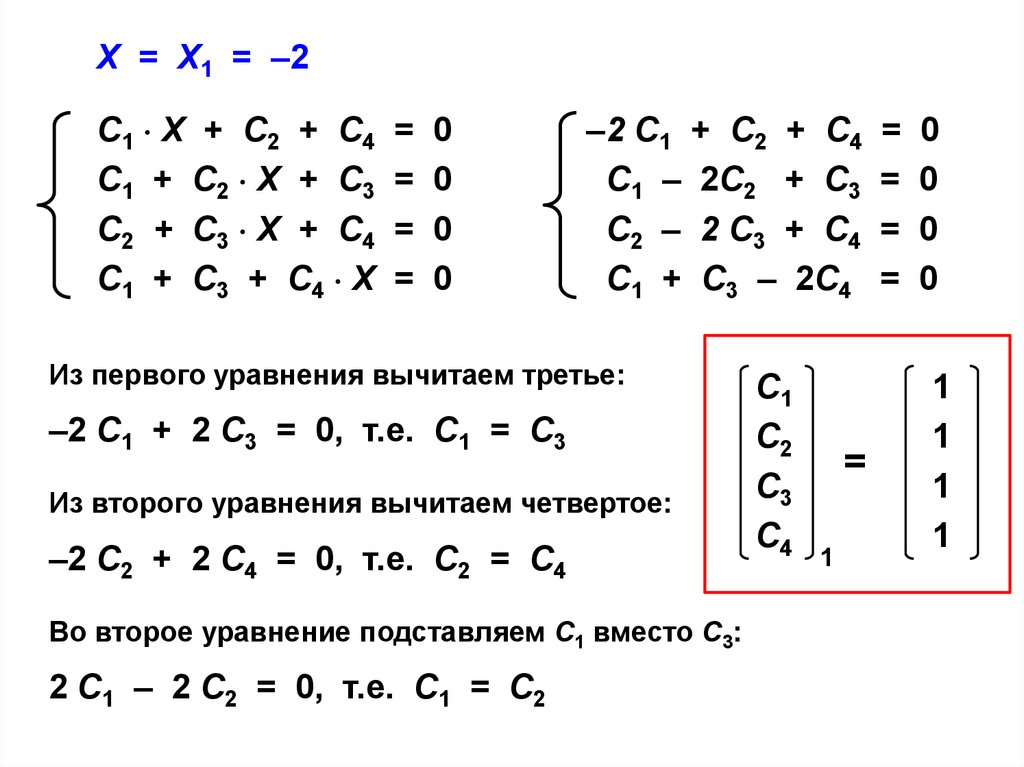
Х = Х1 = –2С1 Х + С2 + С4
С1 + С2 Х + С3
С2 + С3 Х + С4
С1 + С3 + С4 Х
=
=
=
=
0
0
0
0
–2 С1 + С2 + С4
С1 – 2С2 + С3
С2 – 2 С3 + С4
С1 + С3 – 2С4
Из первого уравнения вычитаем третье:
–2 С1 + 2 С3 = 0, т.е. С1 = С3
Из второго уравнения вычитаем четвертое:
–2 С2 + 2 С4 = 0, т.е. С2 = С4
Во второе уравнение подставляем С1 вместо С3:
2 С1 – 2 С2 = 0, т.е. С1 = С2
С1
С2
С3
С4
=
1
=
=
=
=
0
0
0
0
1
1
1
1
68.
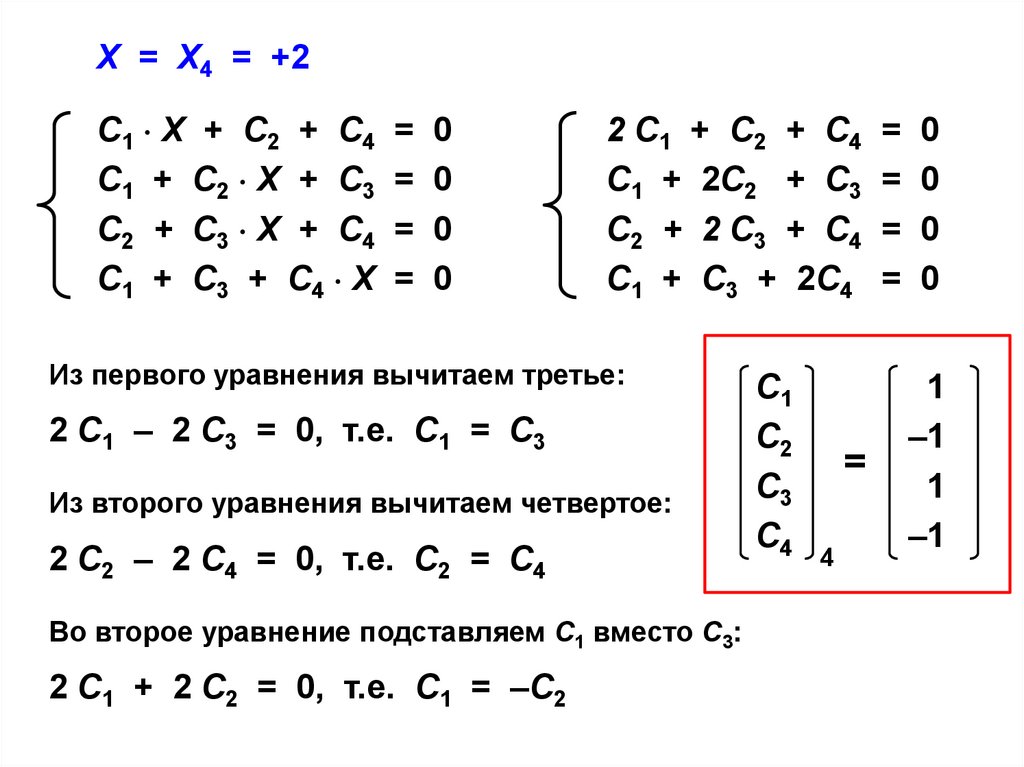
Х = Х4 = +2С1 Х + С2 + С4
С1 + С2 Х + С3
С2 + С3 Х + С4
С1 + С3 + С4 Х
=
=
=
=
0
0
0
0
2 С1 + С2 + С4
С1 + 2С2 + С3
С2 + 2 С3 + С4
С1 + С3 + 2С4
Из первого уравнения вычитаем третье:
2 С1 – 2 С3 = 0, т.е. С1 = С3
Из второго уравнения вычитаем четвертое:
2 С2 – 2 С4 = 0, т.е. С2 = С4
Во второе уравнение подставляем С1 вместо С3:
2 С1 + 2 С2 = 0, т.е. С1 = –С2
С1
С2
С3
С4
=
4
=
=
=
=
0
0
0
0
1
–1
1
–1
69.
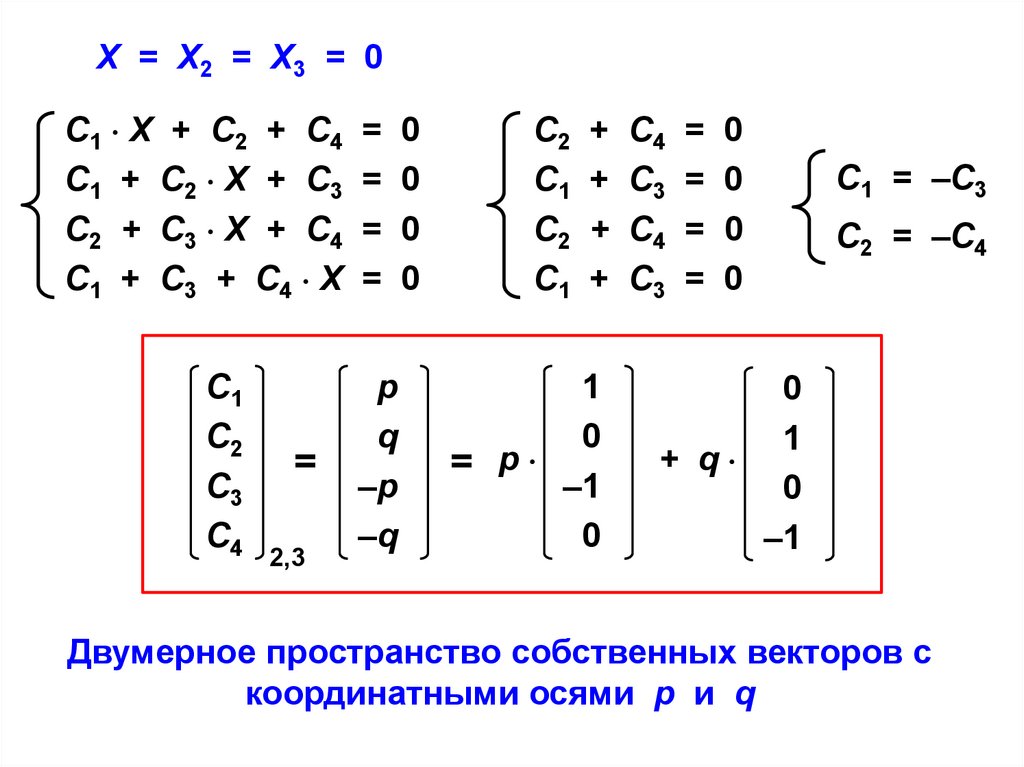
Х = Х2 = Х3 = 0С1 Х + С2 + С4
С1 + С2 Х + С3
С2 + С3 Х + С4
С1 + С3 + С4 Х
С1
С2
С3
С4
=
2,3
=
=
=
=
p
q
–p
–q
0
0
0
0
С2
С1
С2
С1
+
+
+
+
1
0
= p
–1
0
С4
С3
С4
С3
=
=
=
=
0
0
0
0
С1 = –С3
С2 = –С4
0
1
+ q
0
–1
Двумерное пространство собственных векторов с
координатными осями p и q
70.
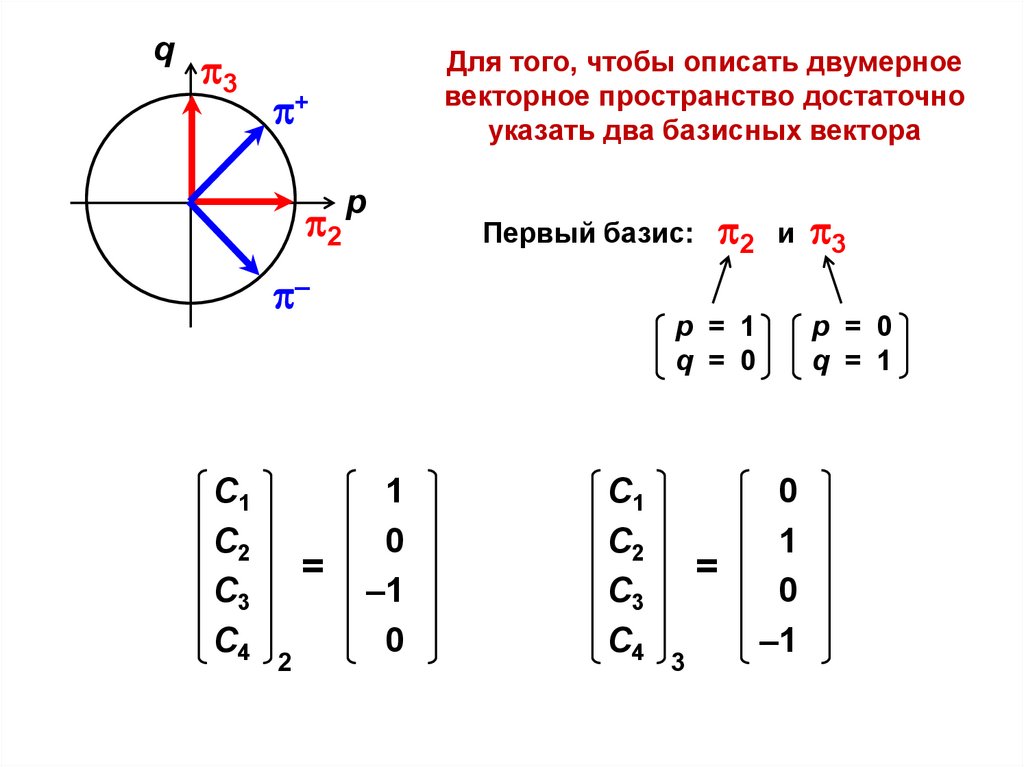
q3
Для того, чтобы описать двумерное
векторное пространство достаточно
указать два базисных вектора
+
2
p
Первый базис:
–
С1
С2
С3
С4
=
2
2
и
p = 1
q = 0
1
0
–1
0
С1
С2
С3
С4
=
3
3
p = 0
q = 1
0
1
0
–1
71.
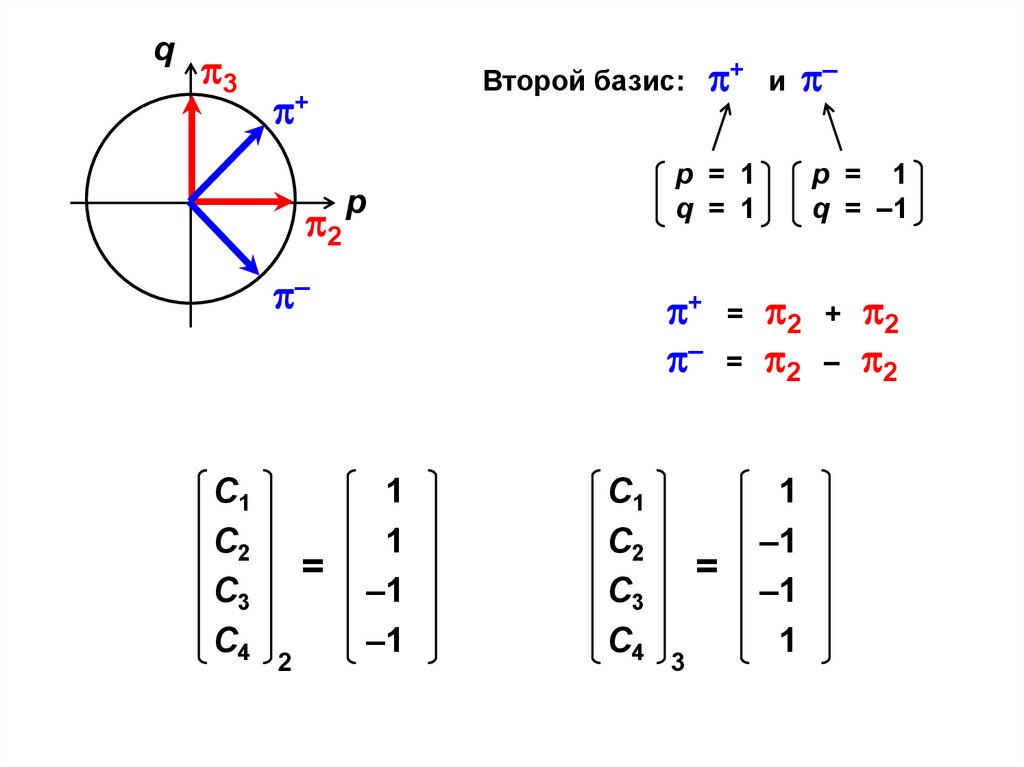
q3
+
2
p
=
2
+
–
1
1
–1
–1
и
–
p = 1
q = 1
–
С1
С2
С3
С4
+
Второй базис:
С1
С2
С3
С4
=
3
=
=
p = 1
q = –1
2
2
1
–1
–1
1
+
–
2
2
72.
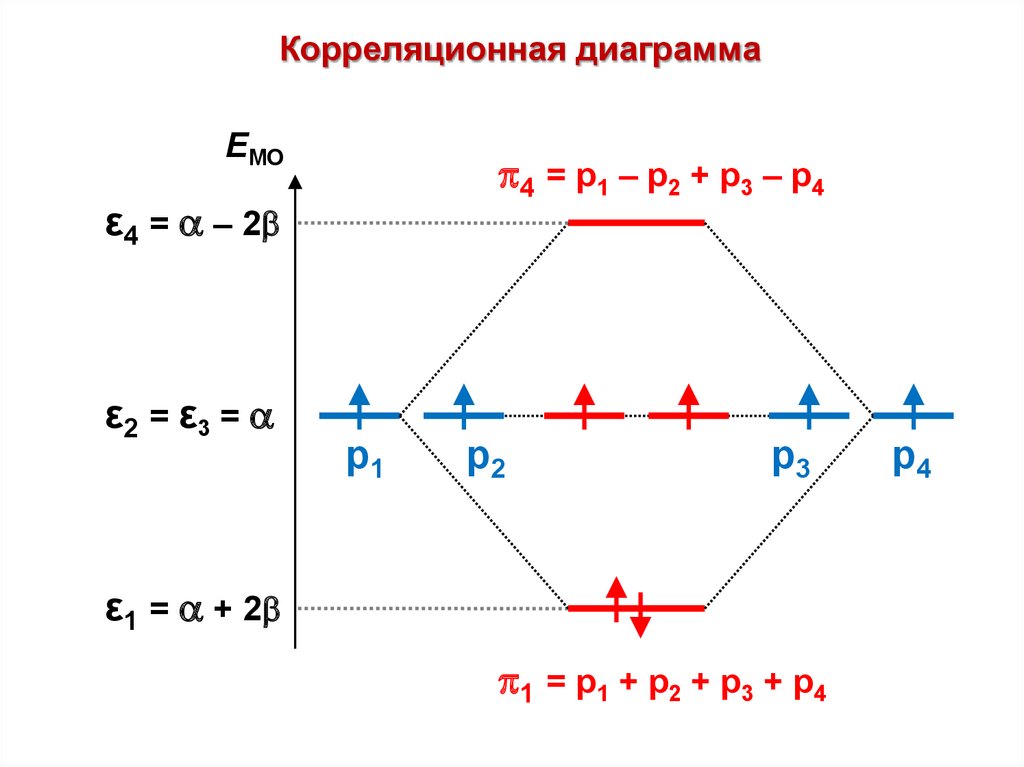
Корреляционная диаграммаEМО
4 = р1 – р2 + р3 – р4
ε4 = – 2
ε2 = ε3 =
р1
р2
р3
ε1 = + 2
1 = р1 + р2 + р3 + р4
р4
73.
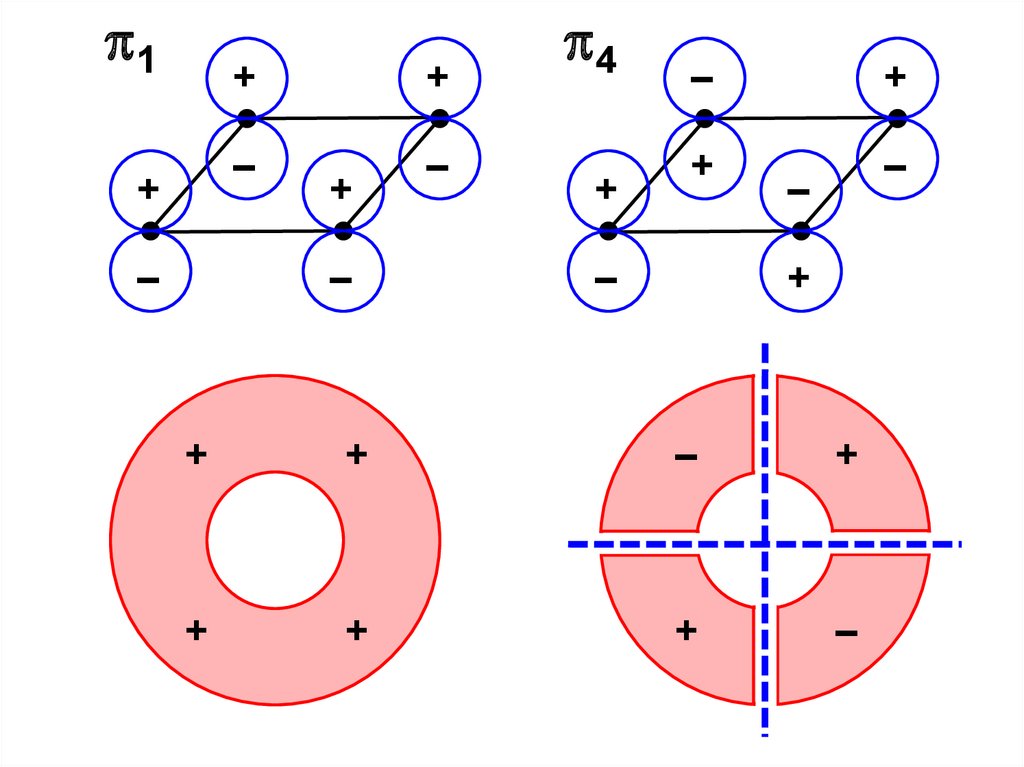
1+
–
+
+
–
–
+
–
4
+
–
+
+
–
–
–
+
+
+
–
+
+
+
+
–
74.
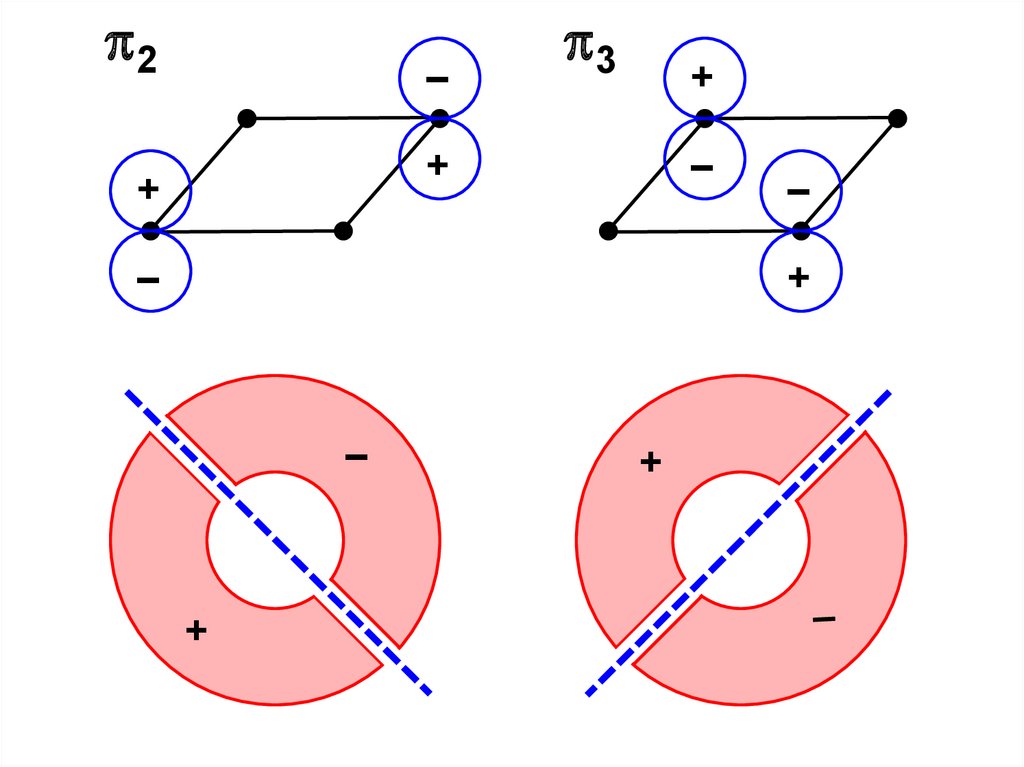
2–
3
+
–
+
+
–
–
+
+
+
–
75.
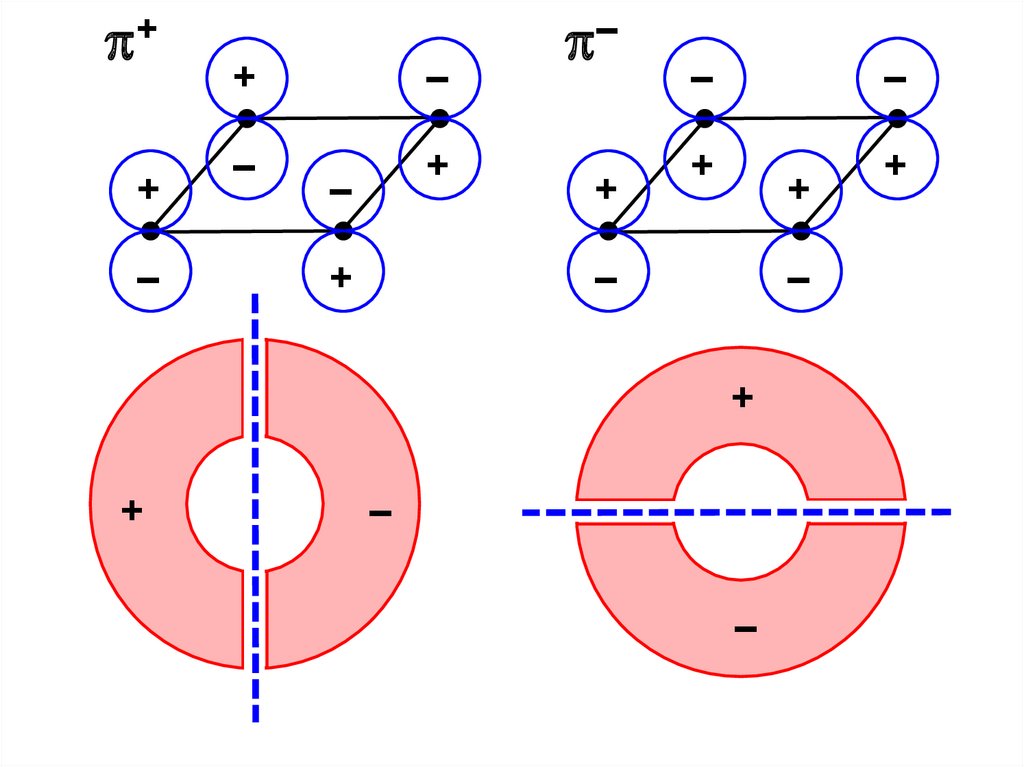
++
–
+
–
–
+
–
–
+
–
–
+
+
+
–
+
–
+
+
–
–
76.
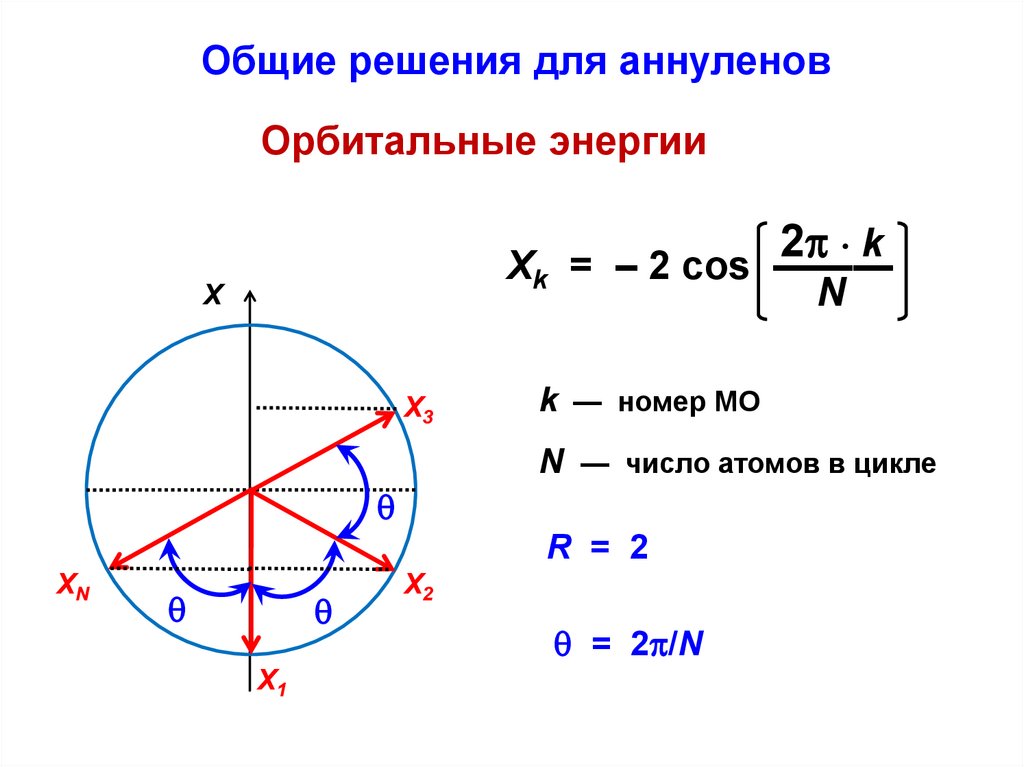
Общие решения для аннуленовОрбитальные энергии
2
k
Xk = – 2 cos ———
N
Х
Х3
k — номер МО
N — число атомов в цикле
R = 2
ХN
Х1
Х2
= 2 /N
77.
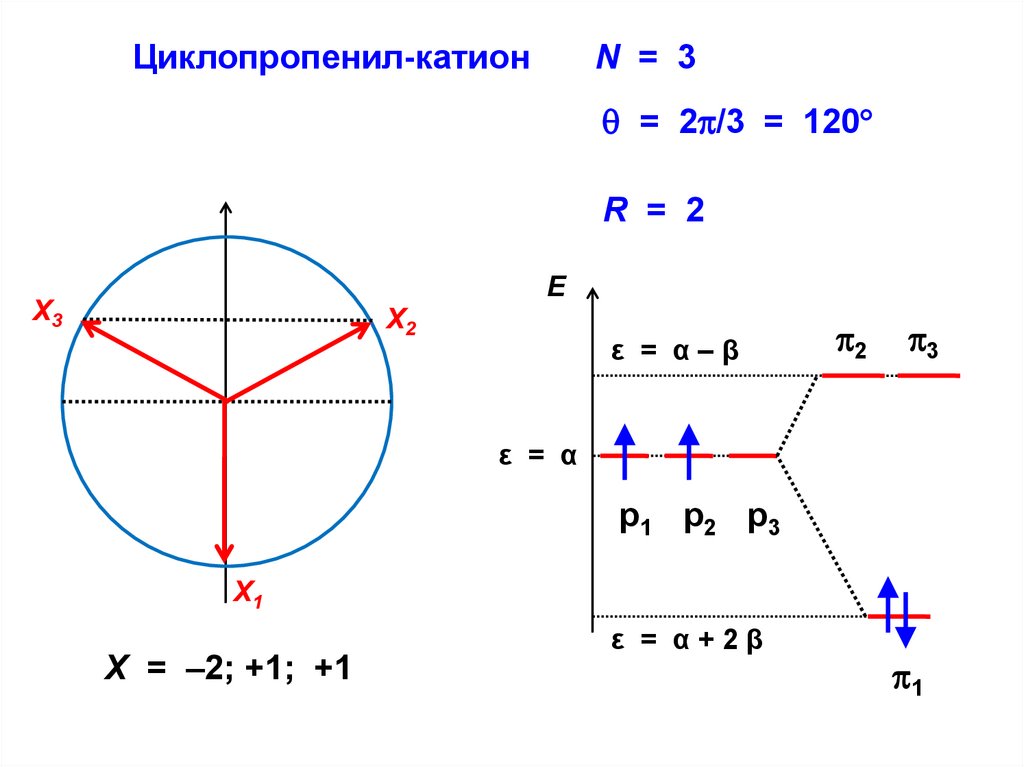
Циклопропенил-катионN = 3
= 2 /3 = 120
R = 2
E
Х3
Х2
ε = α–β
2
3
ε = α
p1 p2 p3
Х1
X = –2; +1; +1
ε = α+2β
1
78.
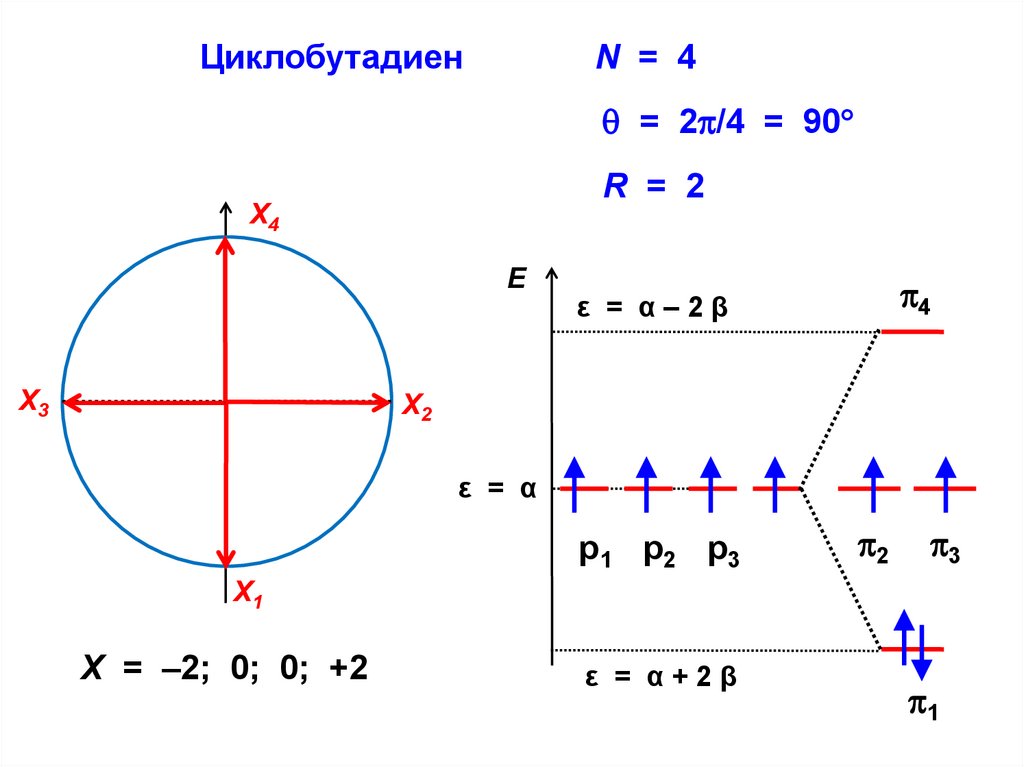
ЦиклобутадиенN = 4
= 2 /4 = 90
R = 2
Х4
E
Х3
4
ε = α–2β
Х2
ε = α
p1 p2 p3
2
3
Х1
X = –2; 0; 0; +2
ε = α+2β
1
79.
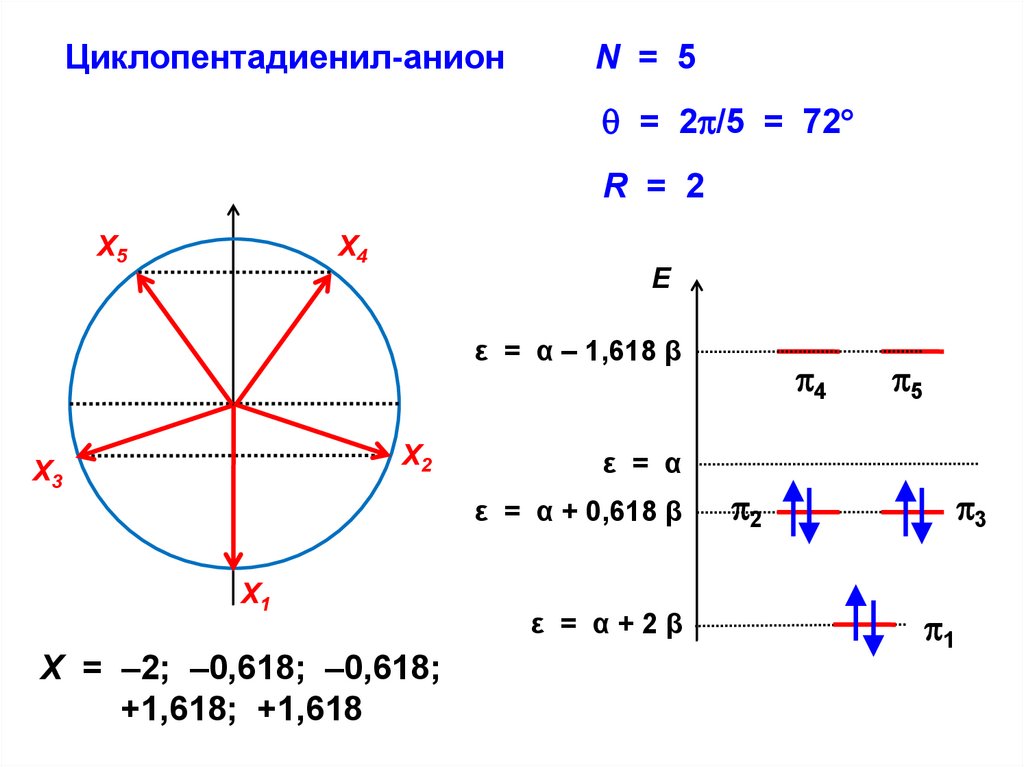
Циклопентадиенил-анионN = 5
= 2 /5 = 72
R = 2
Х5
Х4
E
ε = α – 1,618 β
Х2
Х3
X = –2; –0,618; –0,618;
+1,618; +1,618
5
ε = α
ε = α + 0,618 β
Х1
4
ε = α+2β
2
3
1
80.
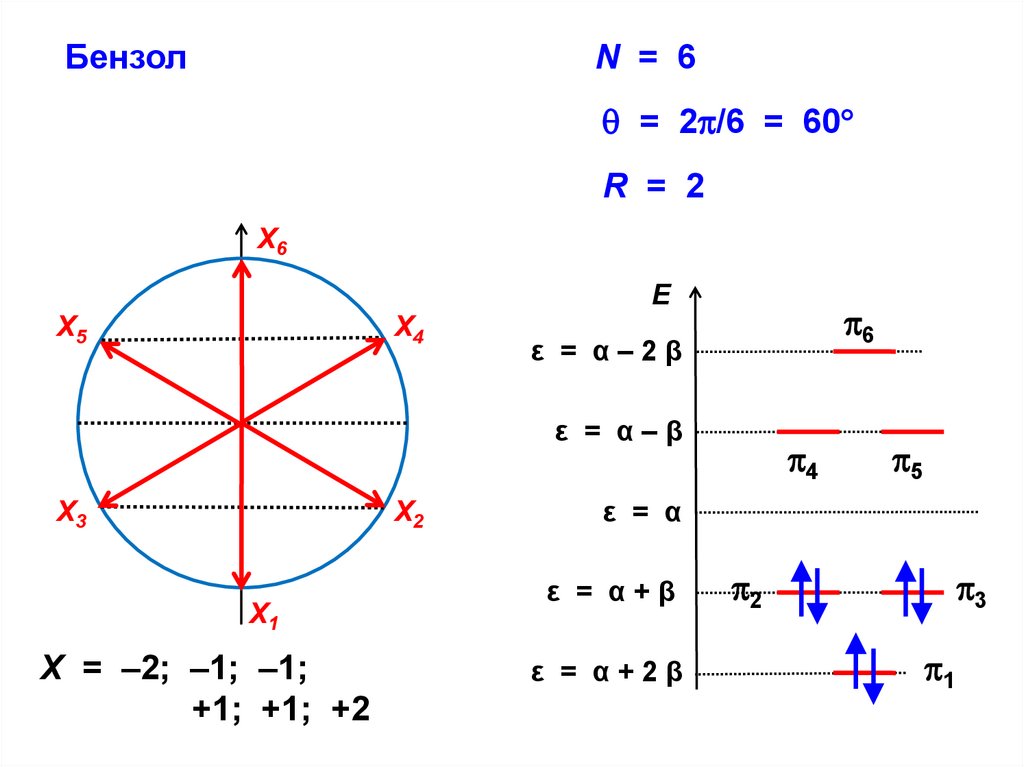
БензолN = 6
= 2 /6 = 60
R = 2
Х6
E
Х5
Х4
6
ε = α–2β
ε = α–β
Х3
Х2
Х1
X = –2; –1; –1;
+1; +1; +2
4
5
ε = α
ε = α+β
ε = α+2β
2
3
1
81.
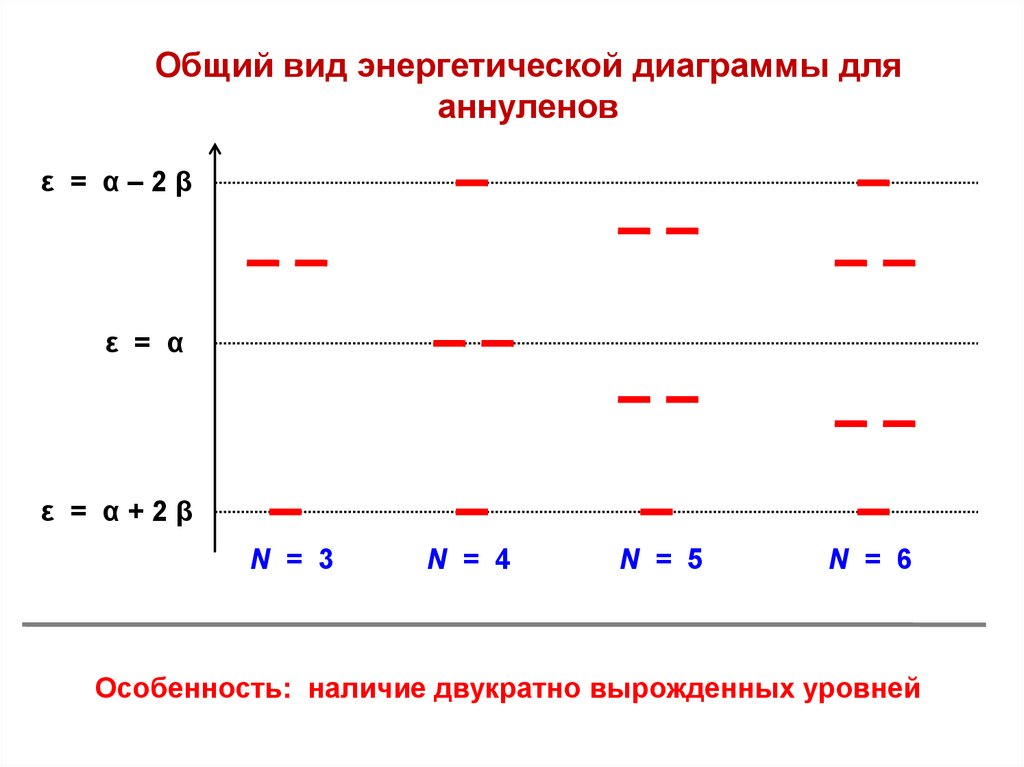
Общий вид энергетической диаграммы дляаннуленов
ε = α–2β
ε = α
ε = α+2β
N = 3
N = 4
N = 5
N = 6
Особенность: наличие двукратно вырожденных уровней
82.
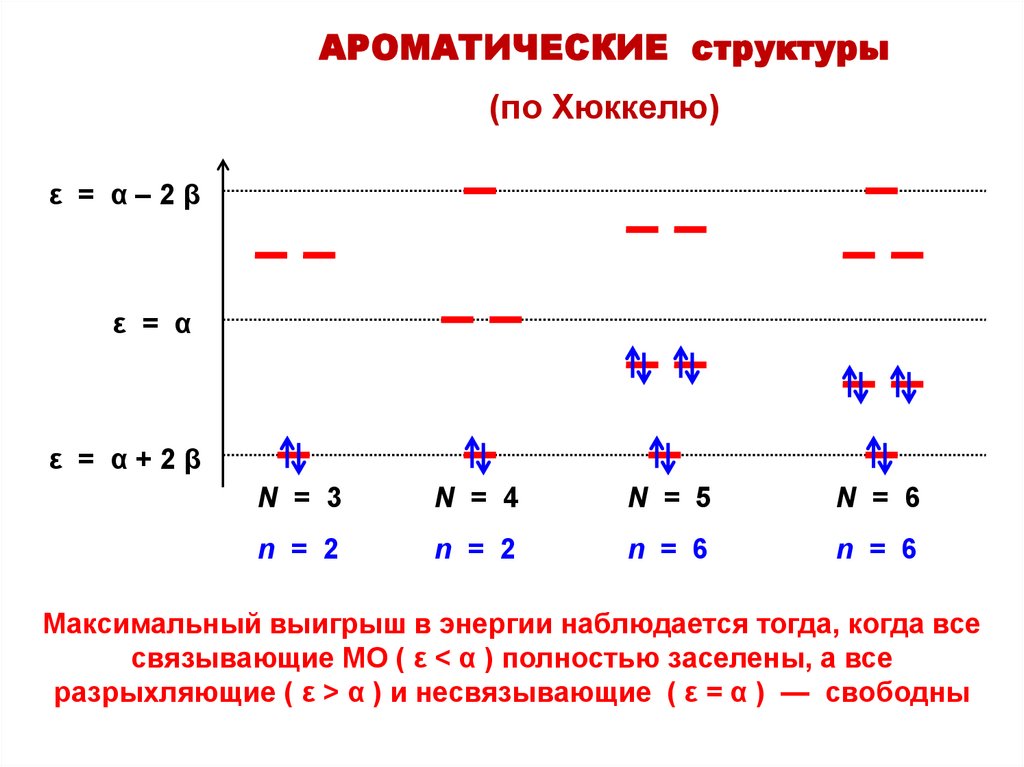
АРОМАТИЧЕСКИЕ структуры(по Хюккелю)
ε = α–2β
ε = α
ε = α+2β
N = 3
N = 4
N = 5
N = 6
n = 2
n = 2
n = 6
n = 6
Максимальный выигрыш в энергии наблюдается тогда, когда все
связывающие МО ( ε < α ) полностью заселены, а все
разрыхляющие ( ε > α ) и несвязывающие ( ε = α ) — свободны
83.
Число связывающих МО всегда нечетно и его можновыразить формулой
(2k + 1),
где k = 0, 1, 2, … (любое целое число)
Суммарная емкость всех связывающих МО равна
2 (2k + 1) = 4k + 2
(т.е. 2, 6, 10, …)
Молекулы аннуленов, в которых число -электронов
удовлетворяет формуле
n = 4k + 2
(т.е. n = 2, 6, 10, …)
должны отличаться повышенной стабильностью и
пониженной химической активностью
Правило Хюккеля
84.
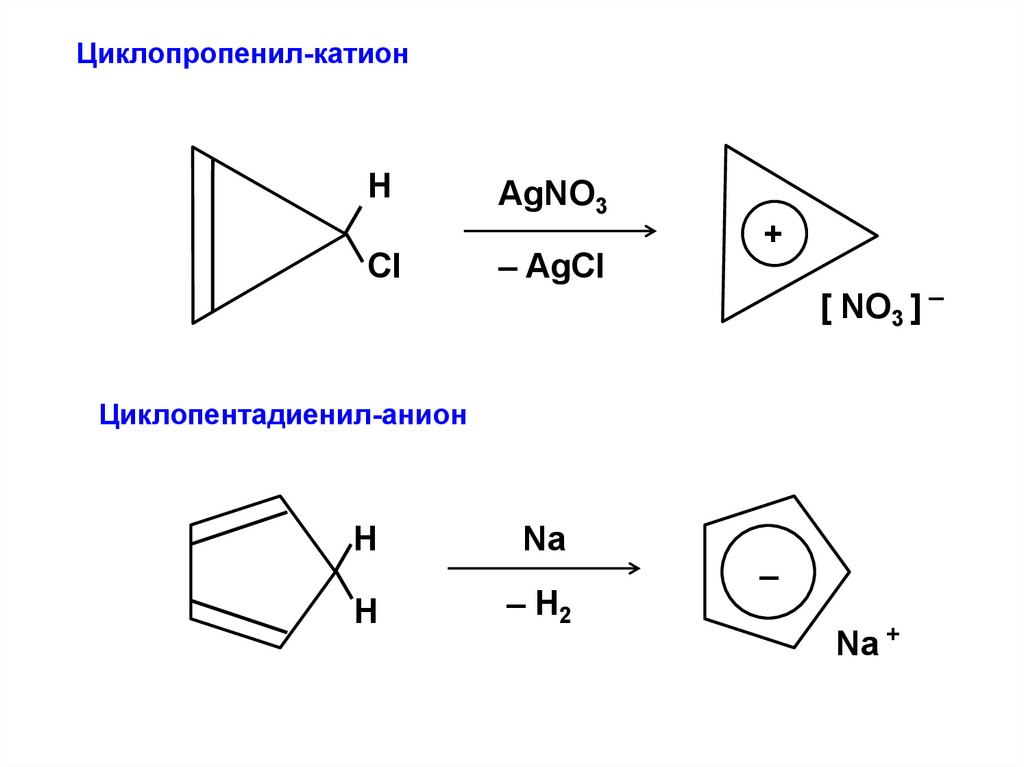
Циклопропенил-катионН
Cl
AgNO3
– AgCl
+
[ NO3 ] –
Циклопентадиенил-анион
Н
Na
Н
– H2
–
Na +
85.
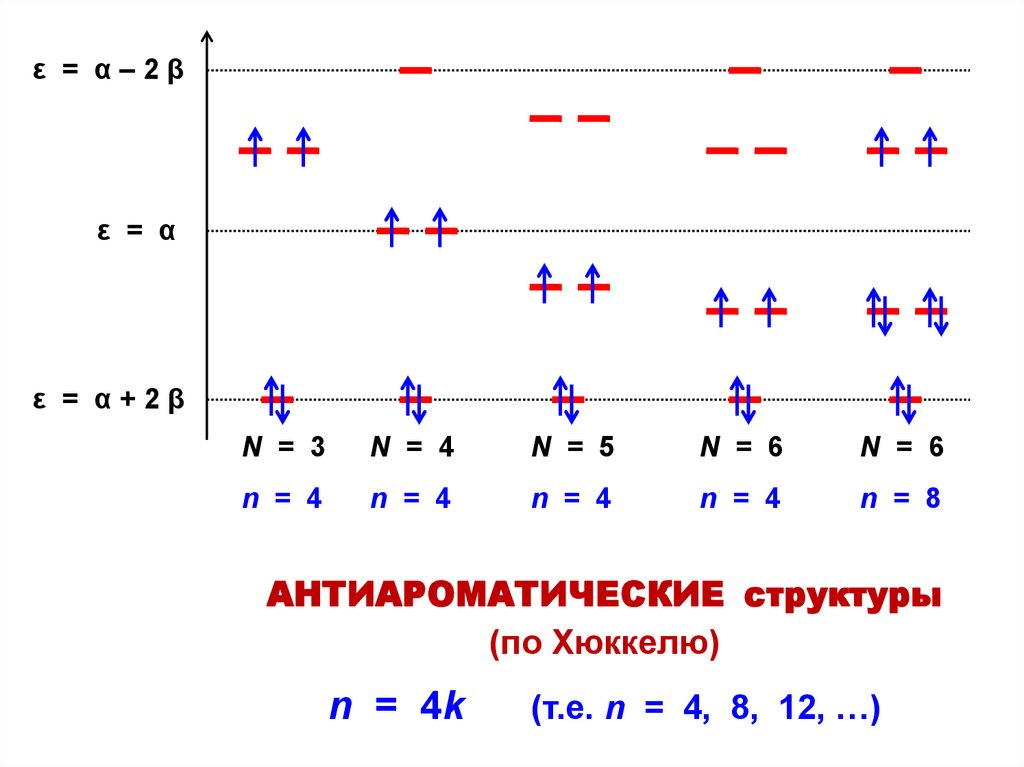
ε = α–2βε = α
ε = α+2β
N = 3
N = 4
N = 5
N = 6
N = 6
n = 4
n = 4
n = 4
n = 4
n = 8
АНТИАРОМАТИЧЕСКИЕ структуры
(по Хюккелю)
n = 4k
(т.е. n = 4, 8, 12, …)
86.
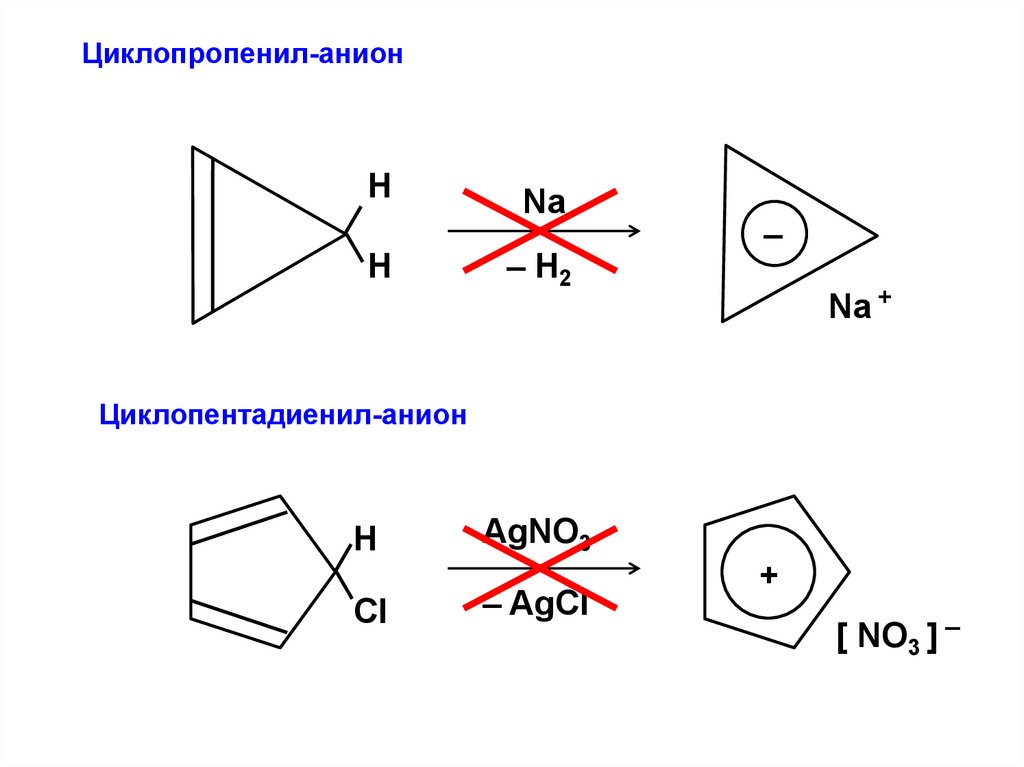
Циклопропенил-анионН
Н
Na
– H2
–
Na +
Циклопентадиенил-анион
Н
Cl
AgNO3
– AgCl
+
[ NO3 ] –
87.
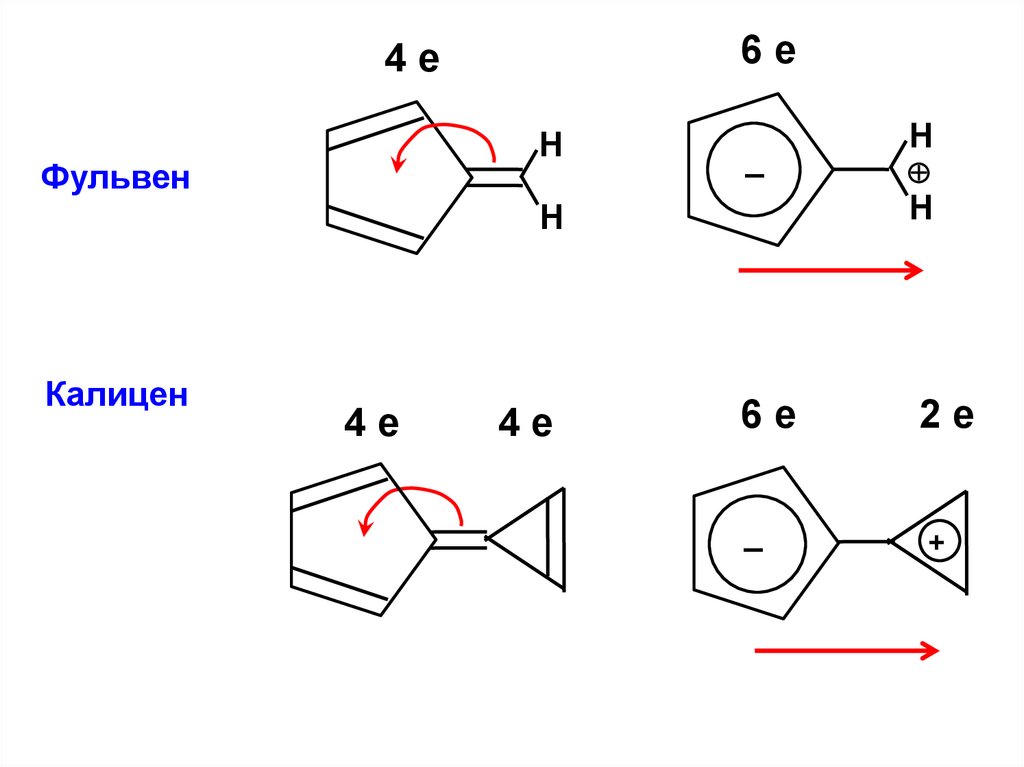
6е4е
Н
Фульвен
–
Н
Калицен
4е
4е
6е
–
Н
Н
2е
+
88.
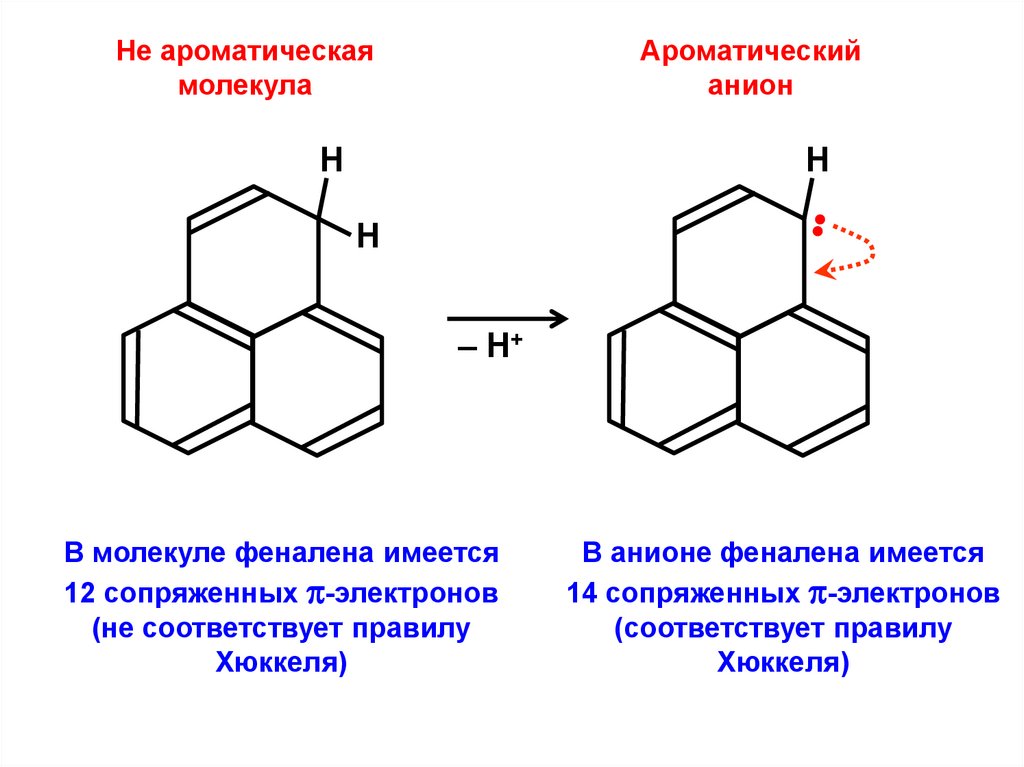
Не ароматическаямолекула
Ароматический
анион
Н
Н
Н
– Н+
В молекуле феналена имеется
12 сопряженных -электронов
(не соответствует правилу
Хюккеля)
В анионе феналена имеется
14 сопряженных -электронов
(соответствует правилу
Хюккеля)
89.
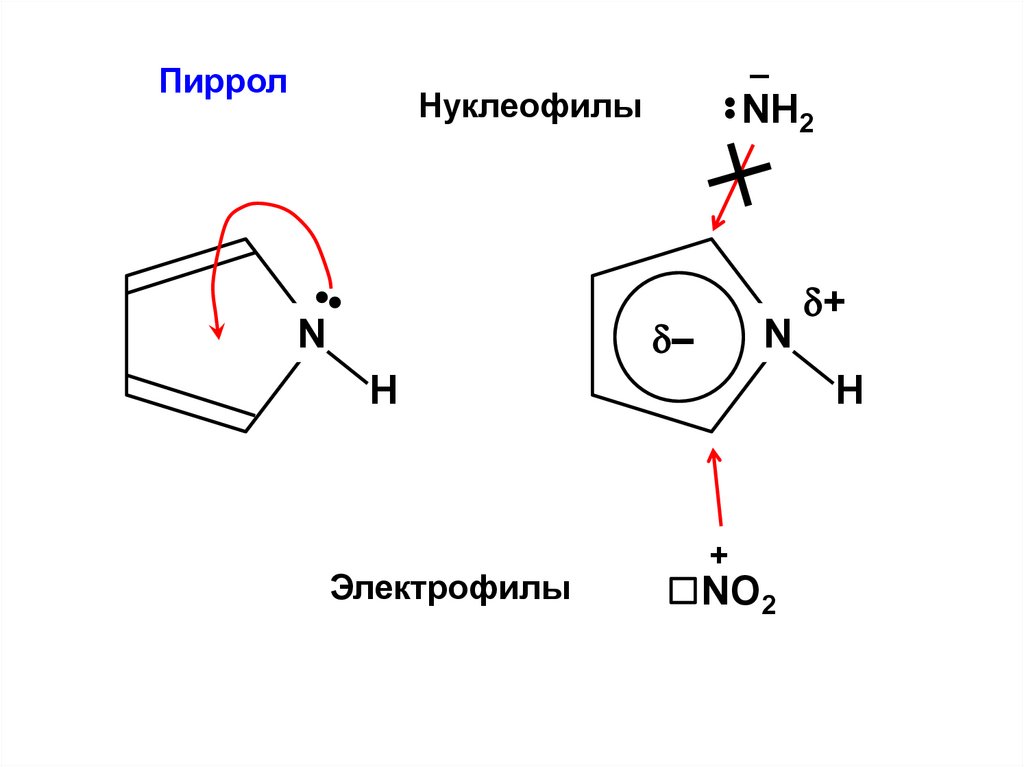
Пиррол–
Нуклеофилы
•
NH2
–
N
N
H
Электрофилы
+
H
+
NO2
90.
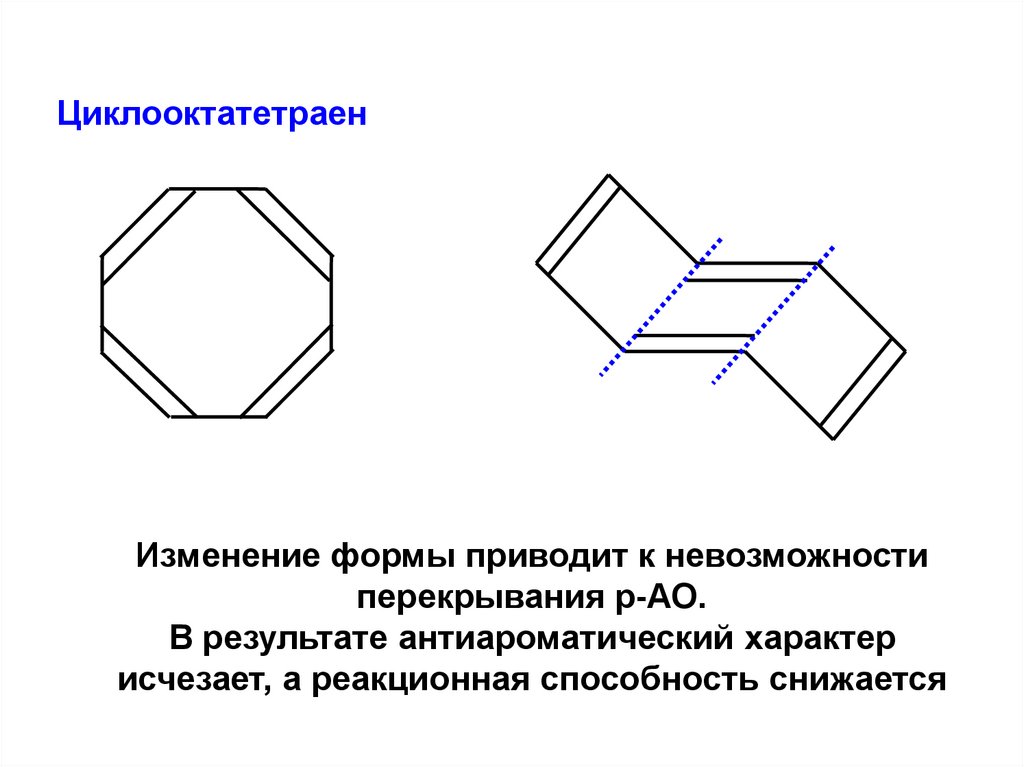
ЦиклооктатетраенИзменение формы приводит к невозможности
перекрывания р-АО.
В результате антиароматический характер
исчезает, а реакционная способность снижается
91.
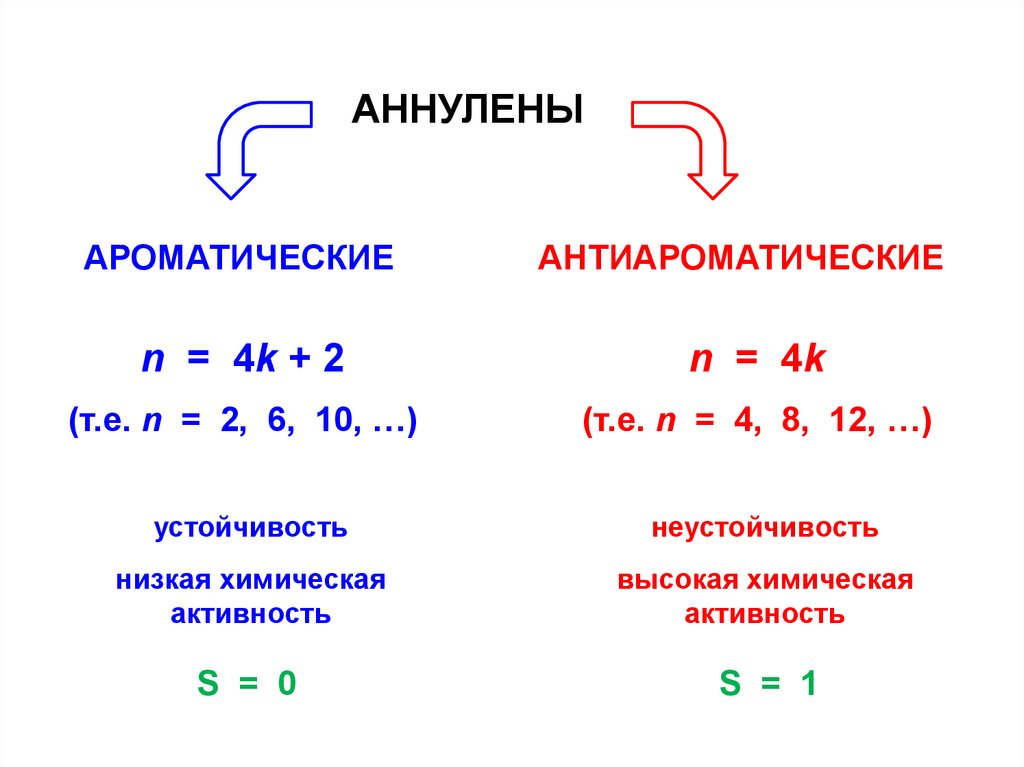
АННУЛЕНЫАРОМАТИЧЕСКИЕ
АНТИАРОМАТИЧЕСКИЕ
n = 4k + 2
n = 4k
(т.е. n = 2, 6, 10, …)
(т.е. n = 4, 8, 12, …)
устойчивость
неустойчивость
низкая химическая
активность
высокая химическая
активность
S = 0
S = 1
92.
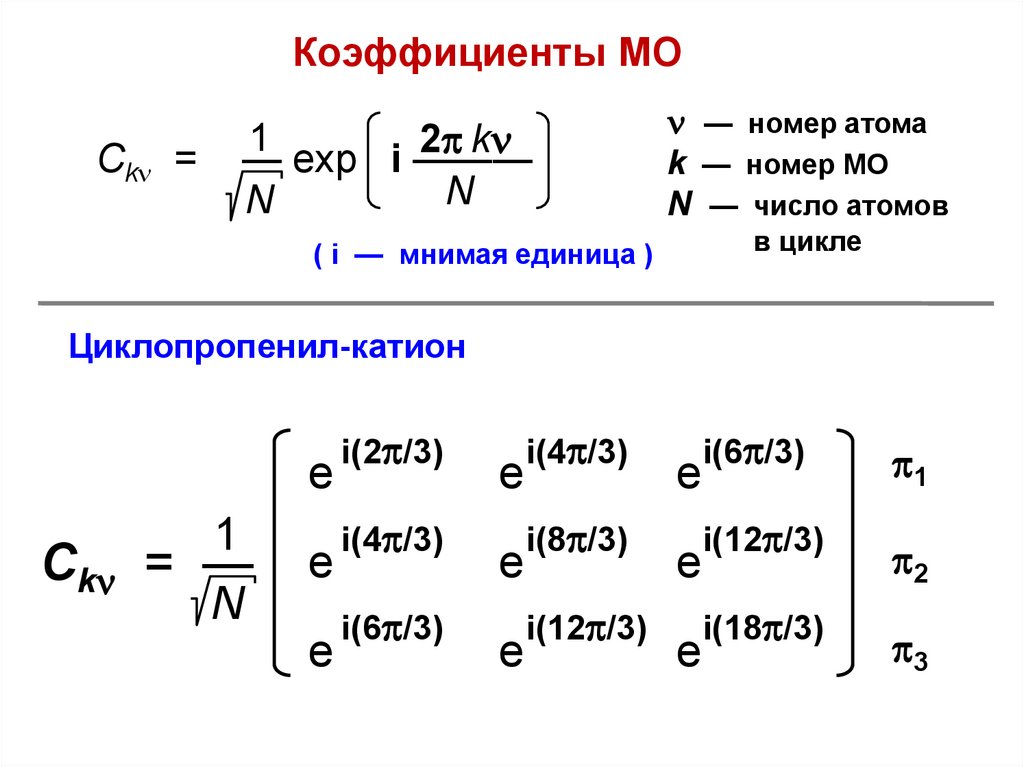
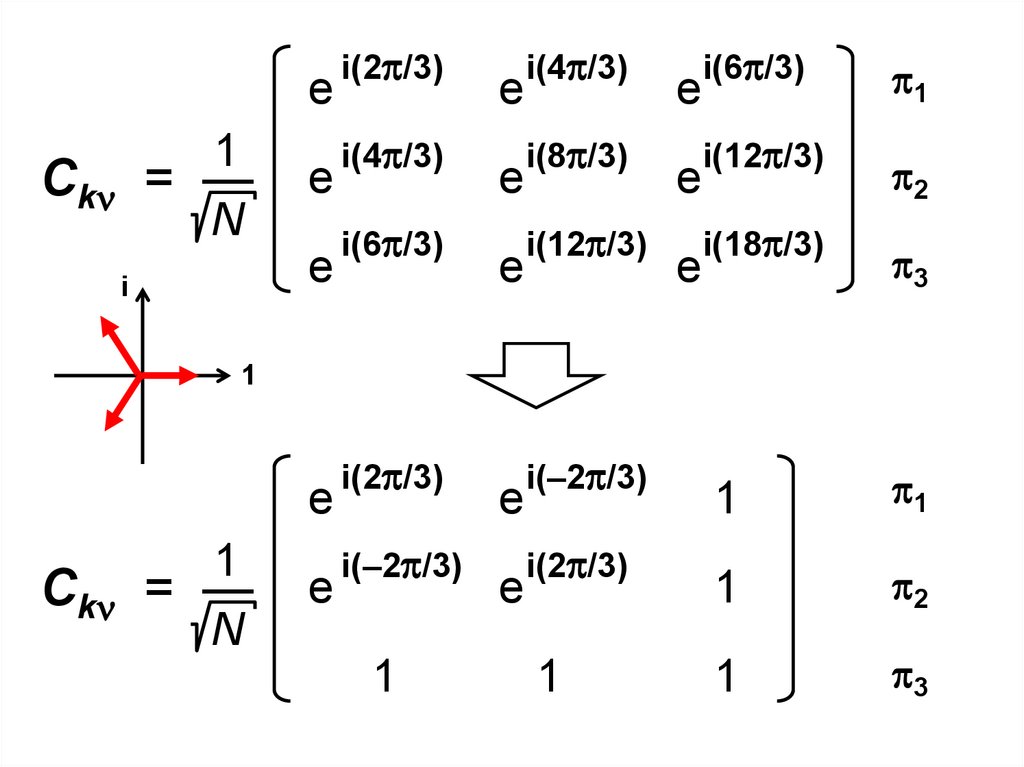
Коэффициенты МО1
2 k
— exp i ———
N
N
Сk =
— номер атома
k — номер МО
N — число атомов
в цикле
( i — мнимая единица )
Циклопропенил-катион
е
1
Сk = —
N
е
е
i(2 /3)
i(4 /3)
i(6 /3)
е
е
е
i(4 /3)
i(8 /3)
i(12 /3)
е
е
е
i(6 /3)
i(12 /3)
i(18 /3)
1
2
3
93.
е1
Сk = —
N
i
е
е
i(2 /3)
i(4 /3)
i(6 /3)
е
е
е
i(4 /3)
i(8 /3)
i(12 /3)
е
е
е
i(6 /3)
i(12 /3)
i(18 /3)
1
2
3
1
е
1
Сk = —
N
е
i(2 /3)
i(–2 /3)
1
е
е
i(–2 /3)
i(2 /3)
1
1
1
1
2
1
3
94.
е1
Сk = —
3
е
i(2 /3)
i(–2 /3)
1
+
= 1/ 2 ( 1 + 2)
1
Сk = —
3
е
е
i(–2 /3)
i(2 /3)
1
1
1
1
2
1
3
= 1/ 2 ( 1 – 2)
–
2 sin(2 /3) – 2 sin(2 /3)
0
–
2 cos(2 /3)
2
+
1
3
1
2 cos(2 /3)
1
95.
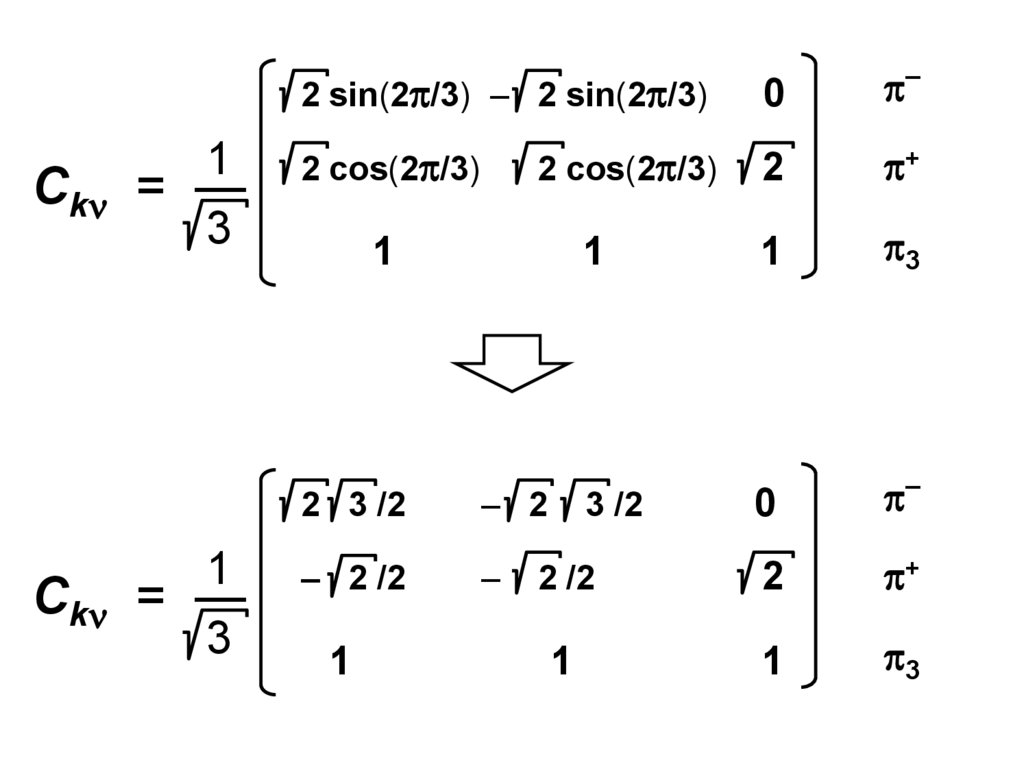
1Сk = —
2 sin(2 /3) – 2 sin(2 /3)
0
–
2 cos(2 /3)
2
+
1
3
0
–
2 /2
2
+
1
1
3
3
1
Сk = —
3
2 cos(2 /3)
1
1
2 3 /2
– 2
– 2 /2
–
1
3 /2
96.
1Сk = —
3
Сk =
0
–
2 /2
2
+
1
1
3
2 3 /2
– 2
– 2 /2
–
1
3 /2
2 /2
– 2 /2
0
–
–1/ 6
–1/ 6
2 / 3
+
1/ 3
1/ 3
1/
3
3
97.
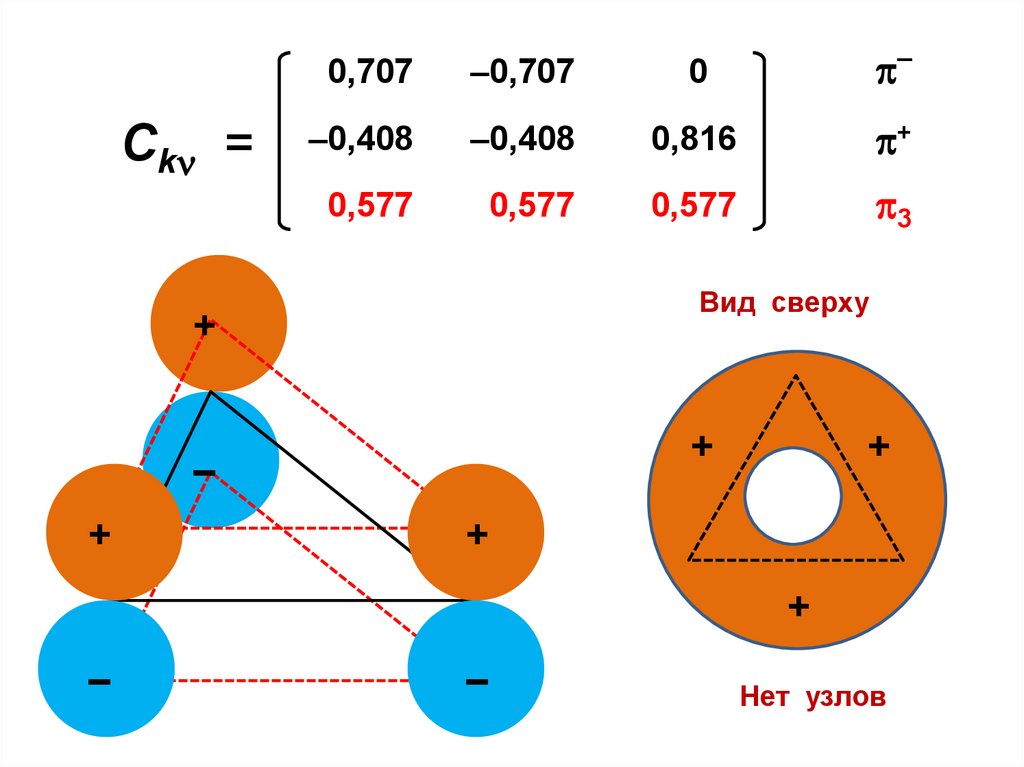
Сk =0,707
–0,707
0
–
–0,408
–0,408
0,816
+
0,577
0,577
0,577
3
Вид сверху
+
+
–
+
+
+
+
–
–
Нет узлов
98.
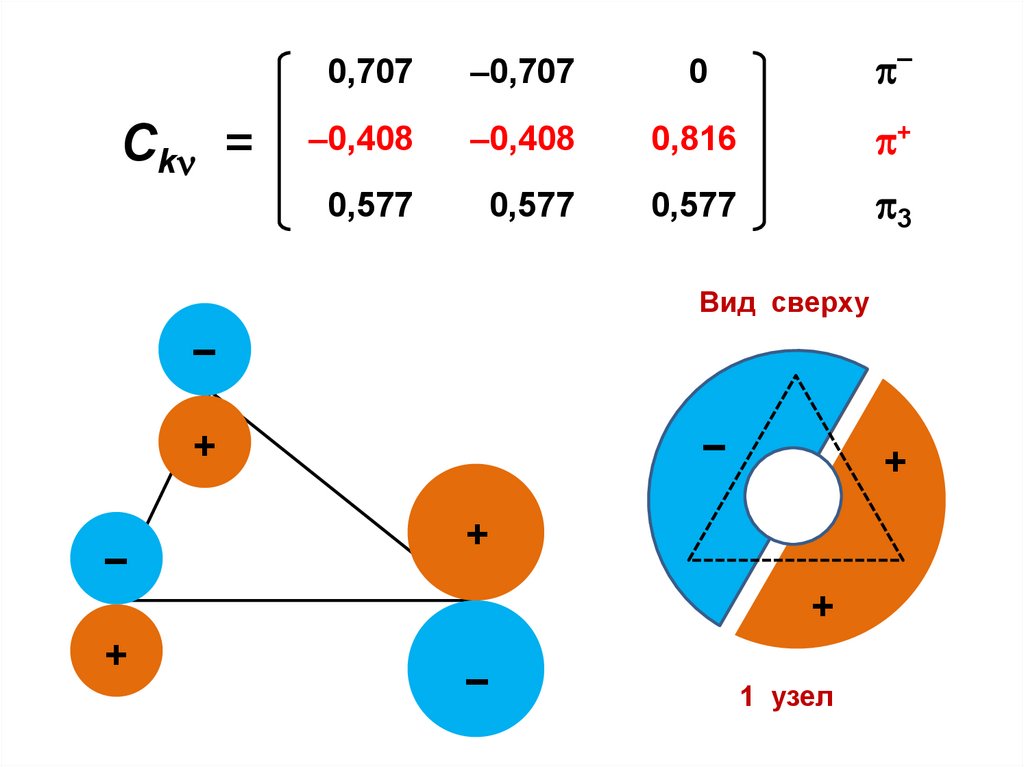
Сk =0,707
–0,707
0
–
–0,408
–0,408
0,816
+
0,577
0,577
0,577
3
Вид сверху
–
––
+
–
+
+
+
+
–
1 узел
99.
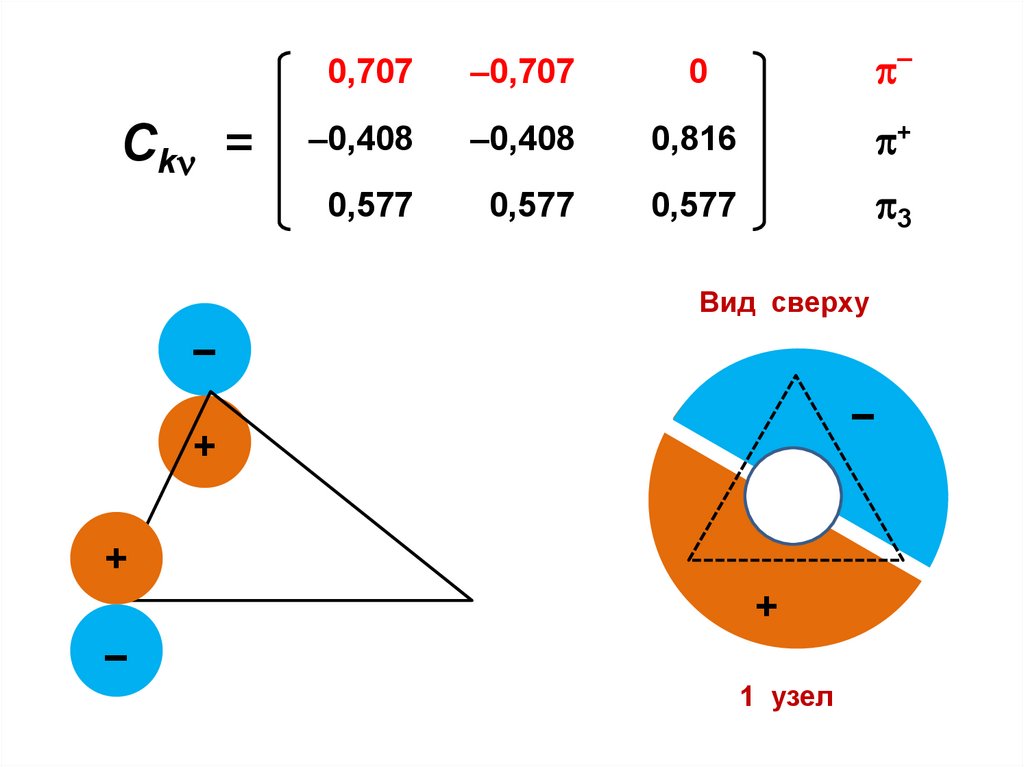
Сk =0,707
–0,707
0
–
–0,408
–0,408
0,816
+
0,577
0,577
0,577
3
Вид сверху
–
+
––
–
+
+
–
1 узел
100.
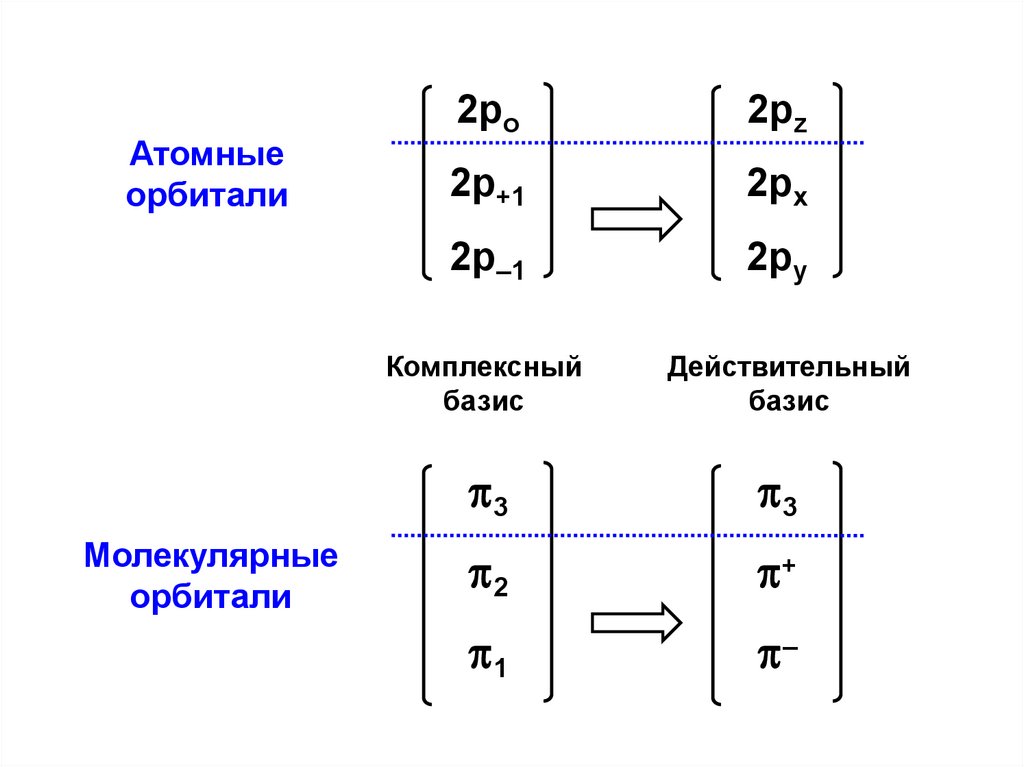
Атомныеорбитали
2ро
2рz
2р+1
2рx
2р–1
2рy
Комплексный
базис
Молекулярные
орбитали
Действительный
базис
3
3
2
+
1
–
101.
Процедура преобразования к действительному базисувозможна для любого аннулена
( – 1) 1
Е
Ck, = (–1)
= k
= –3
= +3
= –2
= +2
= –1
= +1
= 0
—
N
2
——–
N
C– , =
2
— sin
N
C+ , =
2
2
— cos ——–
N
N
1
Co, = —
N
102.
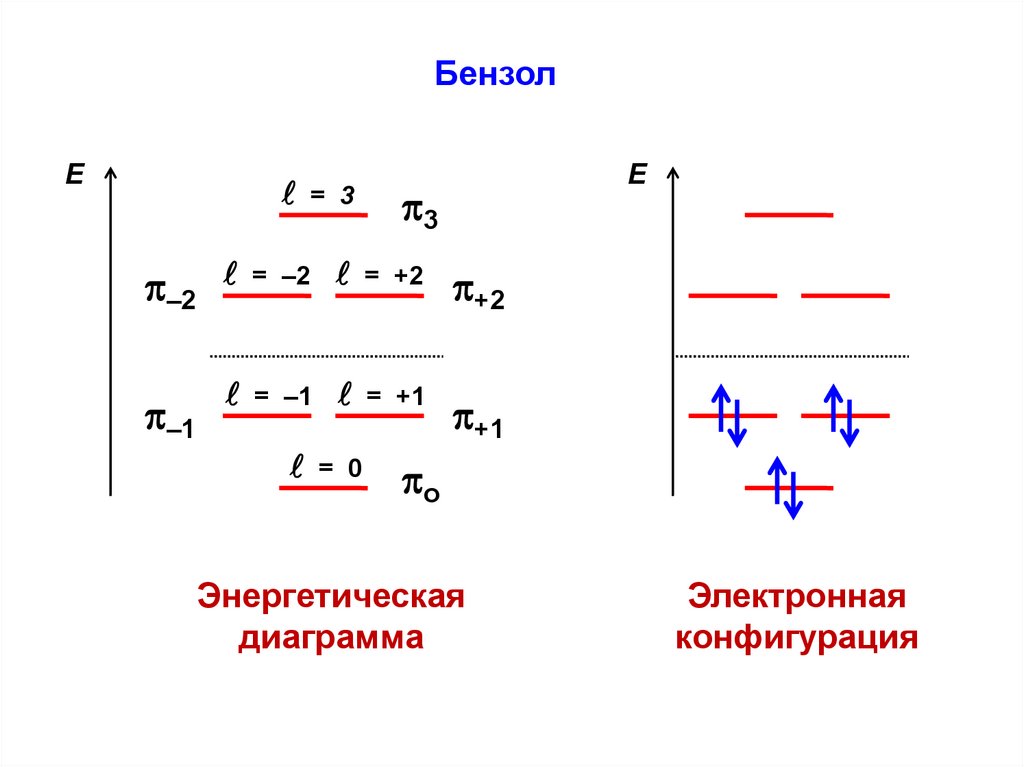
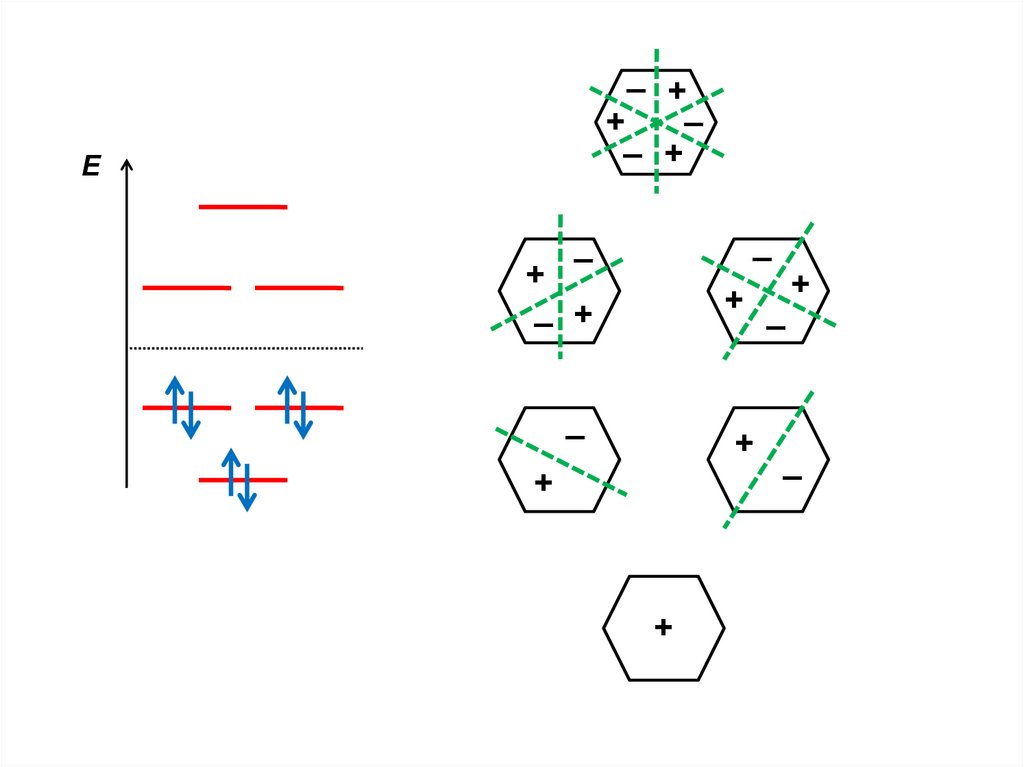
БензолЕ
= 3
Е
3
–2
= –2
= +2
+2
= –1
= +1
+1
–1
= 0
о
Энергетическая
диаграмма
Электронная
конфигурация
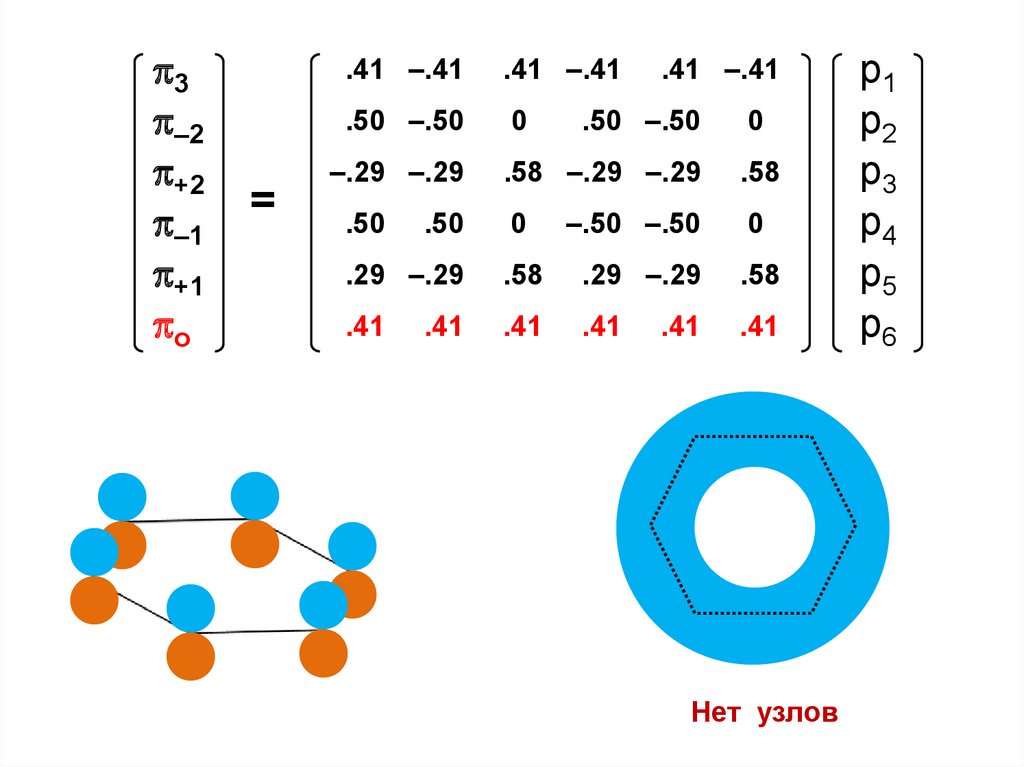
103.
3–2
+2
–1
+1
о
=
.41 –.41
.41 –.41
.50 –.50
0
–.29 –.29
.41 –.41
.50 –.50
.58 –.29 –.29
0
.58
0
–.50 –.50
0
.29 –.29
.58
.29 –.29
.58
.41
.41
.41
.41
.50
.50
.41
.41
Нет узлов
р1
р2
р3
р4
р5
р6
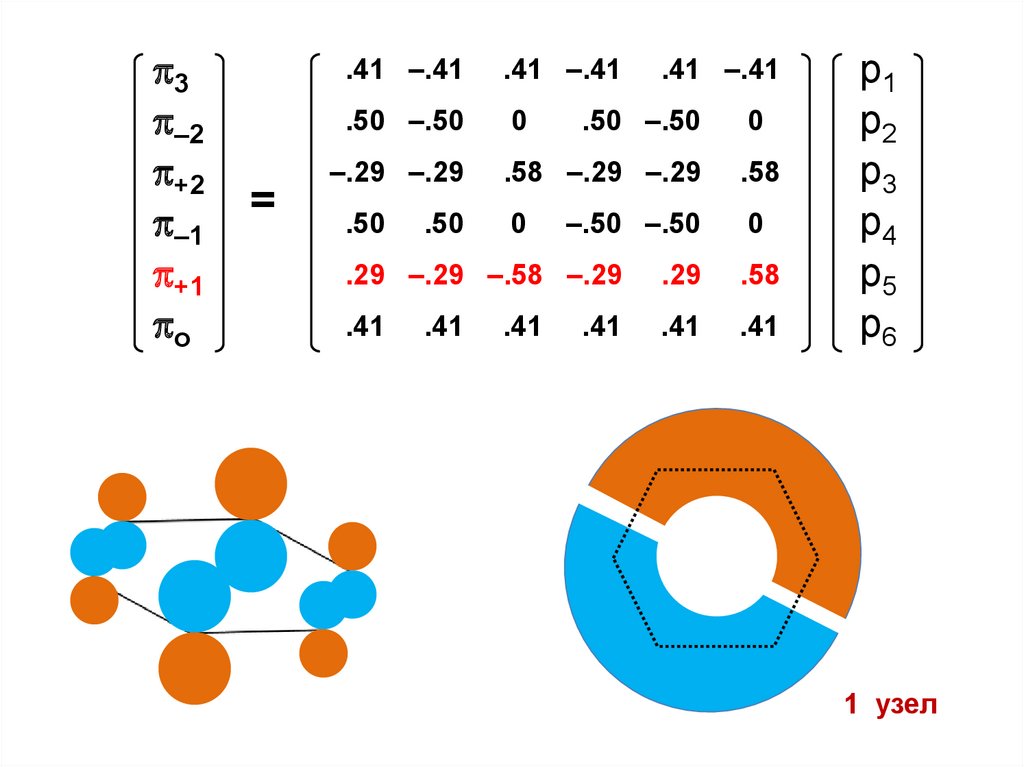
104.
3–2
+2
–1
+1
о
=
.41 –.41
.41 –.41
.50 –.50
0
–.29 –.29
.50
.50
.41 –.41
.50 –.50
.58 –.29 –.29
0
–.50 –.50
0
.58
0
.29 –.29 –.58 –.29
.29
.58
.41
.41
.41
.41
.41
.41
р1
р2
р3
р4
р5
р6
1 узел
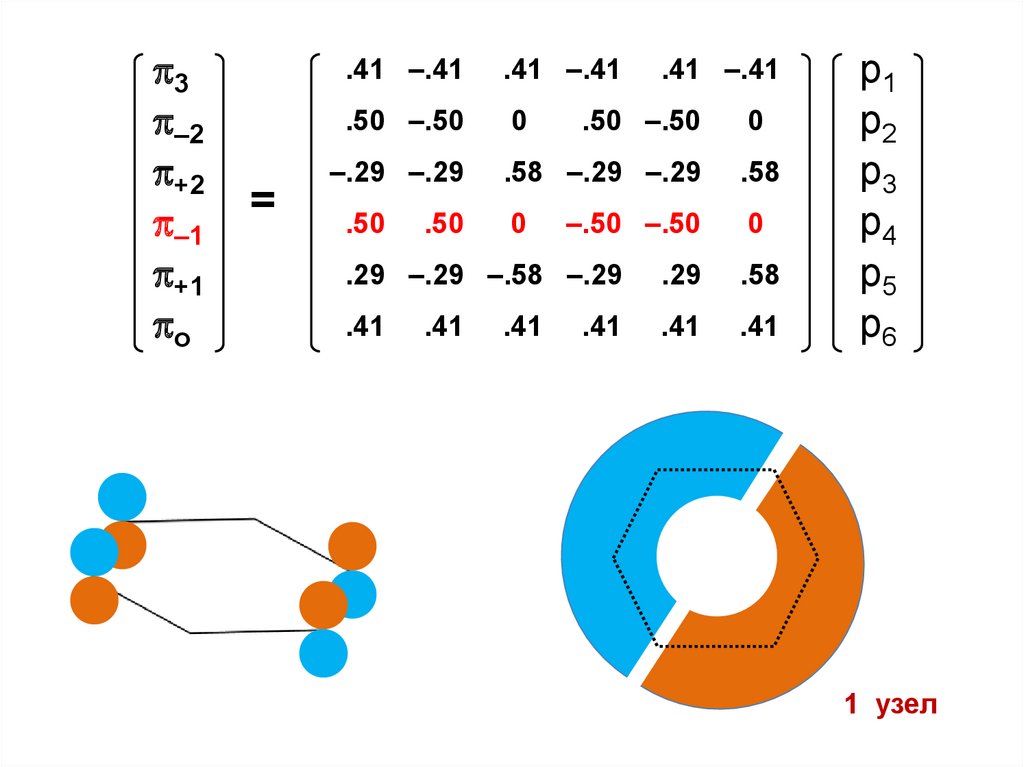
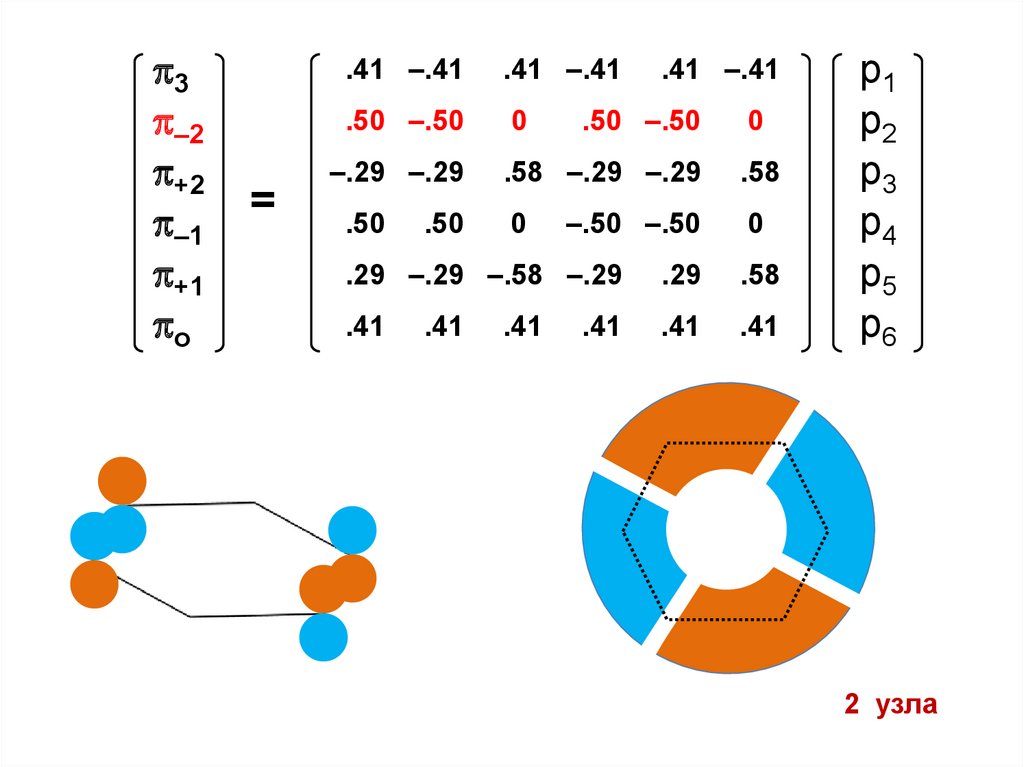
105.
3–2
+2
–1
+1
о
=
.41 –.41
.41 –.41
.50 –.50
0
–.29 –.29
.50
.50
.41 –.41
.50 –.50
.58 –.29 –.29
0
–.50 –.50
0
.58
0
.29 –.29 –.58 –.29
.29
.58
.41
.41
.41
.41
.41
.41
р1
р2
р3
р4
р5
р6
1 узел
106.
3–2
+2
–1
+1
о
=
.41 –.41
.41 –.41
.50 –.50
0
–.29 –.29
.50
.50
.41 –.41
.50 –.50
.58 –.29 –.29
0
–.50 –.50
0
.58
0
.29 –.29 –.58 –.29
.29
.58
.41
.41
.41
.41
.41
.41
р1
р2
р3
р4
р5
р6
2 узла
107.
3–2
+2
–1
+1
о
=
.41 –.41
.41 –.41
.50 –.50
0
–.29 –.29
.50
.50
.41 –.41
.50 –.50
.58 –.29 –.29
0
–.50 –.50
0
.58
0
.29 –.29 –.58 –.29
.29
.58
.41
.41
.41
.41
.41
.41
р1
р2
р3
р4
р5
р6
2 узла
108.
3–2
+2
–1
+1
о
=
.41 –.41
.41 –.41
.50 –.50
0
–.29 –.29
.50
.50
.41 –.41
.50 –.50
.58 –.29 –.29
0
–.50 –.50
0
.58
0
.29 –.29 –.58 –.29
.29
.58
.41
.41
.41
.41
.41
.41
р1
р2
р3
р4
р5
р6
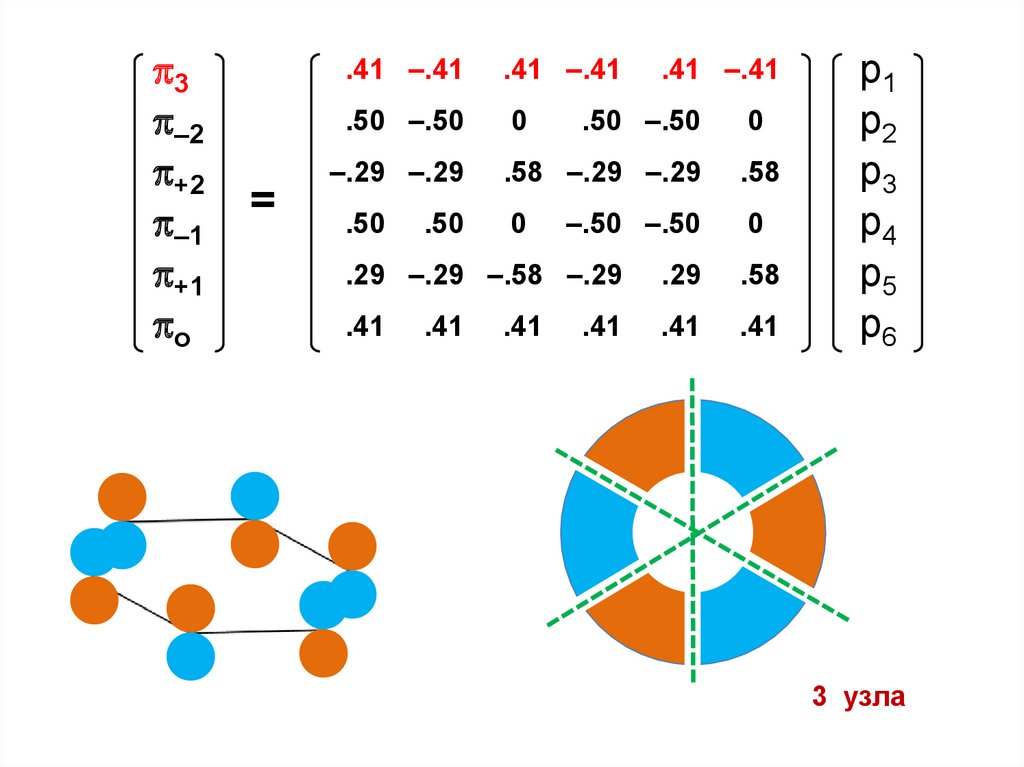
3 узла
109.
– ++
–
– +
Е
–
+ –
– +
+
–
+
+
+
+
–
–
110.
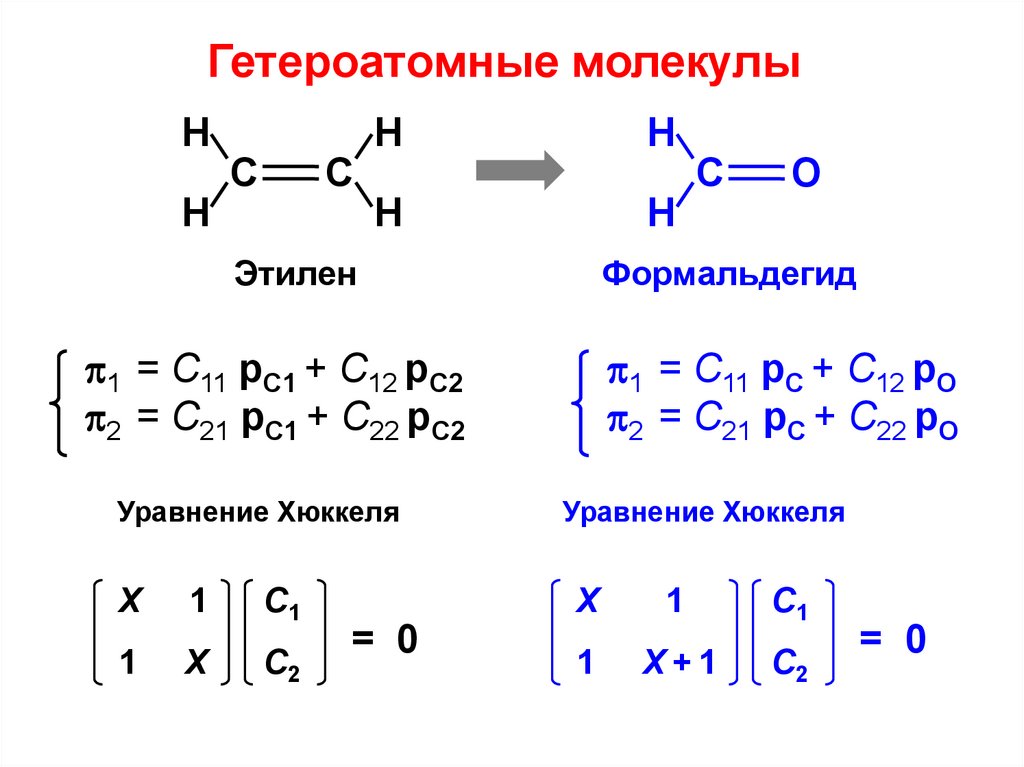
Гетероатомные молекулыН
Н
С
С
Н
Н
Н
Н
Этилен
Х
1
1
Х
С1
С2
1 = С11 pС + C12 pО
2 = С21 pС + C22 pО
Уравнение Хюккеля
Х
= 0
О
Формальдегид
1 = С11 pС1 + C12 pС2
2 = С21 pС1 + C22 pС2
Уравнение Хюккеля
С
1
1
Х+1
С1
С2
= 0
111.
Характеристическое уравнениеХ2 – 1 = 0
Х2 + Х – 1 = 0
Х1 = +1
Х2 = –1
Х1 = + 0,618
Х2 = – 1,618
Σ Xi = 0
Σ Xi = –1
Орбитальные энергии
ε1 = α – β
ε1 = α – 0,618 β
ε2 = α + β
ε2 = α + 1,618 β
112.
Коэффициенты МОХ
1
С1
1
Х+1
С2
= 0
При Х = + 0,618
0,618 С1 + С2 = 0
С2 = – 0,618 С1
1 =
1
–0,618
С1 Х + С2 = 0
С1 + С2 Х + С2 = 0
При Х = – 1,618
–1,618 С1 + С2 = 0
С2 = 1,618 С1
2 =
1
1,618
113.
Атомно-молекулярная матрицаэтилен
1
2
=
0,707
–0,707
р1
0,707
0,707
р2
0,851
–0,526
рС
0,526
0,851
рО
формальдегид
1
2
=
114.
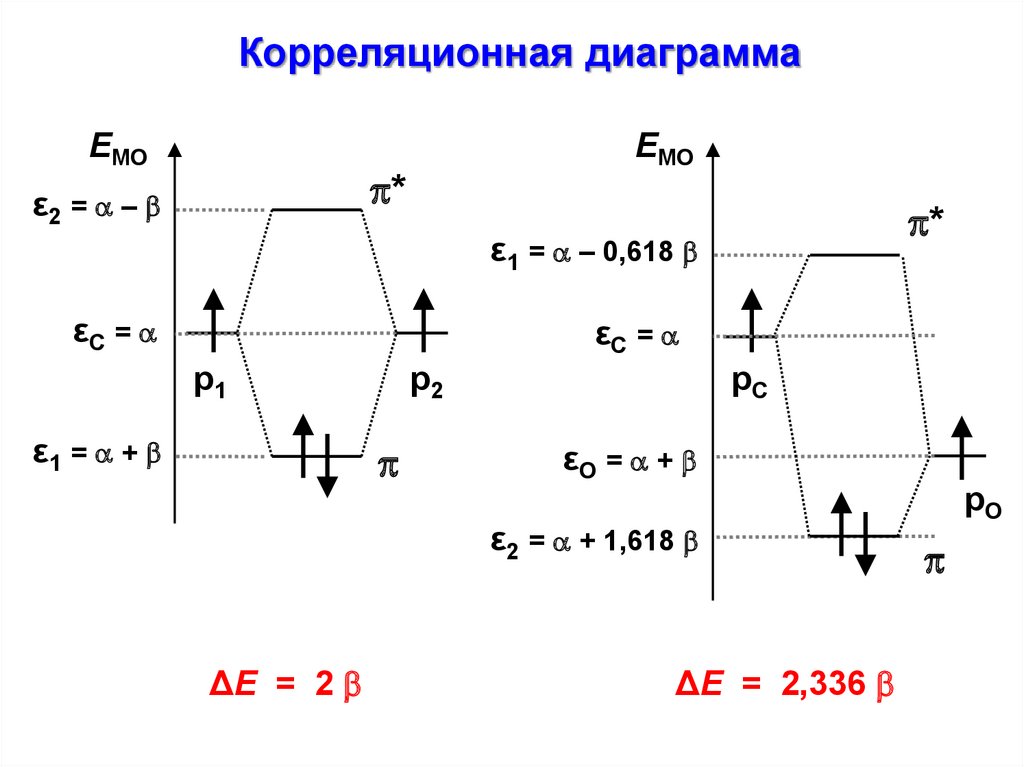
Корреляционная диаграммаEМО
EМО
*
ε2 = –
*
ε1 = – 0,618
εС =
εС =
р1
ε1 = +
р2
рС
εО = +
ε2 = + 1,618
ΔЕ = 2
ΔЕ = 2,336
рО
115.
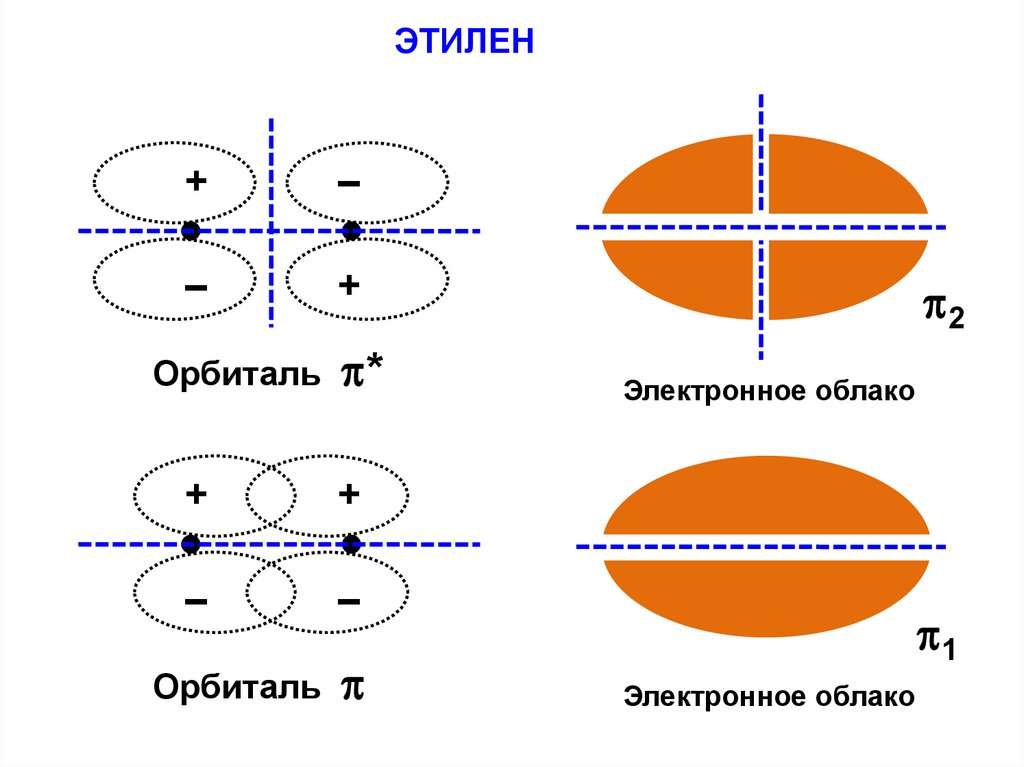
ЭТИЛЕН+
–
–
+
Орбиталь
*
+
+
–
–
Орбиталь
2
Электронное облако
1
Электронное облако
116.
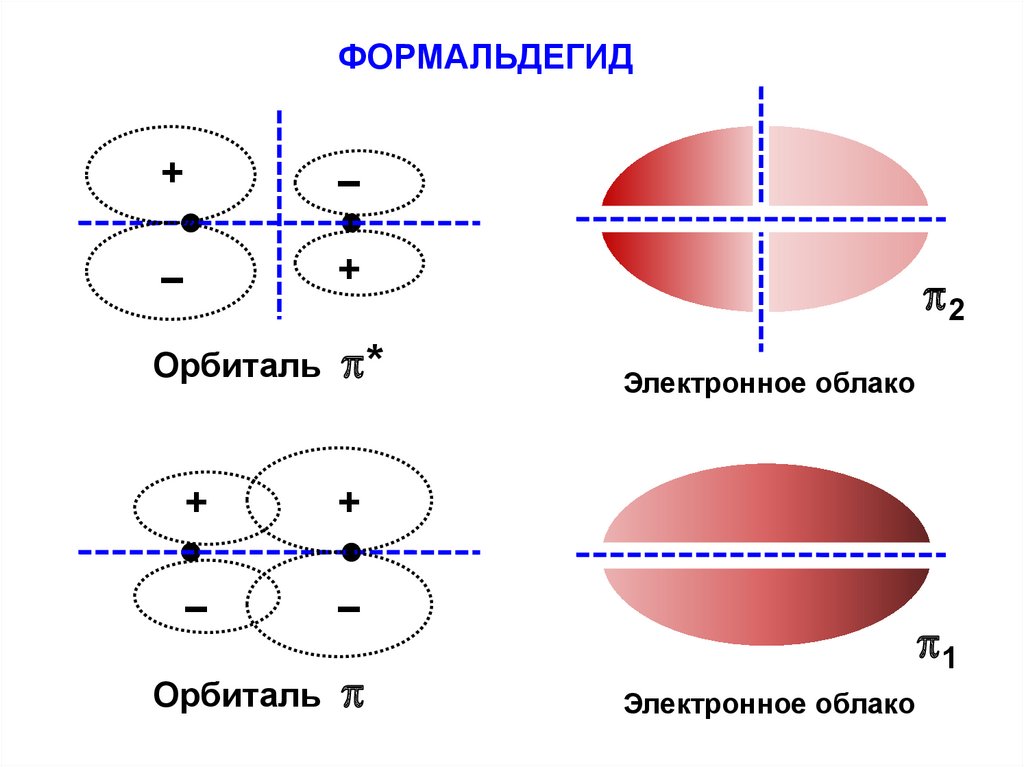
ФОРМАЛЬДЕГИД+
–
–
+
Орбиталь
*
+
+
–
–
Орбиталь
2
Электронное облако
1
Электронное облако
117.
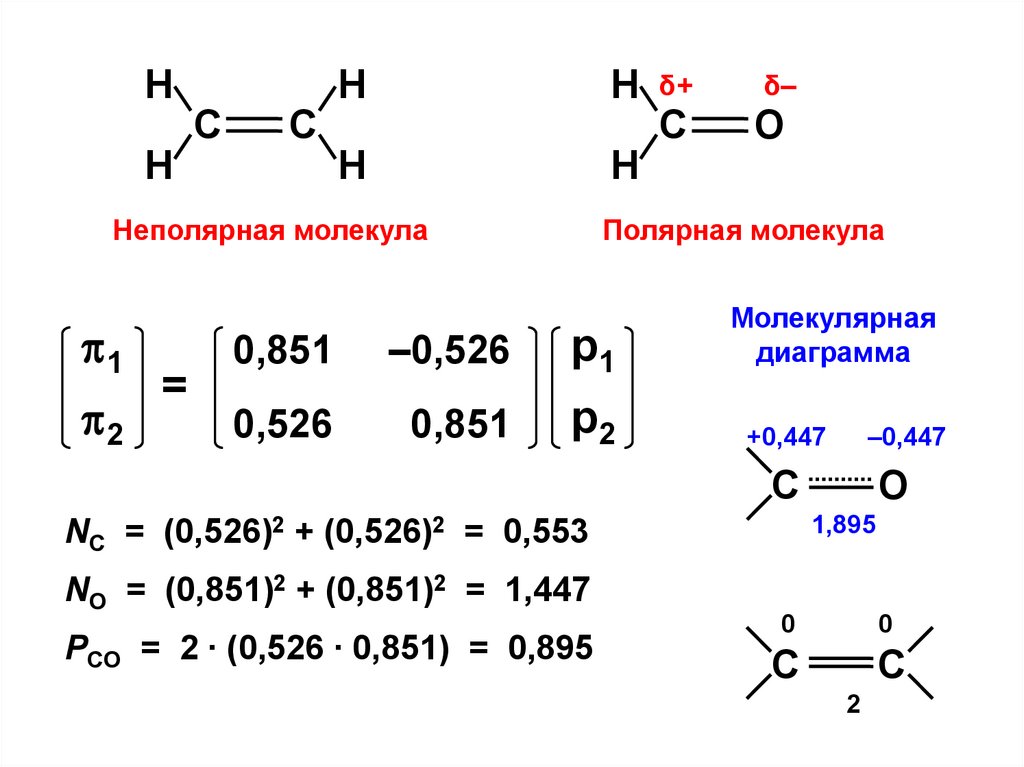
НН
С
С
Н
Н
Н
Н
Неполярная молекула
1
2
=
δ+
С
δ–
О
Полярная молекула
0,851
–0,526
р1
0,526
0,851
р2
Молекулярная
диаграмма
–0,447
+0,447
C
1,895
NC = (0,526)2 + (0,526)2 = 0,553
NO = (0,851)2 + (0,851)2 = 1,447
PCO = 2 ∙ (0,526 ∙ 0,851) = 0,895
O
0
0
C
С
2
118.
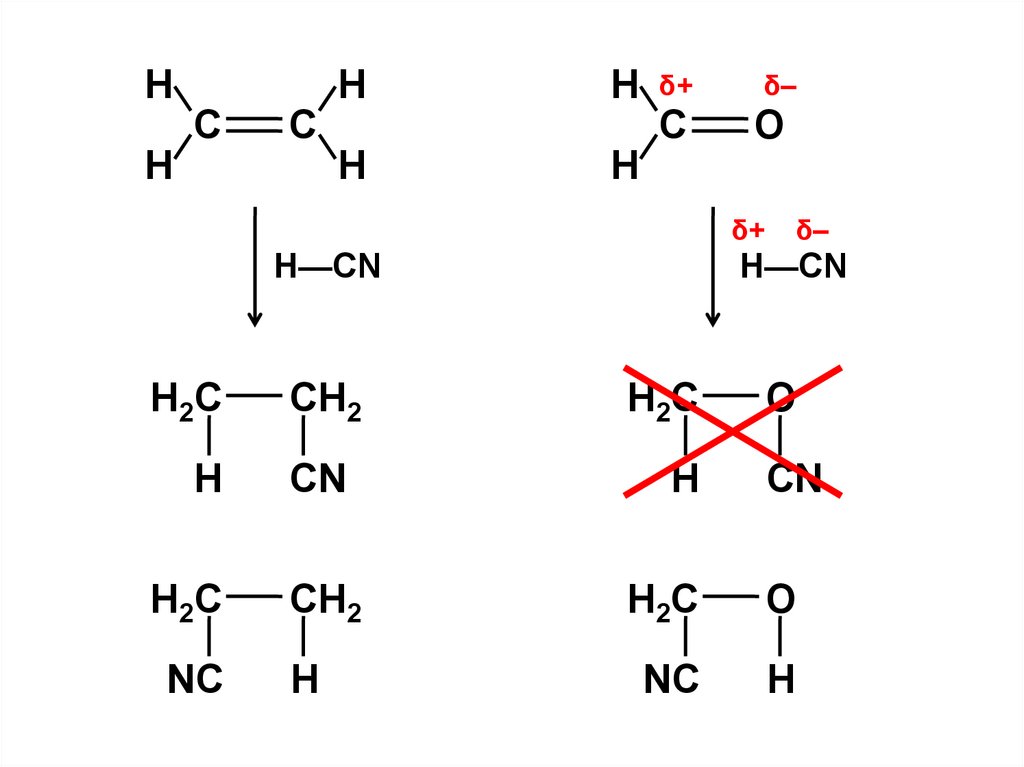
НН
С
С
Н
Н
Н
Н
δ+
С
δ–
О
δ+
H—CN
H2С
H
H2С
NC
СH2
CN
СH2
H
δ–
H—CN
H2С
H
O
CN
H2С
O
NC
H
119.
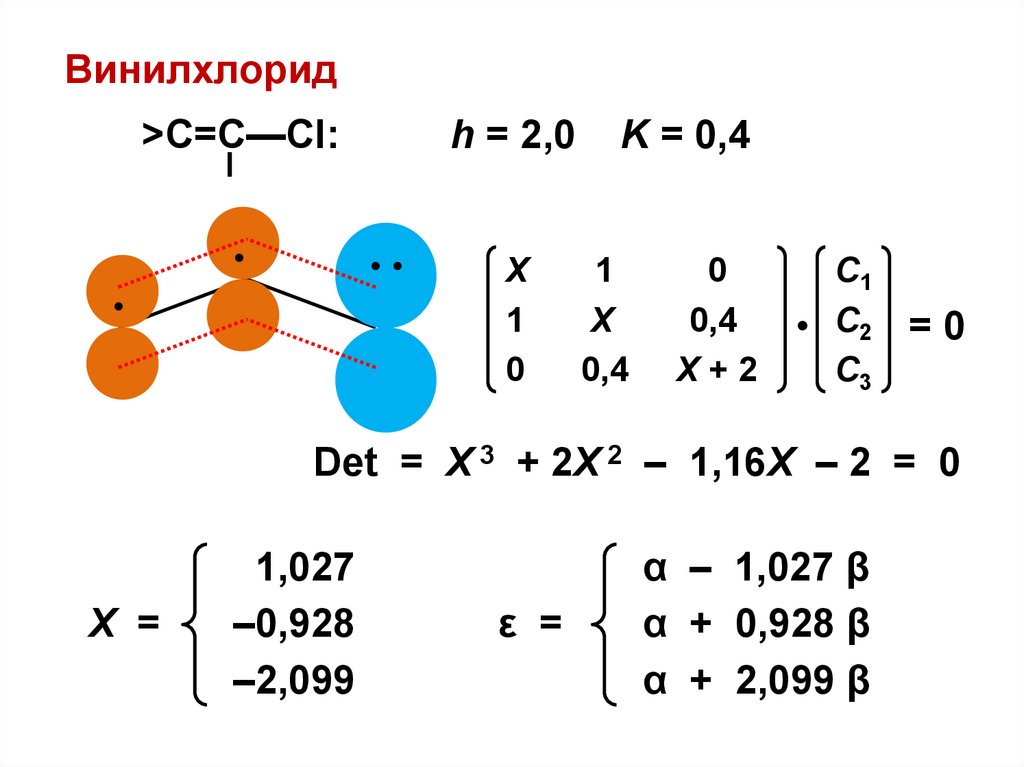
Винилхлорид>C=C—Cl:
h = 2,0
•
Х
1
0
K = 0,4
1
Х
0,4
0
0,4
Х+2
С1
• С2
С3
=0
Det = Х 3 + 2Х 2 – 1,16Х – 2 = 0
X =
1,027
–0,928
–2,099
ε =
α – 1,027 β
α + 0,928 β
α + 2,099 β
120.
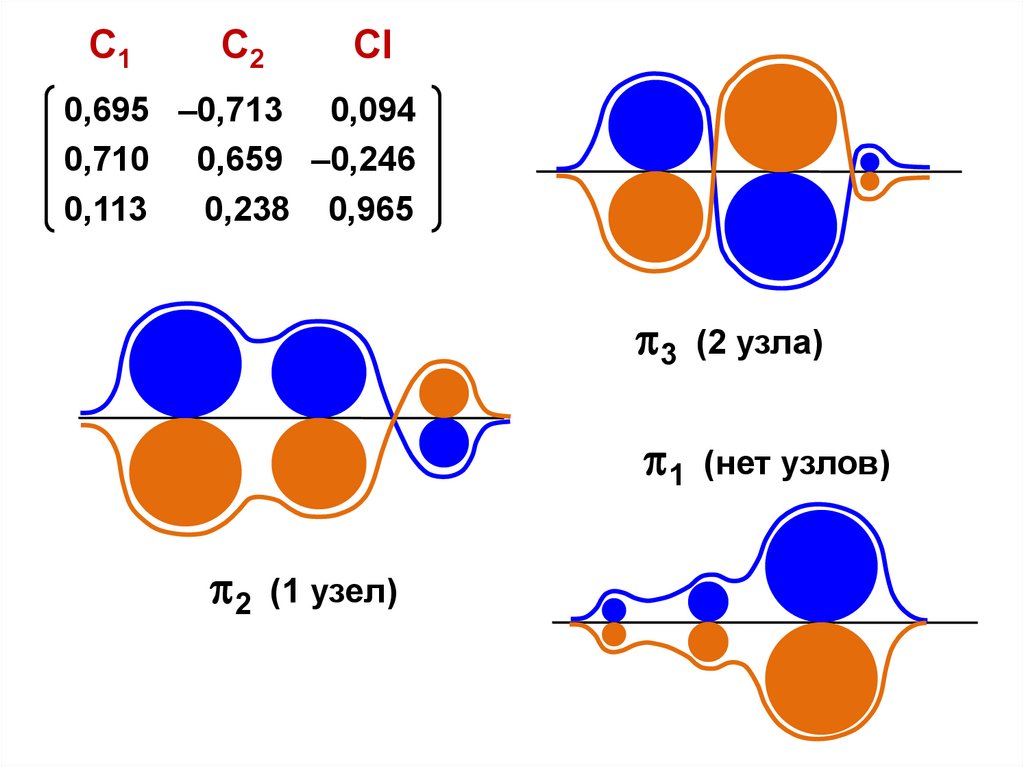
C1=
C2
Cl
0,695 –0,713 0,094
0,710 0,659 –0,246
0,113
0,238 0,965
p1
p2
p3
0
2
2
nC1 = 1,035
no = 1
Q = – 0,035
nC2 = 0,983
no = 1
Q = + 0,017
nCl = 1,982
no = 2
Q = + 0,018
PC-C = 0,991
PC-Cl = 0,134
121.
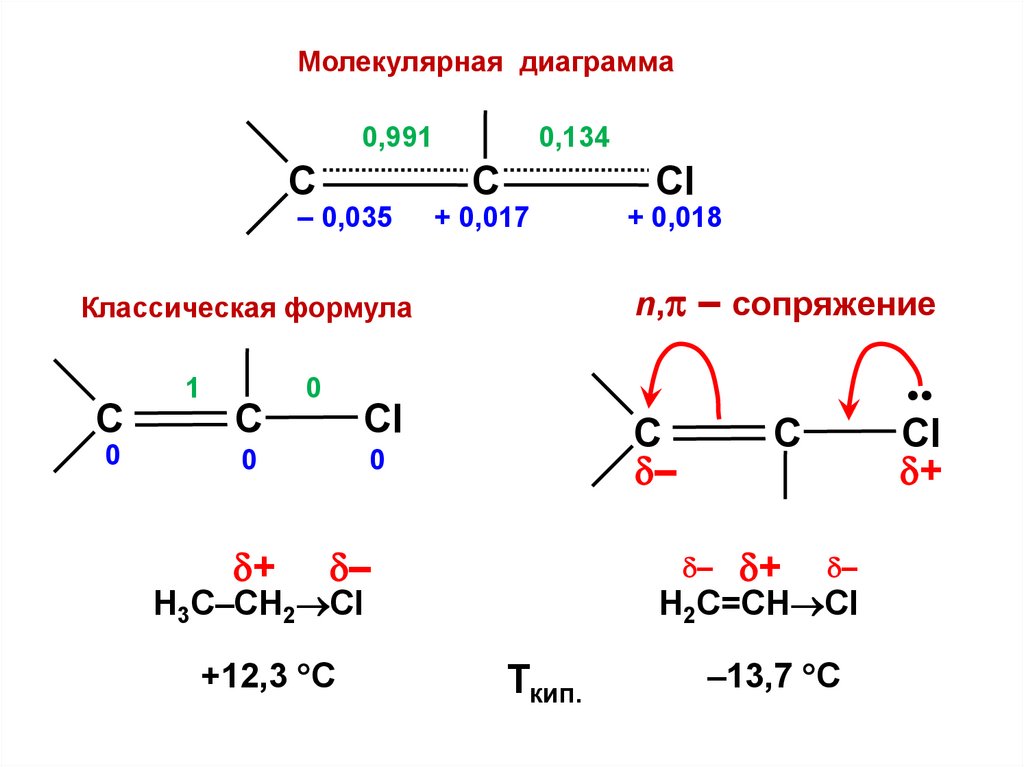
Молекулярная диаграмма0,991
C
– 0,035
0,134
C
Cl
+ 0,017
+ 0,018
n, – сопряжение
Классическая формула
1
•
Cl
+
0
C
C
Cl
0
0
0
+
C
–
–
–
H3C–CH2 Cl
+12,3 С
C
+
–
H2C=CH Cl
Ткип.
–13,7 С
122.
C1C2
Cl
0,695 –0,713 0,094
0,710 0,659 –0,246
0,113
0,238 0,965
2
(1 узел)
3
(2 узла)
1
(нет узлов)
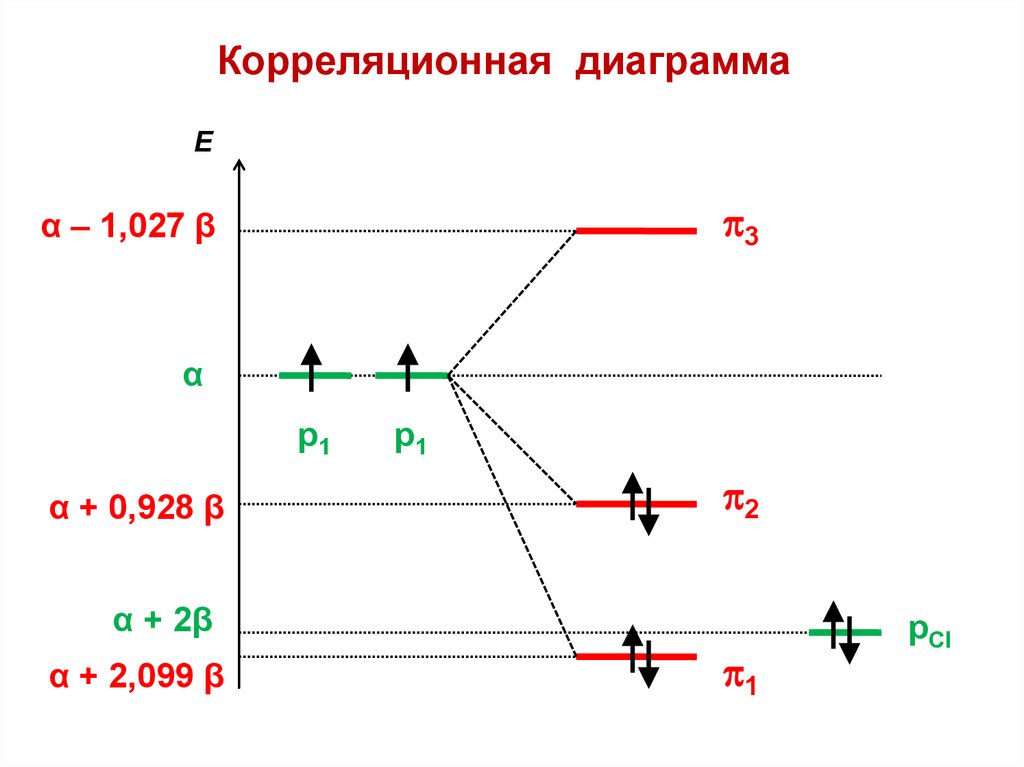
123.
Корреляционная диаграммаЕ
3
α – 1,027 β
α
р1
α + 0,928 β
р1
2
α + 2β
α + 2,099 β
1
рCl
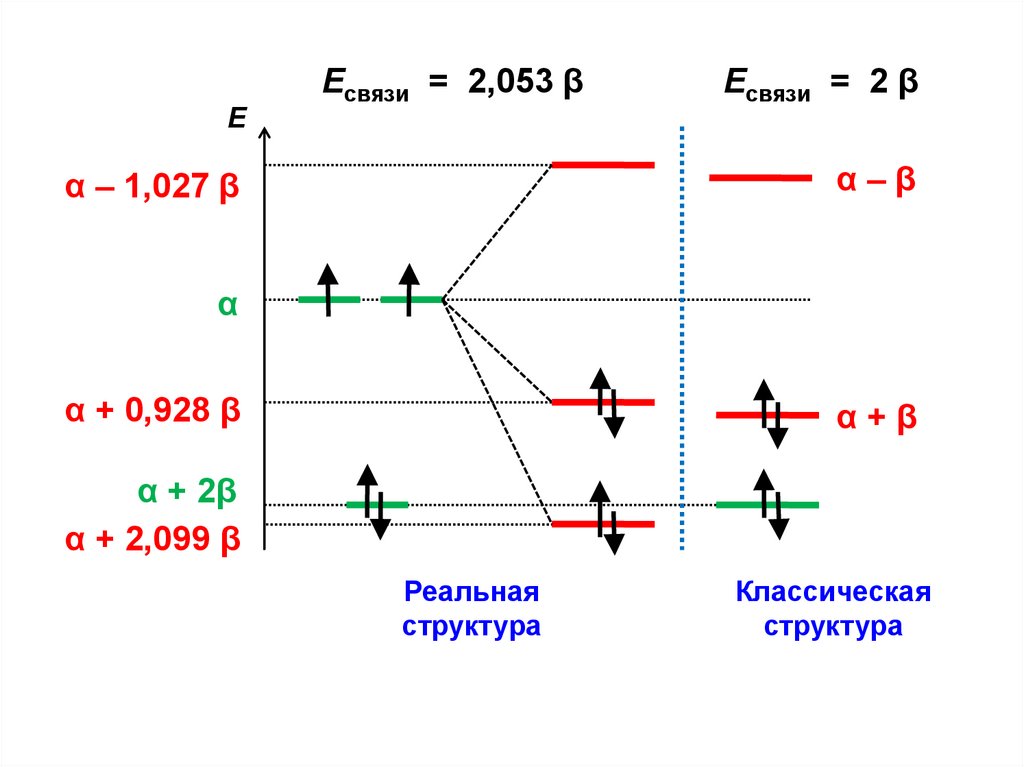
124.
ЕЕсвязи = 2,053 β
Есвязи = 2 β
α–β
α – 1,027 β
α
α + 0,928 β
α+β
α + 2β
α + 2,099 β
Реальная
структура
Классическая
структура
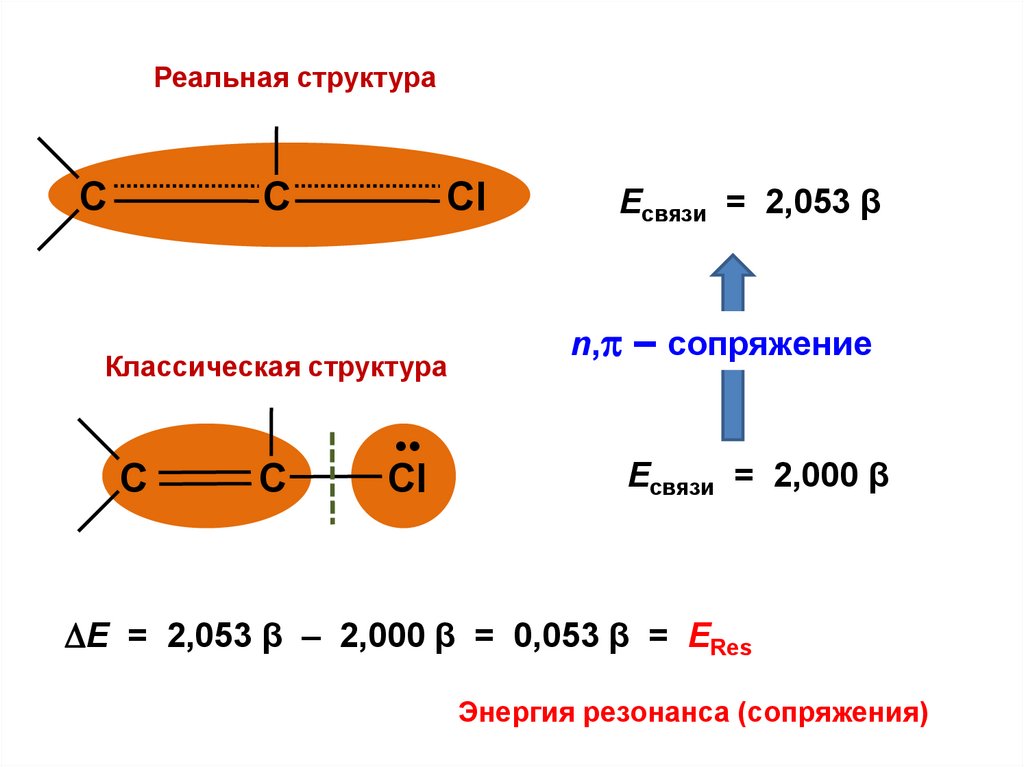
125.
Реальная структураC
C
Cl
Классическая структура
C
C
•
Cl
Есвязи = 2,053 β
n, – сопряжение
Есвязи = 2,000 β
Е = 2,053 β – 2,000 β = 0,053 β = ЕRes
Энергия резонанса (сопряжения)
126.
127.
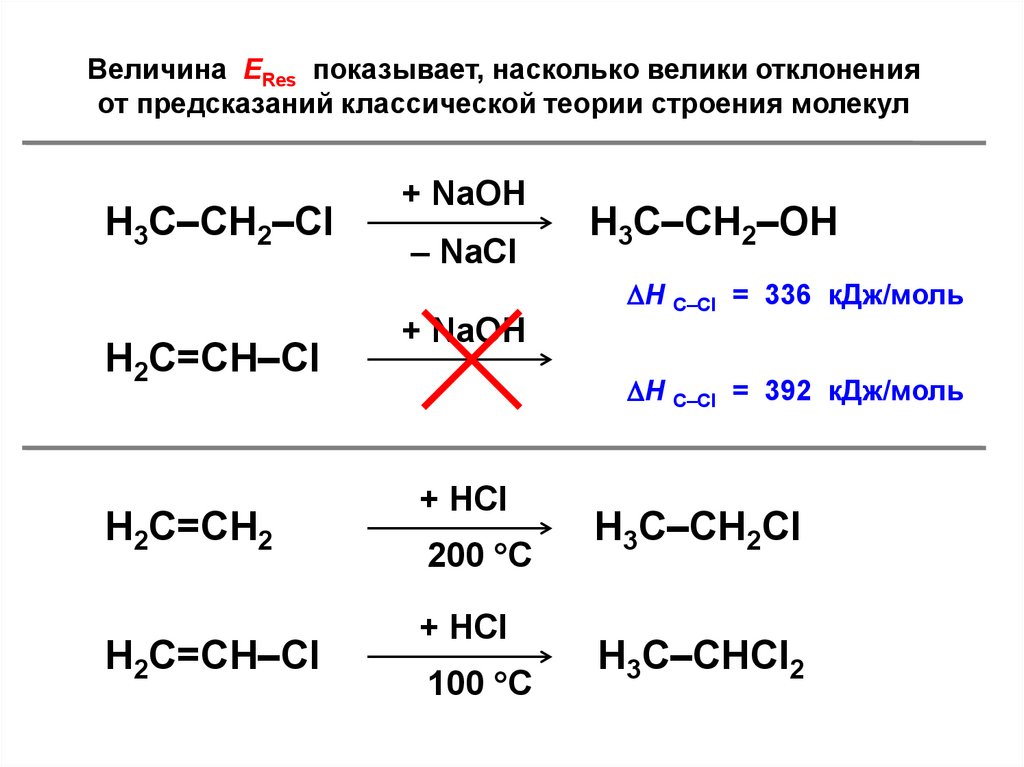
Величина ЕRes показывает, насколько велики отклоненияот предсказаний классической теории строения молекул
Н3С–СН2–Cl
+ NaOH
– NaCl
Н3С–СН2–OH
Н С–Cl = 336 кДж/моль
Н2С=СН–Cl
Н2С=СН2
Н2С=СН–Cl
+ NaOH
Н С–Cl = 392 кДж/моль
+ HCl
200 C
+ HCl
100 C
Н3С–СН2Cl
Н3С–СНCl2
128.
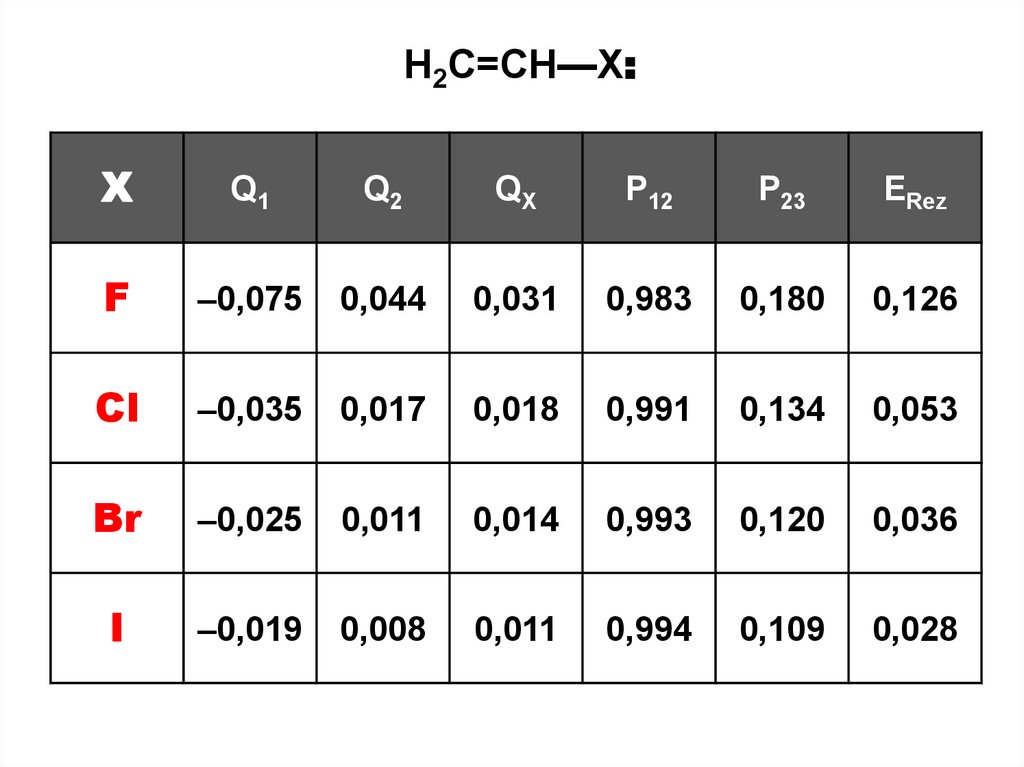
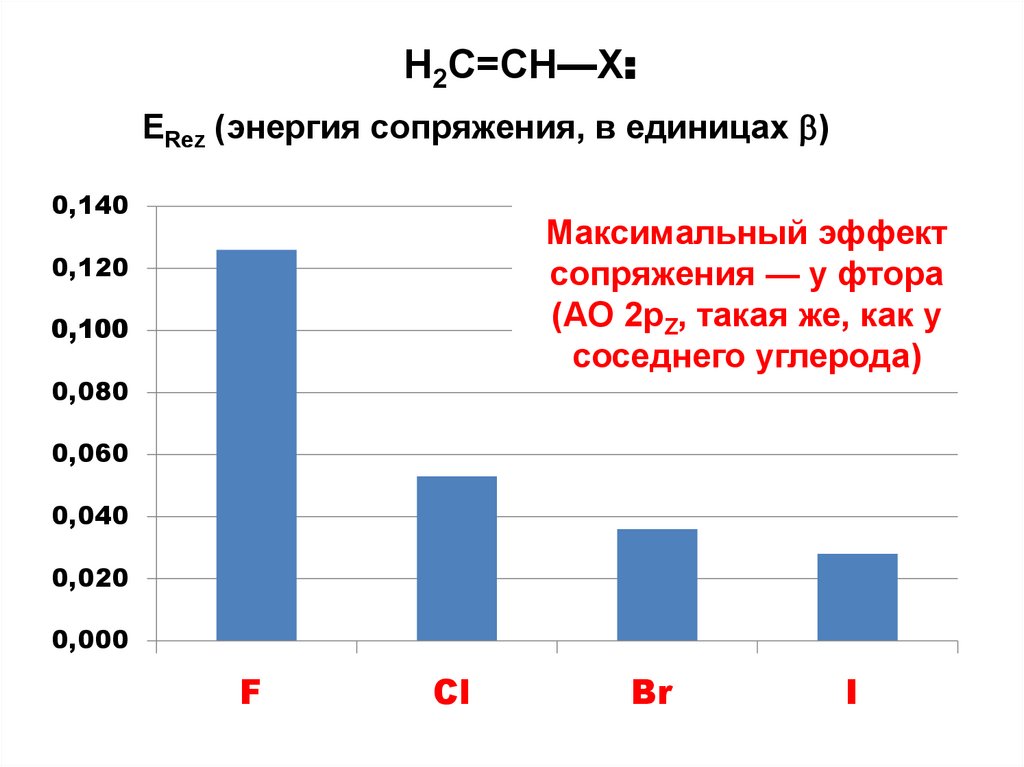
H2C=CH—X:X
Q1
Q2
QХ
P12
P23
ERez
F
–0,075
0,044
0,031
0,983
0,180
0,126
Cl
–0,035
0,017
0,018
0,991
0,134
0,053
Br
–0,025
0,011
0,014
0,993
0,120
0,036
I
–0,019
0,008
0,011
0,994
0,109
0,028
129.
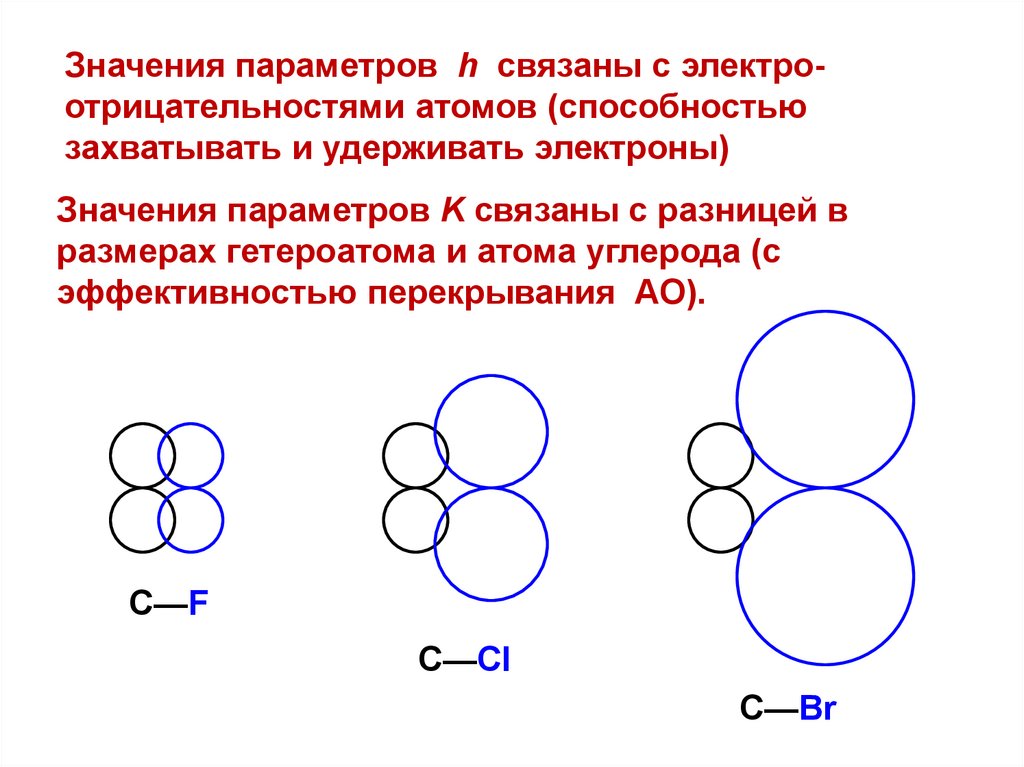
Значения параметров h связаны с электроотрицательностями атомов (способностьюзахватывать и удерживать электроны)
Значения параметров K связаны с разницей в
размерах гетероатома и атома углерода (с
эффективностью перекрывания АО).
С—F
С—Cl
С—Br
130.
H2C=CH—X:ERez (энергия сопряжения, в единицах )
0,140
Максимальный эффект
сопряжения — у фтора
(АО 2pZ, такая же, как у
соседнего углерода)
0,120
0,100
0,080
0,060
0,040
0,020
0,000
F
Cl
Br
I
131.
Виниловый спирт•
>C=C—О—Н
•
h = 2,0
K = 0,8
Х
1
0
0
0,8
Х+2
1
Х
0,8
С1
• С2
С3
=0
Det = Х 3 + 2Х 2 – 1,64Х – 2 = 0
X =
1,108
–0,773
–2,336
ε =
α – 1,108 β
α + 0,773 β
α + 2,336 β
132.
C1=
C2
О
0,658 –0,729 0,188
0,735 0,568 –0,370
0,163 0,382 0,910
p1
p2
p3
0
2
2
nC1 = 1,134
no = 1
Q = – 0,134
nC2 = 0,937
no = 1
Q = + 0,063
nО = 1,929
no = 2
Q = + 0,071
PC-C = 0,960
PC-О = 0,274
133.
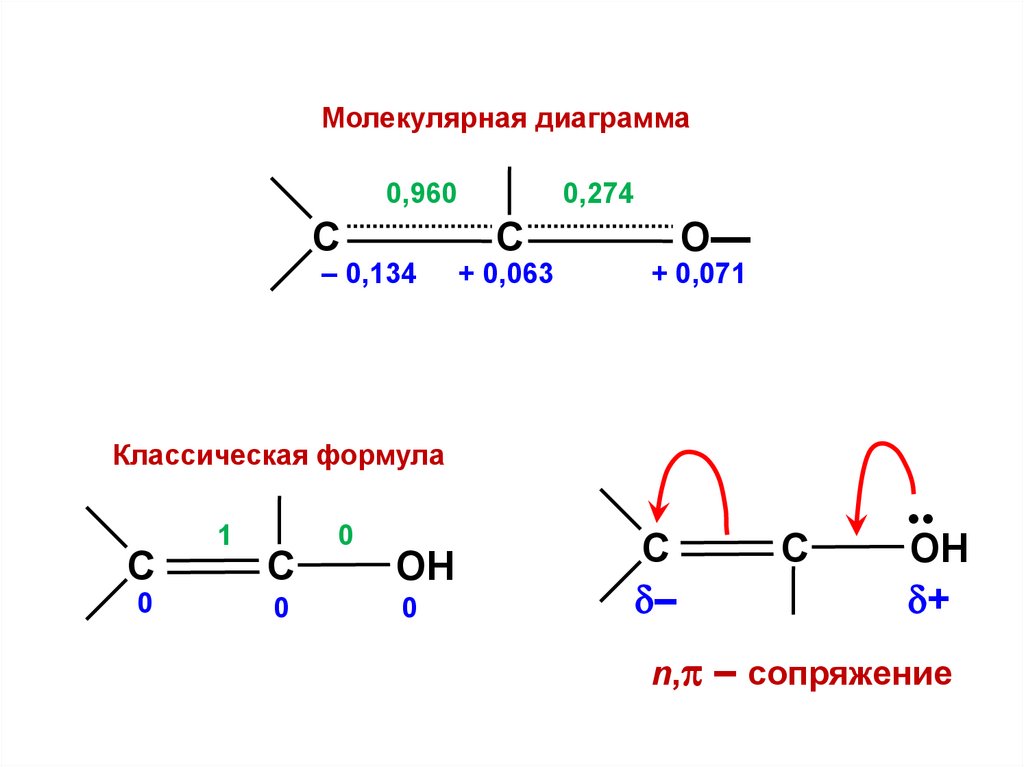
Молекулярная диаграмма0,960
C
– 0,134
0,274
О—
C
+ 0,063
+ 0,071
Классическая формула
1
0
C
C
ОН
0
0
0
C
–
C
•
ОН
+
n, – сопряжение
134.
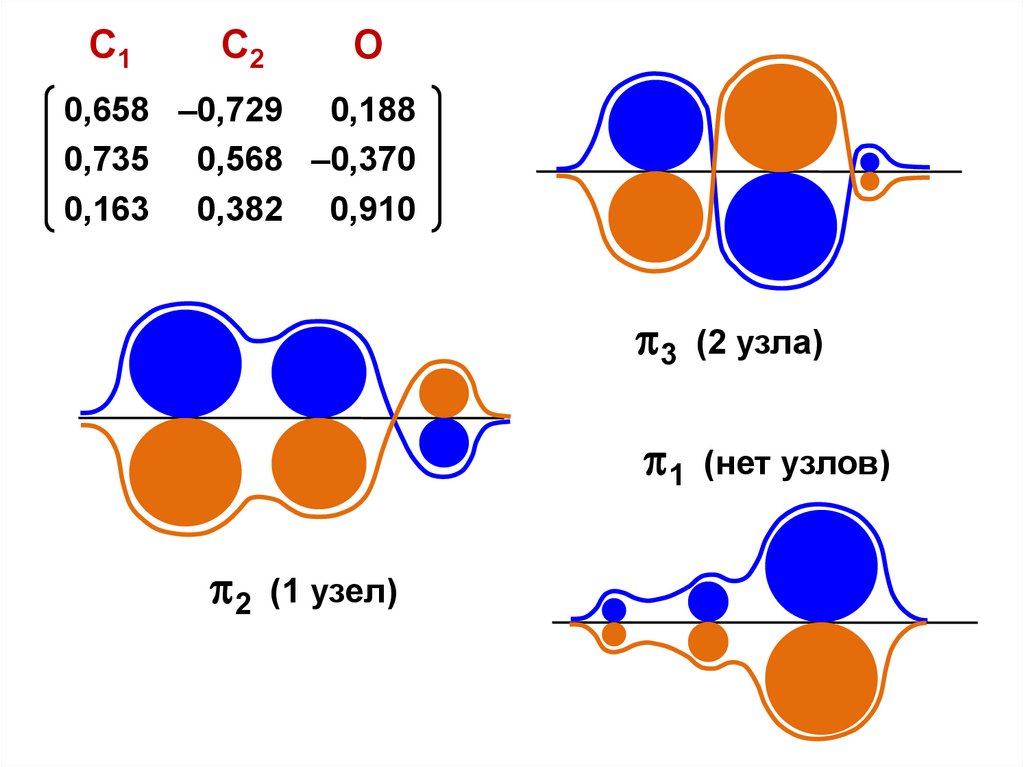
C1C2
О
0,658 –0,729 0,188
0,735 0,568 –0,370
0,163 0,382 0,910
2
(1 узел)
3
(2 узла)
1
(нет узлов)
135.
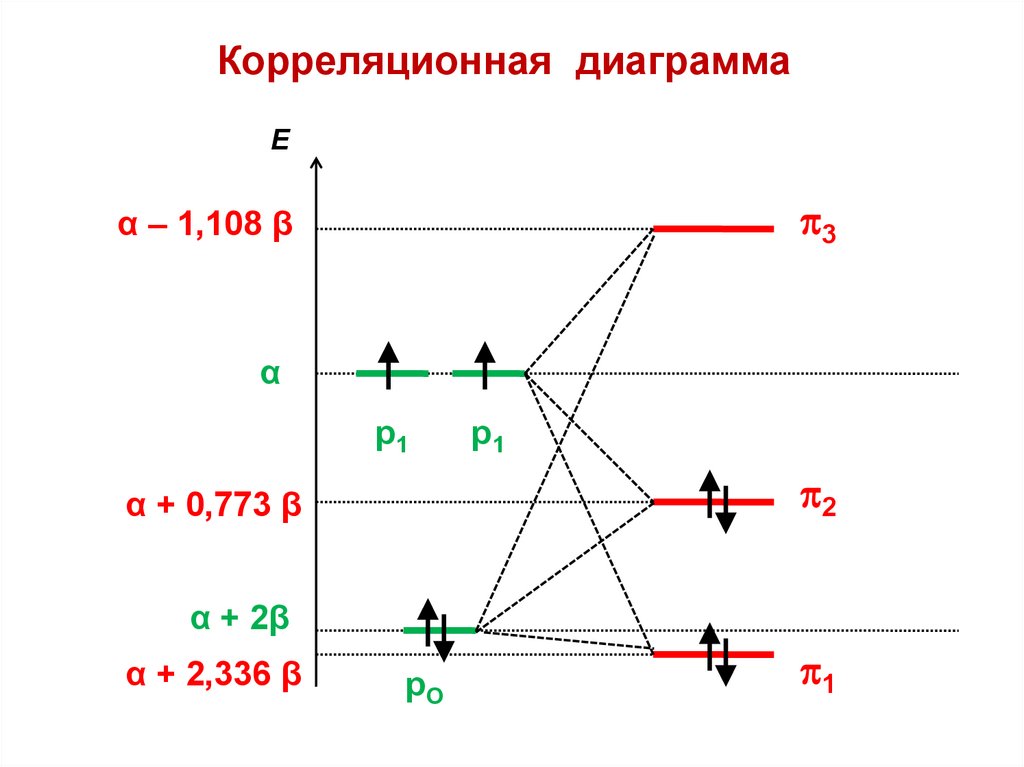
Корреляционная диаграммаЕ
3
α – 1,108 β
α
р1
р1
2
α + 0,773 β
α + 2β
α + 2,336 β
рО
1
136.
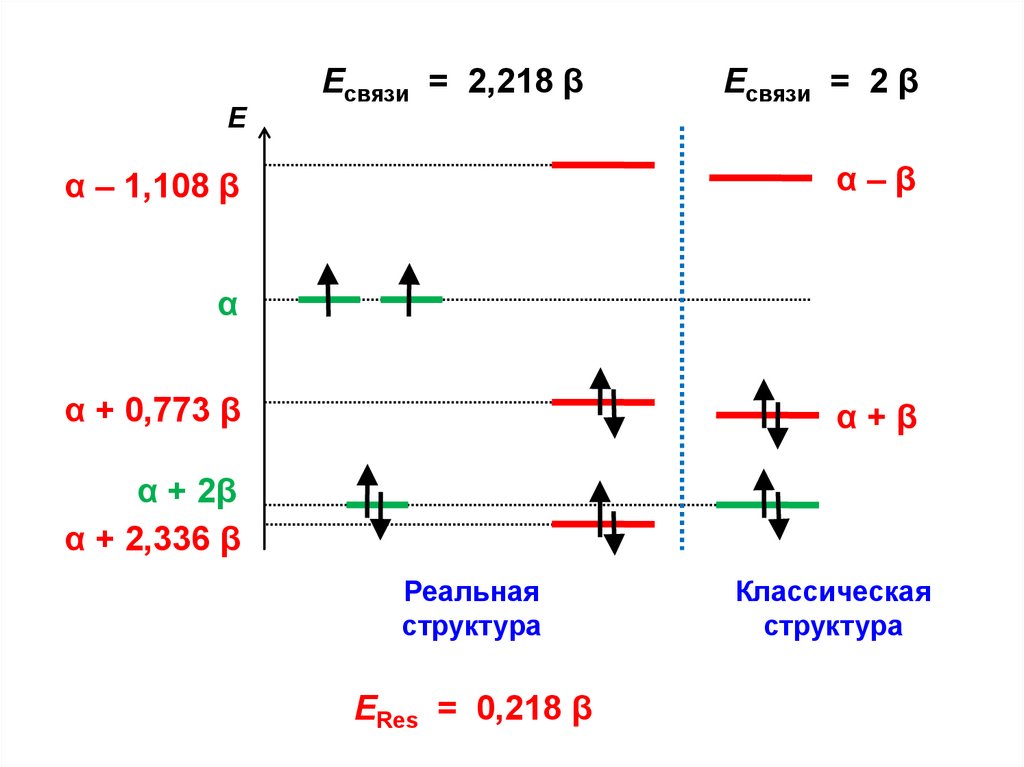
ЕЕсвязи = 2,218 β
Есвязи = 2 β
α–β
α – 1,108 β
α
α + 0,773 β
α+β
α + 2β
α + 2,336 β
Реальная
структура
ERes = 0,218 β
Классическая
структура
137.
Реальная структураC
О
C
Классическая структура
C
C
•
О
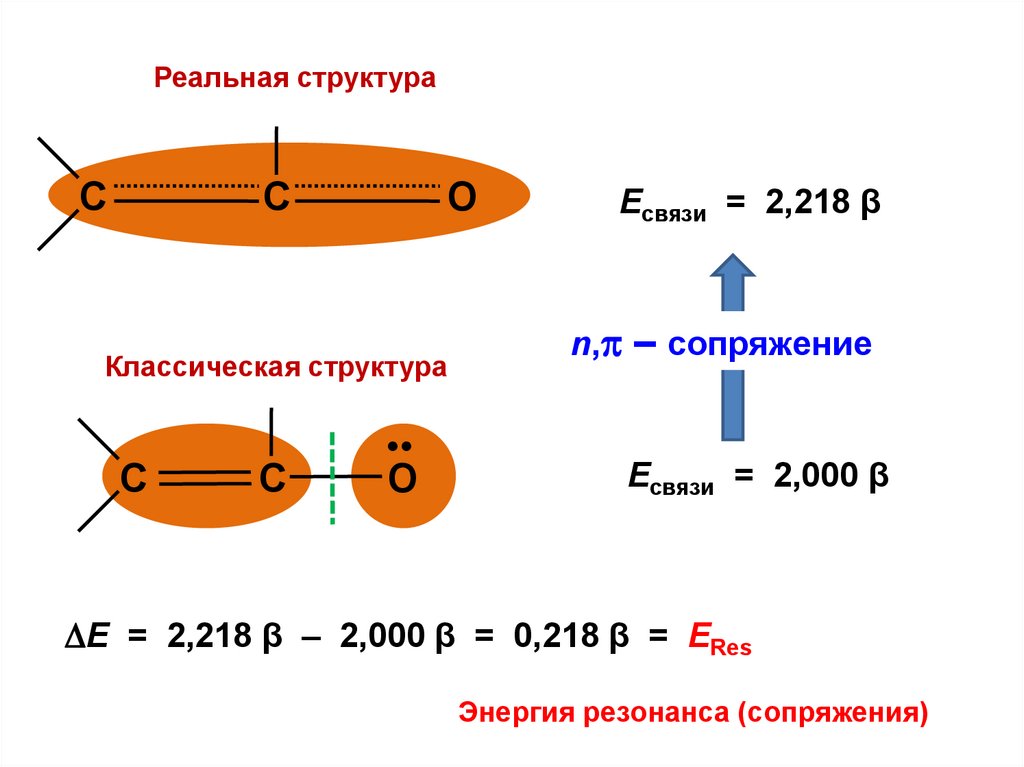
Есвязи = 2,218 β
n, – сопряжение
Есвязи = 2,000 β
Е = 2,218 β – 2,000 β = 0,218 β = ЕRes
Энергия резонанса (сопряжения)
138.
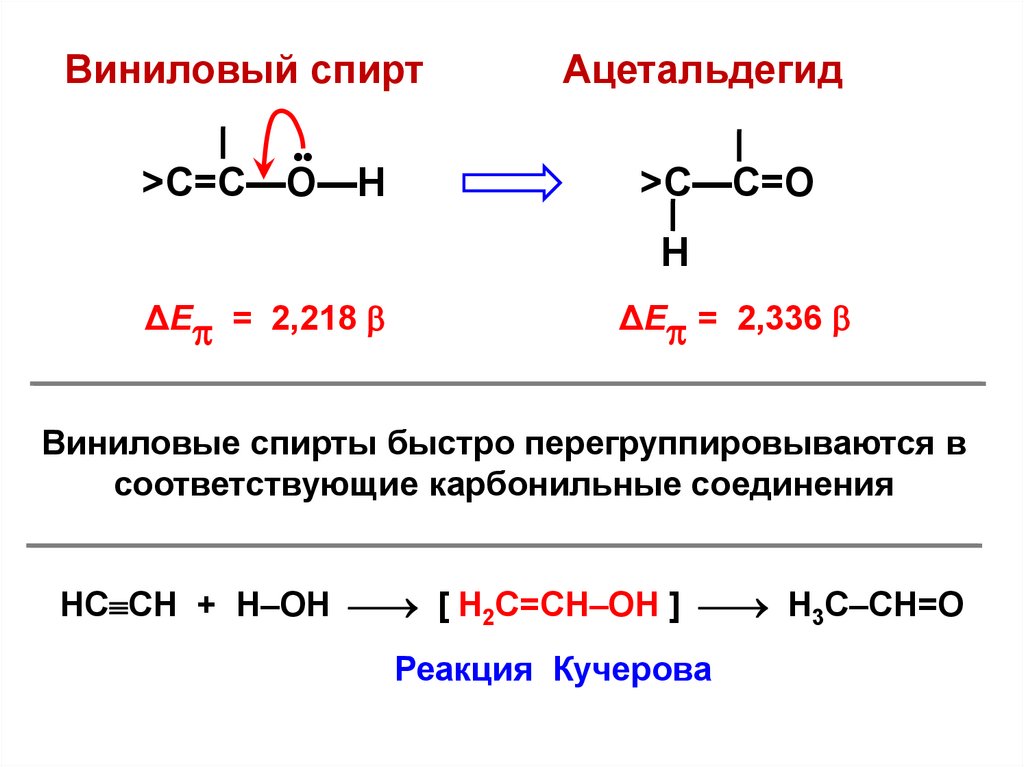
Виниловый спирт•
>C=C—О—Н
Ацетальдегид
>C—C=О
Н
ΔЕ = 2,218
ΔЕ = 2,336
Виниловые спирты быстро перегруппировываются в
соответствующие карбонильные соединения
НС СН + Н–ОН [ Н2С=СН–ОН ] Н3С–СН=О
Реакция Кучерова
139.
Амидная группаO
C
•
N
•
hO = 1,0
KO = 1,0
hN = 1,5
KN = 0,8
Х+1 1
1
Х
0
0,8
0
С1
0,8
• С2
Х + 1,5
С3
=0
Det = Х 3 + 2,5Х 2 – 0,14Х – 2,14 = 0
X =
0,824
–1,257
–2,067
ε =
α – 0,824 β
α + 1,257 β
α + 2,067 β
140.
O=
C
–0,460
0,749
0,476
N
0,840 –0,289
0,193 –0,634
0,508 0,717
p1
p2
p3
0
2
2
nO = 1,575
no = 1
Q = – 0,575
nC = 0,592
no = 1
Q = + 0,408
nN = 1,833
no = 2
Q = + 0,167
PO-C = 0,773
PC-N = 0,484
141.
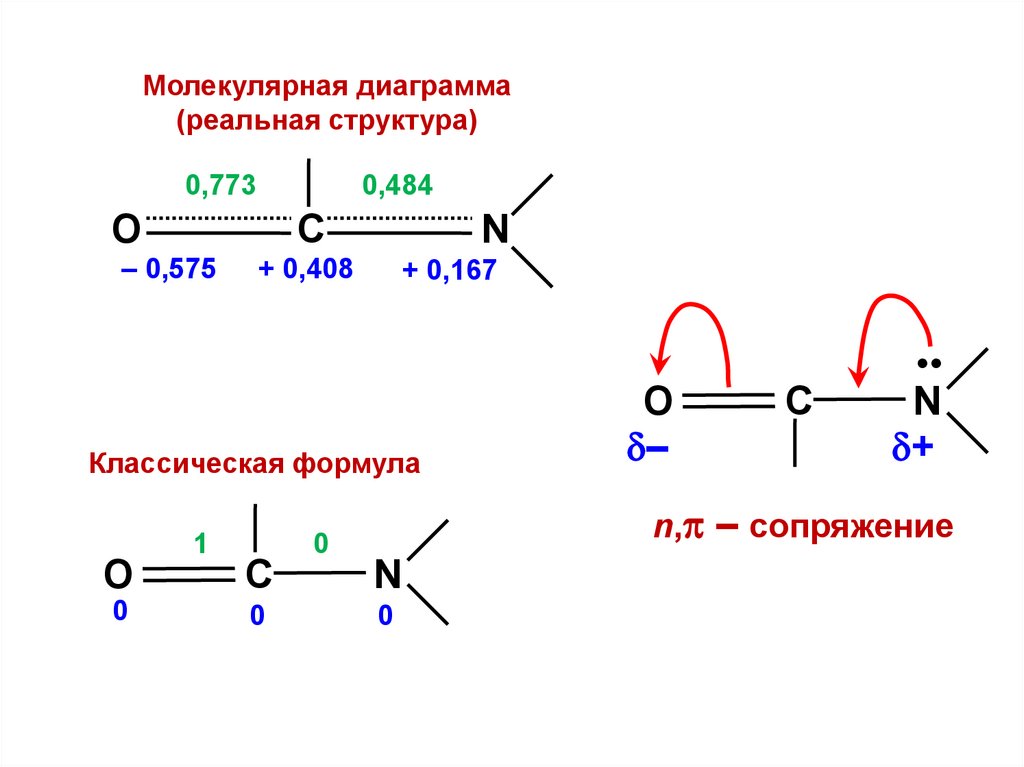
Молекулярная диаграмма(реальная структура)
0,773
0,484
O
C
– 0,575
N
+ 0,408
+ 0,167
Классическая формула
1
O
–
C
•
N
+
n, – сопряжение
0
O
C
N
0
0
0
142.
OC
N
0,460
0,749
0,476
–0,840
0,193
0,508
0,289
–0,634
0,717
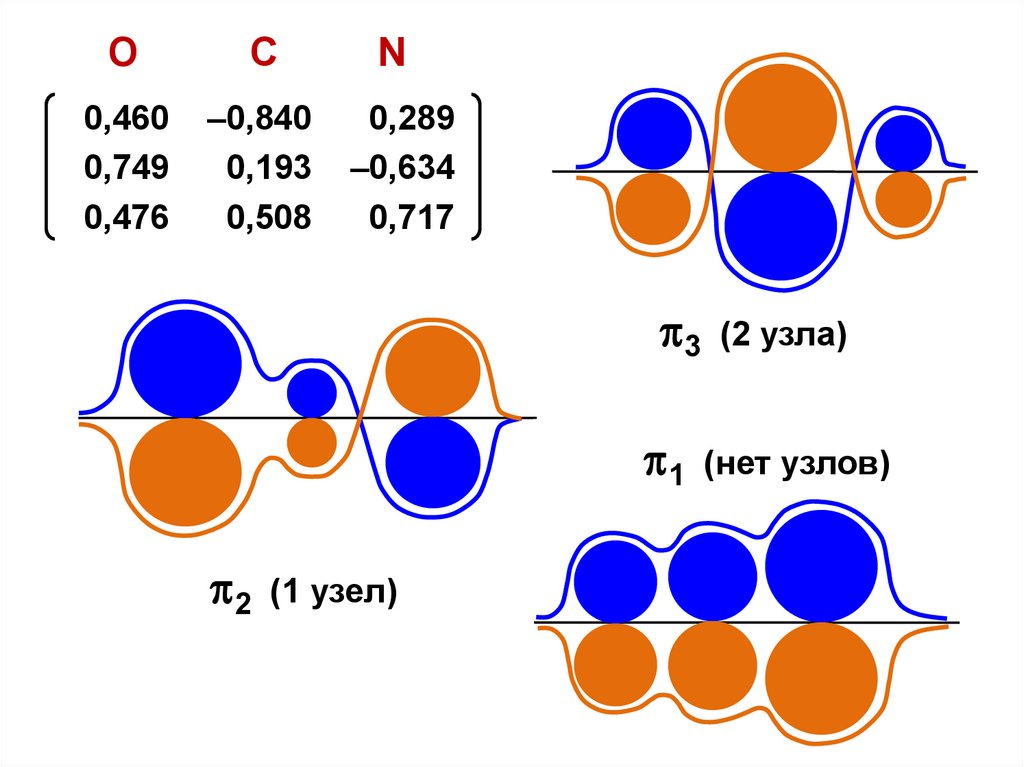
3
1
2
(1 узел)
(2 узла)
(нет узлов)
143.
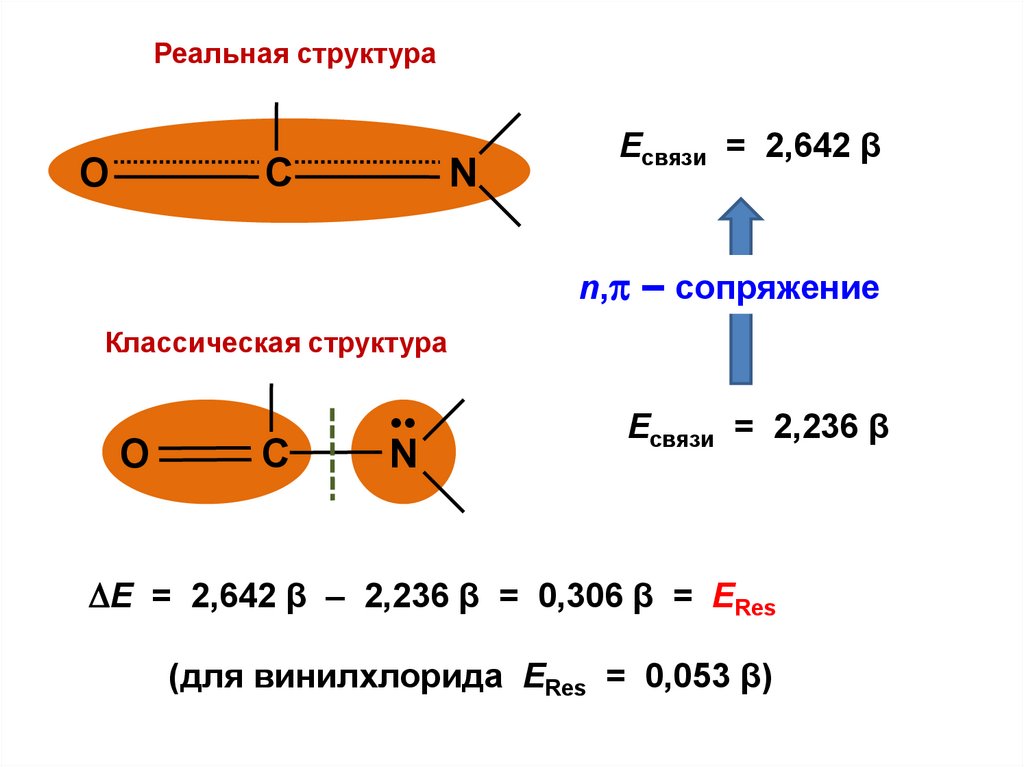
Реальная структураО
C
N
Есвязи = 2,642 β
n, – сопряжение
Классическая структура
O
C
•
N
Есвязи = 2,236 β
Е = 2,642 β – 2,236 β = 0,306 β = ЕRes
(для винилхлорида ЕRes = 0,053 β)
144.
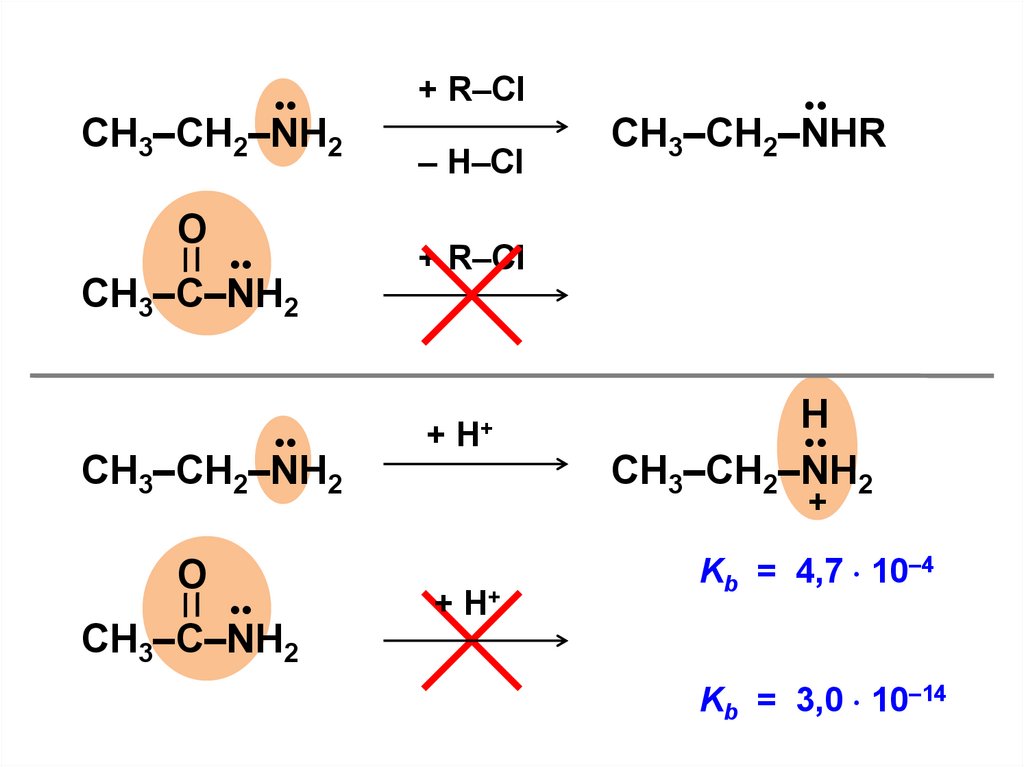
•СН3–СН2–NH2
O
•
СН3–С–NH2
•
СН3–СН2–NH2
O
•
СН3–С–NH2
+ R–Cl
– H–Cl
•
СН3–СН2–NHR
+ R–Cl
+ H+
Н
•
СН3–СН2–NH2
+
+ H+
Kb = 4,7 10–4
Kb = 3,0 10–14
145.
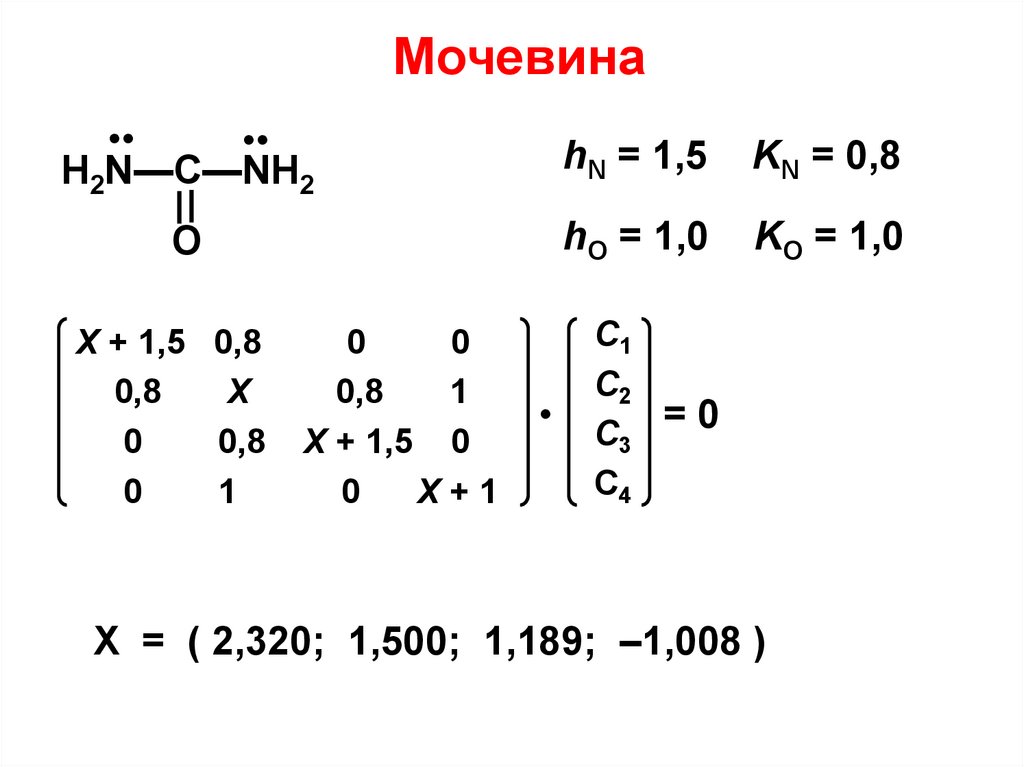
Мочевина•
•
H2N—C—NH2
hN = 1,5
KN = 0,8
O
hO = 1,0
KO = 1,0
Х + 1,5 0,8
0,8
Х
0
0,8
0
1
0
0
0,8
1
Х + 1,5 0
0
X+1
С1
С2
=0
С3
C4
X = ( 2,320; 1,500; 1,189; –1,008 )
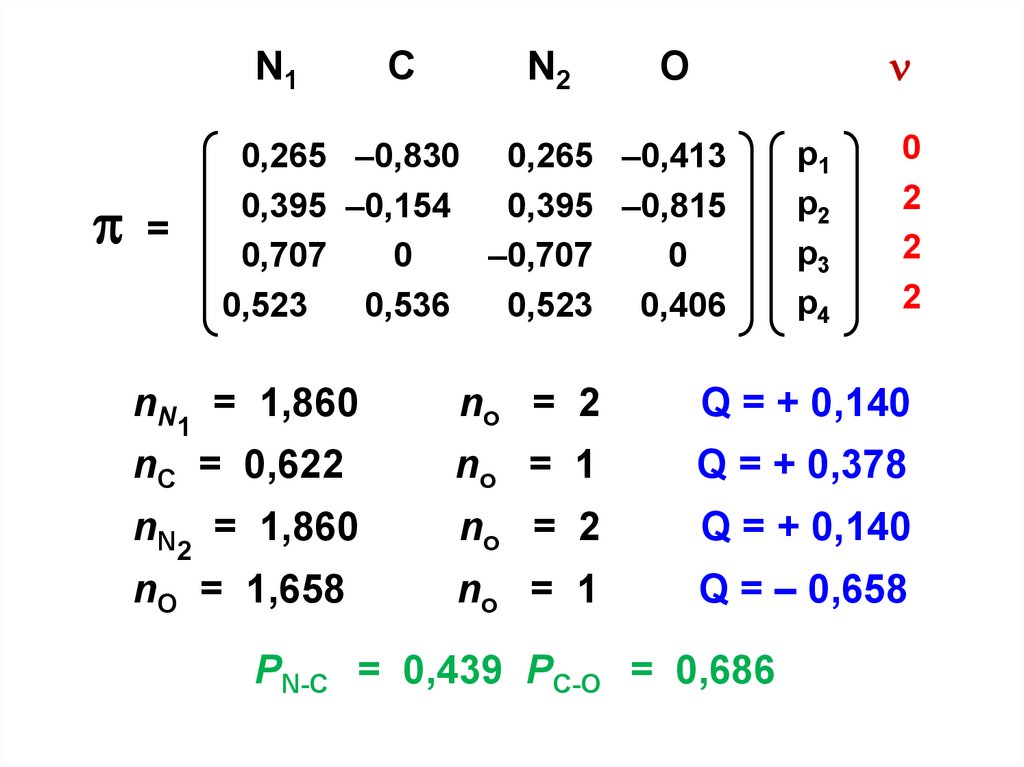
146.
N1=
C
N2
O
0,265 –0,830 0,265 –0,413
0,395 –0,154
0,395 –0,815
0,707
0
–0,707
0
0,523
0,536
0,523 0,406
p1
p2
p3
р4
0
2
2
2
nN1 = 1,860
no = 2
Q = + 0,140
nC = 0,622
no = 1
Q = + 0,378
nN2 = 1,860
no = 2
Q = + 0,140
nO = 1,658
no = 1
Q = – 0,658
PN-C = 0,439 PC-O = 0,686
147.
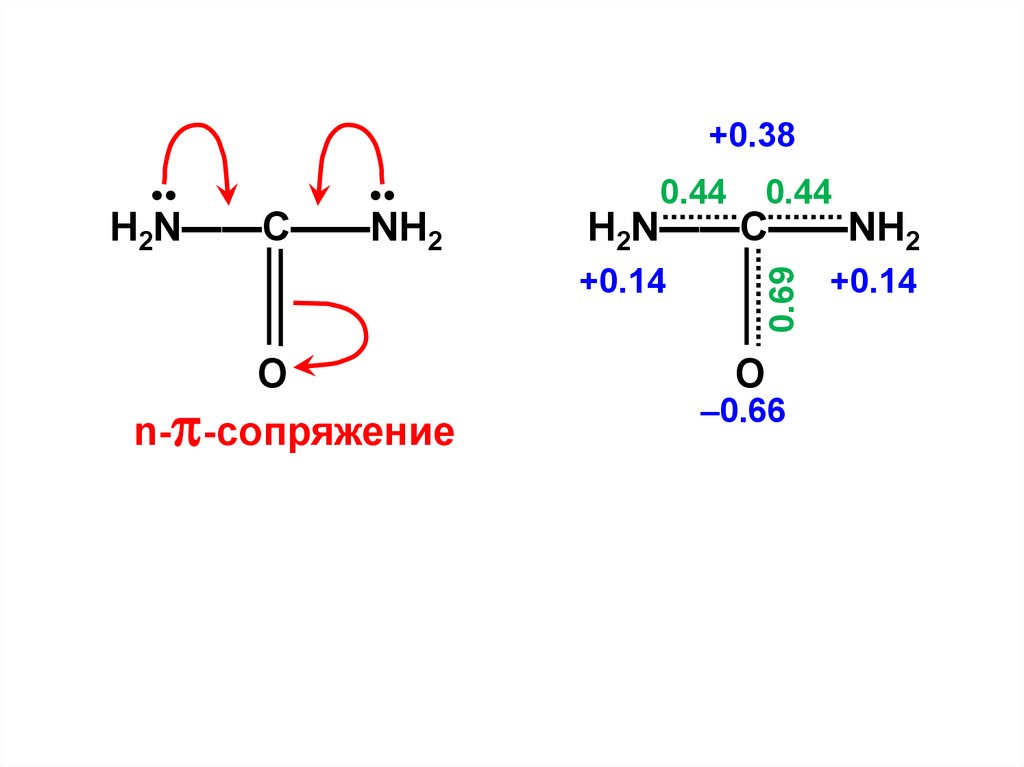
+0.380.44
0.44
H2N——C——NH2
0.69
•
•
H2N——C——NH2
+0.14
O
n- -сопряжение
O
–0.66
+0.14
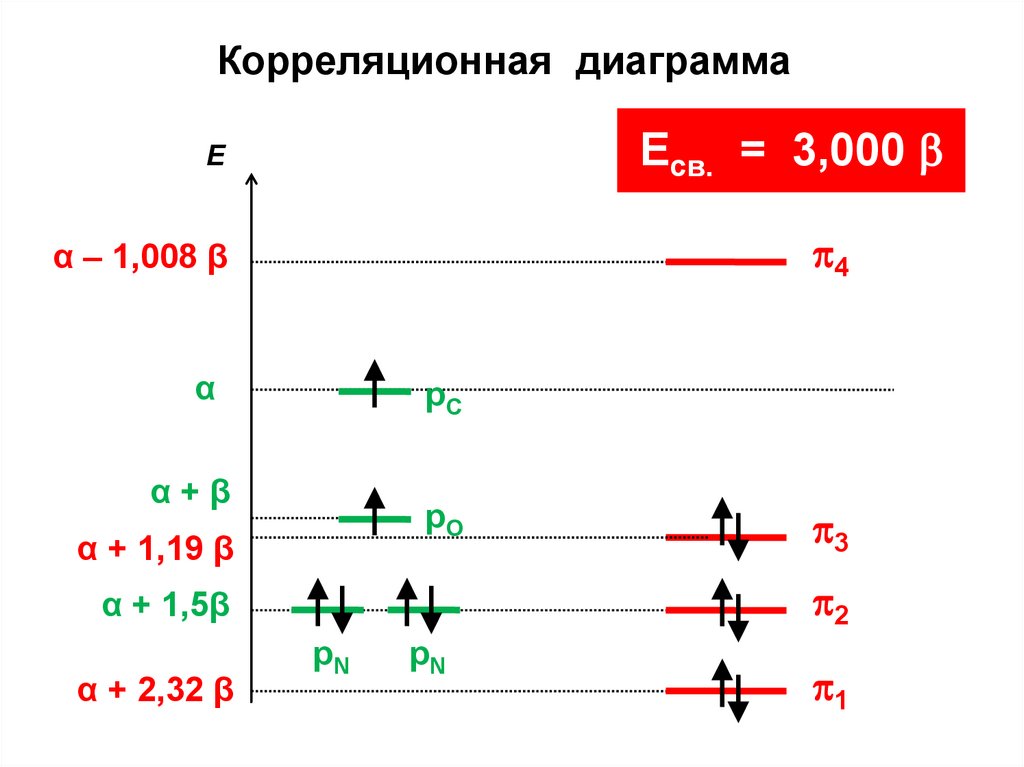
148.
Корреляционная диаграммаEсв. = 3,000
Е
4
α – 1,008 β
α
рС
α+β
рО
α + 1,19 β
2
α + 1,5β
α + 2,32 β
3
рN
рN
1
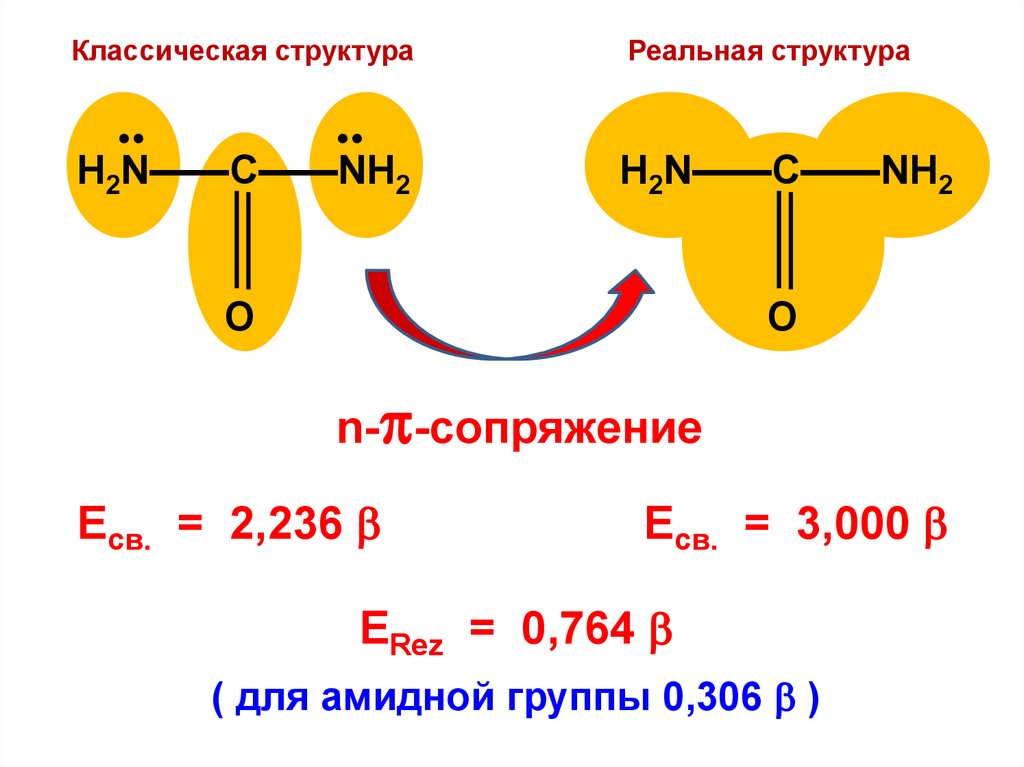
149.
Классическая структураРеальная структура
•
•
H2N——C——NH2
H2N——C——NH2
O
O
n- -сопряжение
Eсв. = 2,236
Eсв. = 3,000
ERez = 0,764
( для амидной группы 0,306 )
150.
С1
3
2
4
О
151.
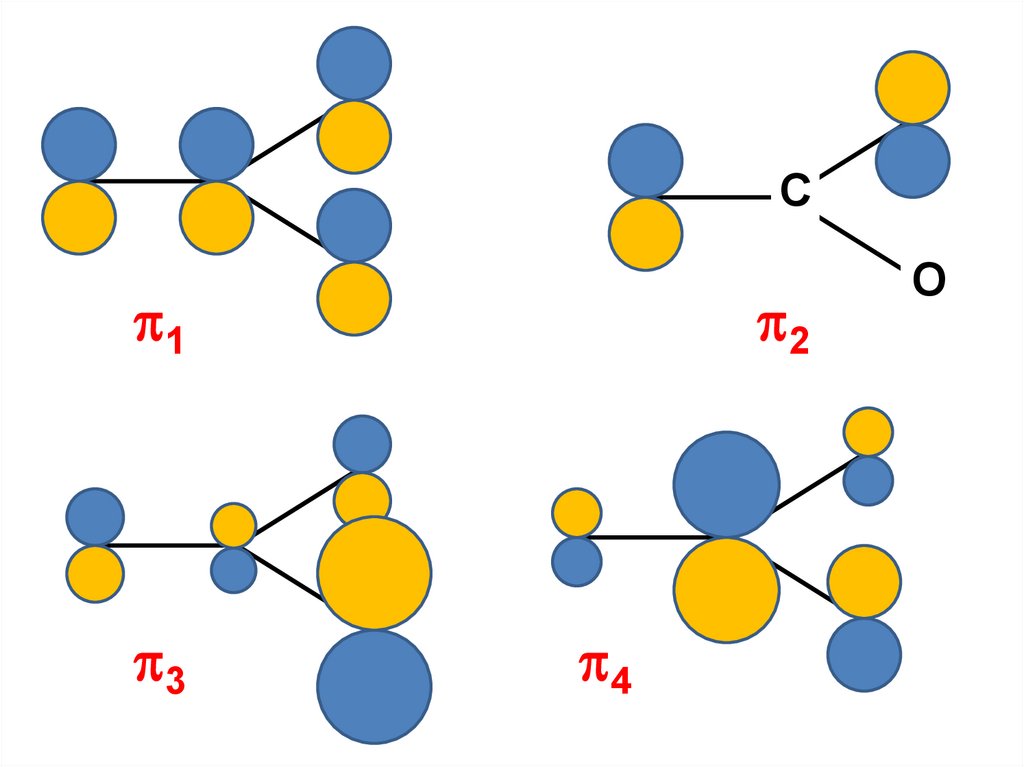
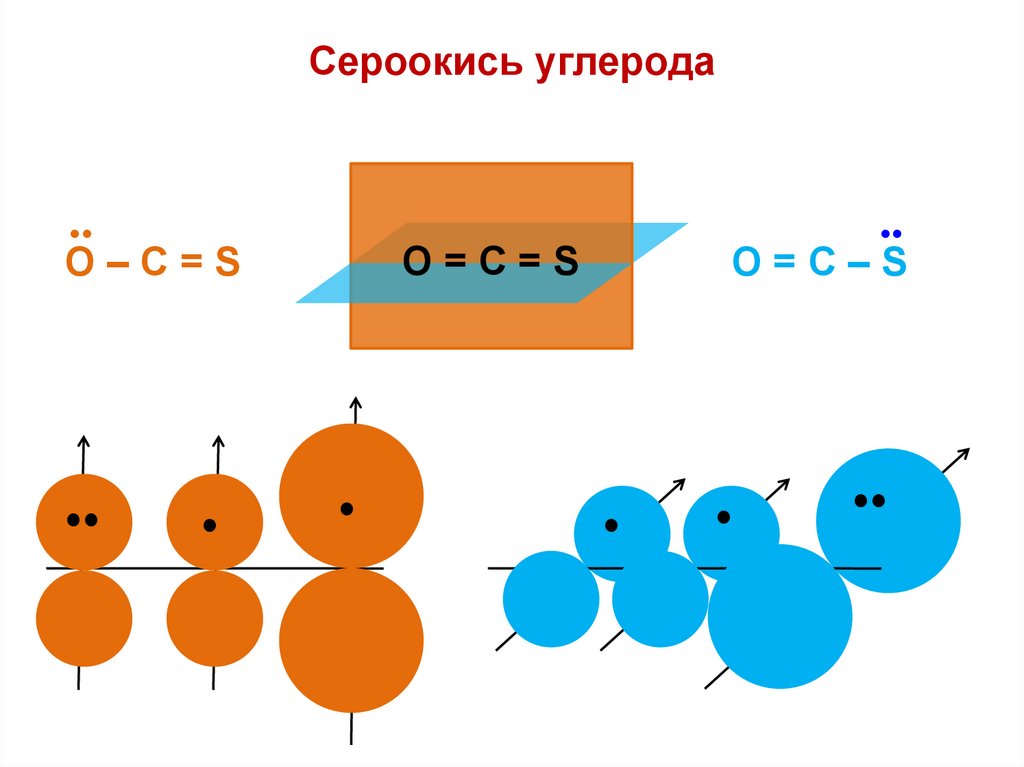
Сероокись углерода•
O=С=S
O–С=S
•
•
O=С–S
•
152.
•O–С=S
•
hO = 2,0
KO = 0,8
hS = 0,4
KS = 1,0
Х + 2 0,8
0,8
Х
0
1,0
0
С1
1,0
• С2
Х + 0,4
С3
=0
Det = Х 3 + 2,4Х 2 – 0,84Х – 2,256 = 0
X =
0,955
–1,006
–2,349
ε =
α – 0,955 β
α + 1,006 β
α + 2,349 β
153.
O=
C
0,213 –0,786
–0,385 0,478
0,898 0,391
S
0,580
0,789
0,201
p1
p2
p3
0
2
2
nO = 1,909
no = 2
Q = + 0,091
nC = 0,765
no = 1
Q = + 0,235
nS = 1,326
no = 1
Q = – 0,326
PO-C = 0,334
PC-S = 0,911
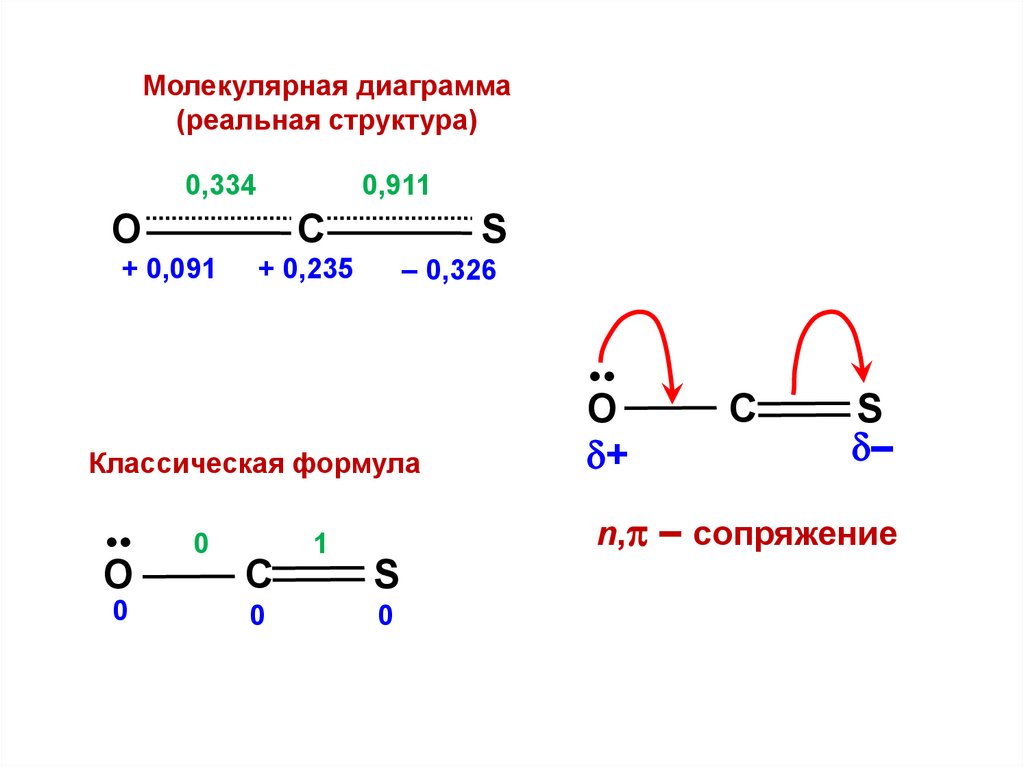
154.
Молекулярная диаграмма(реальная структура)
0,334
0,911
O
C
+ 0,091
S
– 0,326
+ 0,235
Классическая формула
•
O
0
0
•
O
+
C
S
–
n, – сопряжение
1
C
S
0
0
155.
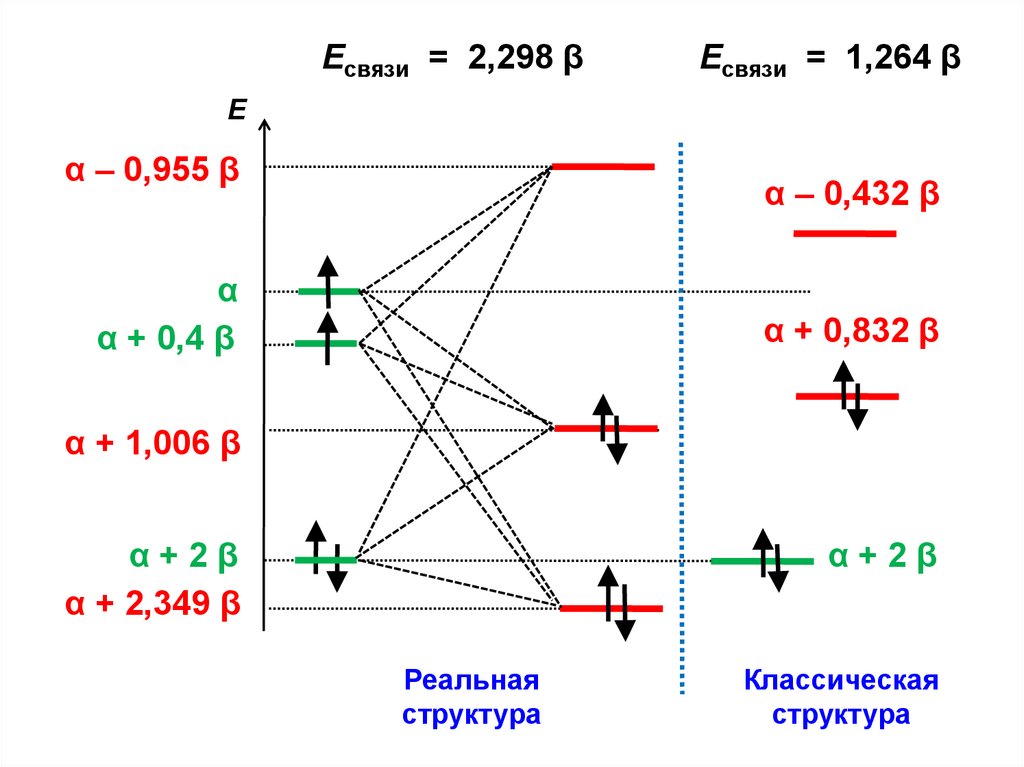
Есвязи = 2,298 βЕсвязи = 1,264 β
Е
α – 0,955 β
α – 0,432 β
α
α + 0,4 β
α + 0,832 β
α + 1,006 β
α+2β
α + 2,349 β
α+2β
Реальная
структура
Классическая
структура
156.
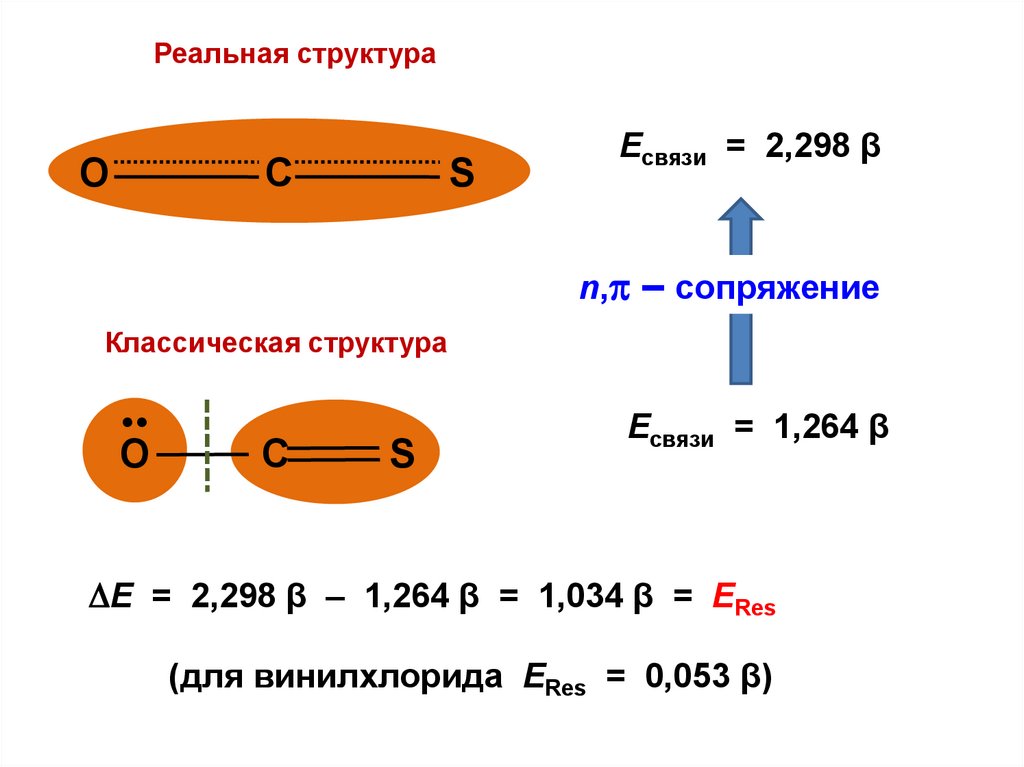
Реальная структураО
C
S
Есвязи = 2,298 β
n, – сопряжение
Классическая структура
•
O
C
S
Есвязи = 1,264 β
Е = 2,298 β – 1,264 β = 1,034 β = ЕRes
(для винилхлорида ЕRes = 0,053 β)
157.
•O=С–S
•
hO = 1,0
KO = 1,0
hS = 1,3
KS = 0,6
Х + 1 1,0
1,0
Х
0
0,6
0
С1
0,6
• С2
Х + 1,3
С3
=0
Det = Х 3 + 2,3Х 2 – 0,06Х – 1,66 = 0
X =
0,748
–1,203
–1,845
ε =
α – 0,748 β
α + 1,203 β
α + 1,845 β
158.
O=
C
S
0,481 –0,841 0,246
0,612 0,125 –0,781
0,623 0,526 0,579
p1
p2
p3
0
2
2
nO = 1,525
no = 1
Q = – 0,525
nC = 0,585
no = 1
Q = + 0,415
nS = 1,890
no = 2
Q = + 0,110
PO-C = 0,808
PC-S = 0,414
159.
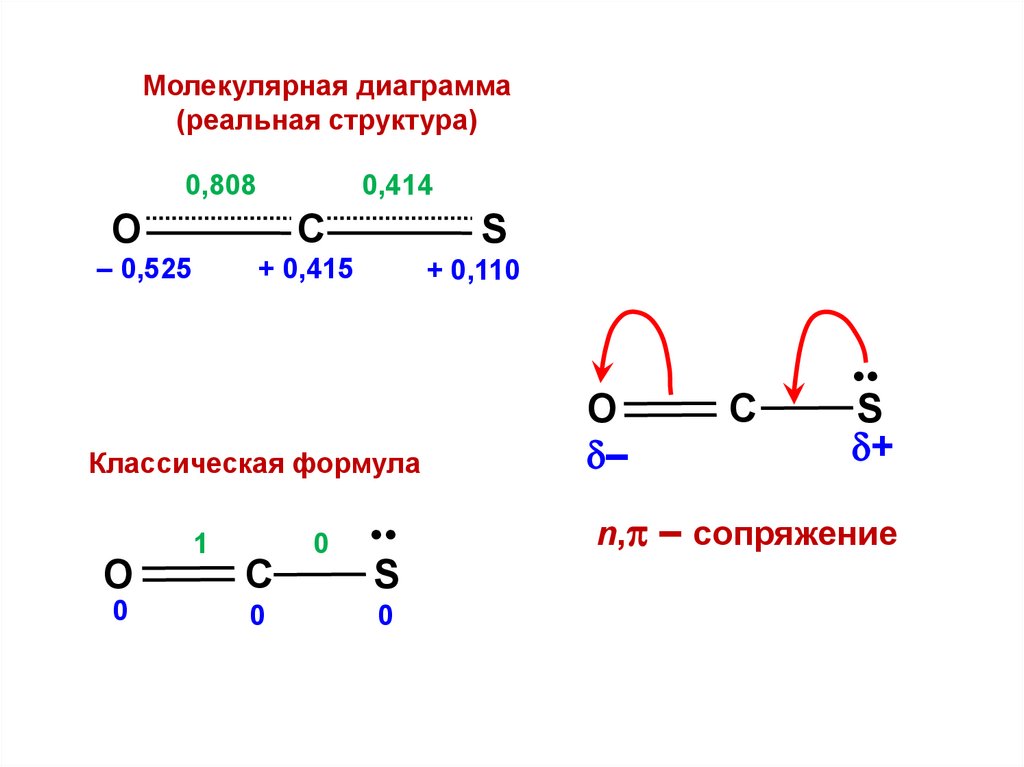
Молекулярная диаграмма(реальная структура)
0,808
0,414
O
C
– 0,525
S
+ 0,415
+ 0,110
Классическая формула
O
C
•
S
0
0
0
1
0
O
–
C
•
S
+
n, – сопряжение
160.
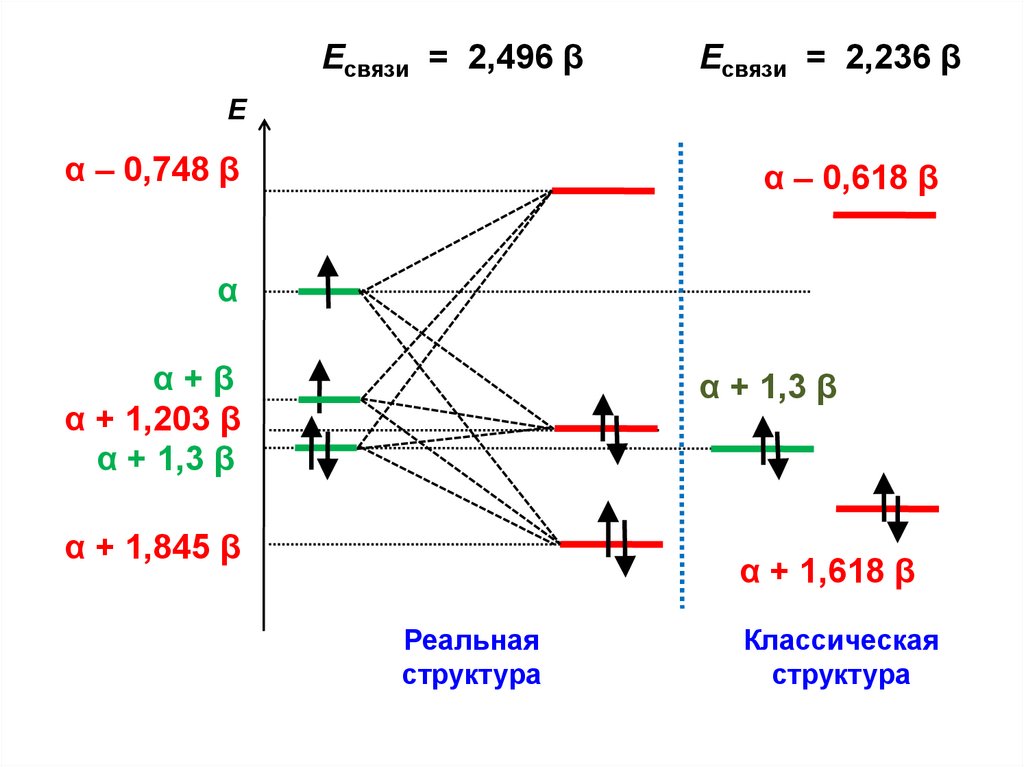
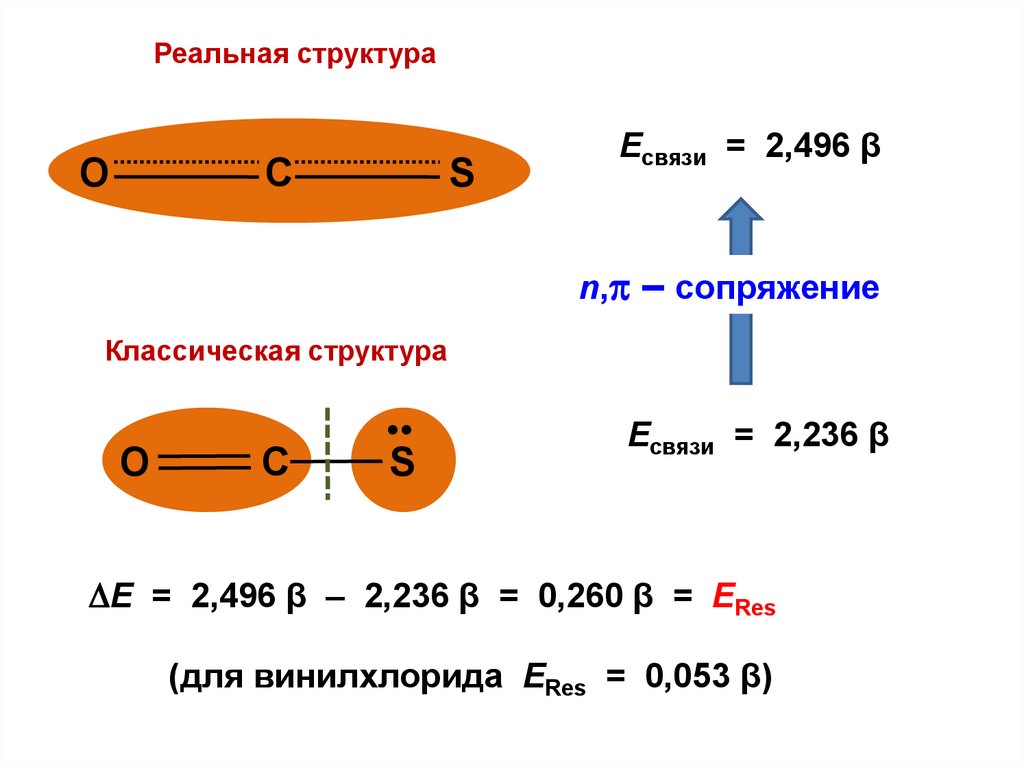
Есвязи = 2,496 βЕсвязи = 2,236 β
Е
α – 0,748 β
α – 0,618 β
α
α+β
α + 1,203 β
α + 1,3 β
α + 1,3 β
α + 1,845 β
α + 1,618 β
Реальная
структура
Классическая
структура
161.
Реальная структураО
C
S
Есвязи = 2,496 β
n, – сопряжение
Классическая структура
O
C
•
S
Есвязи = 2,236 β
Е = 2,496 β – 2,236 β = 0,260 β = ЕRes
(для винилхлорида ЕRes = 0,053 β)
162.
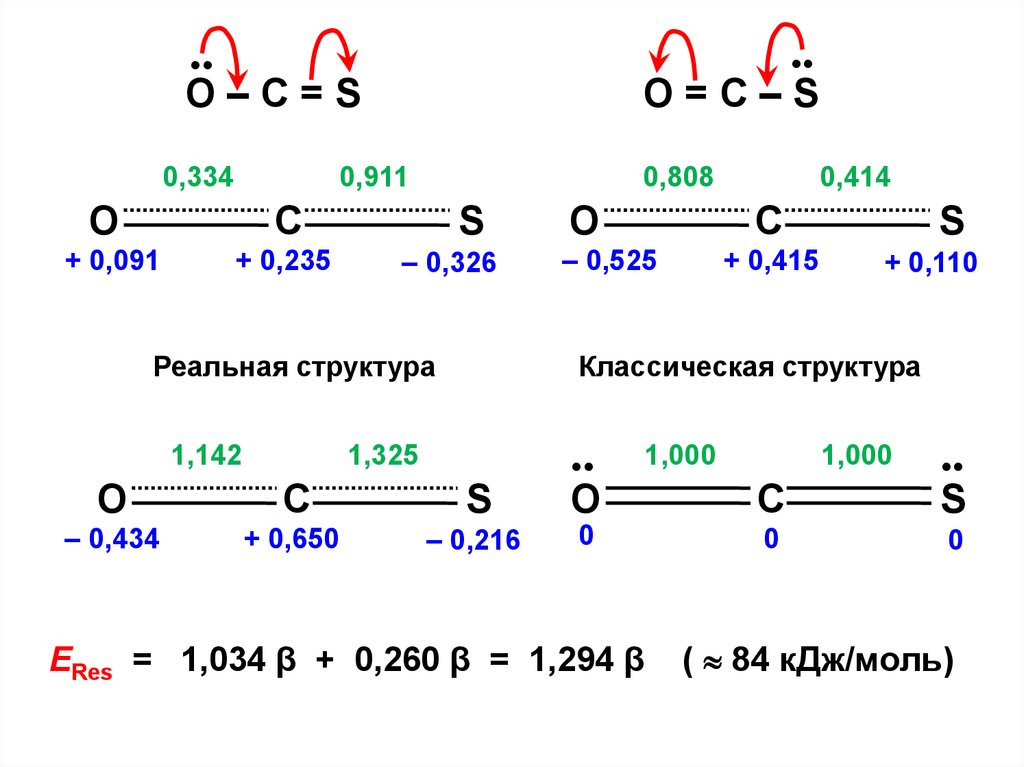
••
O–С=S
0,334
O=С–S
0,911
O
C
+ 0,091
+ 0,235
0,808
S
– 0,326
Реальная структура
1,142
O
0,414
C
– 0,525
+ 0,415
S
+ 0,110
Классическая структура
1,325
O
C
S
– 0,434
+ 0,650
– 0,216
•
1,000
1,000
O
C
0
0
ЕRes = 1,034 β + 0,260 β = 1,294 β
•
S
0
( 84 кДж/моль)
163.
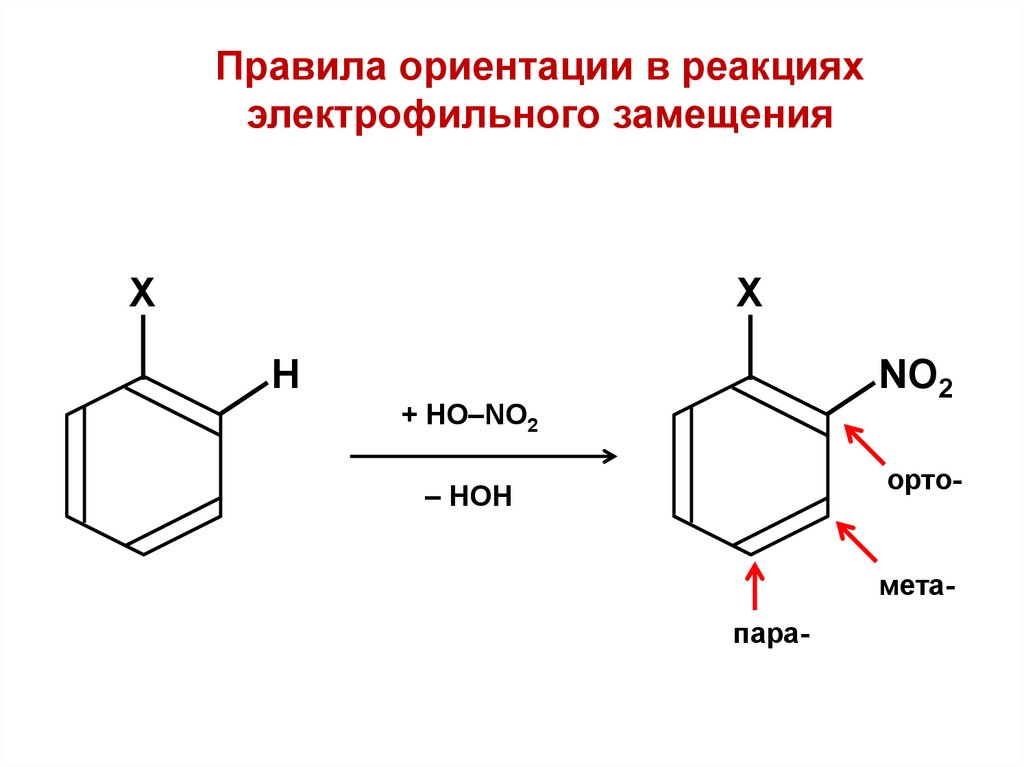
Правила ориентации в реакцияхэлектрофильного замещения
Х
Х
Н
NO2
+ HO–NO2
орто-
– HOH
метапара-
164.
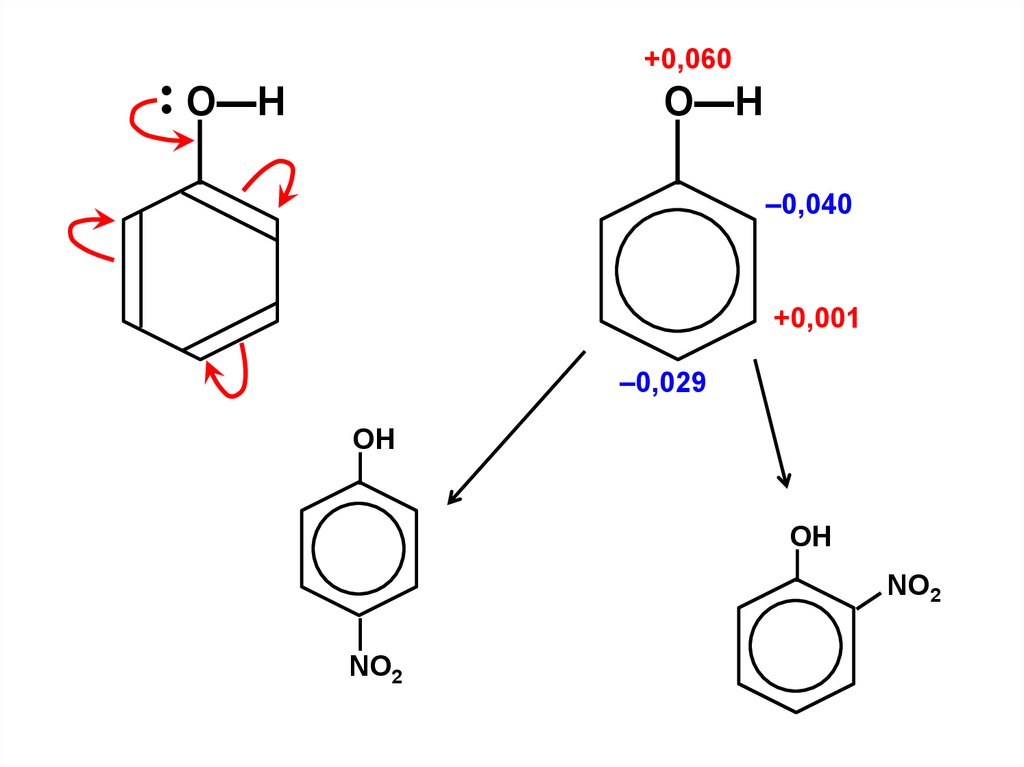
•+0,060
О—Н
О—Н
–0,040
+0,001
–0,029
ОН
ОН
NО2
NО2
165.
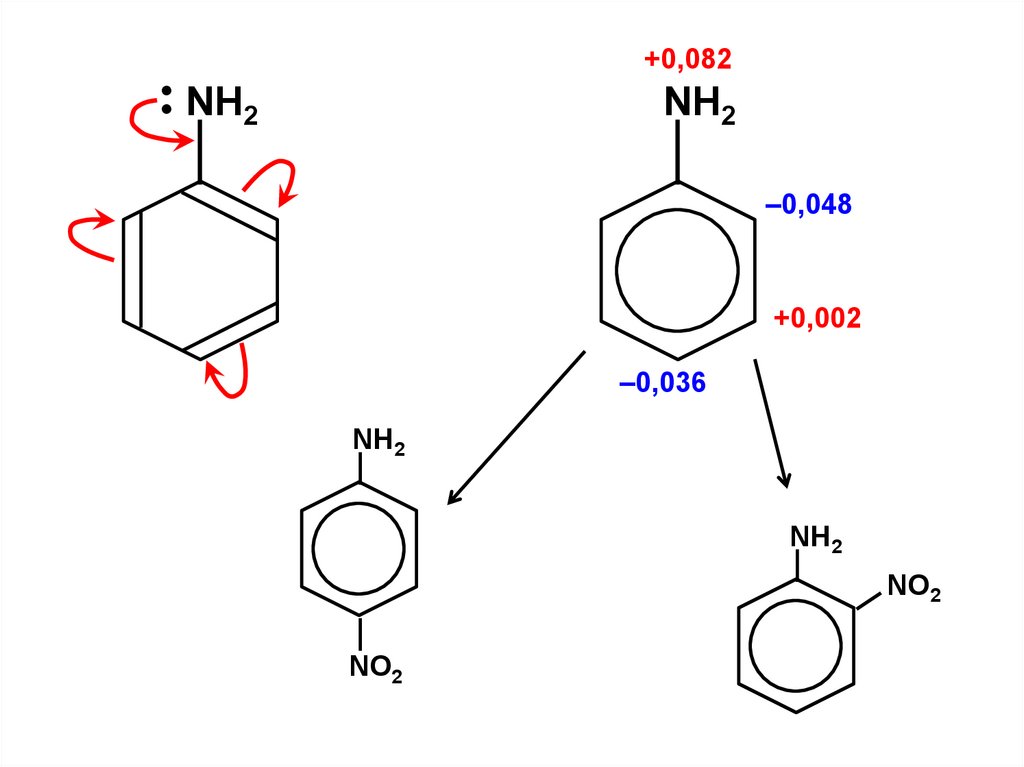
•+0,082
NН2
NН2
–0,048
+0,002
–0,036
NН2
NН2
NО2
NО2
166.
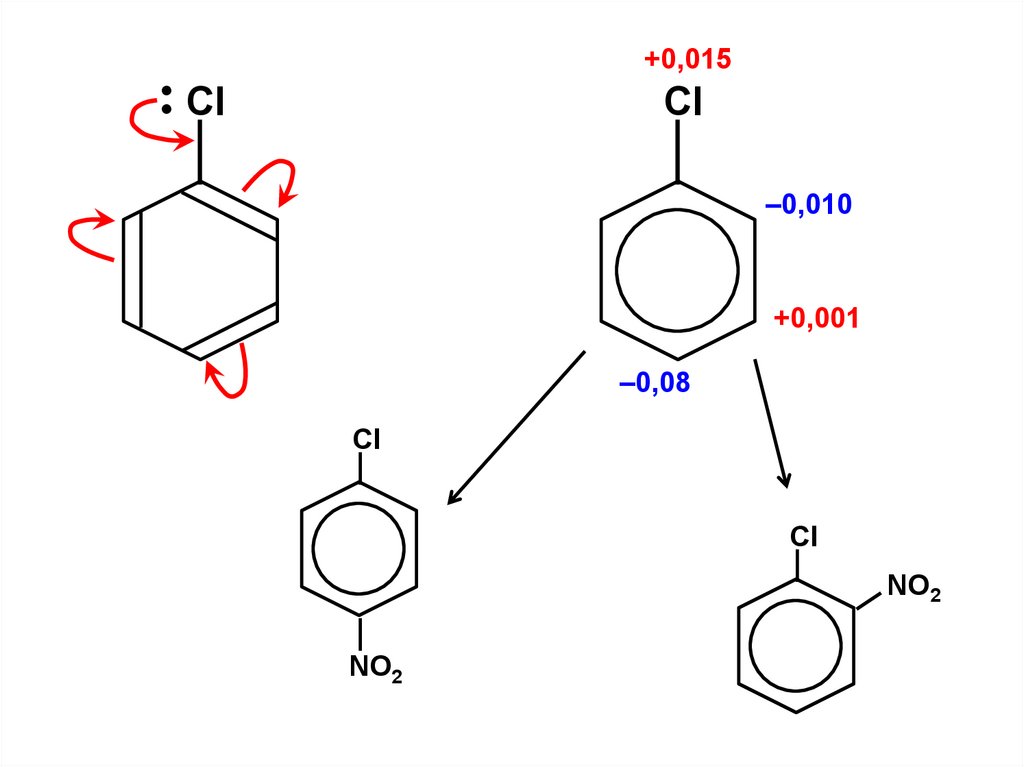
•+0,015
Cl
Cl
–0,010
+0,001
–0,08
Cl
Cl
NО2
NО2
167.
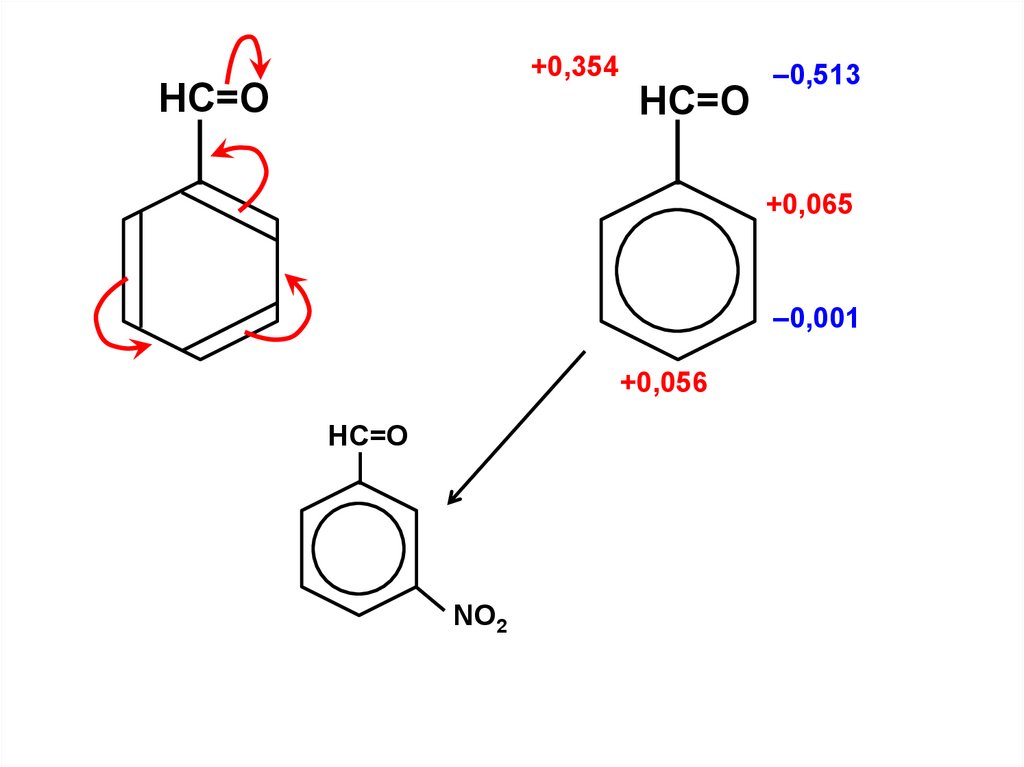
+0,354НC=O
НC=O
–0,513
+0,065
–0,001
+0,056
НC=O
NО2
168.
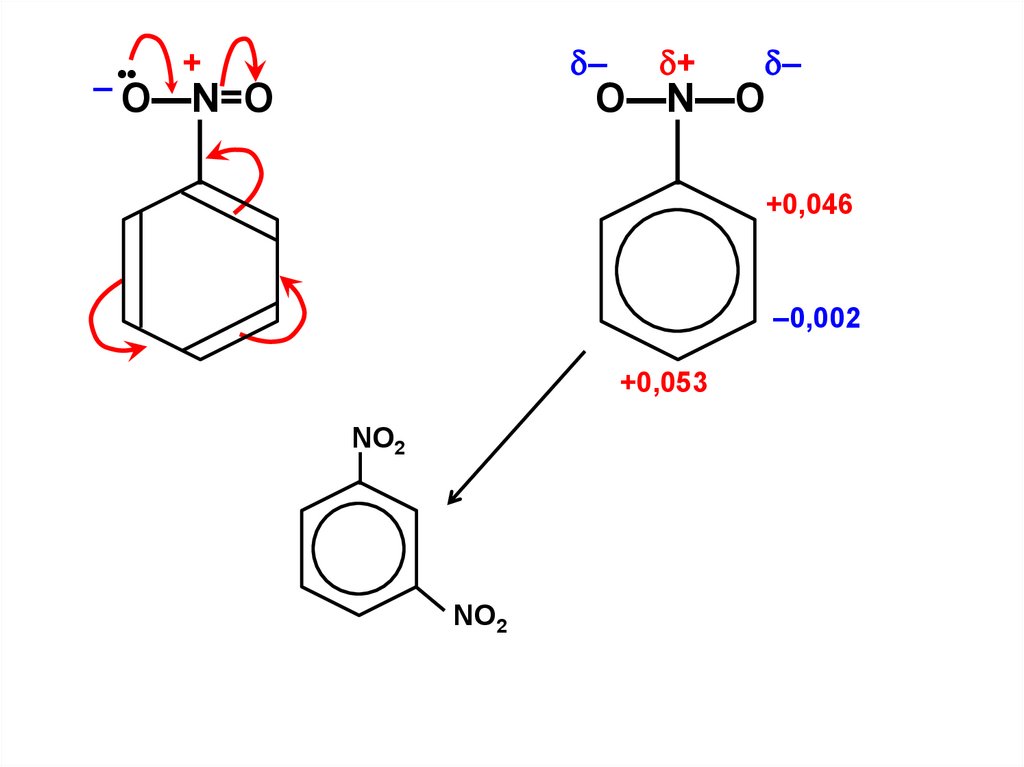
– •–
+
O—N=O
+
–
O—N—O
+0,046
–0,002
+0,053
NO2
NО2
169.
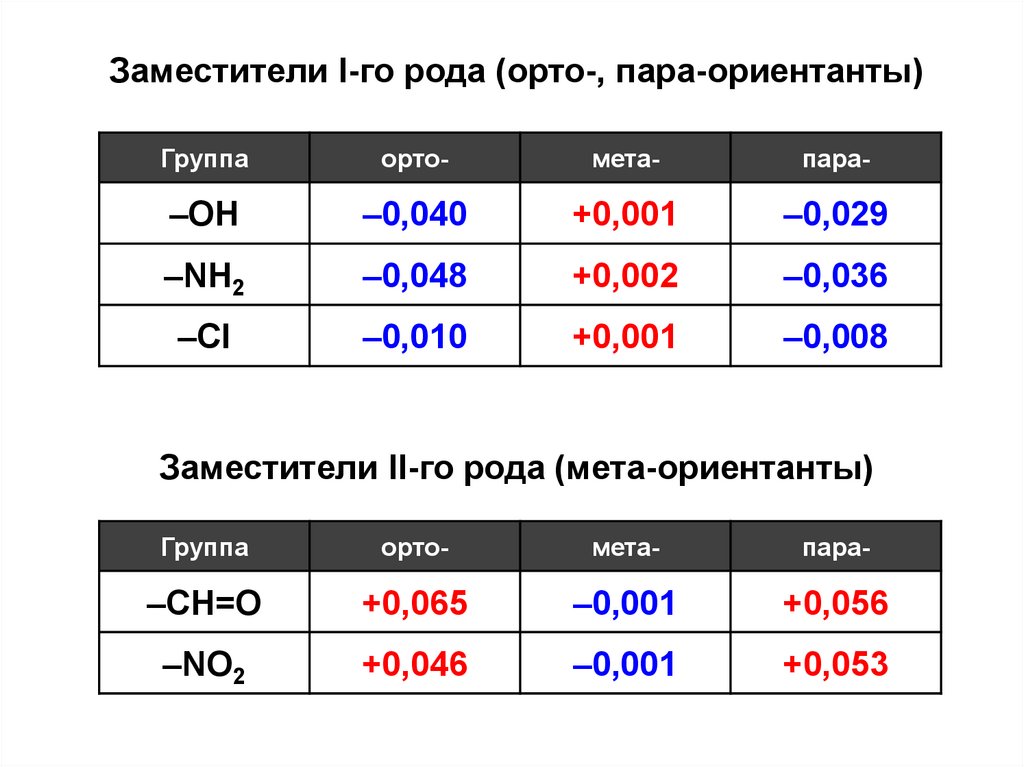
Заместители I-го рода (орто-, пара-ориентанты)Группа
орто-
мета-
пара-
–OH
–0,040
+0,001
–0,029
–NH2
–0,048
+0,002
–0,036
–Cl
–0,010
+0,001
–0,008
Заместители II-го рода (мета-ориентанты)
Группа
орто-
мета-
пара-
–CH=O
+0,065
–0,001
+0,056
–NO2
+0,046
–0,001
+0,053
170.
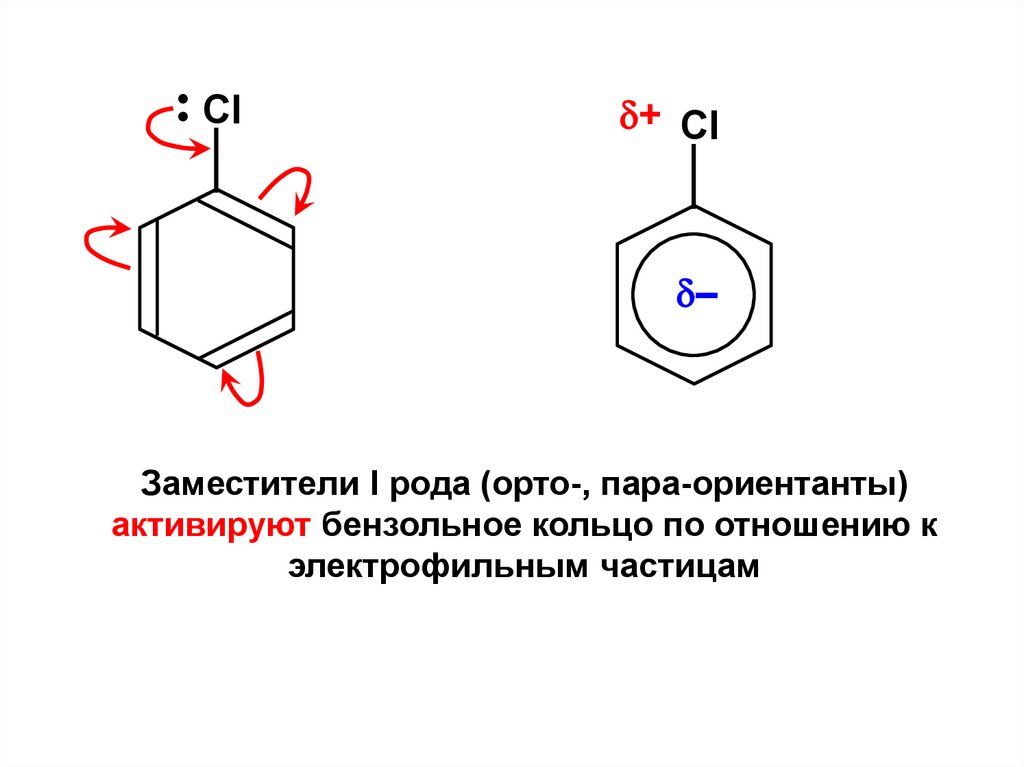
•Cl
+ Cl
–
Заместители I рода (орто-, пара-ориентанты)
активируют бензольное кольцо по отношению к
электрофильным частицам
171.
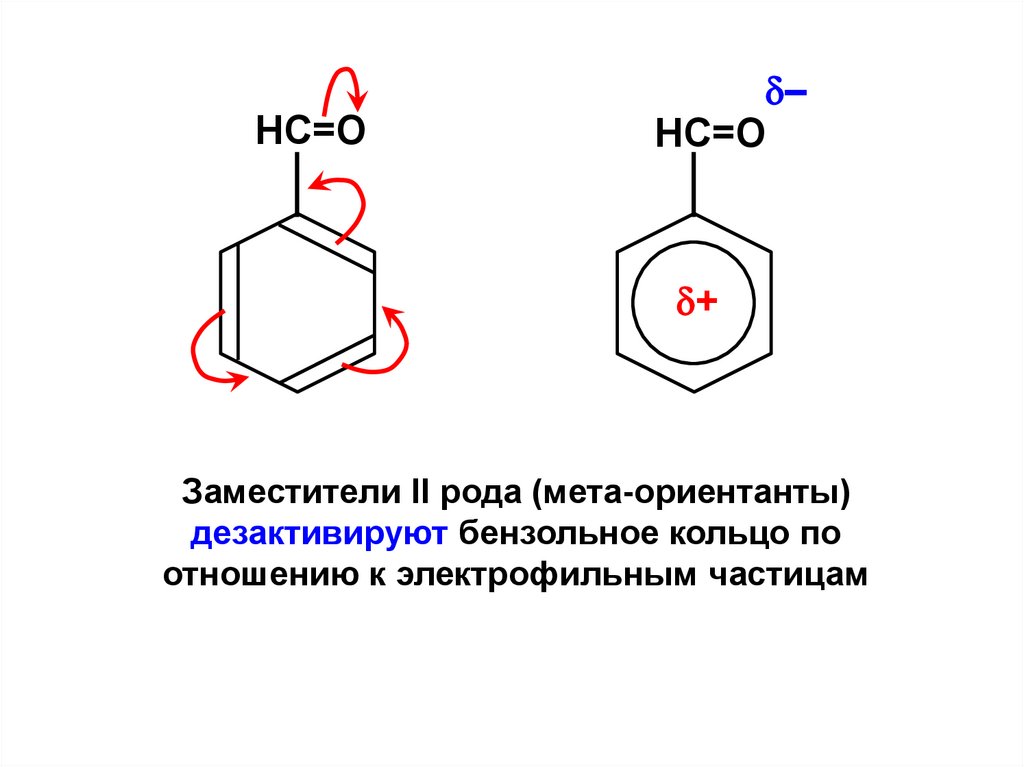
НC=O–
НC=O
+
Заместители II рода (мета-ориентанты)
дезактивируют бензольное кольцо по
отношению к электрофильным частицам
172.
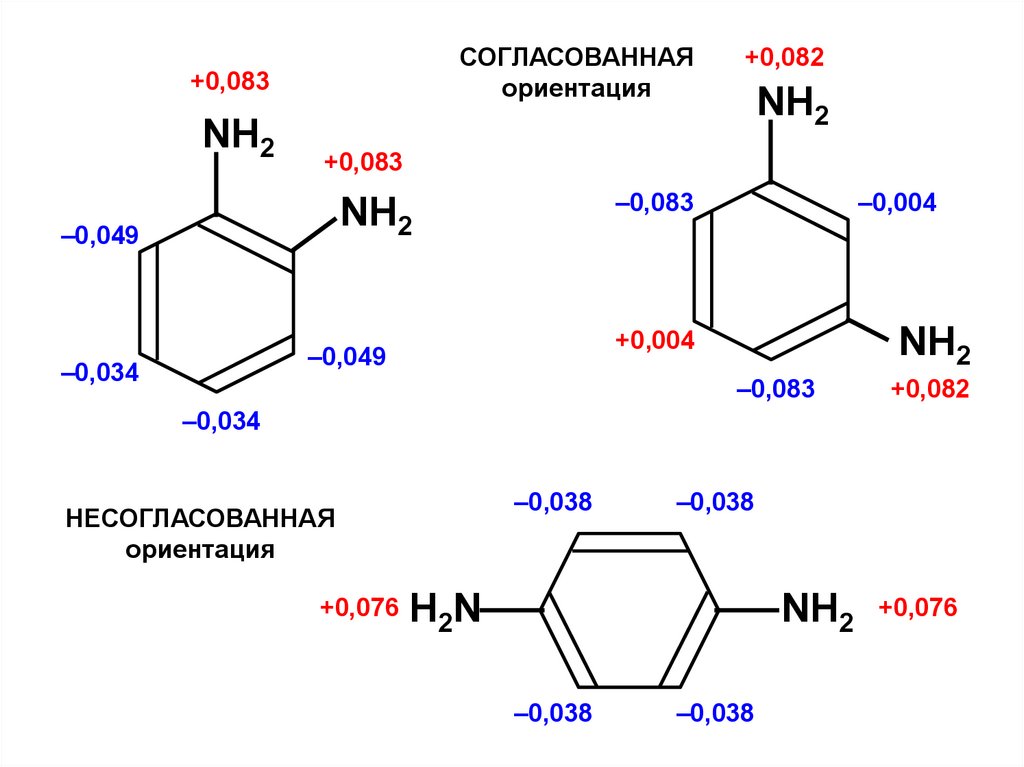
СОГЛАСОВАННАЯориентация
+0,083
NН2
NН2
+0,083
–0,083
NН2
–0,049
–0,004
NН2
+0,004
–0,049
–0,034
+0,082
–0,083
+0,082
–0,034
–0,038
НЕСОГЛАСОВАННАЯ
ориентация
+0,076
–0,038
Н2N
NН2
–0,038
–0,038
+0,076
173.
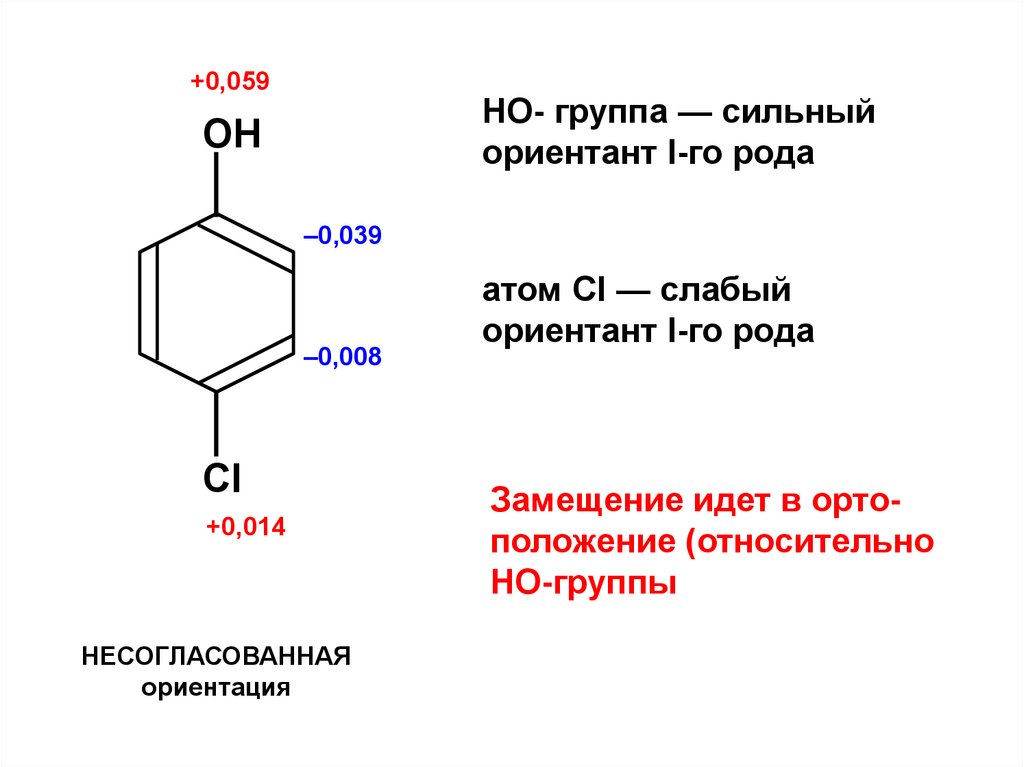
+0,059HO- группа — сильный
ориентант I-го рода
ОН
–0,039
–0,008
Cl
+0,014
НЕСОГЛАСОВАННАЯ
ориентация
атом Cl — слабый
ориентант I-го рода
Замещение идет в ортоположение (относительно
НО-группы
174.
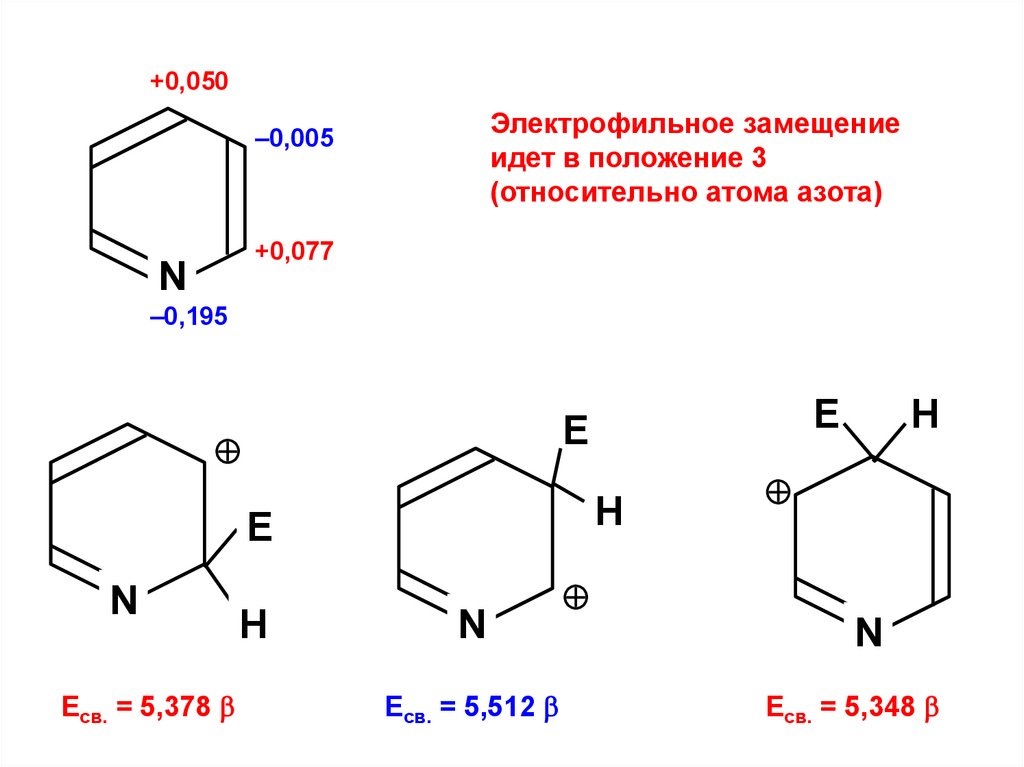
+0,050Электрофильное замещение
идет в положение 3
(относительно атома азота)
–0,005
+0,077
N
–0,195
Н
Е
N
Есв. = 5,378
Е
Е
Н
N
Есв. = 5,512
Н
N
Есв. = 5,348
175.
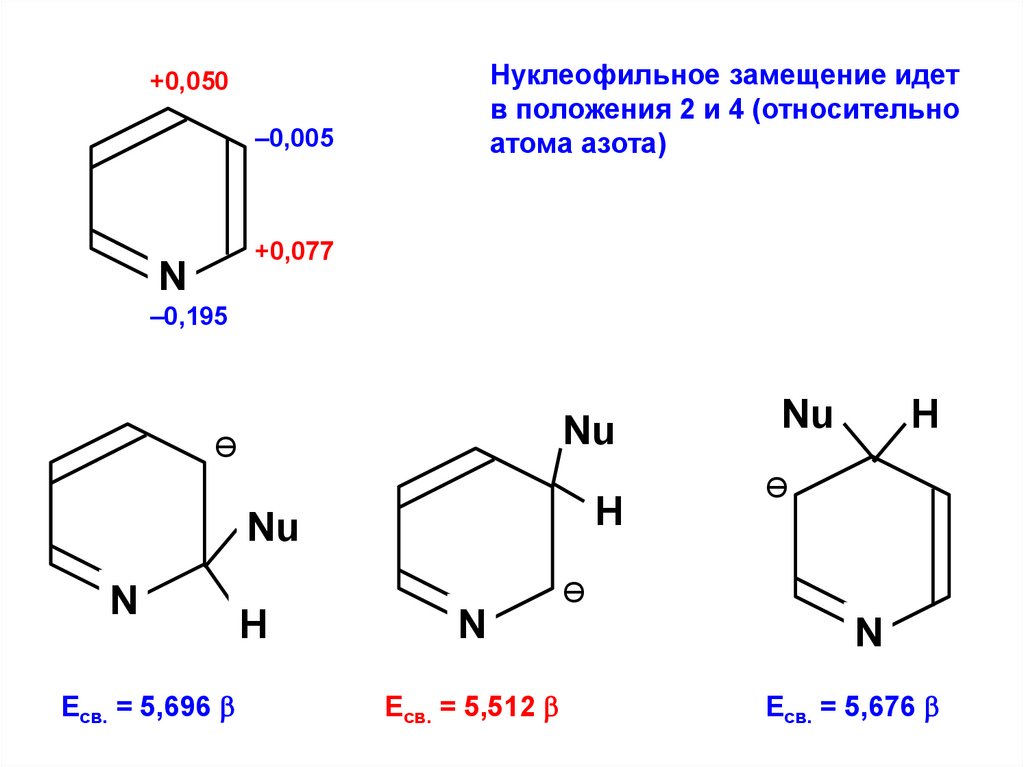
Нуклеофильное замещение идетв положения 2 и 4 (относительно
атома азота)
+0,050
–0,005
+0,077
N
–0,195
Nu
Ө
Н
Nu
N
Есв. = 5,696
Н
Н
Nu
Ө
Ө
N
Есв. = 5,512
N
Есв. = 5,676
176.
Ө:Nu
Nu
Ө
N
N
Е
Н
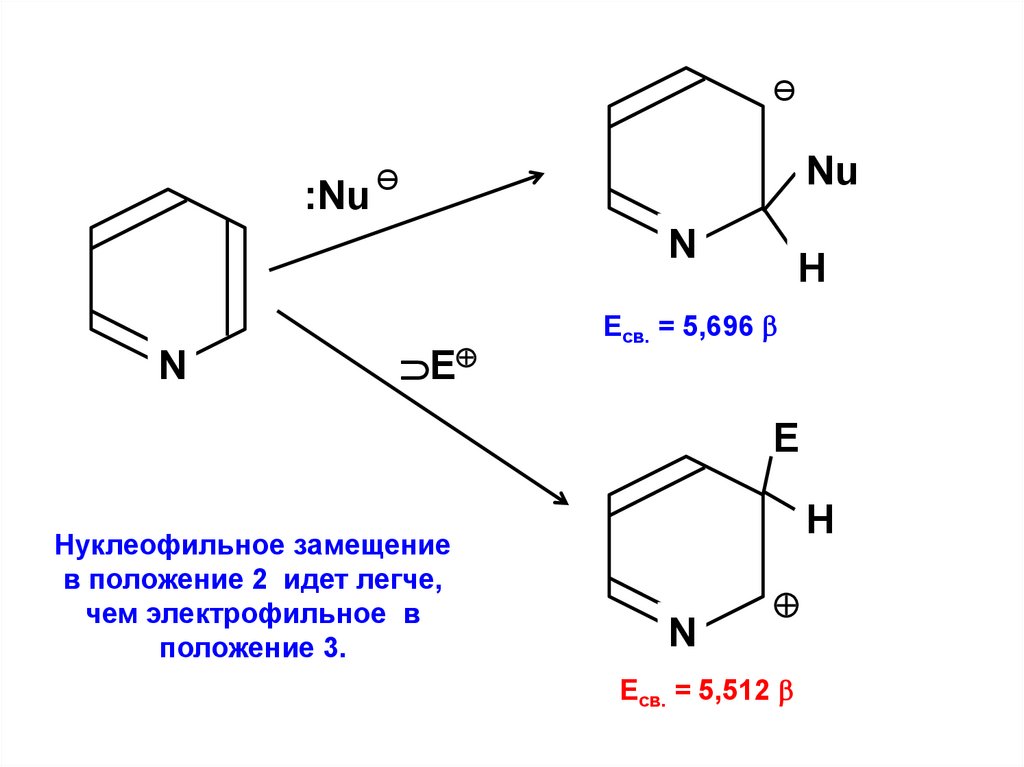
Есв. = 5,696
Е
Нуклеофильное замещение
в положение 2 идет легче,
чем электрофильное в
положение 3.
Н
N
Есв. = 5,512
177.
–0,106–0,035
•
N
N +0,280
H
H
+0,050
–0,005
N
–0,195
+0,077
178.
•N
H
H
E
E
•
N
H
H
Есв. = 4,820
•
N
H
Есв. = 4,454
179.
•N
H
H
Ө
Nu
Nu
•
N
H
Ө
H
Есв. = 4,448
•
N
H
Есв. = 3,826
180.
•N
E
:NuӨ
H
Ө
E
Nu
•
N
H
•
N
H
Есв. = 4,820
H
H
Есв. = 4,448
181.
Задача 8.3.Для гетероатомной молекулы типа
•
•
X—CH=CH—Y
по заданным величинам поправок h и K и корням
характеристического уравнения вычислить:
1) матрицу коэффициентов MO (Сij) в
нормированном виде
2) электрические заряды атомов X, C1, C2, Y
3) порядки -связей X–C1, C1–C2, C2–Y
4) энергию сопряжения ( ERes ) в единицах β
182.
1. Составить уравнение Хюккеля с учетомпоправок на гетероатомы
Х + hX
KCX
0
0
KCX
Х
1
0
0
0
1
0
Х
KCY
KCY X + hY
С1
С2
=0
С3
C4
2. По очереди подставить в это уравнение корни
характеристического уравнения:
Х = (Х1; Х2; Х3; Х4)
183.
3. Решить полученные 4 экземпляра уравненияХюккеля и из решений (предварительно
пронормированных) составить атомномолекулярную матрицу:
=
X
C1
C2
Y
C11
C21
C31
C41
C12
C22
C32
C42
C13
C23
C33
C43
C14
C24
C34
C44
p1
p2
p3
р4
0
2
2
2
184.
4. Вычислить средние электронные плотности(N) и локальные заряды атомов (Q)
NX = …..
no = 2
Q = …..
NC1 = …..
no = 1
Q = …..
NC2 = …..
no = 1
Q = …..
nY = …..
no = 2
Q = …..
5. Вычислить порядки связей (Р)
PX-C1 = …..
PC1-C2 = …..
PC2-Y = …..
185.
6. Вычислить орбитальные энергии по формуле:i = – Xi
7. Построить энергетические диаграммы:
а) для исходных атомных орбиталей
б) для КМО
в) для ЛМО
8. Вычислить энергии связи для КМО и ЛМО
9. Вычислить энергию резонанса: ЕRes = ЕКМО – ЕЛМО
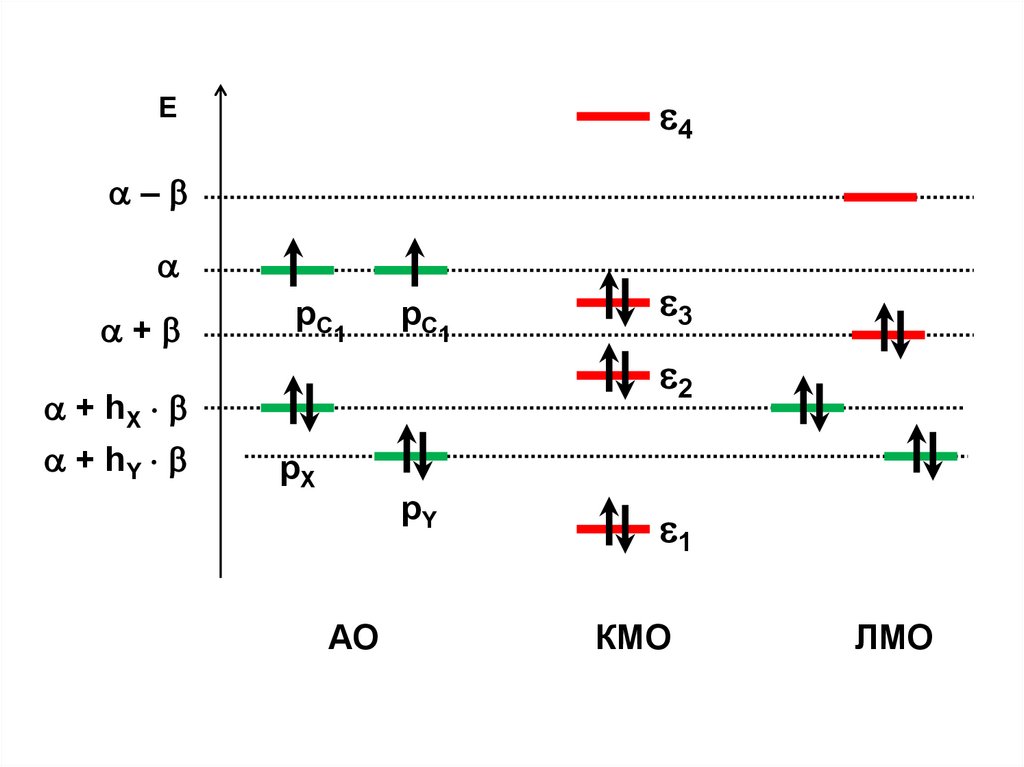
186.
4Е
–
+
рС1
рС1
2
+ hX
+ hY
3
рX
рY
АО
1
КМО
ЛМО
187.
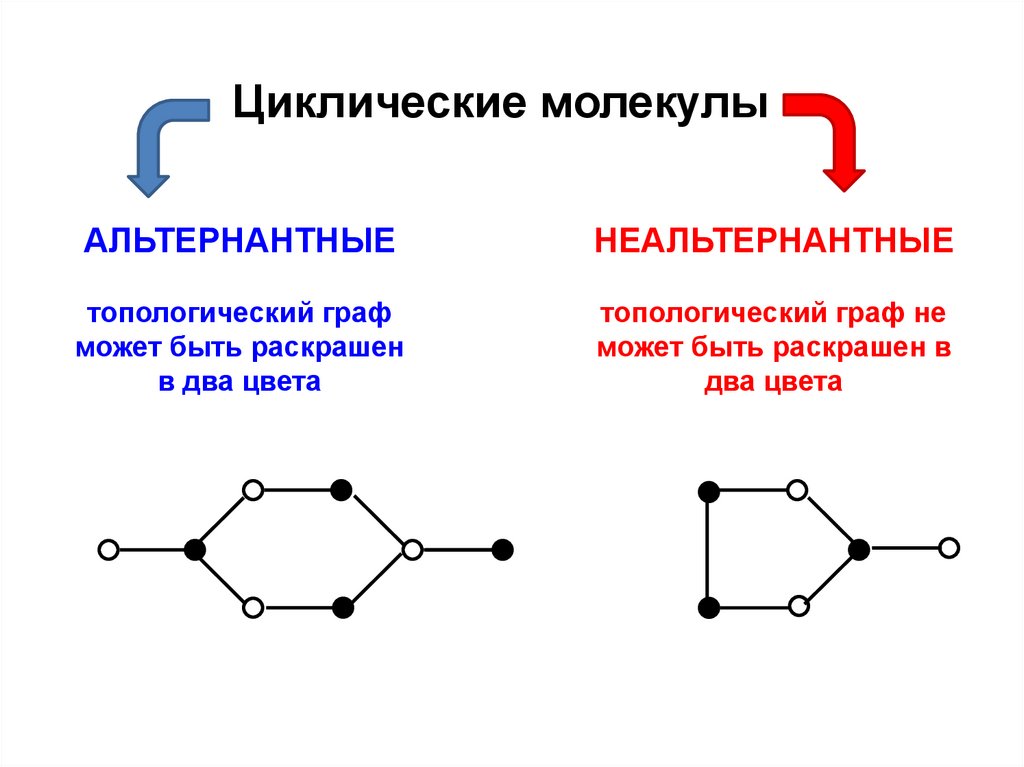
Циклические молекулыАЛЬТЕРНАНТНЫЕ
НЕАЛЬТЕРНАНТНЫЕ
топологический граф
может быть раскрашен
в два цвета
топологический граф не
может быть раскрашен в
два цвета
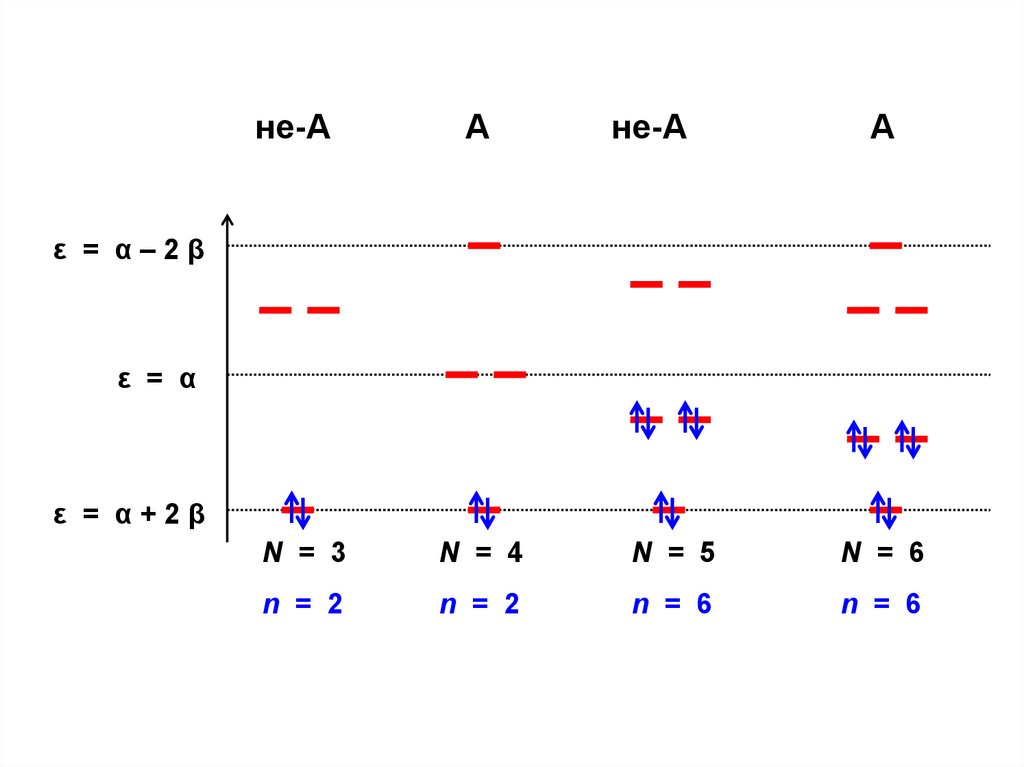
188.
Для альтернантных молекул всегда имеютсядважды вырожденные уровни, которые
располагаются симметрично, относительно
нулевого уровня с
Для неальтернантных молекул дважды
вырожденные уровни располагаются
несимметрично, относительно нулевого уровня и
среди них нет уровня с (несвязывающей МО)
189.
не-АА
не-А
А
ε = α–2β
ε = α
ε = α+2β
N = 3
N = 4
N = 5
N = 6
n = 2
n = 2
n = 6
n = 6
190.
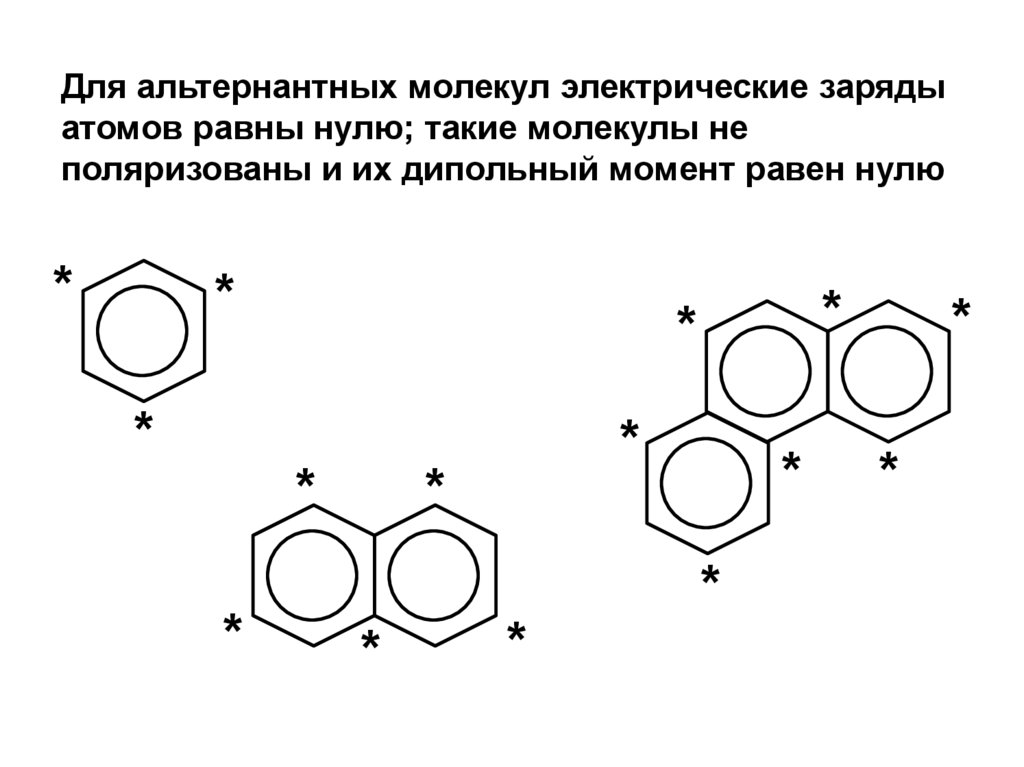
Для альтернантных молекул электрические зарядыатомов равны нулю; такие молекулы не
поляризованы и их дипольный момент равен нулю
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
191.
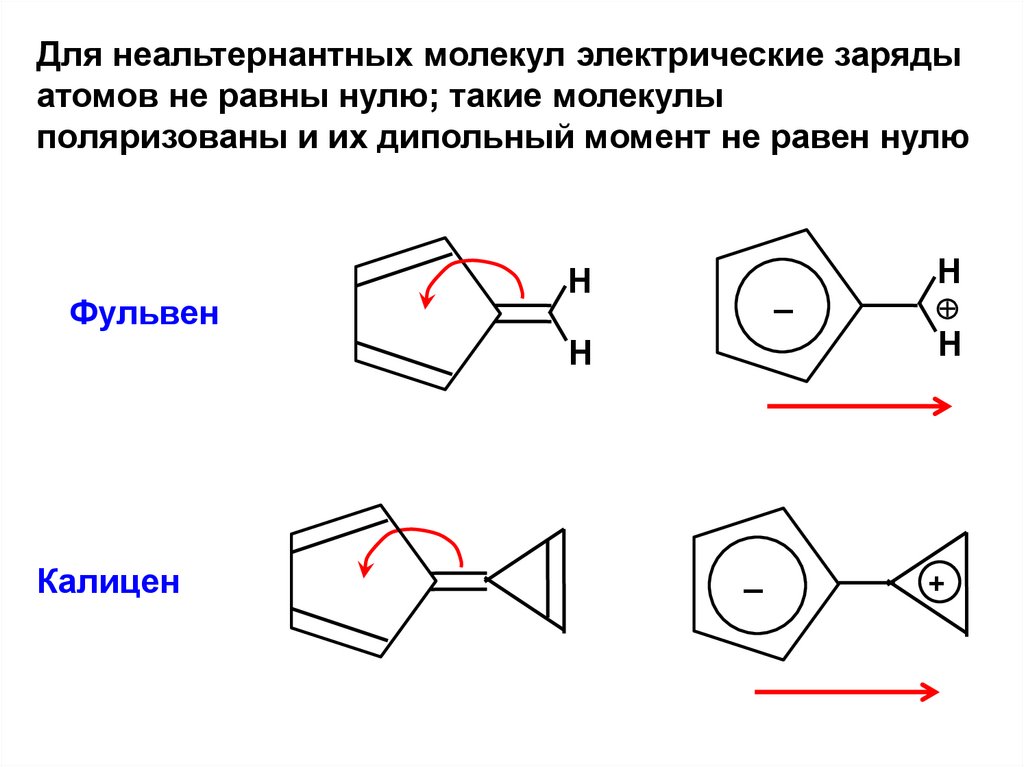
Для неальтернантных молекул электрические зарядыатомов не равны нулю; такие молекулы
поляризованы и их дипольный момент не равен нулю
Фульвен
Н
–
Н
Калицен
–
Н
Н
+












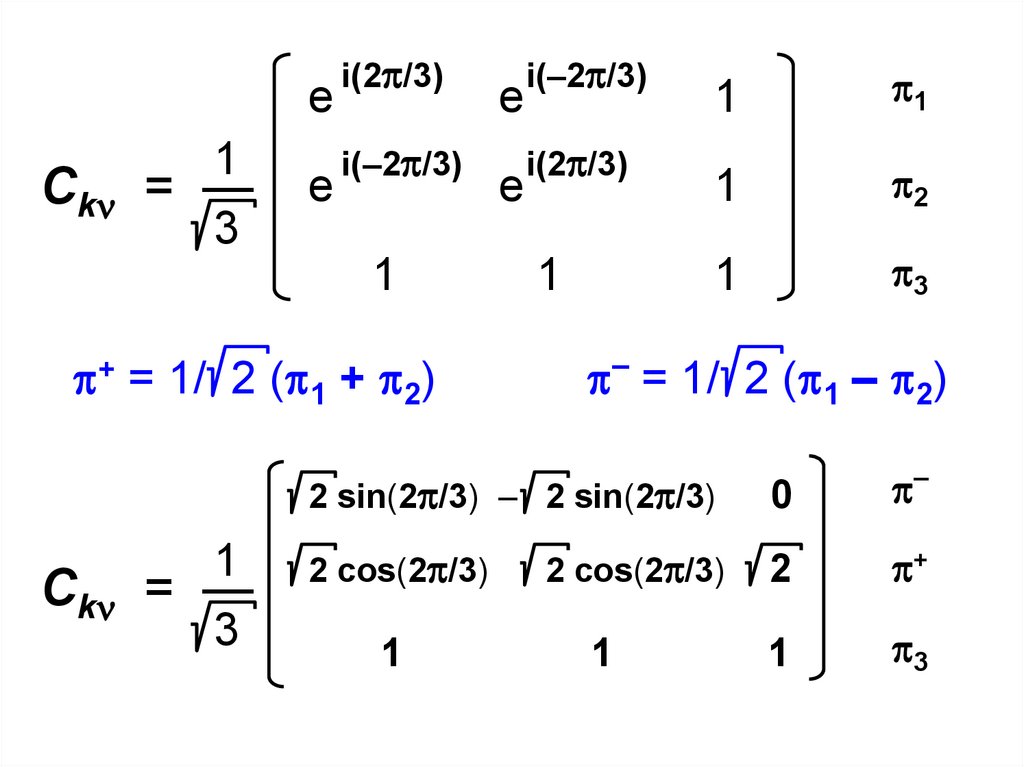
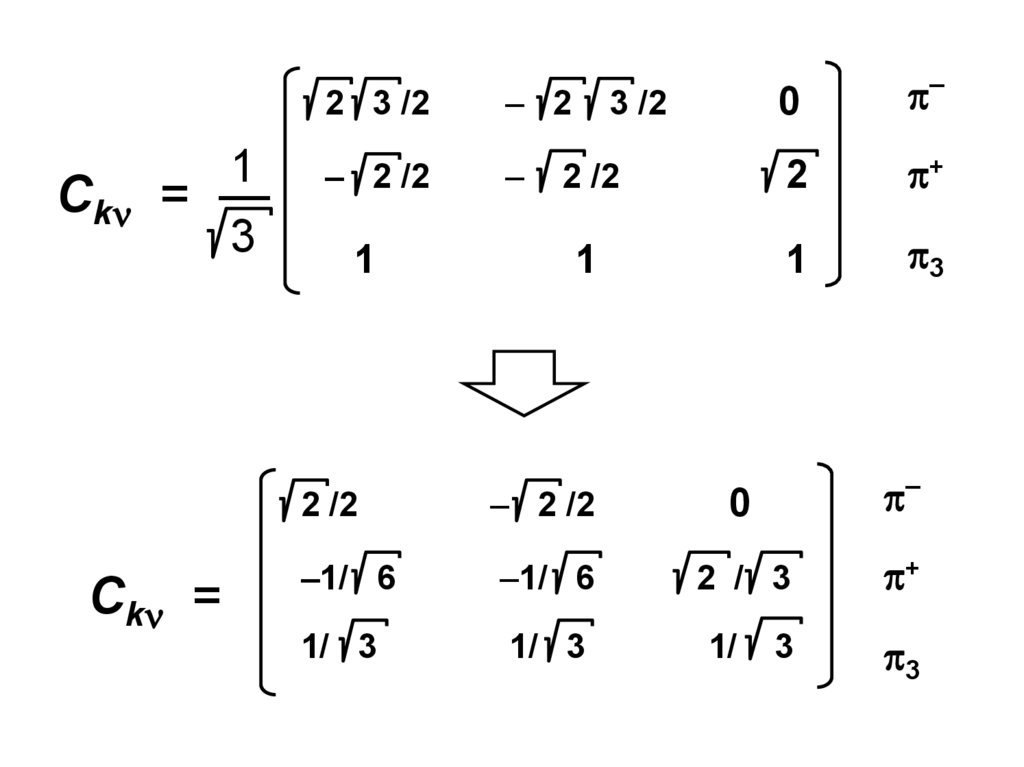

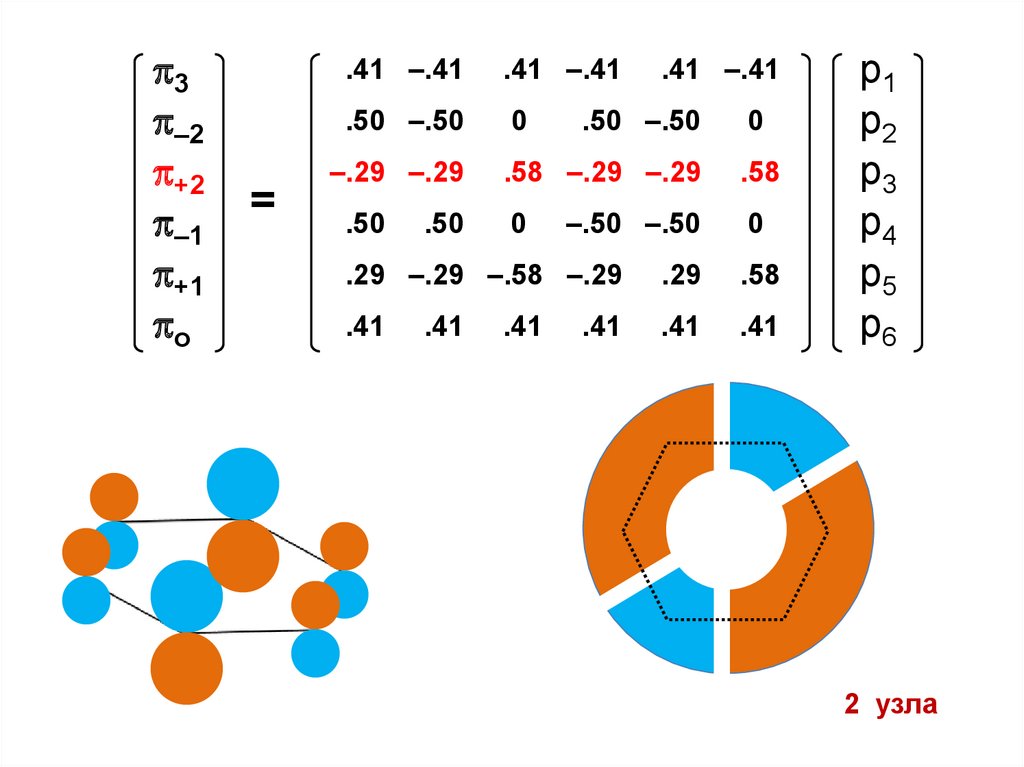








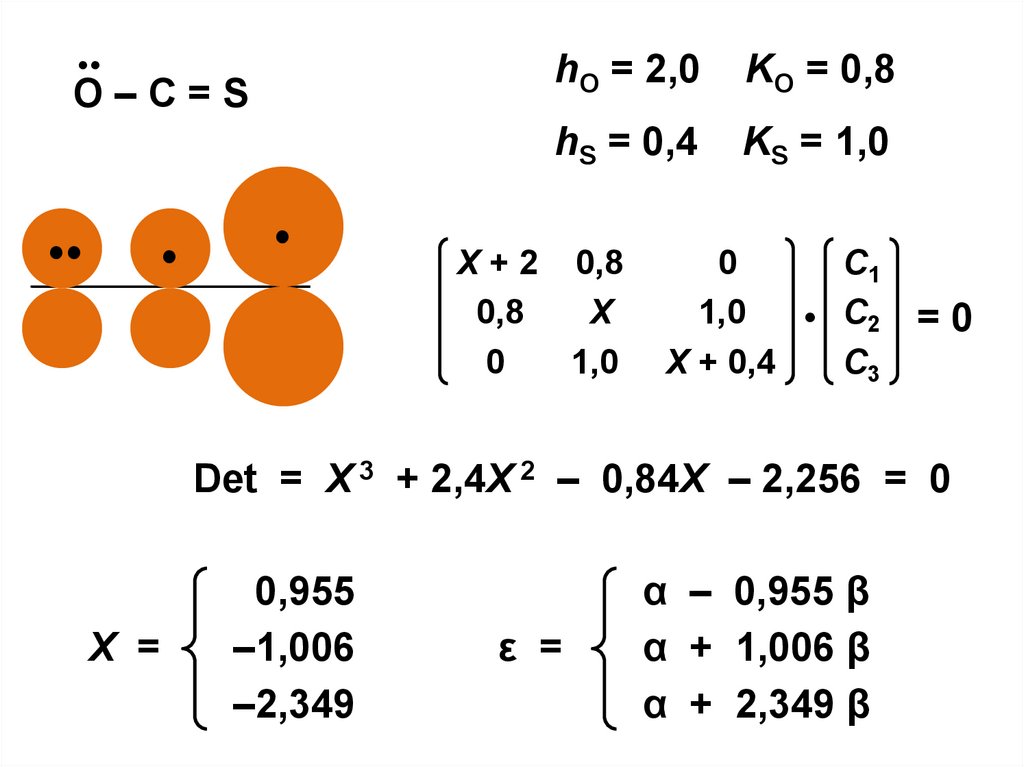









 chemistry
chemistry