Similar presentations:
Поверхности второго порядка
1. Поверхности второго порядка
Лекция 72. Формирование линий 2-го порядка
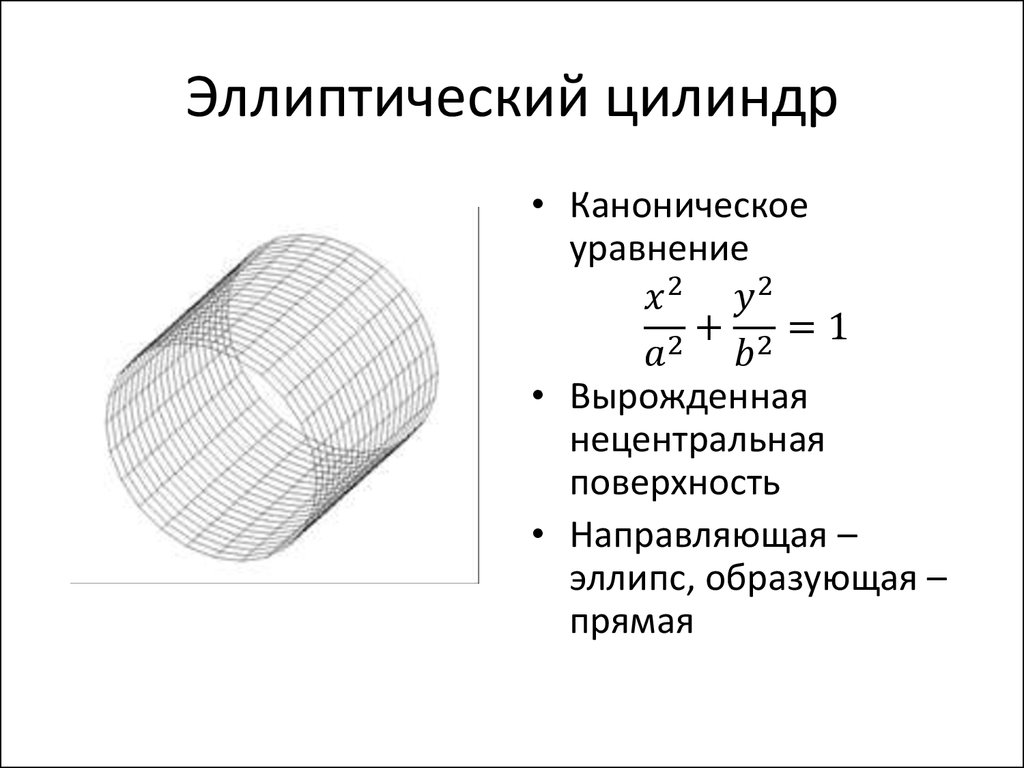
• Все поверхности 2-го порядка получаютсяперемещением линий 1-го или 2-го
порядка – образующих, вдоль линий 1-го
или 2-го порядка – направляющих
3. Линии 2-го порядка
• Линии 2-го порядка являются плоскимилиниями, т.е. любые три их точки
принадлежат одной плоскости
• В плоскости Z = 0, уравнение кривой 2-го
порядка имеет вид:
A*x2 + B*y2 + 2*C*x*y + 2*D*x + 2*E*y + F = 0
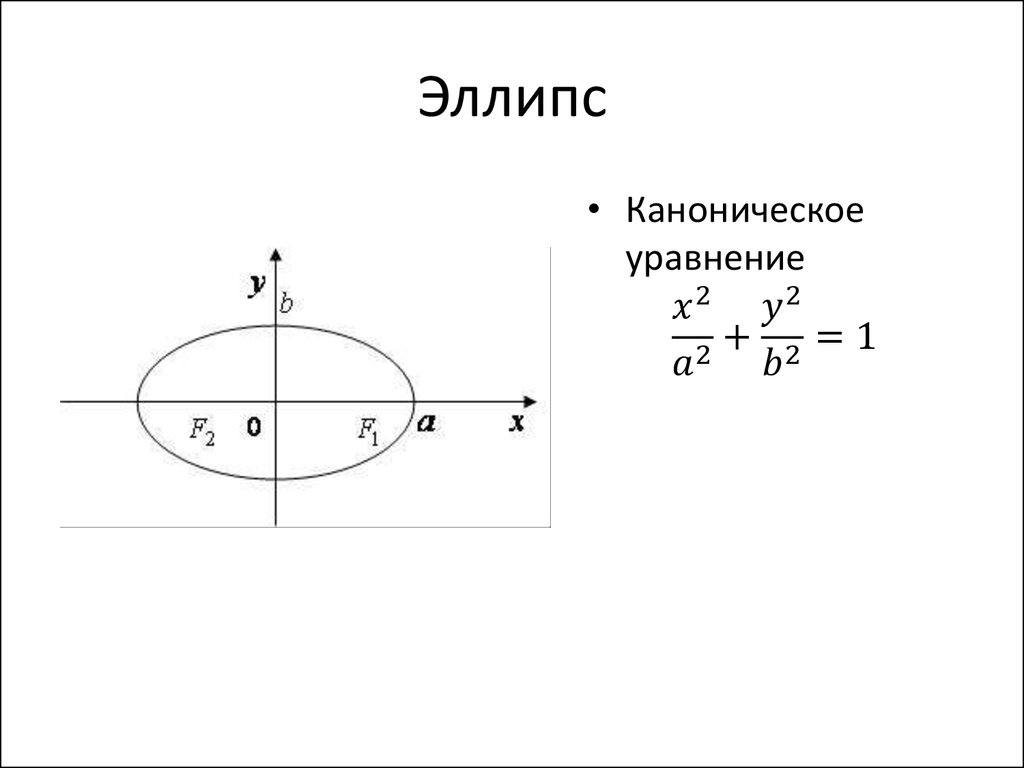
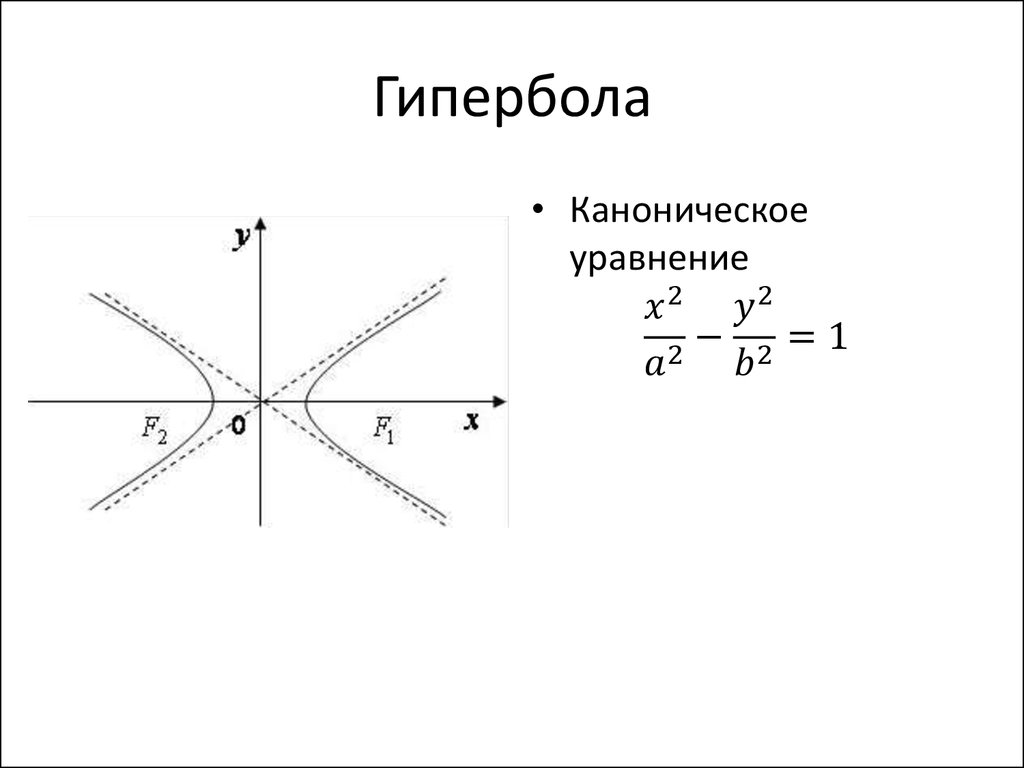
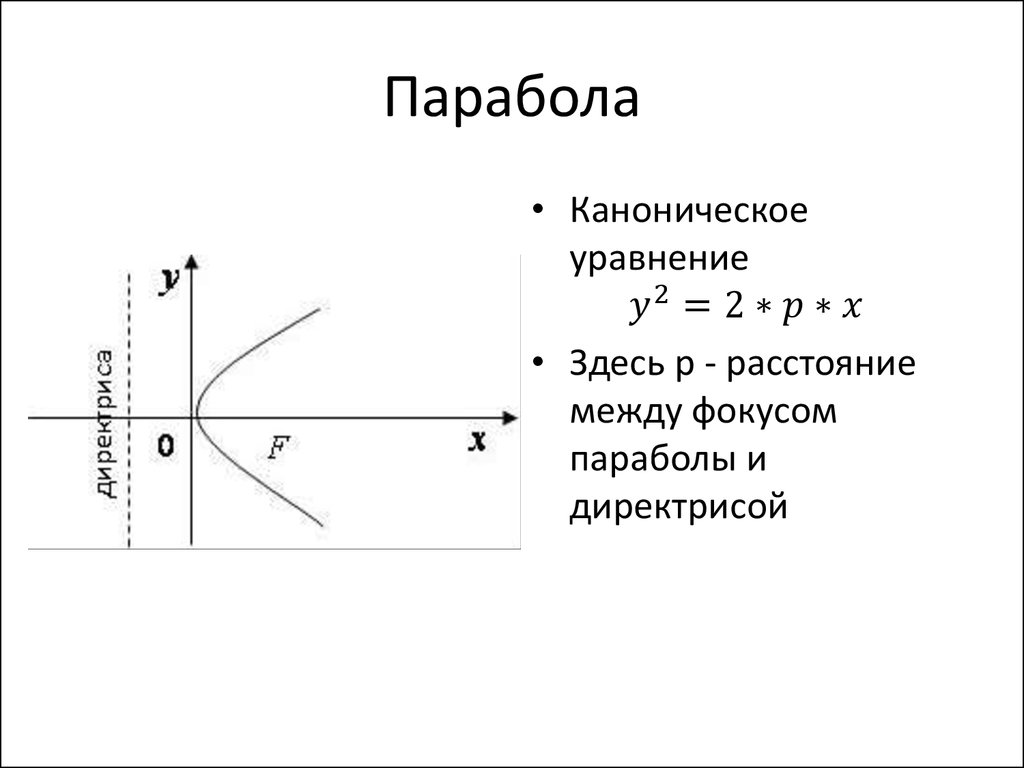
• К кривым второго порядка относятся:
эллипс, гипербола, парабола
4. Условия на коэффициенты
• Эти три вида кривых различаютсяусловиями, которым удовлетворяют
коэффициенты A и C
– если A*C > 0, то эллипс (окружность)
– если A*C < 0, то гипербола
– если A*C = 0, то парабола
5. Матричное представление
• Неявное уравнение кривой 2-го порядкаможно представить в матричном виде:
























 mathematics
mathematics








